Журнал вычислительной математики и математической физики, 2022, T. 62, № 8, стр. 1360-1373

Обнаружение двумерных структур типа “палец” в неравновесной системе уравнений с частными производными с помощью адаптивных подвижных сеток

П. А. Зегелинг^*

Утрехтский университет
Утрехт, Нидерланды

Поступила в редакцию 10.10.2021
После доработки 03.03.2022
Принята к публикации 11.04.2022

EDN: EJXHNK
DOI: 10.31857/S0044466922080166

Аннотация

Рассматривается метод сеточной адаптации, примененный к проблеме бифуркации в неравновесном уравнении Ричардса, возникающем в задачах гидрологии. Расширение этой модели дифференциальных уравнений с частными производными для водонасыщенности с учетом дополнительных эффектов динамической памяти приводит к появлению дополнительного члена третьего порядка – смешанной производной по пространству-времени в дифференциальном уравнении. В случае одномерного пространства предсказывается образование крутых немонотонных нелинейных волн, зависящих от параметра неравновесности. В двумерном пространстве анализ по параметру неравновесности и частоте при малом возмущающем члене предсказывает, что волны могут стать неустойчивыми, тем самым инициируя так называемые гравитационные пальцы. Для выявления крутых подвижных фронтов в решениях нестационарных уравнений используется достаточно изощренный метод построения адаптивной подвижной сетки, основанный на масштабируемой следящей функции. Библ. 25. Фиг. 10.

Ключевые слова: бегущие волны, (не)монотонность, структуры типа “палец”, пористые материалы, адаптивные подвижные сетки.

1. ВВЕДЕНИЕ

В статье обсуждается важность как анализа, так и вычислений в связи с проблемой бифуркации в неравновесном уравнении Ричардса из гидрологии. Расширение этой модели дифференциальных уравнений (ДУ) с частными производными для водонасыщенности с учетом дополнительных эффектов динамической памяти было предложено Хасанизадом и Грэйем (см. [1]) в конце прошлого века. Это приводит к появлению дополнительного члена третьего порядка – смешанной производной по пространству-времени. В одномерном пространстве анализ бегущей волны предсказывает образование крутых немонотонных волн, зависящих от параметра неравновесности. Показано, что в этом случае аналитические оценки, высокоточные численные решения ДУ с частными производными, а также экспериментальные лабораторные наблюдения (см. [2], [3]) могут быть хорошо согласованы. В двумерном пространстве параметр неравновесности $\tau $ и частота (появляющаяся в малом члене возмущения) предсказывают, что волны могут стать неустойчивыми, тем самым инициируя так называемые гравитационные пальцы. Это явление может быть проанализировано с помощью линейного анализа устойчивости и подтверждено численными экспериментами двумерной модели нестационарных ДУ с частными производными. Для этой цели мы использовали эффективную технику адаптивной подвижной сетки, основанную на масштабируемой следящей функции. Численные эксперименты в одно- и двумерных пространствах подтверждают теоретические оценки и показывают эффективность адаптивного сеточного решателя.

2. НЕРАВНОВЕСНАЯ МОДЕЛЬ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

Двумерная модель ДУ с частными производными, описывающая неравновесные эффекты в двухфазной пористой среде, описывается следующим образом (см. [1], [4]–[8]):

(1)

$\begin{gathered} {{S}_{t}} = \nabla \cdot (\mathcal{D}(S)\nabla S) + {{[f(S)]}_{z}} + \tau \nabla \cdot [f(S)\nabla ({{S}_{t}})], \\ (x,z,t) \in [{{x}_{L}},{{x}_{R}}] \times [{{z}_{L}},{{z}_{R}}] \times (0,T], \\ \end{gathered} $

где $S$ – водонасыщенность, $\tau $ – параметр неравновесности, $\mathcal{D}(S)$ – функция диффузии, $f(S)$ – так называемая функция фракционного потока.

2.1. Одномерный случай

Сначала давайте кратко рассмотрим одномерный случай. Для этого, предполагая постоянную диффузию и линеаризованный член неравновесности, модель ДУ (1) может быть упрощена до

(2)

${{S}_{t}} = \mathcal{D} {{S}_{{zz}}} + {{[f(S)]}_{z}} + \tau {{S}_{{zzt}}},\quad (z,t) \in [{{z}_{L}},{{z}_{R}}] \times (0,T],$

с начальным условием $S(z,0) = {{S}_{0}}(z)$.

Водонасыщение в одномерном пространстве представлено переменной $S(z,t) \in [0,1]$, $\mathcal{D} > 0$ – коэффициент диффузии и $\tau \geqslant 0$ – параметр неравновесности (см. также [1], [5], [6]). Функция $f$ удовлетворяет условиям

$f(0) = 0,\quad f(1) = 1,\quad f{\kern 1pt} '(S) > 0$

и связана с функцией фракционного потока в модели пористой среды (см. [5]). В частности, рассматриваются два варианта функции $f$. Первый – это выпуклая функция, представляющая однофазную ситуацию (только вода), т.е.

$f(S) = \frac{{{{S}^{2}}}}{2},$

а вторая – выпукло-вогнутая функция, указывающая на наличие двух фаз (присутствуют и вода, и воздух):

$f(S) = \frac{{{{S}^{2}}}}{{{{S}^{2}} + {{{(1 - S)}}^{2}}}}.$

На пространственных границах накладываются условия Дирихле

$S({{z}_{L}},t) = {{S}_{ - }}\quad {\text{и}}\quad S({{z}_{R}},t) = {{S}_{ + }}.$

Начальная водонасыщенность ${{S}_{0}}(z)$, границы пространственной области, конечное время $T$ и значения $0 \leqslant {{S}_{ - }} < {{S}_{ + }} \leqslant 1$, $\mathcal{D}$ и $\tau $ будут указаны в описании численных экспериментов.

2.2. Бифуркационная диаграмма и бегущие волны

Рассмотрим решения модели дифференциальных уравнений (2) в виде бегущих волн (БВ). Для простоты предположим, что $f(S) = {{S}^{2}}$. Выпукло-вогнутый случай рассматривается в [5], [6], что приводит к еще более богатой структуре динамики (фиг. 1). Подход к описанию БВ, предполагающий положительную постоянную скорость $c$, может быть записан как

$S(z,t) = \varphi (z + ct): = \varphi (\eta ),\quad \eta \in ( - \infty , + \infty ),\quad c > 0.$

Подстановка этой функции в дифференциальное уравнение (2) дает обыкновенное дифференциальное уравнение (ОДУ) третьего порядка

(3)

$c\varphi {\kern 1pt} ' = D \varphi {\kern 1pt} '{\kern 1pt} '\; + [{{\varphi }^{2}}]{\kern 1pt} ' + c\tau \varphi {\kern 1pt} '{\kern 1pt} '{\kern 1pt} ',$

где $'$ означает взятие производных по отношению к переменной БВ $\eta $. Интегрируя (3) между $ - \infty $ и $\eta $ и используя тот факт, что $\varphi ( - \infty ) = {{S}_{ - }}$, $\varphi {\kern 1pt} '( - \infty ) = \varphi {\kern 1pt} '{\kern 1pt} '( - \infty ) = 0$, получаем следующую систему ОДУ первого порядка:

(4)

$\begin{gathered} \varphi {\kern 1pt} ' = \psi , \hfill \\ \psi {\kern 1pt} ' = \frac{{c(\varphi - {{S}_{ - }}) + S_{ - }^{2} - {{\varphi }^{2}} - D \psi }}{{c \tau }}. \hfill \\ \end{gathered} $

БВ для (2) в исходной системе координат $(x,t)$ представляется траекторией в $(\varphi ,\psi )$-плоскости, соединяющей неустойчивую стационарную точку (при $\eta = - \infty $) системы (4) с устойчивой точкой (при $\eta = + \infty $). В системе (4) есть только две стационарные точки:

$(\varphi ,\psi ) = ({{S}_{ - }},0)\quad {\text{и}}\quad (\varphi ,\psi ) = ({{S}_{ + }},0).$

Из этого можно сделать вывод, что немонотонные БВ существуют для

$\tau > {{\tau }_{c}} = \frac{{{{\mathcal{D}}^{2}}}}{{{{S}_{ + }} - {{S}_{ - }}}}.$

Эта ситуация проясняется на бифуркационной диаграмме (фиг. 2а) и на графике фазовой плоскости (фиг. 2б). Для $\tau = 0$ известно, что только монотонные волны удовлетворяют модели дифференциальных уравнений с частными производными (см. [4]). Поскольку мы ищем немонотонные волны, то для описания таких явлений нам нужен дополнительный $\tau $-член в ДУ (2).

Фиг. 1.

(а) – Решения в одномерном пространстве для выпуклой функции фракционного потока, (б) – для выпукло-вогнутого случая при различных значениях параметра неравновесности $\tau \geqslant 0$.

Фиг. 2.

Бифуркационная диаграмма (а), показывающая существование монотонных и немонотонных волн в зависимости от параметров $\mathcal{D}$ и $\tau $. Черная кривая задается так: $\mathcal{D} = \sqrt {\tau ({{S}_{ + }} - {{S}_{ - }})} $. (б) – Траектории в фазовой плоскости $(\varphi ,\psi )$ для трех различных значений параметра $\tau $. Красная и синяя кривые соответствуют немонотонным волнам ($\tau > {{\tau }_{c}} > 0$), а черная кривая обозначает монотонную волну ($\tau = 0$).

2.3. Одномерная адаптивная подвижная сетка

Для численного расчета модельных ДУ (2) в одномерном пространстве мы используем технику адаптивной подвижной сетки, основанную на общем преобразовании координат от $(z,t)$ к $(\xi ,\theta )$ (подробнее см. [7], [9]–[13]). Преобразованные ДУ в новых переменных $\xi $ и $\theta $ связаны с ДУ адаптивной сетки:

$[\sigma (\mathcal{J}) + {{\tau }_{s}} {{\mathcal{J}}_{\vartheta }}) \mathcal{M}{{]}_{\xi }} = 0,\quad {{\tau }_{s}} \geqslant 0,$

где $\mathcal{J} = {{z}_{\xi }}$ – матрица Якоби преобразования, $ \mathcal{M}: = \sqrt {1 + {{{[{{S}_{z}}]}}^{2}}} $ – мониторная функция, отражающая зависимость неоднородной сетки от пространственной производной решения ДУ.

Оператор

$\sigma : = \mathcal{I} + {{\kappa }_{s}}({{\kappa }_{s}} + 1)\frac{{{{\partial }^{2}}}}{{\partial {{\xi }^{2}}}}$

применяется для получения более плавного преобразования сетки в пространстве. Первая константа адаптивности, ${{\kappa }_{s}} > 0$ ($ = \,{\kern 1pt} \mathcal{O}(1)$) является параметром пространственного сглаживания (или фильтрации). Вторая константа адаптивности ${{\tau }_{s}}$ ($ = \,{\kern 1pt} \mathcal{O}{{(10}^{{ - 3}}})$) заботится о сглаживании в направлении времени. Для ${{\kappa }_{s}} > 0$ и ${{\tau }_{s}} > 0$ после полудискретизации можно показать (см. [11]), что пространственная неоднородная сетка удовлетворяет условию

$\frac{{{{\kappa }_{s}}}}{{{{\kappa }_{s}} + 1}} \leqslant \frac{{\Delta {{z}_{{i + 1}}}}}{{\Delta {{z}_{i}}}} \leqslant \frac{{{{\kappa }_{s}} + 1}}{{{{\kappa }_{s}}}}$

для всех точек сетки ${{z}_{i}}$ и любого времени $t > 0$. Заметим, что для ${{\kappa }_{s}} = {{\tau }_{s}} = 0$ (без сглаживания) мы возвращаемся к основному принципу равномерного распределения:

${{[{{z}_{\xi }} \mathcal{M}]}_{\xi }} = 0.$

Более подробную информацию об адаптивной сетке и операторах сглаживания можно найти в [11]–[13]. Преобразованное ДУ и ДУ адаптивной сетки одновременно дискретизируются в пространстве с использованием метода линий. Используются центральные разности второго порядка для преобразованных производных в направлении $\xi $. Интегрирование по времени полученной связанной системы ОДУ производится методом BDF с переменным шагом по времени в среде DASSL (см. [14]).

2.4. Численные результаты в одномерном пространстве

Опишем несколько численных экспериментов для иллюстрации точности и эффективности адаптивной подвижной сетки в одномерном пространстве, а также для подтверждения оценок для БВ из п. 2.2. Параметры адаптивной сетки выбраны следующим образом: ${{\kappa }_{s}} = 2$ и ${{\tau }_{s}} = 0.001$, а допустимая погрешность интегрирования по времени в DASSL установлена ${{10}^{{ - 4}}}$. Начальным условием является крутая волна, начинающаяся на правой границе области и имеющая вид

(5)

$S(z,0) = {{S}_{0}}(z) = {{S}_{ - }} + \frac{1}{2}({{S}_{ + }} - {{S}_{ - }})(1 + \tanh (R(z - {{z}_{0}})),$

где ${{z}_{L}} = 0$, ${{z}_{R}} = 1.4$, ${{S}_{ - }} = 0$, ${{S}_{ + }} = 0.6$, $R = 50$, и параметры уравнения $\tau {{ = 10}^{{ - 4}}}$ и $\mathcal{D}{{ = 10}^{{ - 3}}}$. На фиг. 3а показаны численные решения для $\tau = 0$ с $N = 51$ адаптивными подвижными точками сетки. В этом случае, как мы знаем, существуют только монотонные решения. Видно, что адаптивная сетка прекрасно отслеживает монотонную волну. Кроме того, график с историей времени адаптивной сетки иллюстрирует плавное распределение и поведение сетки во времени при постоянной скорости волны. На фиг. 3б, в показана разница между выпуклым и выпукло-вогнутым случаями: немонотонные БВ и плоские волны. Эти волны предсказаны анализом в п. 2.2 и [5].

Фиг. 3.

История по времени адаптивной сетки (справа), решения в несколько моментов времени (слева) для трех характерных случаев в модели пористой среды: $\tau = 0$ (а), выпуклая $f$ (б) и выпукло-вогнутая $f$ (в). Красные прямые линии показывают точные (асимптотические) скорости волн для трех случаев, как предсказывает формула (6).

Из системы ОДУ (4) можно вывести, что для асимптотической скорости БВ $c$ выполнено равенство

(6)

$c = \frac{{f({{S}_{ + }}) - f({{S}_{ - }})}}{{{{S}_{ + }} - {{S}_{ - }}}}.$

Это дает соответственно для выпуклого случая $c = 0.3$ и для выпукло-вогнутого случая $c \approx 1.1538$. На фиг. 3 красными линиями обозначены постоянные скорости БВ. Мы видим, что адаптивная подвижная сетка очень точно следует за всеми волнами.

3. ДВУМЕРНЫЙ СЛУЧАЙ

Для двумерного случая модели (1) используем следующие упрощенные формулы для функции фракционного потока $f$ и функции диффузии $\mathcal{D}$:

(7)

$f(S) = {{S}^{\alpha }},\quad \mathcal{D}(S) = \beta {{S}^{{\alpha - \beta - 1}}},\quad \alpha > \beta + 1.$

3.1. Немонотонные волны и неустойчивости

В отличие от одномерного случая, для которого как монотонные, так и немонотонные волны устойчивы при малых возмущениях, двумерная модель может привести к неустойчивости (структуры типа “палец”). Можно показать, что для определенных значений $\tau > 0$ немонотонные волны могут стать неустойчивыми. Анализ основан на следующих наблюдениях, также упомянутых в [15] и [16].

Во-первых, неравновесное ДУ (1) переписывается как система двух уравнений – одно для насыщения $S$ и одно для давления $p$:

(8)

$\begin{gathered} {{S}_{t}} = \nabla \cdot (\mathcal{D}(S)\nabla p) + {{[f(S)]}_{z}}, \hfill \\ \tau {{S}_{t}} = p - \mathcal{P}(S), \hfill \\ \end{gathered} $

где $\mathcal{P}(S)$ – равновесное давление. Далее ДУ записываются в координатах БВ, как это сделано в п. 2.2. Волны насыщения и давления затем возмущаются следующим образом:

(9)

$\begin{gathered} S = {{S}_{0}}(\zeta ) + \epsilon {\kern 1pt} e{{{\kern 1pt} }^{{i{{\omega }_{x}} + i{{\omega }_{z}} + kt}}}{{S}_{1}}(\zeta ) + \mathcal{O}(\epsilon {{{\kern 1pt} }^{2}}), \hfill \\ p = {{p}_{0}}(\zeta ) + \epsilon {\kern 1pt} e{{{\kern 1pt} }^{{i{{\omega }_{x}} + i{{\omega }_{z}} + kt}}}{{p}_{1}}(\zeta ) + \mathcal{O}(\epsilon {{{\kern 1pt} }^{2}}). \hfill \\ \end{gathered} $

Эти возмущенные величины подставляются в систему двух уравнений БВ, членами высшего порядка пренебрегают, и в итоге выводятся уравнения для анализа линейной устойчивости. Из них следует, что для $\tau = 0$ фактор роста $k$ всегда будет отрицательным, тогда как для $\tau > 0$ и для определенных частот $\omega $ фактор роста может быть положительным, тем самым инициируя неустойчивые волны. Это может быть связано с так называемыми структурами типа “палец”, как мы увидим в п. 3.3.

3.2. Адаптивная подвижная сетка в двумерном пространстве

Метод адаптивной сетки в двумерном пространстве следует принципам, аналогичным с одномерной ситуацией, но с некоторыми дополнительными особенностями. Более подробную информацию можно найти, например, в [10], [11], [17]–[19]. Обобщая процедуру, можно сказать, что преобразование двумерной сетки выглядит следующим образом:

(10)

$\begin{array}{*{20}{l}} {x = z(\xi ,\eta ,\vartheta ),}&{} \\ {z = z(\xi ,\eta ,\vartheta ),}&{} \\ {t = t(\xi ,\eta ,\vartheta ) = \vartheta .}&{} \end{array}$

На фиг. 4а показана типичная двумерная ситуация преобразования крутого решения ДУ в исходных координатах в более пологое в преобразованных координатах. В качестве примера, первый член нелинейной диффузии с правой стороны в модели ДУ (1) преобразуется в

(11)

${{(\mathcal{D}(S){{S}_{x}})}_{x}} = \frac{1}{\mathcal{J}}\left[ {{{{\left( {\frac{{\mathcal{D}(S)z_{\eta }^{2}}}{\mathcal{J}}{{S}_{\xi }}} \right)}}_{\xi }} - {{{\left( {\frac{{\mathcal{D}(S){{z}_{\xi }}{{z}_{\eta }}}}{\mathcal{J}}{{S}_{\eta }}} \right)}}_{\xi }}} \right. - \left. {{{{\left( {\frac{{\mathcal{D}(S){{z}_{\xi }}{{z}_{\eta }}}}{\mathcal{J}}{{S}_{\xi }}} \right)}}_{\eta }} + {{{\left( {\frac{{\mathcal{D}(S)z_{\xi }^{2}}}{\mathcal{J}}{{S}_{\eta }}} \right)}}_{\eta }}} \right],$

где $\mathcal{J} = {{x}_{\xi }}{{z}_{\eta }} - {{x}_{\eta }}{{z}_{\xi }}$ обозначает якобиан двумерного преобразования (10). Базовый одномерный принцип равномерного распределения, ${{[ \mathcal{M}{{z}_{\xi }}]}_{\xi }} = 0$, распространяется на систему двух связанных нелинейных эллиптических ДУ с частными производными:

$\begin{gathered} \nabla \cdot ( \mathcal{M}\nabla x) = 0,\quad \nabla : = {{\left[ {\frac{\partial }{{\partial \xi }},\frac{\partial }{{\partial \eta }}} \right]}^{{\text{т}}}}, \hfill \\ \nabla \cdot ( \mathcal{M}\nabla z) = 0. \hfill \\ \end{gathered} $

Здесь следящая функция $M$ теперь определяется следующим образом:

$ \mathcal{M} = \gamma (t) + \sqrt {\nabla S \cdot \nabla S} \quad {\text{с}}\quad \gamma (t) = \iint\limits_{{{\Omega }_{c}}} {\sqrt {\nabla S \cdot \nabla S} d\xi d\eta }.$

На фиг. 4б показана двумерная адаптивная сетка с точки зрения минимизации функционала “энергии сетки” для системы пружин (соединенные ребрами точки сетки) и сил (контролируемые значения). Очевидно, что можно было бы использовать более сложные следящие функции, но для модели ДУ в данной работе эта относительно простая следящая функция оказалась достаточно эффективной. Отметим, что мы добавили функцию адаптивности, зависящую от времени $\gamma (t)$, которая вычисляется автоматически в процессе интегрирования по времени. Она обеспечивает дополнительное сглаживание распределения сетки и добавляет масштабирование в пространстве и в направлении решения (см. [17] для дополнительной информации об этом выборе). Можно показать, что адаптивное преобразование сетки, следуя этому принципу двумерного эквидистантного распределения с упомянутой следящей функцией $ \mathcal{M}$, остается несингулярным.

Фиг. 4.

Преобразование двумерной сетки: (а) – показано, как преобразование переводит крутое решение в более пологое, (б) – адаптивную сетку можно представить как систему пружин с силой пружины $F$, расположенной в точке ${\mathbf{x}}(i,j)$ по значениям следящей функции $\omega $.

Теорема (подробную информацию о доказательстве см. [20]). Пусть $ \mathcal{M} > 0$, $ \mathcal{M} \in {{C}^{1}}({{\Omega }_{c}})$ и $ {{\mathcal{M}}_{\xi }}, {{\mathcal{M}}_{\eta }} \in {{C}^{\gamma }}({{\bar {\Omega }}_{c}})$ для $\gamma \in (0,1)$. Тогда существует единственное решение $(x,z) \in {{C}^{2}}({{\bar {\Omega }}_{c}})$, которое является биекцией из ${{\bar {\Omega }}_{c}}$ в себя. Более того, якобиан $\mathcal{J}$ удовлетворяет неравенству

$\mathcal{J} = {{x}_{\xi }}{{z}_{\eta }} - {{x}_{\eta }}{{z}_{\xi }} > 0.$

Некоторые важные компоненты доказательства включают теорему о кривой Жордана, теорему Карлемана–Хартмана–Винтнера и принцип максимума для эллиптических ДУ.

В [21] дан глубокий анализ обратимости более общих, так называемых $\sigma $-гармонических отображений. Преобразованная модель ДУ пространственно дискретизируется на равномерной декартовой сетке в координатах $\xi ,\eta $. Для численного интегрирования по времени преобразованного двумерного неравновесного ДУ и уравнений адаптивной сетки мы использовали подход IMplicitEXplicit (см. [22], [23]). В качестве примера диффузионный член (11) аппроксимируется следующим образом:

(12)

$\begin{gathered} \left. {{{{(\mathcal{D}(S){{S}_{x}})}}_{x}}} \right|_{{i,j}}^{n} \approx \frac{1}{{\mathcal{J}_{{i,j}}^{n}}}\left[ {\frac{{\left. {{{C}_{1}}} \right|_{{i + 1,j}}^{n} + \left. {{{C}_{1}}} \right|_{{i,j}}^{n}}}{2}\frac{{S_{{i + 1,j}}^{{n + 1}} - S_{{i,j}}^{{n + 1}}}}{{{{{(\Delta \xi )}}^{2}}}} - \frac{{\left. {{{C}_{1}}} \right|_{{i,j}}^{n} + \left. {{{C}_{1}}} \right|_{{i - 1,j}}^{n}}}{2}\frac{{S_{{i,j}}^{{n + 1}} - S_{{i - 1,j}}^{{n + 1}}}}{{{{{(\Delta \xi )}}^{2}}}}} \right. - \\ - \; \left. {{{C}_{2}}} \right|_{{i + 1,j}}^{n}\frac{{S_{{i + 1,j + 1}}^{{n + 1}} - S_{{i + 1,j - 1}}^{{n + 1}}}}{{4\Delta \xi \Delta \eta }} + \left. {{{C}_{2}}} \right|_{{i - 1,j}}^{n}\frac{{S_{{i - 1,j + 1}}^{{n + 1}} - S_{{i - 1,j - 1}}^{{n + 1}}}}{{4\Delta \xi \Delta \eta }} - \left. {{{C}_{2}}} \right|_{{i,j + 1}}^{n}\frac{{S_{{i + 1,j + 1}}^{{n + 1}} - S_{{i - 1,j + 1}}^{{n + 1}}}}{{4\Delta \xi \Delta \eta }} + \\ + \;\left. {{{C}_{2}}} \right|_{{i,j - 1}}^{n}\frac{{S_{{i + 1,j - 1}}^{{n + 1}} - S_{{i - 1,j - 1}}^{{n + 1}}}}{{4\Delta \xi \Delta \eta }} + \frac{{\left. {{{C}_{3}}} \right|_{{i,j + 1}}^{n} + \left. {{{C}_{3}}} \right|_{{i,j}}^{n}}}{2}\frac{{S_{{i,j + 1}}^{{n + 1}} - S_{{i,j}}^{{n + 1}}}}{{{{{(\Delta \eta )}}^{2}}}} - \frac{{\left. {{{C}_{3}}} \right|_{{i,j}}^{n} + \left. {{{C}_{3}}} \right|_{{i,j - 1}}^{n}}}{2}\frac{{S_{{i,j}}^{{n + 1}} - S_{{i,j - 1}}^{{n + 1}}}}{{{{{(\Delta \eta )}}^{2}}}}, \\ \end{gathered} $

где

${{C}_{1}}: = \frac{1}{\mathcal{J}}\mathcal{D}(S)z_{\eta }^{2},\quad {{C}_{2}}: = \frac{1}{\mathcal{J}}\mathcal{D}(S){{z}_{\xi }}{{z}_{\eta }},\quad {{C}_{3}}: = \frac{1}{\mathcal{J}}\mathcal{D}(S)z_{\xi }^{2}$

соответственно. Вместо “умных” операторов сглаживания в пространстве и времени, используемых в одномерном режиме, здесь, как в [18], [19], на каждом временном шаге следующим образом несколько раз применяется фильтр для следящей функции:

$\begin{gathered} {{{\tilde {\mathcal{M}}}}_{{i,j}}} = \frac{1}{4} {{\mathcal{M}}_{{i,j}}} + \frac{1}{8}[ {{\mathcal{M}}_{{i - 1,j}}} + {{\mathcal{M}}_{{i + 1,j}}} + {{\mathcal{M}}_{{i,j - 1}}} + {{\mathcal{M}}_{{i,j + 1}}}] + \\ \, + \frac{1}{{16}}[ {{\mathcal{M}}_{{i - 1,j - 1}}} + {{\mathcal{M}}_{{i + 1,j - 1}}} + {{\mathcal{M}}_{{i - 1,j + 1}}} + {{\mathcal{M}}_{{i + 1,j + 1}}}]. \\ \end{gathered} $

Эта модификация позволяет получить более гладкое распределение сетки и улучшает процесс интегрирования по времени.

3.3. Численные результаты

Для подтверждения и подкрепления теоретических предсказаний в анализе в п. 3.1 мы проводим некоторые численные эксперименты для двумерной модели. Пространственная область определяется прямоугольником $[0,10] \times [0,60]$, и начальным решением является функция типа “тангенс”, как и в одномерной модели, определенная в уравнении (5), но теперь расположенная около значения $z = 55$. Мы добавляем небольшое периодическое возмущение с частотой $\omega $ для проверки устойчивости двумерных волн. В численных экспериментах, если не указано иное, используется пространственная сетка с $41 \times 121$ узлами.

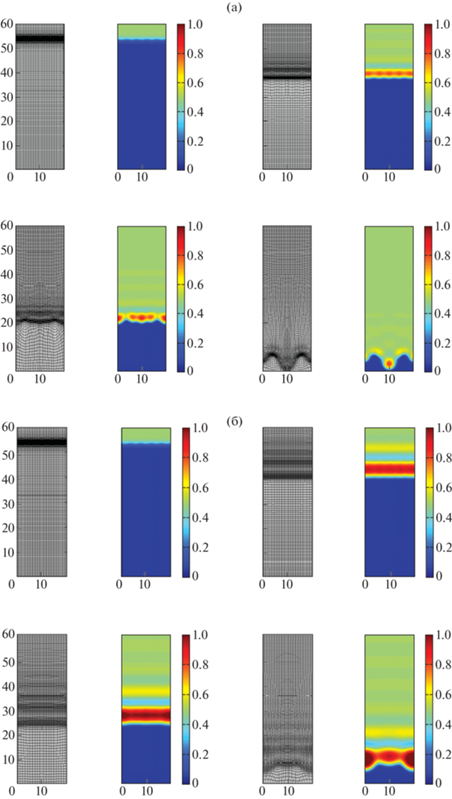
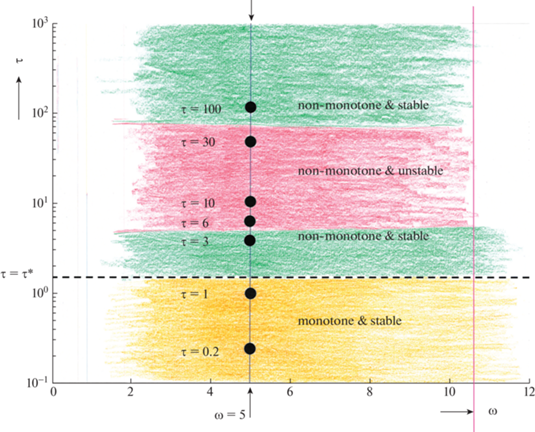
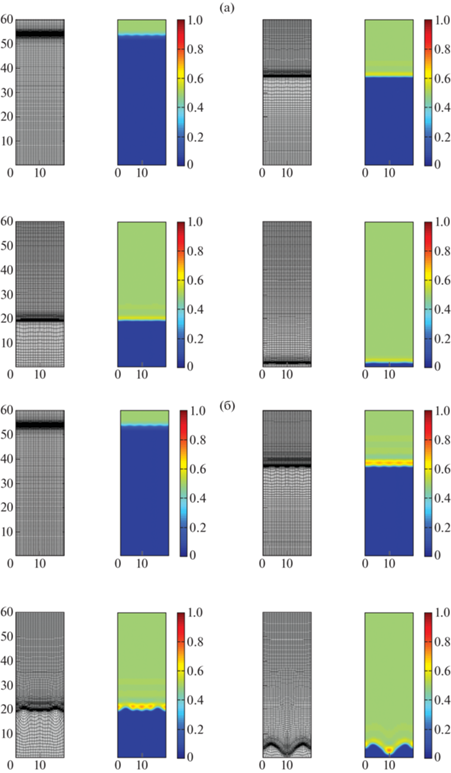
Фигура 5 действительно подтверждает и иллюстрирует анализ устойчивости, проведенный в [15] и [16], также кратко описанный в п. 3.1. На фиг. 5а показан численно рассчитанный коэффициент роста $k$ возмущения как функции начальной частоты $\omega $ для нескольких значений параметра неравновесности $\tau $, используя метод адаптивной сетки из п. 3.2. На фиг. 5б показана очень похожая зависимость $k(\omega )$. Фигуру 6 можно извлечь из фиг. 5, если построить диаграмму зависимости $\tau $ от частоты $\omega $. Семь черных точек обозначают семь значений $\tau $ для $\omega = 5$ в численных экспериментах. Для $\tau = 0.2$ и $\tau = 1$ можно найти монотонную и стабильную волну, как и предсказывалось (см. фиг. 7). Для $\tau = 3$ (фиг. 8а) возникает немонотонная стабильная волна. На фиг. 8б мы видим появление немонотонной и неустойчивой волн для $\tau = 6$. На фиг. 9а для $\tau = 10$ и для $\tau = 30$ (фиг. 9б) мы видим больше немонотонных и неустойчивых волн. Можно также предсказать, что для $\omega = 5$ и $\tau \gg 1$ (в данном случае $\tau = 100$) немонотонные волны снова “становятся” стабильными из-за дополнительного эффекта диффузии при больших значениях параметра неравновесности. Это видно на фиг. 10а. Наконец, на фиг. 10б мы уменьшили коэффициент диффузии $\mathcal{D}$ с 1 до 0.1, тем самым создав еще более неустойчивые структуры в виде “пальцев”. Все расчеты проводились с параметрами $\alpha = 3$, $\beta = 0.5$, c пространственной сеткой $41 \times 121$ узлами, 4000 шагов по времени и частотой $\omega = 5$ в возмущенном начальном состоянии.

Фиг. 5.

(а) – Определенный численно фактор роста $k$ как функция волнового числа $\omega $ возмущения для различных значений $\tau $, (б) – теоретическое предсказание, взятое из [10]. Обращаем внимание, что масштабы по обеим осям на этих двух рисунках разные: для (а) $\omega $ – это численная частота, добавленная к начальному условию, тогда как для (б) $\omega $ получена из теоретического анализа. Глобальное поведение одинаково, но точные значения различны. Аналогичное замечание справедливо и для фактора роста $k$.

Фиг. 6.

$(\omega ,\tau )$-Диаграмма, отображающая зависимость свойств устойчивости и монотонности решения ДУ в двумерном пространстве. Семь черных точек соответствуют семи численным экспериментам на фиг. 7–10 .

Фиг. 7.

(а) – Для $t = 0,100,150,250$ показаны численные результаты для случая $\tau = 0.2 < {{\tau }_{*}}$ (монотонная устойчивая волна), (б) – для $\tau = 1 < \tau {\kern 1pt} *$.

Фиг. 8.

(а) – Для $t = 0,100,150,250$ показаны численные результаты для случая $\tau = 3 > {{\tau }_{*}}$ (немонотонная устойчивая волна), (б) – для $\tau = 6 > {{\tau }_{*}}$ (немонотонная и неустойчивая волна).

Фиг. 9.

(а) – Для $t = 0,100,150,250$ показаны численные результаты для случая $\tau = 10 > {{\tau }_{*}}$, (б) – для $\tau = 30 > {{\tau }_{*}}$ (обе волны немонотонные и неустойчивые).

Фиг. 10.

(а) – Для $t = 0,100,150,250$ показаны численные результаты для случая $\tau = 100 \gg {{\tau }_{*}}$ (снова немонотонная устойчивая волна), (б) – для $\mathcal{D} = 0.1$ вместо $\mathcal{D} = 1$ ( неустойчивая структура типа “палец”).

Список литературы

Alessandrini G., Nesi V. Univalent $\sigma $-harmonic mappings // Arch. Rational Mech. Anal. 2001. V. 158. P. 155–171.
Budd C., Huang W., Russell R. Adaptivity with moving grids // Acta Numerica. 2009. P. 1–131.
Clement Ph., Hagmeijer R., Sweers G. On the invertibility of mappings arising in 2D grid generation problems // Numerische Mathematik. 1996. V. 73. No. 1. P. 37–52.
Cuesta C., van Duijn C.J., Hulshof J. Infiltration in porous media with dynamic capillary pressure: travelling waves // Eur. J. Appl. Math. 2000. V. 11. P. 397.
van Dam A., Zegeling P.A. A robust moving mesh finite volume method applied to 1d hyperbolic conservation laws from magnetohydrodynamics // J. of Comput. Phys. 2006. V. 216. P. 526–546.
van Dam A., Zegeling P.A. Balanced monitoring of flow phenomena in moving mesh methods // Commun. Comput. Phys. 2010. V. 7. P. 138–170.
DiCarlo D. Experimental measurements of saturation overshoot on infiltration // Water Resources Res. 2004. V. 40. W04215.
van Duijn C.J., Fan Y., Peletier L.A., Pop I.S. Travelling wave solutions for a degenerate pseudo-parabolic equation modelling two-phase flow in porous media // Nonlin. Anal. Real World Appl. 2013. P. 1361–1383.
van Duijn C.J., Hassanizadeh S.M., Pop I.S., Zegeling P.A. Non-equilibrium models for two-phase flow in porous media: the occurence of saturation overshoot // Proc. of the Fifth Inter. Conf. on Appl. of Porous Media, Cluj-Napoca, 2013.
Egorov A.G., Dautov R.Z., Nieber J.L., Sheshukov A.Y. Stability analysis of gravity-driven infiltrating flow // Water Resources Res. 2003. V. 39. P. 1266.
Hassanizadeh S.M., Gray W.G. Thermodynamic basis of capillary pressure on porous media // Water Resources Res. 1993. V. 29. P. 3389–3405.
Hilfer R., Doster F., Zegeling P.A. Nonmonotone saturation profiles for hydrostatic equilibrium in homogeneous porous media // Vadose Zone J. 2012. V. 11. No. 3. P. 201.
Hu G., Zegeling P.A. Simulating finger phenomena in porous media with a moving finite element method // J. of Comp. Phys. 2011. YJCPH 3432.
Huang W., Russell R.D. Analysis of moving mesh partial differential equations with spatial smoothing // SIAM J. Num. Anal. 1997. V. 34. P. 1106–1126.
Huang W., Russell R.D. Adaptive moving mesh methods. Springer, New York, 2011, XVII, 432 p.
Hundsdorfer W., Verwer J. Numerical solution of ‘time-dependent advection-diffusion-reaction equations. Springer, Berlin, 1993.
Nicholl M.J., Glass R.J. Infiltration into an analog fracture: experimental observations of gravity-driven fingering // Vadose Zone J. 2005. V. 4. P. 1123–1151.
Kampitsis A.E., Adam A., Salinas P., Pain C.C., Muggeridge A.H., Jackson M.D. Dynamic adaptive mesh optimisation for immiscible viscous fingering // Comput. Geoscienc. 2020. V. 24. P. 1221–1237.
Nieber J.L., Dautov R.Z., Egorov A.G., Sheshukov A.Y. Dynamic capillary pressure mechanosm for instability in gravity-driven flows; review and extension to very dry conditions // Transp. Porous Media. 2005. V. 58. P. 147–172.
Petzold L.R. A Description of DASSL: A Differential/Algebraic System Solver, in: IMACS Transact. on Scient. Comput., Eds.: R.S. Stepleman, 1983. P. 65–68.
Ruuth S.J. Implicit-explicit methods for reaction-diffusion problems in pattern formation // J. of Math. Biolog. 1995. V. 34. P. 148–176.
Tang T., Tang H. Adaptive mesh methods for one- and two-dimensional hyperbolic conservation laws // SIAM J. on Numer. Anal. 2003. V. 41. Iss. 2. P. 487–515.
Zegeling P.A. On resistive MHD models with adaptive moving meshes // J. of Scient. Comput. 2005. V. 24. No. 2. P. 263–284.
Zegeling P.A., Lagzi I., Izsak F. Transition of Liesegang precipitation systems: simulations with an adaptive grid PDE method // Commun. in Comput. Phys. 2011. V. 10. No. 4. P. 867–881.
Zegeling P.A. Theory and application of adaptive moving grid methods, Chapter 7 in Adaptive Computations: Theory and Computation, Sci. Press, Beijing, 2007.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал