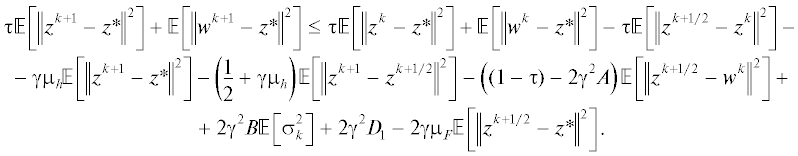Журнал вычислительной математики и математической физики, 2023, T. 63, № 2, стр. 189-217

Унифицированный анализ методов решения вариационных неравенств: редукция дисперсии, сэмплирование, квантизация и покомпонентный спуск

А. Н. Безносиков¹, А. В. Гасников^{1, 2, 3, *}, К. Э. Зайнуллина¹, А. Ю. Масловский¹, Д. А. Пасечнюк^1, 2

¹ Московский физико-технический институт (национальный исследовательский университет)
141701 М.о., Долгопрудный, Институтский пер., 9, Россия

² Институт проблем передачи информации им. А.А. Харкевича
127051 Москва, Большой Каретный пер., 19, стр. 1, Россия

³ Кавказский математический центр Адыгейского государственного университета
385000 Майкоп, ул. Первомайская, 208, Республика Адыгея, Россия

^* E-mail: gasnikov@yandex.ru

Поступила в редакцию 28.01.2022
После доработки 28.01.2022
Принята к публикации 14.10.2022

EDN: BMKMVF
DOI: 10.31857/S0044466923020059

Полный текст (PDF)

Аннотация

Предлагается унифицированный анализ методов для такого широкого класса задач, как вариационные неравенства, который в качестве частных случаев включает в себя задачи минимизации и задачи нахождения седловой точки. Предлагаемый анализ развивается на основе экстраградиентного метода, являющегося стандартным для решения вариационных неравенств. Рассматриваются монотонный и сильно монотонный случаи, которые соответствуют выпукло-вогнутым и сильно-выпукло-сильно-вогнутым задачам нахождения седловой точки. Теоретический анализ основан на параметризованных предположениях для итераций экстраградиентного метода. Следовательно, он может служить прочной основой для объединения уже существующих методов различных типов, а также для создания новых алгоритмов. В частности, чтобы показать это, мы разрабатываем некоторые новые надежные методы, в том числе метод с квантизацией, покомпонентный метод, распределенные рандомизированные локальные методы и др. Большинство из упомянутых подходов прежде никогда не рассматривались в общности вариационных неравенств и применялись лишь для задач минимизации. Стабильность новых методов подтверждается предоставляемыми численными экспериментами по обучению моделей GAN. Библ. 35. Фиг. 3. Табл. 1.

Ключевые слова: экстраградиентный метод, стохастические вариационные неравенства, квантизация, редукция дисперсии.

1. ВВЕДЕНИЕ

Основная постановка задачи, рассматриваемой в настоящей статье, - решение вариационного неравенства (ВН) – имеет следующий вид:

(1)

${\text{найти}}\quad z{\kern 1pt} * \in \mathcal{Z}\quad {\text{такое,}}\;{\text{что}}\quad \left\langle {F(z{\kern 1pt} *),z - z{\kern 1pt} *} \right\rangle + h(z) - h(z{\kern 1pt} *) \geqslant 0\quad \forall z \in \mathcal{Z},$

где $h{\kern 1pt} :\;{{\mathbb{R}}^{d}} \to \mathbb{R} \cup \{ + \infty \} $ – подходящая полунепрерывная снизу выпуклая функция, $F{\kern 1pt} :\;{{\mathbb{R}}^{d}} \to {{\mathbb{R}}^{d}}$ – оператор, $\mathcal{Z}$ – непустое замкнутое выпуклое подмножество ${{\mathbb{R}}^{d}}$.

Приведем сразу некоторые классические примеры задач, которые могут быть представлены в виде (1).

Задача минимизации. Положим, что $F(x)$ является градиентом некоторой функции $f(x)$, а $h(x) = {{\delta }_{\mathcal{X}}}(x)$ – индикаторная функция множества $\mathcal{X}$. В частности, при $\mathcal{X} = {{\mathbb{R}}^{d}}$, $x{\kern 1pt} * \in \mathcal{X}$ является решением (1) тогда и только тогда, когда $\nabla f(x{\kern 1pt} *) = 0$. В случае выпуклой функции ему соответствует глобальный экстремум.

Задача нахождения седловой точки (СТ). Рассмотрим минимаксную задачу

(2)

$\mathop {\min }\limits_{x \in \mathcal{X}} \mathop {\max }\limits_{y \in \mathcal{Y}} f(x,y).$

Эта задача может быть также представлена в виде (1). Достаточно выбрать $F$ и $g$ следующим образом:

$F(z) = \left( {\begin{array}{*{20}{c}} {{{\nabla }_{x}}f(x,y)} \\ { - {{\nabla }_{y}}f(x,y)} \end{array}} \right),\quad h(z) = {{\delta }_{\mathcal{X}}}(x) + {{\delta }_{\mathcal{Y}}}(y).$

Как и в случае задачи минимизации, неравенство (1) является необходимым условием оптимальности. В частности, если $f(x,y)$ выпукло-вогнута и $\mathcal{X} = {{\mathbb{R}}^{{{{d}_{x}}}}}$, $\mathcal{Y} = {{\mathbb{R}}^{{{{d}_{y}}}}}$, это условие является также и достаточным, причем решение $(x{\kern 1pt} *,y{\kern 1pt} *)$ вариационного неравенства тогда является глобальной седловой точкой:

$f(x{\kern 1pt} *,y) \leqslant f(x,y) \leqslant f(x,y{\kern 1pt} *)\quad \forall x \in \mathcal{X},\quad y \in \mathcal{Y}.$

Эти примеры показывают, что класс задач ВН достаточно широк. В частности, задачи минимизации могут рассматриваться в общности ВН. Но обычно предпочитают проводить анализ задачи минимизации отдельно и независимо. На данный момент анализ задач минимизации разработан гораздо шире и глубже, чем для задач ВН. Это связано со сложностью задачи ВН: многие техники из минимизации еще не перенесены или не могут быть перенесены на ВН. Поэтому прежде всего решение ВН интересно с точки зрения нахождения СТ.

Задачи СТ имеют множество практических приложений. Как, например, хорошо известные классические примеры из теории игр и оптимального управления (см. [1]). В последние годы задачи СТ стали популярными и в нескольких других отношениях. Можно отметить ветвь работ, посвященных решению негладких задач путем их переформулирования в виде задачи СТ (см. [2], [3]), а также применение таких подходов к задачам обработки изображений (см. [4], [5]). Однако в первую очередь интересны приложения седловых задач в машинном обучении. Конечно, прежде всего здесь стоит упомянуть о GAN. В классической формулировке [6] обучение этих моделей является минимаксной задачей.

Довольно большая часть прикладных задач, в том числе задачи машинного обучения, являются стохастическими, поэтому естественно сосредоточиться на случае, когда невыгодно (или даже невозможно) вычислить полное значение градиента и когда вместо этого используются некоторые стохастические оценки. Например, для функции из (2), имеющей вид f(x, y) = $ = {{\mathbb{E}}_{{{{p}_{x}} \sim {{D}_{x}},{{p}_{y}} \sim {{D}_{y}}}}}\left[ {{{f}_{{{{p}_{x}},{{p}_{y}}}}}(x,y)} \right]$. В частности, в случае GAN $f$ есть функция потерь, а переменные $x$ и $y$ интерпретируются как относящиеся к двум моделям: $x$ – параметры дискриминатора, а $y$ – генератора, ${{p}_{x}}$ – обучающий пример из реального набора данных, ${{p}_{y}}$ – случайный вектор, который генератор использует для создания поддельных копий реального набора данных. Стандартное предположение статистического обучения состоит в том, что распределение данных ${{D}_{x}}$ неизвестно, а потому полный градиент ${{\nabla }_{x}}f(x,y)$ не может быть вычислен, тогда как можно легко вычислить градиент для некоторых отдельных данных. Возвращаясь к основной проблеме (1) этой статьи, интерпретируем сказанное выше следующим образом: предположим, что мы не имеем доступа к “честному” $F(z)$, а только к некоторой несмещенной стохастической оценке $F(z,\xi )$:

(3)

$F(z) = {{\mathbb{E}}_{{\xi \sim P}}}\left[ {F(z,\xi )} \right].$

В настоящей работе нас также будет интересовать другая стохастическая постановка задачи (1), это тот случай, когда значение $F$ – это среднее значение большого числа операторов:

(4)

$F(z) = \frac{1}{M}\sum\limits_{m = 1}^M \,{{F}_{m}}(z).$

Такие постановки возникают в результате применения подхода интегрирования Монте-Карло. Например, пусть для (2) имеется $M$ частей набора данных, тогда можно вычислить градиенты ${{\nabla }_{x}}{{f}_{m}}(x,y)$, ${{\nabla }_{y}}{{f}_{m}}(x,y)$ для каждой из этих частей, тогда как вычисление полных градиентов ${{\nabla }_{x}}f(x,y)$, ${{\nabla }_{y}}f(x,y)$ будет очень дорогим и потребует много времени. Отсюда кажется естественным выбирать случайный индекс $m$ части набора данных на каждой итерации и учитывать градиенты только на ней. Этот подход обычно используется при практическом решении задач обучения.

Приведенный выше взгляд на (4) справедлив в случае, когда у нас есть только одно устройство для вычислений. Однако в случае распределенного обучения можно просто обмениваться данными между устройствами, и тогда каждому устройству будет соответствовать свой ${{F}_{m}}$. В такой постановке задачу также можно рассматривать в виде (4), но мы предпочтем переписать ее следующим образом:

(5)

$F(Z) = \Phi (Z) + \lambda (Z - \bar {Z}),$

где векторы $\Phi (Z) = [F_{1}^{T}({{z}_{1}}), \ldots ,F_{M}^{T}({{z}_{M}})] \in {{\mathbb{R}}^{{Md}}}$, $Z = [z_{1}^{T}, \ldots ,z_{M}^{T}] \in {{\mathbb{R}}^{{Md}}}$ и $\bar {Z} = [{{\bar {z}}^{T}}, \ldots ,{{\bar {z}}^{T}}] \in {{\mathbb{R}}^{{Md}}}$ для $\bar {z} = \frac{1}{M}\sum\nolimits_{m = 1}^M \,{{z}_{m}}$. Легко проверить, что задача минимизации ${{\min }_{{{{x}_{1}}, \ldots {{x}_{M}}}}}\left[ {\sum\nolimits_{m = 1}^M \,{{f}_{m}}({{x}_{m}})} \right. + $ $ + \;\frac{\lambda }{2}\left. {\sum\nolimits_{m = 1}^M {{{\left\| {{{x}_{m}} - \bar {x}} \right\|}}^{2}}} \right]$ соответствует ВН с оператором (5). Аналогично, задача СТ

$\mathop {\min }\limits_{{{x}_{1}}, \ldots {{x}_{M}}} \mathop {\max }\limits_{{{y}_{1}}, \ldots {{y}_{M}}} \left[ {\sum\limits_{m = 1}^M \,{{f}_{m}}({{x}_{m}},{{y}_{m}}) + \frac{\lambda }{2}\sum\limits_{m = 1}^M {{{\left\| {{{x}_{m}} - \bar {x}} \right\|}}^{2}} - \frac{\lambda }{2}\sum\limits_{m = 1}^M {{{\left\| {{{y}_{m}} - \bar {y}} \right\|}}^{2}}} \right]$

также соответствует ВН с оператором (5) (как построить ВН из задачи минимизации и задачи нахождения седловой точки описано выше). Разобравшись в интуиции, переходим к интерпретации: ${{z}_{1}}, \ldots {{z}_{M}}$ – локальные модели на каждом устройстве, $\bar {z}$ – глобальная модель, полученная усреднением всех локальных моделей. Понятно, что нужно выбрать параметр регуляризации $\lambda $ достаточно большим, чтобы решения задач (4) и (5) были примерно одинаковыми: ${{z}_{m}} \approx \bar {z}$. Но имеет ли смысл брать $\lambda $ малым (например, когда $\lambda = 0$, мы имеем просто локальные модели)? Оказывается, да: такая постановка задачи с переменной $\lambda $, значение которой может варьироваться, породила целую тенденцию в персонализированном федеративном обучении – федеративное обучение со смешиванием (см. [7], [8]). Постановка (5) будет последней из формулировок задачи (1), которые будут исследоваться в рамках предлагаемого унифицированного анализа.

1.1. Экстраградиентный метод

Стохастический градиентный спуск по-прежнему является основным методом минимизации, он используется для большого количества задач машинного обучения, несмотря на наличие более современных методов. Основным же методом решения гладких вариационных неравенств является экстраградиентный метод (см. [9]). В простом виде методы такого рода записываются следующим образом:

(6)

${{z}^{{k + 1/2}}} = {\text{pro}}{{{\text{x}}}_{{\gamma h}}}({{z}^{k}} - \gamma {{g}^{k}}),\quad {{z}^{{k + 1}}} = {\text{pro}}{{{\text{x}}}_{{\gamma h}}}({{z}^{k}} - \gamma {{g}^{{k + 1/2}}}),$

где ${\text{pro}}{{{\text{x}}}_{{\gamma h}}}(z) = \arg {{\min }_{x}}\left\{ {\gamma h(x) + \frac{1}{2}{{{\left\| {z - x} \right\|}}^{2}}} \right\}$. В классическом, детерминированном, варианте ${{g}^{k}} = F({{z}^{k}})$ и ${{g}^{{k + 1/2}}} = F({{z}^{{k + 1/2}}})$. Этот метод оптимален с точностью до численных констант для гладких монотонных и сильно монотонных вариационных неравенств (см. [10]). Причем на практике этот метод показывает себя лучше, чем спуск с итерацией обычного вида ${{z}^{{k + 1}}} = {{z}^{k}} - \gamma {{g}^{k}}$. Более того, известно, что метод без дополнительного шага расходится для наиболее распространенных билинейных задач. Следовательно, вычисление ${{z}^{{k + 1/2}}}$ является ключевым. В настоящей работе для нашего унифицированного анализа мы используем метод (6) с несколько более сложной структурой:

(7)

${{\bar {z}}^{k}} = \tau {{z}^{k}} + (1 - \tau ){{w}^{k}},\quad {{z}^{{k + 1/2}}} = {\text{pro}}{{{\text{x}}}_{{\gamma h}}}({{\bar {z}}^{k}} - \gamma {{g}^{k}}),\quad {{z}^{{k + 1}}} = {\text{pro}}{{{\text{x}}}_{{\gamma h}}}({{\bar {z}}^{k}} - \gamma {{g}^{{k + 1/2}}}),$

где ${{w}^{{k + 1}}} = {{z}^{{k + 1}}}$ с вероятностью $(1 - \tau )$ или ${{w}^{k}}$ – иначе. Видно, что при $\tau = 0$ верно ${{w}^{k}} = {{z}^{k}}$, и метод (7) в точности соответствует (6). Метод (7) был впервые предложен в [11].

1.2. От минимизации к ВН

Метод SGD используется для решения задач минимизации с середины прошлого века (см. [12]) и с того времени был расширен огромным количеством различных модификаций. Это методы уменьшения дисперсии (см. [13]), квантования (см. [14]), координатные методы (см. [15]) и т.д. (различные варианты SGD см. в [16]). В отличие от задач минимизации, вариационные неравенства и седловые задачи не имеют такого широкого набора теоретических результатов, хотя базовый метод для задачи ВН и более сложен, и дает широкий простор для творчества. Но в то же время развитие тех же идей, что и для задач минимизации, для ВН происходит значительно медленнее, в том числе и из-за того, что ВН более общи и сложны в теоретическом анализе. Далее мы перечислим основные достижения в области решения ВН касательно конструирования методов, подобных уже существующим методам минимизации.

Базовые методы. Как отмечалось ранее, базовым методом решения ВН является экстраградиентный метод (см. [9]); еще более общая его версия называется Mirror Prox (см. [3]). Анализ в стохастическом случае с ограниченной дисперсией шума описан в [10]. Стоит обратить внимание на интересные модификации этого метода: с одним дополнительным вызовом оракула (см. [17]) и с повторным вызовом (см. [18]). Можно также причислить классические методы, отличающиеся по структуре от экстраградиентного из [19], [20].

Редукция дисперсии. Направление разработки методов редукции дисперсии для задач ВН и СТ развивалось, начиная с работы [21], где представлен метод, основанный на сильно выпукло–сильно вогнутых седлах (сильно монотонных ВН). Также в [22] был предложен метод для сильно монотонных ВН. Наконец, стоит выделить работу [11], которая пересекается с прошлыми результатами или повторяет их, предоставляя методы редукции дисперсии для монотонных и сильно монотонных ВН. Отметим, что приведенные выше методы сильно отличаются друг от друга, более того, они далеки от классической редукции дисперсии для задач минимизации.

Покомпонентные и квантизованные методы. Покомпонентные методы для задач СТ и ВН изучены не слишком хорошо. Можно выделить работы, посвященные конкретным покомпонентным методам для каких-то определенных классов задач СТ (см. [23], [24]), а также работы по безградиентным методам (см. [25]). Методы же с квантизацией, специализированные для задач СТ, до сих пор совсем не предлагались.

Локальные методы. Направление разработки локальных методов изучено совсем не в той мере (см. [26], [27]), как это сделано для задач минимизации. В настоящей работе мы обращаем внимание не на детерминированные методы типа Local SGD, а на рандомизированные, которые могут быть применены для решения задачи (5), например, как описанные в [7]. Суть этих методов в том, что мы с некоторой вероятностью вызываем и делаем шаг только по оракулу для $\Phi (Z)$, иначе обращаемся к $\lambda (Z - \bar {Z})$. Вызов $\Phi (Z)$ соответствует локальной итерации, а вызов $\lambda (Z - \bar {Z})$ – коммуникации.

1.3. Наш вклад

Унифицированный анализ. В настоящей работе предлагается унифицированный теоретический анализ для методов типа (6) и (7) в сильно монотонном и монотонном случаях. Анализ основан на параметризованных предположениях, поэтому он позволяет легко конструировать и анализировать огромное количество новых методов.

Улучшенные оценки для существующих методов. В исходном анализе Past ES из [17] в стохастическом сильно монотонном случае достигается сублинейная скорость сходимости, тогда как мы можем гарантировать линейную скорость в детерминированном члене и сублинейную в стохастическом члене. Более того, мы предоставляем оценки для Past ES и в стохастическом монотонном случае. Кроме того, мы покрываем результаты для некоторых других существующих методов или немного их обобщаем.

Пять новых методов. Более важным, чем обобщение других результатов, является получение новых надежных методов. В отличие от [16], к моменту написания которой большинство анализируемых там методов уже были описаны в других работах, в нашей работе более половины методов являются новыми. Это покомпонентные методы, методы с квантизацией, методы с сэмплированием по важности, локальные рандомизированные методы.

Эксперименты. Мы предоставляем сравнение методов на примере практической задачи, в котором демонстрируем, что предлагаемые нами новые методы могут превосходить по эффективности существующие. Эксперименты проводятся на искусственной билинейной задаче и в некоторых случаях на GAN.

2. ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ

Для начала введем основные определения. Мы используем аннотацию $\langle x,y\rangle : = \sum\nolimits_{i = 1}^n \,{{x}_{i}}{{y}_{i}}$ для скалярного произведения векторов $x,y \in {{\mathbb{R}}^{d}}$. Оно порождает ${{\ell }_{2}}$-норму в пространстве ${{\mathbb{R}}^{d}}$ в таком виде: $\left\| x \right\|: = \sqrt {\langle x,x\rangle } $.

2.1. Основные предположения

Далее нам потребуются два основных предположения. Наше первое предположение относится к монотонности оператора $F$ из (1) и сильной выпуклости $g$. В частности, мы рассматриваем строго монотонный и монотонный случаи. С точки зрения задачи поиска седловой точки это соответствует сильно выпукло-сильно вогнутому и выпукло-вогнутому случаям.

Предположение 1. (СМ) Сильная монотонность/сильная выпуклость. Существуют неотрицательные ${{\mu }_{F}},{{\mu }_{h}}$ такие, что ${{\mu }_{h}} + {{\mu }_{F}} > 0$ и следующие неравенства верны для всех ${{z}_{1}},{{z}_{2}} \in \mathcal{Z}$:

$\left\langle {F({{z}_{1}}) - F({{z}_{2}}),{{z}_{1}} - {{z}_{2}}} \right\rangle \geqslant {{\mu }_{F}}{{\left\| {{{z}_{1}} - {{z}_{2}}} \right\|}^{2}},$

$h({{z}_{1}}) - h({{z}_{2}}) - \left\langle {\nabla h({{z}_{2}}),{{z}_{1}} - {{z}_{2}}} \right\rangle \geqslant \frac{{{{\mu }_{h}}}}{2}{{\left\| {{{z}_{1}} - {{z}_{2}}} \right\|}^{2}}.$

(M) Монотонность/выпуклость. Для всех ${{z}_{1}},{{z}_{2}} \in \mathcal{Z}$

$\left\langle {F({{z}_{1}}) - F({{z}_{2}}),{{z}_{1}} - {{z}_{2}}} \right\rangle \geqslant 0,\quad h({{z}_{1}}) - h({{z}_{2}}) - \left\langle {\nabla h({{z}_{2}}),{{z}_{1}} - {{z}_{2}}} \right\rangle \geqslant 0.$

Второе предположение ключевое и позволяет нам рассматривать разные методы для решения ВН в унифицированном виде. Суть этого предположения проста, аналогично с [16], мы вводим неравенства для основных членов, которые необходимо оценить при анализе экстра-градиентных методов.

Предположение 2. Пусть последовательности $\{ {{z}^{k}}\} $ и $\{ {{w}^{k}}\} $ были получены в результате случайных итераций (7). Предположим, что стохастические операторы ${{g}^{{k + 1/2}}}$ не смещены для всех $k$:

(10)

$\mathbb{E}\left[ {{{g}^{{k + 1/2}}}\,|\,{{z}^{{k + 1/2}}}} \right] = F({{z}^{{k + 1/2}}}).$

Далее предположим, что существуют неотрицательные $A,\;B,\;C,\;E,$ ${{D}_{1}},\;{{D}_{2}},\;{{D}_{3}}$ и $\rho \in (0;1]$ и рандомная последовательность $\{ {{\sigma }^{k}}\} $ (может быть нулевой), что выполняются следующие неравенства:

$\mathbb{E}\left[ {{{{\left\| {{{g}^{{k + 1/2}}} - {{g}^{k}}} \right\|}}^{2}}} \right] \leqslant A{\kern 1pt} \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + B{\kern 1pt} \mathbb{E}\left[ {\sigma _{k}^{2}} \right] + {{D}_{1}},$

(11)

$\mathbb{E}\left[ {\sigma _{{k + 1}}^{2}} \right] \leqslant (1 - \rho ){\kern 1pt} \mathbb{E}\left[ {\sigma _{k}^{2}} \right] + C{\kern 1pt} \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + {{D}_{2}},$

$\mathbb{E}\left[ {{{{\left\| {{{g}^{{k + 1/2}}} - F({{z}^{{k + 1/2}}})} \right\|}}^{2}}} \right] \leqslant E{\kern 1pt} \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + {{D}_{3}}.$

Похожие неравенства могут быть найдены в анализе методов (6) и (7) (см. [10], [11]). Это первая работа, которая рассматривает вариационные неравенства в такой общности.

2.2. Унифицированная теорема

Мы готовы представить основной теоретический результат данной статьи. Для начала введем функцию Ляпунова, с помощью которой будем анализировать сходимость:

${{V}^{k}} = \tau {{\left\| {{{z}^{{k + 1}}} - z{\kern 1pt} *} \right\|}^{2}} + {{\left\| {{{w}^{{k + 1}}} - z{\kern 1pt} *} \right\|}^{2}} + T{{\gamma }^{2}}\sigma _{k}^{2},$

где константа $T > 0$. Этот критерий используется в сильно монотонном случае.

Для монотонного случая используется другой критерий – функция зазора (см. [3], [10]):

${\text{Gap}}(z) = \mathop {\max }\limits_{u \in \mathcal{C}} \left[ {\langle F(u),z - u\rangle + h(z) - h(u)} \right].$

Здесь максимум берется не по всему множеству $\mathcal{Z}$ (как в классической версии), а по $\mathcal{C}$ – компактному подмножеству множества $\mathcal{Z}$. Таким образом, мы можем рассматривать неограниченные множества $\mathcal{Z}$. Это допустимо, так как такой вариант критерия верен, если решение $z{\kern 1pt} *$ лежит в $\mathcal{C}$ (см. [20]).

Теорема 1. Пусть выполнено предположение $2$. Тогда, если дополнительно выполняется одно из условий предположения $1$, верны следующие оценки:

• для сильно монотонного/сильно выпуклого случаев с $\gamma \leqslant \min \left\{ {\frac{{\sqrt {1 - \tau } }}{{2\sqrt {2A + TC} }};\frac{{1 - \tau }}{{4\left( {{{\mu }_{F}} + {{\mu }_{h}}} \right)}}} \right\}$ и $T \geqslant \frac{{4B}}{\rho }$:

$\mathbb{E}\left[ {{{V}_{K}}} \right] \leqslant \max \left\{ {{{{\left( {1 - \gamma \frac{{{{\mu }_{F}} + {{\mu }_{h}}}}{{16}}} \right)}}^{{K - 1}}};{{{\left( {1 - \frac{\rho }{2}} \right)}}^{{K - 1}}}} \right\}{{V}_{0}} + \frac{{{{\gamma }^{2}}(2{{D}_{1}} + T{{D}_{2}})}}{{\min \left\{ {\gamma \frac{{{{\mu }_{F}} + {{\mu }_{h}}}}{{16}};\frac{\rho }{2}} \right\}}};$

• для монотонного/выпуклого случаев с $\gamma \leqslant \frac{{\sqrt {1 - \tau } }}{{2\sqrt {2A + TC + E} }}$ и $T \geqslant \frac{{2B}}{\rho }$

$\mathbb{E}\left[ {{\text{Gap}}({{{\bar {z}}}^{K}})} \right] \leqslant \frac{{8\mathop {\max }\limits_{u \in \mathcal{C}} \left[ {{{{\left\| {{{z}^{0}} - u} \right\|}}^{2}}} \right] + 4{{\gamma }^{2}}T\sigma _{0}^{2}}}{{\gamma K}} + \gamma (7{{D}_{1}} + 3T{{D}_{2}} + {{D}_{3}}),$

где ${{\bar {z}}^{K}} = \frac{1}{K}\sum\nolimits_{k = 0}^{K - 1} {{{z}^{{k + 1/2}}}} $.

Метод (7) в условиях предположения 2 сходится линейно в сильно монотонном случае и сублинейно $( \sim {\kern 1pt} 1{\text{/}}K)$ в монотонном случае до определенного радиуса осцилляции сходимости, который зависит от второго члена в теореме 1. Формально можно добиться сходимости по этому члену за фиксированное число шагов. Для этого необходимо правильно выбрать шаг $\gamma $ (см. [28]). Для некоторых методов мы используем это, чтобы получить классические оценки сходимости (см. подробнее об этом в п. 2.3). Оптимальный выбор шага для каждого метода находится в приложении, соответствующем этому методу.

Далее приведем доказательство теоремы 1. Для начала докажем лемму.

Лемма 1. Пусть $h$ ${{\mu }_{h}}$ – сильно выпуклая и ${{z}^{ + }} = {\text{pro}}{{{\text{x}}}_{{\gamma h}}}(z)$. Тогда для всех $x \in {{\mathbb{R}}^{d}}$ справедливо следующее неравенство:

$\left\langle {{{z}^{ + }} - z,x - {{z}^{ + }}} \right\rangle \geqslant \gamma \left( {h({{z}^{ + }}) - h(x) + \frac{{{{\mu }_{h}}}}{2}{{{\left\| {{{z}^{ + }} - x} \right\|}}^{2}}} \right).$

Доказательство. Мы используем $\gamma \mu $-сильно выпуклость функции $\gamma h$ (9):

$\gamma \left( {h(x) - h({{z}^{ + }})} \right) - \left\langle {\gamma \nabla h({{z}^{ + }}),x - {{z}^{ + }}} \right\rangle \geqslant \frac{{\gamma {{\mu }_{h}}}}{2}{{\left\| {x - {{z}^{ + }}} \right\|}^{2}}.$

Вместе с определением ${\text{prox}}$ и необходимым условием оптимума: $\gamma \nabla h({{z}^{ + }}) = z - {{z}^{ + }}$, это завершает доказательство.

Доказательство теоремы 1. По лемме 1 для ${{z}^{{k + 1/2}}} = {\text{pro}}{{{\text{x}}}_{{\gamma h}}}({{\bar {z}}^{k}} - \gamma {{g}^{k}})$ и ${{z}^{{k + 1}}} = {\text{pro}}{{{\text{x}}}_{{\gamma h}}}({{\bar {z}}^{k}} - \gamma {{g}^{{k + 1/2}}})$ для $x = u$ получаем

$\begin{gathered} \left\langle {{{z}^{{k + 1}}} - {{{\bar {z}}}^{k}} + \gamma {{g}^{{k + 1/2}}},u - {{z}^{{k + 1}}}} \right\rangle \geqslant \gamma \left( {h({{z}^{{k + 1}}}) - h(u) + \frac{{{{\mu }_{h}}}}{2}{{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}}} \right), \\ \left\langle {{{z}^{{k + 1/2}}} - {{{\bar {z}}}^{k}} + \gamma {{g}^{k}},{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\rangle \geqslant \gamma \left( {h({{z}^{{k + 1/2}}}) - h({{z}^{{k + 1}}}) + \frac{{{{\mu }_{h}}}}{2}{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right). \\ \end{gathered} $

Далее суммируем два неравенства и проводим некоторые перестановки:

$\begin{gathered} \left\langle {{{z}^{{k + 1}}} - {{{\bar {z}}}^{k}},u - {{z}^{{k + 1}}}} \right\rangle + \left\langle {{{z}^{{k + 1/2}}} - {{{\bar {z}}}^{k}},{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\rangle + \gamma \left\langle {{{g}^{{k + 1/2}}} - {{g}^{k}},{{z}^{{k + 1/2}}} - {{z}^{{k + 1}}}} \right\rangle + \\ + \;\gamma \left\langle {{{g}^{{k + 1/2}}},u - {{z}^{{k + 1/2}}}} \right\rangle \geqslant \gamma \left( {h({{z}^{{k + 1/2}}}) - h(u) + \frac{{{{\mu }_{h}}}}{2}{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}} + \frac{{{{\mu }_{h}}}}{2}{{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}}} \right). \\ \end{gathered} $

Умножая на 2 и используя определение ${{\bar {z}}^{k}}$ из (7), получаем

$\begin{gathered} 2\tau \left\langle {{{z}^{{k + 1}}} - {{z}^{k}},u - {{z}^{{k + 1}}}} \right\rangle + 2(1 - \tau )\left\langle {{{z}^{{k + 1}}} - {{w}^{k}},u - {{z}^{{k + 1}}}} \right\rangle + 2\tau \left\langle {{{z}^{{k + 1/2}}} - {{z}^{k}},{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\rangle + \\ + \;2(1 - \tau )\left\langle {{{z}^{{k + 1/2}}} - {{w}^{k}},{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\rangle + 2\gamma \left\langle {{{g}^{{k + 1/2}}} - {{g}^{k}},{{z}^{{k + 1/2}}} - {{z}^{{k + 1}}}} \right\rangle + 2\gamma \left\langle {{{g}^{{k + 1/2}}},u - {{z}^{{k + 1/2}}}} \right\rangle \geqslant \\ \, \geqslant 2\gamma \left( {h({{z}^{{k + 1/2}}}) - h(u) + \frac{{{{\mu }_{h}}}}{2}{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}} + \frac{{{{\mu }_{h}}}}{2}{{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}}} \right). \\ \end{gathered} $

Для первой и второй строки используем выражение $2\langle a,b\rangle = {{\left\| {a + b} \right\|}^{2}} - {{\left\| a \right\|}^{2}} - {{\left\| b \right\|}^{2}}$ и получаем

$\begin{gathered} \tau \left( {{{{\left\| {{{z}^{k}} - u} \right\|}}^{2}} - {{{\left\| {{{z}^{{k + 1}}} - {{z}^{k}}} \right\|}}^{2}} - {{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}}} \right) + (1 - \tau )\left( {{{{\left\| {{{w}^{k}} - u} \right\|}}^{2}} - {{{\left\| {{\text{|}}{{z}^{{k + 1}}} - {{w}^{k}}} \right\|}}^{2}} - {{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}}} \right) + \\ + \;\tau \left( {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{k}}} \right\|}}^{2}} - {{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}} - {{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right) + (1 - \tau )\left( {{{{\left\| {{{z}^{{k + 1}}} - {{w}^{k}}} \right\|}}^{2}} - {{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right. - \\ \end{gathered} $

$\begin{gathered} - \;\left. {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right) + 2\gamma \left\langle {{{g}^{{k + 1/2}}} - {{g}^{k}},{{z}^{{k + 1/2}}} - {{z}^{{k + 1}}}} \right\rangle + 2\gamma \left\langle {{{g}^{{k + 1/2}}},u - {{z}^{{k + 1/2}}}} \right\rangle \geqslant \\ \geqslant 2\gamma \left( {h({{z}^{{k + 1/2}}}) - h(u) + \frac{{{{\mu }_{h}}}}{2}{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}} + \frac{{{{\mu }_{h}}}}{2}{{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}}} \right). \\ \end{gathered} $

Небольшая перестановка дает

$\begin{gathered} (1 + \gamma {{\mu }_{h}}){{\left\| {{{z}^{{k + 1}}} - u} \right\|}^{2}} \leqslant \tau {{\left\| {{{z}^{k}} - u} \right\|}^{2}} + (1 - \tau ){{\left\| {{{w}^{k}} - u} \right\|}^{2}} - \tau {{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}^{2}} - (1 - \tau ){{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}^{2}} - \\ - \;(1 + \gamma {{\mu }_{h}}){{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}^{2}} + 2\gamma \left\langle {{{g}^{{k + 1/2}}} - {{g}^{k}},{{z}^{{k + 1/2}}} - {{z}^{{k + 1}}}} \right\rangle - 2\gamma \left\langle {{{g}^{{k + 1/2}}},{{z}^{{k + 1/2}}} - u} \right\rangle - 2\gamma (h({{z}^{{k + 1/2}}}) - h(u)). \\ \end{gathered} $

Из простого факта: $2\langle a,b\rangle \leqslant \eta {{\left\| a \right\|}^{2}} + \frac{1}{\eta }{{\left\| b \right\|}^{2}}$ с $a = {{g}^{{k + 1/2}}} - {{g}^{k}},$ $b = {{z}^{{k + 1/2}}} - {{z}^{{k + 1}}},$ $\eta = 2\gamma $, следует

(12)

$\begin{gathered} (1 + \gamma {{\mu }_{h}}){{\left\| {{{z}^{{k + 1}}} - u} \right\|}^{2}} \leqslant \tau {{\left\| {{{z}^{k}} - u} \right\|}^{2}} + (1 - \tau ){{\left\| {{{w}^{k}} - u} \right\|}^{2}} - \tau {{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}^{2}} - (1 - \tau ){{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}^{2}} - \\ \, - \left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right){{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}^{2}} + 2{{\gamma }^{2}}{{\left\| {{{g}^{{k + 1/2}}} - {{g}^{k}}} \right\|}^{2}} - 2\gamma \left\langle {{{g}^{{k + 1/2}}},{{z}^{{k + 1/2}}} - u} \right\rangle - 2\gamma (h({{z}^{{k + 1/2}}}) - h(u)). \\ \end{gathered} $

Далее рассмотрим разные случаи теоремы. Начнем с сильно монотонного/выпуклого случая. Заменим $u = z{\kern 1pt} *$, возьмем полное математическое ожидание и получим

$\begin{gathered} (1 + \gamma {{\mu }_{h}})\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] \leqslant \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + (1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] - \\ \, - (1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] - \left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] + 2{{\gamma }^{2}}\mathbb{E}\left[ {{{{\left\| {{{g}^{{k + 1/2}}} - {{g}^{k}}} \right\|}}^{2}}} \right] - \\ \end{gathered} $

$\begin{gathered} - \;2\gamma \mathbb{E}\left[ {\left\langle {{{g}^{{k + 1/2}}},{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\rangle + h({{z}^{{k + 1/2}}}) - h(z{\kern 1pt} *)} \right] = \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + (1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \\ - \;(1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] - \left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] + 2{{\gamma }^{2}}\mathbb{E}\left[ {{{{\left\| {{{g}^{{k + 1/2}}} - {{g}^{k}}} \right\|}}^{2}}} \right] - \\ - \;2\gamma \mathbb{E}\left[ {\left\langle {\mathbb{E}[{{g}^{{k + 1/2}}}\,|\,{{z}^{{k + 1/2}}}],{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\rangle + h({{z}^{{k + 1/2}}}) - h(z{\kern 1pt} *)} \right]. \\ \end{gathered} $

Далее применим предположение 2, а именно, (10) и (11):

$\begin{gathered} (1 + \gamma {{\mu }_{h}})\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] \leqslant \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + (1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] - \\ - \;(1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] - \left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] + 2{{\gamma }^{2}}\left( {A\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + B\mathbb{E}\left[ {\sigma _{k}^{2}} \right] + {{D}_{1}}} \right) - \\ \end{gathered} $

$\begin{gathered} \, - 2\gamma \mathbb{E}\left[ {\left\langle {F({{z}^{{k + 1/2}}}),{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\rangle + h({{z}^{{k + 1/2}}}) - h(z{\kern 1pt} *)} \right] = \tau \mathbb{E}\left[ {{{{\left| {{{z}^{k}} - z{\kern 1pt} *} \right|}}^{2}}} \right] + \left( {1 - \tau } \right)\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \\ - \;\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] - \left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] - \left( {(1 - \tau ) - 2{{\gamma }^{2}}A} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + 2{{\gamma }^{2}}B\mathbb{E}\left[ {\sigma _{k}^{2}} \right] - \\ \, - 2\gamma \mathbb{E}\left[ {\left\langle {F({{z}^{{k + 1/2}}}),{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\rangle + h({{z}^{{k + 1/2}}}) - h(z{\kern 1pt} *)} \right] + 2{{\gamma }^{2}}{{D}_{1}}. \\ \end{gathered} $

Свойство решения (1) дает

$\begin{gathered} (1 + \gamma {{\mu }_{h}})\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] \leqslant \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \left( {1 - \tau } \right)\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] - \\ \, - \left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] - \left( {(1 - \tau ) - 2{{\gamma }^{2}}A} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + 2{{\gamma }^{2}}B\mathbb{E}\left[ {\sigma _{k}^{2}} \right] - \\ \, - 2\gamma \mathbb{E}\left[ {\left\langle {F({{z}^{{k + 1/2}}}) - F(z{\kern 1pt} *),{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\rangle } \right] + 2{{\gamma }^{2}}{{D}_{1}}. \\ \end{gathered} $

И по предположению 1 в сильно монотонном случае получим

$\begin{gathered} (1 + \gamma {{\mu }_{h}})\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] \leqslant \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \left( {1 - \tau } \right)\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] - \\ \, - \left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] - \left( {(1 - \tau ) - 2{{\gamma }^{2}}A} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + 2{{\gamma }^{2}}B\mathbb{E}\left[ {\sigma _{k}^{2}} \right] - \\ \, - 2\gamma {{\mu }_{F}}\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + 2{{\gamma }^{2}}{{D}_{1}}. \\ \end{gathered} $

С другой стороны,

$\mathbb{E}\left[ {{{{\left\| {{{w}^{{k + 1}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] = (1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \tau \mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right].$

Суммируя два предыдущих неравенства, имеем

Добавив $\mathbb{E}\left[ {{{\gamma }^{2}}T\sigma _{{k + 1}}^{2}} \right]$, мы получим функцию Ляпунова с левой стороны:

$\begin{gathered} \mathbb{E}\left[ {{{V}_{{k + 1}}}} \right] = \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \mathbb{E}\left[ {{{{\left\| {{{w}^{{k + 1}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \mathbb{E}\left[ {{{\gamma }^{2}}T\sigma _{{k + 1}}^{2}} \right] \leqslant \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \\ - \;\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] - 2\gamma {{\mu }_{F}}\mathbb{E}{\text{||}}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \gamma {{\mu }_{h}}\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] - \\ \, - \left( {(1 - \tau ) - 2{{\gamma }^{2}}A} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + 2{{\gamma }^{2}}B\mathbb{E}\left[ {\sigma _{k}^{2}} \right] + \mathbb{E}\left[ {{{\gamma }^{2}}T\sigma _{{k + 1}}^{2}} \right] + 2{{\gamma }^{2}}{{D}_{1}}. \\ \end{gathered} $

С предположением 2 для ${{\sigma }_{{k + 1}}}$ получаем

$\begin{gathered} \mathbb{E}\left[ {{{V}_{{k + 1}}}} \right] \leqslant \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \left( {1 - \rho + \frac{{2B}}{T}} \right)\mathbb{E}\left[ {{{\gamma }^{2}}T\sigma _{k}^{2}} \right] - \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] - \\ - \;\gamma {{\mu }_{h}}\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] - \left( {(1 - \tau ) - 2{{\gamma }^{2}}A - {{\gamma }^{2}}TC} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] - \\ \, - 2\gamma {{\mu }_{F}}\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + {{\gamma }^{2}}(2{{D}_{1}} + T{{D}_{2}}). \\ \end{gathered} $

Используем $ - {{\left\| {{{z}^{{k + 1}}} - z{\kern 1pt} *} \right\|}^{2}} \leqslant - \frac{1}{2}{{\left\| {{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\|}^{2}} + {{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}^{2}}$, что дает

$\begin{gathered} \mathbb{E}\left[ {{{V}_{{k + 1}}}} \right] \leqslant \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \left( {1 - \rho + \frac{{2B}}{T}} \right)\mathbb{E}\left[ {{{\gamma }^{2}}T\sigma _{k}^{2}} \right] - \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] - \\ \, - \left( {(1 - \tau ) - 2{{\gamma }^{2}}A - {{\gamma }^{2}}TC} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] - \left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] - \\ - \;\gamma \left( {2{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{2}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \gamma \left( {2{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{2}} \right)(1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + {{\gamma }^{2}}(2{{D}_{1}} + T{{D}_{2}}). \\ \end{gathered} $

Из простых фактов: ${{\left\| {{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\|}^{2}} \geqslant \frac{1}{2}{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}^{2}} - {{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}^{2}}$ и ${{\left\| {{\text{|}}{{z}^{{k + 1/2}}} - z{\kern 1pt} *} \right\|}^{2}} \geqslant $ $\frac{1}{2}{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}^{2}} - $ $ - {{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}^{2}}$, следует

$\mathbb{E}\left[ {{{V}_{{k + 1}}}} \right] \leqslant \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z} \right\|}}^{2}}} \right] + \mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z} \right\|}}^{2}}} \right] + \left( {1 - \rho + \frac{{2B}}{T}} \right)\mathbb{E}\left[ {{{\gamma }^{2}}T\sigma _{k}^{2}} \right] - $

(13)

$\begin{gathered} - \;\left( {(1 - \tau ) - 2{{\gamma }^{2}}A - {{\gamma }^{2}}TC - \gamma \left( {2{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{2}} \right)(1 - \tau )} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] - \\ - \;\left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] - \left( {1 - \gamma \left( {2{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{2}} \right)} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] - \\ \end{gathered} $

$ - \;\gamma \left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z} \right\|}}^{2}}} \right] - \gamma \left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)(1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z} \right\|}}^{2}}} \right] + {{\gamma }^{2}}(2{{D}_{1}} + T{{D}_{2}}).$

Далее работаем с предпоследней строкой (13):

$\begin{gathered} - \gamma \left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \gamma \left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)(1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] = - \frac{\gamma }{2}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \\ - \;\frac{\gamma }{2}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \gamma \left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)(1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \leqslant - \frac{\gamma }{2}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \\ \end{gathered} $

(14)

$\begin{gathered} - \;\frac{\gamma }{4}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \frac{\gamma }{2}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - {{w}^{k}}} \right\|}}^{2}}} \right] - \gamma \left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)(1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] \leqslant \\ \leqslant - \frac{\gamma }{4}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \frac{\gamma }{4}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \frac{\gamma }{2}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - {{w}^{k}}} \right\|}}^{2}}} \right] \leqslant \\ \end{gathered} $

$\begin{gathered} \leqslant - \frac{\gamma }{4}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \frac{\gamma }{4}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \gamma \left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] + \\ \, + \gamma \left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right]. \\ \end{gathered} $

Подставив (14) в (13), получим

$\mathbb{E}\left[ {{{V}_{{k + 1}}}} \right] \leqslant \tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \left( {1 - \rho + \frac{{2B}}{T}} \right)\mathbb{E}\left[ {{{\gamma }^{2}}T\sigma _{k}^{2}} \right] - $

(15)

$\begin{gathered} - \;\left( {(1 - \tau ) - 2{{\gamma }^{2}}A - {{\gamma }^{2}}TC - \gamma \left( {2{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{2}} \right)} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] - \left( {\frac{1}{2} + \gamma {{\mu }_{h}}} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] - \\ \, - \left( {1 - 3\gamma \left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] - \frac{\gamma }{4}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] - \\ \end{gathered} $

$\, - \frac{\gamma }{4}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)\mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + {{\gamma }^{2}}(2{{D}_{1}} + T{{D}_{2}}).$

Остается только выбрать $\gamma \leqslant \min \left\{ {\frac{{\sqrt {1 - \tau } }}{{2\sqrt {2A + TC} }};\frac{{1 - \tau }}{{4\left( {{{\mu }_{F}} + {{\mu }_{h}}} \right)}}} \right\}$, $T \geqslant \frac{{4B}}{\rho }$ и получить

$\mathbb{E}\left[ {{{V}_{{k + 1}}}} \right] \leqslant \left( {1 - \frac{\gamma }{4}\left( {{{\mu }_{F}} + \frac{{{{\mu }_{h}}}}{4}} \right)} \right)\left( {\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right] + \mathbb{E}\left[ {{{{\left\| {{{w}^{k}} - z{\kern 1pt} *} \right\|}}^{2}}} \right]} \right) + \left( {1 - \frac{\rho }{2}} \right)\mathbb{E}\left[ {{{\gamma }^{2}}T\sigma _{k}^{2}} \right] + {{\gamma }^{2}}(2{{D}_{1}} + T{{D}_{2}}).$

В результате

$\mathbb{E}\left[ {{{V}_{{k + 1}}}} \right] \leqslant \max \left\{ {\left( {1 - \gamma \frac{{{{\mu }_{F}} + {{\mu }_{h}}}}{{16}}} \right);\left( {1 - \frac{\rho }{2}} \right)} \right\}\mathbb{E}\left[ {{{V}_{k}}} \right] + {{\gamma }^{2}}(2{{D}_{1}} + T{{D}_{2}}).$

Выполнение рекурсивных переходов завершает доказательство.

Далее рассмотрим монотонный/выпуклый случай (${{\mu }_{h}} = 0$, ${{\mu }_{F}} = 0$). Начнем с (12) с дополнительным обозначением ${\text{gap}}({{z}^{{k + 1/2}}},u) = \langle F({{z}^{{k + 1/2}}}),{{z}^{{k + 1/2}}} - u\rangle + h({{z}^{{k + 1/2}}}) - h(u)$:

$\begin{gathered} 2\gamma {\text{gap}}({{z}^{{k + 1/2}}},u) + {{\left\| {{{z}^{{k + 1}}} - u} \right\|}^{2}} \leqslant \tau {{\left\| {{{z}^{k}} - u} \right\|}^{2}} + (1 - \tau ){{\left\| {{{w}^{k}} - u} \right\|}^{2}} - \tau {{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}^{2}} - \\ - \;(1 - \tau ){{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}^{2}} + 2{{\gamma }^{2}}{{\left\| {{{g}^{{k + 1/2}}} - {{g}^{k}}} \right\|}^{2}} - 2\gamma \left\langle {{{g}^{{k + 1/2}}} - F({{z}^{{k + 1/2}}}),{{z}^{{k + 1/2}}} - u} \right\rangle . \\ \end{gathered} $

Добавив к обеим частям ${{\left\| {{{w}^{{k + 1}}} - u} \right\|}^{2}}$ и проведя некоторые перестановки, получим

$\begin{gathered} 2\gamma {\text{gap}}({{z}^{{k + 1/2}}},u) \leqslant \left[ {\tau {{{\left\| {{{z}^{k}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{k}} - u} \right\|}}^{2}}} \right] - \left[ {\tau {{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{{k + 1}}} - u} \right\|}}^{2}}} \right] - \tau {{\left\| {{{w}^{k}} - u} \right\|}^{2}} - \\ - \;(1 - \tau ){{\left\| {{{z}^{{k + 1}}} - u} \right\|}^{2}} + {{\left\| {{{w}^{{k + 1}}} - u} \right\|}^{2}} - \tau {{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}^{2}} - (1 - \tau ){{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}^{2}} + \\ \, + 2{{\gamma }^{2}}{{\left\| {{{g}^{{k + 1/2}}} - {{g}^{k}}} \right\|}^{2}} - 2\gamma \left\langle {{{g}^{{k + 1/2}}} - F({{z}^{{k + 1/2}}}),{{z}^{{k + 1/2}}} - u} \right\rangle . \\ \end{gathered} $

Просуммируем по $k = 0,1, \ldots ,K - 1$, возьмем максимум от обеих частей по $z \in \mathcal{C}$, далее возьмем математическое ожидание и получим

$\begin{gathered} 2\gamma \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \,{\text{gap}}({{z}^{{k + 1/2}}},u)} \right] \leqslant \mathop {\max }\limits_{u \in \mathcal{C}} \left[ {\tau {{{\left\| {{{z}^{0}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{0}} - u} \right\|}}^{2}}} \right] + \\ \, + \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ { - \tau {{{\left\| {{{w}^{k}} - u} \right\|}}^{2}} - (1 - \tau ){{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{{k + 1}}} - u} \right\|}}^{2}}} \right]} \right] - \sum\limits_{k = 0}^{K - 1} \left[ {\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] + } \right. \\ + \;(1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] - \left. {2{{\gamma }^{2}}\mathbb{E}\left[ {{{{\left\| {{{g}^{{k + 1/2}}} - {{g}^{k}}} \right\|}}^{2}}} \right]} \right] + 2\gamma \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ {\left\langle {{{g}^{{k + 1/2}}} - F({{z}^{{k + 1/2}}}),u - {{z}^{{k + 1/2}}}} \right\rangle } \right]} \right]. \\ \end{gathered} $

Используя предположение 2 для $\mathbb{E}\left[ {{{{\left\| {{{g}^{{k + 1/2}}} - {{g}^{k}}} \right\|}}^{2}}} \right]$, получаем

$\begin{gathered} 2\gamma \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \,{\text{gap}}({{z}^{{k + 1/2}}},u)} \right] \leqslant \mathop {\max }\limits_{u \in \mathcal{C}} \left[ {\tau {{{\left\| {{{z}^{0}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{0}} - u} \right\|}}^{2}}} \right] + \\ + \;\mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ { - \tau {{{\left\| {{{w}^{k}} - u} \right\|}}^{2}} - (1 - \tau ){{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{{k + 1}}} - u} \right\|}}^{2}}} \right]} \right] - \sum\limits_{k = 0}^{K - 1} \left[ {\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right]} \right. + \\ \, + \left. {(1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] - 2{{\gamma }^{2}}\left( {A{\kern 1pt} \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + B{\kern 1pt} \mathbb{E}\left[ {\sigma _{k}^{2}} \right] + {{D}_{1}}} \right)} \right] + \\ + \;2\gamma \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ {\left\langle {{{g}^{{k + 1/2}}} - F({{z}^{{k + 1/2}}}),u - {{z}^{{k + 1/2}}}} \right\rangle } \right]} \right]. \\ \end{gathered} $

Добавим и вычтем $\sum\nolimits_{k = 0}^{K - 1} {\left[ {{{\gamma }^{2}}T\mathbb{E}\left[ {\sigma _{{k + 1}}^{2}} \right]} \right]} $ и применим предположение 2 для ${{\sigma }_{k}}$, что дает

$\begin{gathered} 2\gamma \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \,{\text{gap}}({{z}^{{k + 1/2}}},u)} \right] \leqslant \mathop {\max }\limits_{u \in \mathcal{C}} \left[ {\tau {{{\left\| {{{z}^{0}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{0}} - u} \right\|}}^{2}}} \right] + \sum\limits_{k = 0}^{K - 1} \left[ {{{\gamma }^{2}}T\mathbb{E}\left[ {\sigma _{{k + 1}}^{2}} \right]} \right] - \sum\limits_{k = 0}^{K - 1} \left[ {{{\gamma }^{2}}T\mathbb{E}\left[ {\sigma _{{k + 1}}^{2}} \right]} \right] + \\ \, + \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ { - \tau {{{\left\| {{{w}^{k}} - u} \right\|}}^{2}} - (1 - \tau ){{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{{k + 1}}} - u} \right\|}}^{2}}} \right]} \right] - \sum\limits_{k = 0}^{K - 1} \left[ {\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right] + } \right. \\ \end{gathered} $

$\begin{gathered} \, + \left. {(1 - \tau - 2{{\gamma }^{2}}A)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right]} \right] + 2{{\gamma }^{2}}K{{D}_{1}} + \sum\limits_{k = 0}^{K - 1} \left[ {2{{\gamma }^{2}}B\mathbb{E}\left[ {\sigma _{k}^{2}} \right]} \right] + \\ + \;2\gamma \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ {\left\langle {{{g}^{{k + 1/2}}} - F({{z}^{{k + 1/2}}}),u - {{z}^{{k + 1/2}}}} \right\rangle } \right]} \right] \leqslant \mathop {\max }\limits_{u \in \mathcal{C}} \left[ {\tau {{{\left\| {{{z}^{0}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{0}} - u} \right\|}}^{2}}} \right] + \\ \end{gathered} $

$\begin{gathered} \, + \sum\limits_{k = 0}^{K - 1} \left[ {{{\gamma }^{2}}T\left( {(1 - \rho )\mathbb{E}\left[ {\sigma _{k}^{2}} \right] + C\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + {{D}_{2}}} \right)} \right] - \sum\limits_{k = 0}^{K - 1} \left[ {{{\gamma }^{2}}T\mathbb{E}\left[ {\sigma _{{k + 1}}^{2}} \right]} \right] + \\ \, + \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ { - \tau {{{\left\| {{{w}^{k}} - u} \right\|}}^{2}} - (1 - \tau ){{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{{k + 1}}} - u} \right\|}}^{2}}} \right]} \right] - \sum\limits_{k = 0}^{K - 1} \left[ {\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right]} \right. + \\ \end{gathered} $

$\begin{gathered} \, + \left. {(1 - \tau - 2{{\gamma }^{2}}A)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right]} \right] + 2{{\gamma }^{2}}K{{D}_{1}} + \sum\limits_{k = 0}^{K - 1} \left[ {2{{\gamma }^{2}}B\mathbb{E}\left[ {\sigma _{k}^{2}} \right]} \right] + \\ + \;2\gamma \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ {\left\langle {{{g}^{{k + 1/2}}} - F({{z}^{{k + 1/2}}}),u - {{z}^{{k + 1/2}}}} \right\rangle } \right]} \right] = \mathop {\max }\limits_{u \in \mathcal{C}} \left[ {\tau {{{\left\| {{{z}^{0}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{0}} - u} \right\|}}^{2}}} \right] + \\ \end{gathered} $

$\begin{gathered} \, + \sum\limits_{k = 0}^{K - 1} \left[ {{{\gamma }^{2}}T\left( {1 + \frac{{2B}}{T} - \rho } \right)\mathbb{E}\left[ {\sigma _{k}^{2}} \right]} \right] - \sum\limits_{k = 0}^{K - 1} \left[ {{{\gamma }^{2}}T\mathbb{E}\left[ {\sigma _{{k + 1}}^{2}} \right]} \right] + \\ + \;\mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ { - \tau {{{\left\| {{{w}^{k}} - u} \right\|}}^{2}} - (1 - \tau ){{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{{k + 1}}} - u} \right\|}}^{2}}} \right]} \right] - \sum\limits_{k = 0}^{K - 1} \left[ {\tau \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{z}^{k}}} \right\|}}^{2}}} \right]} \right. + \\ \end{gathered} $

$\begin{gathered} + \;\left. {(1 - \tau - {{\gamma }^{2}}(2A + TC))\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right]} \right] + {{\gamma }^{2}}K(2{{D}_{1}} + T{{D}_{2}}) + \\ \, + 2\gamma \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ {\left\langle {{{g}^{{k + 1/2}}} - F({{z}^{{k + 1/2}}}),u - {{z}^{{k + 1/2}}}} \right\rangle } \right]} \right]. \\ \end{gathered} $

С $\gamma \leqslant \frac{{\sqrt {1 - \tau } }}{{\sqrt {2A + TC} }}$ и $T \geqslant \frac{{2B}}{\rho }$ получим

(16)

$\begin{gathered} 2\gamma \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \,{\text{gap}}({{z}^{{k + 1/2}}},u)} \right] \leqslant \mathop {\max }\limits_{u \in \mathcal{C}} \left[ {\tau {{{\left\| {{{z}^{0}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{0}} - u} \right\|}}^{2}}} \right] + {{\gamma }^{2}}T\sigma _{0}^{2} + \\ \, + \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ { - \tau {{{\left\| {{{w}^{k}} - u} \right\|}}^{2}} - (1 - \tau ){{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{{k + 1}}} - u} \right\|}}^{2}}} \right]} \right] + \\ + \;2\gamma \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ {\left\langle {{{g}^{{k + 1/2}}} - F({{z}^{{k + 1/2}}}),u - {{z}^{{k + 1/2}}}} \right\rangle } \right]} \right] + {{\gamma }^{2}}K(2{{D}_{1}} + T{{D}_{2}}). \\ \end{gathered} $

Для того чтобы завершить доказательство, надо оценить члены в последних двух строках. Начнем с $\mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\nolimits_{k = 0}^{K - 1} {\left\langle {F({{z}^{{k + 1/2}}}) - {{g}^{{k + 1/2}}},{{z}^{{k + 1/2}}} - u} \right\rangle } } \right]$. Определим последовательность $v$: ${{v}^{0}} = {{z}^{0}}$, ${{v}^{{k + 1}}} = {\text{pro}}{{{\text{x}}}_{{\gamma h}}}({{v}^{k}} - \gamma {{\delta }_{k}})$ с ${{\delta }^{k}} = F({{z}^{{k + 1/2}}}) - {{g}^{{k + 1/2}}}$. Тогда получим

(17)

$\sum\limits_{k = 0}^{K - 1} \left\langle {{{\delta }^{k}},{{z}^{{k + 1/2}}} - u} \right\rangle = \sum\limits_{k = 0}^{K - 1} \left\langle {{{\delta }^{k}},{{z}^{{k + 1/2}}} - {{v}^{k}}} \right\rangle + \sum\limits_{k = 0}^{K - 1} \left\langle {{{\delta }^{k}},{{v}^{k}} - u} \right\rangle .$

По определению ${{v}^{{k + 1}}}$ (свойство prox), для всех $z \in \mathcal{Z}$

$\left\langle {{{v}^{{k + 1}}} - {{v}^{k}} + \gamma {{\delta }^{k}},z - {{v}^{{k + 1}}}} \right\rangle \geqslant 0.$

Переписав это неравенство, получим

$\begin{gathered} \left\langle {\gamma {{\delta }^{k}},{{v}^{k}} - z} \right\rangle \leqslant \left\langle {\gamma {{\delta }^{k}},{{v}^{k}} - {{v}^{{k + 1}}}} \right\rangle + \left\langle {{{v}^{{k + 1}}} - {{v}^{k}},z - {{v}^{{k + 1}}}} \right\rangle \leqslant \left\langle {\gamma {{\delta }^{k}},{{v}^{k}} - {{v}^{{k + 1}}}} \right\rangle + \frac{1}{2}{{\left\| {{{v}^{k}} - z} \right\|}^{2}} - \\ - \;\frac{1}{2}{{\left\| {{{v}^{{k + 1}}} - z} \right\|}^{2}} - \frac{1}{2}{{\left\| {{{v}^{k}} - {{v}^{{k + 1}}}} \right\|}^{2}} \leqslant \frac{{{{\gamma }^{2}}}}{2}{{\left\| {{{\delta }^{k}}} \right\|}^{2}} + \frac{1}{2}{{\left\| {{{v}^{k}} - {{v}^{{k + 1}}}} \right\|}^{2}} + \frac{1}{2}{{\left\| {{{v}^{k}} - z} \right\|}^{2}} - \frac{1}{2}{{\left\| {{{v}^{{k + 1}}} - z} \right\|}^{2}} - \\ \, - \frac{1}{2}{{\left\| {{{v}^{k}} - {{v}^{{k + 1}}}} \right\|}^{2}} = \frac{{{{\gamma }^{2}}}}{2}{{\left\| {{{\delta }^{k}}} \right\|}^{2}} + \frac{1}{2}{{\left\| {{{v}^{k}} - z} \right\|}^{2}} - \frac{1}{2}{{\left\| {{{v}^{{k + 1}}} - z} \right\|}^{2}}. \\ \end{gathered} $

Вместе с (17) это дает

$\begin{gathered} \sum\limits_{k = 0}^{K - 1} \left\langle {{{\delta }^{k}},{{z}^{{k + 1/2}}} - u} \right\rangle \leqslant \sum\limits_{k = 0}^{K - 1} \left\langle {{{\delta }^{k}},{{z}^{{k + 1/2}}} - {{v}^{k}}} \right\rangle + \frac{1}{\gamma }\sum\limits_{k = 0}^{K - 1} \left( {\frac{{{{\gamma }^{2}}}}{2}{{{\left\| {{{\delta }^{k}}} \right\|}}^{2}} + \frac{1}{2}{{{\left\| {{{v}^{k}} - u} \right\|}}^{2}} - \frac{1}{2}{{{\left\| {{{v}^{{k + 1}}} - u} \right\|}}^{2}}} \right) \leqslant \\ \, \leqslant \sum\limits_{k = 0}^{K - 1} \left\langle {{{\delta }^{k}},{{z}^{{k + 1/2}}} - {{v}^{k}}} \right\rangle + \frac{\gamma }{2}\sum\limits_{k = 0}^{K - 1} {{\left\| {{{\delta }^{k}}} \right\|}^{2}} + \frac{1}{{2\gamma }}{{\left\| {{{v}^{0}} - u} \right\|}^{2}}. \\ \end{gathered} $

Берем максимум по $u$ и получаем

$\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left\langle {{{\delta }^{k}},{{z}^{{k + 1/2}}} - u} \right\rangle \leqslant \sum\limits_{k = 0}^{K - 1} \left\langle {{{\delta }^{k}},{{z}^{{k + 1/2}}} - {{v}^{k}}} \right\rangle + \frac{1}{{2\gamma }}\mathop {\max }\limits_{u \in \mathcal{C}} {{\left\| {{{v}^{0}} - u} \right\|}^{2}} + \frac{\gamma }{2}\sum\limits_{k = 0}^{K - 1} {{\left\| {F({{z}^{{k + 1/2}}}) - {{g}^{{k + 1/2}}}} \right\|}^{2}}.$

Берем полное математическое ожидание и получаем

(18)

$\begin{gathered} \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left\langle {{{\delta }^{k}},{{z}^{{k + 1/2}}} - u} \right\rangle } \right] \leqslant \mathbb{E}\left[ {\sum\limits_{k = 0}^{K - 1} \left\langle {{{\delta }^{k}},{{z}^{{k + 1/2}}} - {{v}^{k}}} \right\rangle } \right] + \frac{\gamma }{2}\sum\limits_{k = 0}^{K - 1} \,\mathbb{E}\left[ {{{{\left\| {F({{z}^{{k + 1/2}}}) - {{g}^{{k + 1/2}}}} \right\|}}^{2}}} \right] + \\ + \;\frac{1}{{2\gamma }}\mathop {\max }\limits_{u \in \mathcal{C}} {{\left\| {{{v}^{0}} - u} \right\|}^{2}} = \mathbb{E}\left[ {\sum\limits_{k = 0}^{K - 1} \left\langle {\mathbb{E}\left[ {F({{z}^{{k + 1/2}}}) - {{g}^{{k + 1/2}}}\,|\,{{z}^{{k + 1/2}}} - {{v}^{k}}} \right],{{z}^{{k + 1/2}}} - {{v}^{k}}} \right\rangle } \right] + \\ + \;\frac{\gamma }{2}\sum\limits_{k = 0}^{K - 1} \,\mathbb{E}\left[ {{{{\left\| {F({{z}^{{k + 1/2}}}) - {{g}^{{k + 1/2}}}} \right\|}}^{2}}} \right] + \frac{1}{{2\gamma }}\mathop {\max }\limits_{u \in \mathcal{C}} {{\left\| {{{v}^{0}} - u} \right\|}^{2}} = \frac{\gamma }{2}\sum\limits_{k = 0}^{K - 1} \,\mathbb{E}\left[ {{{{\left\| {F({{z}^{{k + 1/2}}}) - {{g}^{{k + 1/2}}}} \right\|}}^{2}}} \right] + \frac{1}{{2\gamma }}\mathop {\max }\limits_{u \in \mathcal{C}} {{\left\| {{{v}^{0}} - u} \right\|}^{2}}. \\ \end{gathered} $

Далее оценим

$\mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ { - \tau {{{\left\| {{{w}^{k}} - u} \right\|}}^{2}} - (1 - \tau ){{{\left\| {{{z}^{{k + 1}}} + u} \right\|}}^{2}} + {{{\left\| {{{w}^{{k + 1}}} - u} \right\|}}^{2}}} \right]} \right],$

для этого заметим, что

$\begin{gathered} \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ { - \tau {{{\left\| {{{w}^{k}} - u} \right\|}}^{2}} - (1 - \tau ){{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{{k + 1}}} - u} \right\|}}^{2}}} \right]} \right] = \\ \, = \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ { - 2\left\langle {(1 - \tau ){{z}^{{k + 1}}} + \tau {{w}^{k}} - {{w}^{{k + 1}}},u} \right\rangle } \right.} \right. - \left. {\left. {(1 - \tau ){{{\left\| {{{z}^{{k + 1}}}} \right\|}}^{2}} - \tau {{{\left\| {{{w}^{k}}} \right\|}}^{2}} + {{{\left\| {{{w}^{{k + 1}}}} \right\|}}^{2}}} \right]} \right] = \\ = \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ { - 2\left\langle {(1 - \tau ){{z}^{{k + 1}}} + \tau {{w}^{k}} - {{w}^{{k + 1}}},u} \right\rangle } \right]} \right] + \mathbb{E}\left[ {\sum\limits_{k = 0}^{K - 1} - (1 - \tau ){{{\left\| {{{z}^{{k + 1}}}} \right\|}}^{2}} - \tau {{{\left\| {{{w}^{k}}} \right\|}}^{2}} + {{{\left\| {{{w}^{{k + 1}}}} \right\|}}^{2}}} \right]. \\ \end{gathered} $

По определению, ${{w}^{{k + 1}}}$: $\mathbb{E}\left[ {(1 - \tau ){\text{||}}{{z}^{{k + 1}}}{\text{|}}{{{\text{|}}}^{2}} + \tau {\text{||}}{{w}^{k}}{\text{|}}{{{\text{|}}}^{2}} - \;{\text{||}}{{w}^{{k + 1}}}{\text{|}}{{{\text{|}}}^{2}}} \right] = 0$, тогда

Далее можно провести рассуждения аналогично цепочке рассуждений для (18):

$\begin{gathered} \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ {\tau {{{\left\| {{{w}^{k}} - u} \right\|}}^{2}} + (1 - \tau ){{{\left\| {{{z}^{{k + 1}}} - u} \right\|}}^{2}} - {{{\left\| {{{w}^{{k + 1}}} - u} \right\|}}^{2}}} \right]} \right] \leqslant \\ \leqslant \sum\limits_{k = 0}^{K - 1} \,\mathbb{E}\left[ {{{{\left\| {(1 - \tau ){{z}^{{k + 1}}} + \tau {{w}^{k}} - {{w}^{{k + 1}}}} \right\|}}^{2}}} \right] + \mathop {\max }\limits_{u \in \mathcal{C}} {{\left\| {{{v}^{0}} - u} \right\|}^{2}} = \sum\limits_{k = 0}^{K - 1} \,\mathbb{E}\left[ {{{{\left\| {{{\mathbb{E}}_{{{{w}^{{k + 1}}}}}}[{{w}^{{k + 1}}}] - {{w}^{{k + 1}}}} \right\|}}^{2}}} \right] + \\ \end{gathered} $

(19)

$ + \;\mathop {\max }\limits_{u \in \mathcal{C}} {{\left\| {{{v}^{0}} - u} \right\|}^{2}} = \sum\limits_{k = 0}^{K - 1} \,\mathbb{E}\left[ { - {{{\left\| {{{\mathbb{E}}_{{{{w}^{{k + 1}}}}}}[{{w}^{{k + 1}}}]} \right\|}}^{2}} + {{\mathbb{E}}_{{{{w}^{{k + 1}}}}}}{{{\left\| {{{w}^{{k + 1}}}} \right\|}}^{2}}} \right] + \mathop {\max }\limits_{u \in \mathcal{C}} {{\left\| {{{v}^{0}} - u} \right\|}^{2}} = $

$\begin{gathered} = \sum\limits_{k = 0}^{K - 1} \,\mathbb{E}\left[ { - {{{\left\| {(1 - \tau ){{z}^{{k + 1}}} + \tau {{w}^{k}}} \right\|}}^{2}} + (1 - \tau ){{{\left\| {{{z}^{{k + 1}}}} \right\|}}^{2}} + \tau {{{\left\| {{{w}^{k}}} \right\|}}^{2}}} \right] + \mathop {\max }\limits_{u \in \mathcal{C}} {{\left\| {{{v}^{0}} - u} \right\|}^{2}} = \\ \, = \sum\limits_{k = 0}^{K - 1} \,\tau (1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + \mathop {\max }\limits_{u \in \mathcal{C}} {{\left\| {{{v}^{0}} - u} \right\|}^{2}}. \\ \end{gathered} $

Подставив (18) и (19) в (16), получим

Предположение 2 для $\mathbb{E}\left[ {{{{\left\| {F({{z}^{{k + 1/2}}}) - {{g}^{{k + 1/2}}}} \right\|}}^{2}}} \right]$ дает

С $\gamma \leqslant \frac{{\sqrt {1 - \tau } }}{{\sqrt E }}$ приходим к

(20)

$\begin{gathered} 2\gamma \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \,{\text{gap}}({{z}^{{k + 1/2}}},u)} \right] \leqslant \mathop {\max }\limits_{u \in \mathcal{C}} \left[ {(2 + \tau ){{{\left\| {{{z}^{0}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{0}} - u} \right\|}}^{2}}} \right] + (1 - \tau )\sum\limits_{k = 0}^{K - 1} \left[ {\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{w}^{k}}} \right\|}}^{2}}} \right] + } \right. \\ + \;\left. {\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right]} \right] + {{\gamma }^{2}}T\sigma _{0}^{2} + {{\gamma }^{2}}K(2{{D}_{1}} + T{{D}_{2}} + {{D}_{3}}) \leqslant \mathop {\max }\limits_{u \in \mathcal{C}} \left[ {(2 + \tau ){{{\left\| {{{z}^{0}} - u} \right\|}}^{2}} + {{{\left\| {{{w}^{0}} - u} \right\|}}^{2}}} \right] + \\ \, + {{\gamma }^{2}}T\sigma _{0}^{2} + 3(1 - \tau )\sum\limits_{k = 0}^{K - 1} \left[ {\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] + \mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right]} \right] + {{\gamma }^{2}}K(2{{D}_{1}} + T{{D}_{2}} + {{D}_{3}}). \\ \end{gathered} $

Вернемся к (15) с ${{\mu }_{h}} = 0$, ${{\mu }_{F}} = 0$, $T \geqslant \frac{{2B}}{\rho }$, $\gamma \leqslant \frac{{\sqrt {1 - \tau } }}{{2\sqrt {2A + TC} }}$ и получим

$\begin{gathered} \mathbb{E}\left[ {{{V}_{{k + 1}}}} \right] \leqslant \mathbb{E}\left[ {{{V}_{k}}} \right] - \left( {(1 - \tau ) - 2{{\gamma }^{2}}A - {{\gamma }^{2}}TC} \right)\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] - \frac{1}{2}\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] + {{\gamma }^{2}}(2{{D}_{1}} + T{{D}_{2}}) \leqslant \\ \, \leqslant \mathbb{E}\left[ {{{V}_{k}}} \right] - \frac{{(1 - \tau )}}{2}\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}}} \right] - \frac{{(1 - \tau )}}{2}\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] + {{\gamma }^{2}}(2{{D}_{1}} + T{{D}_{2}}). \\ \end{gathered} $

Откуда

(21)

$3(1 - \tau )\mathbb{E}\left[ {{{{\left\| {{{z}^{{k + 1/2}}} - {{w}^{k}}} \right\|}}^{2}} + {{{\left\| {{{z}^{{k + 1}}} - {{z}^{{k + 1/2}}}} \right\|}}^{2}}} \right] \leqslant 6\mathbb{E}\left[ {{{V}_{k}} - {{V}_{{k + 1}}}} \right] + 6{{\gamma }^{2}}(2{{D}_{1}} + T{{D}_{2}}).$

Подставляя (21) в (20), получаем

$\begin{gathered} \leqslant \mathop {\max }\limits_{u \in \mathcal{C}} \left[ {(2 + 7\tau ){{{\left\| {{{z}^{0}} - u} \right\|}}^{2}} + 7{{{\left\| {{{w}^{0}} - u} \right\|}}^{2}}} \right] + 7{{\gamma }^{2}}T\sigma _{0}^{2} + {{\gamma }^{2}}K(14{{D}_{1}} + 7T{{D}_{2}} + {{D}_{3}}) \leqslant \\ \, \leqslant \mathop {\max }\limits_{u \in \mathcal{C}} \left[ {16{{{\left\| {{{z}^{0}} - u} \right\|}}^{2}}} \right] + 7{{\gamma }^{2}}T\sigma _{0}^{2} + {{\gamma }^{2}}K(14{{D}_{1}} + 7T{{D}_{2}} + {{D}_{3}}). \\ \end{gathered} $

Остается немного подкорректировать критерий сходимости на монотонность $F$ и неравенство Йенсена для выпуклых функций:

$\begin{gathered} \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \,{\text{gap}}({{z}^{{k + 1/2}}},u)} \right] = \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ {\left\langle {F({{z}^{{k + 1/2}}}),{{z}^{{k + 1/2}}} - u} \right\rangle + h({{z}^{{k + 1/2}}}) - h(u)} \right]} \right] \geqslant \\ \, \geqslant \mathbb{E}\left[ {\mathop {\max }\limits_{u \in \mathcal{C}} \sum\limits_{k = 0}^{K - 1} \left[ {\left\langle {F(u),{{z}^{{k + 1/2}}} - u} \right\rangle + h({{z}^{{k + 1/2}}}) - h(u)} \right]} \right] \geqslant \\ \, \geqslant \mathbb{E}\left[ {K\mathop {\max }\limits_{u \in \mathcal{C}} \left[ {\left\langle {F(u),{{{\bar {z}}}^{K}} - u} \right\rangle + h({{{\bar {z}}}^{K}}) - h(u)} \right]} \right] = K\mathbb{E}\left[ {{\text{Gap}}({{{\bar {z}}}^{K}})} \right], \\ \end{gathered} $

где мы используем ${{\bar {z}}^{K}} = \frac{1}{K}\sum\nolimits_{k = 0}^{K - 1} {{{z}^{{k + 1/2}}}} $. Что приводит к

$\mathbb{E}\left[ {{\text{Gap}}({{{\bar {z}}}^{K}})} \right] \leqslant \frac{{8{{{\max }}_{{u \in \mathcal{C}}}}\left[ {{{{\left\| {{{z}^{0}} - u} \right\|}}^{2}}} \right] + 4{{\gamma }^{2}}T\sigma _{0}^{2}}}{{\gamma K}} + \gamma (7{{D}_{1}} + 3T{{D}_{2}} + {{D}_{3}}).$

2.3. Анализ для различных методов

Здесь мы устанавливаем связь между единым анализом и конкретными методами, удовлетворяющими предположению 2. В скобках указаны разделы Приложения, где представлен псевдокод соответствующего метода, а также его анализ при предположении 2, основанный на применении теоремы 1. В большинстве случаев анализируются операторы, удовлетворяющие следующему условию.

Предположение 3. $F(z)$ – ограниченно-липшицев с константами $L$ и $D$, т.е. для любых ${{z}_{1}},{{z}_{2}} \in \mathcal{Z}$ верно

${{\left\| {F({{z}_{1}}) - F({{z}_{2}})} \right\|}^{2}} \leqslant {{L}^{2}}{{\left\| {{{z}_{1}} - {{z}_{2}}} \right\|}^{2}} + {{D}^{2}}.$

Заметим, что для $D = 0$ это эквивалентно определению липшицевости. При $D > 0$ это предположение покрывает случай, когда оператор не является липшицевым, но ограничен.

$ \bullet $ Существующие методы (A.1)–(A.3). Прежде всего хотелось бы упомянуть методы, которые соответствуют нашему параметризованному предположению. Это, конечно, классический экстраградиентный (см. [10]) для задачи (1)–(3). Далее отметим методы с однократным вызовом оракула (см. [17]); отличие этих методов от классического экстраградиентного в том, что на каждой итерации они вычисляют новое значение оператора $F$ лишь один раз. Например, этого можно добиться, используя значение $F$ с предыдущей итерации: ${{g}^{k}} = F({{z}^{{k - 1/2}}}),$ ${{g}^{{k + 1/2}}} = F({{z}^{{k + 1/2}}})$ (в экстраградиентном методе имеем ${{g}^{k}} = F({{z}^{k}}),\;{{g}^{{k + 1/2}}} = F({{z}^{{k + 1/2}}})$). Вариант метода редукции дисперсии (см. 11]), специализированный для задач решения ВН (1)–(4) также удовлетворяет условиям предлагаемого анализа.

Ко-коэрцитивность. Это предположение аналогично липшицевости оператора:

${{\left\| {F({{z}_{1}}) - F({{z}_{2}})} \right\|}^{2}} \leqslant l\left\langle {F({{z}_{1}}) - F({{z}_{2}}),{{z}_{1}} - {{z}_{2}}} \right\rangle .$

Видно, что $l$-коэрцитивный оператор также является $l$-липшицевым (обратное, вообще говоря, неверно). Более того, если $F$ – градиент выпуклой функции, то $l$-липшицевость и $l$-коэрцитивность эквивалентны. В литературе имеется анализ некоторых методов (например, метода редукции дисперсии, см. [22]) с этим дополнительным допущением. Довольно легко проанализировать многие методы решения ВН с предположением ко-коэрцитивности. Мы также могли бы построить унифицированную теорию вокруг него и так перенести многие методы минимизации в контекст ВН. Но основная проблема предположения о ко-коэрцитивности состоит в том, что это свойство не выполняется для самой распространенной, билинейной, задачи. Поэтому такой анализ будет справедлив только для минимизации, а это уже проделано в [16].

Coord-ES для (1)–(3) (A.4). Наш первый новый метод позволяет работать не с полным оператором $F$, а выбирать его случайную координату (координаты) и делать шаг только вдоль нее. Методы этого типа называются координатными (см. [29]). С помощью таких методов можно произвести более тщательный поиск решения – выбрать направления, в которых оператор изменяется в большей степени, и проделывать больше шагов в этих направлениях (см. [30]). Также координатный метод очень близок к безградиентным методам (см. [25]), которые актуальны, когда мы работаем с функциями в соответствии с моделью черного ящика и не можем вычислить оператор F/градиент.

Quant-ES для (1)–(3) (A.5). Суть Quant-ES заключается в использовании так называемого оператора квантизации:

$\mathbb{E}Q(x) = x,\quad \mathbb{E}{{\left\| {Q(x)} \right\|}^{2}} = \omega \left\| x \right\|\quad {\text{для}}\;{\text{любых}}\;\;x.$

Такие операторы могут быть рандомизированными или детерминированными с большим или малым параметром $\omega $ (см. [14], [32]), но все они имеют одну и ту же функцию – сжать вектор $x$. Методы с квантизацией популярны с точки зрения распределенной оптимизации, поскольку основной проблемой там является коммуникация, а сжатие позволяет передавать меньше информации и, следовательно, выигрывать в этом отношении. Мы представляем метод для вариационных неравенств, который может использовать квантизованный оператор.

QVR-ES for (1)–(4) (A.6). QVR-ES сочетает методы редукции дисперсии и квантизации, т.е. сначала мы выбираем случайную функцию с номером $m$ из $M$ вариантом, а затем также квантизуем ее. В простейшем виде это выглядит так: $Q({{F}_{m}}(z))$, в нашем методе это делается немного в другом виде, но суть остается той же. Этот метод красочно демонстрирует гибкость нашего подхода и возможность создания различных комбинаций методов с использованием параметризованного предположения 2.

IS-ES (1)–(4) (5.7). В этом случае мы рассматриваем задачу более общую, чем (1)–(4). Здесь предполагаем, что мы не вызываем функции случайно и равномерно от $1$ до $M$. Теперь каждый оператор ${{F}_{m}}$ имеет свой вес, в зависимости от которого его можно вызывать чаще или реже.

Local-ES for (1)–(5) (5.8). Этот метод относится к так называемым локальным методам, которые делают ряд локальных обновлений между периодическими коммуникациями. Наш метод является рандомизированным (см. [7]) и основан на методе из предыдущего абзаца, а также использует технику сэмплирования по важности.

3. ЗАКЛЮЧЕНИЕ

В настоящей работе был рассмотрен экстраградиентный подход, базовый подход для решения вариационных неравенств, а также различные его модификации. Мы представили унифицированный анализ, с помощью которого можно единообразно анализировать семейство методов, основанных на экстраградиенте. Полученный унифицированный анализ позволил улучшить оценки сходимости уже существующих методов, а также представить новые методы и их гарантии сходимости. В будущем хотелось бы усовершенствовать анализ, чтобы в его предположения подпадали методы, которые не могут быть описаны текущей версией анализа.

Список литературы

Facchinei F., Pang J. Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer New York, 2007. (Springer Series in Operations Research and Financial Engineering). URL: https://books.google.ru/books?id=lX%5C_7Rce3%5C_Q0C.
Nesterov Y. Smooth minimization of non-smooth functions // Math. Program. 2005. T. 103. № 1. C. 127–152.
Nemirovski A. Prox-method with rate of convergence O (1/t) for variational inequalities with Lipschitz continuous monotone operators and smooth convex-concave saddle point problems // SIAM J. Optimizat. 2004. V. 15. № 1. P. 229–251.
Chambolle A., Pock T. A first-order primal-dual algorithm for convex problems with applications to imaging // J. Math. Imag. and Vis. 2011. V. 40. № 1. P. 120–145.
Esser E., Zhang X., Chan T.F. A general framework for a class of first order primal-dual algorithms for convex optimization in imaging science // SIAM J. Imag. Sci. 2010. V. 3. № 4. P. 1015–1046.
Generative Adversarial Networks / I.J. Goodfellow [и дp.]. 2014. arXiv: 1406.2661[stat.ML].
Hanzely F., Richtárik P. Federated learning of a mixture of global and local models // arXiv preprint a-rXiv:2002.05516. 2020.
Lower bounds and optimal algorithms for personalized federated learning / F. Hanzely [и дp.] // arXiv preprint arXiv:2010.02372. 2020.
Korpelevich G.M. The extragradient method for finding saddle points and other problems // Ekonomika i Matematicheskie Metody. 1976. V. 12. № 4. P. 747–756.
Juditsky A., Nemirovski A., Tauvel C. Solving variational inequalities with stochastic mirror-prox algorithm // Stochastic System. 2011. V. 1. № 1. P. 17–58.
Alacaoglu A., Malitsky Y. Stochastic Variance Reduction for Variational Inequality Methods // arXiv preprint arXiv:2102.08352. 2021.
Robbins H., Monro S. A Stochastic Approximation Method // Ann. Math. Statistic. 1951. V. 22. № 3. P. 400–407. URL: https://doi.org/10.1214/aoms/1177729586
Johnson R., Zhang T. Accelerating stochastic gradient descent using predictive variance reduction // Adv. Neural Informat. Processing System. 2013. V. 26. P. 315–323.
QSGD: Communication-efficient SGD via gradient quantization and encoding / D. Alistarh [и дp.] // Adv. Neural Informat. Processing System. 2017. P. 1709–1720.
Hanzely F., Mishchenko K., Richtarik P. SEGA: Variance reduction via gradient sketching // arXiv preprint a-rXiv:1809.03054. 2018.
Gorbunov E., Hanzely F., Richtarik P. A unified theory of SGD: Variance reduction, sampling, quantization and coordinate descent // Internat. Conf. Artific. Intelligence and Statistic. PMLR. 2020. P. 680–690.
On the convergence of single-call stochastic extra-gradient methods / Y.-G. Hsieh [и дp.]. 2019. arXiv: 1908.08465 [math.OC].
Revisiting stochastic extragradient / K. Mishchenko [и дp.] // Internat. Conf. Artific. Intelligence and Statistic. PMLR. 2020. P. 4573–4582.
Tseng P. A Modified Forward-Backward Splitting Method for Maximal Monotone Mappings // SIAM J. Control and Optimizat. 2000. V. 38. № 2. P. 431–446. https://doi.org/10.1137/S0363012998338806
Nesterov Y. Dual extrapolation and its applications to solving variational inequalities and related problems // Math. Program. 2007. V. 109. № 2. P. 319–344.
Palaniappan B., Bach F. Stochastic Variance Reduction Methods for Saddle- Point Problems // Adv. Neural Informat. Processing System. Т. 29 / Под ред. D. Lee [и др.]. Curran Associates, Inc., 2016. URL: https://proceedings.neurips.cc/paper/2016/file/1aa48fc4880bb0c9b8aPaper.pdf.
Reducing noise in gan training with variance reduced extragradient / T. Chavdarova [и дp.] // arXiv preprint arXiv:1904.08598. 2019.
Sidford A., Tian K. Coordinate methods for accelerating regression and faster approximate maximum flow // 2018 IEEE 59th Ann. Symp. Foundat. of Comput. Sci. (FOCS). IEEE. 2018. P. 922– 933.
Coordinate methods for matrix games / Y. Carmon [и дp.] // arXiv preprint arXiv:2009.08447. 2020.
Zeroth-Order Algorithms for Smooth Saddle-Point Problems / A. Sadiev [и дp.] // arXiv preprint ar-Xiv:2009.09908. 2020.
Deng Y., Mahdavi M. Local Stochastic Gradient Descent Ascent: Convergence Analysis and Communication Efficiency // Internat. Conf. Artific. Intelligence and Statistic. PMLR. 2021. P. 1387–1395.
Beznosikov A., Samokhin V., Gasnikov A. Distributed Saddle-Point Problems: Lower Bounds, Optimal Algorithms and Federated GANs // arXiv preprint arXiv:2010.13112. 2021.
Stich S.U. Unified optimal analysis of the (stochastic) gradient method // arXiv preprint arXiv:1907.04232. 2019.
Wright S.J. Coordinate descent algorithms // Math. Program. 2015. V. 151. № 1. C. 3–34.
Nesterov Y. Efficiency of coordinate descent methods on huge-scale optimization problems // SIAM J. Optimizat. 2012. V. 22. № 2. P. 341–362.
On Biased Compression for Distributed Learning / A. Beznosikov [и дp.] arXiv preprint arXiv:2002.12410. 2020.
Barratt S., Sharma R. A note on the inception score // arXiv preprint arXiv:1801.01973. 2018.
Radford A., Metz L., Chintala S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. 2016. arXiv: 1511.06434 [cs.LG].
Mirza M., Osindero S. Conditional generative adversarial nets // arXiv preprint arXiv:1411.1784. 2014.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал