Журнал вычислительной математики и математической физики, 2023, T. 63, № 2, стр. 336-348

ВВЕДЕНИЕ

В кинетической теории газов выделяются два асимптотических режима течения: свободномолекулярный режим при ${\text{Kn}} \to \infty $ и режим сплошной среды, описываемый уравнениями Навье–Стокса при ${\text{Kn}} \to 0$. Между этими предельными режимами лежит переходный режим течения, в котором необходимо решать уравнение Больцмана [1–3]. На практике границы перечисленных режимов определяются сильными неравенствами ${\text{Kn}} \gg 1$ и ${\text{Kn}} \ll 1$ соответственно. Более точные границы зависят от других параметров и особенностей течения, а также от требуемой точности расчета. По оценкам [4], для обеспечения 2% точности, граница перехода от уравнения Больцмана к решению уравнений Навье–Стокса лежит между значениями ${\text{Kn}} = 0.01$ и ${\text{Kn}} = 0.001$.

Для течений, которые можно отнести к режиму сплошной среды, имеются области, где уравнения Навье–Стокса не применимы. У поверхности обтекаемого тела образуется слой Кнудсена толщиной в длину свободного пробега молекул, в котором функция распределения испытывает разрыв в пространстве скоростей, вызванный рассеянием молекул поверхностью. По мере удаления от поверхности, разрыв сглаживается, и функция распределения молекул приближается к локально-максвелловской функции. Слой Кнудсена и примыкающая к нему область течения относятся к переходному режиму и требуют решения уравнения Больцмана.

При расчете течений на основе уравнений Навье–Стокса, слой Кнудсена учитывается заданием граничных условий скольжения, получаемых из приближенного анализа функции распределения у поверхности [2], [3]. Такой подход применялся до появления численных методов решения кинетических уравнений [5]. Современным методом является сращивание решений уравнения Больцмана вблизи границы с решением уравнений Навье–Стокса во внешней области течения [6–10]. Методика сращивания основана на использовании функции распределения Энскога–Чепмена

где Здесь ${{c}_{i}} = {{\xi }_{i}} - {{u}_{i}}\,,$ ${\mathbf{u}}$ – средняя скорость газа, $\mu $ и $\lambda $ – коэффициенты вязкости и теплопроводности, $n$ – концентрация газа, $m$ – масса молекулы, $T$ – температура, $k$ – постоянная Больцмана. Корректность выбора границы сращивания решений можно оценить по величине производных в (0.2), которые должны быть порядка ${\text{Kn}}$, однако это возможно только после решения задачи с уже выбранной границей. Сложной проблемой сращивания решений является необходимость обеспечить непрерывность потоков массы, импульса и энергии через границу областей [6], [9].

В настоящей работе изучается возможность решения уравнения Больцмана при ${\text{Kn}} \ll 1$ во всей области течения, без сращивания с уравнениями Навье–Стокса. Трудность решения уравнения Больцмана при малых числах Кнудсена хорошо известна и определяется двумя причинами. Первая связана с большой в масштабе длины свободного пробега молекул областью решения в физическом пространстве, что резко увеличивает объем вычислений. Вторая причина более существенна и состоит в необходимости высокой точности вычисления интеграла столкновений, достаточной чтобы выделить вклад от второго приближения (в терминах работы [1]) в асимптотическом разложении (0.1). Этот вклад пропорционален производным от температуры и скорости газа и имеет первый порядок по числу Кнудсена. Добиться такой точности при вычислении многомерного интеграла за счет измельчения скоростной сетки и увеличения мощности кубатурной сетки практически невозможно.

Преодолеть указанную трудность позволяет представленный в [11], [12] вариант проекционного метода вычисления интеграла столкновений Больцмана, который дает точное нулевое значение интеграла от функции ${{f}_{M}}$– главного члена асимптотического разложения. Метод широко использовался для моделирования дозвуковых и сверхзвуковых течений простого газа и газовых смесей [13]. В [14] было найдено улучшение, позволившее более чем на порядок ускорить вычисление интеграла столкновений за счет уменьшения необходимой мощности кубатурной сетки. В [15] эта оптимизация была проверена на расчете течения при числе Маха M = 0.001, которое требует высокой точности вычислений.

1. МЕТОД РЕШЕНИЯ УРАВНЕНИЯ БОЛЬЦМАНА

Уравнение Больцмана решается на равномерной сетке из ${{N}_{0}}$ узлов ${{{\mathbf{\xi }}}_{\gamma }} \in {{\Sigma }_{0}}$, которые являются центрами кубов с ребром $h$ в области $\Omega $ с объемом $V$ в пространстве скоростей, и на произвольной пространственной сетке

На шаге по времени $\tau $ используется симметричный метод расщепления [16], имеющий второй порядок точности по времени где ${{\Lambda }_{\tau }}$ – решение на шаге $\tau $ уравнения адвекции, ${{\Theta }_{\tau }}$ – решение уравнения релаксации. Интеграл столкновений ${{I}_{\gamma }}$ вычисляется проекционным методом, который обеспечивает точное выполнение законов сохранения вещества, импульса и энергии, а также условие Здесь ${{f}_{{M,\gamma }}}$ – максвелловская функция распределения, заданная в узлах ${{{\mathbf{\xi }}}_{\gamma }}$. Дадим краткое описание метода и опишем его оптимизацию, позволившую значительно сократить объем вычислений. В непрерывном скоростном пространстве интеграл столкновений в узле ${{{\mathbf{\xi }}}_{\gamma }}$ запишем в виде Здесь $f \equiv f({\mathbf{\xi }},{\mathbf{x}},t),$ $f{\kern 1pt} ' \equiv f({\mathbf{\xi }}{\kern 1pt} ',{\mathbf{x}},t),$ $f_{*}^{{}} \equiv f({\mathbf{\xi }}_{*}^{{}},{\mathbf{x}},t),$ $f_{*}^{'} \equiv f({\mathbf{\xi }}_{*}^{'},{\mathbf{x}},t)$, ${\mathbf{\xi }}{\kern 1pt} '$ и ${\mathbf{\xi }}_{*}^{'}$ – скорости после столкновений молекул со скоростями ${\mathbf{\xi }}$ и ${{{\mathbf{\xi }}}_{*}}$, $g = {\text{|}}{\mathbf{\xi }} - {{{\mathbf{\xi }}}_{*}}{\text{|}}$, ${{b}_{m}}$ – максимальное значение прицельного параметра $b$, $\sigma = {{b}^{2}}{\text{/}}2$, ${{\Phi }_{1}} = \delta ({\mathbf{\xi }}{\kern 1pt} '\; - {{{\mathbf{\xi }}}_{\gamma }}) + \delta ({\mathbf{\xi }}_{*}^{'} - {{{\mathbf{\xi }}}_{\gamma }}) - \delta ({\mathbf{\xi }} - {{{\mathbf{\xi }}}_{\gamma }}) - \delta ({{{\mathbf{\xi }}}_{*}} - {{{\mathbf{\xi }}}_{\gamma }})$, $\delta ({\mathbf{\xi }} - {{{\mathbf{\xi }}}_{с}})$ – трехмерная дельта-функция.

Вычисление 8-мерного интеграла (1.4) осуществляется на равномерной кубатурной сетке ${{\Sigma }_{\nu }}$ из ${{N}_{\nu }}$ узлов. Каждый узел сетки включает значения непрерывных переменных ${{\sigma }_{\nu }},\;{{\varphi }_{\nu }}$ и сеточные узлы ${{{\mathbf{\xi }}}_{{{{\alpha }_{\nu }}}}} \in {{\Sigma }_{0}}$, ${{{\mathbf{\xi }}}_{{{{\beta }_{\nu }}}}} \in {{\Sigma }_{0}}$. В общем случае скорости после столкновения ${\mathbf{\xi }}_{{{{\alpha }_{\nu }}}}^{'} \notin {{\Sigma }_{0}}$, ${\mathbf{\xi }}_{{{{\beta }_{\nu }}}}^{'} \notin {{\Sigma }_{0}}$. При вычислении интеграла столкновений они заменяются двумя парами ближайших симметрично расположенных сеточных узлов ${{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }}}}}$, ${{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }} + {{s}_{\nu }}}}}$ и ${{{\mathbf{\xi }}}_{{{{\mu }_{\nu }}}}}$, ${{{\mathbf{\xi }}}_{{{{\mu }_{\nu }} - {{s}_{\nu }}}}}$, где ${{s}_{\nu }}$ – вектор единичного сдвига по сетке ${{\Sigma }_{0}}$. Из закона сохранения импульса при столкновении следует ${{{\mathbf{\xi }}}_{{{{\alpha }_{\nu }}}}} + {{{\mathbf{\xi }}}_{{{{\beta }_{\nu }}}}} = {\mathbf{\xi }}_{{{{\alpha }_{\nu }}}}^{'} + {\mathbf{\xi }}_{{{{\beta }_{\nu }}}}^{'} = {\mathbf{k}}h$, где ${\mathbf{k}} = ({{k}_{x}},{{k}_{y}},{{k}_{z}})$ – целочисленный вектор. Пусть ${\mathbf{\xi }}_{{{{\alpha }_{\nu }}}}^{'} = {{{\mathbf{k}}}_{1}}h + \Delta {\mathbf{h}}$, $\Delta {\mathbf{h}} = (\Delta {{h}_{x}},\Delta {{h}_{y}},\Delta {{h}_{z}})$, тогда ${\mathbf{\xi }}_{{{{\beta }_{\nu }}}}^{'} = {{{\mathbf{k}}}_{2}}h - \Delta {\mathbf{h}}$, что доказывает симметричное расположение скоростей ${\mathbf{\xi }}_{{{{\alpha }_{\nu }}}}^{'}$ и ${\mathbf{\xi }}_{{{{\beta }_{\nu }}}}^{'}$ относительно узлов ${{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }}}}} = {{{\mathbf{k}}}_{1}}h$ и ${{{\mathbf{\xi }}}_{{{{\mu }_{\nu }}}}} = {{{\mathbf{k}}}_{2}}h$, а также относительно узлов ${{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }} + {{s}_{\nu }}}}}$ и ${{{\mathbf{\xi }}}_{{{{\mu }_{\nu }} - {{s}_{\nu }}}}}$. Для перехода в (1.4) к сумме по узлам скоростной сетки заменяем соответствующие $\delta $-функции, входящие в ${{\Phi }_{1}}$ разложениями

Узлы ${{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }}}}}$, ${{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }} + {{s}_{\nu }}}}}$ и ${{{\mathbf{\xi }}}_{{{{\mu }_{\nu }}}}}$, ${{{\mathbf{\xi }}}_{{{{\mu }_{\nu }} - {{s}_{\nu }}}}}$ выбираются так, чтобы выполнялось одно из неравенств ${{E}_{1}} \leqslant {{E}_{0}} < {{E}_{2}}$, или ${{E}_{2}} \leqslant {{E}_{0}} < {{E}_{1}}$, где ${{E}_{0}} = {{({{{\mathbf{\xi }}}_{{{{\alpha }_{\nu }}}}})}^{2}} + {{({{{\mathbf{\xi }}}_{{{{\beta }_{\nu }}}}})}^{2}}$, ${{E}_{1}} = {{({{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }}}}})}^{2}} + {{({{{\mathbf{\xi }}}_{{{{\mu }_{\nu }}}}})}^{2}}$, ${{E}_{2}} = {{({{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }} + {{s}_{\nu }}}}})}^{2}} + {{({{{\mathbf{\xi }}}_{{{{\mu }_{\nu }} - {{s}_{\nu }}}}})}^{2}}$. Коэффициент ${{r}_{\nu }}$ находится из условия сохранения энергии ${{E}_{0}} = (1 - {{r}_{\nu }}){{E}_{1}} + {{r}_{\nu }}{{E}_{2}}$, откуда следует $0 \leqslant {{r}_{\nu }} < 1$. Сохранение массы обеспечивается приведенным условием на ${{r}_{\nu }}$, а сохранение импульса следует из симметричного расположения пар узлов ${{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }}}}}$, ${{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }} + {{s}_{\nu }}}}}$ и ${{{\mathbf{\xi }}}_{{{{\mu }_{\nu }}}}}$, ${{{\mathbf{\xi }}}_{{{{\mu }_{\nu }} - {{s}_{\nu }}}}}$ относительно скоростей ${\mathbf{\xi }}_{{{{\alpha }_{\nu }}}}^{'}$ и ${\mathbf{\xi }}_{{{{\beta }_{\nu }}}}^{'}$ соответственно. Выбор сеточных узлов ${{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }} + {{s}_{\nu }}}}}$ и ${{{\mathbf{\xi }}}_{{{{\mu }_{\nu }} - {{s}_{\nu }}}}}$ не однозначен и может осуществляться на основе различных критериев. В данной работе использовался критерий их близости по энергии к не сеточным значениям, ${\mathbf{\xi }}_{{{{\alpha }_{\nu }}}}^{'}$ и ${\mathbf{\xi }}_{{{{\beta }_{\nu }}}}^{'}$: выбирались узлы с наименьшей по величине разностью энергий $\Delta {{E}_{2}} = {\text{|}}{{E}_{2}} - {{E}_{0}}{\text{|}}$, противоположной по знаку разности $\Delta {{E}_{1}} = {\text{|}}{{E}_{1}} - {{E}_{0}}{\text{|}}$. Получаем явное выражение для интегральной суммы где ${{\delta }_{{\alpha ,\beta }}}$ – символ Кронекера, ${{\Delta }_{\nu }} = ({{f}_{{{{\alpha }_{\nu }}}}}{{f}_{{{{\beta }_{\nu }}}}} - f_{{{{\alpha }_{\nu }}}}^{'}f_{{{{\beta }_{\nu }}}}^{'}){{g}_{\nu }}$, $B = {{N}_{0}}V\pi b_{m}^{2}{\text{/}}(4{{N}_{\nu }})$.

В [11], [12] представлены два основных варианта консервативного проекционного метода вычислений интеграла столкновений: “Проекционно-Интерполяционный Метод” (ПИМ) и “Симметричный Проекционный Метод” (СПМ). В ПИМ произведение $f_{{{{\alpha }_{\nu }}}}^{'}f_{{{{\beta }_{\nu }}}}^{'}$ находится интерполяцией по сеточным значениям функции распределения. Для ${\text{Kn}} \ll 1$ в [17] была предложена интерполяция, точная для максвелловской сеточной функции ${{f}_{{M,\gamma }}}$

Для функции ${{f}_{{M,\gamma }}}$ получаем ${{\Delta }_{\nu }} = 0$, откуда следует свойство (1.3). Доказано [18], что при интерполяции (1.6) дискретная форма интеграла столкновений (1.5) обладает свойством не возрастания $H$-функции Для произвольной функции погрешность формулы (1.6) в зависимости от шага сетки имеет оценку $О(h)$, а для функции вида ${{f}_{\gamma }} = {{f}_{{M,\gamma }}} + {\text{Kn}} \cdot f_{\gamma }^{{(1)}}$, ${\text{Kn}} \ll 1$, погрешность составит ${\text{Kn}} \cdot О(h)$, что важно для течений при малых числах Кнудсена.

Однако ПИМ имеет существенный недостаток, связанный с необходимостью обеспечить неотрицательность решения. Ниже рассмотрим способ решения данной проблемы.

Применение формулы (1.5) на стадии релаксации в схеме (1.2) должно исключить отрицательные решения, которые могут возникнуть из-за конечной величины шага по времени $\tau $. Для этого оператор релаксации ${{\Theta }_{\tau }}(f)$ построен как решение интегрального уравнения по схеме непрерывного счета. На шаге $\tau $ решается уравнение

Интервал $\tau $ делится на ${{N}_{\nu }}$ равных частей ${{\tau }_{\nu }} = \tau {\text{/}}{{N}_{\nu }}$и осуществляется решение уравнения (1.7) по неявной схеме Здесь $f_{\gamma }^{{t + j{{\tau }_{\nu }}}}$ – промежуточное решение после $j$ шагов, $j = 1,...,{{N}_{\nu }}$, $\Delta I_{\gamma }^{{t + j{{\tau }_{\nu }}}}$ – вклад в сумму (1.5) от $j$-го узла кубатурной формулы. Схема (1.8) используется для контроля неотрицательности получаемого решения: вклад в интеграл на шаге $\nu $ отвергается, если решение в одном из узлов сетки становится отрицательным. Относительное число таких исключений не должно превышать заданного критерия, типичное значение которого ${{\varepsilon }_{{tol}}} = 0.5 \times {{10}^{{ - 4}}}$, однако, желательно добиваться его нулевого значения. Исключение части вкладов искажает интеграл столкновений и может привести к нестабильности счета.

Определим условие неотрицательности решения при заданном шаге $\tau $. Начальное и конечное значения промежуточного решения обозначим индексами $j$ и $j + 1$, соответственно, индекс $\nu $ опускаем. Каждый вклад совершается в 6 узлов ${{{\mathbf{\xi }}}_{\gamma }} \in {{\Sigma }_{0}}$ при индексе $\gamma $, принимающем значения $\alpha ,\beta ,\lambda ,\mu ,\lambda + s,\mu - s$. Запишем эти вклады подробно

Из (1.9), используя значение $B = {{N}_{0}}V\pi b_{m}^{2}{\text{/}}(4{{N}_{\nu }})$, получаем искомое условие необходимой мощности кубатурной сетки ${{N}_{\nu }}$для функций $f_{\alpha }^{{j + 1}}$ и $f_{\beta }^{{j + 1}}$Здесь ${{g}_{{\max }}}$ – максимальное значение относительной скорости при столкновении, равное диаметру области $\Omega $ пространства скоростей, ${{f}_{{\max }}}$ – максимальное значение сеточной функции $f_{\gamma }^{j}$. Перейдем к оценке функций из (1.10) и (1.11). Эти формулы отличаются множителем перед вкладом ${{\Delta }^{j}}$, поэтому достаточно рассмотреть первую формулу из (1.10). Получаем цепочку неравенств и искомое условие в ее конце Условие (1.14) отличается от (1.13) множителем ${{\chi }^{j}} = (1 - r){{(f_{{\lambda + s}}^{j}{\text{/}}f_{\lambda }^{j})}^{r}}$, в который входит отношение функций в соседних узлах сетки. Несмотря на близость узлов, этот множитель может быть большим на границе газ-поверхность и на периферии области $\Omega $, где значения функции распределения близки к нулю и подвержены случайным флуктуациям. Указанные флуктуации делают невозможным выбор числа узлов ${{N}_{\nu }}$ кубатурной сетки, гарантирующего неотрицательность решения. Для обеспечения приемлемого значения коэффициента ${{\varepsilon }_{{tol}}}$ необходимо многократное увеличение мощности кубатурной сетки.

Чтобы распространить условие (1.13) на все узлы сетки и ускорить вычисления, в [14] предложен способ пересчета вкладов, для которых решение становится отрицательным. Для пересчета используется СПМ, в котором условие (1.3) выполняется с точностью $O(h)$. Он менее точен для слабо возмущенных течений, но успешно применялся для сверхзвуковых течений с ударными волнами. Дадим краткий вывод дискретной формы интеграла столкновений в СПМ с учетом перехода к интегрированию по $\sigma = {{b}^{2}}{\text{/}}2$.

Разделим интеграл (1.4) на две части. Первую, которая содержит $f{{f}_{*}}$ и дает вклад от “прямых” столкновений, и вторую, включающую $f{\kern 1pt} '{\kern 1pt} f_{*}^{'}$ и описывающую “обратные” столкновения. Для первой части используем ту же функцию ${{\Phi }_{1}}({{{\mathbf{\xi }}}_{\gamma }})$, что при выводе (1.5). Во второй части заменим выражение под интегралом на следующую аппроксимацию:

Здесь вклад “обратных” столкновений из точек ${\mathbf{\xi }}_{{{{\alpha }_{\nu }}}}^{'},\;{\mathbf{\xi }}_{{{{\beta }_{\nu }}}}^{'}$ заменяется вкладами “обратных” столкновений из узлов ${{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }}}}},\;{{{\mathbf{\xi }}}_{{{{\mu }_{\nu }}}}}$с весом $1 - r_{\nu }^{*}$, и из узлов ${{{\mathbf{\xi }}}_{{{{\lambda }_{\nu }} + {{s}_{\nu }}}}},\;{{{\mathbf{\xi }}}_{{{{\mu }_{\nu }} - {{s}_{\nu }}}}}$с весом $r_{\nu }^{*}$. Коэффициент $r_{\nu }^{*}$ определяется из равенства энергии $(1 - r_{\nu }^{*}){{E}_{{1,\nu }}}{{\Delta }_{{1,\nu }}} + r{\kern 1pt} *{\kern 1pt} {{E}_{{2,\nu }}}{{\Delta }_{{2,\nu }}} = [(1 - r_{\nu }^{*}){{\Delta }_{{1,\nu }}} + r_{\nu }^{*}{{\Delta }_{{2,\nu }}}]{{E}_{{0,\nu }}}$, где ${{\Delta }_{{1,\nu }}} = {{f}_{{{{\lambda }_{\nu }}}}}{{f}_{{{{\mu }_{\nu }}}}}{{g}_{\nu }}$, ${{\Delta }_{{2,\nu }}} = {{f}_{{{{\lambda }_{\nu }} + {{s}_{\nu }}}}}{{f}_{{{{\mu }_{\nu }} - {{s}_{\nu }}}}}{{g}_{\nu }}$.

Получаем $r_{\nu }^{*} = {{r}_{\nu }}{{\Delta }_{{1,\nu }}}{\text{/}}[{{r}_{\nu }}{{\Delta }_{{1,\nu }}} + (1 - {{r}_{\nu }}){{\Delta }_{{2,\nu }}}]$.

Пусть ${{\Delta }_{{0,\nu }}} = {{f}_{{{{\alpha }_{\nu }}}}}{{f}_{{{{\beta }_{\nu }}}}}{{g}_{\nu }}$. Интеграл (1.4) в дискретной форме примет вид

Погрешность аппроксимации (1.15) имеет порядок $O(h)$ и не уменьшается при близости решения к ${{f}_{{M,\gamma }}}$.

Подробно вклады в сеточные узлы выражаются формулами (индекс $\nu $ опускаем)

Анализ этих формул показывает неотрицательность решения для всех сеточных узлов при выполнении условия (1.13).

Предлагается следующий алгоритм вычислений (1.8) в цикле по $j = 1,...,{{N}_{\nu }}$.

1. На шаге $j$ проводятся вычисления по формулам (1.9)–(1.12);

2. Проверяется неотрицательность полученных значений во всех узлах;

3. Если хотя бы одно из полученных значений отрицательное, то производится пересчет по формулам (1.17)–(1.20).

4. Если хотя бы одно из вновь полученных значений отрицательное, то вклад исключается, и счетчик исключенных вкладов увеличивается на единицу.

5. По окончании цикла вычисляется коэффициент ${{\varepsilon }_{{{\text{tol}}}}}$, на основе которого делается вывод о достаточности числа узлов ${{N}_{\nu }}$ кубатурной сетки.

Заметим, что пересчет не приводит к замедлению основного цикла, так как число исключений на шаге 2 при выполнении условия (1.13) обычно не превышает долей процента. Асимптотическое свойство (1.3) сохраняется для тех вкладов, где функция распределения близка к максвелловской. Пересчет выпавших вкладов позволяет значительно сократить необходимое число узлов кубатурной сетки, чем достигается значительное ускорение вычисления интеграла столкновений.

При вычислении суммы (1.5) применяется равномерная кубатурная сетка Коробова [19], которая имеет оценку сходимости по числу узлов ${{N}_{\nu }}$ кубатурной сетки $O\left( {\frac{{\alpha \ln {{N}_{\nu }}}}{{N_{\nu }^{\alpha }}}} \right)$, где $\alpha \geqslant 1$ и зависит от гладкости интегрируемой функции. На каждом новом шаге по времени используется новая интеграционная сетка, которая получается из основной сетки периодическим сдвигом на случайный 8-мерный вектор: $\Sigma _{\nu }^{{t + \tau }} = \{ \Sigma _{\nu }^{t} + R_{8}^{{t + \tau }}\} $. Фигурные скобки обозначают периодический сдвиг сетки, а верхние индексы отмечают момент времени. Получается новая кубатурная сетка с теми же свойствами, что и основная. Эта сетка используется во всех узлах физического пространства, чем достигается лучшая гладкость решения по пространству. Одинаковая кубатурная сетка позволяет значительно уменьшить объем вычислений, так как наиболее затратные вычисления (скорости после столкновения, коэффициент ${{r}_{\nu }}$, сеточные узлы) находятся до входа в цикл (1.9)–(1.12) вычисления вкладов в интегралы столкновений по узлам кубатурной и пространственной сеток. Вклады в узлы пространственной сетки вычисляются параллельно на имеющемся числе процессов.

2. ОБТЕКАНИЕ ПЛОСКОЙ ПЛАСТИНЫ В РЕЖИМЕ СПЛОШНОЙ СРЕДЫ

Рассмотрим продольное обтекание плоской пластины при числе Маха $M = 0.5$ и числах Кнудсена ${\text{Kn}} = (0.01,0.001,0.0001)$. Первый случай близок к границе перехода в режим сплошной среды, в третьем и четвертом основное течение происходит заведомо в режиме сплошной среды.

Течение происходит в плоскости $x,\;y$. Пластина занимает отрезок $0 \leqslant x \leqslant L$ оси $x$. Поток газа с плотностью ${{n}_{0}}$, температурой ${{T}_{0}}$ и скоростью ${{u}_{0}}$ натекает слева вдоль оси $x$, которая является линией симметрии течения. Задача решается в области ${{x}_{{\min }}} \leqslant x \leqslant {{x}_{{\max }}},$ $0 \leqslant y \leqslant {{y}_{{\max }}}$ методом установления: в момент времени $t = 0$ пластина помещается в невозмущенный поток газа. На внешних границах области ставится условие невозмущенного потока с массовой скоростью ${{{\mathbf{u}}}_{0}} = ({{u}_{0}},0,0)$, соответствующей заданному числу Маха

На пластине ставится условие диффузного отражения в форме (2.1) с температурой стенки, равной температуре набегающего потока, но при нулевом значении ${{{\mathbf{u}}}_{0}}$ и при замене плотности ${{n}_{0}}$ на плотность отраженного потока ${{n}_{w}}$, которая определяется из условия непроницаемости пластины.

В уравнении Больцмана перейдем к безразмерным параметрам, переменным и функциям. Плотность и температуру газа будем относить к значениям ${{n}_{0}}$ и ${{T}_{0}}$ в невозмущенном потоке. В качестве характерных масштабов берем скорость ${{v}_{0}} = \sqrt {k{{T}_{0}}{\text{/}}m} $, длину свободного пробега молекул $\lambda = 1{\text{/}}(\sqrt 2 \pi {{n}_{0}}{{d}^{2}})$ и характерное время ${{\tau }_{0}} = \lambda {\text{/}}{{v}_{0}}$. В этих масштабах безразмерная скорость потока для $M = 0.5$ равна ${{u}_{0}} = 0.645$. Выберем молекулярную модель газа из твердых сфер диаметра $d = {{b}_{m}}$. Определим безразмерную функцию распределения $\tilde {f} = (n_{0}^{{ - 1}}v_{T}^{{ - 3}})f$ и безразмерный интеграл столкновений $\tilde {I} = n_{0}^{{ - 1}}\lambda v_{T}^{{ - 4}}I$. При сохранении для безразмерных величин прежних обозначений уравнение (1.1) запишется в виде

Интеграл столкновений и искомое решение являются четными функциями по компоненте скорости ${{\xi }_{z}}$, что позволяет вдвое уменьшить число узлов ${{N}_{0}}$ скоростной сетки ${{\Sigma }_{0}}$ и решать уравнение (2.2) только для положительных значений ${{\xi }_{z}}$. При вычислении интеграла столкновений по формулам (1.5) и (1.16) значения функции распределения для ${{\xi }_{z}} < 0$ берутся из зеркально отраженных узлов ${{\xi }_{z}} > 0$.

С учетом множителя перед интегралом и симметрии по ${{\xi }_{z}}$, коэффициент $B$ в формулах предыдущей главы изменится на $\tilde {B} = {{h}^{3}}N_{0}^{2}{\text{/}}(2\sqrt 2 {{N}_{\nu }})$, где произведена замена $V = {{h}^{3}}{{N}_{0}}$.

Область решения в физическом пространстве покрывается прямоугольной неравномерной сеткой. По оси $y$ сетка растягивается с шагом ${{h}_{{y,k + 1}}} = {{h}_{{y,k}}}(1 + {{d}_{y}})$начиная с $y = 0$. Аналогичное растяжение шага сетки применяется в двух направлениях по оси $x$ начиная от передней кромки пластины, и в двух направлениях по оси $x$ начиная от задней кромки. Коэффициенты растяжения ${{d}_{y}},\;{{d}_{x}}$ выбирались в диапазоне от 0.05 до 0.13. Коэффициенты ${{d}_{x}}$ отличаются у передней и задней кромок пластины, а также в зависимости от направлений изменения шага: внутрь пластины или от нее. Сетка строится так, чтобы шаги у пластины по оси $y$ и шаги по оси $x$ около передней и задней кромок пластины были существенно меньше длины свободного пробега. В других областях течения шаги сетки достигают нескольких длин свободного пробега для ${\text{Kn}} = 0.01$, десятков длин свободного пробега для ${\text{Kn}} = 0.001$ и сотен длин свободного пробега для ${\text{Kn}} = 0.0001$. Скоростная сетка ${{\Sigma }_{0}}$ строится в области $\Omega {\text{/}}2$, которая является полусферой радиуса ${{u}_{R}}$ с центром в ${{u}_{0}}$, следующим образом. Сначала создается равномерная сетка в прямоугольной области $ - {{u}_{R}} + {{u}_{0}} \leqslant {{\xi }_{x}} \leqslant {{u}_{R}} + {{u}_{0}}$, $ - {{u}_{R}} \leqslant {{\xi }_{y}} \leqslant {{u}_{R}}$, $0 \leqslant {{\xi }_{z}} \leqslant {{u}_{R}}$. Затем в эту область вписывается полусфера и оставляются только узлы – центры ячеек, которые лежат внутри полусферы. Объем области $\Omega {\text{/}}2$ равен $V{\text{/}}2 = {{N}_{0}}{{h}^{3}}$, где ${{N}_{0}}$ – число узлов внутри полусферы. Аналогично строится кубатурная сетка ${{\Sigma }_{\nu }}$ в пространстве скоростей ${\mathbf{\xi }},\;{{{\mathbf{\xi }}}_{*}}$, но исходная область является гиперкубом, включающим также отрицательные значения ${{\xi }_{z}}$, а $\Omega \times \Omega $ есть 6-мерная сфера радиуса ${{u}_{R}}$ с центром ${{u}_{0}}$.

При расчетах было взято ${{u}_{R}} = 5.6{{v}_{0}} = 4{{v}_{T}}$, где ${{v}_{T}}$ – тепловая скорость. При таком размере области решения в скоростном пространстве функция распределения набегающего потока на границе области ${{f}_{M}}({{u}_{R}}) < {{10}^{{ - 7}}}{{f}_{M}}({{u}_{0}})$, а отраженная от пластины функция ${{f}_{W}}({{u}_{R}}) < {{10}^{{ - 5}}}{{f}_{W}}(0)$. Скоростная сетка состояла из ${{N}_{0}} = 3604$ узлов, которые остаются в полусфере, вписанной в полу-куб из $24 \times 24 \times 12$ узлов, или из ${{N}_{0}} = 7164$ узлов, остающихся из $30 \times 30 \times 15$ узлов в полу-кубе. Кубатурная сетка, в зависимости от шага $\tau $ и числа узлов ${{N}_{0}}$, насчитывала от ${{N}_{\nu }} = 25\,000$ до ${{N}_{\nu }} = 75\,000$ узлов. Во всех расчетах обеспечивалось условие ${{\varepsilon }_{{{\text{tol}}}}} = 0$.

Решение уравнения адвекции в методе расщепления (1.2) осуществлялось по схеме второго порядка точности типа предиктор-корректор [20], которая ранее использовалась в работах [6–9]. С учетом симметричного расщепления на два этапа, шаг по времени $\tau $ выбирался из условия $\tau = 0.9{{h}_{y}}{\text{/}}{{u}_{R}}$, где ${{h}_{y}}$ – минимальный шаг пространственной сетки, равный первому шагу по оси $y$ около пластины.

В качестве иллюстраций приводятся поля плотности, температуры и нормальной к пластине компоненты скорости газа $v(x,y){\text{/}}{{u}_{0}}$, а также графики скорости скольжения на пластине ${{u}_{W}}(x) = u(x,0){\text{/}}{{u}_{0}}$ и трения ${{F}_{w}}(x) = {{P}_{{xy}}}(x,0){\text{/}}{{J}_{p}}$. Для нормировки использованы скорость потока газа ${{u}_{0}}$ и характерный поток импульса ${{J}_{p}} = u_{0}^{2}{\text{/}}2$. Величины $u(x,0)\,,{{P}_{{xy}}}(x,0)\,$ вычисляются как соответствующие суммы от граничной функции $f_{i}^{{(w)}}({{{\mathbf{\xi }}}_{\gamma }})$, определенной на прилежащих к пластине гранях ячеек. Функция $f_{i}^{{(w)}}({{{\mathbf{\xi }}}_{\gamma }})$ состоит из двух частей: функции в центре ячейки ${{f}_{{i,1}}}({{{\mathbf{\xi }}}_{\gamma }})$ для ${{\xi }_{{\gamma ,y}}} < 0$, и отраженной от пластины функции ${{f}_{{M,i}}}({{{\mathbf{\xi }}}_{\gamma }})$ при ${{\xi }_{{\gamma ,y}}} > 0$:

Все расстояния на фигурах отнесены к длине пластины. Передняя кромка пластины находится в точке $x = 0,$ $y = 0$, задняя кромка в точке $x = 1,$ $y = 0$. На графиках полей плотности и температуры приведены значения $n{\kern 1pt} * = 100(n(x,y) - 1)$ и $T{\kern 1pt} * = 100 \cdot (T(x,y) - 1)$.

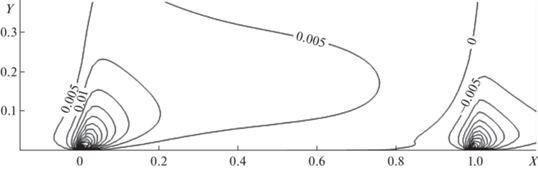
Для случая ${\text{Kn}} = 0.01$ было проведено два расчета при разных скоростных сетках. Число узлов пространственной сетки равнялось ${{k}_{x}}{{k}_{y}} = 166 \times 61$, минимальные шаги сетки ${{h}_{{x,0}}} = 0.333,$ ${{h}_{{y,0}}} = 0.2$. На фиг. 1 представлены поля плотности, полученные на скоростной сетке из N₀ = ${\text{ = }}\;7164$ узлов (сплошные линии) и на сетке из ${{N}_{0}} = 3604$ (штриховые линии). Поля плотности на разных сетках отличаются незначительно. Такой же результат дает сравнение полей температуры и поперечной скорости. Графики скорости скольжения и трения практически совпадают. Можно сделать вывод, что сетка из ${{N}_{0}} = 3604$ скоростных узлов является достаточной. На фиг. 2 изображено поле температуры. Интересной особенностью является образование области с небольшим, порядка 0.5%, понижением температуры.

На фиг. 3 показано поле поперечной скорости. У передней кромки поток газа отклоняется вверх, а у задней кромки и на довольно большом расстоянии за ней возникает возвратный поток к оси течения.

Расчеты для $Kn = 0.001$ осуществлялись на двух разных скоростных и пространственных сетках. Первый расчет при ${{N}_{0}} = 3604$, ${{h}_{{x,0}}} = 0.333,$ ${{h}_{{y,0}}} = 0.2$, ${{k}_{x}}{{k}_{y}} = 250 \times 80$, второй – при ${{N}_{0}} = 7164$, ${{h}_{{x,0}}} = 0.5,$ ${{h}_{{y,0}}} = 0.333$, ${{k}_{x}}{{k}_{y}} = 222 \times 68$. На фиг. 4 показано сравнение полей плотности по первому расчету (сплошные линии) и по второму (штриховые линии).

На фиг. 5 и 6 показаны, соответственно, поля температуры и поперечной скорости, рассчитанные по первому набору параметров.

Области пониженной температуры не наблюдается. Потоки газа от пластины у передней кромки и к линии симметрии у задней кромки менее интенсивны и разделены областью с нулевой поперечной скоростью.

Наиболее трудоемким является расчет для ${\text{Kn}} = 0.0001$. Были выбраны следующие параметры счета: ${{N}_{0}} = 3604$, ${{h}_{{x,0}}} = 0.5,$ ${{h}_{{y,0}}} = 0.333$, ${{k}_{x}}{{k}_{y}} = 300 \times 112$. Шаг по времени $\tau = 0.06$, число узлов кубатурной сетки было равно ${{N}_{\nu }} \approx 25\,000$ в первом расчете и ${{N}_{\nu }} \approx 50\,000$ во втором. Результаты расчетов полностью совпали. Поля плотности, температуры, поперечной скорости представлены на фиг. 7–9 соответственно. Основное изменение плотности и поперечной скорости происходит вблизи поверхности пластины. На фиг. 7 и 9 показана именно эта область течения. Газ прогревается в значительно большей области, что видно на фиг. 8, где показана вся расчетная область.

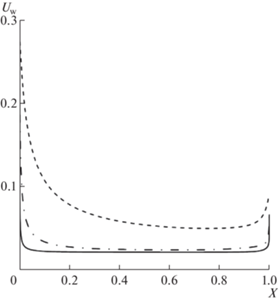
На фиг. 10 и 11 для разных чисел Кнудсена представлены распределения по длине пластины скорости скольжения ${{U}_{w}}$ и силы трения ${{F}_{w}}$ соответственно. Сплошной линией показаны данные для ${\text{Kn}} = 0.0001$, штрихпунктирной – для ${\text{Kn}} = 0.001$ и штриховой – для ${\text{Kn}} = 0.01$. Для всех чисел Кнудсена имеются локальные максимумы скорости скольжения и трения у передней и задней кромок пластины. Скорость скольжения в центральной части пластины заметно отличается от нуля. Таким образом, при расчете рассмотренных течений на основе уравнений Навье–Стокса следует использовать условия скольжения, отражающие указанные особенности.

Контроль сходимости к стационарному состоянию осуществлялся на основе сравнения полей течения и графиков аэродинамических реакций на пластине. Характерным масштабом времени для сходимости является t_Kn = ${{\tau }_{0}}{\text{/}}(\sqrt {3{\text{/}}2} \operatorname{Kn} )$ = $0.8{{\tau }_{0}}{\text{/Kn}}$ – время распространения звука от передней до задней кромок пластины. Для Kn = 0.01 потребовалось время стабилизации t_st = 8t_Kn, для Kn = 0.001 время стабилизации составило t_st = 2t_Kn, для Kn = 0.0001 сходимость наступает при t_st = 1.2t_Kn. Быстрая сходимость при Kn = 0.0001 объясняется тем, что возмущенная область близко прилегает к пластине.

Наибольшее процессорное время потребовалось для Kn = 0.0001 и составило 125 ч при N_ν ≈ 25 000, и 180 ч при N_ν ≈ 50 000 на 8-ядерном процессоре i7-11800H, 2.30 GHz. Отношение времени счета стадии релаксации к полному времени счета в первом варианте равно 0.46, во втором равно 0.62.

ЗАКЛЮЧЕНИЕ

Были представлены примеры решения уравнения Больцмана для продольного дозвукового обтекания плоской пластины при трех отличающихся на порядок значений числа Кнудсена: Kn = (0.01, 0.001, 0.0001). Течение при Kn = 0.01 можно отнести к границе режима сплошной среды. Два других примера относятся к режиму течения, в большей части области счета описываемому уравнениями Навье–Стокса. Решения получены на основе консервативного проекционного метода вычислений интеграла столкновений Больцмана, сохраняющего главный член асимптотики Энскога–Чепмена. Была применена оптимизация метода, которая обеспечивает стабильность счета и значительно увеличивает скорость вычислений. Расчеты выполнены на персональном компьютере средней производительности.

Современным способом моделирования течений в режиме сплошной среды является сращивание решения уравнений Навье–Стокса в основной области с решением кинетического уравнения вблизи поверхности тела. Этот метод позволяет значительно сократить область физического пространства, где решается кинетическое уравнение. Он намного экономичнее, чем представленный в данной статье, однако содержит две существенные проблемы при его реализации. Первая состоит в корректном выборе границ сращивания уравнений Больцмана и Навье–Стокса. Вторая – в обеспечении строгого баланса потоков массы, импульса и энергии через границу сращивания при сохранении не отрицательности функции распределения. Для этого метода требуется более сложный код, который включает решение кинетического уравнения, решение уравнений Навье–Стокса, сращивание этих решений на границах областей, проверку правильности выбора границ сращивания. Представленный в статье метод прост в реализации, но требует значительно более интенсивных вычислений. Его возможности будут возрастать с прогрессом вычислительных устройств.

В работе [21] приведены расчеты течений сплошной среды, выполненные методом прямого статистического моделирования (DSMC) на суперкомпьютере большой мощности. В этом методе асимптотическое свойство решения не используется, что сделало расчеты исключительно интенсивными.

Сравнение с решением уравнений гидродинамики и оценка существующих моделей граничных условий скольжения заслуживают отдельного исследования.