Автоматика и телемеханика, № 8, 2019
Оптимизация, системный анализ
и исследование операций
© 2019 г. Е.А. ВОРОНЦОВА, канд. физ.-мат. наук (vorontsovaea@gmail.com)
(Дальневосточный федеральный университет, Владивосток;
Университет Гренобль Альпы, Гренобль),
А.В. ГАСНИКОВ, д-р физ.-мат. наук (gasnikov@yandex.ru)
(Московский физико-технический институт;
Национальный исследовательский университет
“Высшая школа экономики”, Москва;
Кавказский математический центр,
Адыгейский государственный университет, Майкоп),
Э.А. ГОРБУНОВ (ed-gorbunov@yandex.ru)
(Московский физико-технический институт),
П.Е. ДВУРЕЧЕНСКИЙ, канд. физ.-мат. наук (pavel.dvurechensky@gmail.com)
(Институт прикладного анализа и стохастики им. Вейерштрасса, Берлин)
УСКОРЕННЫЕ БЕЗГРАДИЕНТНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ
С НЕЕВКЛИДОВЫМ ПРОКСИМАЛЬНЫМ ОПЕРАТОРОМ1
Предлагается ускоренный безградиентный метод с неевклидовым прок-
симальным оператором, связанным с p-нормой (1 ≤ p ≤ 2). Получены
оценки скорости сходимости метода в условиях малого шума, возникаю-
щего при вычислении значения функции. Представлены результаты вы-
числительных экспериментов.
Ключевые слова: ускоренные методы оптимизации, выпуклая оптимиза-
ция, безградиентные методы, неточный оракул, неевклидов проксималь-
ный оператор, прокс-структура.
DOI: 10.1134/S0005231019080117
1. Введение
В данной статье рассматриваются безградиентные методы выпуклой
оптимизации, называемые также методами нулевого порядка [1-3]. Основной
1 Исследование в разделе 3 выполнено за счет Российского научного фонда (про-
ект № 17-11-01027). В остальных разделах исследование А.В. Гасникова выполнено в
рамках господдержки ведущих университетов Российской Федерации “5-100”, а также
было поддержано Российским фондом фундаментальных исследований (проект № 18-
31-20005 мол-а-вед), работа Э.А. Горбунова была поддержана грантом Президента РФ
МД-1320.2018.1, работа П.Е. Двуреченского и Е.А. Воронцовой была поддержана Россий-
ским фондом фундаментальных исследований (проект № 18-29-03071 мк).
149
особенностью этих методов является предположение о доступности только
значения целевой функции, но недоступности градиента или гессиана. Такая
ситуация возникает, например, если значение функции вычисляется с помо-
щью некоторой вспомогательной компьютерной программы и доработка этой
программы для вычисления градиента стоит дороже, чем машинное время.
Кроме того, в отличие от вычисления значения функции, вычисление гради-
ента может быть вычислительно нестабильным, например, в глубинных ней-
ронных сетях при использовании обратной прогонки (backpropagation) [4-7].
В [8, 9] были предложены ускоренные методы нулевого порядка 2 (безгра-
диентные методы) решения задач гладкой выпуклой безусловной оптимиза-
ции. В отличие от известных до [8, 9] методов ускоренные методы обладают
более высокой скоростью сходимости. В рассуждениях [9] существенным об-
разом использовалось то, что был выбран именно евклидов проксимальный
оператор (далее будем называть его прокс-структурой, это выпуклая глад-
кая функция, порождающая расстояние, и 1-сильно выпуклая относительно
какой-то нормы; строгое определение вводится в разделе 3). Такой выбор
прокс-структуры для задач безусловной оптимизации является вполне есте-
ственным (см., например, [11]). Однако в ряде задач имеется дополнительная
информация, которая, например, позволяет рассчитывать на разреженность
решения (когда в решении большая часть компонент нулевые). В частности,
во многих задачах анализа данных существенным оказывается небольшое
число признаков (потому и решения соответствующих задач обучения оказы-
ваются разреженными). Кроме того, во многих задачах обучения с подкреп-
лением одновременно выполняются два условия: 1) нет возможности считать
градиент, есть только возможность считать зашумленное значение целевой
функции (см., например, [12]); 2) при выборе параметрической модели часто
сложно сразу правильно угадать параметрическое представление и часть па-
раметров оказываются малозначимыми (лишними), что и обеспечивает раз-
реженность. Кроме того, тот же эффект наблюдается, если выбирать точку
старта так, чтобы разность между точкой старта и решением была разре-
женным вектором. Наконец, даже если вдруг это не выполняется, получен-
ные результаты свидетельствуют о том, что предложенный в статье метод с
неевклидовой прокс-структурой будет работать не хуже, чем в евклидовом
случае.
В [13] был предложен ускоренный спуск (опирающийся на метод из [14])
по случайному направлению и получена оценка скорости сходимости. В [13]
метод использовал проекцию градиента на случайное направление. В данной
статье используется не сама проекция градиента на случайное направление, а
ее аппроксимация конечной разностью, т.е. приближение, которое не исполь-
зует градиент. Кроме того, рассматривается случай, когда значения функции
известны с некоторым ограниченным по абсолютной величине шумом.
2 Здесь и далее термин “ускоренный” для безградиентных методов означает точно то
же самое, что и для методов первого порядка (градиентных), см., в частности, описание
основополагающего и очень популярного в последние годы ускоренного (быстрого, момент-
ного) градиентного метода Нестерова [10]. Ускоренный метод имеет скорость сходимости,
пропорциональную 1/k2, где k - номер итерации. В отличие от него неускоренный метод
имеет скорость сходимости по значению целевой функции, пропорциональную 1/k.
150
2. Постановка задачи
Рассматривается разрешимая задача гладкой выпуклой оптимизации
(1)
f (x) → min ,
x∈Rn
где функция f (x), заданная на Rn, имеет липшицев градиент с константой L
в 2-норме
(2)
∥∇f (y) - ∇f (x)∥2 ≤ L∥y - x∥2
∀ x, y ∈ Rn.
При этом в точке минимума x∗ выполнено равенство ∇f (x∗) = 0.
В [13] для решения задачи (1) вместо обычного градиента использовалась
его стохастическая аппроксимация, построенная на базе производной по слу-
чайно выбранному направлению [15]
g (x, e) = n 〈∇f (x) , e〉 e,
где e — случайный вектор, равномерно распределенный на Sn2 (1) — единич-
ной сфере в 2-норме в пространстве Rn (e ∈ RSn2 (1) — под этой записью бу-
дем понимать, что случайный вектор e имеет равномерное распределение на
n-мерной единичной евклидовой сфере с центром в нуле), а угловые скоб-
ки 〈·, ·〉 обозначают стандартное скалярное произведение векторов.
В отличие от [13], будем использовать не 〈∇f(x), e〉 e, а приближенный
аналог
f (x + te) - f(x)
e, t > 0.
t
Более того, предположим, что оракул3 может выдавать значение функции в
любой точке, но с некоторым шумом δ(x), т.е. от оракула получаем значения
f (x) = f(x) + δ(x), поэтому на практике будем вынуждены использовать
f (x + te)
f (x)
e
t
вместо 〈∇f(x), e〉 e.
Итак в силу сделанных предположений теперь работаем не с истинной
производной по направлению, а с ее приближенным аналогом4
= (〈∇f(x), e〉 + δ∇(x, t, e)) e,
3 Здесь и далее под оракулом понимается подпрограмма расчета значений целевой
функции и/или градиента (его части), а оптимальность метода на классе задач понимается
в смысле Бахвалова-Немировского [16] — как число обращений (по ходу работы метода) к
оракулу для достижения заданной точности (по функции).
4 Строго говоря, вектор
∇δ,tf(x) определяется из приведенного выражения не един-
ственным образом, однако данное обозначение крайне удобно использовать для записи
метода и доказательств. Кроме того, нигде в работе авторы не пользуются конкретным вы-
бором
∇δ,tf(x), везде существенную роль играет выражение 〈∇δ,tf(x), e〉e, которое опре-
деляется однозначно.
151
где δ∇(x, t, e) — ошибка приближения значения 〈∇f(x), e〉, связанная с вы-
числительной ошибкой (значения функции известны с некоторым шумом) и
с аппроксимационной ошибкой метода приближения, т.е.
δ(x + te) - δ(x)
f (x + te) - f(x)
δ∇(x, t, e) =
+
- 〈∇f(x), e〉
t
t
!
!
вычислительная ошибка
ошибка метода
Ограничимся рассмотрением следующей концепции абсолютной неточно-
сти оракула. Пусть про шум известно, что ∀ x ∈ Rn ↪→ |δ(x)| ≤ δ. Оценим
|δ∇(x, e, t)|:
|δ(x + te)| + |δ(x)|
f (x + te) - f(x)
2δ
Lt
|δ∇(x, e, t)| ≤
+
- 〈∇f(x), e〉≤
+
,
t
t
t
2
где последнее слагаемое в правой части возникает в силу неравенства
L
f (x + te) - f(x) - 〈∇f(x), x + te - x〉 ≤
||x + te - x||22,
2
которое следует из (2). Выберем параметр t = t∗ так, чтобы минимизировать
значение верхней оценки на δ∇(x, e, t). Параметр t∗ находится из условия
√
2δ
L
δ
-
+
=0 ⇒ t∗ =2
(t∗)2
2
L
Тогда
√
(3)
|δ∇(x, e, t∗)| ≤ 2
= δ
Везде далее будем использовать параметр t = t∗, поэтому можно писать
δ∇(x, e, t∗) = δ∇(x, e). Кроме того, для упрощения нотации будем исполь-
зовать обозначение∇f(x) вместо∇δ,tf(x).
3. Ускоренный безградиентный метод
Введем дивергенцию Брэгмана Vz (y), связанную с p-нормой:
= d(y) - d(z) - 〈∇d(z), y - z〉,
где функция d(x) является непрерывно дифференцируемой и сильно выпук-
лой с константой сильной выпуклости, равной единице (и называется прокс-
функцией, или прокс-структурой, связанной с p-нормой). Например, для p =
= 1 функцию d(x) можно взять такой:
1
d(x) =
||x||2a,
2(a - 1)
2 log n
где a =
. Кроме того, пусть q — такое число, что 1p + 1q = 1.
2 log n-1
152
Введем следующие объекты:
+
,
1
= x-
∇f (x), e e,
L
{ +
+
,
,
}
= argmin α n
∇f (x) , e e, y - z + Vz (y)
,
y∈Rn
где
= (〈∇f(x), e〉 + δ∇(x, e)) e.
Также обозначим (см. теорему 1 из [17], формулировка приведена в Прило-
жении)
√
2
(4)
=
3min{2q - 1,32ln n - 8}n
q
+1.
Опишем ускоренный безградиентный метод (Accelerated by Coupling
Derivative-Free Method — ACDF) (см. алгоритм 1). Обращение к оракулу це-
левой функции происходит на шагах вычисления значений Gradek+1 (xk+1) и
Mirrek+1 (xk+1, zk, αk+1).
Алгоритм. (ACDF)
Вход: оракул, выдающий значение функции f (выпуклой дифференцируе-
мой функции на Rn с липшицевым градиентом с константой L по от-
ношению к 2-норме) в любой точке x с некоторым шумом δ(x); x0 —
некоторая стартовая точка; N — количество итераций.
Выход: точка yN .
1: y0 ← x0, z0 ← x0
2: for k = 0, . . . , N - 1 do
k+2
1
2
3:
αk+1 ←
, τk ←
=
4LCn,q
2αk+1LCn,q
k+2
4:
Генерируется ek+1 ∈ RSn2 (1), независимо от предыдущих итераций
5:
xk+1 ← τkzk + (1 - τk)yk
6:
yk+1 ← Gradek+1(xk+1)
7:
zk+1 ← Mirrek+1(xk+1, zk, αk+1)
8: end for
9: return yN
Схема доказательства оценки скорости сходимости ACDF близка к схе-
ме доказательства теоремы в [13] и опирается на две следующие леммы, в
которыхδ определена в (3).
153
1
Лемма 1. Если τk =
, то для всех u ∈ Rn верны неравенства
2αk+1LCn,q
αk+1〈∇f(xk+1), zk - u〉 ≤
≤ 2α2
LCn,q(f(xk+1) - Eek+1[f(yk+1)]) + Vzk (u) - Eek+1[Vzk+1(u)] +
(5)
k+1
7
+
α2k+1Cn,qδ2 +
√nδαk+1||u - zk||p, q ≥ 2, n ≥ 8.
4
Лемма 2. Для всех u ∈ Rn выполнено
2α2k+1LCn,qEe
[f(yk+1) | e1, . . . , ek] -
k+1
− (2α2
LCn,q - αk+1)f(yk) + Eek+1[Vzk+1(u)] - Vzk (u) -
(6)
k+1
7
−
α2k+1Cn,qδ2 -
√nδαk+1||u - zk||p ≤ αk+1f(u), q ≥ 2, n ≥ 8.
4
Теорема. Пусть f(x) — выпуклая дифференцируемая функция на Rn с
константой Липшица для градиента, равной L, d(x) — 1-сильно выпуклая
в p-норме функция на Rn, N ∈ NN. Тогда ACDF на выходе даст точку yN ,
удовлетворяющую неравенству
√
16ΘLCn,q
35Nδ
16
2ΘnLδ
8nN2δ
(7)
E[f(yN )] - f(x∗) ≤
+
+
+
,
N2
4
N2
Cn,q
= Vx0(x∗), q ≥ 2,n ≥ 8, а Cn,q определено в (4).
Таким образом, теорема утверждает, что алгоритм ACDF через N итера-
ций выдаст точку yN , удовлетворяющую неравенству E[f(yN )] - f(x∗) ≤ ε,
(√
)
ΘLCn,q
5
ε > 0, если N = O
и шум δ такой, что
ε
(
{
})
ε2
C2n,qΘL
ε2
δ = O min
√
,
,
=
ΘLCn,q
n
nΘL
(8)
(
{
})
2
ε2
ε
= O min
√
,
ΘLCn,q
nΘL
√
5 Если N ∼ΘLCn,q
(оценивается порядок величины, числовые константы не учиты-
ε
ваются), то
√
(
)
7(N + 2)(2N + 3)δ
ΘLCn,q
ε2
∼Nδ ∼
δ ⇒ δ=O
√
,
6(N + 1)
ε
ΘLCn,q
√
√
)
16
2ΘnLδ
ε
nδ
(ΘLC2n,q
∼
√
⇒ δ=O
,
(N + 1)2
ΘLCn,q
n
(
)
8nN4δ
nN2δ
nΘLδ
ε2
∼
∼
⇒ δ=O
Cn,q (N + 1)2
Cn,q
ε
nΘL
154
√
2
По определению (см. (4)) Cn,q =
3 min{2q - 1, 32ln n - 8}nq +1, а в случае
p = 2, q = 2 можно взять Cn,q = n2, что видно из теоремы 1 в [17] и лем-
мы B.10 из [18] (формулировки приведены в Приложении), поэтому минимум
достигается на втором аргу (нте, т.е)если не учитывать еще и константы Θ
(
)
√
ε2
ΘLn2
и L, то δ = O
иN =O
n
ε
√
Если же p = 1, q = ∞, то Cn,q = n
3 (32 ln n - 8) и
(√
)
(
{
})
ΘLn lnn
ε2
ε2
N =O
,
δ = O min
√
,
ε
ΘLn ln n
nΘL
4. Неускоренный безградиентный метод
Для сопоставления рассмотрим неускоренный метод
{
}
xk+1 = argmin
α〈n〈∇f(xk), ek+1〉ek+1, y - xk〉 + Vx
(y)
k
y∈Rn
Можно показать, что данный метод за N итераций генерирует последова-
тельность точек x0, x1, . . . , xN , такую что
√
16ΘLCn,q
8
2nΘLδ
8n2Nδ
(9)
E[f(xN )] - f(x∗) ≤
+
+ 3nδ +
,
nN
N
Cn,q
(
)
1
∑N-1
ε2
где xN =
xk. Оказывается, что нужно брать δ = O
(как и в
N k=0
n
ускоренном случае), чтобы получить ε-решение по функции.
5. Численные эксперименты
Для практического применения предложенный ускоренный безградиент-
ный метод ACDF был реализован на языке программирования Python. Так-
же была реализована концепция неточно заданного оракула. Был рассмотрен
случай, когда неточность порождается только неточностью вычисления целе-
вой функции. Зашумления производились на каждой итерации, независимо
от предыдущих, случайным образом из отрезка [-δ, δ], где максимально воз-
можная для шума граница δ вычислялась по (8). Код метода и демонстрация
вычислительных свойств метода с построением графиков сходимости доступ-
ны как Jupyter Notebook и выложены в свободном доступе на Github [19].
Рассмотрим следующую з а д а ч у. Пусть A — матрица размеров n × n
со случайными независимыми элементами, равномерно распределенными
A⊤A
на [0, 1], а матрица B =
, где λmax(A⊤A) — максимальное соб-
λmax(A⊤A)
ственное значение матрицы A⊤A.
Необходимо минимизировать функцию
1
(10)
f (x) =
〈x - x∗, B(x - x∗)〉 , x ∈ Rn,
2
155
100
101
102
103
104
0
200
400
600
800
1000
1200
1400
N
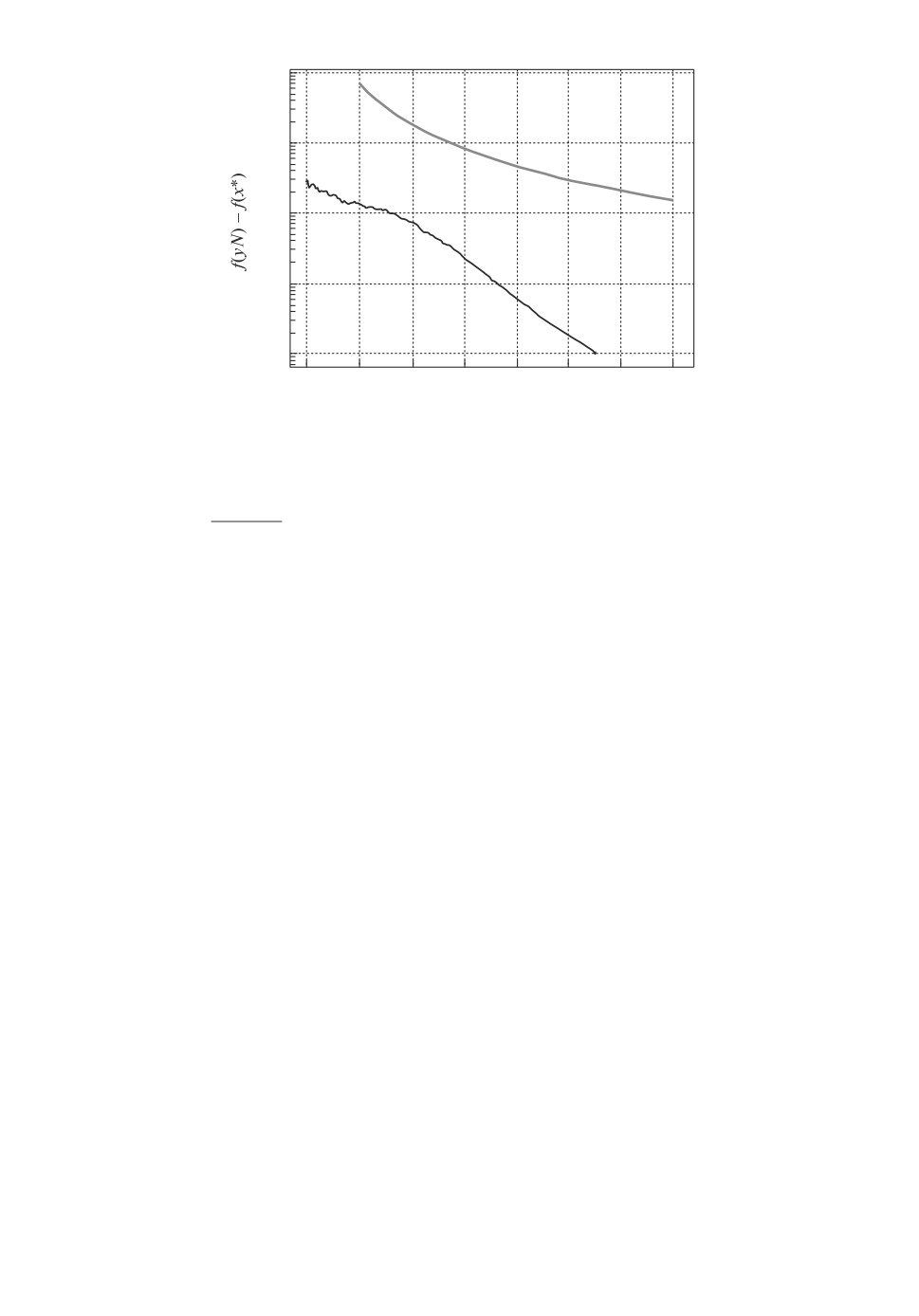
Рис. 1. Сходимость метода ACDF для функции (10), размерность n = 10. По-
казана практическая зависимость точности нахождения минимума f(yN ) -
- f(x∗) от числа итераций N алгоритма — темный график и теоретическая
(
)
16ΘLCn,q
оценка O
— светлый график.
N2
где x∗ = (1, 0, 0, . . . , 0)⊤. Решение этой задачи известно и равно x∗, f(x∗) =
= 0. Начальная точка x0 для всех экспериментов выбиралась как δ′, где δ′ ∈
∈ [-δ, δ]. Константа Липшица градиента целевой функции L = 1.
Для различных n, заданной точности ε и заданной границы максимально-
го шума δ были рассчитаны теоретически требуемые значения числа итера-
ций по теореме 3 и проведена проверка сходимости на практике. Для данной
задачи во всех случаях практическая скорость сходимости по функции была
выше. Так, например, для n = 10, ε = 10-4, δ = 2,1715 · 10-10 заданная точ-
ность была достигнута за 1106 итераций (см. рис. 1), а теоретическая оценка
числа итераций дает 17215 итераций. Далее, для n = 103, ε = 10-4 теорети-
ческая оценка числа итераций дает не более чем 527756 итераций. По факту
алгоритм завершил работу за 141476 итераций (см. рис. 2).
При проведении численных экспериментов также были подтверждены ре-
зультаты зкспериментов в [13]: и для ускоренного безградиентного метода
преимущество выбора проксимального оператора, связанного с 1-нормой, воз-
никает только для задач средней и большой размерности (от n = 1000). Будет
ли иметь преимущество предложенный метод, можно определить, сравнив
теоретические оценки числа итераций из теоремы 3 для разных p. На рис. 2
показаны случаи, когда ускоренный безградиентный метод с неевклидовой
прокс-структурой работает быстрее ускоренного безградиентного метода с ев-
клидовой прокс-структурой. Сравнение этого эксперимента для ускоренного
безградиентного метода (с неточным оракулом) с таким же, но для ускорен-
ного спуска по случайному направлению (с точным оракулом) из [13] (см.
рис. 2,б ), показывает, что принципиальный результат тот же, но скорость
сходимости оказывается хуже, что вполне естественно для метода нулевого
порядка с неточным оракулом.
156
104
а
104
б
3,0
3,0
4
2,5
2,5
3
2
2,0
2,0
1,5
1,5
1
1,0
1,0
0
40 000
80 000
120 000
0
40 000
80 000
120 000
N
N
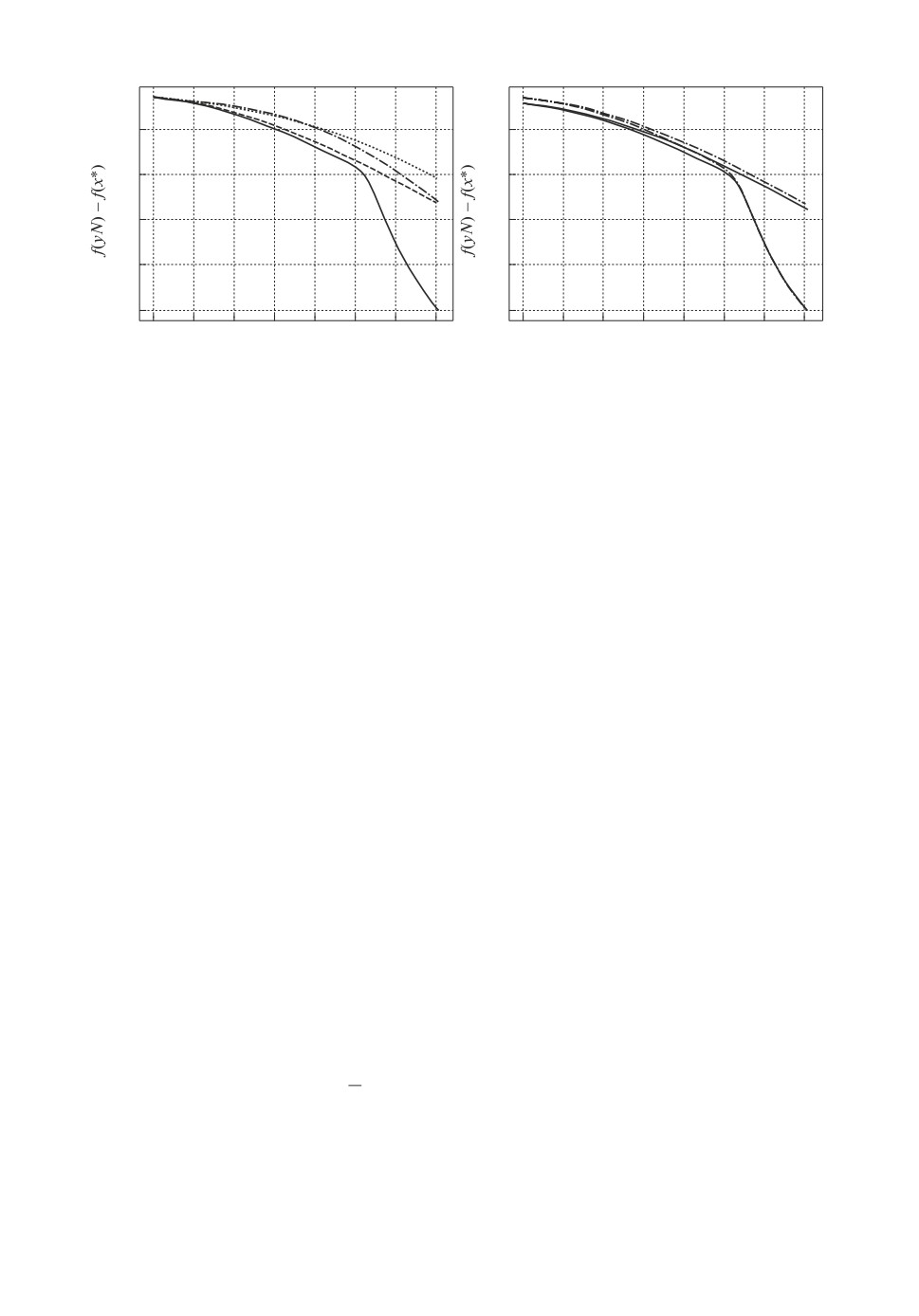
Рис. 2. Сходимость метода ACDF для функции (10), размерность n = 103,
точность ε = 10-4. Показана практическая зависимость точности нахождения
минимума f(yN ) - f(x∗) от числа итераций N алгоритма (а), график 1. Также
для сравнения на рис. 2,а приведены результаты работы метода при других p
(евклидова норма — график 2; p = 1,8 — график 3; p = 1,9 — график 4) при
одних и тех же генерируемых ek и точке старта x0. На рис. 2,б приведены
результаты сравнения на той же задаче работы метода ACDF (пунктирная
линия) и ускоренного неевклидового спуска ACDS [13] (сплошная линия, гра-
фик 1), предназначенного для работы с точным оракулом первого порядка.
Также на рис. 2,б приведены результаты работы указанных методов при p = 2
(график 2, штрихпунктирная линия —ACDF, сплошная линия —ACDS).
В целом, численные эксперименты с ускоренным безградиентным методом
подтверждают теоретические результаты.
6. Заключение
В статье предложен ускоренный безградиентный метод и рассмотрен
неускоренный безградиентный метод. Безградиентные методы рассматрива-
ются в условиях наличия малого шума, возникающего при вычислении зна-
чения функции. Полученные оценки скорости сходимости ускоренного без-
градиентного метода в условиях малого шума подтверждены результатами
вычислительных экспериментов.
В отличие от известных вариантов безградиентных методов (см., напри-
мер, [9]) в данной статье рассматриваются безградиентные методы с неевкли-
довым проксимальным оператором. В случае, когда 1-норма решения близка
к 2-норме решения (это имеет место, например, если решение задачи раз-
режено — имеет много нулевых компонент), предлагаемый подход улучшает
оценку на необходимое число итераций, полученную оптимальным методом
из [9], приблизительно в
√n раз, где n — размерность пространства, в кото-
ром происходит оптимизация.
Данная статья продолжает цикл работ, открытый публикацией [13] (см.
также [20]). Далее планируется распространить приведенные в настоящей
статье результаты на задачи стохастической оптимизации и распространить
все эти результаты на случай сильно выпуклой функции.
157
ПРИЛОЖЕНИЕ
Доказательство леммы 1. Во-первых,
(Π.1)
αk+1〈n〈∇f(xk+1), ek+1〉ek+1, zk - u〉 =
= 〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk - zk+1〉 +
○
+ 〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk+1 - u〉
≤
○
≤ 〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk - zk+1〉 + 〈-∇Vz
=
k
○
○
= 〈αk+1n〈∇
f (xk+1), ek+1〉 ek+1, zk - zk+1〉 + Vzk (u) - Vzk+1 (u) - Vzk (zk+1)
≤
(
)
○
≤
〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk - zk+1〉 -1||zk - zk+1||2
p
+
2
+ Vzk(u) - Vzk+1(u),
где ○ выполнено в силу того, что
{
}
zk+1 = argmin
Vzk (z) + αk+1〈n〈∇f(xk+1), ek+1〉ek+1, z〉 ,
z∈Rn
откуда следует, что 〈∇Vzk (zk+1) + αk+1n〈∇f(xk+1), ek+1〉 ek+1, u - zk+1〉 ≥ 0
для всех u ∈ Rn, ○ выполнено в силу равенства треугольника для дивер-
генции Брэгмана6, ○ выполнено, так как Vx(y) ≥12 ||x - y||2p в силу сильной
выпуклости прокс-функции d(x).
Аналогично доказательству (П.3) из [13] можно показать, что
〈αk+1n〈∇f(xk+1), ek+1〉 ek+1, zk - zk+1〉 -1||zk - zk+1||2p ≤
2
α2k+1n2
≤
|〈∇f(xk+1), ek+1〉|2||e||2q =
2
α2k+1n2
○
(Π.2)
=
(〈∇f(xk+1), ek+1〉 + δ∇(xk+1, ek+1))2||e||2q
≤
2
○
○
≤ α2k+1n2〈∇f(xk+1), ek+1〉2||ek+1||2q + α2k+1n2δ2∇(xk+1,ek+1)||ek+1||2q
≤
○
≤ α2k+1n2〈∇f(xk+1), ek+1〉2||ek+1||2q + α2k+1n2δ2||ek+1||2q,
6 Действительно,
∀x, y ∈ Rn
〈-∇Vx(y), y - u〉 = 〈∇d(x) - ∇d(y), y - u〉 = (d(u) - d(x) - 〈∇d(x), u - x〉)-
-(d(u) - d(y) - 〈∇d(y), u - y〉) - (d(y) - d(x) - 〈∇d(x), y - x〉) = Vx(u) - Vy(u) - Vx(y).
158
где ○ следует из неравенства (a + b)2 ≤ 2a2 + 2b2,δ определена в (3), ○ выпол-
нено в силу |δ∇(x, e)| ≤δ ∀ x, e ∈ Rn. Используя неравенство (Π.2), из нера-
венства (Π.1) можно получить, что
αk+1〈n〈∇f(xk+1), ek+1〉ek+1, zk - u〉 ≤
(Π.3)
≤ α2k+1n2〈∇f(xk+1), ek+1〉2||ek+1||2q + α2k+1n2δ2||ek+1||2q +
+ Vzk(u) - Vzk+1(u),
что можно записать в виде
αk+1〈n〈∇f(xk+1), ek+1〉ek+1, zk - u〉 ≤
≤ α2k+1n2〈∇f(xk+1), ek+1〉2||ek+1||2q + α2k+1n2δ2||ek+1||2q +
(Π.4)
+ Vzk(u) - Vzk+1(u) + αk+1n〈δ∇(xk+1, ek+1)ek+1, u - zk〉 ≤
≤ α2k+1n2〈∇f(xk+1), ek+1〉2||ek+1||2q + Vz
(u) - Vzk+1 (u) +
k
+ α2k+1n2δ2||ek+1||2q + αk+1n|〈δ∇(xk+1, ek+1)ek+1, u - zk〉|.
√
2
В силу теоремы 1 из [17] и того что Cn,q равно
3 min{2q -1,32ln n-8}n
q
+1,
получаем:
α2k+1Cn,q
Eek+1[α2k+1n2〈∇f(xk+1), ek+1〉2||ek+1||2q] ≤
||∇f(xk+1)||22,
n
Eek+1[α2k+1n2δ2||ek+1||2q] ≤3α2k+1Cn,qδ2,
4
Eek+1[αk+1n|〈δ∇(xk+1, ek+1)ek+1, u - zk〉|] =
(Π.5)
○
= Eek+1[αk+1n|δ∇(xk+1, ek+1)| · |〈ek+1, u - zk〉|]
≤
√
○
○
≤ αk+1nδEe
[|〈ek+1, u - zk〉|] ≤ αk+1nδ Ee
[|〈ek+1, u - zk〉|2]
≤
k+1
k+1
√
○
||u - zk||22
≤αk+1nδ
=
≤
√nδαk+1||u - zk||p,
n
где
○ следует из |δ∇(xk+1, ek+1)| ≤δ, ○ выполнено в силу леммы B.10 из
[18], ○ получено при помощи следующего факта: ∀ x ∈ Rn ∀ 1 ≤ p ≤ q ≤
≤ ∞ ↪→ ||x||p ≥ ||x||q (данное неравенство доказывается, например, при по-
мощи рассмотрения p-нормы для фиксированного x как функции, зависящей
от p, а точнее логарифма p-нормы7). Беря от (Π.4) математическое ожидание
(∑n
)1
(∑n
)
= ln ||x||p = ln
|xk|p
p =1
ln
|xk|p
. Тогда
k=1
p
k=1
∑
(
)
ln(|xk|) · |xk|p
∑
dgx(p)
1
1
=-
ln
|xk|p
+
· k=1
n
dp
p2
p
k=1
|xk|p
k=1
159
по ek+1 и пользуясь неравенствами (Π.5), получим, что
αk+1〈∇f(xk+1), zk - u〉 ≤
α2k+1Cn,q
≤
||∇f(xk+1)||22 + Vz
(u) - Eek+1 [Vzk+1 (u)] +
(Π.6)
k
n
3
+
α2k+1Cn,qδ2 +
√nδαk+1||u - zk||p.
4
Покажем теперь, что
(Π.7)
||∇f(xk+1)||22 ≤ 2nL(f(xk+1) - Ee
[f(yk+1)]) + nδ2.
k+1
Во-первых, для всех x, y ∈ R в силу (2)
∫1
f (y) - f(x) =
〈∇f(x + τ(y - x)), y - x〉dτ =
0
∫1
= 〈∇f(x), y - x〉 +
〈∇f(x + τ(y - x)) - ∇f(x), y - x〉dτ ≤
0
∫1
≤ 〈∇f(x), y - x〉 +
||∇f(x + τ(y - x)) - ∇f(x)||2 · ||y - x||2dτ ≤
0
∫1
≤ 〈∇f(x), y - x〉 + τL||y - x||2 · ||y - x||2dτ =
0
L
= 〈∇f(x), y - x〉 +
||y - x||22,
2
Так как ln y — вогнутая по y функция, то по неравенству Йенсена получаем, что
⎛
⎞
(
)-1
∑
p
∑
dgx(p)
1
1
|xk|p
⎟
≤
ln
|xk|p
+
ln⎜
|xk| ·
⎟
dp
p
p
⎝
∑
⎠=
k=1
k=1
|xk|p
k=1
⎛
⎞
⎛
⎞
∑
∑
⎜
|xk|p+1
⎟
|xk|p+1
1
⎜
⎟
1
⎜
⎟
⎜
k=1
⎟
⎜
k=1
⎟
ln
≤
ln
0,
p
⎜(
)p+1
⎟
p
∑
p+1
⎠=
⎝
∑
p
⎠
(|xk|p)p
|xk|p
k=1
k=1
т.е. функция gx(p) — невозрастающая функция на [1, +∞).
160
т.е.
L
-〈∇f(x), y - x〉 -
||y - x||22 ≤ f(x) - f(y).
2
Беря в последнем неравенстве
x=xk+1,
1
y = Gradek+1(xk+1) = xk+1 -
〈∇f(xk+1), ek+1〉ek+1,
L
получим, что
1
f (xk+1) - f(yk+1) ≥
〈∇f(xk+1), ek+1〉 · 〈∇f(xk+1), ek+1〉 -
L
1
-
〈∇f(xk+1), ek+1〉2 · ||ek+1||22 =
2L
1
1
=
〈∇f(xk+1), ek+1〉2 +
〈∇f(xk+1), ek+1〉δ∇(xk+1, ek+1) -
L
L
1
1
−
〈∇f(xk+1), ek+1〉2 -
〈∇f(xk+1), ek+1〉δ∇(xk+1, ek+1) -
2L
L
1
1
1
−
δ2∇(xk+1,ek+1) =
〈∇f(xk+1), ek+1〉2 -
δ2∇(xk+1,ek+1),
2L
2L
2L
откуда получаем неравенство
〈∇f(xk+1), ek+1〉2 ≤ 2L(f(xk+1) - f(yk+1)) + δ2∇(xk+1, ek+1) ≤
≤ 2L(f(xk+1) - f(yk+1)) + δ2,
так как ∀x, e ∈ Rn ↪→ |δ∇(x, e)| ≤δ. Возьмем от этого неравенства условное
математическое ожидание Eek+1 [ · ], используя лемму B.10 из [18], и полу-
чим (Π.7).
Наконец, из (Π.6) и (Π.7) получим, что
αk+1〈∇f(xk+1), zk - u〉 ≤
≤ 2α2k+1LCn,q(f(xk+1) - Ee
[f(yk+1)]) + Vzk (u) - Eek+1 [Vzk+1 (u)] +
k+1
7
+
α2k+1Cn,qδ2 +
√nδαk+1||u - zk||p.
4
Лемма 1 доказана.
161
Доказательство леммы 2. Запишем цепочку неравенств:
αk+1(f(xk+1) - f(u)) ≤
≤ αk+1〈∇f(xk+1), xk+1 - u〉 =
=
○
○
(1 - τk)αk+1
=
〈∇f(xk+1), yk - xk+1〉 + αk+1〈∇f(xk+1), zk - u〉
≤
τk
○
○
(1 - τk)αk+1
≤
(f(yk) - f(xk+1)) + αk+1〈∇f(xk+1), zk - u〉
≤
τk
○
(1 - τk)αk+1
≤
(f(yk) - f(xk+1))+
τk
+2α2k+1LCn,q · (f(xk+1) - Ee
[f(yk+1) | e1, e2, . . . , ek]) +
k+1
+ Vzk(u) - Eek+1[Vzk+1(u) | e1, e2, ..., ek]+
7
+
α2k+1Cn,qδ2 +
=
4
○
= (2α2
LCn,q - αk+1)f(yk) - 2α2k+1LCn,qEe
[f(yk+1) | e1, e2, . . . , ek] +
k+1
k+1
+ αk+1f(xk+1) + Vzk(u) - Eek+1[Vzk+1(u) | e1, e2, ... , ek] +
7
+
α2k+1Cn,qδ2 +
√nδαk+1||u - zk||p.
4
Действительно, ○ выполнено, так как
= τkzk + (1 - τk)yk ⇔ τk(xk+1 - zk) = (1 - τk)(yk - xk+1),
○ следует из выпуклости f(·) и неравенства 1 - τk ≥ 0, ○ справедливо в силу
леммы 1 и в ○ используется равенство
1
τk =
2αk+1LCn,q
Лемма 2 доказана.
Доказательство теоремы. Заметим, что в силу выбора αk =k+14LC
n,p
выполняется равенство
1
(Π.8)
2α2kLCn,q = 2α2k+1LCn,q - αk+1 +
8LCn,q
162
Действительно,
2
(k + 1)
2α2kLCn,q =
,
8LCn,q
2
1
(k + 2)
k+2
1
2α2k+1LCn,q - αk+1 +
=
-
+
=
8LCn,q
8LCn,q
4LCn,q
8LCn,q
2
(k + 1)2 + 2(k + 1) + 1 - 2(k + 2) + 1
(k + 1)
=
=
= 2α2kLCn,q.
8LCn,q
8LCn,q
Возьмем для k = 0, 1, . . . , N - 1 математическое ожидание по e1, e2, . . . , eN от
неравенств (6) и сложим получившиеся неравенства, учитывая (Π.8):
∑
E[f(yk)]
2α2N LCn,qE[f(yN )] +
+ E[VzN (u)] - Vz0 (u) -
8LCn,q
k=1
(Π.9)
∑
∑
∑
7
√
δ2
-
Cn,q
α2k+1 -
nδ
αk+1E[||u - zk||p] ≤
αk+1f(u)
4
k=0
k=0
k=0
для любого u ∈ Rn, здесь такжеδ определена в (3). Положим u = x∗. Так
∑N
как
αk =N(N+3)8LC
, E[f(yk)] ≥ f(x∗) и Vz0(x∗) = Vx0 (x∗) = Θ, то из (Π.9)
k=1
n,q
следует, что
)
(N + 1)2
(N(N + 3)
N-1
E[f(yN )] -
-
f (x∗) ≤
8LCn,q
8LCn,q
8LCn,q
(Π.10)
∑
∑
7
δ2
≤ Θ - E[VzN(x∗)] +
Cn,q
α2k+1 +
√nδ
αk+1E[Rk],
4
k=0
k=0
= ||x∗ - zk||p. После простых преобразований неравенство (Π.10) за-
пишется в виде
2
(N + 1)
0≤
(E[f(yN )] - f(x∗)) ≤
8LCn,q
(Π.11)
∑
∑
7
δ2
≤ Θ - E[VzN(x∗)] +
Cn,q
α2k+1 +
√nδ
αk+1E[Rk],
4
k=0
k=0
откуда следует еще одно полезное неравенство:
7
∑
∑
δ2
(Π.12)
E[VzN (x∗)] ≤ Θ +
Cn,q
α2k+1 +
√nδ
αk+1E[Rk
].
4
k=0
k=0
163
Докажем индукцией по N неравенство
∑
∑
7
δ2
Θ+
Cn,q
α2k+1 +
√nδ
αk+1E[Rk] ≤
4
k=0
k=0
(Π.13)
⎛A
⎞2
B
B
∑
√
δ
√
N2δ
≤⎝√Θ +7Cn,qδ2
α2k+1 +
2Θn
+
2n
⎠ .
4
2LCn,q
4LCn,q
k=0
Для N = 1 неравенство (Π.13) выполнено, так как
7
○
Θ+
Cn,qδ2α21 +
√nδα1 E[R0]
≤
4
!
R0
○
√
δ
7
≤Θ+
Cn,qδ2α21 +
2Θn
≤
4
2LCn,q
⎛√
⎞2
√
δ
√
δ
≤⎝ Θ +7
Cn,qδ2α21 +
2Θn
+
2n
⎠ ,
4
2LCn,q
4LCn,q
√
√
где ○ следует из неравенства R0 ≤
2Vz0 (x∗) =
2Θ (Vx(y) ≥12 ||x - y||2p в
2
=
=
4LCn,q
1
=
. Таким образом, база индукции доказана. Докажем теперь шаг ин-
2LCn,q
дукции: предположим, что (Π.13) выполнено для некоторого натурального N
и докажем, что тогда оно выполнено и для N + 1. Во-первых, из предполо-
жения индукции и (Π.12) следует, что
(Π.12)
1
1
(E[RN ])2 ≤
E[R2N ] ≤ E[Vz
(x∗)]
≤
N
2
2
(Π.12)
∑
∑
(Π.13)
7
δ2
≤ Θ+
Cn,q
α2k+1 +
nδ
αk+1E[Rk]
≤
4
k=0
k=0
⎛A
⎞2
B
(Π.13)
B
∑
√
δ
√
N2δ
≤
⎝√Θ +7Cn,qδ2
α2k+1 +
2Θn
+
2n
⎠ ,
4
2LCn,q
4LCn,q
k=0
откуда следует, что
⎛
A
⎞
B
√
√
B
∑
√
2Θnδ
N2δ
(Π.14)
E[RN ] ≤
2⎝
√Θ +7Cn,qδ2
α2k+1 +
+
2n
⎠.
4
2LCn,q
4LCn,q
k=0
164
Тогда получаем оценку
∑
∑
7
δ2
Θ+
Cn,q
α2k+1 +
√nδ
αk+1E[Rk] ≤
4
k=0
k=0
⎛A
⎞2
B
B
∑
√
δ
√
N2δ
≤⎝√Θ +7Cn,qδ2
α2k+1 +
2Θn
+
2n
⎠ +
4
2LCn,q
4LCn,q
k=0
7
+
Cn,qδα2N+1 +
≤
4
(Π.14)
∑
√
δ
7
δ2
≤ Θ+
Cn,q
α2k+1 +
2Θn
+
4
2LCn,q
k=0
A
B
(
)2
√
B
∑
√
δ
√
N2δ
N2δ
+2
2n
√Θ +7Cn,qδ2
α2k+1 +
2Θn
+
2n
+
4LCn,q
4
2LCn,q
4LCn,q
k=0
⎛A
⎞
B
√
√
B
∑
√
○
2Θnδ
N2δ
+
2nδαN+1 ⎝
√Θ +7Cn,qδ2
α2k+1 +
+
2n
⎠
≤
4
2LCn,q
4LCn,q
k=0
○
∑
√
δ
√
7
(N + 1)2 δ
δ2
≤Θ+
Cn,q
α2k+1 +
2Θn
+2
2n
×
4
2LCn,q
4LCn,q
k=0
A
B
(
)2
B
∑
√
δ
√
(N + 1)2 δ
×
√Θ +7Cn,qδ2
α2k+1 +
2Θn
+
2n
=
4
2LCn,q
4LCn,q
k=0
⎛A
⎞2
B
B
∑
√
δ
√
(N + 1)2 δ
=⎝√Θ +7Cn,qδ2
α2k+1 +
2Θn
+
2n
⎠ ,
4
2LCn,q
4LCn,q
k=0
где ○ следует из неравенств
2N2
2N2
N+2
2(N + 1)2
+αN+1 =
+
≤
,
4LCn,q
4LCn,q
4LCn,q
4LCn,q
(
)2
√
N2δ
√
√
N2δ
2n
+
2nδαN+1 ·
2n
=
4LCn,q
4LCn,q
(
)2
(
)2
√
δ
√
(N + 1)2 δ
=
2n
(N4 + (N + 2)N2) ≤
2n
,
4LCn,q
4LCn,q
165
A
B
B
∑
√
δ
√Θ +7Cn,qδ2
α2k+1 +
2Θn
≤
4
2LCn,q
k=0
A
B
B
∑
√
δ
≤
√Θ +7Cn,qδ2
α2k+1 +
2Θn
4
2LCn,q
k=0
Итак, неравенство (Π.13) доказано.
Из (Π.11), (Π.13) и VzN (x∗) ≥ 0 получаем неравенство
2
(N + 1)
0≤
(E[f(yN )] - f(x∗)) ≤
8LCn,q
⎛A
⎞2
B
B
∑
√
δ
√
○
N2δ
≤⎝√Θ +7Cn,qδ2
α2k+1 +
2Θn
+
2n
⎠
≤
4
2LCn,q
4LCn,q
k=0
√
○
∑
○
(Π.15)
7
2Θnδ
nN4δ2
δ2
≤ 2Θ +
Cn,q
α2k+1 +
+
≤
2
LCn,q
4L2C2n,q
k=0
√
○
7δ2(N + 1)(N + 2)(2N + 3)
2Θnδ
nN4δ2
○
≤ 2Θ +
+
+
=
192L2Cn,q
LCn,q
4L2C2n,q
√
○
7(N + 1)(N + 2)(2N + 3)δ
2
2Θnδ
nN4
= 2Θ +
+
√
+
δ,
48LCn,q
LCn,q
LC2n,q
где ○ следует из неравенства (a + b)2 ≤ 2a2 + 2b2
∀ a, b ∈ R, ○ получается из
неравенства
∑
∑
∑
(k + 2)2
1
α2k+1 =
=
k2 =
16L2C2n,q
16L2C2
k=0
k=0
n,q k=2
(
)
1
(N + 1)(N + 2)(2N + 3)
(N + 1)(N + 2)(2N + 3)
=
·
-1
≤
,
16L2C2n,q
6
96L2C2n,q
а ○ верно в силу (3). Поделим неравенство (Π.15) на (N+1)2 и получим окон-8LC
n,q
чательно, что
16ΘLCn,q
7(N + 2)(2N + 3)δ
E[f(yN )] - f(x∗) ≤
+
+
(N + 1)2
6(N + 1)
√
16
2ΘnLδ
8nN4δ
+
+
(N + 1)2
Cn,q(N + 1)2
Теорема доказана.
Приводим формулировку теоремы 1 из [17].
166
Теорема П.1. Пусть e ∈ RSn2(1), n ≥ 8, s ∈ Rn, тогда
2
1
(Π.16)
E[||e||2q] ≤ min{q - 1, 16 ln n - 8}n q-
,
2 ≤ q ≤ ∞,
√
(Π.17)
E[〈s, e〉2||e||2q] ≤
3||s||22 min{2q - 1, 32 ln n - 8}nq -2
,
2 ≤ q ≤ ∞,
где под знаком || · ||q понимается векторная q-норма.
Кроме того, приводим формулировку леммы B.10 из [18]. Отметим, что
в доказательстве нигде не использовалось, что второй вектор в скалярном
произведении (помимо e) есть градиент функции f(x) (поэтому утверждение
леммы остается верным для произвольного вектора s ∈ Rn вместо ∇f(x)).
Лемма П.1. Пусть e ∈ RSn2(1) и вектор s ∈ Rn — некоторый вектор.
Тогда
||s||22
Ee[〈s, e〉2] =
n
СПИСОК ЛИТЕРАТУРЫ
1.
Rosenbrock H.H. An Automatic Method for Finding the Greatest or Least Value of a
Function // Comput. J. 1960. V. 3. Iss. 3. P. 175-184. doi: 10.1093/comjnl/3.3.175.
2.
Brent R.P. Algorithms for Minimization Without Derivatives // Dover Books
on Mathematics. Dover Publications, 1973. ISBN 9780486419985. URL: https://
books.google.de/books?id=6Ay2biHG-GEC.
3.
Spall J.C. Introduction to Stochastic Search and Optimization. 1 edition. N.Y.: John
Wiley & Sons, Inc., 2003.
4.
Rumelhart D.E., Hinton G.E., Williams R.J. Learning Representations by Back-
Propagating errors // Nature. 1986. № 323. P. 533-536.
5.
Schmidhuber J. Deep Learning in Neural Networks: An Overview // Neural
Networks. 2015. V. 61. P. 85-117. arXiv:1404.7828
6.
Goodfellow I., Bengio Y., Courville A. Deep Learning. Cambridge: MIT Press, 2016.
7.
Николенко С., Кадурин А., Архангельская Е. Глубокое обучение. Погружение в
мир нейронных сетей. СПб.: Питер, 2018.
8.
Nesterov Yu. Random Gradient-Free Minimization of Convex Functions // Universite
catholique de Louvain, Center for Operations Research and Econometrics (CORE).
№ 2011001, 2011.
9.
Nesterov Yu., Spokoiny V. Random Gradient-Free Minimization of Convex
Functions // Found. Comput. Math. 2017. V. 17. Iss. 2. P. 527-566.
10.
Nesterov Yu.E. A Method of Solving a Convex Programming Problem with
Convergence Rate O(1/k2) // Soviet Math. Dokl. 1983. V. 27. No. 2. P. 372-376.
11.
Гасников А.В., Двуреченский П.Е., Нестеров Ю.Е. Стохастические градиент-
ные методы с неточным оракулом // Тр. МФТИ. 2016. Т. 8. № 1. С. 41-91. arXiv
preprint arXiv:1411.4218.
12.
Chopra P. Reinforcement Learning without Gradients: Evolving Agents using
without-gradients-evolving-agents-using-genetic-algorithms-8685817d84f.
13.
Воронцова Е.А., Гасников А.В., Горбунов Э.А. Ускоренные спуски по случайно-
му направлению с неевклидовой прокс-структурой // АиТ. 2019. № 4. С. 126-143.
arXiv:1710.00162.
167
14. Allen-Zhu Z., Orecchia L. Linear Сoupling: An Ultimate Unification of Gradient and
Mirror Descent // arXiv preprint arXiv:1407.1537.
15. Dvurechensky P., Gasnikov A., Tiurin A. Randomized Similar Triangles Method:
A Unifying Framework for Accelerated Randomized Optimization Methods
(Coordinate Descent, Directional Search, Derivative-Free Method) // arXiv preprint
arXiv:1707.08486.
16. Немировский А.С., Юдин Д.Б. Сложность задач и эффективность методов оп-
тимизации. М.: Наука, 1979.
17. Горбунов Э.А., Воронцова Е.А., Гасников А.В. О верхней оценке математическо-
го ожидания нормы равномерно распределенного на сфере вектора и явлении
концентрации равномерной меры на сфере // arXiv preprint arXiv:1804.03722.
18. Bogolubsky L., Dvurechensky P., Gasnikov A., Gusev G., Nesterov Y., Raigorod-
skii A., Tikhonov A., Zhukovskii M. Learning Supervised PageRank with Gradient-
Based and Gradient-Free Optimization Methods
// D.D. Lee, M. Sugiyama,
U.V. Luxburg, I. Guyon, R. Garnett, ed. Proc. NIPS’16 Proc. 30th Int. Conf. on
Neural Information Processing Systems. P. 4914-4922. Curran Associates, Inc., 2016.
arXiv:1603.00717.
20. Гасников А.В. Эффективные численные методы поиска равновесий в больших
транспортных сетях // Дисс. д.ф.-м.н. по специальности 05.13.18 - Математиче-
ское моделирование, численные методы, комплексы программ. М.: МФТИ, 2016.
arXiv preprint arXiv:1607.03142.
Статья представлена к публикации членом редколлегии А.В. Назиным.
Поступила в редакцию 21.04.2018
После доработки 05.11.2018
Принята к публикации 08.11.2018
168