БИОФИЗИКА, 2022, том 67, № 2, с. 301-318

БИОФИЗИКА КЛЕТКИ

УДК 571.3

МАТЕМАТИЧЕСКИЙ АНАЛИЗ МОДЕЛИ ЭПИДЕМИИ COVID-19

С ИСПОЛЬЗОВАНИЕМ ДАННЫХ ЭПИДЕМИОЛОГИЧЕСКИХ

ПАРАМЕТРОВ БОЛЕЗНЕЙ, РАСПРОСТРАНЕННЫХ В ИНДИИ

*Высшая школа Чандрахати Дилип Кумар, Чандрахати, Западная Бенгалия, 712504, Индия

**Национальный технологический институт Пудучерри, Караикал, 609609, Индия

***Технологический университет имени Азада Маулана Абул Калама, Калькутта, 700064, Индия

E-mail: pal.debkumar@gmail.com

Поступила в редакцию 09.02.2021 г.

После доработки 18.04.2021 г.

Принята к публикации 23.12.2021 г.

Сделана попытка описания вспышки возбудителя тяжелого острого респираторного синдрома

SARS-CoV 2 (COVID-19) с помощью эпидемической модели. Вирус имеет различные проявления в

разных странах. а количество новых подтвержденных случаев коронавирусной инфекции стреми-

тельно увеличивается по всему земному шару. Индия сейчас проходит вторую стадию распростра-

нения COVID-19, которая очень быстро примет характер эпидемии, если не будут предприняты

надлежащие меры защиты, основанные на базе данных передачи заболевания. В данной работе те-

кущие данные по COVID-19 были использованы для математического моделирования с последую-

щим анализом динамики. Предложен новый тип представления данных для оценки и контроля ин-

фекционного заболевания COVID-19 через модель пандемии SEQIR, которая основана на предло-

жении отправлять на карантин на время инкубационного периода инфицированных людей, у

которых инфекция не определяется по результатам анализа. В течение инкубационного периода,

если кто-либо из людей инфицируется COVID-19, их изолируют, и применяется необходимое лече-

ние, чтобы они не заражали других жителей местности. Динамика модели SEQIR представлена ос-

новным числом воспроизведения R₀ и детальным анализом стабильности. Численные результаты

приводятся на графиках по данным пяти штатов и всей Индии.

Ключевые слова: новый коронавирус, модель SEQIR, число воспроизведения, самоизоляция, стабиль-

ность.‘

DOI: 10.31857/S0006302922020132

COVID-19 быстро распространился из Уханя

Математическая формулировка моделей бо-

по всему Китаю [1]. На 1 апреля 2020 года в Китае

лезней очень эффективна для понимания эпиде-

было диагностировано 81589 случаев (из них

миологических прототипов болезней, также она

3318 смертей), из которых 67802 - в провинции

помогает принимать необходимые меры в сфере

Хубэй, причем 50007 - в городе Ухань, столице

здравоохранения через контроль распростране-

провинции Хубэй [3]. Коронавирусы впервые

ния заболеваний. В начале декабря 2019 года на-

были обнаружены в 1965 г., после этого произо-

селение Уханя в китайской провинции Хубэй бы-

шли три жизненно значимых вспышки корона-

ло инфицировано возбудителем неизвестной

вирусных инфекций. В 2003 г. первая вспышка

пневмонии [1, 2]. Эта пневмония была вызвана

возникла в материковом Китае. Она была названа

новым коронавирусом, обычно называемым

тяжелым острым респираторным синдромом

2019-nCoV, или SARS-CoV-2 по классификации

(SARS - Severe Acute Respiratory Syndrome) [4, 5].

международного комитета таксономии вирусов;

Вторая вспышка - ближневосточного респира-

официально по предложению Всемирной орга-

торного синдрома (MERS) - произошла в 2012 г. в

низации здравоохранения это заболевание назы-

Саудовской Аравии [6, 7]. Третья вспышка в фор-

вается COVID-19.

ме MERS имела место в 2015 г. в Южной Корее

[8]. В четвертый раз коронавирусная инфекция

Сокращения: SARS - тяжелый острый респираторный

возникла как COVID-19 в Китае и далее распро-

синдром, MERS - ближневосточный респираторный син-

дром.

странилась по всему земному шару. Отмечается,

301

302

ПАЛ и др.

что в США намного больше пациентов с проявле-

смертей - 0), Ладакх (подтвержденных случаев -

ниями COVID-19, чем в Китае, стране, с которой

14, из них смертей - 0) , Западная Бенгалия (под-

началась вспышка. Теперь этот вирус играет свою

твержденных случаев - 53, из них смертей - 3)

разрушительную роль уже в таких странах, как

(по данным на 03.04.2020 г.) [16]. В таких штатах,

Индия, Иран, Пакистан, Бангладеш, Шри-Ланка

как Одиша (подтвержденных случаев - 5, из них

и другие страны Южной Азии.

смертей - 0), Пудучерри (подтвержденных случа-

ев - 5, из них смертей - 0), Мизорам (подтвер-

Основные симптомы COVID-19 почти такие

жденных случаев - 1, из них смертей - 0), Гима-

же, как у инфекций SARS-CoV и MERS-CoV. Па-

чал-Прадеш (подтвержденных случаев - 6, из них

циенты с COVID-19 страдают от сухого кашля,

смертей - 1), Гоа (подтвержденных случаев - 6,

высокой температуры, слабости, затруднений

дыхания и двустороннего поражения легких в тя-

из них смертей - 0), распространение шло очень

медленно (по данным на 03.04.2020 г.) [16].

желых случаях [9]. Кроме того, некоторые паци-

енты с COVID-19 испытывают тошноту, рвоту и

Федеральное правительство Индии и все пра-

диарею без всяких симптомов расстройства дыха-

вительства штатов предприняли надлежащие ме-

тельной системы [10]. Китайское министерство

ры сдерживания распространения COVID-19 в

здравоохранения объявило [11], что анализы па-

Индии с 21 марта 2020 г. В Индии 22 марта 2020 г.

циентов могут сначала давать отрицательные ре-

был введен обязательный 14-часовой комендант-

зультаты, но через несколько последовательных

ский час в общественных местах [17]. Также пре-

тестов появляются положительные результаты

мьер-министр Индии объявил полный 21-днев-

обнаружения COVID-19. Благодаря нескольким

ный локдаун с 24 марта 2020 г. [17]. Правительство

исследованиям [11, 12] было установлено, что

приняло множество мер, таких, как поддержание

возбудитель COVID-19 передается от человека к

определенной социальной дистанции, повыше-

человеку. В результате распространение вируса

ние общественной сознательности и мер предо-

не ограничилось Китаем, а произошло по всему

сторожности, как ношение масок в обществен-

миру. Теперь оно приобрело характер пандемии,

ных местах, карантин для инфицированных и так

затронув 205 стран с 900306 подтвержденными

далее. Более того, до сих пор (до конца работы над

случаями, а также 45693 подтвержденными смер-

данной рукописью), количество подтвержденных

тями (на 2 апреля 2020 г. [13]). Ситуация ухудша-

случаев COVID-19 растет день ото дня.

ется в таких странах, как Италия, США, Испа-

Не только медицинские и биологические ис-

ния, Франция, Германия и т.д. Поскольку вирус

следования, но и методы математического моде-

передается от человека к человеку, страны с вы-

лирования вовлекаются в сотрудничество и игра-

сокой плотностью населения, в особенности Ин-

ют ключевую роль в остановке распространения

дия, находятся в угрожающем положении. Если

COVID-19. Методами математического модели-

не предпринять правильную стратегию для защи-

рования мы можем предсказывать начало инфек-

ты от распространения вируса COVID-19, то и

ции и время конца эпидемии. Это также помогает

Индию ждет эпидемия, которая будет причиной

нам принимать правильные решения по необхо-

смерти многих индийцев.

димым мерам для ограничения распространения

Первой жертвой COVID-19 в Индии был сту-

болезней. В 2019 г. вирус COVID-19 широко рас-

дент из округа Тхиссур в Керале, приехавший до-

пространялся по всему миру. Следовательно, сей-

мой из Уханя (Китай) и идентифицированный

час имеет место тревожная ситуация, становяща-

как подтвержденный вирусоноситель 30 января

яся глобальной пандемией [18] из-за тяжести это-

2020 г. [15]. В настоящем сценарии мы наблюдаем

го вирусного заболевания. Поэтому необходимы

быстрый, умеренный и медленный темпы рас-

реальные эпидемиологические данные со всего

пространения инфекции в ряде штатов Индии. В

мира для улучшения понимания ситуации и уве-

Махараштре (подтвержденных случаев - 335, из

домления о вовлечении [19]. Не так давно, когда

них смертей - 16), Керале (подтвержденных слу-

случались такие пандемии, как SARS, пандемия

чаев - 286, из них смертей - 2), Тамил Наду (под-

гриппа 2009 г. или вспышка лихорадки Эбола

твержденных случаев - 309, из них смертей - 1),

[20-23], в течение первых нескольких недель при

Дели (подтвержденных случаев - 219, из них смер-

анализе реальной ситуации уделялось внимание

тей - 4), Телангане (подтвержденных случаев - 158,

тяжести, контагиозности и естественной истории

из них смертей - 7), Уттар-Прадеше (подтвержден-

новообразованного патогена. И в этом случае ма-

ных случаев - 172, из них смертей - 2), Раджастха-

тематическое моделирование, фундированное

не (подтвержденных случаев - 167, из них смер-

динамическими уравнениями [24, 25], может поз-

тей - 0) темп распространения инфекции очень

волить детально охарактеризовать динамику эпи-

быстрый (на 04.04.2020 г.) [16]. Умеренный рост

демий так же подробно, как и статистические ме-

имеет место в таких штатах, как Ассам (подтвер-

тоды

[26,

27]. На ранней стадии пандемии

жденных случаев - 16, из них смертей - 0), Бихар

COVID-19 многие исследования проводились в

(подтвержденных случаев - 29, из них смертей - 1),

облaсти статистического подхода, а равно и мате-

Чандигарх (подтвержденных случаев - 18, из них

матического моделирования, чтобы определить

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКИЙ АНАЛИЗ МОДЕЛИ ЭПИДЕМИИ COVID-19

303

верглась новой завезенной болезни, и количество

пациентов с COVID-19 увеличивается день ото

дня. Из-за недавней ситуации правительство Ин-

дии предприняло некоторые стратегические ме-

ры для предотвращения распространения возбу-

дителя COVID-19. В этом разделе представлена

модель SEQIR для эпидемии COVID-19, осно-

ванная на текущей ситуации с болезнью в услови-

ях Индии. Мы придерживаемся той версии, что

воспроизводит несколько ключевых эпидемио-

логических свойств вируса COVID-19. Настоя-

щая структура модели COVID-19 описывает ди-

намику пяти субпопуляций индийцев, таких, как

субпопуляция, подверженная инфекции (S(t));

Рис. 1. Диаграмма передачи COVID-19 в модели SEQIR.

инфицированная, но не определяемая по резуль-

татам тестов (E(t)); популяция в карантине (Q(t));

популяция с подтвержденной инфекцией в изо-

основные параметры эпидемии, такие как число

ляции (I(t)) и популяция, проживающая в без-

воспроизведения, серийный интервал и время

опасной зоне, не затронутой COVID-19 (R(t)).

удвоения [28, 29].

Мы принимаем общее население Индии за N(t),

Авторы работы [30] сосчитали количество под-

тогда

твержденных случаев передачи инфекции из Уха-

N(t) = S(t) + E(t) + Q(t) + I(t) + R(t).

ня в другие крупные города Китая. В работе [31]

В этой модели карантин вводится для отделе-

была предложена SEIR-модель для предсказания

ния инфицированных людей от общего населе-

распространения болезни по всему миру на осно-

ния Индии, при этом часть популяции инфици-

ве данных, отслеживаемых с 31 декабря 2019 г. по

рована, но не инфекционна. Под инфицирован-

28 января 2020 г. В работе [32] изучалась SEIR-

ной популяцией мы понимаем людей, у которых

модель на COVID-19, а в работе [33] была пред-

подтверждено наличие вируса COVID-19. Под

ставлена передача COVID-19 от человека к чело-

популяцией в безопасной зоне мы понимаем тех

веку и предсказан размер вспышки COVID-19 в

жителей Индии, которые не подвержены корона-

Ухане (Китай). Авторы работы [34] изучили мате-

вирусной инфекции. Чтобы сделать предложен-

матическую модель SIR для того, чтобы умень-

ную модель SEQIR более реалистичной, мы

шить рост новых случаев коронавируса методом

включаем несколько демографических эффек-

введения жестких карантинных процедур.

тов, вводя пропорциональную частоту естествен-

В данной статье мы разработали эпидемиче-

ной смерти (d₁ > 0) в каждой из пяти субпопуля-

скую модель COVID-19, оптимизируя ее под си-

ций Индии. Более того, мы включаем общий при-

туацию в Индии. В данной модельной системе мы

ток подверженных инфекции жителей Индии в

делим население Индии на пять субпопуляций,

страну со скоростью Λ (> 0) в единицу времени. Λ

таких, как подверженная инфекции популяция,

представляет собой интегральный показатель,

инфицированная, но не определяемая по тестам

объединяющий новорожденных детей, иммигра-

популяция, популяция в карантине, популяция с

цию и эмиграцию. Потоковая диаграмма модели

подтвержденной инфекцией в изоляции, и попу-

инфекции COVID-19 описана на рис. 1.

ляция, проживающая в безопасной зоне, не за-

Моделирование подверженной популяции:

тронутой COVID-19. Затем при использовании

данная популяция увеличивается за счет притока

анализа с применением динамического модели-

населения в регион (Индию) со скоростью Λ и

рования нашей целью будет предсказание коли-

уменьшается за счет естественной смертности d₁.

чества подтвержденных случаев COVID-19 в Ин-

дии в будущем с разбивкой для различных шта-

Также подверженная популяция уменьшается за

тов. Мы также анализируем предложенную

счет взаимодействия между подверженной попу-

модель развития болезни математически для по-

ляцией и инфицированной, но не определяемой

нимания динамики передачи COVID-19 от чело-

тестами. Также она уменьшается с постоянными

века к человеку.

коэффициентами скорости σ₁ и β₁ соответствен-

но, отражающими переход в группу в безопасной

зоне и в группу в карантине. В Индии и в самом

РАЗРАБОТКА МОДЕЛИ НОВОГО

деле, в особенности в округах Пурулия, Мурши-

КОРОНАВИРУСНОГО ЗАБОЛЕВАНИЯ

дабад, Бирбхум (Западная Бенгалия), Гайя, Бха-

Разные исследователи ранее разрабатывали

галпур (Бихар) и ряде других подверженная попу-

математическую модель распространения инфек-

ляция прямо переселяется в безопасную зону, по-

ционных заболеваний [35-38]. Индия также под-

скольку жители боятся распространения болезни.

БИОФИЗИКА том 67

№ 2

2022

304

ПАЛ и др.

Эта ситуация возникает вследствие отсутствия

пы инфицированных, но не определяемых по те-

доступного адекватного лечения и тестирования

стам, со скоростью r₁ (инфицированные, не опре-

для значительной части населения Индии. Таким

деляемые тестами, не могут быть все помещены в

образом, скорость изменения подверженной по-

карантин по причине отсутствия возможностей

пуляции определяется следующим дифференци-

помещения в карантин из-за недостатка про-

альным уравнением:

странства или других факторов; инфицирован-

dS/dt = Λ - αSE - σ₁S - β₁S - d₁S.

(1)

ные, но не определяемые тестами индивиды мо-

гут впоследствии стать больными и повторные те-

Моделирование инфицированной популяции,

сты покажут положительные результаты.

не определяемой тестами (E(t)): данная популя-

Поэтому они напрямую попадают в популяцию

ция обозначает тех людей, которые инфицирова-

инфицированных, и этот особый случай очень

ны, но результатами теста инфекция не подтвер-

вреден с точки зрения предотвращения распро-

ждена вследствие неадекватных возможностей

тестирования. Эта популяция увеличивается со

странения COVID-19 в Индии), а также увеличи-

скоростью, отражающей переход из подвержен-

вается со скоростью r₂ из популяции в карантине,

ной популяции в данную группу. Она уменьшает-

как обычно. Инфицированная популяция умень-

ся вследствие перехода в карантин со скоростью

шается со скоростью σ₃ за счет перехода в популя-

β₂ и вследствие естественной смертности со ско-

цию, восстановившуюся после болезни, а также

ростью d₁. Из-за очень большой плотности насе-

за счет естественной смертности. Примем есте-

ления для правительства Индии трудно изолиро-

ственную смертность за d₁ и, для большей реали-

вать некоторых граждан, которые инфицирова-

стичности, введем d₂ как смертность от инфек-

ны, но не определяются по тестам, и отослать их

ции, тогда изменение инфицированной популя-

на карантин. Держа в уме этот факт, примем, что

эта популяция также прямо уменьшается со ско-

ции

будет

определяться

следующим

ростью r₁. Таким образом, изменение популяции

дифференциальным уравнением:

инфицированных людей, не определяемых теста-

dI/dt = r₁E + r₂Q - σ₃I - d₁I - d₂I.

(4)

ми, описывается следующим дифференциаль-

ным уравнением:

Моделирование популяции в безопасной зоне,

не подверженной риску заражения COVID-19

dE/dt = αSE - r₁E - β₂E - d₁E.

(2)

(R(t)): примем, что подверженные инфекции лю-

При моделировании популяции в карантине

ди, жители, находящиеся в карантине и инфици-

(Q(t)) учитываем, что инкубационный период

рованные индивиды восстанавливаются после

COVID-19 составляет от 2 до 14 суток. Этот пери-

болезни соответственно со скоростями σ₁, σ₂и σ₃

од является ключевым для передачи болезни от

и переходят в популяцию безопасной зоны. Эта

индивида к индивиду. Следовательно, необходи-

популяция уменьшается за счет естественной

мо отделять таких индивидов от подверженных и

смертности d₁. Таким образом, изменение попу-

инфицированных, но не определяемых тестами,

ляции безопасной зоны, не подверженной риску

тестируя в течение 14 суток для контроля распро-

заражения вирусом COVID-19, определяется сле-

странения COVID-19 в Индии. Эта упомянутая

дующим дифференциальным уравнением:

популяция также известна как карантинная по-

dR/dt = σ₁S+ σ₂Q + σ₃I - d₁R.

(5)

пуляция. Она увеличивается со скоростью β₁ и β₂,

пополняясь соответственно из подверженной и

Комбинируя уравнения ((1)-(5)), придаем на-

инфицированной, но не определяемой тестами

шей желаемой структуре модели следующую

популяции. Эта популяция уменьшается со ско-

форму:

ростью r₂ и σ₂за счет перехода соответственно в

dS/dt = Λ - αSE - σ₁S - β₁S - d₁S,

инфицированную популяцию и популяцию в без-

опасной зоне. Примем скорость естественной

dE/dt = αSE - r₁E - β₂E - d₁E,

смертности в этой популяции за d₁, тогда ско-

dQ/dt = β₁S + β₂E - r₂Q - σ₂Q - d₁Q,

(6)

рость изменения карантинной популяции выгля-

дит следующим образом:

dI/dt = r₁E + r₂Q - σ₃I - d₁I - d₂I,

dQ/dt = β₁S + β₂E - r₂Q - σ₂Q - d₁Q.

(3)

dR/dt = σ₁S+ σ₂Q + σ₃I - d₁R,

Моделирование популяции с подтвержденной

с начальными плотностями S(0) > 0, E(0) ≥ 0,

инфекцией (I(t)): инфицированная популяция, у

I(0) ≥ 0, Q(0) ≥ 0, R(0) > 0.

которой наличие COVID-19 было подтверждено

Все параметры и соответствующий им биоло-

тестами, увеличивается за счет перехода из груп-

гический смысл представлены в табл. 1.

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКИЙ АНАЛИЗ МОДЕЛИ ЭПИДЕМИИ COVID-19

305

Таблица 1. Объяснение параметров, используемых в предложенной структуре модели SEQIR

Параметр

Смысл

Скорость притока новых индивидов в население Индии

Скорость перехода из подверженной популяции в популяцию инфицированных, но не

определяемых тестами индивидов

β₁

Коэффициент перехода из подверженной популяции в популяцию на карантине

Коэффициент перехода из инфицированной, но не определяемой тестами популяции в

β₂

популяцию на карантине

σ₁

Коэффициент перехода из подверженной популяции в популяцию в безопасной зоне

Коэффициент перехода из инфицированной, но не определяемой тестами популяции в

σ₂

популяцию в безопасной зоне

σ₃

Коэффициент перехода из популяции на карантине в популяцию в безопасной зоне

Коэффициент перехода из инфицированной, но не определяемой тестами популяции в

r₁

инфицированную популяцию, получающую лечение

Коэффициент перехода из популяции на карантине в инфицированную популяцию, получающую

r₂

лечение

d₂

Смертность инфицированной популяции от COVID-19

d₁

Естественная смертность всех пяти субпопуляций

Приведенная выше формула для модели

где А = σ₁+ β₁+ d, B = r₁+ β₂+ d₁, С = r₂+ σ₂ + d₁,

SEQIR (6) может быть переписана в виде

D = σ₃ + d₁+ d₂.

dS/dt = Λ - αSE - AS,

dE/dt = αSE - BE,

ЧИСЛЕННАЯ ВЕРИФИКАЦИЯ

И ПРЕДСКАЗАНИЯ

dQ/dt = β₁S + β₂E - CQ,

(7)

Для оптимизации нашей модели COVID-19 (6)

dI/dt = r₁E + r₂Q - DI,

с целью соответствия ежедневным сообщениям о

новых случаях COVID по всей Индии и отдельно

dR/dt = σ₁S+ σ₂Q + σ₃I - d₁R,

по пяти штатам (Дели, Керала, Махараштра, Ут-

Таблица 2. Значения параметров модельной системы уравнений (6) для Индии

Параметры

Значения

Ссылка

4⋅10⁴

[49]

β₁

4⋅10^-7

Предположение

β₂

0.1

Оценка

σ₁

5⋅10^-4

Предположение

σ₂

5⋅10^-2

Предположение

σ₃

6⋅10^-3

Оценка

r₁

1⋅10^-2

Оценка

r₂

1⋅10^-3

Оценка

d₂

197⋅10^-5

Оценка

d₁

2⋅10^-5

Оценка

БИОФИЗИКА том 67

№ 2

2022

306

ПАЛ и др.

Таблица 3. Начальные плотности в модельной системе (2.6) для Индии

S(0)

E(0)

Q(0)

I(0)

R(0)

8⋅10⁸

15⋅10²

5⋅10⁴

284

4⋅10⁸

Таблица 4. Значение R₀ для различных α для Индии

2.1⋅10^-10

2.5⋅10^-10

2.8⋅10^-10

R₀

0.35847

0.42675

0.47796

тар-Прадеш и Западная Бенгалия) мы провели в

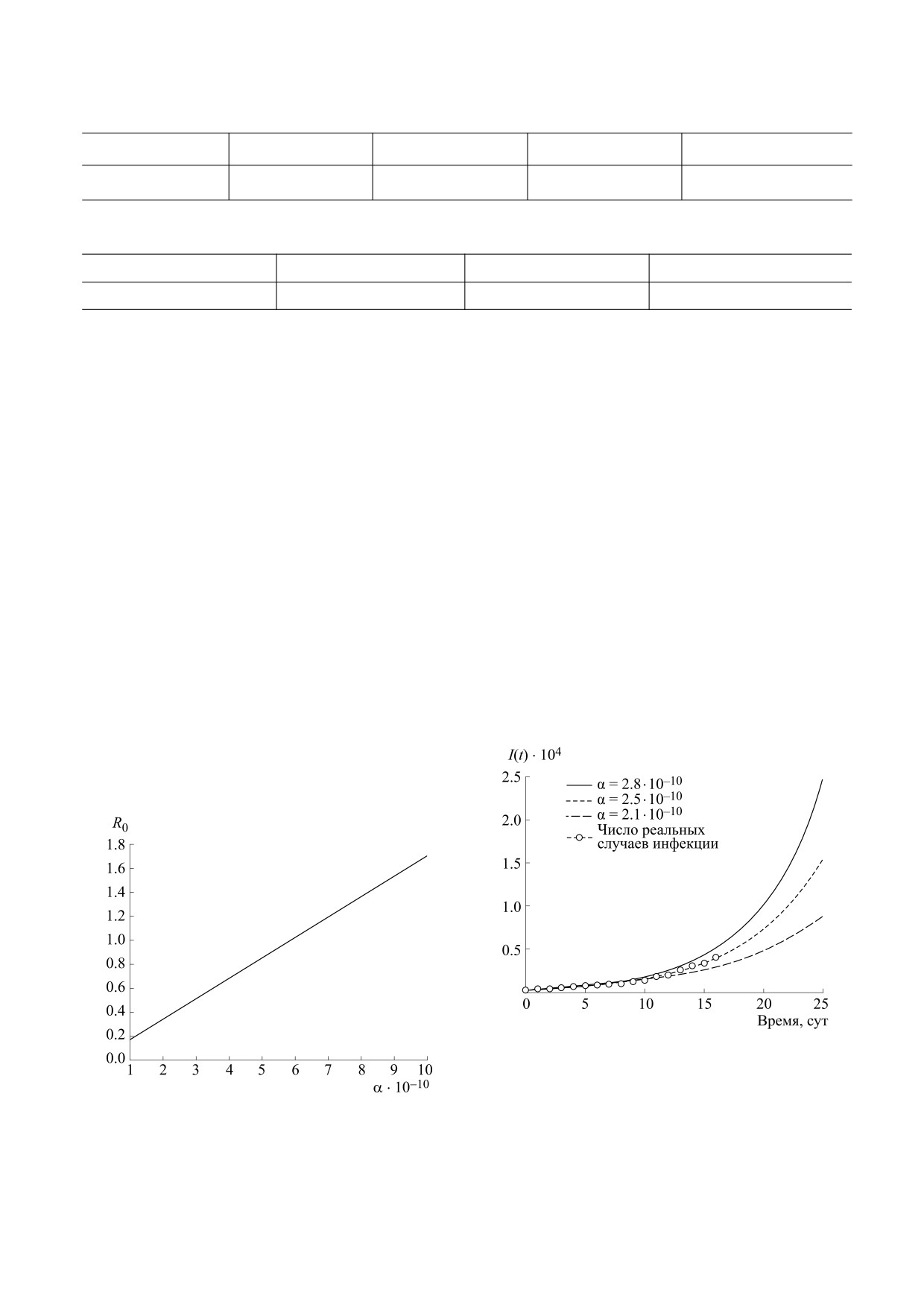
На данном рисунке мы видим, что при увели-

этой части численное моделирование. Данные

чении значений α увеличивается и R₀. Также на-

были взяты с официального сайта Индийского

блюдается, что после определенных значений α

совета по медицинским исследованиям и Все-

величина R₀ становится больше единицы. Следо-

мирной организации здравоохранения [47, 48].

вательно, до определенных значений α равнове-

Сначала мы оценили значения различных пара-

сие, свободное от болезни, является стабильным,

метров модели, приведенные в табл. 2.

а за пределами этих значений оно нестабильно. В

Изначальные плотности на 21 марта 2020 г.

данном конкретном состоянии нас интересует

приводятся в табл. 3.

инфицированная популяция I(t), изменяющаяся

В предложенной нами модельной системе

с каждым днем. Таким образом, изобразим вре-

менные ряды инфицированной популяции при

наиболее чувствительным параметром является

α - скорость перехода из подверженной популя-

принятии начальных значений плотностей из

ции в популяцию инфицированных, но не опре-

табл. 3.

деляемых тестами. Поэтому мы в основном стре-

Рис.

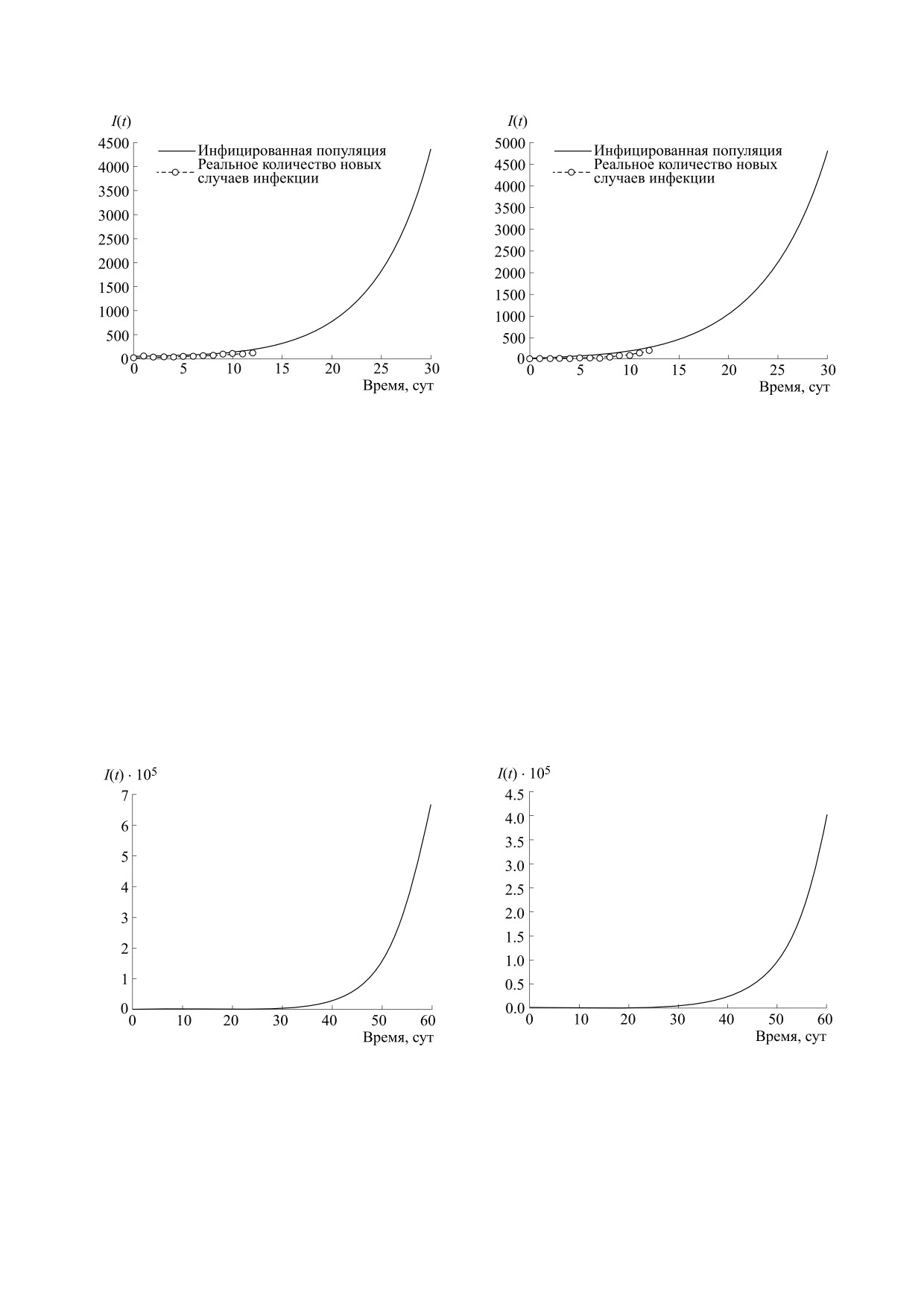
3 очень интересен, поскольку при

мимся увидеть именно эффект α на скорость рас-

α = 2.5⋅10^-10 количество подтвержденных случаев

пространения COVID-19. Для разных значений α

инфекции в модели точно ложится на реальные

значение R₀ представлено в табл. 4.

подтвержденные случаи в Индии в недавнее

Из вышеприведенной таблицы мы наблюдаем,

время.

что все значения R₀ менее единицы. Следователь-

На рис. 4 представлен пик инфекции для дол-

но, эндемическое уравнение E₁ не является ло-

говременного течения эпидемии. Этот рисунок

кально асимптотически стабильным для этих

значений R₀ и соответствующих значений α. Да-

вайте теперь построим график R₀ относительно α

(рис. 2).

Рис. 3. Графики временных рядов инфицированной

популяции для α = 2.1·10^-10, 2.5·10^-10 и

2.8·10^-10.

Начальные условия и значения параметров приводятся

в табл. 2 и 3 соответственно. По оси абсцисс - время в

сутках, по оси ординат - инфицированная популяция

Рис. 2. Изменение R₀ в зависимости от наиболее чув-

I(t). Кружками отмечено число реальных случаев

ствительного параметра α.

инфекции.

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКИЙ АНАЛИЗ МОДЕЛИ ЭПИДЕМИИ COVID-19

307

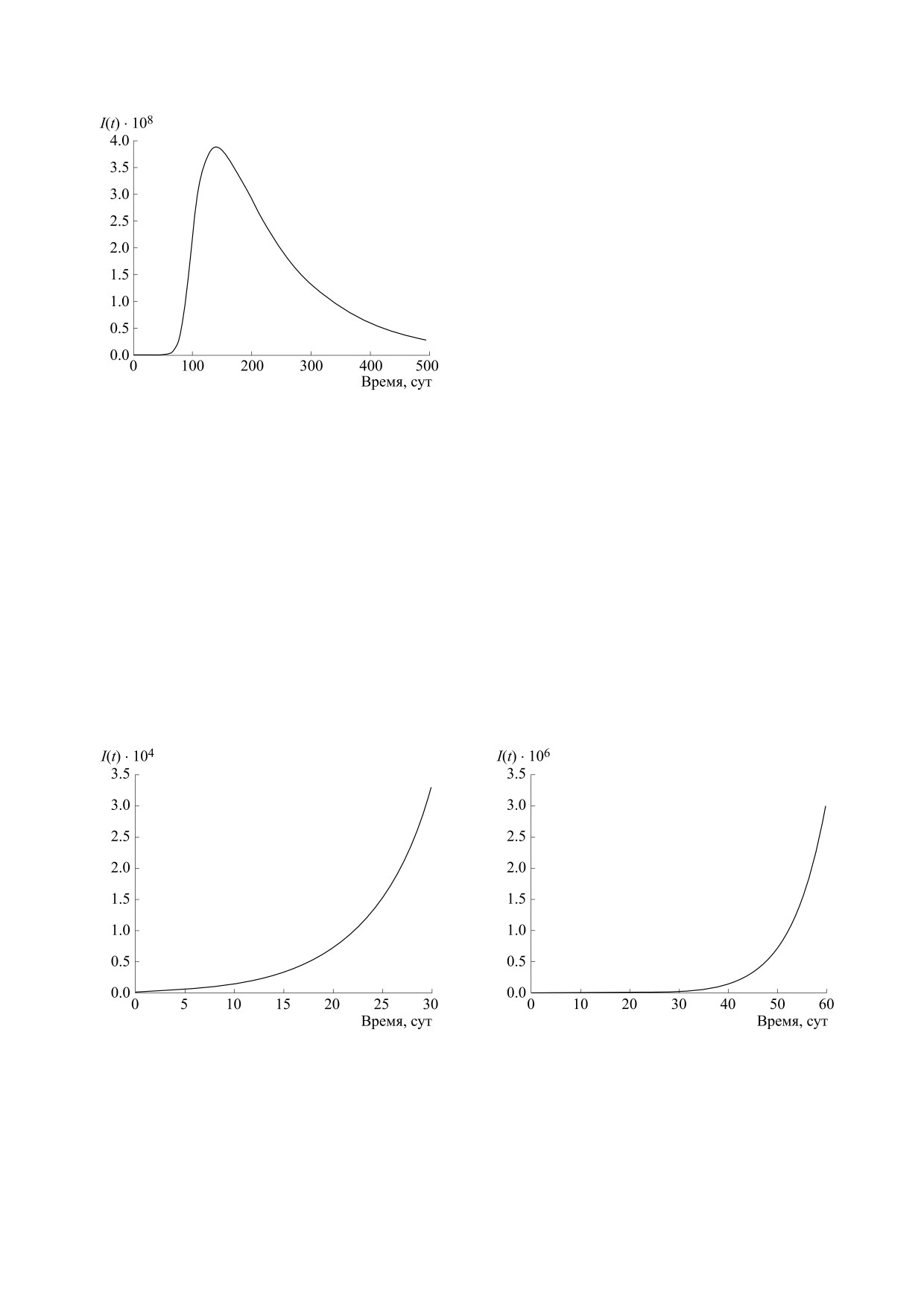
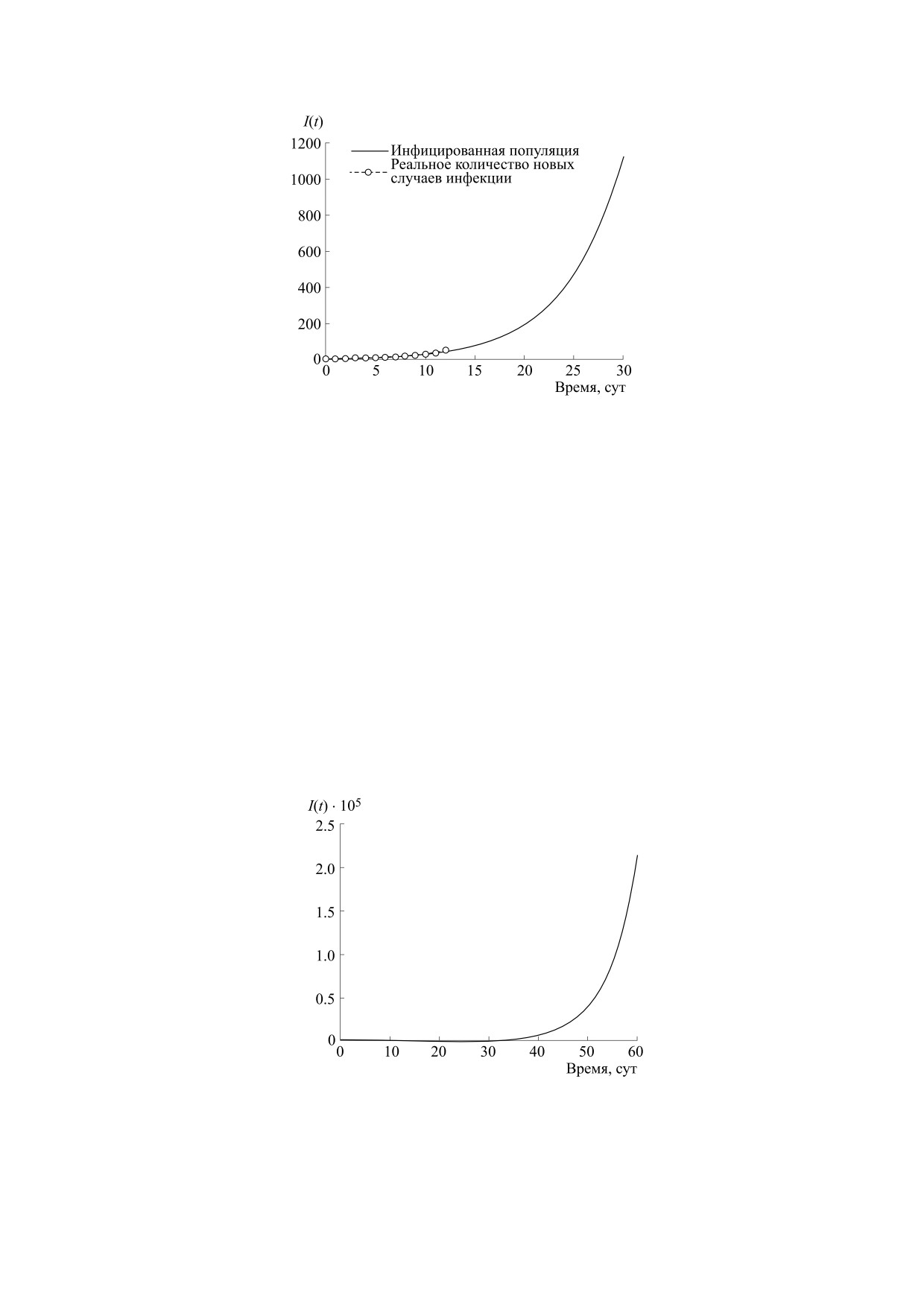
Краткосрочное поведение предложенной на-

ми модели в течение 30 и 60 суток после ограни-

чительныx мер, начатых правительством Индии,

описывается на рис. 5 и 6 соответственно.

Таким образом, при введении правительствен-

ных ограничений, в нашей математической моде-

ли из рис. 5 и 6 можно вывести, что за 30 суток ко-

личество инфицированных жителей Индии при-

близится к 32000. За 60 суток оно станет равно

3000000.

Поскольку после определенного периода пра-

вительство меняет ограничительные меры, пара-

метры системы после этого периода меняются.

Следовательно, в нынешней ситуации нам неин-

тересна инфицированная популяция на долгом

отрезке времени.

Теперь мы моделируем ежедневные новые

случаи подтвержденного заболевания COVID-19

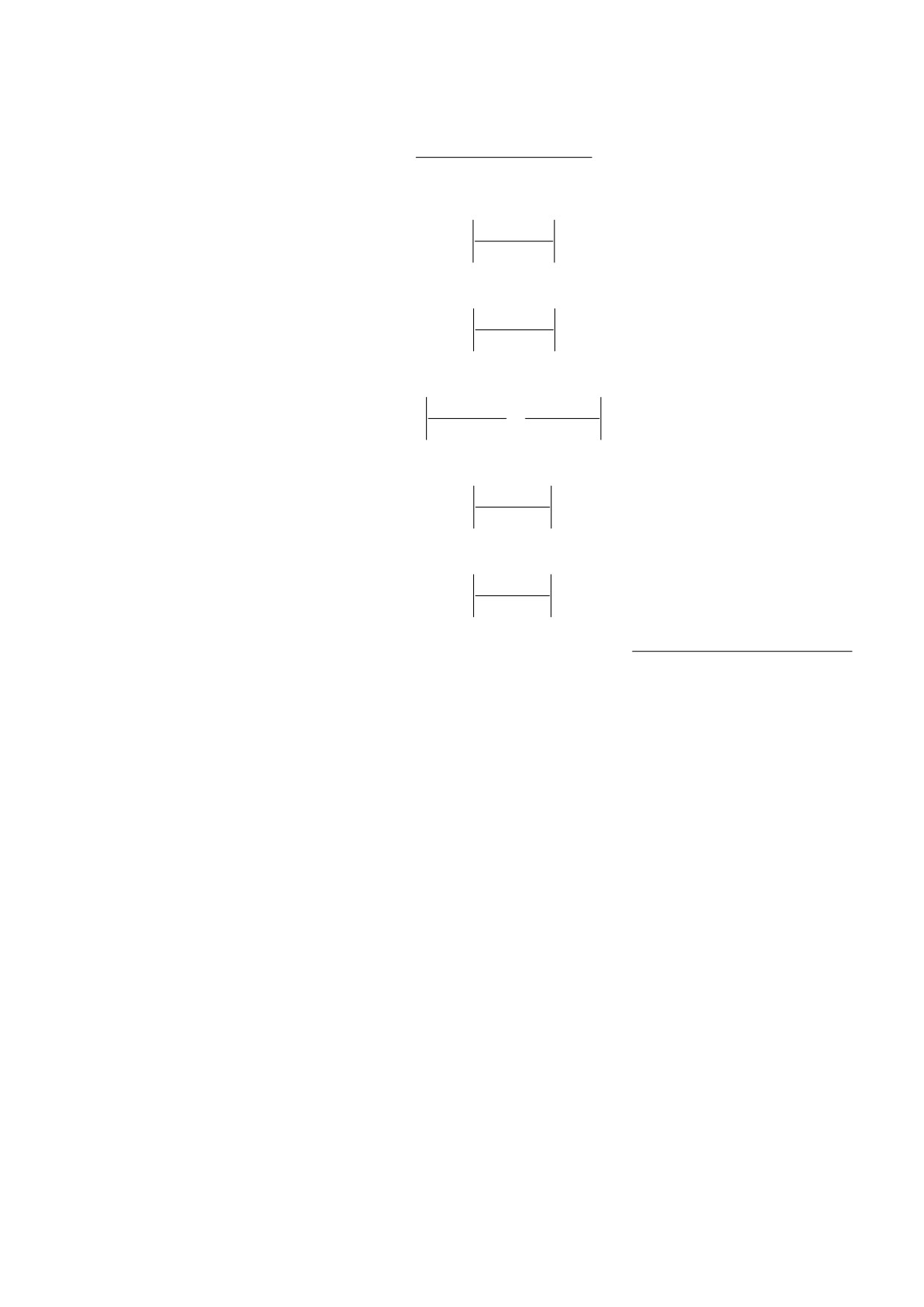
Рис. 4. График инфицированной популяции на длитель-

для пяти штатов Индии - Махараштра, Керала,

. Началь-

ном временном промежутке при α = 2.5·10^-10

Уттар-Прадеш, Дели и Западная Бенгалия, начи-

ные условия и значения параметров приведены в табл. 2

ная с 21 марта 2020 г. Попытаемся оптимизиро-

и 3 соответственно. По оси абсцисс - время в сутках, по

вать модель (6) к ежедневным новым случаям

оси ординат - инфицированная популяция I(t).

подтвержденного COVID-19 в этих пяти штатах.

Здесь мы также принимаем для α (скорости пере-

для инфицированной популяции в предложен-

хода из подверженной популяции в популяцию

инфицированных, но не определяемых тестами

ной нами модели показывает, что при введении

индивидов) то же значение, что и раньше. Оце-

ограничительных мер правительством Индии

ненные начальные плотности на 21 марта 2020 г.

21 марта 2020 г. пик инфекции (максимум количе-

приведены в табл. 5, а скорости притока населе-

ства случаев в день) ожидается почти через четы-

ния и смертность от инфекции для пяти штатов

ре месяца (120 суток). После этого, если продол-

Индии - в табл. 6. Наконец, остальные оценен-

жится такой же уровень ограничений, скорость

ные параметры приведены в табл. 7.

распространения инфекции постепенно умень-

Используя эти оценочные параметры, фикси-

шится.

рованные параметры и начальные плотности

Рис. 5. График временного ряда инфицированной

Рис. 6. График временного ряда инфицированной

популяции при α = 2.5·10^-10 на временном промежутке

в один месяц. Начальные условия и значения

в два месяца. Начальные условия и значения

параметров приведены в табл. 2 и 3 соответственно. По

оси абсцисс - время в сутках, по оси ординат -

инфицированная популяция I(t).

БИОФИЗИКА том 67

№ 2

2022

308

ПАЛ и др.

Таблица 5. Оценочные значения начальных плотностей на 21 марта 2020 г.

Штат

S(0)

E(0)

Q(0)

I(0)

R(0)

Махараштра

75000000

225

800

30000000

Керала

10000000

200

1000

10050000

Уттар-Прадеш

150000000

120

1500

50000000

Дели

10000000

150

800

500000

Западная Бенгалия

50000000

200

30000000

Таблица 6. Скорость притока населения и смертность от инфекции для пяти штатов Индии

Параметры

Махараштра

Керала

Уттар-Прадеш

Дели

Западная Бенгалия

3300

405

14200

650

3490

d₂

0.0032

0.00029

0.0049

0.00067

0.0024

Таблица 7. Оценочные параметры для пяти штатов Индии

Параметры

Махараштра

Керала

Уттар-Прадеш

Дели

Западная Бенгалия

β₁

0.0000004

β₂

0.005

σ₁

0.0005

σ₂

0.1

σ₃

0.005

0.012

0.0038

0.0016

0.0078

r₁

0.04

0.05

0.02

0.05

r₂

0.002

0.001

0.0012

0.00093

0.0005

d₁

0.000015

0.000018

0.00002

0.00001

0.000016

(табл. 5 и 7), мы можем графически представить

Чтобы проиллюстрировать ситуацию с

инфицированные популяции для разных штатов.

COVID-19 в штате Керала на основе значений па-

Рис. 7 и 8 показывают графическое представле-

раметров, приведенных в табл. 5-7, приведем

ние инфицированной популяции для штата Ма-

следующие два графика.

хараштра.

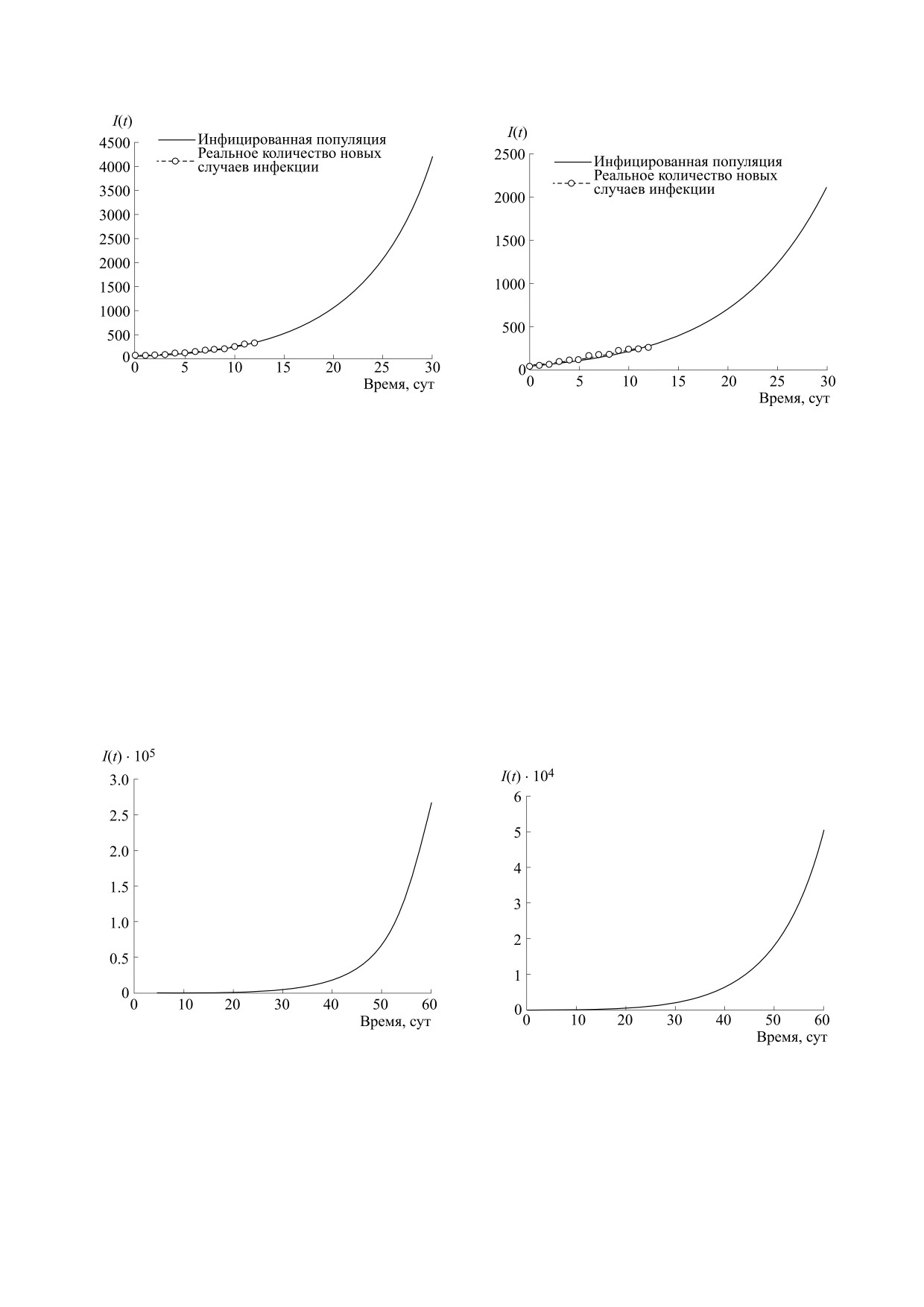
Рис. 9 показывает, что за 30 суток инфициро-

По рис. 7 мы можем наблюдать, что после при-

менения правительством Индии ограничитель-

ванная популяция в Керале достигнет 2100. Мы

ных мер общее количество инфицированных жи-

также наблюдаем, что реальное количество новых

телей Махараштры за 30 суток достигнет 4100 с

случаев инфекции перекрывается с моделируе-

21 марта 2020 г. Также можно заметить, что дей-

мой кривой новых случаев в течение 13 суток. Ри-

ствительное количество инфицированных жите-

сунок 10 показывает, что количество инфициро-

лей совпадает с предсказанным нашей системой

ванных индивидов в Керале спустя 60 суток с

количеством индивидов с COVID-19 в течение

21 марта 2020 г. достигнет 50000. Но недавние

13 суток с 21 марта 2020 г.

тренды показывают, что количество новых инфи-

Из рис. 8 можно вывести, что общее количе-

цированных намного меньше, чем ожидаемое

ство инфицированных достигнет 260000 через два

нами число. Это можно объяснить тем, что пра-

месяца. Но в реальности этого может и не слу-

читься, поскольку правительство постоянно ме-

вительство Кералы предприняло строгие ограни-

няет ограничительные меры, стремясь остано-

чительные меры для предотвращения распро-

вить распространение COVID-19.

странения вируса COVID-19.

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКИЙ АНАЛИЗ МОДЕЛИ ЭПИДЕМИИ COVID-19

309

Рис. 7. График временного ряда инфицированной

популяции при α = 2.5⋅10^-9 на временном промежутке в

Рис. 9. Временной ряд инфицированной популяции в

один месяц (с 22 марта 2020 г.) для штата Махараштра с

Керале при α = 0.0000000164 с данными из табл. 5-7 для

применением данных из табл. 5-7. По оси абсцисс -

периода в один месяц (с 22 марта 2020 г.). По оси

время в сутках, по оси ординат - инфицированная

абсцисс

- время в сутках, по оси ординат

популяция I(t). Кружками отмечено реальное

инфицированная популяция I(t). Кружками отмечено

количество новых случаев инфекции.

реальное количество новых случаев инфекции.

Следующие два рисунка (рис. 11 и 12) показы-

Аналогичным образом представим следующие

два графика для штата Дели (рис. 13 и 14). Они по-

вают ситуацию с COVID-19 в штате Уттар-Пра-

казывают, что для нашей модели количество ин-

деш.

фицированных в Дели спустя 30 и 60 суток с

Рис. 11 и 12 показывают, что для наших по-

21 марта 2020 г. достигнет 4600 и 400000 соответ-

строений инфицированная популяция в Уттар-

ственно.

Прадеше за 30 и 60 суток достигнет 4400 и 620000

Наконец, возможная ситуация с пандемией

соответственно, начиная с 21 марта 2020 г.

COVID-19 по Западной Бенгалии представлена

на рис. 15 и 16. Как и ранее, рис. 15 и 16 показыва-

Рис. 8. График временного ряда инфицированной

популяции при α = 2.5⋅10^-9 на временном промежутке в

Рис. 10. Временной ряд инфицированной популяции в

два месяца (с 22 марта 2020 г.) для штата Махараштра с

Керале при α = 0.0000000164 с данными из табл. 5-7

применением данных из табл. 5-7. По оси абсцисс -

для периода в два месяца (с 22 марта 2020 г.). По оси

время в сутках, по оси ординат - инфицированная

абсцисс

- время в сутках, по оси ординат

популяция I(t).

инфицированная популяция I(t).

БИОФИЗИКА том 67

№ 2

2022

310

ПАЛ и др.

Рис. 11. Временной ряд инфицированной популяции в

Рис. 13. Временной ряд инфицированной популяции в

штате Уттар-Прадеш при α = 0.000000020 с данными из

штате Дели при α = 0.000000021 с данными из табл. 5-7

табл. 5-7 для периода в один месяц (с 22 марта 2020 г.).

для периода в один месяц (с 22 марта 2020 г.). По оси

По оси абсцисс - время в сутках, по оси ординат -

абсцисс

- время в сутках, по оси ординат

инфицированная популяция I(t). Кружками отмечено

реальное количество новых случаев инфекции.

ют, что инфицированная популяция в Западной

чаев COVID-19 растет день ото дня во всем мире.

Бенгалии через 30 и 60 суток с 21 марта 2020 г. до-

Исходя из этого, предсказание количества инфи-

стигнет 1100 и 210000 соответственно.

цированных индивидов чрезвычайно важно для

принятия надлежащих мер здравоохранения.

Также важно контролировать скорость распро-

ОБСУЖДЕНИЕ И ВЫВОДЫ

странения COVID-19, ограничивая количество

новых случаев. Наше математическое исследова-

В данной статье мы сформулировали и изучи-

ние основано на распространении вируса

ли эпидемиологическую модель для вируса бо-

лезни COVID-19, передаваемой от человека к че-

COVID-19 в Индии. Мы попытались оптимизи-

ловеку. Сейчас количество подтвержденных слу-

ровать нашу модель к случаю распространения

Рис. 12. Временной ряд инфицированной популяции в

Рис. 14. Временной ряд инфицированной популяции в

штате Уттар-Прадеш при α = 0.000000020 с данными из

штате Дели при α = 0.000000021 с данными из табл. 5-7

табл. 5-7 для периода в два месяца (с 22 марта 2020 г.).

для периода в два месяца (с 22 марта 2020 г.). По оси

По оси абсцисс - время в сутках, по оси ординат -

абсцисс

- время в сутках, по оси ординат

инфицированная популяция I(t).

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКИЙ АНАЛИЗ МОДЕЛИ ЭПИДЕМИИ COVID-19

311

Рис. 15. Временной ряд инфицированной популяции в штате Западная Бенгалия при α = 0.0000000047 с данными из табл.

5-7 для периода в один месяц (с 22 марта 2020 г.). По оси абсцисс - время в сутках, по оси ординат - инфицированная

популяция I(t). Кружками отмечено реальное количество новых случаев инфекции.

COVID-19 в Индии, поскольку объем доступных

В данном исследовании наша главная цель -

данных достаточно ограничен. Основной пара-

математически предсказать количество инфици-

рованных жителей Индии с COVID-19. Для до-

метр взаимодействия R₀ рассчитан для нашей

стижения цели мы провели подробное численное

ожидаемой модели. Наблюдается, что при R₀ < 1

моделирование предложенной системы. Сначала

величина E₀ для равновесия, свободного от бо-

мы провели моделирование развития COVID-19 в

лезни, глобально асимптотически стабильна. Да-

Индии, а затем в пяти различных штатах (Маха-

лее, из анализа чувствительности R₀ мы наблюда-

раштра, Керала, Уттар-Прадеш, Дели и Западная

Бенгалия) выполнили численное предсказание

ем, что самый чувствительный параметр нашей

через графический подход, используя программу

модельной структуры - α (скорость перехода из

Matlab. Мы оценили значения параметров и на-

подверженной популяции в популяцию инфици-

чальных условий, исходя из данных, доступных

рованных, но не определяемых тестами индиви-

на момент 21 марта 2020 г.

дов). Также эндемическое равновесие E₁ суще-

Видно, что α - наиболее чувствительный пара-

ствует и стабильно при R₀ > 1.

метр нашей системы. Поэтому для разных значе-

Рис. 16. Временной ряд инфицированной популяции в штате Западная Бенгалия при α = 0.0000000047 с данными из табл.

5-7 для периода в два месяца (с 22 марта 2020 г.). По оси абсцисс - время в сутках, по оси ординат - инфицированная

популяция I(t).

БИОФИЗИКА том 67

№ 2

2022

312

ПАЛ и др.

ний α популяционные кривые представлены на

будет принимать надлежащие меры раз за разом,

рис. 3. Мы наблюдаем, что для α = 2.5⋅10^-10инфи-

инфицированная популяция будет отличаться от

цированная популяция наилучшим образом сов-

предсказанных нами значений с течением време-

падает с реальным количеством инфицирован-

ни, и Индия излечится от этой вирусной инфек-

ных индивидов в течение 13 суток с 21 марта

ции в ближайшем будущем. Наконец, мы должны

2020 г. Долгосрочное развитие эпидемиии можно

сказать, что индийское общество должно помочь

наблюдать на рис. 4. Этот рисунок показывает,

правительству бороться с опасным заболеванием

что для данной модели и доступных данных пик

COVID-19, описанным представленной моделью.

инфекции должен быть достигнут в течение

120 суток с 21 марта 2020 г. Таким образом, оце-

ночная дата достижения пика инфекции по

Приложение А

нашему предсказанию - 21 июля 2020 г., если

ОСНОВНЫЕ СВОЙСТВА

ограничительные меры, объявленные правитель-

Неотрицательность решения.

ством Индии 21 марта 2020 г., будут неизменны-

Теорема 1 (А1). Каждое решение структуры мо-

ми. Краткосрочные предсказания размера инфи-

дели SEQIR (7) при предварительных ограниче-

цированной популяции приведены на рис. 5 и 6

ниях существует в интервале (0, ∞), при этом

соответственно.

S(t) > 0, Е(t) ≥ 0, I(t) ≥ 0, а также R(t) > 0 для всех

Согласно этим двум рисункам, количество па-

значений t больше нуля.

циентов с COVID-19 через 30 и 60 суток с 21 марта

Доказательство. Поскольку правая часть

2020 г. составит 32000 и 3000000 соответственно.

структуры модели SEQIR (7) полностью непре-

Теперь взглянем на ситуацию в разных штатах.

рывна и локально на C является функцией Лип-

Рис. 7 и 8 показывают, что количество инфициро-

шица, решение (S(t), E(t), I(t), R(t)) уравнения (7)

ванных индивидов в штате Махараштра достиг-

нет соответственно 4100 и 260000 в течение 30 и

с начальными условиями существует и является

60 суток. Для Кералы эти числа составят 2100 и

единственным на (0, ξ); где 0 < ξ < +∞.

50000 (при α

= 0.0000000164) соответственно

Из системы (7) с начальным условием имеем

(рис. 9 и 10). В Уттар-Прадеше, согласно рис. 11 и

dS/dt ≥ -AS(t),

12, при α = 0.000000020 предсказанное количество

инфицированных жителей составит

4400 и

S(t) ≥ S(0)exp[-At] > 0.

620000; 4600 и 400000 человек будет инфицирова-

но через в Дели (рис. 13 и 14). Наконец, в Запад-

Из второго уравнения системы (7) следует, что

ной Бенгалии соответственно 1100 и 210000 жите-

dE/dt ≥ -BE(t). Используя начальное условие, по-

лей будет инфицировано вирусом COVID-19 че-

лучаем E(t) ≥ E(0)exp[-Bt] ≥ 0. Вновь из третьего и

рез 30 и 60 суток (рис. 15 и 16).

четвертого уравнений системы (7) с помощью на-

Таким образом, анализ всех результатов пред-

чального условия находим

ложенной нами модели и наблюдение за ситуаци-

Q(t) ≥ Q(0)ехр[-Ct] ≥ 0 и I(t) ≥ I(0)ехр[-Dt] ≥ 0.

ей в разных странах позволяет нам сделать вывод,

Кроме того, последнее уравнение (7) дает

что в ближайшем будущем Индию ожидают очень

большие проблемы из-за COVID-19. Во избежа-

dR/dt ≥ -d₁R → R(t) ≥ R(0)exp[-d₁t] > 0.

ние этих проблем правительство Индии должно

Отсюда видно, что S(t) > 0, E(t) ≥ 0, I(t) ≥ 0,

принять более строгие меры помимо карантина,

R(t) > 0, ∀t ≥ 0. Это завершает доказательство тео-

локдауна и т. д. В настоящее время индийское

ремы.

правительство постоянно меняет меры противо-

действия COVID-19. Недавно все округа Индии

Инвариантная область.

были классифицированы в три группы, назван-

Теорема 2 (А2). Все решения структуры модели

ные красными зонами (тревожные зоны), оран-

SEQIR (7), инициирующиеся в R⁵⁺, ограничены

жевыми зонами (зоны меньшего уровня тревоги)

и входят в область Ω, определяемую равенством

и зелеными зонами (безопасные зоны). По пред-

варительным данным, 170 округов Индии явля-

Ω = {(S, E, Q, I, R) ∈ R⁵⁺: 0 < N(t) ≤ Λ/ζ} при t → ∞,

ются тревожными зонами, в которых мощности

где ζ = min{d₁, d₁ + d₂}.

экспресс-тестирования быстро развертываются и

Доказательство. Предположим, что N(t) =

становятся доступными для общества. С течени-

= S(t) + E(t) + I(t) + R(t), где (S(t), E(t), Q(t), I(t),

ем времени все больше стратегических мер при-

R(t)) - структура модели SEQIR (7). Дифферен-

нимается правительством Индии и всеми прави-

цируя обе части по t, имеем

тельствами штатов для остановки распростране-

ния COVID-19 в Индии. Таким образом, мы

dN(t)/dt = dS(t)/dt + dE(t)/dt +

можем оценить, что если правительство Индии

+ dQ(t)/dt + dI(t)/dt + dR(t)/dt.

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКИЙ АНАЛИЗ МОДЕЛИ ЭПИДЕМИИ COVID-19

313

Подставив значения dS(t)/dt, dE(t)/dt, dQ(t)/dt,

фицирование, производимое одиночным инфи-

dI(t)/dt и dR(t)/dt из уравнения (7), получим

цированным индивидуумом на протяжении его

или ее активной инфекционной эпохи при введе-

dN(t)/dt = Λ - d₁S - d₁E - d₁Q - d₁R - (d₁ + d₂)I.

нии в крайне восприимчивое население, находя-

Таким образом, имеем

щееся в равновесии.

dN(t)/dt + ζN(t) = Λ - (d₁ - ζ)S - (d₁ - ζ)E -

Чтобы найти базовое число воспроизводства в

- (d₁ - ζ)Q - (d₁ + d₂)I - (d₁ - ζ)R →

предлагаемой нами структуре модели SEQIR (7),

воспользуемся формулировкой из нового поко-

→ dN(t)/dt + ζN(t) ≤ Λ,

ления матричного метода [41]. Предположим, что

где ζ = min{d₁, d₁ + d₂}. Теперь, используя теорему

y = (E, Q, I, R, S)^T , тогда систему (7) можно пере-

сравнения, получаем

писать в виде

0 < N(t) ≤ N(0)ехр(-ζt) + Λ/ζ.

dy/dt = F(y) - v(y),

При t → ∞ имеем 0 < N(t) ≤ Λ/ζ. Следователь-

но, все решения структуры модели (7) входят в

⎡αSE⎤

⎡

⎤

область Ω = {(S, E, Q, I, R) ∈ R⁵⁺: 0 < N(t) ≤ Λ/ζ}.

⎢

⎥

⎢

⎥

−β

E +CQ

Таким образом, мы завершили требуемое доказа-

⎢

⎥

⎢

⎥

где F(y) =

тельство.

⎢

⎥

⎢

−r

E -r

Q+DI

⎥

⎢

⎥

⎢

⎥

−σ

I + d

⎢

⎥

⎢

⎥

Приложение B

⎣

⎦

⎣

-Λ + αSE +ΛS

⎦

Равновесие без болезни и базовое число воспро-

Величина F известна как передаточная часть,

изводства. Равновесие без болезни в предложен-

которая отражает возникновение новой инфек-

ной модели SEQIR (7) достигается установкой

ции, а v - как переходная часть, которая объясня-

E = 0, Q = 0, I = 0 и R = 0. Полученное равновесие

ет изменение состояния.

без болезней равно E₀(Λ/А, 0, 0, 0, 0).

Базовое число воспроизводства [39-42] - это

Матрицы Якоби F(y) и v(y) в равновесии без

число, определяемое как новообразованное ин- болезни E0^{задаются выражением}

⎡

⎤

⎡F

3×3

0 0⎤

⎢V

3×3

⎥

⎢

⎥

⎢

⎥

DF(E

)

Dv(E

)

−σ

⎢

⎥

⎢

⎥

⎣0

0⎦

⎢αΛ

⎥

⎣

⎦

Таким образом, FV^-1 является матрицей следу-

⎡αΛ

⎤

0 0

ющего поколения структуры модели SEQIR (7).

⎢

⎥

⎡B

⎤

где

⎢

⎥

⎢

⎥

Так, согласно работе [41] R₀ = ρ(FV^-1), где ρ -

−δ

⎢

⎥

⎢

⎥

спектральный радиус матрицы следующего поко-

−

D⎦

⎢

⎥

⎣-

⎣

⎦

ления FV^-1. Следовательно,

−1

αΛ

=ρ(FV

)

(

β +σ +

)(r

+β +

)

Примечательно, что L/A представляет количе-

тельности для проверки чувствительности основ-

ство восприимчивых лиц в равновесии без болез-

ного числа воспроизведения. Как указывали

ней E₀.

авторы работы [43], мы рассчитали нормализо-

Анализ чувствительности R₀. На основе каждо-

ванный индекс прямой чувствительности по от-

го из параметров R₀ выполняется анализ чувстви- ношению к каждому из параметров:

БИОФИЗИКА том 67

№ 2

2022

314

ПАЛ и др.

∂R₀

∂R

∂α

(β

+σ

)(r

+β

)

∂R0

∂R

−β

β₁

∂β

+σ

β₁

∂R0

∂R

−σ

∂σ

+σ

σ₁

(B1)

∂R

−d

d₁

−

∂d

+σ

+β

d₁

∂

R₀

∂R

−r

∂

∂r

+β

∂R₀

∂R

−β

∂β

+β

Из приведенных выше расчетов очевидно, что

распространения коронавирусной болезни в та-

базовое число воспроизводства R₀ в основном

кой стране, как Индия. Следуя той же концеп-

ции, правительство Индии, а также правитель-

чувствительно к изменениям в α. Значение R₀ бу-

ства всех индийских штатов предприняли необ-

дет увеличено, если мы увеличим значение α. На-

ходимые действия, такие как изоляция, кампания

оборот, в той же пропорции значение R₀ умень-

против болезни и т. д., для защиты от вспышки

шится, если мы уменьшим значение α. Также бы-

этой опасной болезни.

ло замечено, что параметры β₁, σ₁, d₁, r₁ и β₂

Анализ устойчивости равновесия без болезни.

связаны с R₀ обратно пропорционально. Следо-

Этот раздел построен с целью изучения природы

вательно, при любом увеличении значения любо-

устойчивости равновесия без болезни E0 с

го из упомянутых параметров обязательно будет

помощью следующих теорем.

уменьшаться значение R₀. Но уменьшающееся

Теорема 3. Структура модели SEQIR (7) при

значение R₀ будет относительно меньшим. По-

равновесии без болезни E₀(Λ/A, 0, 0, 0, 0) локаль-

скольку влияние параметров β₁, σ₁, d₁, r₁ и β₂ на

но асимптотически устойчива при условии R₀ < 1

R₀ очень мало; будет разумно сосредоточить уси-

и становится неустойчивой при R₀ > 1.

лия на снижении α (скорости передачи, при кото-

Доказательство. Якобиан системы (7) при

рой восприимчивый индивидуум превращается в

равновесии без болезни E₀(Λ/A, 0, 0, 0, 0) имеет

подвергающегося воздействию индивидуума).

следующий вид:

Таким образом, детальный анализ базового числа

⎡

αΛ

⎤

воспроизводства подчеркнул, что профилактика

−A

−

⎢

⎥

лучше, чем лечение. Иными словами, меры по

⎢

⎥

усилению профилактики более эффективны в

⎢0

^αΛ -

0⎥

борьбе с распространением болезни COVID-19,

⎢

⎥

чем в увеличении числа людей, получающих до-

–C

⎢

⎥

ступ к лечению, поскольку пока нет надлежащих

⎢

⎥

–D

вакцин, что доказано с медицинской точки зре-

⎢

⎥

ния, этот метод очень эффективен для контроля

−

⎣

⎦

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКИЙ АНАЛИЗ МОДЕЛИ ЭПИДЕМИИ COVID-19

315

Характеристическое уравнение матрицы JE0

Доказательство. Мы можем переписать систе-

задается выражением

му дифференциальных уравнений (7) в следую-

щем виде:

det(JE0 - λI) = 0,

(B2)

dX/dt = F(X, V),

где λ — собственное значение матрицы JE0. Та-

dV/dt = G(X, V), G(X, 0) = 0,

ким образом, корнями уравнения (B2),

т.е. собственными значениями матрицы JE0, яв-

где X = (S, R) ∈ R² (число компартментов незара-

ляются λ₁ = -A < 0, λ₂ = αΛ/A - B, λ₃ = -C < 0,

женных особей), V = (E, Q, R) ∈ R³ (количество

λ₄ = -D < 0, а также λ₅ = -d₁ < 0. Поэтому систе-

компартментов инфицированных особей), а так-

ма (7) локально асимптотически находится в рав-

же E₀(Λ/A, 0, 0, 0, 0) - равновесие без болезни

новесии без болезни E₀(Λ/A, 0, 0, 0, 0), если

структуры модели SEQIR (7). E₀ является гло-

λ₂ < 0. Теперь λ₂ < 0 влечет

бально стабильным, если выполняются следую-

щие два условия:

αΛ

−

⇒

1) при dX/dt = F(X, V) X* глобально асимптотиче-

Следовательно, равновесие без болезни

ски устойчиво,

E₀(Λ/A, 0, 0, 0, 0) локально асимптотически

2) G(X, V) = BV - Ĝ(X, V), Ĝ(X, V) ≥ 0 for (X, V) ∈ Ω,

устойчиво при условии R₀ < 1.

где B = D_VG(X*, 0) - матрица Метцлера и Ω - по-

Теорема 4. Структура модели SEQIR (7) при

ложительно инвариантное множество относи-

равновесии без болезни E₀(Λ/A, 0, 0, 0, 0) гло-

тельно модели (7). Вслед за авторами работы [44]

бально асимптотически устойчива при условии

проверяем указанные выше условия. Для предло-

R₀ < 1 и становится неустойчивой при R₀ > 1.

женной нами структуры модели (7) имеем:

⎡−B

⎤

⎡αSE⎤

⎡Λ-

⎤

⎢

⎥

⎢

⎥

F(X, 0)

–C

and

G(X,V)

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

⎣

–D⎦

⎣

⎦

Очевидно, что Ĝ(X,V) ≥ 0 каждый раз, когда

мического равновесия, а также демонстрирует его

переменные состояния находятся в пределах Ω.

устойчивый характер. Чтобы обнаружить энде-

Также очевидно, что X* = (L/A, 0) является гло-

мическое равновесие E₁(S*, E*, Q*, I*, R*) в на-

бальным асимптотически устойчивым равнове-

шей предлагаемой структуре SEQIR (7), мы счи-

сием системы dX/dt = F(X, 0). Следовательно, тео-

таем следующее:

рема доказана.

S > 0, E > 0, Q > 0, I > 0, R > 0,

а также

Приложение С

dS/dt = dE/dt = dQ/dt = dI/dt = dR/dt = 0. (C1)

Наличие эндемической точки равновесия и ее

устойчивость. Этот раздел отражает наличие энде-

Решая систему уравнений (C1), получаем

B +r

α(r

Cr E*

0[R

0],

αC

αCD

{

+β

(σ

+σ

)}

+α

{β

+σ

(

Cr E*

αd1CD

Из первого уравнения (C1) имеем

Δ-

Λ-

AS*

AAR

(ввод значения

S),

αS

AR₀

⎡

⎤

1−

⎢

⎥

⎣

⎦

[

−

]

αΛ

БИОФИЗИКА том 67

№ 2

2022

316

ПАЛ и др.

Следовательно, E* имеет единственное поло-

нению, чем другие параметры. Если считать, что

жительное значение, если R₀ - 1 > 0, т. е. R₀ > 1.

R₀ = 1, то имеем

Сокращая приведенные выше рассуждения и рас-

α* = АВ/Λ.

(C3)

суждения в предыдущих разделах, мы пришли к

следующей теореме.

Теперь якобиан линеаризованной системы

Теорема 5 (C1). Структура модели SEQIR (7)

(C1) через (C2) при равновесии без болезни E₀,

имеет уникальное равновесие без болезни

когда α* = α, выглядит следующим образом:

E₀(Λ/A, 0, 0, 0, 0) для всех значений параметров,

также система (7) имеет уникальное эндемиче-

⎡−A

–B

0⎤

ское равновесие E₁(S*, E*, Q*, I*, R*) при условии

⎢

⎥

⎢

⎥

R₀ > 1.

J(α*)

=⎢β

–C

0⎥.

(C4)

Следующая теорема устанавливает локальную

⎢

⎥

–D

устойчивость эндемического равновесия E₁(S*,

⎢

⎥

⎣⎢σ

–d

⎦

E*, Q*, I*, R*):

g₁ = Λ - αSE - AS,

Собственные значения матрицы (C4) задаются

g₂ = αSE - BE,

как (0, -A, -C, -D, -d₁)^T. Заметим, что матрица

(C4) имеет простое нулевое собственное значе-

g₃ = β₁S + β₂E - CQ,

(C2)

ние, а ее остальные собственные значения отри-

g₄ = r₁E + r₂Q - DI,

цательны. Сейчас мы находимся на этапе приме-

нения теории центрального многообразия [45]

g₅ = σ₁S + σ₂Q + σ₃I - d₁R.

для анализа динамики системы (C1). Нулевому

собственному значению соответствует правиль-

Мы предполагаем, что α* = α как параметр би-

фуркации, при этом, как было объяснено в (B1),

ный собственный вектор ω = (ω₁, ω₂, ω₃, ω₄, ω₅)^T

R₀ преимущественно более чувствителен к изме-

матрицы (C4) определяется выражениями

=- ω

−β

(

)

⎡

⎤

−β

⎣

(

)

⎦

⎡

⎤

−β

(

)

{

(

)}

⎣

⎦

A C

A D

со свободным ω₂. Более того, J(a*) имеет соответ-

v₃, v₄, v₅), где v₁ = 0, v₂ = 0, v₃ = 0, v₄ = 0, v₅ = 0 со

ствующий левый собственный вектор v = (v₁, v₂,

свободным v₂. Таким образом, мы имеем

∂

α =

ωω

(0,0)

ωω

(0,0)

(0,0),

∑

k i j

∑

k i j

∑

ki, j=1

∂x

ki, j=

∂

i, j=1

∂x

∂

(0,0)

(0,0).

∑

k i

∑

i=1

∂x

Подставляя значения всех производных вто-

Поскольку a < 0 и b > 0 при α* = α, то, исходя

рого порядка, рассчитанных для равновесия без

из замечания 1 к теореме 4.1, сформулированной

болезни, а также α* = α, получаем

в работе [44], имеем транскритическую бифурка-

цию при R₀ = 1, а неподражаемое эндемическое

a = -(2/Λ)B² < 0 и b = Λ/A > 0.

равновесие локально асимптотически устойчиво

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКИЙ АНАЛИЗ МОДЕЛИ ЭПИДЕМИИ COVID-19

317

благодаря R₀ > 1. Таким образом, мы завершаем

14.

Coronavirus disease 2019 (COVID-19) Situation Report -

доказательство.

73 (World Health Organization,

2020), https://

www.who.int/docs/default-source/coronaviruse/situ-

ation-reports/20200402-sitrep-73-covid-19.pdf?

БЛАГОДАРНОСТИ

sfvrsn=5ae25bc7_2. Retrieved: 2020-04-02.

Авторы выражают благодарность главному ре-

15.

Timeline of the 2020 coronavirus pandemic in India,

дактору, секретарю редакции и рецензентам за

2020,

https://en.wikipedia.org/wiki/Timeline_of_

поддержку и конструктивные замечания при до-

the_2020_coronavirus_pandemic_in_India#Janu-

работке статьи.

ary. Retrieved: 2020-04-02.

16.

Ministry of Health and Family Welfare (Government of

КОНФЛИКТ ИНТЕРЕСОВ

India, 2020), https://www.mohfw.gov.in/. Retrieved:

Авторы заявляют об отсутствии конфликта

03.04.2020.

интересов.

17.

2020 coronavirus pandemic in India,

2020,

https://en.wikipedia.org/wiki/2020_coronavirus_

pandemic_in_India#cite_note-2-10.

Retrieved:

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

03.04.2020.

Настоящая работа не содержит описания ис-

18.

Statement on the second meeting of the international

следований с использованием людей и животных

health regulations (2005) emergency committee regarding

в качестве объектов.

the outbreak of novel coronavirus (2019-ncov) (Geneva:

World health organization,

2020), https://www.

СПИСОК ЛИТЕРАТУРЫ

who.int/, 2019. Retrieved: 2020-09-04.

C. Huang, Y. Wang, X. Li, et al., Lancet 395 (10223),

19.

C. Rivers, J. P. Chretien, S. Riley, et al., Nature Com-

497 (2020).

mun. 10 (1), 1 (2019).

N. Zhu, D. Zhang, W. Wang, et al., N. Engl. J. Med.

20.

G. Chowell, S. M. Bertozzi, M. A. Colchero, et al., N.

382, 727 (2020).

Engl. J. Med. 361 (7), 674 (2009).

National Health Commission of the People’s Republic of

21.

G. Chowell, S. Echevarria-Zuno, C. Viboud, et al.,

China, http://www.nhc.gov.cn/xcs/yqfkdt/202004/

PLoS Med. 8 (5), e1000436 (2011).

be27dc3c4a9544b081e2233537e762c3.shtml. Acces-

22.

C. Fraser, C. A. Donnelly, S. Cauchemez, et al., Sci-

sed April 02, 2020.

ence 324 (5934), 1557 (2009).

A. B. Gumel, S. Ruan, T. Day, et al., Proc. Roy. Soc.

23.

M. Lipsitch, T. Cohen, B. Cooper, et al., Science 300

Lond. Ser. B: Biological Sciences 271 (1554), 2223

(5627), 1966 (2003).

(2004).

24.

A. J. Kucharski, T. W. Russell, C. Diamond, et al.,

W. Li, M. J. Moore, N. Vasilieva, et al., Nature 426

Lancet Infect Dis. 20, 553 (2020).

(6965), 450 (2003).

25.

B. Tang, X. Wang, Q. Li, et al., J. Clin. Med. 9 (2), 2

R. J. Groot, S. C. Baker, R. S. Baric, et al., J. Virology

(2020).

87 (14), 7790 (2013).

26.

T. Zeng, Y. Zhang, Z. Li, X. Liu, B. Qiu, ArXiv 2020,

E. Wit, N. Doremalen, D. Falzarano, and V. J. Mun-

04945 (2020).

ster, Nature Rev. Microbiol. 14 (8), 523 (2016).

27.

N. E. Huang and F. Qiao, Sci. Bull. 65 (6), 425 (2020).

B. J. Cowling, M. Park, V. J. Fang, et al., Eur. Com-

28.

S. Lai, I. Bogoch, N. Ruktanonchai, A. Watts, et al.,

mun. Dis. Bull. 20 (25) (2015).

medRxiv (2020). DOI: 10.1101/2020.02.04.20020479

L. E. Gralinski and V. D. Menachery, Viruses 12 (2),

29.

K. Muniz-Rodriguez, G. Chowell, C. Cheung, et al.,

135 (2020).

Emerging Infect. Dis. 26 (8), 1912 (2020).

10.

Centers for disease control and prevention: 2019 novel

30.

Nowcasting and Forecasting the Wuhan 2019-nCoV Out-

coronavirus, https://www.cdc.gov/coronavirus/2019-

break, https://les.sph.hku.hk/download/wuhan_ex-

ncov. Retrieved: 2020-03-10.

portation_preprint.pdf, 2020. Retrieved: 2020-04-09.

11.

J. F.-W. Chan, S. Yuan, K. Kok, et al., Lancet 395

31.

J. T. Wu, K. Leung, and G. M. Leung, Lancet, 395

(10223), 514 (2020).

(10225), 689 (2020).

12.

Z. J. Cheng and J. Shan, Infection 48 (2), 155 (2020).

32.

J. M. Read, J. R. E. Bridgen, D. A. Cummings, et al.,

13.

Coronavirus disease (COVID-19) Situation Dashboard

Phil. Trans. R. Soc. B 376, 20200265 (2020). DOI:

(World Health Organization, 2020), https://experi-

10.1098/rstb.2020.0265

ence.arcgis.com/experience/685d0ace521648f8a5-

33.

N. Imai, A. Cori, I. Dorigatti, et al., Report 3: trans-

beeeee1b9125cd. Retrieved: 2020-04-02.

missibility of 2019-ncov. Reference Source (2020).

БИОФИЗИКА том 67

№ 2

2022

318

ПАЛ и др.

34.

V. Volpert, M. Banerjee, and S. Petrovskii, Math.

43. L. Arriola and J. Hyman, Lecture notes, Forward and

Model. Nat. Phenom. 15, 24 (2020).

adjoint sensitivity analysis: with applications in Dynami-

35.

R. M. May, Infectious diseases of humans: dynamics and

cal Systems, Linear Algebra and Optimization (Mathe-

control (Oxford University Press, 1991).

matical and Theoretical Biology Institute, 2005).

36.

O. Diekmann and J. A. P. Heesterbeek, Mathematical

44. C. Castillo-Chavez, Z. Feng, and W. Huang, In Math-

epidemiology of infectious diseases: model building, anal-

ematical Approaches for Emerging and Reemerging In-

ysis and interpretation (John Wiley & Sons, 2000),

fectious Diseases: An Introduction (Springer-Verlag,

vol. 5.

New York, 2002), pp. 229-250.

37.

H. W. Hethcote, SIAM Rev. 42 (4), 599 (2000).

45. J. Carr, Applications of Center Manifold Theory

38.

S. Sharma and G. P. Samanta, J. Biol. Syst. 22, 1

(Springer-Verlag, New York, 1981).

(2014).

46. C. Castillo-Chavez and B. Song, Math. Biosci. Engi-

39.

R. M. Anderson and R. M. May, Nature 280, 361

neer. 1 (2), 361 (2004).

(1979).

47. Coronavirus disease (covid-19) outbreak, https://www.

40.

F. Brauer and C. Castillo-Chavez, Mathematical Mod-

who.int/emergencies/diseases/novelcoronavirus-2019.

els in Population Biology and Epidemiology (Springer,

Retrieved: 2020-04-14.

Berlin, 2001).

48. Indian Council of Medical research,

2019,

41.

P. Van Den Driessche and J. Watmough, Math.

https://www.icmr.nic.in/. Retrieved: 2020-04-14.

Biosci. 180, 29 (2002).

42.

F. Nyabadza and S. D. Hove-Musekwa, Math. Biosci.

49. Knoema, https://knoema.com/atlas/India/Birth-rate.

225, 132 (2010).

Retrieved: 2020-04-08.

Mathematical Analysis of a COVID-19 Epidemic Model by using Data Driven

Epidemiological Parameters of Diseases Spread in India

D. Pal*, D. Ghosh**, P.K. Santra***, and G.S. Mahapatra**

*Chandrahati Dilip Kumar High School, Chandrahati 712504, West Bengal, India

**National Institute of Technology Puducherry, Karaikal-609609, India

***Maulana Abul Kalam Azad University of Technology, Kolkata-700064, India

This paper attempts to describe the outbreak of SARS-CoV 2 (COVID-19) via an epidemic model. This virus

has dissimilar effects in different countries. The number of new active coronavirus cases is increasing gradu-

ally across the globe. India is now in the second stage of COVID-19 spreading, it will be an epidemic very

quickly if proper protection is not undertaken based on the database of the transmission of the disease. This

paper is using the current data of COVID-19 for the mathematical modeling and its dynamical analysis. We

bring in a new representation to appraise and manage the outbreak of infectious disease COVID-19 through

SEQIR pandemic model, which is based on the supposition that the infected but undetected by testing indi-

viduals are send to quarantine during the incubation period. During the incubation period if any individual

be infected by COVID-19, then that confirmed infected individuals are isolated and the necessary treatments

are arranged so that they cannot taint the other residents in the community. Dynamics of the SEQIR model

is presented by basic reproduction number R₀ and the comprehensive stability analysis. Numerical results are

depicted through apt graphical appearances using the data of five states and India.

Keywords: novel coronavirus, SEQIR model, reproduction number, lockdown, stability

БИОФИЗИКА том 67

№ 2

2022