Акустические методы
УДК 620.179.162:534.87; 517.958:5
ОПРЕДЕЛЕНИЕ ГЕОМЕТРО-АКУСТИЧЕСКИХ СВОЙСТВ СВАРНОГО
СОЕДИНЕНИЯ КАК РЕШЕНИЕ ОБРАТНОЙ КОЭФФИЦИЕНТНОЙ ЗАДАЧИ
ДЛЯ СКАЛЯРНОГО ВОЛНОВОГО УРАВНЕНИЯ
© 2021 г. Е.Г. Базулин1,*, А.В. Гончарский2,3,**, С.Ю. Романов 2,3,***, С.Ю. Серёжников 2,3,****
1ООО ЭХО+, Россия 123458 Москва, Технопарк Строгино
2МГУ им. Ломоносова, Россия 119992 Москва, Воробьевы горы, 1, стр.4
3Московский центр фундаментальной и прикладной математики, Россия 119992 Москва
E-mail: *bazulin@echoplus.ru; **gonchar@srcc.msu.ru;
***romanov60@gmail.com; ****s2110sj@gmail.com
Поступила в редакцию 03.09.2021 г.; после доработки 20.09.2021 г.
Принята к публикации 20.09. 2021 г.
Разработаны ультразвуковые томографические методы неразрушающего контроля объектов с целью определения
геометрии сварного соединения и оценки поля скоростей в нем. Предложено решение обратной коэффициентной задачи
для схемы регистрации эхосигналов в зеркально-теневом режиме. Проведено численное моделирование для различных
томографических схем на образцах с акустическими параметрами и геометрией, соответствующими реальному экспе-
рименту с использованием антенной решетки с рабочей частотой 2.25 МГц. Численными методами проведена оптими-
зация томографических схем для разных прикладных задач. Показано, что с помощью разработанных томографических
схем можно не только обнаружить границы сварного соединения, но и определить поле скоростей внутри объекта кон-
троля.
Ключевые слова: обратные задачи, ультразвуковая томография, ультразвуковой неразрушающий контроль, антенная
решетка, скорость продольной волны, FMC, C-SAFT, цифровая фокусировка антенной (ЦФА).
DOI: 10.31857/S0130308221110014
1. ВВЕДЕНИЕ
Задача контроля сварных соединений является одной из важнейших и актуальных задач дефек-
тоскопии при контроле объектов повышенной опасности, таких как трубопроводы и оборудование
атомных станций, магистральные и промысловые газопроводы, компрессорные станции, уникаль-
ные изделия машиностроения и так далее. Одним из способов ее решения является получение
высококачественных изображений внутреннего объема объекта контроля. В настоящее время для
этого широко используются ультразвуковые антенные решетки, работающие в режиме физической
фокусировки и в режиме цифровой фокусировки антенной (ЦФА) [1]. Метод ЦФА позволяет вос-
становить изображения отражателей со сплошной фокусировкой во всех точках области восста-
новления изображения (ОВИ). На первом этапе регистрируются эхосигналы для всех комбинаций
излучатель—приемник элементов антенной решетки. Такой режим называется режим двойного
сканирования (в зарубежной литературе FullMatrixCapture (FMC) [2]). Набор эхосигналов при
излучении одним элементом антенной решетки называется выстрел. На втором этапе по измерен-
ным эхосигналам методом комбинационного Synthetic Aperture Focusing Technique (SAFT)
(C-SAFT) [3] восстанавливается изображение отражателей. В отличии от ФАР-технологии, ЦФА-
технология позволяет получать изображение с лучшей фокусировкой по всей ОВИ и, главное,
применять самые разнообразные методы восстановления изображения отражателей, в том числе с
учетом многократного отражения импульсов от границ анизотропно-неоднородного объекта кон-
троля с учетом трансформации типа волны при отражении и преломлении [4—6]. Однако методу
ЦФА свойственны и недостатки. Для того, чтобы восстанавливать высококачественные изображе-
ния отражателей нужно использовать акустические схемы с учетом отражения от дна объекта
контроля и с учетом неоднородного распределения скорости распространения звука в основном
металле и в сварном соединении. Но проблема в том, что эти параметры, как правило, неизвестны
с достаточной точностью, и получение высококачественного изображения отражателя разбивается
на две задачи. Первая — это определение геометро-акустических свойств объекта контроля, а вто-
рая — это непосредственное восстановление ЦФА-изображения по многим акустическим схемам
с учетом информации, полученной при решении первой задачи. Отсутствие достоверной инфор-
мации о свойствах объекта контроля приводит к тому, что ультразвуковой контроль часто прово-
дится только на прямом луче [7—9]. Еще один недостаток метода ЦФА в том, что с его помощью
информация об отражателях восстанавливается в виде амплитуды вторичных источников, порож-
4
Е.Г. Базулин, А.В. Гончарский, С.Ю. Романов, С.Ю. Серёжников
денных падающей волной на границах контрастных несплошностей. Поэтому для выравнивания
пространственно-временной чувствительности в пределах ОВИ для выделения отражателей, пре-
вышающих браковочный уровень, необходимо проводить специальную настройку дефектоскопа.
Кроме того, работая с амплитудой вторичных источников, крайне сложно сделать вывод об акусти-
ческих свойствах разных областей объекта контроля. Поэтому возникает необходимость в разра-
ботке таких алгоритмов визуализации внутренней структуры объекта контроля, которые были бы
свободны от этих недостатков. Отметим также исследования по применению лучевых моделей в
томографии для нахождения скорости распространения и поглощения звука в объекте контроля
[10, 11]. Существуют направления «topological imaging», «time reverse», в которых основные уси-
лия направлены на обнаружение границ неоднородных включений в отраженном излучении
[12—18].
В настоящее время для проведения ультразвукового контроля начинают использоваться более
сложные методы волновой томографии, которые хорошо зарекомендовали себя в медицине и в
сейсмике [19—23]. Решение коэффициентной обратной задачи позволяет получать изображение в
виде значения скорости распространения звука в объекте контроля (поле скоростей), а задача опре-
деления геометро-акустических свойств объекта контроля и задача восстановления изображения
решаются одновременно, что является принципиальным отличием обратной коэффициентной
задачи от методов подобным ЦФА. В сейсмике итерационные методы решения коэффициентной
обратной задачи волновой томографии получили название «full wave form inversion» [24—26]. В
работах [27, 28] было показано, что можно решить обратную коэффициентную задачу для твердо-
го тела, когда источники и приемники ультразвука располагались со всех сторон от исследуемого
объекта. Однако такая постановка задачи характерна для медицинской диагностики, а не для уль-
тразвукового контроля. Поэтому необходимо оценить возможность решения обратной задачи уль-
тразвукового неразрушающего контроля методами волновой томографии в зеркально-теневом
режиме, когда антенную решетку или решетки можно разместить только на внешней поверхности
объекта контроля [29, 30, 11].
В работе исследована томографическая схема зондирования объекта при размещении ультра-
звуковой антенной решетки на внешней поверхности объекта контроля с целью восстановления
поля скоростей и формы как сварного соединения, так и основного металла. Использование эхо-
сигналов, отраженных от дна объекта контроля, является принципиальным, поскольку позволяет
значительно увеличить количество ракурсов зондирования и регистрировать проходящие через
сварное соединение волны. В статье проведены результаты численного моделирования для раз-
личных томографических схем, что позволяет провести оптимизацию томографических схем для
разных прикладных задач. Рассматриваемые томографические обратные задачи ультразвукового
неразрушающего контроля требуют больших объемов вычислений. Для решения таких задач необ-
ходимо использовать высокопроизводительные вычислительные системы [28, 31].
2. ПОСТАНОВКА ОБРАТНОЙ ЗАДАЧИ УЛЬТРАЗВУКОВОЙ ТОМОГРАФИИ ОБЪЕКТОВ
С ПЛОСКОПАРАЛЛЕЛЬНЫМИ ГРАНИЦАМИ И СПОСОБ ЕЕ РЕШЕНИЯ
Ограничимся рассмотрением волн, описываемых скалярным волновым уравнением. В силу
своей относительной простоты скалярная волновая модель широко используется при проведении
расчетов в ультразвуковом неразрушающем контроле. Она позволяет рассчитывать скалярное вол-
новое поле u(r, t) по заданным начальным данным, пользуясь уравнением:
c(r)utt(r, t) - Δ u(r, t) = δ(r - r0)g(t);
(1)
u(r, t = 0) = ut(r, t = 0) = 0.
(2)
Здесь c-0,5(r) = v(r) — скорость продольной волны в среде, r∈R2; ∆ — оператор Лапласа по
переменной r; δ — функция Дирака, которая задает положение точечного источника в точке r0,
который излучает зондирующий импульс вида g(t). Уравнение (1) хорошо описывает явления диф-
ракции, рефракции волн и перерассеивания на неоднородностях объекта контроля.
Проведем постановку обратной задачи томографической ультразвуковой диагностики плоских
объектов. Рассмотрим простейшую двумерную задачу (рис. 1), в которой области 1 и 2 (основной
металл) изготовлены из одного и того же материала и разделены областью из другого материала 3
(сварное соединение). Скорость распространения продольной волны v(r) в областях 1 и 2 постоян-
на и равна v(r) = const = v0. Скорость волны v(r) в области 3 может быть неоднородна и ее форма
Дефектоскопия
№ 11
2021
Определение геометро-акустических свойств сварного соединения...
5
A
3
1
2
4
5
Рис. 1. Схема томографического эксперимента при размещении антенной решетки на внешней поверхности объекта
контроля.
точно неизвестна. На верхней границе пластин располагается линейная антенная решетка, обо-
значенная буквой A. Цифрой 4 на рис. 1 обозначена нижняя граница областей 1, 2 и 3. Ниже гра-
ницы 4 располагается однородная среда 5 (например, воздух или вода). Скорость продольной
волны v(r) в области 5 постоянна и известна, эта скорость сильно отличается от скоростей в обла-
стях 1, 2, 3. Из-за большого изменения импеданса на границе 4 ультразвуковые волны, излучаемые
антенной решеткой A, отражаются от границы 4 и регистрируются ею.
Будем считать, что излучаемые источниками ультразвуковые волны отражаются от нижней
границы 4 по какому-либо одному из стандартных законов:
k
∂
u r,t)
= p r,t),
(k = либо 0, либо 1),
(3)
n
k
где
u r,
)
∂
t
при k = 1 обозначает производную вдоль нормали к границе 4, а при k = 0 обозначает
n
значение функции u(r, t) на границе 4; p(r, t) — некоторая известная функция. Значение параметра
k определяется типом отражения и для каждой конкретной задачи известно. К подобной постанов-
ке граничных условий приводит, например, случай свободной поверхности или неподвижной
границы (в этих случаях p(r, t) = 0).
На верхней границе областей 1, 2 и 3 в численном эксперименте будем ставить условие
2
2
2
∂
u
1
∂
u v
∂
u
«неотражения» второго порядка точности в виде
−
+
=
0
[32]. Заметим, что в
2
2
∂ ∂t v ∂t
2
∂y
реальном эксперименте на верхней границе происходит отражение волн, однако при решении
обратной задачи волнами, отраженными от этой границы, можно пренебречь. Для этого время T
окончания регистрации эхосигналов на элементах антенной решетки выбирается так, чтобы
отсечь прием этих импульсов. Надо отметить, что учет многократно отраженных волн от границ
объекта контроля должен привести к более устойчивому и точному решению обратной коэффи-
циентной задачи. Условие «неотражения» поставим также на боковых границах: левая граница
области 1 и правая граница области 2.
В численном эксперименте использовалась следующая схема измерений ультразвуковых волн.
Антенная решетка A работает в режиме, когда заданные элементы излучают зондирующий
импульс, распространяются в областях 1, 2, 3, однократно отражаются от границы 4, а эхосигналы
измеряются всеми элементами решетки A.
Обозначим зарегистрированные антенной решеткой эхосигналы через Uij(t), где индекс j соот-
ветствует элементам, излучающим импульс (j = 1, …, M), i — соответствует элементам, принима-
ющим импульс (i = 1, …, M), М — количество элементов на антенной решетке. Обозначим через
uij (t) значение волнового поля u(r, t), рассчитанное из уравнений (1) — (3) в точке i -го приемного
элемента при излучении источником номер j. Таким образом, можно записать для разных положе-
ний источников и приемников уравнение:
uij (t)=Uij (t).
(4)
Совокупность уравнений (1) — (4) описывает задачу.
Обратная задача ультразвуковой томографической диагностики в скалярной модели заключа-
ется в реконструкции по уравнениям (1)—(4) неизвестной функции v(r)в области 3, форма и поло-
жение которой неизвестно, по экспериментально измеренному волновому полю Uij (t) на принима-
ющих элементах при зондировании излучающими элементами c известной функцией g(t), при
известных положениях элементов антенной решетки.
Дефектоскопия
№ 11
2021
6
Е.Г. Базулин, А.В. Гончарский, С.Ю. Романов, С.Ю. Серёжников
Прямая задача описывается уравнениями (1)—(3) и позволяет для произвольной функции c(r),
которая определяется функцией скоростей v(r) по формуле c(r) = v-2(r), вычислить волновое поле
u(r, t; c). Рассмотрим функционал невязки Φ(c) от аргумента c(r) между экспериментальными
данными Uij(t) и рассчитанным при заданном c(r) полем на детекторах:
M M
T
1
ij
ij
Φ
(c)
=
(
u
(
t;c
)
−U t))2
dt
(5)
∑∑ ∫
j
=1
i
=1
2
0
Здесь uij(t; c) — значения волнового поля при решении прямой задачи (1)—(3) при заданном коэф-
фициенте c(r). При использовании нескольких источников зондирующего излучения функционал
невязки представляет собой сумму по j = 1, …, M значений невязки, полученных для каждого
источника. При каждом фиксированном источнике j функционал интегрируется по времени (0,T)
и суммируется по всем приемникам i = 1, …, M, принимающим сигналы для выбранного источни-
ка. Математически обратная задача ставится как задача поиска функции c (r), минимизирующей
функционал невязки (5)
c
(
r
)
: min
Φ c)=Φ
(
c).
Функция c (r) принимается за приближенное
c
(
r
)
решение обратной коэффициентной задачи.
Эффективными методами минимизации функционала невязки Φ(c) являются градиентные
методы. Имея явное выражение для градиента, можно построить различные достаточно быстрые
итеративные алгоритмы первого порядка минимизации функционала невязки. Численная оценка
градиента функционала невязки, когда нет аналитического выражения расчета градиента, является
вычислительно очень трудоемкой задачей даже для современных высокопроизводительных кла-
стеров.
Кратко опишем процедуру прямого вычисления градиента функционала невязки. Рассмотрим
задачу, которую назовем сопряженной к основной задаче (1)—(3):
c(r) wtt (r, t) - ∆w(r, t) = u(r, t) |Г - U(t);
(6)
w(r, t = T) = wt (r, t = T) = 0;
(7)
∂ nk w(r, t) = 0,
(8)
где u(r, t) есть решение прямой задачи (1)—(3); ∂nkw(r, t) (k = 0 или 1) при k = 1— производная
вдоль нормали к границе 4, при k = 0 — значение функции w(r, t) на границе 4. Значение k такие
же, что и в формуле (3). По аналогии с работами [22, 34] для приведенной постановки обратной
задачи можно получить выражение для градиента функционала Φ(c):
T
Φ′ c)
=∫w
(
r,t
)
u
(
r,t
)
dt
(9)
c
t
t
0
Здесь u(r, t) — решение прямой задачи (1)—(3), а w(r, t) — решение сопряженной задачи (6)—(8)
при заданном c(r). Таким образом, для вычисления градиента функционала необходимо решить
основную и сопряженную задачи и рассчитать Φс'(c) по формуле (9).
Сформулированная задача восстановления скорости волны является нелинейной коэффици-
ентной обратной задачей, так как U(t) нелинейно зависит от c(r). Количество неизвестных даже
для двумерной задачи может быть больше 5·105, и для ее решения необходимо использовать высо-
копроизводительные вычислительные системы [33—36].
Особенность рассматриваемой томографической задачи в неразрушающем ультразвуком кон-
троле состоит в том, что доступ к объекту контроля не может быть обеспечен с разных сторон, в
отличие от постановки аналогичной задачи в медицинской диагностике. Источники и приемники
обычно могут быть расположены только на внешней поверхности объекта контроля. Схема экс-
перимента, представленная на рис. 1, является типичной для задач контроля сварных соединений.
В рассматриваемой в статье томографическойпостановке помимо волн, отраженных от границ
неоднородностей, регистрируются также проходящие через неоднородности волны, отразившиеся
от дна. Дополнительный учет этих волн при решении обратной задачи позволяет определять ско-
рость внутри неоднородностей, что чрезвычайно важно в задачах диагностики. Более того, инфор-
Дефектоскопия
№ 11
2021
Определение геометро-акустических свойств сварного соединения...
7
мация о скорости в сварном соединении позволяет учесть ее при восстановлении изображения
методом ЦФА [11] и повысить качество изображения отражателей.
3. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ
Модельные расчеты проводились для обратной 2D-задачи томографического неразрушающего
ультразвукового контроля сварных соединений. Одной из проблем в задаче контроля сварных
соединений плоских объектов, когда доступ к объекту возможен только на верхней границе, явля-
ется отсутствие точной информации о расположении нижней границы, в том числе нижней грани-
цысварного соединения. Эта информация важна как с точки зрения диагностики качества сварки,
так и для корректного решения обратной задачи методом ЦФА, учитывающим неоднородность
акустических свойств объекта контроля.
В настоящем разделе проведены численные эксперименты по определению положения нижней
границы сварного соединения. Конечно, идеальный вариант для решения обратной задачи — когда
положение границы 4 известно. Однако такое, как правило, недостижимо на практике: толщина
трубы и скорость звука в нем известны с ошибкой порядка 0,5 %, а форма сварного соединения на
внутренней стороне объекта контроля вообще неизвестна.
Относительно положения нижней границы 4 (см. рис. 1) будут рассмотрены три варианта. В
первой постановке будем считать, что положение границы 4 известно, то есть известен верти-
кальный размер областей 1, 2 и 3. Во второй постановке положение границы 4 неизвестно, а в
третьем варианте положение границы 4 известно только частично в области основного металла
(области 1 и 2).
3.1. Определение формы нижней границы и скорости звука сварного соединения
3.1.1. Антенная решетка со 150 элементами
Область 3 модельного образца имитирует аустенитное сварное соединение и основной
металл (области 1 и 2). Вертикальный размер областей 1 и 2 равен 45 мм. Под областью 3 гра-
ница 4 имеет выступ вниз размером 1,5 мм по вертикали. Он моделирует натек корня шва (про-
висание), который может возникнуть при сварке. Ширина области 3 на внешней границе равна
19 мм, на внутренней — 10 мм. Нижняя граница 4 под областями 1 и 2 задавалась ровной и
параллельной горизонтальной оси. Расчетная область представляет собой объединение областей
1, 2, 3 и 5. В области 5 скорость полагалась постоянной и равной скорости звука в воде. На внеш-
них границах расчетной области ставилось граничное условие «неотражения». После решения
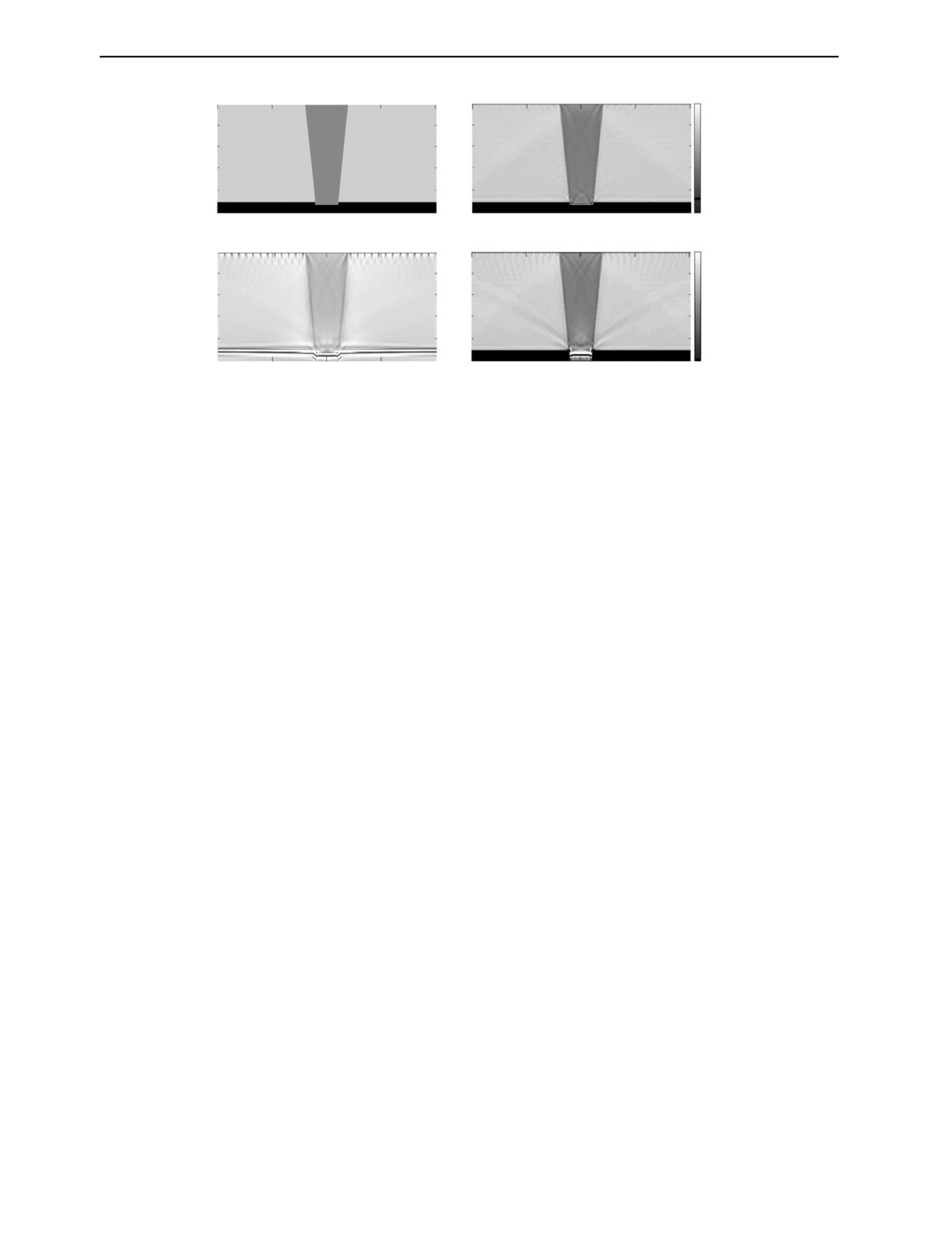
прямой задачи для уравнения (1) в неоднородной модельной среде, изображенной на рис. 2а,
рассчитанные эхосигналы uij(t)для каждого источника j сохранялись и использовались в качестве
«экспериментально измеренных» эхосигналов Uij(t) для последующего решения обратной зада-
чи. Предполагалось, что зондирующие импульсы для каждого излучающего элемента одинаковы
и представляют собой короткий импульс с центральной частотой 2,25 МГц.
В численных расчетах использовались следующие значения параметров. Скорость распростра-
нения звука в областях 1 и 2 была равна v0= 5,9 мм/мкс (сталь), скорость распространения звука в
области 3 (сварное соединение) — 5,7 мм/мкс (аустенитная сталь) и отличается от v0 примерно на
3,4 %. Скорость распространения звука в области 5 была равна v1= 1,5 мм/мкс и отличается от v0
почти в 4 раза. Длина волны λ центральной частоты широкополосного импульса равна λ = 2,62 мм,
размер расчетной области —200×50 мм, размер разностной сетки 800×200 точек. Антенная решет-
ка состоит из 150 элементов шириной 1 мм с шагом 1,2 мм и расположена на верхней границе
образца (см. рис. 2а). В расчетах для уменьшения объема вычислений в качестве источника
использовался каждый третий элемент антенной решетки, всего около 50 положений источников.
Для восстановления изображения использовалось 7 050 эхосигналов. Модельные расчеты показа-
ли, что использование всех элементов решетки в качестве источников принципиально не улучшает
реконструированное поле скоростей, но объем вычислений увеличивается в 3 раза.
Приведем результаты решения обратных задач по определению положения нижней границы
сварного соединения. На всех последующих рисунках для удобства восприятия будем приводить
только фрагмент центральной части восстановленного изображения. На рис. 2б приведены резуль-
таты реконструкции в случае, когда положение нижней границы 4 известно полностью, то есть,
например, известен вертикальный размер областей 1, 2 и 3. В качестве начального приближения
итерационного процесса решения обратной задачи в областях 1, 2 и 3 на рис. 1 была выбрана
Дефектоскопия
№ 11
2021
8
Е.Г. Базулин, А.В. Гончарский, С.Ю. Романов, С.Ю. Серёжников
а
б
0
0
V, мм/мкс
5,9
5,7
40
40
Y, мм
Y, мм
50
100
125
Х, мм
50
100
125
Х, мм
в
г
V, мм/мкс
0
0
5,9
5,7
40
40
Y, мм
Y, мм
50
100
125
Х, мм
50
100
125
Х, мм
Рис. 2. Численное моделирование: исходное распределение скорости звука (а); изображение, реконструированное в
случае известной нижней границы (б); изображение, реконструированное в случае неизвестного положения нижней
границы 4 (в); изображение, восстановленное в случае частично известной нижней границы (г).
константа v0 = 5,9 мм/мкс. В области 5 скорость полагалась v1 = 1,5 мм/мкс и не менялась на ите-
рациях. Видно, что значения скорости продольной волны в сварном соединении (область 3) в
среднем восстановлено правильно и составило около 5,7 мм/мкс, небольшие (около 2 %) по раз-
меру флуктуации скорости заметны в нижней части.
На рис. 2в приведены результаты решение обратной задачи в постановке, когда положение
отражающей границы 4 неизвестно. Начальное приближение функции скорости для итерационно-
го решения в этом случае выбиралось v0 = 5,9 мм/мкс во всей расчетной области. Узкая осцилли-
рующая полоса в нижней части рисунка соответствует восстановленной границе 4. Видно, что
качество реконструкции поля скоростей области 3 стало хуже. Хотя очертания области 3 восстано-
вились, однако значение скорости в области 3 составило в среднем около 5,8 мм/мкс, что сильно
отличается от модельного значения 5,7 мм/мкс. Это связано с тем, что восстановленная граница 4
в центральной части в целом смещена вниз на 0,6 мм от своего реального положения в образце.
Скорость в области 5 полагалась известной.
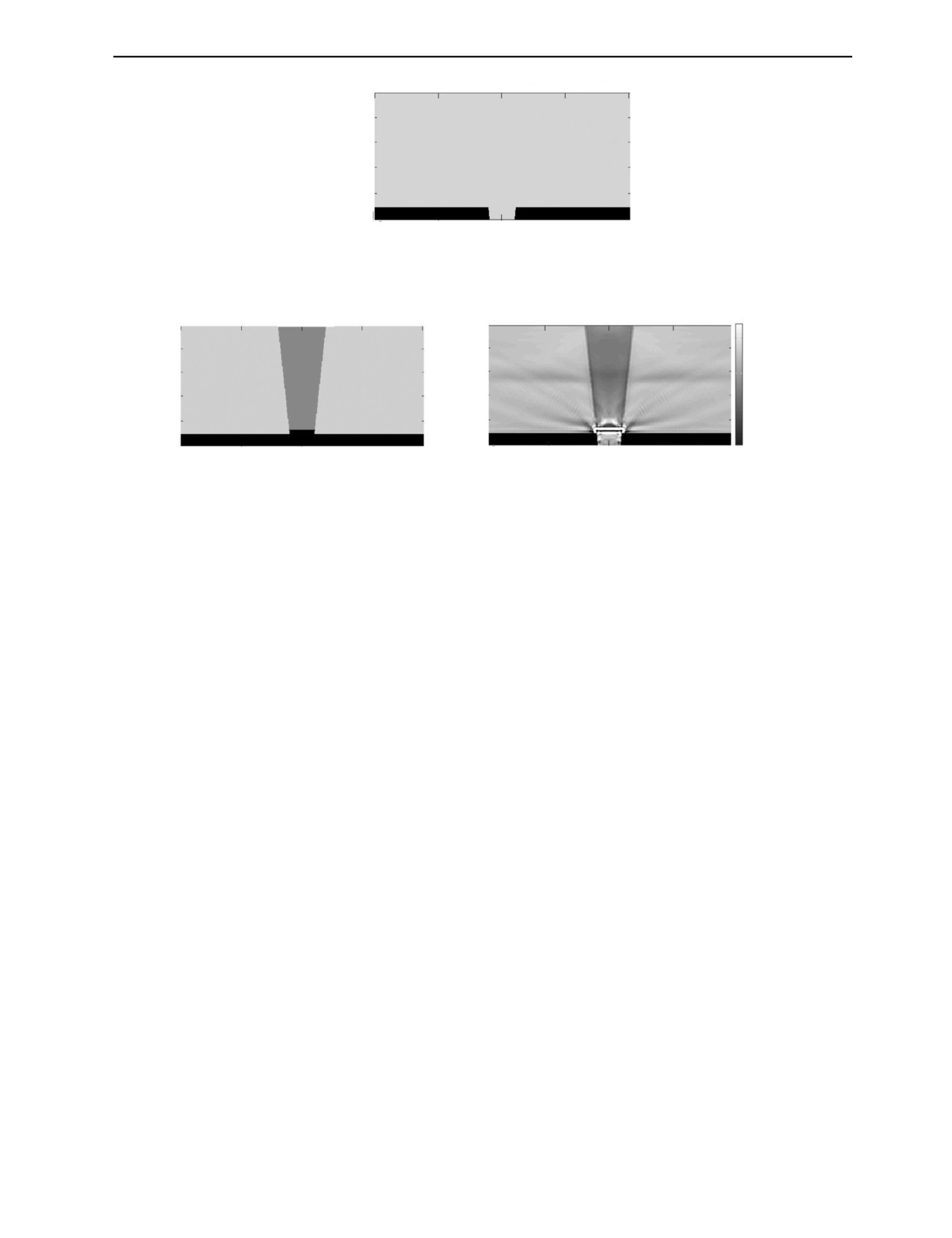
Используя априорную информацию о том, что толщина областей 1 и 2 известна, решим
обратную задачу в предположении, что положение границы 4 известно частично, только
между областью 5 и областями 1, 2. В статье [37] был предложен безэталонный метод опреде-
ления толщины объекта с плоскопараллельными границами и скорости продольной волны в
нем по эхосигналам, измеренным антенной решеткой. Форма сварного соединения (область 3)
неизвестна. Начальное приближение функции скорости для итерационного процесса решения
обратной задачи в этом случае выбиралось следующее. В областях 1, 2, 3 полагалось v0 =
= 5,9 мм/мкс, а в области 5 на каждой итерации полагалось v1 = 1,5 мм/мкс. Начальное при-
ближение поля скоростей приведено на рис. 3. На рис. 2г приведены результаты решения
обратной задачи в постановке, когда положение нижней границы области 3 неизвестно. Видно,
что качество реконструкции скоростного разреза области 3 стало заметно лучше. Остались
артефакты вблизи участка с неизвестным положением границы 4. Однако отчетливо видно,
что под областью 3 реконструированная граница имеет выступ вниз по вертикали. Максимум
осциллирующей полосы в области границы 4 совпадает с реальным положением границы с
точностью размера 1 пикселя около 0,2 мм.
На рис. 4б представлены результаты решения обратной задачи для образца с вогнутостью
корня шва (утяжина), показанного на рис. 4а. В отличие от модельного образца, на рис. 2а под
областью 3 граница 4 имеет смещение не вниз, а вверх размером 1,5 мм по вертикали. Обратная
задача решалась в постановке, когда положение отражающей границы 4 известно частично, то есть
неизвестно положение границы только под областью 3. На рис. 4б хорошо видно, что в отличие от
рис. 2г, под областью 3 реконструированная граница имеет смещение вверх по вертикали.
Начальное приближение при решении обратной задачи в этом случае, так же как и при реконструк-
ции изображения, приведенного на рис. 2г, было выбрано как на рис. 3.
Дефектоскопия
№ 11
2021
Определение геометро-акустических свойств сварного соединения...
9
0
40
Y, мм
50
100
125
Х, мм
Рис. 3. Начальное приближение в случае, когда положение границы 4 частично известно. В области серого цвета ско-
рость равна 5,9 мм/мкс, а в области черного цвета равна 1,5 мм/мкс.
а
б
V, мм/мкс
0
0
5,9
5,7
40
40
Y, мм
Y, мм
50
100
125
Х, мм
50
100
125
Х, мм
Рис. 4. Численное моделирование: исходное поле скоростей образца (а); поле скоростей восстановленное, как и
на рис. 2г, в случае частично известной нижней границы (б).
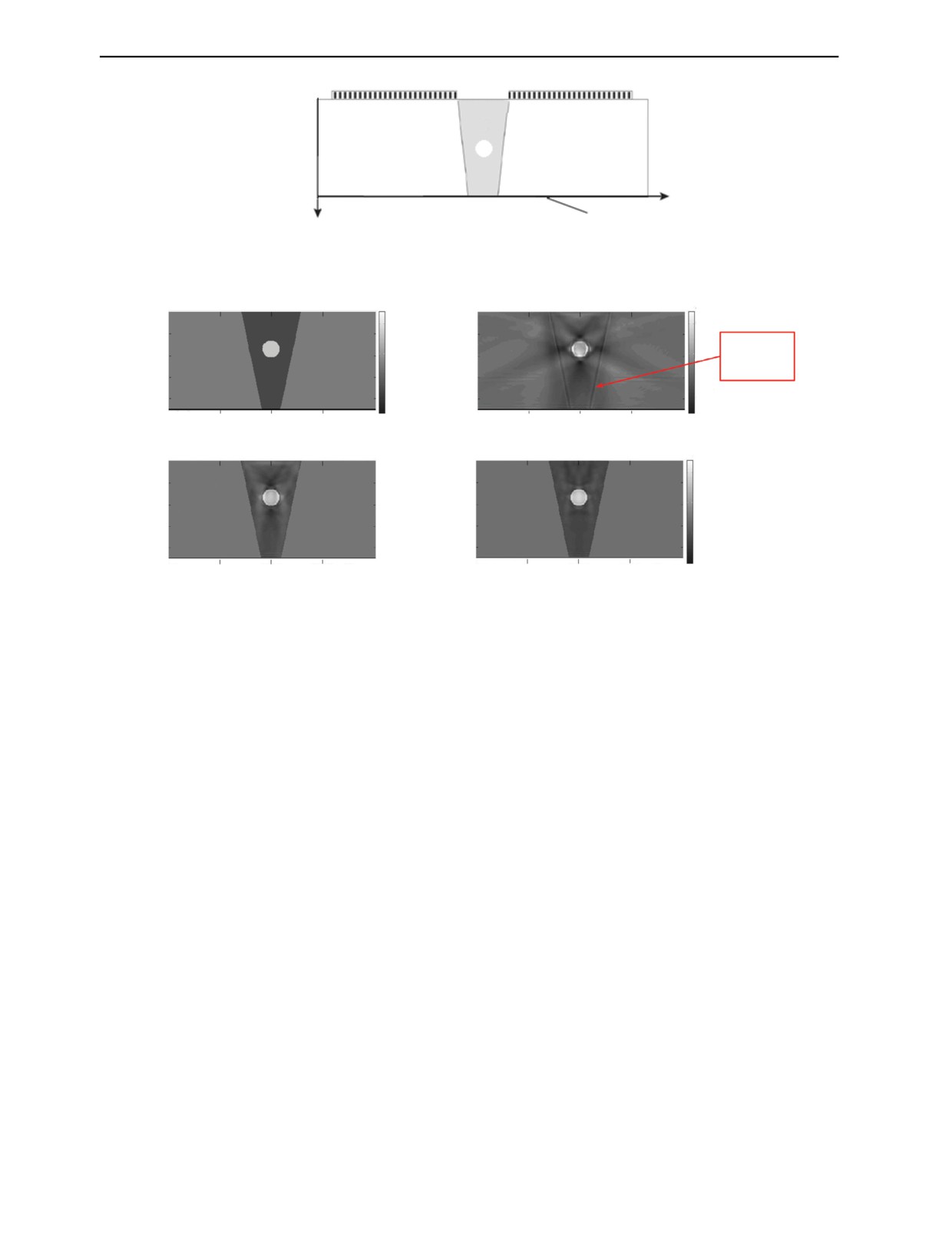
3.1.2. Две антенные решетки со 100 элементами при наличии валика усиления
В практике ультразвукового контроля сварных соединений нередко возникает ситуация, когда
трудно или невозможно расположить источники и приемники непосредственно над сварным сое-
динением, например, при наличии валика усиления. В этом случае схема эксперимента выглядит
как на рис. 5, на котором, в отличие от схемы на рис. 1, отсутствуют источники и приемники над
областью 3. В эксперименте каждый пятый элемент антенных решеток слева и справа от области
3 последовательно излучает зондирующие импульсы, при этом все элементы обоих антенных
решеток регистрируют эхосигналы. Модельные расчеты показали, что использование всех элемен-
тов антенных решеток в качестве источников не улучшает реконструированное поле скоростей,
однако объем вычислений возрастает в 5 раз.
Скорость распространения звука в областях 1 и 2 составляла v0 = 5,9 мм/мкс, скорость рас-
пространения звука в области 3 — 5,78 мм/мкс и отличается от v0 примерно на 2 % (рис. 6а).
Скорость распространения звука в круглой вставке диаметром 7,7 мм равна 6,2 мм/мкс.
Положение нижней границы 4 предполагается 45 мм. Расчетная область представляет собой объ-
единение областей 1, 2 и 3. Размер расчетной области составляет 260 × 45 мм, размер разностной
сетки — 1020 × 175 точек. Обе антенные решетки с рабочей частотой 2,25 МГц содержат по 100
элементов с шагом 1,2 мм.
На рис. 6б показано восстановленное поле скоростей в области сварки в схеме эксперимента,
изображенной на рис. 5. Качество восстановленного скоростного разреза в этой схеме эксперимен-
та невысокое. Изображение содержит артефакты, возникающие из-за неполноты углового диапа-
зона зондирования, поскольку не регистрируются эхосигналы, распространяющиеся по вертикаль-
ным траекториям. Однако по изображению на рис. 6б можно с точностью до пиксела восстановить
форму правой и левой границы области 3.
Будем считать, что имеется полная информация об областях основного металла, то есть извест-
на скорость звука и геометрия областей 1 и 2 (см. рис. 5). Известна геометрия сварного соединения
(область 3), то есть известно положение правой и левой границы области 3, но неизвестна скорость
звука в области 3. Эти предположения использовались при реконструкции изображения, приведен-
ного на рис. 6в. Из рис. 6в видно, что качество восстановленного поля скоростей повысилось по
сравнению с рис. 6б. Скорость в областях 1 и 2 равна 5,9 мм/мкс и предполагалась постоянной на
каждой итерации. Скорость в области 3 варьирует около правильного значения 5,78 мм/мкс,
Дефектоскопия
№ 11
2021
10
Е.Г. Базулин, А.В. Гончарский, С.Ю. Романов, С.Ю. Серёжников
3
1
2
y
4
x
Рис. 5. Схема томографического эксперимента в случае неполных данных на верхней поверхности.
а
б
V, мм/мкс
V, мм/мкс
0
0
6,2
6,2
Граница
6,0
6,0
сварного
соединения
5,8
5,8
40
40
Y, мм
Y, мм
80
130
155
Х, мм
80
130
155
Х, мм
в
г
V, мм/мкс
0
0
6,2
6,0
5,8
40
40
Y, мм
Y, мм
80
130
155
Х, мм
80
130
155
Х, мм
Рис. 6. Численное моделирование: исходное поле скоростей в образце (а); изображение получено в схеме эксперимента
на рис. 6а (б); изображение получено при наличии полной информации об областях 1 и 2 (в); изображение получено
с одним дополнительным источником над областью 3 (г).
причем величина варьирования не превышает 0,05 мм/мкс. Более того, достаточно добавить к
схеме эксперимента, изображенного на рис. 5, один дополнительный источник над областью 3, как
качество реконструкции становится еще выше (см. рис. 6г). Отметим, что в практике ультразвуко-
вого контроля можно использовать локальную иммерсионную ванну, которая позволяет размещать
антенную решетку над валиком усиления [38]. Но численные эксперименты с таким способом
регистрации эхосигналов потребуют нового цикла моделирования.
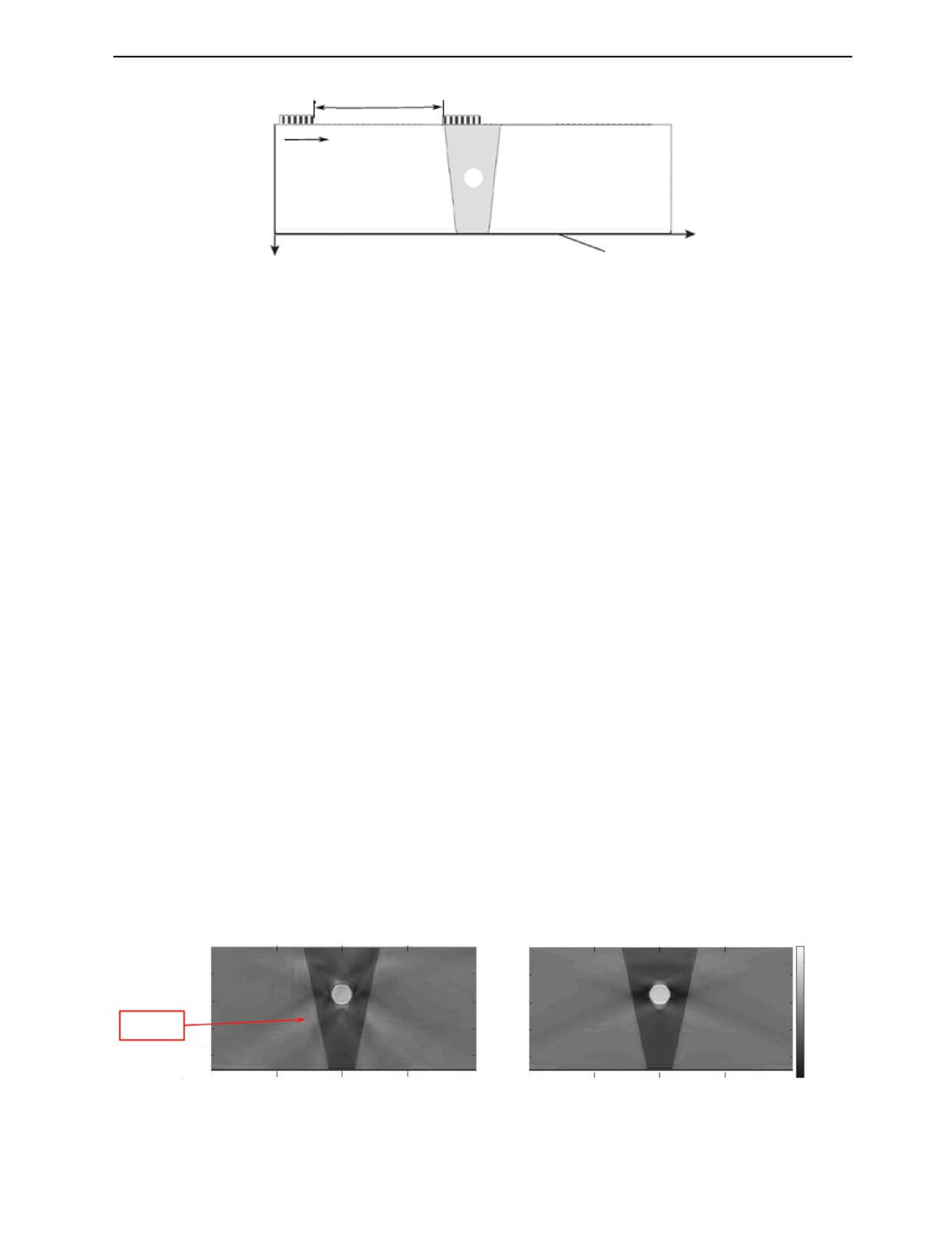
3.2. Два варианта сканирования антенными решетками с 20 элементами
Использование антенной решетки с числом элементов более 128 в настоящий момент времени
достаточно затруднительно, так как наиболее популярные ЦФА-дефектоскопы имеют 32 или 64
канала излучения и измерения эхосигналов. Поэтому были рассмотрены схемы проведения реги-
страции эхосигналов двумя сканирующими антенными решетками с 20 элементами с рабочей
частотой 2,25 МГц.
В первой схеме эксперимента, изображенной на рис. 7, две одинаковые линейные антенные
решетки A и B размещены на верхней границе объекта контроля на фиксированном расстоянии
друг от друга, равном 84 мм. Сначала каждый пятый элемент решеток A и B последовательно
излучает зондирующие импульсы, при этом все элементы решеток A и B регистрируют эхосигна-
лы. Затем решетки A и B синхронно смещаются вправо на расстояние Δ xw , равное размерам антен-
ной решетки вдоль оси x, и процесс регистрации эхосигналов повторяется. За 6 шагов Δ xw антен-
ная решетка A достигает области 2 и изменения прекращаются. Такая схема регистрации эхосиг-
налов называется тройным сканированием [1]. Она применяется при проведении контроля антен-
ными решетками с малым числом элементов с целью увеличения размеров области сканирования
для повышения разрешающей способности изображения и для уменьшения уровня шума.
Дефектоскопия
№ 11
2021
Определение геометро-акустических свойств сварного соединения...
11
84 мм
A
B
3
Направление
смещения
1
2
y
4
x
Рис. 7. Регистрация эхосигналов в режиме тройного сканирования.
Использование такой схемы регистрации эхосигналов увеличивает набор углов зондирования объ-
екта контроля, что повышает качество восстановления его поля скоростей. Однако для реализации
режима тройного сканирования требуется более сложная система сканирования с двумя двигате-
лями для синхронного перемещения антенных решеток не только вдоль сварного соединения, но
и поперек его (вдоль оси x). Понятно, что сканирование по двум координатам увеличивает время
регистрации эхосигналов, но для восстановления изображения использовалось всего 3 120 эхосиг-
налов.
Во второй схеме эксперимента две антенные решетки A и B также перемещаются по верхней
границе образца, однако расстояние между решетками может изменяться. Измерения эхосигналов
по такой схеме требует еще более сложной системы сканирования с тремя двигателями для неза-
висимого перемещения антенных решеток A и B поперек сварного соединения. При таком режиме
сканирования в начальном положении антенные решетки A и B размещаются как в первой схеме
эксперимента. Антенная решетки A фиксируется, а антенная решетка B перемещается 6 раз вправо
со сдвигом Δxw, равным размерам антенной решетки вдоль оси x. Затем антенная решетки A пере-
мещается на Δxw вправо, а антенная решетка B снова перемещается 6 раз вправо c шагом Δxw,
начиная от границы областей 1 и 3. Такой способ измерения эхосигналов предполагает уже 36
измерений двумя антенными решетками A и B при их независимом сканировании вдоль оси x. Эта
схема регистрации эхосигналов фактически еще ближе, чем режим тройного сканирования, к
схеме регистрации, изображенной на рис. 1, когда одна неподвижная антенная решетка A из 150
элементов располагается на верхней границе образца, но требует значительно больше времени для
регистрации эхосигналов и сложную систему сканирования с тремя двигателями. Для восстанов-
ления изображения использовалось уже 18 720 эхосигналов. В численных расчетах использова-
лись те же значения параметров и тот же образец, что и в разделе 3.1.1.
Как и прежде, для удобства восприятия на рисунках будем приводить только фрагмент цен-
тральной части реконструированного изображения. На рис. 8а показано восстановленное поле
скоростей при регистрации эхосигналов в режиме тройного сканирования. Хотя поле скоростей
внутри сварного соединения удалось восстановить, но оно содержит артефакты, возникающие
из-за неполноты углового диапазона зондирования. Можно видеть вытянутые шлейфы, идущие
влево и вправо от круглой вставки. Углы, под которыми шлейфы идут от круглой вставки, при-
а
б
V, мм/мкс
0
0
6,2
6,0
Шлейф
40
40
5,8
Y, мм
Y, мм
80
130
155
Х, мм
80
130
155
Х, мм
Рис. 8. Численное моделирование: изображение, реконструированное в схеме эксперимента по первому варианту
(тройное сканирование) (а); изображение, реконструированное в схеме эксперимента по второму варианту (б).
Дефектоскопия
№ 11
2021
12
Е.Г. Базулин, А.В. Гончарский, С.Ю. Романов, С.Ю. Серёжников
мерно совпадают с углами, под которыми зондирующие импульсы от антенной решетки А прохо-
дят через круглую вставку, отражаются от дна и принимаются элементами антенной решетки B.
На рис. 8б показано поле скоростей, восстановленное по эхосигналам, измеренным по второму
варианту эксперимента. Качество восстановленного изображения в этой схеме эксперимента
выше, чем на рис. 8а, так как для реконструкции использовалось гораздо больше углов зондирова-
ния, чем для рис. 8а. Скорость в круглой вставке на рис. 8б можно оценить как 6,2 мм/мкс, а на
рис. 8а — как 6,1 мм/мкс. Отклонение определенной скорости продольной волны в области шлей-
фа от исходного на рис. 8а в среднем равно 0,05 мм/мкс, а на рис. 8б в среднем равно 0,03 мм/мкс.
4. ВЫВОДЫ
Таким образом, по результатам исследований, изложенных в данной статье, можно сделать
следующие выводы.
1. Численное моделирование показало возможность восстановить поле скоростей и форму свар-
ного соединения при регистрации эхосигналов антенной решеткой в зеркально-теневом режиме.
2. Результаты численных экспериментов для различных схем регистрации эхосигналов позво-
ляют провести оптимизацию томографических схем для разных прикладных задач.
3. Показано, что в случае, когда положение дна образца известно полностью, то качество
реконструкции поля скоростей достаточно высокое — ошибка не превышает 0,03—0,05 мм/мкс.
Если положение отражающего дна неизвестно, удается восстановить форму дна объекта контроля,
но ошибки определения скорости продольной волны значительны и составляют около 0,1 мм/мкс.
Перспективным представляется использование априорной информации о толщине основного
металла и скорости звука в нем, в этом случае удается определить размер провисания или утяжи-
ны.
4. Проведено сравнение результатов решения обратной задачи для двух схем модельного экс-
перимента с двумя сканирующими антенными решетками с малым числом элементов. Качество
реконструкции поля скоростей при регистрации эхосигналов двумя независимо сканирующими
антенными решетками близко к качеству изображения, восстановленному при использовании
антенной решетки с 150 элементами. Однако для ее реализации нужно использовать сложное ска-
нирующее устройство с тремя двигателями, что значительно увеличивает время эксперимента и
примерно в три раза увеличивает объем данных у измеряемых эхосигналов.
5. Показано, что при наличии валика усиления, когда над сварным соединением невозможно
разместить источники излучения, тем не менее удается с точностью 0,05 мм/мкс восстановить в
сварном соединении поле скоростей звука и его форму.
В статье расчеты проводились на СPU-разделе суперкомпьютера «Ломоносов-2» МГУ [39] с
использованием около 50 вычислительных ядер CPU. Для каждого решения обратной задачи коли-
чество итераций составило около 100—150, время расчета составило около 0,5—1 ч.
Работа выполнена при финансовой поддержке Минобрнауки РФ в рамках реализации програм-
мы Московского центра фундаментальной и прикладной математики по соглашению № 075-15-
2019-1621. Работа выполнена с использованием оборудования Центра коллективного пользования
сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова.
СПИСОК ЛИТЕРАТУРЫ
1. Базулин Е.Г. Сравнение систем для ультразвукового неразрушающего контроля, использующих
антенные решетки или фазированные антенные решетки // Дефектоскопия. 2013. № 7. С. 51—74.
2. Hunter A.J., Drinkwater B.W., Wilcox P.D. The Wavenumber Algorithm for Full-Matrix Imaging Using
and Ultrasonic Array // NDT Int. 2006. V. 39. No. 7. P. 525—541.
3. Ковалев А.В., Козлов В.Н., Самокрутов А.А., Шевалдыкин В.Г., Яковлев Н.Н. Импульсный эхо-
метод при контроле бетона. Помехи и пространственная селекция. Дефектоскопия. 1990. № 2.
С. 29—41.
4. Самокрутов А.А., Шевалдыкин В.Г. Возможности оценки характера несплошности металла уль-
тразвуковым томографом с цифровой фокусировкой антенной решетки // Контроль. Диагностика. 2011.
№ 10. С. 63—70.
5. Deleye X., Hörchens L., Chougrani K. Experimental comparison of wave-field based ultrasonic imag-
ing with other advanced ultrasonic weld inspection techniques / 18th World Conference on Nonde-structive
Testing. 16—20 April 2012. Durban. South Africa.
6. Базулин Е.Г. Определение типа отражателя по изображению, восстановленному по эхосигналам,
измеренным ультразвуковыми антенными решетками // Дефектоскопия. 2014. № 3. С. 12—22.
Дефектоскопия
№ 11
2021
Определение геометро-акустических свойств сварного соединения...
13
7. Blitz J., Simpson G. Ultrasonic Methods of Non-destructive Testing. London: Springer, 1995. 264 p.
8. Langenberg K.-J., Marklein R., Mayer K. Ultrasonic Nondestructive Testing. Boca Raton: CRC Press,
2012. 772 p.
9. Качанов В.К., Соколов И.В., Тимофеев Д.В., Туркин М.В., Шалимова Е.В. Обнаружение отражаю-
щих плоскостей при ультразвуковой томографии строительных конструкций из бетона // Дефектоско-
пия. 2010. № 5. С. 36—44.
10. Кошевой В.В., Кривин Е.В., Муравьев А.М., Романишин И.М. Особенности ультразвуковой томо-
графии толстолистовых изделий // Дефектоскопия. 2004. № 7. С. 3—16.
11. Базулин Е.Г., Садыков М.С. Определение скорости продольной ультразвуковой волны в изотроп-
ном однородном сварном соединении по эхосигналам, измеренным двумя антенными решетками //
Дефектоскопия. 2018. № 5. С. 3—15.
12. Bellis C., Bonnet M. Crack identification by 3D time-domain elastic or acoustic topological sensitivity
// C.R. Mecanique. 2009. V. 337. № 3. P. 124—130.
13. Lubeigt E., Mensah S., Rakotonarivo S., Chaix J-F., Baquѐ F., Gobillot G. Topological imaging in
bounded elastic media // Ultrasonics. 2017. V. 76. P. 145—153.
14. Dominguez N., Gibiat V. Non-destructive imaging using the time domain topological energy //
Ultrasonics. 2010. V. 50. № 3. P. 367—372.
15. Rodriguez S., Deschamps M., Castaings M., Ducasse E. Guided wave topological imaging of isotropic
plates // Ultrasonics. 2014. V. 54. № 7. P. 1880—1890.
16. Metwally K., Lubeigt E., Rakotonarivo S., Chaix J.F., Baqué F., Gobillot G., Mensah S. Weld inspection
by focused adjoint method // Ultrasonics. 2018. V. 83. P. 80—87.
17. Bachmann E., Jacob X., Rodriguez S., Gibiat V. Three-dimensional and real-time two-dimensional
topological imaging using parallel computing // The Journal of the Acoustical Society of America. 2015.
V. 138. № 3. P. 1796.
18. Kocur G.K., Saenger E.H., Grosse C.U., Vogel T. Time reverse modeling of acoustic emissions in a
reinforced concrete beam // Ultrasonics. 2016. V. 65. P. 96—104.
19. Virieux J., Operto S. An overview of full-waveform inversion in exploration geophysics // Goephysics.
2009. V. 74. № 6. P. WCC1 — WCC26.
20. Vinard N., Martiartu N.K., Boehm C., Balic I.J., Fichtner A. Optimized transducer configuration for
ultrasound waveform tomography in breast cancer detection / In: N. Duric, B.C. Byram (eds.). Medical
Imaging 2018: Ultrasonic Imaging and Tomography. Proc. SPIE. 2018. V. 10580. P. 1058001.
21. Klibanov M.V., Kolesov A.E., Nguyen D.-L. Convexification method for an inverse scattering problem
and its performance for experimental backscatter data for buried targets // SIAM J. Imaging Sci. 2019. V. 12.
P. 576—603.
22. Goncharsky A.V., Romanov S.Y. Iterative methods for solving coefficient inverse problems of wave
tomography in models with attenuation // Inverse Problems. 2017. V. 33. № 2. P. 025003.
23. Seidl R., Rank E. Iterative time reversal based flaw identification // Computers & Mathematics with
Applications. 2016. V. 72. № 4. P. 879—892.
24. Marty P., Boehm C., Fichtner A. Acoustoelastic full-waveform inversion for transcranial ultrasound
computed tomography / In: B.C. Byram, N.V. Ruiter (eds.). Medical Imaging 2021: Ultrasonic Imaging and
Tomography. Proc. SPIE. 2021. V. 11602. P. 1160211.
25. Pérez-Liva M., Herraiz J.L., Udías J.M., Miller E., Cox B.T., Treeby B.E. Time domain reconstruction
of sound speed and attenuation in ultrasound computed tomography using full wave inversion // The Journal
of the Acoustical Society of America. 2017. V. 141. No. 3. P. 1595—1604.
26. Rao J., Ratassepp M., Fan Z. Guided Wave Tomography Based on Full Waveform Inversion // IEEE
Trans Ultrason Ferroelectr Freq Control. 2016. V. 63. № 5. P. 737—745.
27. Bazulin E.G., Goncharsky A.V. Inverse Problems of Ultrasonic Tomography in Nondestructive Testing:
Mathematical Methods and Experiment // Russian Journal of Nondestructive Testing. 2019. V. 55. No. 6.
P. 453—462. [Базулин Е.Г., Гончарский А.В., Романов С.Ю., Сережников С.Ю. Обратные задачи ультра-
звуковой томографии в неразрущающем контроле: математические методы и эксперимент // Дефекто-
скопия. 2019. № 6. С. 30—39. DOI: 10.1134/S0130308219060046]
28. Bazulin E.G., Goncharsky A.V., Romanov S.Y., Seryozhnikov S.Y. Parallel CPU- and GPU-algorithms
for inverse problems in nondestructive testing // Lobachevskii Journal of Mathematics. 2018. V. 39. № 4.
29. Juengert A., Dugan S., Homann T., Mitzscherling S., Prager J., Pudovikov S., Schwender T. Advanced
ultrasonic techniques for nondestructive testing of austenitic and dissimilar welds in nuclear facilities // AIP
30. Chassignole B., Villard D., Dubuget M., Baboux J.C., El Guerjouma R. Characterization of austenitic
stainless steel welds for ultrasonic NDT // AIP Conference Proceedings. 2000. V. 509. P. 1325—1332. https://
doi.org/10.1063/1.1307835
31. Romanov S.Y. Supercomputer simulations of ultrasound tomography problems of flat objects //
Lobachevskii Journal of Mathematics. 2020. V. 41. No 8. P. 1563—1570. DOI: 10.1134/S199508022008017X
Дефектоскопия
№ 11
2021
14
Е.Г. Базулин, А.В. Гончарский, С.Ю. Романов, С.Ю. Серёжников
32. Ильгамов М.А., Гильманов A.H. Неотражающие условия на границах расчетной области.
М.: Физматлит, 2003.
33. Engquist B., Majda A. Absorbing boundary conditions for the numerical simulation of waves // Math.
Comput. 1977. V. 31. P. 629—651.
34. Goncharsky A.V., Romanov S.Y. A method of solving the coefficient inverse problems of wave
tomography.
// Computers and Mathematics with Applications.
2019. V.
77. P.
967—980.
35. Natterer F. Possibilities and limitations of time domain wave equation imaging / In: Contemporary
conm/559
36. Klibanov M.V., Kolesov A.E. Convexification of a 3-D coefficient inverse scattering problem //
Computers & Mathematics with Applications. 2019. V. 77. No 6. P. 1681—1702.
37. Bazulin E.G.,Vopilkin A.Kh. Reference-Free Method for Thickness Gaging of a Test Object and
Measuring the Speed of Longitudinal and Transverse Waves in It Based on Echo Signals Picked by an
Antenna Array // Russian Journal of Nondestructive Testing. 2019. V. 55. No. 6. P. 463—475. [Базулин Е.Г.,
Вопилкин А.Х. Безэталонный метод измерения толщины объекта контроля и скорости продольной и
поперечной волны в нем по эхосигналам, измеренным антенной решеткой // Дефектоскопия. 2019.
№ 6. С. 40—52.]
38. Базулин А.Е., Базулин Е.Г. Применение антенных решеток и кремнийорганического полимера в
качестве иммерсионной среды для проведения ультразвукового контроля объектов с неровной поверх-
ностью // Дефектоскопия. 2014. № 7. С. 3—11.
39. Voevodin Vl., Antonov A., Nikitenko D., Shvets P., Sobolev S., Sidorov I., Stefanov K., Voevodin
Vad., Zhumatiy S. Supercomputer Lomonosov-2: large scale, deep monitoring and fine analytics for the
user community
// Supercomputing Frontiers and Innovations.
2019. V.
6. No
2. P.
4—11.
DOI:10.14529/jsfi190201
Дефектоскопия
№ 11
2021