ЖЭТФ, 2020, том 158, вып. 6 (12), стр. 1188-1214

ВОЛНОВЫЕ ПРОЦЕССЫ ВО ВРАЩАЮЩИХСЯ СЖИМАЕМЫХ

ТЕЧЕНИЯХ АСТРОФИЗИЧЕСКОЙ ПЛАЗМЫ

С УСТОЙЧИВОЙ СТРАТИФИКАЦИЕЙ

М. А. Федотоваa*, А. С. Петросян^a,b

^a Институт космических исследований Российской академии наук

117997, Москва, Россия

^b Московский физико-технический институт

41700, Долгопрудный, Московская обл., Россия

Поступила в редакцию 21 июня 2020 г.,

после переработки 21 июня 2020 г.

Принята к публикации 28 июня 2020 г.

Теоретически исследуются волновые процессы во вращающемся слое сжимаемой астрофизической плаз-

мы с устойчивой стратификацией и линейным профилем энтропии. Учет сжимаемости осуществляется

в неупругом приближении. В этом приближении акустические волны отфильтрованы, система содержит

слагаемые с потенциальной температурой (энтропией), а уравнение непрерывности — исходный стра-

тифицированный профиль плотности. Сила Кориолиса в магнитогидродинамических уравнениях сжи-

маемой астрофизической плазмы рассматривается в четырех различных приближениях: стандартной

f-плоскости, нестандартной f-плоскости (с учетом горизонтальной компоненты силы Кориолиса), стан-

дартной β-плоскости и нестандартной β-плоскости. Для каждого рассматриваемого приближения силы

Кориолиса развиты линейная и нелинейная теории волновых процессов. Найдены новые типы волн, вос-

станавливающими механизмами которых служат вращение, магнитное поле, гравитация и сжимаемость.

Эффекты сжимаемости представлены в новых дисперсионных уравнениях частотой Брента - Вяйсяля

для сжимаемых стратифицированных течений, зависящей как от исходного профиля плотности, так и от

исходного профиля давления. С помощью качественного анализа дисперсионных кривых выявлены все

реализующиеся типы трехволновых взаимодействий. Методом многомасштабных разложений получена

система уравнений для амплитуд взаимодействующих волн и инкременты параметрических неустойчи-

востей.

DOI: 10.31857/S0044451020120172

цессов в солнечном тахоклине

[1-6], устойчиво-

стратифицированных областях в недрах звезд (из-

1. ВВЕДЕНИЕ

лучающей зоны) и планет (внешний жидкий слой

ядра) [7], астрофизических дисках [8], экзоплане-

Работа посвящена теоретическому исследованию

тах [9], а также для анализа осцилляций враща-

волновых процессов во вращающейся сжимаемой

ющихся звезд и Солнца [10-12]. Учет стратифи-

астрофизической плазме с линейным профилем эн-

кации позволяет существенно расширить возмож-

тропии. Генерация, распространение и взаимодей-

ности для интерпретации имеющихся данных на-

ствие волн в астрофизике играют важную роль в

блюдений крупномасштабных волн Россби на Солн-

понимании свойств и изменчивости множества аст-

це [11, 13-15]. Экспериментальное обнаружение волн

рофизических объектов и явлений, влияют на их

магнито-Россби на Солнце инициировало разви-

динамику, формируют различные плазменные тече-

тие моделей для описания поведения волн магни-

ния, являются частью нелинейных процессов.

то-Россби во вращающихся течениях астрофизичес-

Исследования эффектов стратификации в маг-

кой плазмы [16-18].

нитогидродинамических моделях вращающейся аст-

рофизической плазмы важны для анализа про-

Отметим важные исследования влияния волн

магнито-Россби на солнечные сезоны [12, 19] и, как

^* E-mail: fedotova.maria.04@gmail.com

следствие, их существенную роль в объяснении яв-

1188

ЖЭТФ, том 158, вып. 6 (12), 2020

Волновые процессы во вращающихся сжимаемых течениях. . .

лений космической погоды [20]. Также отметим важ-

пределе дисперсионное соотношение на стандартной

ные работы по исследованию крупномасштабных

и нестандартной β-плоскостях имеет решение в ви-

волн Россби в геофизической гидродинамике [21,22].

де волны магнито-Россби, аналогичной полученной

Полная система уравнений магнитной гидродина-

в приближении двуслойной мелкой воды. Диспер-

мики вращающейся стратифицированной плазмы в

сионные кривые всех найденных типов волн каче-

поле силы тяжести представляет собой практиче-

ственно проанализированы для выявления выпол-

ски неразрешимую проблему как для аналитическо-

нения условия синхронизма, обеспечивающего на-

го исследования, так и для численного моделиро-

личие трехволновых взаимодействий. Для всех най-

вания. Эффективной моделью для описания стра-

денных типов трехволновых взаимодействий полу-

тифицированной плазмы, опирающейся на магнито-

чены амплитудные уравнения, описаны возможные

гидродинамическую теорию мелкой воды [16,23], яв-

параметрические неустойчивости и найдены их ин-

ляется модель n слоев плазмы различной плотности,

кременты. Отметим, что приближение Буссинеска

наложенных друг на друга.

применимо, когда градиент плотности пропорцио-

Первым шагом в учете стратификации при ис-

нален только градиенту температуры, и описывает

следовании волновых процессов во вращающей-

несжимаемые стратифицированные течения [25].

ся плазме стал вывод магнитогидродинамических

Важной принципиальной особенностью течений

уравнений мелкой воды во внешнем магнитном по-

астрофизической плазмы является свойство сжи-

ле, которые учитывают стратификацию в модели

маемости, характеризующее большинство наблюда-

двух слоев плазмы различной, но постоянной плот-

емых объектов во Вселенной. Именно исследова-

ности, выполненный в работе [17]. На основе данной

нию фундаментальной роли сжимаемости в крупно-

модели получены линейные волны магнито-Россби,

масштабных течениях вращающейся астрофизиче-

найдены поправки к ним, связанные с различием в

ской плазмы с устойчивой стратификацией посвя-

плотностях слоев, показано влияние стратификации

щена данная работа. Отметим, что первые экспе-

в данной модели на групповые и фазовые скорости

риментальные наблюдения крупномасштабных те-

полученных волн, развита слабонелинейная теория

чений астрофизической плазмы выполнены на осно-

волн магнито-Россби и предсказаны параметриче-

ве изучения магнитных полей или методами астро-

ские неустойчивости на основе полученных ампли-

сейсмологии, что естественным образом мотивирует

тудных уравнений трех взаимодействующих волн.

развитие магнитогидродинамической теории с уче-

Подробный обзор результатов исследования волно-

том как сжимаемости, так и магнитных полей. Учет

вых процессов в астрофизической плазме в прибли-

сжимаемости в магнитогидродинамических моде-

жении мелкой воды можно найти в работе [24].

лях вращающейся плазмы существенно повыша-

Магнитогидродинамическая теория мелкой во-

ет возможность интерпретации астросейсмологиче-

ды является двумерной, исключает вертикальные

ских данных, например, данных о широтной зависи-

ускорения и учет вертикального изменения гори-

мости собственных мод солнечных осцилляций [11].

зонтальных составляющих. Следующий существен-

Мы используем неупругое приближение (anelstic

ный шаг, являющийся принципиальным для реаль-

approximation) в полных уравнениях магнитной гид-

ных астрофизических течений с непрерывной стра-

родинамики сжимаемой плазмы для описания тече-

тификацией, выполнен в работе [18], в которой изу-

ний плазмы при наличии вращения. В таком при-

чены трехмерные волновые процессы в магнито-

ближении акустические волны отсутствуют, а гра-

гидродинамических течениях вращающейся страти-

диент плотности зависит как от градиента давле-

фицированной плазмы в приближении Буссинеска.

ния, так и от градиента температуры [26]. Магнито-

В рассмотренном в работе [18] случае магнитных

гидродинамическая система уравнений в неупругом

течений, в отличие от течений нейтральной жид-

приближении не содержит акустических волн и по-

кости, решения содержат новые типы волн вслед-

лучается из полной системы сжимаемых уравнений

ствие присутствия дополнительной восстанавлива-

магнитной гидродинамики в предположении малых

ющей силы, а именно силы Лоренца, наряду с си-

возмущений плотности и описывает течения с ма-

лой Кориолиса и силой плавучести. В работе [18]

лыми числами Маха.

получены законы дисперсии различных типов маг-

Подробный качественный анализ эффектов ма-

нитных инерционно-гравитационных волн, магнито-

лых чисел Маха в астрофизике приведен в рабо-

строфических волн и волн магнито-Россби, динами-

те [27], которая посвящена разработке нового чис-

ка которых определяется силами Лоренца, Корио-

ленного алгоритма для описания объектов плазмен-

лиса и плавучести. Показано, что в низкочастотном

ной астрофизики. В этой работе приведено краткое,

1189

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

но информативное сравнение различных типов при-

Задача о фильтрации акустических волн в круп-

ближений, используемых при численном моделиро-

номасштабных моделях геофизической гидродина-

вании течений с малым числом Маха. Наиболее про-

мики была впервые сформулирована в работе [29]

стым является приближение несжимаемой жидкос-

с целью упростить численное моделирование теп-

ти, предполагающее постоянство фоновой плотнос-

ловой конвекции в геофизике, поскольку присут-

ти и давления по координате. В данном приближе-

ствие акустических волн в полной сжимаемой си-

нии при движении плотность жидкости можно счи-

стеме уравнений требует очень малого временного

тать постоянной вдоль всего объема жидкости в те-

шага в численной схеме конечно-разностного инте-

чение всего времени движения.

грирования. Отметим работу [30], в которой показа-

Следующим важным приближением при усло-

на возможность использования неупругого прибли-

вии несжимаемого потока жидкости является при-

жения для исследования внутренних гравитацион-

ближение Буссинеска. В нем по-прежнему считает-

ных волн при малых числах Маха, а также рабо-

ся постоянным фоновое состояние, однако в урав-

ты [31-35], в которых исследуются математические

нение для импульса при массовых силах включены

свойства неупругого приближения для течений ней-

эффекты плавучести. Как в несжимаемом прибли-

тральной жидкости.

жении, так и в приближении Буссинеска уравнение

Упомянем также работы по развитию теории

непрерывности переходит в условие бездивергент-

неупругого приближения в рамках задач земной

ности поля скоростей в силу отсутствия эффектов

конвекции и геодинамо [36-39], которые иницииро-

сжимаемости.

вали применение неупругого приближения для изу-

Следующие два приближения, неупругое и псев-

чения астрофизических течений. Говоря о развитии

донесжимаемое, основаны на стратифицированном

неупругого приближения в астрофизике и физике

фоновом состоянии (исходном состоянии равнове-

планет, отметим работы [40, 41], в которых исполь-

сия). В обоих этих приближениях элемент жидко-

зуется неупругое приближение в нейтральной жид-

сти может расширяться или сжиматься при движе-

кости, и работы [42-48], в которых используются

нии по вертикали относительно фонового состояния

магнитогидродинамические уравнения в неупругом

в ответ на изменение давления окружающей сре-

приближении для исследования конвекции и дина-

ды. Уравнение непрерывности в неупругом прибли-

мо на Солнце и в звездах.

жении является условием бездивергентности произ-

Отметим важные для дальнейшего понимания

ведения фоновой плотности и скорости. Уравнение

работы [26, 49]. В работе [26] выполнен вывод урав-

непрерывности в псевдосжимаемом приближении

нений для нейтрального газа в неупругом прибли-

имеет более сложный вид, а именно, ненулевую ди-

жении с введением уменьшенного давления (reduced

вергенцию произведения скорости и фонового дав-

pressure), наиболее адекватный для астрофизичес-

ления, возведенного в степень 1/γ (γ = c_p/c_v — по-

ких задач. Метод, предложенный в работе [26], при-

казатель адиабаты). При этом уравнения в псевдо-

менен в [49] для магнитогидродинамических те-

сжимаемом приближении сводятся к уравнениям в

чений без вращения. На основе данной методики

неупругом приближении в случае малых возмуще-

вывода уравнений в настоящей работе выведены

ний плотности и температуры, но сами по себе не

магнитогидродинамические уравнения вращающей-

предполагают малости таких изменений. Кроме то-

ся стратифицированной плазмы с линейным профи-

го, псевдосжимаемые уравнения учитывают локаль-

лем энтропии в поле силы тяжести в неупругом при-

ные эффекты нагрева.

ближении. Новые дисперсионные соотношения, по-

Впервые неупругое приближение предложено в

лученные в данной работе, описывают различные

работе [28] для решения задач геофизической гид-

типы волн, восстанавливающими механизмами ко-

родинамики. В ней с использованием масштабно-

торых являются магнитное поле, вращение, грави-

го анализа приведен вывод уравнений на основе

тация и сжимаемость.

предположения о том, что распределение давления,

В разд. 2 получена система магнитогидродина-

плотности и потенциальной температуры газа всег-

мических уравнений в неупругом приближении для

да близки к модели адиабатически стратифициро-

вращающихся сжимаемых стратифицированных те-

ванной атмосферы, а временной масштаб определя-

чений астрофизической плазмы с линейным про-

ется частотой Брента - Вяйсяля. Такие предположе-

филем энтропии и проведена ее линеаризация. В

ния и приближения при выводе уравнений привели

разд. 3.1 найдены дисперсионные соотношения для

к отсутствию в них акустических волн, хотя это не

линейных сжимаемых магнитных инерционно-гра-

было непосредственной целью исследования.

витационных волн и сжимаемых магнитострофи-

1190

ЖЭТФ, том 158, вып. 6 (12), 2020

Волновые процессы во вращающихся сжимаемых течениях. . .

ческих волн в неупругом приближении на f-плос-

тьях, мы сочли полезным для читателей привести

кости. В разд. 3.2 получены дисперсионные соот-

в данной работе подробный вывод системы магни-

ношения для различных типов линейных сжимае-

тогидродинамических уравнений в неупругом при-

мых магнитных инерционно-гравитационных волн и

ближении для вращающейся стратифицированной

линейных сжимаемых магнитострофических волн в

плазмы. Таким образом, выведенная в данной ра-

неупругом приближении на нестандартной f-плос-

боте система уравнений в неупругом приближении

кости. В разд. 4.1 найдены дисперсионные соот-

является новой относительно используемых ранее в

ношения для линейных сжимаемых волн магнито-

различных работах уравнений в неупругом прибли-

Россби в неупругом приближении на β-плоскости.

жении, так как содержит одновременно силу Корио-

В разд.

4.2

получены дисперсионные соотноше-

лиса и магнитное поле, а также предполагает посто-

ния для различных типов линейных сжимаемых

янное ненулевое магнитное поле в исходном состоя-

магнитных инерционно-гравитационных и магни-

нии равновесия. Для вывода системы магнитогидро-

тострофичеких волн и сжимаемых волн магни-

динамических уравнений сжимаемой стратифици-

то-Россби в неупругом приближении на нестандарт-

рованной вращающейся плазмы в неупругом при-

ной β-плоскости. В разд. 5.1 описаны возможные

ближении воспользуемся методикой, предложенной

для всех найденных в предыдущих разделах типов

в работе [26]. В качестве исходной используем пол-

волн трехволновые взаимодействия, удовлетворяю-

ную систему магнитогидродинамических уравнений

щие условию синхронизма. В разд. 5.2 выведена сис-

сжимаемой плазмы при наличии вращения:

тема уравнений для амплитуд взаимодействующих

∂v

∇p

[b × [∇ × b]]

волн. Полученные дифференциальные операторы и

+(v·∇)v+[f ×v] = -

+g-

(1)

∂t

4πρ

коэффициенты для трехволновых взаимодействий

на f-плоскости и на нестандартной f-плоскости при-

∂S

ведены в разд. 5.2.1, а в разд. 5.2.2 — на β-плоскости

+ (v · ∇)S = 0,

(2)

∂t

и на нестандартной β-плоскости. В разд. 5.2.3 по-

∂b

лучены инкременты параметрических неустойчиво-

= [∇ × [v × b]],

(3)

стей: распада и усиления.

∂t

∂ρ

+ ∇(ρ · v) = 0,

(4)

∂t

2. МАГНИТОГИДРОДИНАМИЧЕСКИЕ

УРАВНЕНИЯ ВРАЩАЮЩЕЙСЯ

(∇ · b) = 0,

(5)

СЖИМАЕМОЙ СТРАТИФИЦИРОВАННОЙ

ρ = ρ(p,S),

(6)

ПЛАЗМЫ В НЕУПРУГОМ ПРИБЛИЖЕНИИ

состоящую из уравнения Навье - Стокса (1), урав-

Получим уравнения магнитной гидродинами-

нения для энтропии (2), уравнения индукции для

ки сжимаемой стратифицированной вращающейся

идеально проводящей плазмы (3), уравнения непре-

плазмы в неупругом приближении. Неупругое при-

рывности (4), уравнения бездивергентности магнит-

ближение является одним из приближений, исполь-

ного поля (5) и уравнения состояния (6). В системе

зуемых при исследовании течений с малым числом

(1)-(6) ρ — плотность плазмы, v — вектор скорос-

Маха, в котором характерный временной масштаб

ти, f = 2Ω — вектор силы Кориолиса, Ω — вектор

изучаемых течений астрофизической плазмы значи-

скорости вращения, p — давление, g = (0, 0, -g) —

тельно превышает время распространения акусти-

ускорение свободного падения, b — вектор магнит-

ческих волн. В неупругом приближении для страти-

ного поля, S — энтропия. Для удобства дальнейше-

фицированной плазмы элемент жидкости при дви-

го анализа перейдем от энтропии к потенциальной

жении по вертикали меняет свой объем вследствие

температуре θ, используя их простую зависимость,

изменения давления окружающей среды. Таким об-

заданную выражением dS = c_pd ln θ. Уравнение со-

разом, неупругое приближение учитывает эффек-

стояния (6) запишем в виде

ты сжимаемости во вращающейся астрофизической

плазме. Кроме того, в неупругом приближении воз-

мущение плотности полагается малым, что отлича-

d ln θ =

d ln p - d ln ρ.

(7)

ет его от псевдосжимаемого приближения. В силу

разрозненности учета различных физических эф-

В качестве исходного рассмотрим состояние рав-

фектов в системе уравнений в неупругом прибли-

новесия плазмы (v₀ = 0) в постоянном магнитном

жении и особенностей их вывода в различных ста-

поле (b₀ = const) при наличии стратификации ρ₀(z).

1191

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

Тогда давление в равновесии удовлетворяет уравне-

Запишем слагаемое ρ^′/ρ₀ в уравнении На-

нию гидростатики

вье - Стокса (11), используя уравнение состояния

для возмущенных величин (16) и уравнение состоя-

∇p₀

= g,

(8)

ния для невозмущенных величин (9), следующим

ρ₀

образом:

а уравнение состояния (7) для невозмущенных ве-

ρ^′

p^′

θ^′

p^′∇p₀

θ^′

∇p₀

θ^′

личин сводится к виду

= ω

(17)

ρ₀

γp₀

θ₀

γp₀ρ₀g

θ₀

γp₀g

∇θ₀

∇p₀

∇ρ₀

(9)

где ω = p^′/ρ₀ (reduced pressure) [26, 49].

θ₀

γp₀

ρ₀

Пренебрежем в уравнении (11) всеми слагаемы-

Для получения уравнений магнитной гидроди-

ми, пропорциональными ω, за исключением слагае-

намики вращающейся плазмы в неупругом прибли-

мых, содержащих градиент ω. Используемый метод

жении рассмотрим возмущение исходного состояния

обеспечивает выполнение условия сохранения энер-

равновесия:

гии в системе. Получим магнитогидродинамическое

уравнение Навье - Стокса при наличии вращения в

v=v^′, b=b₀ +b^′, p=p₀ +p^′,

следующем виде:

(10)

ρ=ρ₀ +ρ^′, θ=θ₀ +θ^′,

∂v^′

θ^′

+ (v^′ · ∇)v^′ + [f × v^′] = -∇ω -

полагая возмущение плотности малым (ρ^′ ≪ ρ₀).

∂t

θ₀

Линеаризуя уравнения (1), (4), (7) по ρ^′ и за-

[b₀ × [∇ × b^′]]

[b^′ × [∇ × b^′]]

мыкая систему уравнениями (2), (3), (5), получим

(18)

4πρ₀

систему магнитогидродинамических уравнений для

возмущенных переменных в неупругом приближе-

Полученная таким образом система уравнений

нии:

(12)-(14), (18) удобна для дальнейшего исследова-

ния, поскольку не включает в явном виде слага-

∂v^′

∇p^′

ρ^′

емых, содержащих возмущение плотности. Систе-

+ (v^′ · ∇)v^′ + [f × v^′] = -

∂t

ρ₀

ма (12)-(14), (18) описывает течения вращающейся

[b₀ × [∇ × b^′]]

[b^′ × [∇ × b^′]]

сжимаемой астрофизической плазмы в неупругом

−

(11)

4πρ₀

приближении и используется в работе для развития

линейной и слабонелинейной теорий волновых вза-

∂θ^′

+ (v^′ · ∇)θ₀ + (v^′ · ∇)θ^′ = 0,

(12)

имодействий. Отметим, что система линейна отно-

∂t

сительно термодинамических переменных и сохра-

∂b^′

няет нелинейность для поля скорости и магнитного

= [∇ × [v^′ × b₀]] + [∇ × [v^′ × b^′]],

(13)

∂t

поля. Линеаризованная система магнитогидродина-

∇(ρ₀ · v^′) = 0,

(14)

мических уравнений в неупругом приближении для

вращающейся плазмы (12)-(14), (18) имеет вид

(∇ · b^′) = 0,

(15)

θ^′

p^′

ρ^′

∂v^′

[b₀ × [∇ × b^′]]

(16)

+ [f × v^′] = -∇ω - T^′g -

(19)

θ₀

γp₀

ρ₀

∂t

4πρ₀

Ключевые отличия системы уравнений в неупру-

∂θ^′

гом приближении от уравнений в приближении Бус-

+ (v^′ · ∇)θ₀ = 0,

(20)

∂t

синеска [18] заключаются в уравнении энергии, за-

∂b^′

писанном для потенциальной температуры, в урав-

= [∇ × [v^′ × b₀]],

(21)

∂t

нении непрерывности, включающем в себя исходный

стратифицированный профиль плотности, и в урав-

∇(ρ₀ · v^′) = 0.

(22)

нении состояния, определяющем функцию плотно-

Полученные системы уравнений (12)-(14), (18)

сти как функцию не только давления, но и потен-

и (19)-(22) допускают аналитическое исследование

циальной температуры (энтропии). Таким образом,

для стратифицированного слоя плазмы с исходным

в неупругом приближении изменение давления и

устойчивым линейным профилем энтропии

плотности жидкости связаны не только с силой пла-

вучести, как в приближении Буссинеска, но и с из-

∂S₀

1 ∂θ₀

= const.

(23)

менением потенциальной температуры (энтропии).

∂z

θ0 ∂z

1192

ЖЭТФ, том 158, вып. 6 (12), 2020

Волновые процессы во вращающихся сжимаемых течениях. . .

В этом случае уравнение состояния для невозму-

вектор Кориолиса направлен по вертикали и при ма-

щенных величин (9) определяет связь между плот-

лых изменениях широты слабо меняется, приближе-

ностью и потенциальной температурой:

ние нестандартной β-плоскости, когда учтена гори-

зонтальная составляющая вектора Кориолиса, а он

1 ∂θ₀

ρ₀g

g ∂ρ0

(24)

сам при малых изменениях широты меняется слабо.

θ0 ∂z

γp₀

g ρ0 ∂z

Введем понятие частоты Брента - Вяйсяля в

сжимаемых течениях стратифицированной астро-

3. ЛИНЕЙНАЯ ТЕОРИЯ ВОЛНОВЫХ

физической плазмы:

ПРОЦЕССОВ В СЖИМАЕМОМ

СТРАТИФИЦИРОВАННОМ

)

⁽ 1 ∂ρ₀

gρ₀

g ∂θ0

ВРАЩАЮЩЕМСЯ СЛОЕ ПЛАЗМЫ С

N2θ = -g

(25)

ЛИНЕЙНЫМ ПРОФИЛЕМ ЭНТРОПИИ

ρ0 ∂z

γp₀

θ0 ∂z

Учет сжимаемости в выражении (25) приводит к за-

3.1. Приближение стандартной f-плоскости

висимости частоты Брента - Вяйсяля не только от

Получим дисперсионные уравнения для волн

плотности, но и от давления. Первое слагаемое в

в сжимаемом стратифицированном вращающемся

частоте Брента - Вяйсяля N2θ для сжимаемых тече-

слое плазмы с линейным профилем энтропии на

ний в неупругом приближении с линейным профи-

f-плоскости. Вектор Кориолиса f в стандартном

лем энтропии (25) имеет вид, аналогичный частоте

приближении f-плоскости полагается постоянным и

Брента - Вяйсяля в приближении Буссинеска,

направленным по вертикали: f = (0, 0, f_V ). В таком

g ∂ρ

случае слагаемое [f ×v^′] в уравнении (19) принимает

N² = -

ρ₀ ∂z

вид f_V v^′x ŷ - f_V v^′y x, где x и ŷ — единичные векторы

вдоль осей соответственно x и y. Преобразуем ли-

где ρ₀ — постоянная фоновая плотность, а ρ — ли-

неаризованную систему магнитогидродинамических

нейный профиль плотности, обеспечивающий устой-

уравнений в неупругом приближении (19)-(22) для

чивую стратификацию. В случае сжимаемых те-

вращающегося слоя сжимаемой стратифицирован-

чений в неупругом приближении предполагается

ной плазмы в приближении f-плоскости с линейным

стратификация исходного профиля плотности ρ₀(z),

профилем энтропии (24) к следующему виду:

обеспечивающая линейность и устойчивость профи-

ля энтропии (∂_z ln ρ₀ = const). Для удобства даль-

∂v^′

нейшего анализа мы обозначим первое слагаемое в

-f_Vv^′yx+f_Vv^′xŷ=

∂t

(25) следующим образом:

= -∇ω - T^′g - [B₀ × [∇ × B^′]],

(27)

g ∂ρ0

N² = -

(26)

ρ0 ∂z

∂T^′

′

= 0,

(28)

∂t

Кроме того, введем переобозначения для потенци-

альной температуры и магнитного поля:

∂B^′

= [∇ × [v^′ × B₀]],

(29)

′

√

∂t

T^′ =

b₀ =

4πρ₀B₀, b^′ =

4πρ₀B^′.

θ₀

N²

(∇ · v^′) - v^′z

= 0.

(30)

Полученные в данном разделе магнитогидроди-

намические уравнения в неупругом приближения

записаны для полной силы Кориолиса. Для даль-

Представим переменные возмущения исходного

нейшего исследования используем четыре различ-

состояния равновесия в виде

ных приближения силы Кориолиса: приближение

стандартной f-плоскости, когда вектор Кориолиса

q^′ = q₁ exp[i(ωt - (k · r))].

(31)

предполагается постоянным и направленным по вер-

тикали, приближение нестандартной f-плоскости,

Тогда получим следующее дисперсионное соотноше-

когда вектор Кориолиса предполагается постоян-

ние для волн во вращающемся слое плазмы с линей-

ным и учитывается его горизонтальная составляю-

ным профилем энтропии на стандартной f-плоскос-

щая, приближение стандартной β-плоскости, когда

ти:

1193

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

[

]

f2V k2z

k2hN2θ

Дисперсионное соотношение для трехмерных

ω⁴ - 2(B0 · k)2 +

ω² -

k²

магнитострофических волн в неупругом приближе-

N²(B₀ · k)

нии имеет вид

[f_V k_z (By0 k_x - Bx0 k_y)] ω +

gk²

⎛

[

]

k2h

f2V k2z

k2h

+ (B₀ · k)² (B₀ · k)² -

N²

= 0,

(32)

ωmstrB

= ±^⎝B2z

k2z +

N2θ -

k²

2k²

⎞1/2

где k2h = k2x + k2y.

)₂

Проанализируем решение полученного дисперси-

√(f2_V k2_z

k2h

−

N²

+B2z

k4zf2V

⎠

(36)

онного уравнения в частных случаях. При условии,

когда в состоянии покоя магнитное поле направлено

вдоль вертикальной координаты z (B₀ = (0, 0, Bz0)),

Так же, как и в случае трехмерных магнитных

дисперсионное уравнение (32) принимает вид

инерционно-гравитационных волн, трехмерные маг-

[

]

нитострофические волны в неупругом приближе-

f2V k2z

k2h

нии описываются дисперсионным уравнением, ана-

ω⁴ -

2B2z

k2z +

N²

ω² +

k²

логичным дисперсионному уравнению в прибли-

[

]

k2h

жении Буссинеска ( [18], формула (10)), с учетом

+B2z

k2z B2z

k2z -

N²

(33)

k²

эффектов сжимаемости в частоте Брента - Вяйся-

ля N2θ.

и его решение включает два типа волн: трехмерные

В случае двумерных возмущений, действующих

сжимаемые магнитные инерционно-гравитационные

только в горизонтальном направлении (k_z = 0), дис-

волны и трехмерные сжимаемые магнитострофи-

персионное уравнение (32) принимает вид

ческие волны. Дисперсионное уравнение для трех-

мерных сжимаемых магнитных инерционно-грави-

[

]

тационных волн в неупругом приближении имеет

ω⁴ -

2(B₀ · k)2h - N2θ

ω² +

[

]

вид

+ (B₀ · k)2h

(B₀ · k)2h - N2θ

(37)

⎛

и допускает решение в виде двух типов волн. Пер-

f2V k2z

k2h

ωmigBz = ±^⎝B2z

k2z +

N2θ +

вый тип — волны Альфвена с дисперсионным соот-

2k²

ношением

⎞1/2

√(

)₂

ω_A = ±(B₀ · k)_h.

(38)

f2V k2z

k2h

N²

+B2z0k4zf2V

⎠

(34)

Второй тип — двумерные магнитогравитационные

волны в неупругом приближении с дисперсионным

аналогичный дисперсионному соотношению для

соотношением

трехмерных магнитных инерционно-гравитацион-

√

ных волн в приближении Буссинеска ([18], формула

ω_mg = ± (B₀ · k)2h - N2θ.

(39)

(6)). Однако принципиальным отличием является

присутствие в выражении

(34) частоты Брен-

Выражение (39) в отсутствие магнитного поля

та - Вяйсяля для сжимаемых течений, N2θ, которая

описывает сжимаемые гравитационные волны в ней-

зависит как от исходного профиля плотности, так

тральной жидкости в неупругом приближении с час-

√

и от исходного профиля давления. Таким образом,

тотой ω_g = ±

-N2θ.

для волн, описываемых дисперсионным соотно-

В противоположном случае одномерных верти-

шением

(34) восстанавливающими механизмами

кальных возмущений (k = k_z) дисперсионное урав-

являются не только вращение, магнитное поле и

нение (32) имеет вид

гравитация, но и сжимаемость.

[

]

ω⁴ -

2B2z

k2z + f2V

ω² + B4z

k4z = 0

(40)

В частном случае отсутствия вертикального маг-

нитного поля (Bz0

= 0) выражение (34) пере-

и описывает два типа вертикальных магнитных

ходит в дисперсионное соотношение для трехмер-

волн. Первый тип удовлетворяет дисперсионному

ных инерционно-гравитационных волн в нейтраль-

соотношению

ной жидкости [50]:

√

f2V k2z

k²

f2V

ωz1 = ± B2z

k2z +

+f_V B2z

k2z +

(41)

ωig3D = ±

N2θ

(35)

k²

1194

ЖЭТФ, том 158, вып. 6 (12), 2020

Волновые процессы во вращающихся сжимаемых течениях. . .

которое в случае нейтральной жидкости (при отсут-

f-плоскости с линейным профилем энтропии (24) в

ствии магнитного поля) сводится к уравнению ω =

следующем виде:

= ±f_V . Второй тип магнитных вертикальных волн

удовлетворяет дисперсионному соотношению

∂v^′

+ (f_H v^′z - f_V v^′y)x + f_V v^′x ŷ - f_H v^′xz =

∂t

√

= -∇ω - T^′g - [B₀ × [∇ × B^′]],

(43)

f2V

ωz2 = ± B2z

k2z +

-f_V B2z

k2z +

(42)

∂T^′

N2θ

+v^′

= 0,

(44)

Данный тип волн не имеет аналога в динамике нейт-

∂t

^z g

ральной жидкости.

∂B^′

Выражения (41) и (42) совпадают с дисперсион-

= [∇ × [v^′ × B₀]],

(45)

∂t

ными соотношениями для вертикальных магнитных

N²

волн, найденными в приближении Буссинеска ([18],

(∇ · v^′) - v^′

= 0.

(46)

^z g

формулы (8) и (11)).

Таким образом, в приближении f-плоскости най-

Рассматривая возмущение в виде (31), получим

дены сжимаемые магнитогравитационные, сжимае-

следующее дисперсионное соотношение для волн во

мые магнитострофические и сжимаемые магнитные

вращающемся слое плазмы с линейным профилем

инерционно-гравитационные волны, в которых эф-

энтропии на нестандартной f-плоскости:

фекты сжимаемости представлены слагаемым с час-

тотой Брента - Вяйсяля для сжимаемых течений,

N²k_xf_H

ω⁴ -

ω³ -

включающей в себя зависимость как от исходного

gk²

[

]

профиля плотности, так и от исходного профиля

(f_H k_y + f_V k_z )²

k2hN2θ

давления. Помимо новых типов волн найдены волны

- 2(B₀ · k)² +

ω² +

k²

Альфвена и вертикальные магнитные волны, анало-

N²(B₀ · k)

[

гичные волнам в приближении Буссинеска.

f_H(Bx0k2h + Bz0k_zk_x) -

gk²

- fV k_z(By0k_x - Bx0k_y)]ω + (B₀ · k)2 ×

3.2. Приближение нестандартной

[

]

k2h

f -плоскости

× (B₀ · k)² -

N²

= 0,

(47)

k²

Получим дисперсионные уравнения для волн

где k2h = k2x + k2y.

в сжимаемом стратифицированном вращающемся

Проанализируем решение полученного диспер-

слое плазмы с линейным профилем энтропии на

сионного уравнения в частных случаях. Рассмот-

нестандартной f-плоскости. В приближении нестан-

рим возмущение, направленное вдоль тороидальной

дартной f-плоскости полагаем небольшое отклоне-

компоненты магнитного поля Bx0. Тогда дисперси-

ние вектора Кориолиса f от вертикали. Тогда вектор

онное уравнение (47) принимает вид

Кориолиса с учетом горизонтальной составляющей

принимает вид f = (0, f_H , f_V ), где fV = 2Ω sinθ, а

(

)

ω² - B2x

k2x

f_H = 2Ω cosθ. В таком случае слагаемое [f × v^′] в

(

)

уравнении (19) принимает вид

N²f_H

× ω² -

ω-B2x

k2x + N

= 0.

(48)

gk_x

(f_H v^′z - f_V v^′y)x + f_V v^′x ŷ - f_H v^′xz,

В неупругом приближении слагаемое с массовой си-

где x,

ŷ,

z — единичные векторы вдоль соответ-

лой в уравнении для z-компоненты скорости содер-

ствующих осей. Учет горизонтальной составляющей

жит потенциальную температуру, зависящую как

в нестандартном приближении f-плоскости играет

от плотности, так и от давления. Уравнение непре-

ключевую роль в описании экваториальных тече-

рывности в неупругом приближении включает в се-

ний, для которых вертикальная компонента вектора

бя исходный профиль плотности, в то время как

Кориолиса на экваторе обращается в нуль [51].

в приближении Буссинеска является условием без-

Запишем линеаризованную систему магнитогид-

дивергентности поля скоростей. Таким образом, в

родинамических уравнений в неупругом приближе-

неупругом приближении дисперсионное уравнение

нии для вращающегося слоя сжимаемой стратифи-

(47) для волн на нестандартной f-плоскости имеет

цированной плазмы в приближении нестандартной

значительное различие в выражениях при первой и

1195

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

третьей степенях частоты, что в частном случае рас-

Дисперсионное соотношение (52) в предположении

пространения волн вдоль тороидального магнитно-

отсутствия стратификации плотности (N²

= 0)

го поля приводит к появлению новых типов сжима-

описывает сжимаемые гравитационные волны в

√

емых магнитных инерционно-гравитационных волн.

неупругом приближении с частотой ω =

-N′2θ.

Соотношение (47) описывает три типа волн. Пер-

Третий тип волн

— сжимаемые магнитные

вый тип — одномерные волны Альфвена с диспер-

инерционно-гравитационные волны с дисперсион-

сионным соотношением

ным соотношением

√

ωAx = ±Bx0k_x.

(49)

N²f

N⁴f2H

ωmigx

+B2x

k2x - N2θ,

(53)

Второй тип линейных волн — сжимаемые магнит-

2gk_x

4g²k²

ные инерционно-гравитационные волны с дисперси-

аналогичным полученному выше соотношению (50)

онным соотношением

√

с точностью до знака перед корнем. В предположе-

N²f_H

N⁴f2H

нии отсутствия стратификации плотности (N² = 0)

ωmigx

+B2x

k2x - N2θ.

(50)

2gk_x

4g²k²

данный тип волн переходит в сжимаемые магнито-

гравитационные волны в неупругом приближении с

Выражение (50) значительно отличается от дис-

частотой

√

персионного соотношения (34) для сжимаемых маг-

ωmgx2

=- B2x0k2x -N2θ.

(54)

нитных инерционно-гравитационных волн, получен-

ных в предыдущем разделе, а также и от диспер-

В частном случае отсутствия магнитного поля

сионного соотношения для магнитных инерцион-

(Bx0 = 0) выражение (53) описывает сжимаемые

но-гравитационных волн в приближении Буссинеска

инерционно-гравитационные волны в нейтральной

[18]. Однако восстанавливающие механизмы для

жидкости с частотой

волн, описываемых выражениями (50) и (34), оди-

√

наковы. Тем не менее выражение (50) описыва-

N²f_H

N⁴f2H

ωigx2 =

-N2θ.

(55)

ет физические эффекты, сопровождающие сжима-

2gk_x

4g²k²

емые магнитные инерционно-гравитационные вол-

ны в неупругом приближении с новым законом

В случае полного отсутствия стратификации (N2θ =

дисперсии, восстанавливающими механизмами ко-

= 0, N² = 0) оба типа волн, (50) и (53), переходят

торых являются вращение, гравитация, магнитное

в одномерные волны Альфвена с частотой ωAx =

поле и сжимаемость. Отметим, что исходный про-

= ±Bx0k_x.

филь плотности связан непосредственно с гори-

Рассмотри случай полоидального магнитного по-

зонтальной составляющей силы Кориолиса. Такая

ля в состоянии покоя и одномерное возмущение, на-

связь обусловлена учетом эффектов сжимаемости и

правленное вдоль магнитного поля. Тогда дисперси-

горизонтальной компоненты вектора Кориолиса, а

онное уравнение (47) принимает вид

также распространением волн вдоль тороидально-

[

]

го магнитного поля. В предположении отсутствия

ω⁴ -

2B2y

k2y + f2H - N2θ

ω² +

[

]

стратификации плотности (N2 = 0) вклад силы

+B2y

k2y

B2y

k2y - N2θ

(56)

инерции в дисперсионное соотношение (50) исчезает

и оно описывает одномерные сжимаемые магнито-

и описывает два типа волн: одномерные магнит-

гравитационные волны в неупругом приближении с

ные инерционно-гравитационные волны и одномер-

частотой

√

ные магнитострофические волны. Дисперсионное

ωmgx1

= B2x0k2x -N′2θ,

(51)

соотношение для одномерных магнитных инерцион-

но-гравитационных волн в неупругом приближении

где N′2θ = -g²ρ₀/γp₀.

имеет следующий вид:

В частном случае отсутствия магнитного поля

(Bx0 = 0) дисперсионное соотношение (50) предста-

⎛

вимо в виде

f2H

N2θ

ωmigy = ±^⎝B2y

k2y +

√

N²f_H

N⁴f2H

ωigx1 =

-N2θ

(52)

⎞1/2

2gk_x

4g²k²

)₂

√(f2_H

-N²

+B2y0k2yf2H

⎠

(57)

и описывает одномерные сжимаемые инерцион-

но-гравитационные волны в нейтральной жидкости.

1196

ЖЭТФ, том 158, вып. 6 (12), 2020

Волновые процессы во вращающихся сжимаемых течениях. . .

Такой тип волн, так же как и в случае трехмер-

f слабо меняется при малых изменениях широты и

ных магнитных инерционно-гравитационных волн

раскладывается в ряд:

на стандартной f-плоскости (34), является сжима-

емым аналогом одномерных магнитных инерцион-

f = 2ΩsinΘ ≈ 2ΩsinΘ₀ + 2Ω(Θ - Θ₀)cosΘ₀ ≈

но-гравитационных волн в приближении Буссинеска

≈f₀ +βy,

(60)

([18], формула (33)).

где Ω — угловая скорость вращения, Θ — широта,

В частном случае отсутствия магнитного поля

f₀ = 2Ω sinΘ₀ (f₀ ≡ f_V ), β = ∂f/∂y. Приближение

(By0 = 0) выражение (57) переходит в дисперсион-

β-плоскости, в отличие от приближения f-плоскос-

ное соотношение для одномерных инерционно-гра-

ти, сохраняет первый порядок малости в разложе-

витационных волн в нейтральной жидкости:

нии параметра Кориолиса. Запишем линеаризован-

√

ωigy = ± f2H - N2θ.

(58)

ную систему магнитогидродинамических уравнений

в неупругом приближении для вращающегося слоя

Дисперсионное соотношение для одномерных маг-

сжимаемой стратифицированной плазмы в прибли-

нитострофических волн имеет вид

жении β-плоскости с линейным профилем энтропии

⎛

(24) в следующем виде:

f2H

N2θ

ωmstry = ±^⎝B2y

k2y +

′

∂²v

∂v^′y

∂² ω

∂

-f_V

- βv^′y = -

∂y∂t

∂y

∂y∂x

∂y

⎞1/2

(

)

))

√(

)₂

⁽∂B^′y

∂B^′x

⁽∂B^′z

∂B^′x

f2H

⎠

× By0

+Bz0

(61)

-N²

+B2y0k2yf2H

(59)

∂x

∂y

∂x

∂z

)

аналогичный дисперсионному соотношению для од-

∂v^′y

∂ω

⁽∂B^′z

∂B^′y

номерных магнитострофических волн в прибли-

+f_Vv^′x =-

-B0z

∂t

∂y

∂z

жении Буссинеска ([18], формула (36)), с учетом

)

⁽∂B^′y

∂B^′x

эффектов сжимаемости, представленных частотой

+B0x

(62)

∂x

∂y

Брента - Вяйсяля N2θ.

Таким образом, в приближении нестандартной

)

f-плоскости найдены новые сжимаемые магнитные

∂v^′z

∂ω

⁽∂B^′x

∂B^′z

+T^′g-B0x

инерционно-гравитационные волны с различными

∂t

∂z

∂x

)

законами дисперсии и сжимаемые магнитострофи-

⁽∂B^′z

∂B^′y

ческие волны, в которых эффекты сжимаемости

+B0y

(63)

∂y

∂z

представлены слагаемыми с частотой Брента - Вяй-

сяля для сжимаемых течений, включающей в себя

∂T^′

N2θ

+v^′

= 0,

(64)

зависимость как от исходного профиля плотности,

∂t

^z g

так и от исходного профиля давления. Помимо но-

∂B^′

= [∇ × [v^′ × B₀]],

(65)

вых типов волн найдены волны Альфвена, анало-

∂t

гичные волнам в приближении Буссинеска.

N²

(∇ · v^′) - v^′

= 0.

(66)

^z g

4. ЛИНЕЙНАЯ ТЕОРИЯ ВОЛНОВЫХ

Рассматривая возмущение основного состояния в

ПРОЦЕССОВ В СЖИМАЕМОМ

виде (31), получим дисперсионное соотношение для

СТРАТИФИЦИРОВАННОМ

волн во вращающемся слое плазмы с линейным про-

ВРАЩАЮЩЕМСЯ СЛОЕ ПЛАЗМЫ С

филем энтропии на стандартной β-плоскости:

ЛИНЕЙНЫМ ПРОФИЛЕМ ЭНТРОПИИ С

[

УЧЕТОМ ЭФФЕКТОВ СФЕРИЧНОСТИ

βN²f_Vk_z

k²ω⁴ + βk_xω3 - ω2 f2V k2z +

gk_y

4.1. Приближение стандартной β-плоскости

]

[

(

)

+ 2k²(B₀ · k)²-k2hN²

-ω k_xβ

(B₀ · k)²-N2θ

Получим дисперсионные уравнения для волн

]

в сжимаемом стратифицированном вращающемся

N²fV kz

слое плазмы с линейным профилем энтропии с уче-

(B₀ · k) (By0 k_x - Bx0 k_y)

том эффектов сферичности в приближении β-плос-

[

]

+ (B₀ · k)²

k²(B₀ · k)² - k2hN2θ

(67)

кости. В таком приближении параметр Кориолиса

1197

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

Проанализируем решение полученного дисперсион-

в неупругом приближении с дисперсионным соотно-

ного уравнения в частных случаях. Рассмотрим дву-

шением

мерные возмущения только в горизонтальном на-

[

]

правлении (k_z = 0). Тогда дисперсионное уравнение

ω ≈ (B₀ · k)²

k²(B₀ · k)² - k2hN2θ

[

(67) принимает вид

(

)

× k_xβ

(B₀ · k)² - N2θ

(

)

ω² - (B₀ · k)2h + N2θ

]-1

(

)

N²fV kz

βk_x

(B₀ · k) (By0 k_x - Bx0 k_y)

(75)

× ω² +ω

- (B₀ · k)²

= 0.

(68)

k²

Выражение (75) учитывает эффекты сжимаемо-

Выражение (68) описывает три типа волн. Пер-

сти в низкочастотных трехмерных волнах Россби

вый тип — сжимаемые магнитогравитационные вол-

вследствие зависимости частоты Брента - Вяйсяля

ны в неупругом приближении, аналогичные волнам

для сжимаемых течений, N2θ, не только от исход-

на f-плоскости (39). Второй тип — волны магни-

ного профиля плотности, но и от исходного про-

то-Россби с дисперсионным соотношением

филя давления. Дисперсионное соотношение (75)

√

имеет вид, аналогичный дисперсионному соотноше-

βk_x

β²k2x

нию для трехмерных низкочастотных волн магни-

ωmR1 = -

+ (B₀ · k)2h,

(69)

2k2h

4k⁴

то-Россби в приближении Буссинеска ([18], формула

(47)). Однако в результате учета эффектов сжима-

которое в отсутствие магнитного поля описывает

емости в неупругом приближении выражение (75)

стандартные гидродинамические волны Россби с

имеет дополнительное слагаемое в знаменателе, свя-

частотой

занное со стратификацией плотности, которое исче-

βk_x

ω_R = -

(70)

зает, если в состоянии покоя магнитное поле направ-

k²

лено вдоль вертикали.

Третий тип — волны магнито-Россби с дисперсион-

Таким образом, в приближении стандартной

ным соотношением

β-плоскости найдены сжимаемые магнитогравита-

√

ционные волны и сжимаемые трехмерные низкоча-

βk_x

β²k2x

стотные волны магнито-Россби, в которых эффекты

ωmR2 = -

+ (B₀ · k)2h.

(71)

2k2h

4k⁴

сжимаемости представлены слагаемыми с частотой

Брента - Вяйсяля для сжимаемых течений, включа-

Такой тип волн не имеет аналога в динамике нейт-

ющей в себя зависимость как от исходного профиля

ральной жидкости.

плотности, так и от исходного профиля давления.

В случае одномерных возмущений, направлен-

Помимо новых типов волн найдены волны Альфве-

ных только вдоль полоидальной составляющей маг-

на и волны магнито-Россби, аналогичные волнам в

нитного поля, дисперсионное уравнение (67) прини-

приближении Буссинеска.

мает вид

4.2. Приближение нестандартной

ω⁴ -ω²(2B2y

k2y -N2θ)+B2y

k2y(B2y

k2y -N2θ) = 0. (72)

β-плоскости

Выражение (72) описывает два типа волн: одномер-

Получим дисперсионные уравнения для волн

ные волны Альфвена с дисперсионным соотношени-

в сжимаемом стратифицированной вращающемся

ем

слое плазмы с линейным профилем энтропии с

ωAy = ±By0k_y

(73)

учетом эффектов сферичности на нестандартной

β-плоскости. В приближении нестандартной β-плос-

и одномерные сжимаемые магнитогравитационные

кости предполагаем отклонение вектора Кориолиса

волны в неупругом приближении с дисперсионным

f от вертикали, а также его незначительное изме-

соотношением

нение при малых изменениях широты. Горизонталь-

√

ная и вертикальная компоненты вектора Кориолиса

ωmgy = ± B2y

k2y - N2θ.

(74)

раскладываются в ряд, и параметр Кориолиса вы-

глядит следующим образом:

В низкочастотном пределе уравнение (67) описы-

вает сжимаемую трехмерную волну магнито-Россби

f = (0,f_H + γy,f_V + βy),

(76)

1198

ЖЭТФ, том 158, вып. 6 (12), 2020

Волновые процессы во вращающихся сжимаемых течениях. . .

]

где

^[N²

f_H

k_z

k²ω⁴ - k_xω³

+γ

-β

k_y

2Ω cosΘ

f_V = 2Ω sinΘ, β =

[

(

)

βN²

- ω² (f_Hk_y + fV k_z)² +

f_H + f_V

k_y

]

2Ω sinΘ

f_H = 2Ω cosΘ, γ = -

+ 2k²(B₀ · k)² - k2hN²

{

(

)

k_z

N²

Запишем линеаризованную систему магнитогид-

+ ω k_x(B₀

· k)²

-β

+βk_xN2θ+

(B₀ · k) ×

k_y

родинамических уравнений в неупругом приближе-

}

[

]

нии для вращающегося слоя сжимаемой стратифи-

f_H(Bx0k2h + Bz0k_xk_z)+f_V k_z(Bx0k_y-By0k_x)

цированной плазмы в приближении нестандартной

[

]

β-плоскости с линейным профилем энтропии (24) в

+ (B₀ · k)²

k²(B₀ · k)² - k2hN2θ

(83)

виде

Проанализируем решение полученного диспер-

сионного уравнения в частных случаях. Рассмот-

∂²v^′x

∂v^′y

∂v^′z

-f_V

- βv^′

+f_H

+γv^′z =

рим исходное состояние равновесия с тороидальным

∂y∂t

∂y

магнитным полем. Для двумерных возмущений, на-

(

)

правленных только в горизонтальном направлении

∂² ω

∂

⁽∂B^′y

∂B^′x

By0

(k_z = 0), таких что k_y ≪ k_x и k2y/k2h ≪ 1, k2x/k2h ∼ 1,

∂y∂x

∂y

∂x

∂y

дисперсионное уравнение (83) принимает вид

))

⁽∂B^′z

∂B^′x

(

)

+ Bz0

(77)

βk_x

∂x

∂z

ω² +

ω-B2x

k²

(

)

N²f_Hk_x

× ω

² -

ω-B2x

k2x + N²

(84)

)

k2hg

∂v^′y

∂ω

⁽∂B^′z

∂B^′y

+f_Vv^′x =-

-B0z

и допускает решение в виде четырех типов волн.

∂t

∂y

∂z

Первый тип — волны магнито-Россби с частотой

)

√

⁽∂B^′y

∂B^′x

+B0x

(78)

βk_x

β²k2x

∂x

∂y

ωmR1 = -

+B2x0k2x.

(85)

2k2h

Выражение (85) аналогично дисперсионному соот-

)

∂v^′z

∂ω

⁽∂B^′x

∂B^′z

ношению (69) для волн магнито-Россби на β-плос-

-f_Hv^′x =-

+T^′g-B0x

∂t

∂z

∂x

кости с учетом однокомпонентности магнитного по-

ля (B = (Bx0, 0, 0)).

)

⁽∂B^′z

∂B^′y

Второй тип — волны магнито-Россби с частотой

+B0y

(79)

∂y

∂z

√

βk_x

β²k2x

ωmR2 = -

+B2x0k2x.

(86)

2k²

4k⁴

∂T^′

N2θ

+v^′

= 0,

(80)

∂t

^z g

Выражение (86) аналогично дисперсионному соот-

ношению (71) для волн магнито-Россби на β-плос-

кости с учетом однокомпонентности магнитного по-

∂B^′

= [∇ × [v^′ × B₀]],

(81)

ля (B = (Bx0, 0, 0)).

∂t

Третий тип — сжимаемые магнитные инерцион-

но-гравитационные волны с дисперсионным соотно-

(∇ · v^′) - v^′

= 0.

(82)

шением

^z g

√

N²f_Hk_x

N⁴f2Hk2x

ω_mig′

+B2x0k2x -N2θ,

(87)

Рассматривая возмущение в виде (31), получим

2k2hg

4k4hg²

следующее дисперсионное соотношение для волн во

вращающемся слое плазмы с линейным профилем

которое аналогично соотношению (50), полученному

энтропии на нестандартной β-плоскости:

при изучении волн на нестандартной f-плоскости.

1199

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

Четвертый тип — сжимаемые магнитные инер-

метр β, характерный для волн магнито-Россби, ко-

ционно-гравитационные волны с дисперсионным со-

торые непосредственно связаны с градиентом про-

отношением

филя плотности и горизонтальной составляющей

√

силы Кориолиса. Такая связь обсуловлена учетом

N²f_Hk_x

N⁴f2Hk2x

эффектов сжимаемости и горизонтальной компо-

ω_mig′

+B2x

k2x - N2θ,

(88)

2k2hg

4k4hg²

ненты вектора Кориолиса, а также распространени-

ем волн вдоль полоидального магнитного поля.

которое аналогично соотношению (53), полученному

В предположении отстутствия стратификации

при изучении волн на нестандартной f-плоскости.

плотности (N² = 0) дисперсионное соотношение (90)

Рассмотрим случай, когда в состоянии покоя

описывает одномерные магнитные инерционно-гра-

магнитное поле полоидально. Для одномерных воз-

витационные волны, аналогичные волнам на нестан-

мущений, направленных вдоль магнитного поля,

дартной f-плоскости (57). В частном случае отсут-

дисперсионное уравнение (83) записывается в виде

ствия магнитного поля (By0 = 0) дисперсионное со-

[

]

отношение (90) описывает новый тип сжимаемых

βN²f_H

ω⁴ - ω2 f2H +

+ 2B2y

k2y - N²

инерционно-гравитационных волны в нейтральной

gk²

жидкости с частотой

[

]

+B2y

k2y

B2y

k2y - N2θ

= 0.

(89)

√

βN²f_H

В неупругом приближении слагаемое с массо-

ω= f2H +

-N2θ.

(91)

gk²

вой силой в уравнении для z-компоненты скорости

содержит потенциальную температуру, зависящую

Выражение (91) в предположении отстутствия стра-

как от плотности, так и от давления. Уравнение

тификации плотности (N² = 0) переходит в выраже-

непрерывности в неупругом приближении включа-

ние (58), которое также описывает инерционно-гра-

ет в себя исходный профиль плотности, в то время

витационные волны в нейтральной жидкости.

как в приближении Буссинеска является условием

Дисперсионное соотношение для сжимаемых

бездивергентности поля скоростей. Таким образом,

магнитострофических волн, являющееся решением

в неупругом приближении дисперсионное уравнение

дисперсионного уравнения (89), имеет вид

для волн на нестандартной β-плоскости (83) имеет

значительное различие в выражениях при первой,

⎡

второй и третьей степенях частоты, что в частном

βN²f_H

N2θ

ωmstrβ =⎣fH

+B2y

k2y -

случае распространения волн вдоль полоидального

2gk2y

магнитного поля (89) приводит к появлению новых

)₂

типов сжимаемых магнитных инерционно-гравита-

[(f2_H

βN²f_H

N2θ

−

ционных и сжимаемых магнитострофических волн.

2gk2y

Дисперсионное соотношение для сжимаемых

⎤

]1/2

1/2

магнитных инерционно-гравитационных волн имеет

f_HβN²B2y

⎦

+f2HB2y

k2y +

(92)

вид

⎡

βN²f_H

N2θ

Волны, описываемые дисперсионным соотношени-

ωmigβ =⎣fH

+B2y

k2y +

2gk2y

ем (92), не имеют аналога в динамике нейтральной

[(

)₂

жидкости. Выражение (92) имеет вид, аналогичный

f2H

βN²f_H

N2θ

дисперсионному соотношению для сжимаемых маг-

2gk2y

нитострофических волн, полученных в предыдущих

]1/2⎤

1/2

разделах. Однако дисперсионное соотношение (92)

f_HβN²B2y

включает в себя параметр β, характерный для волн

⎦

+ f2HB2y

k2y +

(90)

магнито-Россби, который, как и в случае со сжима-

емыми магнитными инерционно-гравитационными

который аналогичен дисперсионному соотношению

волнами с частотой (90), неразрывно связан с гра-

для сжимаемых магнитных инерционно-гравитаци-

диентом профиля плотности и горизонтальной со-

онных волн, полученных в предыдущих разделах.

ставляющей силы Кориолиса. В предположении от-

Однако дисперсионное соотношение (90) имеет до-

стутствия стратификации плотности (N² = 0) дис-

полнительные слагаемые, включающие в себя пара-

персионное соотношение (92) описывает одномерные

1200

ЖЭТФ, том 158, вып. 6 (12), 2020

Волновые процессы во вращающихся сжимаемых течениях. . .

сжимаемые магнитострофические волны, аналогич-

5. ТРЕХВОЛНОВЫЕ ВЗАИМОДЕЙСТВИЯ И

ные волнам на нестандартной f-плоскости (59).

ПАРАМЕТРИЧЕСКИЕ НЕУСТОЙЧИВОСТИ

ВОЛН В НЕУПРУГОМ ПРИБЛИЖЕНИИ

В случае полного отсутствия стратификации

(N2θ = 0, N² = 0) оба типа волн, (90) и (92), пе-

5.1. Качественный анализ дисперсионных

реходят в одномерные волны Альфвена с частотой

соотношений

ωAy = ±By0k_y.

Ниже проанализируем дисперсионные соотноше-

В низкочастотном пределе дисперсионное урав-

ния, полученные в предыдущих разделах, и най-

нение (83) допускает решение в виде сжимаемой

дем условия синхронизма, обеспечивающие трехвол-

трехмерной волны магнито-Россби в неупругом при-

новые взаимодействия. Для существования взаимо-

ближении с частотой

действия между тремя волнами необходимо, что-

бы их дисперсионные соотношения удовлетворяли

условию синхронизма [52]

{

[

]}

ω≈

(B₀ · k)²

k²(B₀ · k)² - k2hN2θ

{

(

)

ω(k₁) + ω(k₂) = ω(k₁ + k₂), k₁ + k₂ = k₃.

(94)

k_z

× k_x(B₀

· k)²

β-γ

- βk_xN2θ -

k_y

Чтобы проверить выполнение условия синхронизма

(94), используем качественный анализ дисперсион-

[

(B₀ · k)

f_H(Bx0k2h + Bz0k_xk_z) +

ных кривых. В таком случае пересечение двух дис-

}-1

персионных кривых, одна из которых смещена отно-

сительно начала координат на некоторый волновой

+ fV k_z(Bx0k_y - By0k_x)]

(93)

вектор k_c, обеспечивает выполнение условия синхро-

низма [53].

Выражение (93) учитывает эффекты сжимаемос-

5.1.1. Условие синхронизма для волн на

ти в низкочастотных трехмерных волнах Россби

стандартной f -плоскости и нестандартной

вследствие зависимости частоты Брента - Вяйсяля

f -плоскости. Трехволновые взаимодействия

для сжимаемых течений, N2θ, не только от исход-

ного профиля плотности, но и от исходного про-

Проверим выполнение условия синхронизма (94)

филя давления. Дисперсионное соотношение (93)

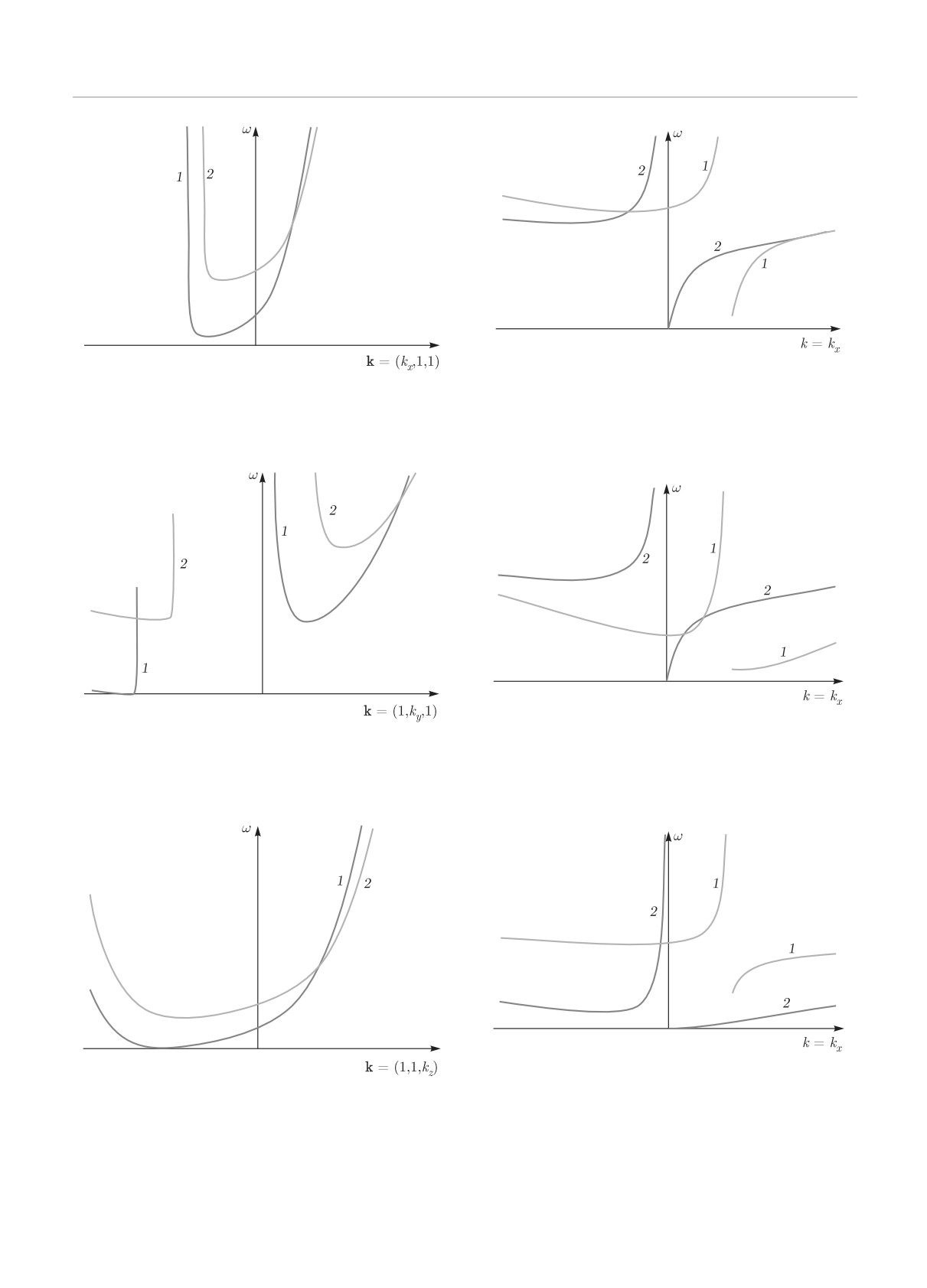
для волн на f-плоскости. Изобразим на рис. 1 дис-

имеет вид, аналогичный дисперсионному соотноше-

персионную кривую для волны Альфвена с частотой

нию для трехмерных низкочастотных волн магни-

ω_A (38) и дисперсионную кривую для сжимаемой

то-Россби в приближении Буссинеска на нестан-

магнитогравитационной волны в неупругом прибли-

дартной β-плоскости ( [18], формула (64)). Кроме

жении с частотой ω_mg (39), смещенную относитель-

того, в результате учета эффектов сжимаемости в

но начала координат. Пересечение двух дисперси-

неупругом приближении выражение (93) имеет до-

онных кривых в некоторой точке (ω(k₃), k₃) означа-

полнительное слагаемое в знаменателе, связанное со

ет выполнение условия синхронизма (94). На рис. 1

стратификацией плотности, которое, однако, не ис-

изображено пересечение двух дисперсионных кри-

чезает при отсутствии горизонтальных компонент

вых, определяющее трехволновое взаимодействие

магнитного поля, как в случае стандартного при-

ближения β-плоскости.

Таким образом, в приближении нестандарт-

ной β-плоскости найдены сжимаемые магнитные

инерционно-гравитационные и магнитострофичес-

кие волны с различными законами дисперсиии

и сжимаемые трехмерные низкочастотные волны

магнито-Россби, в которых эффекты сжимаемости

представлены слагаемыми с частотой Брента - Вяй-

сяля для сжимаемых течений, включающей в себя

зависимость как от исходного профиля плотности,

Рис. 1. Условие синхронизма для двух сжимаемых маг-

так и от исходного профиля давления. Помимо

нитогравитационных волн и волны Альфвена: 1 — ω =

новых типов волн найдены волны магнито-Россби,

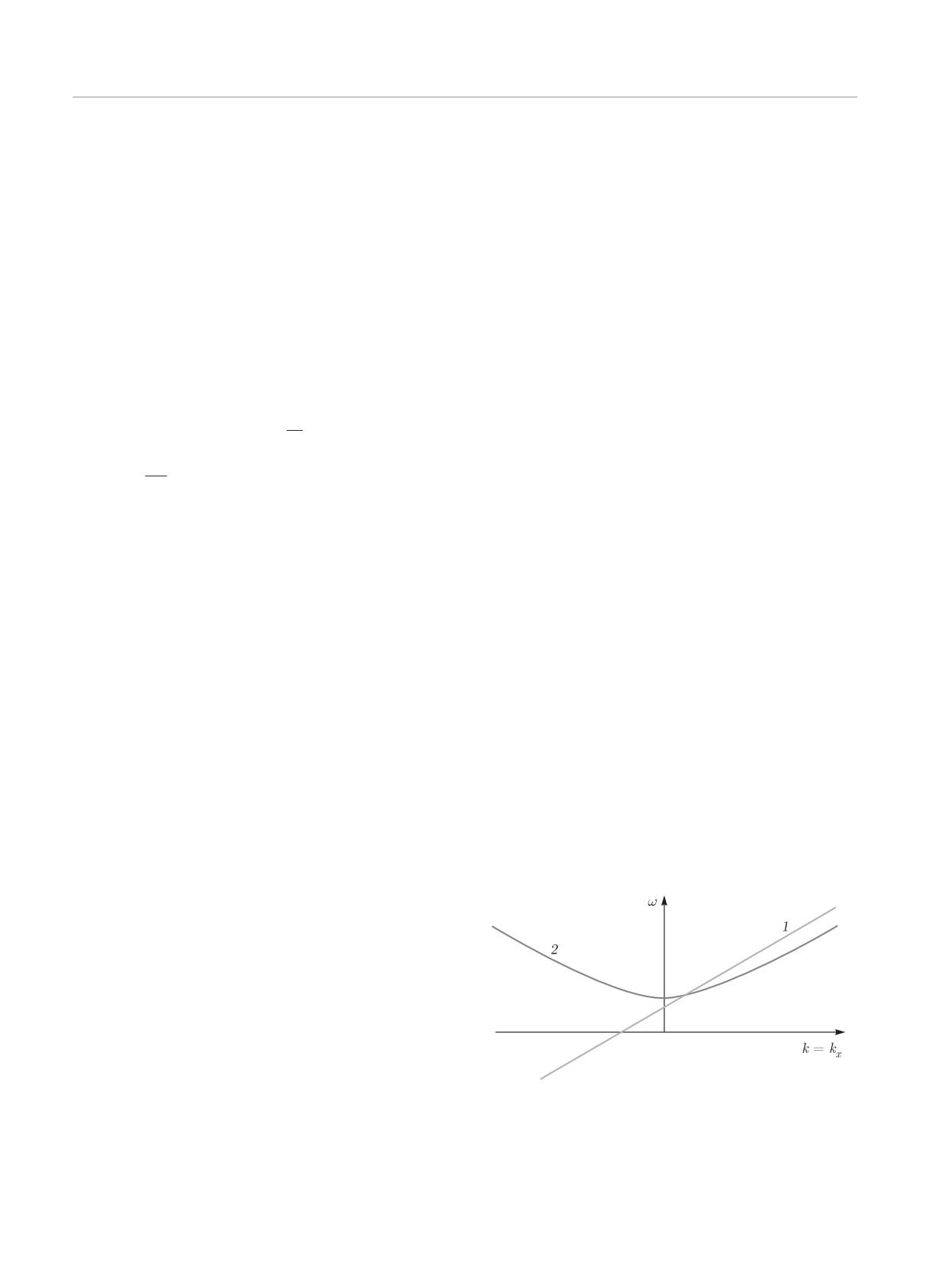
= ωmg(kx); 2 — ω = ωA(kx - kxc) + ωmg(kxc )

аналогичные волнам в приближении Буссинеска.

1201

ЖЭТФ, вып. 6 (12)

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

Рис. 2. Условие синхронизма для двух сжимаемых магнитных инерционно-гравитационных волн и сжимаемой магнито-

строфической волны при k = kx (а) и при k = kz (б): 1 — ω = ωmig_Bz (k); 2 — ω = ωmstr_Bz (k - kc) + ωmig_Bz (kc)

Рис. 3. Условие синхронизма для двух сжимаемых магнитных инерционно-гравитационных волн и сжимаемой магнито-

строфической волны при k = kx (а) и при k = kz (б): 1 — ω = ωmstr_Bz (k); 2 — ω = ωmig_Bz (k - kc) + ωmig_Bz (kc)

волны Альфвена и двух сжимаемых магнитогра-

маемой магнитной инерционно-гравитационной

витационных волн в неупругом приближении. По-

волны при взаимодействии сжимаемых магни-

скольку вертикальные магнитные волны с частота-

тострофической волны и сжимаемой магнитной

ми ωz1 (41) и ωz2 (42) идентичны волнам на f-плос-

инерционно-гравитационной волны (рис.

2); воз-

кости в приближении Буссинеска [18], для них будут

никновение сжимаемой магнитострофической

существовать идентичные трехволновые взаимодей-

волны при взаимодействии двух сжимаемых

ствия, а именно, взаимодействие двух вертикальных

магнитных инерционно-гравитационных волн

магнитных волн с частотой ωz1 и вертикальной маг-

(рис. 3); возникновение сжимаемой магнитостро-

нитной волны с частотой ωz2 ([18], рис. 4); взаимо-

фической волны при взаимодействии сжимаемой

действие трех вертикальных магнитных волн с час-

магнитной инерционно-гравитационной волны и

тотой ωz2 ([18], рис. 5).

сжимаемой магнитострофической волны (рис. 4);

возникновение сжимаемой магнитной инерционно-

Для сжимаемых трехмерных магнитных инер-

гравитационной волны при взаимодействии двух

ционно-гравитационных

(34) и магнитострофи-

сжимаемых магнитострофических волн (рис.

5);

ческих (36) волн проведен качественный анализ

возникновение сжимаемой магнитострофической

дисперсионных кривых при k = (k_x, 0, 1) и k =

волны при взаимодействии двух сжимаемых магни-

= (1, 0, k_z). В обоих случаях найдены следующие

тострофических волн (рис. 6).

трехволновые взаимодействия: возникновение сжи-

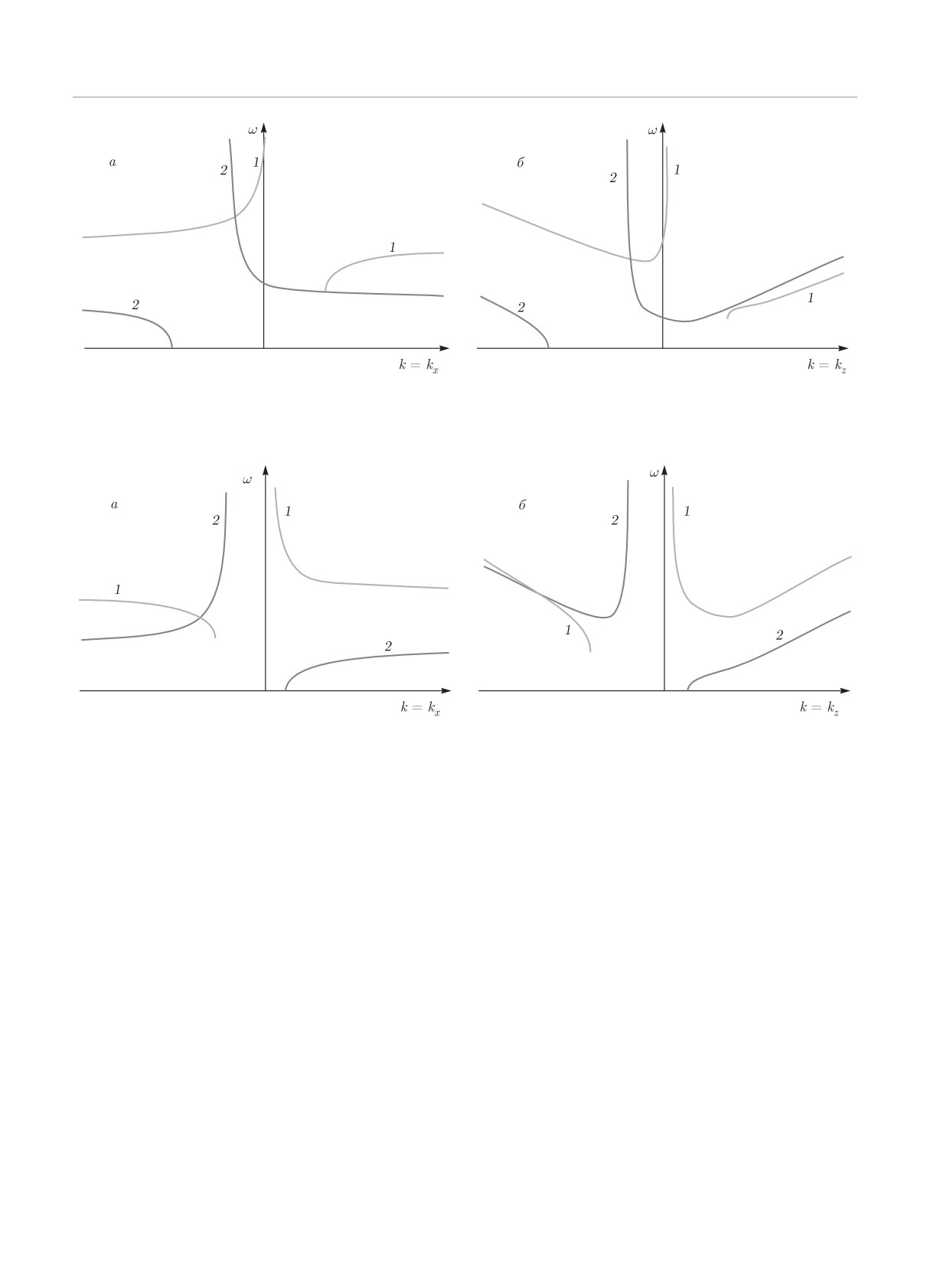
1202

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

в ней трехволновые взаимодействия, а именно:

при малой горизонтальной составляющей силы

Кориолиса (f_H

< 1) возникает сжимаемая маг-

нитная инерционно-гравитационная волна (57) при

взаимодействии двух сжимаемых магнитостро-

фических волн (59) ( [18], рис. 8); при большой

горизонтальной составляющей силы Кориолиса

(f_H

≫ 1) помимо предыдущего трехволнового

взаимодействия возникает сжимаемая магнитная

инерционно-гравитационная волна (57) при взаимо-

действии сжимаемой магнитострофической (59) и

сжимаемой магнитной инерционно-гравитационной

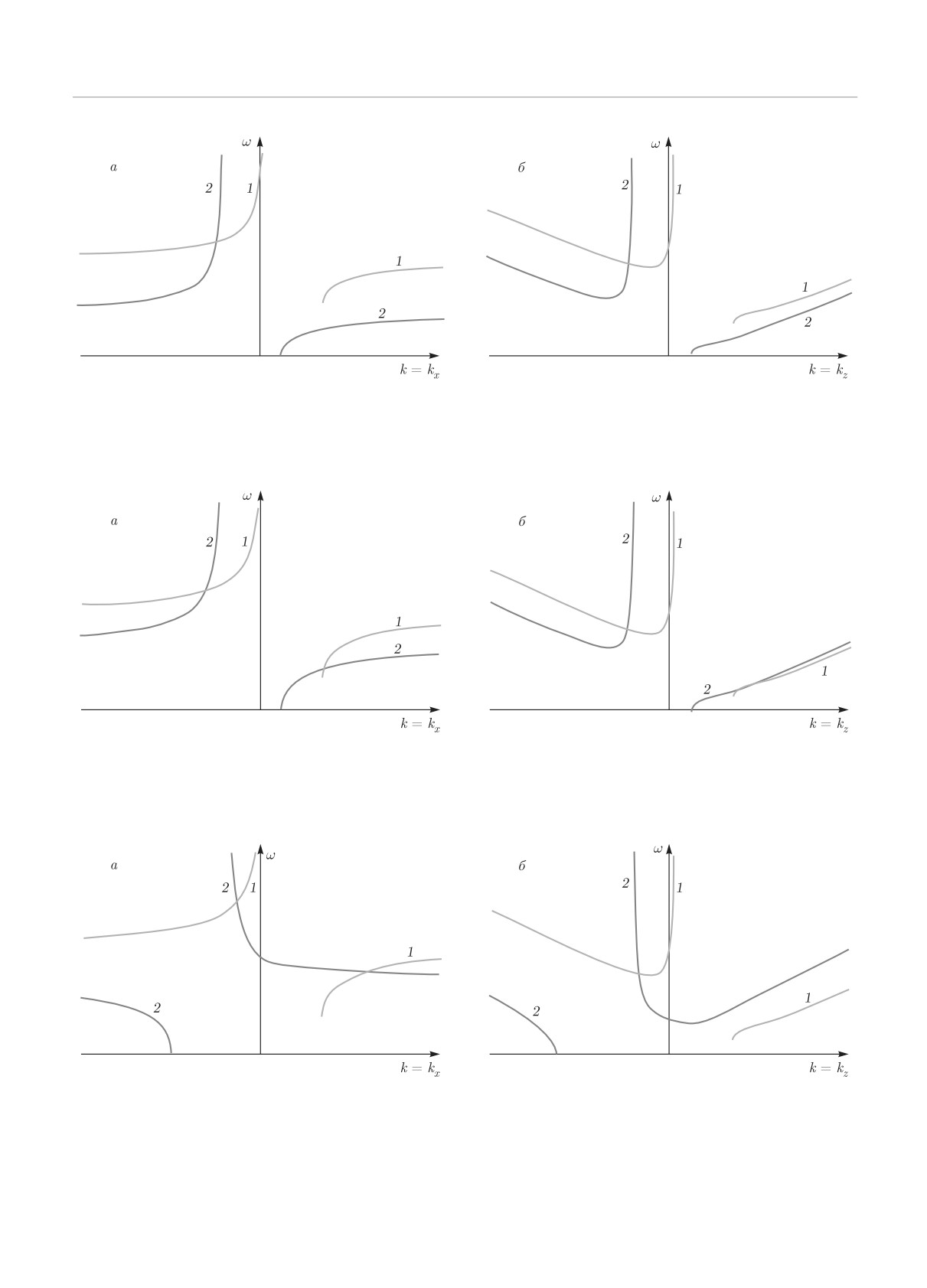
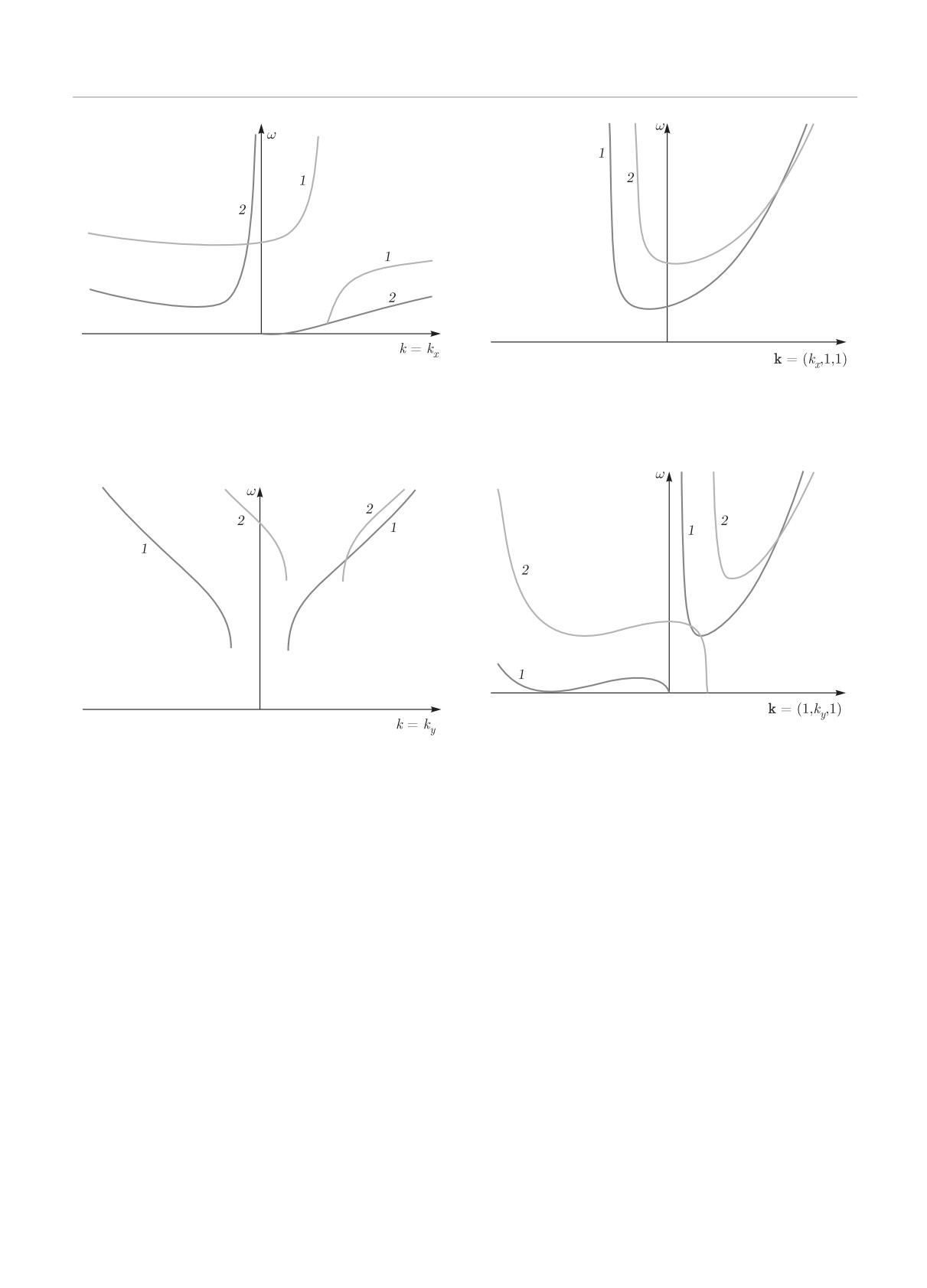
Рис. 7. Условие синхронизма для двух сжимаемых магнит-

волн (57) ([18], рис. 10).

ных инерционно-гравитационных волн и волны Альфвена:

1 — ω = ωmigx1 (kx); 2 — ω = ωAx(kx - kxc) + ωmigx1 (kxc)

5.1.2. Условие синхронизма для волн на

стандартной β-плоскости и нестандартной

β-плоскости. Трехволновые взаимодействия

Перейдем теперь к проверке выполнения усло-

вия синхронизма (94) для волн на стандартной и

нестандартной β-плоскостях. Для найденных волн

(73), (74) на β-плоскости картина пересечения дис-

персионных кривых аналогична пересечению волн

на f-плоскости (см. рис. 1). Условие синхронизма

обеспечивает взаимодействие волны Альфвена (73)

и двух сжимаемых магнитогравитационных волн

(74). Для волн на β-плоскости, аналогичных волнам,

полученным в работе [18], существуют следующие

трехволновые взаимодействия: возникновение вол-

Рис. 8. Условие синхронизма для трех сжимаемых маг-

ны магнито-Россби (69) при взаимодействии двух

нитных инерционно-гравитационных волн:

— ω

волн магнито-Россби (69) ([18], рис. 13); возникнове-

= ωmigx₁ (kx); 2 — ω = ωmigx₁ (kx - kxc ) + ωmigx₁ (kxc )

ние сжимаемой магнитогравитационной волны (39)

при взаимодействии волны магнито-Россби (69) и

сжимаемой магнитогравитационной (39) волны ([18],

Для волн на нестандартной f-плоскости изоб-

рис. 14); возникновение волны магнито-Россби (69)

ражено пересечение дисперсионных кривых, со-

при взаимодействии сжимаемой магнитогравитаци-

ответствующее выполнению условия синхронизма

онной волны (39) и волны магнито-Россби (69) ([18],

(рис. 7), которое определяет возникновение сжима-

рис. 15).

емой магнитной инерционно-гравитационной волны

Для сжимаемых низкочастотных волн магнито-

(50) при взаимодействии волны Альфвена (49) и

Россби (75) выполняется условие синхронизма, обес-

сжимаемой магнитной инерционно-гравитационной

печивающее взаимодействие трех сжимаемых волн

волны

(50). На рис.

изображено пересечение

магнито-Россби при k = (k_x, 1, 1) (рис. 9), при k =

дисперсионных кривых, обеспечивающее выпол-

= (1, k_y, 1) (рис. 10) и при k = (1, 1, k_z) (рис. 11).

нение условия синхронизма для трех сжимаемых

Перейдем к анализу дисперсионных кривых на

магнитных инерционно-гравитационных волн (50).

нестандартной β-плоскости. На рис. 12 изображено

Для волн

(57),

(59), имеющих дисперсионные

пересечение дисперсионных кривых, обеспечива-

соотношения, аналогичные полученным в работе

ющее условие синхронизма, которое определяет

по исследованию волн в приближении Буссинеска

возникновение сжимаемой магнитной инерцион-

([18], формулы (33), (34)) с учетом замены частоты

но-гравитационной волны при взаимодействии

Брента - Вяйсяля для несжимаемых течений на

сжимаемой магнитной инерционно-гравитационной

частоту Брента - Вяйсяля для сжимаемых тече-

волны

(87) и волны магнито-Россби

(69), на

ний, выполняются, соответственно, и найденные

рис.

— возникновение сжимаемой магнитной

1204

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

Рис.

15. Условие синхронизма для двух волн маг-

Рис. 17. Условие синхронизма для трех сжимаемых низ-

нито-Россби и сжимаемой магнитной инерционно-гра-

кочастотных волн магнито-Россби: 1 — ω = ω(kx); 2 —

витационной волны:

— ω

= ωmR₁(kx);

—

ω = ω(kx - kxc) + ω(kxc)

ω=ω_mig′

(kx - kxc ) + ωmR1 (kxc )

Рис. 18. Условие синхронизма для трех сжимаемых низ-

Рис. 16. Условие синхронизма для двух сжимаемых маг-

кочастотных волн магнито-Россби: 1 — ω = ω(ky); 2 —

нитных инерционно-гравитационных волн и сжимаемой

ω = ω(ky - kyc) + ω(kyc)

магнитострофической волны: 1 — ω = ωmig_β (ky); 2 —

ω = ωmig_β(ky - kyc) + ωmstrβ(kyc⁾

чивающее взаимодействие трех сжимаемых волн

магнито-Россби при k = (kx, 1, 1) (рис. 17), при

инерционно-гравитационой волны (87) при взаи-

k = (1,k_y,1) (рис. 18) и при k = (1,1,k_z) (рис. 19).

модействии двух сжимаемых волн магнито-Россби

(69), на рис.

— возникновение волны магни-

5.2. Слабонелинейные взаимодействия волн

то-Россби (69) при взаимодействии двух сжимаемых

в сжимаемой стратифицированной

магнитных инерционно-гравитационных волн (87),

вращающейся плазме. Амплитудные

на рис. 15 — возникновение волны магнито-Россби

уравнения и инкременты неустойчивостей

(69) при взаимодействии сжимаемой магнитной

инерционно-гравитационной волны (87) и волны

Для анализа слабонелинейных волновых взаи-

магнито-Россби (69), на рис. 16 — возникновение

модействий во вращающейся сжимаемой стратифи-

сжимаемой магнитной инерционно-гравитационной

цированной плазме воспользуемся асимптотическим

волны (90) при взаимодействии сжимаемой маг-

методом многомасштабных разложений. Для крат-

нитной инерционно-гравитационной волны (90) и

кости ограничимся схематическим описанием мето-

сжимаемой магнитострофической волны (92). Для

да и приведем лишь полученные амплитудные урав-

сжимаемых низкочастотных волн магнито-Россби

нения и коэффициенты взаимодействия волн. Де-

(93) выполняется условие синхронизма, обеспе-

тали метода многих масштабов в магнитогидроди-

1206

ЖЭТФ, том 158, вып. 6 (12), 2020

Волновые процессы во вращающихся сжимаемых течениях. . .

В системе уравнений во втором порядке мало-

сти по ε, полученной после представления решения

в виде (95), можно избавиться от резонансных сла-

гаемых. Запишем систему уравнений во втором по-

рядке малости по ε в следующем виде:

Aq₂ = -NL₁(q₀, q₁) - NL₂(q₁, q₁),

(97)

где A — линейный оператор системы (19)-(22), за-

висящий от q₀, T₀, X₀, Y₀, Z₀, а правая часть систе-

мы содержит резонансные слагаемые. Воспользуем-

ся условием совместности, а именно, свойством ор-

тогональности правой части системы (97) ядру ли-

нейного оператора. Для этого домножим систему

Рис. 19. Условие синхронизма для трех сжимаемых низ-

(97) слева и справа на собственный вектор z линей-

кочастотных волн магнито-Россби: 1 — ω = ω(kz); 2 —

ного оператора A. Последовательно выписывая сла-

ω = ω(kz - kzc) + ω(kzc)

гаемые правой части, пропорциональные exp(iϑ₁),

exp(iϑ₂) и exp(iϑ₃), получим следующую систему

намических течениях вращающейся плазмы можно

уравнений для амплитуд трех взаимодействующих

найти в работах [16, 23, 53].

волн, удовлетворяющих условию синхронизма (94):

В методе многомасштабных разложений реше-

s₁φ = f₁ψ^∗χ,

ние исследуемой системы уравнений представляет-

ся в виде асимптотически сходящегося ряда по ма-

s₂ψ = f₂φ^∗χ,

(98)

лому параметру ε, характеризующему слабую нели-

s₃χ = f₃φψ,

нейность:

где s_i — дифференциальный оператор по медлен-

q = q₀ + εq₁ + ε²q₂ + ...,

ным переменным, который имеет вид

где q₀ — исходное состояние равновесия, q₁ — ре-

s_i = r_i∂T1 + p_i∂X1 + q_i∂Y1 + w_i∂Z1 ,

(99)

шение линейной системы (19)-(22), а q₂ — слагае-

мое, описывающее эффекты квадратичной нелиней-

а коэффициенты f_i зависят только от начальных

ности. В таком представлении система во втором

условий и характеристик взаимодействующих волн.

порядке малости по ε содержит резонансные сла-

Отметим, что именно в выражениях для опе-

гаемые, нарушающие условия сходимости ряда. Ис-

раторов s_i и коэффициентов f_i состоит различие

ключение таких слагаемых осуществляется введени-

в амплитудных уравнениях (98) для всех типов

ем медленно меняющихся амплитуд и выполнением

взаимодействующих волн, найденных в предыду-

условия совместности. Представим решение иссле-

щих разделах. Приведем ниже полученные выраже-

дуемой системы в виде суммы трех взаимодействую-

ния для дифференциальных операторов и коэффи-

щих волн с медленно меняющимися амплитудами φ,

циентов взаимодействия волн в магнитной гидро-

ψ, χ:

динамике сжимаемой стратифицированной враща-

ющейся плазмы в неупругом приближении для каж-

q₁(T₁, X₁, Y₁, Z₁)×

дого из приближений силы Кориолиса.

× exp(iωT₀ - ik_xX₀ - ik_yY₀ - ik_zZ₀) =

5.2.1. Дифференциальные операторы и

= φa(k₁) exp(iϑ₁) + ψa(k₂) exp(iϑ₂) +

коэффициенты амплитудных уравнений для

+ χa(k₁) exp(iϑ₃) + c.c.,

(95)

трехволновых взаимодействий на стандартной и

нестандартной f -плоскостях

где взаимосвязь «медленных» переменных (с индек-

сом «1») и «быстрых» (с индексом «0») определена

Запишем полученные выражения для дифферен-

следующим образом:

циальных операторов sif и коэффициентов взаимо-

действия fif волн в магнитной гидродинамике стра-

∂_t = ∂T0 + ε∂T1 ,

∂_x = ∂X0 + ε∂X1,

тифицированной вращающейся плазмы в неупругом

(96)

∂_y = ∂Y0 + ε∂Y1,

∂_z = ∂Z0 + ε∂Z1.

приближении на f-плоскости. Коэффициент rif при

1207

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

производной по медленному времени T₁ в (99) в при-

κ2i

= iγ[kxm(a₁

a∗2

-a₄

a^∗

ближении стандартной f-плоскости имеет вид

∗

+ kzm(a₃

a∗2

-a₆

5_km

)] -

∑

− i[kyi (a²²

+a²⁴

+a²

6_lm

rif = zjaj +z4a8 + zjaj-1.

(100)

+k_x

(a∗1

a₂

-a∗4

5_kl

j=1

j=5

+ k_zl(a∗3

a₂

-a∗6

5_kl

)],

(106)

Выражение (100) совпадает с выражением, анало-

гичным полученному в работе [18] (формула (18)) с

различием в слагаемых, содержащих эффекты сжи-

κ3i

= iγ[kxm(a₁

a∗3

-a₄

a^∗

6_km

маемости, а именно в собственном векторе z и ком-

поненте a₈.

+ kym(a₂

a∗3

-a₅

a^∗

6_km

)] -

Коэффициент p_i

при производной по медленной

− i[kzi (a²³

+a²⁴

+a²

5_lm

координате X₁ в (99) в приближении стандартной

+k_x

(a∗1

a₃

-a^∗k

6_kl

f-плоскости имеет вид

+k_y

(a∗2

a₃

-a∗5

a₆

)],

(107)

pif = z₁ (a₇+By0 a₅+Bz0 a₆)-Bx0 (z₂a₅+z₃a₆ +

+ z₆a₂ + z₇a₃) + a1 (By0z₆ + Bz0z₇) + z₈a₁.

(101)

∗

κ4if = iγ[a₁

kxm + a2kl kym + a3kl kzm ]a

8_km

Коэффициент qif при производной по медленной

− i[a∗1

kxl + a∗2

kyl + a∗3

kzl ]a

8_kl

(108)

координате Y₁ в (99) в приближении стандартной

f-плоскости имеет вид

κ5if = ikyi (â₁₅ - â₂₄) + ikzi (â₁₆ - â₃₄),

(109)

κ6if = ikxi (â₂₄ - â₁₅) + ikzi(â₂₆ - â₃₅),

(110)

qif = z2 (a7+Bz0a6+Bx0a4)-By0 (z1a4+z3a6 +

+ z₅a₁ + z₇a₃) + a2 (Bx0z₅ + Bz0z₇) + z₈a₂.

(102)

κ7if = ikxi (â₃₄ - â₁₆) + ikyi(â₃₅ - â₂₆).

(111)

В выражениях (105)-(111) использованы обозна-

Коэффициент wif при производной по медлен-

чения

ной координате Z₁ в (99) в приближении стандарт-

ной f-плоскости имеет вид

a2n

=ankla^∗n

ân1n2 = an1kl aⁿ2km+an1km^a

n2kl

wif = z₃ (a₇+Bx0 a₄+By0a₅)-Bz0 (z₁a₄ + z₂a₅ +

Выражения (105)-(108) аналогичны полученным

+ z₅a₁ + z₆a₂) + a3 (Bx0z₅ + By0z₆) + z₈a₃.

(103)

в работе [18] (формулы (23)-(29)) с отличием в соб-

ственном векторе z и компоненте a₈.

Здесь и далее a = a(k_i) — собственный волновой

Полученные выражения для коэффициентов

вектор, в котором a₁ ≡ vx1, a₂ ≡ vy1 , a₃ ≡ vz1 , a₄ ≡

дифференциальных операторов s^′ и коэффици-_i

≡Bx1, a₅ ≡By1, a₆ ≡Bz1,a₇ ≡ ω₁, a₈ ≡θ₁.

ентов взаимодействия f^′ волн в приближении_i

Коэффициенты fif , зависящие от начальных

нестандартной f-плоскости имеют такой же вид,

условий и характеристик взаимодействующих волн

как и операторы sif (100)-(103) и коэффициенты

на f-плоскости, запишем в виде суммы:

fif (105)-(111) на стандартной f-плоскости и отли-

∑

чаются только собственным вектором z линейного

fif = zsκsif ,

(104)

оператора системы (43)-(46).

s=1

Для всех найденных типов взаимодействий су-

ществует следующее соотношение между индек-

где κ8if = 0. Для слагаемых κ_si

в сумме (104) в слу-

сами в полученных коэффициентах: индексы «i»,

чае волн на f-плоскости получаем следующие выра-

«m», «l» соответствуют одной из трех волн, удовле-

жения:

творяющих условию синхронизма. Следовательно,

при взаимодействии трех волн с частотами ω₁(k₁),

κ1if = iγ[kym (a₂

a∗1

-a5kla^∗

4_km

ω₂(k₂) и ω₃(k₃) индексы i, m, l = 1 будут соответ-

+ kzm(a₃

a∗1

-a6kla^∗

4_km

)] -

ствовать первой волне, индексы i, m, l = 2 — вто-

− i[kxi (a²¹

+a²⁵

+a²

6_lm

рой, а индексы i, m, l = 3 — третьей. Индексы «m»,

«l», параметр γ и комплексное сопряжение вектора

+ kyl(a∗2

a1kl - a∗5

4_kl

a связаны с индексом «i» следующим образом: если

+ kzl(a∗3

a1kl - a∗6

a4kl)],

(105)

i = 1, то l = 3, m = 2, γ = 1; если i = 2, то l = 3,

1208

ЖЭТФ, том 158, вып. 6 (12), 2020

Волновые процессы во вращающихся сжимаемых течениях. . .

m = 1, γ = 1; если i = 3, то l = 1, m = 2, γ = -1,

дартной и нестандартной f-плоскостей. Эффекты

а комплексно-сопряженные компоненты вектора a

сжимаемости представлены в полученных выраже-

заменяются на действительные (a^∗n → a_n).

ниях слагаемым с потенциальной температурой a₈,

Таким образом, для волн на f-плоскости нами

а также собственным вектором z системы магнито-

выявлены взаимодействие волны Альфвена (ω₁ =

гидродинамических уравнений вращающейся сжи-

= ω_A(k₁)) и двух сжимаемых магнитогравитацион-

маемой астрофизической плазмы в неупругом при-

ных волн (ω₂ = ω_mgr(k₂), ω₃ = ω_mgr(k₃)); взаимо-

ближении.

действие двух вертикальных магнитных волн с ча-

стотами ω₁ = ωz1(kz1 ), ω₂ = ωz1 (kz2 ) и вертикальной

5.2.2. Дифференциальные операторы и

магнитной волны с частотой ω₃ = ωz2(kz3); взаимо-

коэффициенты амплитудных уравнений для

действие трех вертикальных магнитных волн с ча-

трехволновых взаимодействий на стандартной и

стотами ω₁ = ωz2(kz1 ), ω₂ = ωz2 (kz2 ), ω₃ = ωz2 (kz3 );

нестандартной β-плоскостях

возникновение сжимаемой магнитной инерцион-

Запишем теперь полученные выражения для

но-гравитационной волны (ω₃

= ωmigB

(k₃)) при

дифференциальных операторов s_i

и коэффициен-

взаимодействии сжимаемой

магнитострофичес-

тов взаимодействия fiβ волн в магнитной гидроди-

кой (ω₁

= ωmstrBz(k₁)) и сжимаемой магнитной

намике стратифицированной вращающейся плазмы

инерционно-гравитационной волн (ω₂ = ωmigB

(k₂))

в неупругом приближении на β-плоскости. Коэффи-

или при взаимодействии двух сжимаемых маг-

циент riβ при производной по медленному времени

нитострофических волн (ω1 = ωmstrBz(k1), ω2 =

T₁ в (99) в приближении стандартной β-плоскости

= ωmstrBz(k₂)); возникновение сжимаемой маг-

имеет вид

нитострофической волны (ω₃

= ωmstrBz(k₃))

при взаимодействии либо двух сжимаемых

∑

магнитных инерционно-гравитационных волн

ri_β = -ikyi z1a1+

z_ja_j+z₄a₈+

z_jaj-1,

(112)

(ω₁

= ωmigBz(k₁), ω₂

= ωmigBz(k₂)), либо

j=2

j=5

двух сжимаемых магнитострофических волн

(ω1 = ωmstrBz(k1), ω2 = ωmstrBz(k2)), либо сжи-

аналогичный полученному в работе [18] (формула

маемой магнитной инерционно-гравитационной

(52)) с отличием в собственном векторе z и компо-

(ω₁

= ωmigBz(k₁)) и сжимаемой магнитострофи-

ненте a₈.

ческой волн (ω₂

= ωmstrBz(k₂)). Качественный

Коэффициент piβ при производной по медленной

анализ дисперсионных соотношений на нестан-

координате X₁ в (99) в приближении стандартной

дартной f-плоскости показывает возникновение

β-плоскости имеет вид

сжимаемой магнитной инерционно-гравитационной

волны (ω₃

= ωmigx1(kx3)) при взаимодействии

piβ = -iz₁kyi (a₇ + By0 a₅ + Bz0 a₆) -

волны Альфвена (ω₁ = ωAx(kx1)) и сжимаемой маг-

- Bx0 (z₂a₅ + z₃a₆ + z₆a₂ + z₇a₃) +

нитной инерционно-гравитационной волны (ω₂

+ a1 (By0z₆ + Bz0z₇) + z₈a₁.

(113)

= ωmigx1(kx2)) или при взаимодействии двух сжима-

емых магнитных инерционно-гравитационных волн

Коэффициент qiβ при производной по медленной

(ω₁ = ωmigx

(kx1 ), ω₂ = ωmigx1 (kx2 )); возникновение

координате Y₁ в (99) в приближении стандартной

волны Альфвена (ω₃ = ωAx(kx3)) при взаимодей-

β-плоскости имеет вид

ствии двух сжимаемых магнитных инерцион-

но-гравитационных волн (ω₁

= ωmigx1(kx1),

ω₂

= ωmigx1(kx2)); возникновение сжимаемой

qiβ = iz₁ [ωa₁ + if_va₂ - kxi a₇ -

магнитной инерционно-гравитационной волны

- By0(kxia₅ + 2kyia₄)+

(ω₃ = ωmigy (ky3 )) при взаимодействии двух сжима-

+Bz0(kzi a₄ - kxi a₆)] +

емых магнитострофических волн (ω₁ = ωmstry (ky1 ),

+ z2 (a₇ + Bz0a₆ + Bx0a₄) -

ω₂

= ωmstry(ky2)) или при взаимодействии сжи-

маемой магнитострофической (ω₁ = ωmstry (ky1)) и

- By0(z₃a₆ + z₅a₁ + z₇a₃)+

сжимаемой магнитной инерционно-гравитационной

+ a2 (Bx0z₅ + Bz0z₇) + z₈a₂.

(114)

(ω₂ = ωmigy (ky2 )) волн при f_H ≫ 1.

Таким образом, получены дифференциальные

Коэффициент wiβ при производной по медлен-

операторы и коэффициенты трехволновых взаимо-

ной координате Z₁ в (99) в приближении стандарт-

действий для сжимаемых волн в приближении стан-

ной β-плоскости имеет вид

1209

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

w_i

= z3 (a₇ + Bx0a₄ + By0a₅) -

«l», параметр γ и комплексное сопряжение вектора

a связаны с индексом «i» следующим образом: если

- Bz0 (iz₁kyia₄ + z₂a₅ + z₅a₁ + z₆a₂) +

i = 1, то l = 3, m = 2, γ = 1; если i = 2, то l = 3,

+ a3 (Bx0z₅ + By0z₆) + z₈a₃.

(115)

m = 1, γ = 1; если i = 3, то l = 1, m = 2, γ = -1,

Здесь и далее ω = ω(k_i).

а комплексно-сопряженные компоненты вектора a

Коэффициенты f_i

, зависящие от начальных

заменяются на действительные (a^∗n → a_n).

условий и характеристик взаимодействующих волн

Для волн на β-плоскости нами выявлены возник-

на β-плоскости, представим в виде суммы:

новение волны магнито-Россби (ω₃ = ωmR1(k₃)) при

взаимодействии двух волн магнито-Россби (ω₁

∑

= ωmR1(k₁), ω₂ = ωmR1(k₂)) или при взаимодейст-

f_i

= z_sκ_si

(116)

вии сжимаемой магнитогравитационной волны

s=1

(ω₁

= ω_mgr(k₁)) и волны магнито-Россби (ω₂

где κ8i

= 0.

= ωmR1(k₂)); возникновение сжимаемой магнито-

Слагаемое κ1i

имеет вид

гравитационной волны (ω₃ = ω_mgr(k₃)) при взаи-

модействии волны магнито-Россби (ω₁ = ωmR1(k₁))

κ1iβ = γkyi [kym (a₂

a∗1

-a5kla^∗

4_km

и сжимаемой магнитогравитационной волны

+ kzm(a₃

a∗1

-a6kla^∗

4_km

)] -

(ω₂

= ω_mgr(k₂)); возникновение сжимаемой

низкочастотной волны магнито-Россби (ω₃) при

− kyi[kxi(a²¹

+a²⁵

+a²

6_lm

взаимодействии двух сжимаемых низкочастотных

+ kyl(a∗2

a1kl - a∗5

4_kl

волн магнито-Россби (ω₁, ω₂).

+ kzl(a∗3

a1kl - a∗6

4_kl

)].

(117)

Для волн на нестандартной β-плоскости нами

выявлены возникновение сжимаемой магнит-

Остальные слагаемые в сумме (116) отличаются от

ной инерционно-гравитационной волны (ω₃

слагаемых в сумме (104) только собственным векто-

= ωmig1(k₃)) при взаимодействии либо волны

ром z линейного оператора системы (61)-(66).

магнито-Россби (ω₁

= ωmR1(k₁)) и сжимаемой

Отметим, что выражения для коэффициентов

магнитной инерционно-гравитационной волны

r^′i

, p^′i

, w^′i

дифференциальных операторов s^′ и_i

(ω2 = ωmig1(k2)), либо двух волн магнито-Россби

коэффициентов взаимодействия f^′ волн в прибли-_i

(ω₁ = ωmR1(k₁), ω₂ = ωmR1(k₂)), либо двух сжи-

жении нестандартной β-плоскости имеют такой же

маемых магнитных инерционно-гравитационных

вид, как и коэффициенты riβ (112), p_i

(113), wiβ

волн (ω₁

= ωmig1(k₁), ω₂

= ωmig1(k₂)); возник-

(115) дифференциальных операторов siβ и коэффи-

новение волны магнито-Россби (ω₃

= ωmR1(k₃))

циенты fiβ (116) на стандартной β-плоскости и от-

при взаимодействии либо двух сжимаемых маг-

личаются только собственным вектором z линейного

нитных инерционно-гравитационных волн (ω₁

оператора системы (77)-(82). Коэффициент q^′ при_i

= ωmig1(k₁), ω₂

= ωmig1(k₂)), либо сжимаемой

медленной переменной Y₁ в (99) на нестандартной

магнитной инерционно-гравитационной волны

β-плоскости имеет вид

(ω1 = ωmig1(k1)) и волны магнито-Россби (ω2 =

= ωmR1(k₂)), либо двух волн магнито-Россби

qiβ = iz₁ [ωa₁ - if_Ha₃ + if_va₂ - kxi a₇ -

(ω1 = ωmR1(k1), ω2 = ωmR1(k2)); возникновение

- By0(kxia₅ + 2kyia₄) + Bz0(kzia₄ - kxia₆)] +

сжимаемой магнитной инерционно-гравитационной

+ z2 (a₇ + Bz0a₆ + Bx0a₄)-

волны (ω₃ = ω_mig

(k₃)) при взаимодействии сжи-

- By0(z₃a₆ + z₅a₁ + z₇a₃)+

маемой магнитной инерционно-гравитационной

волны (ω₁ = ω_mig

(k₁)) и сжимаемой магнитостро-

+ a2 (Bx0z₅ + Bz0z₇) + z₈a₂.

(118)

фической волны (ω₂ = ω_mstr

(k₂)); возникновение

Для всех найденных типов взаимодействий су-

сжимаемой низкочастотной волны магнито-Россби

ществует следующее соотношение между индекса-

(ω₃) при взаимодействии двух сжимаемых низкочас-

ми в полученных коэффициентах: индексы «i», «m»,

тотных волн магнито-Россби (ω₁, ω₂).

«l» соответствуют одной из трех волн, удовлет-

Таким образом, получены дифференциальные

воряющих условию синхронизма. Таким образом,

операторы и коэффициенты трехволновых взаимо-

при взаимодействии трех волн с частотами ω₁(k₁),

действий для сжимаемых волн в приближении стан-

ω₂(k₂) и ω₃(k₃) индексы i, m, l = 1 будут соответ-

дартной и нестандартной β-плоскостей. Эффекты

ствовать первой волне, индексы i, m, l = 2 — вто-

сжимаемости представлены в полученных выраже-

рой, а индексы i, m, l = 3 — третьей. Индексы «m»,

ниях слагаемым с потенциальной температурой a₈,

1210

ЖЭТФ, том 158, вып. 6 (12), 2020

Волновые процессы во вращающихся сжимаемых течениях. . .

а также собственным вектором z системы магнито-

волн, либо двух сжимаемых магнитострофических

гидродинамических уравнений вращающейся сжи-

волн (ω₂ = ωmstrB

(k₂), ω₃ = ωmstrB

(k₃)); распад

маемой астрофизической плазмы в неупругом при-

или усиление сжимаемой магнитной инерцион-

ближении.

но-гравитационной волны (ω₁

= ωmigB

(k₁)) при

участии либо сжимаемой магнитной инерцион-

5.2.3. Параметрические неустойчивости во

но-гравитационной (ω₂ = ωmigB

(k₂)) и сжимаемой

вращающейся сжимаемой стратифицированной

магнитострофической (ω₃

= ωmstrB

(k₃)) волн,

плазме в неупругом приближении

либо двух сжимаемых магнитострофических волн

Система уравнений (98) является универсаль-

(ω₂ = ωmstrB

(k₂), ω₃ = ωmstrB

(k₃)).

ной для описания параметрических неустойчиво-

Для волн на нестандартной f-плоскости име-

стей трехволновых взаимодействий. Различия, свя-

ют место распад или усиление сжимаемой маг-

занные с выбором приближения силы Кориоли-

нитной инерционно-гравитационной волны (ω₁

са, содержатся только в коэффициентах взаимодей-

= ωmigx

(kx1 )) при участии либо двух сжимае-

ствия и дифференциальных операторах, приведен-

мых магнитных инерционно-гравитационных волн

ных выше в разд. 5.2.1, 5.2.2. Поэтому в магнито-

(ω₂

= ωmigx

(kx2 ), ω₃

= ωmigx

(kx3 )), либо сжи-

гидродинамических течениях стратифицированной

маемой магнитной инерционно-гравитационной вол-

вращающейся плазмы в неупругом приближении ре-

ны (ω₂ = ωmigx

(kx2 )) и волны Альфвена (ω3 =

ализуются два типа параметрических неустойчивос-

= ωAx(kx3)); распад или усиление волны Альфве-

тей [16,53]. Первый тип — распад волны с частотой

на (ω₁ = ωAx(kx1 )) при участии двух сжимаемых

ω₁ на две волны c частотами ω₂ и ω₃ и инкрементом

магнитных инерционно-гравитационных волн (ω₂ =

неустойчивости

√

= ωmigx1(kx2), ω₃ = ωmigx

(kx3 )); распад или усиле-

Γ=

|f₂f₃|/|r₂r₃||φ₀| > 0

ние сжимаемой магнитострофической волны (ω₁ =

)) при участии либо сжимаемой маг-

= ωmstry(ky1

— реализуется, когда в начальный момент времени

нитострофической (ω₂

= ωmstry(ky2)) и сжимае-

амплитуда одной из волн много больше амплитуд

мой магнитной инерционно-гравитационной (ω₃ =

двух других (φ = φ₀ ≫ ψ, χ). Второй тип парамет-

= ωmigy(ky3)) волн, либо двух сжимаемых маг-

рической неустойчивости — усиление волны с час-

нитных инерционно-гравитационных волн (ω₂

тотой ω₁ двумя волнами c частотами ω₂ и ω₃ и ко-

= ωmigy(ky2), ω₃ = ωmigy(ky3)) при f_H ≫ 1.

эффициентом усиления

Для волн на β-плоскости имеют место рас-

пад или усиление волны магнито-Россби (ω₁

Γ = (|f₁|/|r₁|)|ψ₀χ₀| > 0

= ωmR1(k₁)) при участии либо двух волн магни-

— реализуется, когда в начальный момент времени

то-Россби (ω₂

= ωmR1(k₂), ω₃

= ωmR1(k₃)), ли-

амплитуда одной из волн много меньше амплитуд

бо двух сжимаемых магнитогравитационных волн

двух других (φ ≪ ψ = ψ₀, χ = χ₀).

(ω₂

= ω_mgr(k₂), ω₃

= ω_mgr(k₃)); распад или

Таким образом, суммируя, для волн на f-плос-

усиление сжимаемой магнитогравитационной вол-

кости имеют место распад или усиление волны

ны (ω₁ = ω_mgr(k₁)) при участии двух волн магни-

Альфвена (ω₁ = ω_A(k₁)) при участии двух сжимае-

то-Россби (ω2 = ωmR1(k2), ω3 = ωmR1(k3)); рас-

мых магнитогравитационных волн (ω₂ = ω_mgr(k₂),

пад или усиление сжимаемой низкочастотной волны

ω₃ = ω_mgr(k₃)); распад или усиление вертикальной

магнито-Россби (ω₁) при участии двух сжимаемых

магнитной волны с частотой ω₁

= ωz1(kz1) при

низкочастотных волн магнито-Россби (ω₂,ω₃).

участии двух вертикальных магнитных волн с

Для волн на нестандартной β-плоскости име-

частотами ω₂ = ωz1(kz2 ) и ω₃ = ωz2(kz3 ); распад

ют место распад или усиление волны магни-

или усиление вертикальной магнитной волны с

то-Россби (ω₁

= ωmR1(k₁)) при участии либо

частотой ω1 = ωz2(kz1) при участии двух верти-

двух волн магнито-Россби (ω₂

= ωmR1(k₂),

кальных магнитных волн с частотами ω₂ = ωz2(kz2)

ω₃

= ωmR1(k₃)), либо двух сжимаемых магнит-

и ω₃ = ωz2(kz3); распад или усиление сжимаемой

ных инерционно-гравитационных волн (ω₂

магнитострофической волны (ω₁

= ωmstrBz(k₁))

= ωmig1(k₂), ω₃

= ωmig1(k₃)), либо волны

при участии либо двух сжимаемых магнитных

магнито-Россби (ω₂

= ωmR1(k₂)) и сжимаемой

инерционно-гравитационных волн (ω₂ = ωmigB

(k₂),

магнитной инерционно-гравитационной волны

ω₃ = ωmigB

(k₃)), либо сжимаемой магнитострофи-

(ω₃

= ωmig1(k₃)); распад или усиление сжимае-

ческой (ω₂ = ωmstrB

(k₂)) и сжимаемой магнитной

мой магнитной инерционно-гравитационной волны

инерционно-гравитационной (ω₃

= ωmigBz(k3))

(ω₁

= ωmig1(k₁)) при участии либо двух сжи-

1211

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

маемых магнитных инерционно-гравитационных

мерные сжимаемые магнитогравитационные волны

волн (ω₂ = ωmig1(k₂), ω₃ = ωmig1 (k₃)), либо сжи-

(39); вертикальные магнитные волны, аналогичные

маемой магнитной инерционно-гравитационной

найденным в работе [18].

волны (ω2 = ωmig1(k2)) и волны магнито-Россби

На нестандартной f-плоскости найдены диспер-

(ω3 = ωmR1(k3)), либо двух волн магнито-Россби

сионные соотношения, описывающие следующие ти-

(ω₂

= ωmR1(k₂), ω₃

= ωmR1(k₃)); распад или

пы волн: одномерные волны Альфвена (49); одно-

усиление сжимаемой магнитной инерционно-гра-

мерные сжимаемые магнитные инерционно-гравита-

витационной волны (ω₁ = ω_mig

(k₁)) при участии

ционные волны с новыми законами дисперсии (50),

сжимаемой магнитной инерционно-гравитаци-

(53), которые при равенстве нулю горизонтальной

онной волны (ω₂

= ω_mig

(k₂)) и сжимаемой

компоненты вектора Кориолиса переходят в одно-

магнитострофической волны (ω₃

= ω_mstr

(k₃));

мерные сжимаемые магнитогравитационные волны

распад или усиление сжимаемой низкочастотной

(51), (54), а в отсутствие магнитного поля переходят

волны магнито-Россби (ω₃) при участии двух

в сжимаемые инерционно-гравитационные волны с

сжимаемых низкочастотных волн магнито-Россби

новыми законами дисперсии (52), (55); одномерные

(ω₁, ω₂).

сжимаемые магнитные инерционно-гравитационные

Таким образом, получены инкременты неустой-

(57) и магнитострофические волны (59), аналогич-

чивости двух типов (распад и усиление), имеющей

ные найденным в работе [18], с точностью до слага-

место в системе для амплитуд трех взаимодейству-

емых с частотой Брента - Вяйсяля для сжимаемых

ющих волн в неупругом приближении. Эффекты

течений. Эффекты сжимаемости в найденных типах

сжимаемости в найденных инкрементах неустойчи-

волн представлены слагаемыми с частотой Брен-

вости неявно содержатся в коэффициентах взаимо-

та - Вяйсяля N2θ для сжимаемых стратифицирован-

действия f_i и коэффициентах r_i при производной по

ных течений, зависящей как от исходного профиля

медленному времени, которые включают в себя сла-

плотности, так и от исходного профиля давления.

гаемые с потенциальной температурой a₈, а также

Для сферических течений в приближениях стан-

собственный вектор z системы магнитогидродина-

дартной и нестандартной β-плоскостей также раз-

мических уравнений вращающейся сжимаемой аст-

вита теория линейных волн и получены диспер-

рофизической плазмы в неупругом приближении.

сионные уравнения. В приближении стандартной

β-плоскости получены дисперсионные соотношения,

6. ЗАКЛЮЧЕНИЕ

описывающие следующие типы волн: двумерные

сжимаемые магнитогравитационные волны; волны

В работе получена система магнитогидроди-

магнито-Россби (69), которые в отсутствие магнит-

намических уравнений сжимаемой вращающейся

ного поля переходят в стандартные гидродинами-

плазмы с устойчивой стратификацией в поле силы

ческие волны Россби (70); волны магнито-Россби

тяжести в неупругом приближении. Исследованы

(71), не имеющие аналога в динамике нейтральной

магнитогидродинамические течения в слое сжимае-

жидкости; одномерные волны Альфвена (73); низ-

мой устойчиво-стратифицированной вращающейся

кочастотные сжимаемые трехмерные волны магни-

плазмы с линейным профилем энтропии в неупру-

то-Россби (75).

гом приближении. Развита теория линейных волн в

В приближении нестандартной β-плоскости по-

сжимаемых течениях на стандартной и нестандарт-

лучены дисперсионные соотношения, описывающие

ной f-плоскостях, получены дисперсионные уравне-

следующие типы волн: волны магнито-Россби (85),

ния и найдены решения, описывающие различные

(86), аналогичные волнам на β-плоскости; дву-

типы волн.

мерные сжимаемые магнитные инерционно-грави-

В приближении f-плоскости найдены диспер-

тационные волны с новыми законами дисперсии

сионные соотношения, описывающие следующие

(87), (88), аналогичные волнам на нестандартной

типы волн: сжимаемые трехмерные магнитные

f-плоскости; одномерные сжимаемые магнитные

инерционно-гравитационные волны (34), которые в

инерционно-гравитационные (90) и магнитострофи-

отсутствие магнитного поля переходят в сжимаемые

ческие (92) волны с новыми законами дисперсии,

трехмерные инерционно-гравитационные волны в

включащими слагаемые с параметром β; низкоча-

нейтральной жидкости в неупругом приближении

стотные сжимаемые трехмерные волны магнито-

(35); трехмерные магнитострофические волны (36),

Россби (93). Эффекты сжимаемости в найденных

не имеющие аналога в гидродинамике нейтральной

типах волн представлены слагаемыми с частотой

жидкости; двумерные волны Альфвена (38); дву-

Брента - Вяйсяля N2θ для сжимаемых стратифици-

1212

ЖЭТФ, том 158, вып. 6 (12), 2020

Волновые процессы во вращающихся сжимаемых течениях. . .

рованных течений, зависящей как от исходного про-

фическая волна с частотой ω_mstr

, три сжимаемые

филя плотности, так и от исходного профиля дав-

низкочастотные волны магнито-Россби.

ления.

С использованием метода многомасштабных

В рамках магнитогидродинамических уравне-

разложений получена универсальная система ам-

ний сжимаемой вращающейся стратифицированной

плитудных уравнений для взаимодействующих

плазмы в неупругом приближении для каждого из

волн. В каждом из четырех различных приближе-

четырех различных приближений силы Кориоли-

ний силы Кориолиса выписаны дифференциальные

са развита нелинейная теория волновых процессов.

операторы и коэффициенты в амплитудных урав-

Качественный анализ дисперсионных кривых всех

нениях и для всех найденных типов трехволновых

найденных типов волн выявил существование сле-

взаимодействий показано различие в них. Также

дующих видов трехволновых взаимодействий, удов-

в каждом из перечисленных случаев найдены

летворяющих условию синхронизма. В приближе-

инкременты двух типов неустойчивостей, имеющих

нии стандартной f-плоскости могут взаимодейство-

место в системе, — распада и усиления. Эффекты

вать три вертикальные магнитные волны с час-

сжимаемости в найденных коэффициентах вза-

тотой ωz2 , две вертикальные магнитные волны с

имодействия, дифференциальных операторах и

частотой ωz1 и вертикальная магнитная волна с

инкрементах содержатся в слагаемых с потенци-

частотой ωz2 , две сжимаемые магнитогравитацион-

альной температурой (энтропией) и в собственном

ные волны и волна Альфвена, сжимаемая магнит-

векторе системы магнитогидродинамических урав-

ная инерционно-гравитационная волна с частотой

нений вращающейся сжимаемой астрофизической

и две сжимаемые магнитострофические вол-

плазмы в неупругом приближении.

migBz

ны с частотой ω

, сжимаемая магнитостро-

mstrBz

фическая волна с частотой ω

и две сжимае-

Финансирование. Работа поддержана Фондом

mstrBz

мые магнитные инерционно-гравитационные волны

развития теоретической физики и математики «Ба-

с частотой ω

, три сжимаемые магнитострофи-

зис» и Российским фондом фундаментальных ис-

migBz

ческие волны с частотой ω

следований (грант № 19-02-00016).

mstrBz

В приближении нестандартной f-плоскости

могут взаимодействовать две сжимаемые маг-

ЛИТЕРАТУРА

нитные инерционно-гравитационные волны с

1. M. S. Miesch and P. A. Gilman, Solar Phys. 220, 287

частотой ω

и волна Альфвена, три сжимаемые

migx₁

(2004).

магнитные инерционно-гравитационные волны

с частотой ω

, сжимаемая магнитная инер-

2. D. W. Hughes, R. Rosner, and N. O. Weiss, The Solar

migx₁

ционно-гравитационная волна с частотой ωmigy

Tachocline, Cambridge Univ. Press (2007).

и две сжимаемые магнитострофические волны

3. P. A. Gilman, Astrophys. J. Lett. 544, L79 (2000).

с частотой ωmstry , две сжимаемые магнитные

инерционно-гравитационные волны с частотой

4. M. Dikpati and P. A. Gilman, Astrophys. J. 551(1),

536 (2001).

ωmigy и сжимаемая магнитострофическая волна

с частотой ωmstry при f_H

≫ 1. В приближении

5. T. V. Zaqarashvili, R. Oliver, J. L. Ballester, and

стандартной β-плоскости могут взаимодействовать

B. M. Shergelashvili, Astron. Astrophys. 470, 815

две сжимаемые магнитогравитационные волны

(2007).

и волна Альфвена, три волны магнито-Россби,

6. T. V. Zaqarashvili, R. Oliver, J. L. Ballester et al.,

две сжимаемые магнитогравитационные волны и

Astron. Astropys. 532, A139 (2011).

волна магнито-Россби, две волны магнито-Россби

и сжимаемая магнитогравитационная волна, три

7. J. Philidet, C. Gissinger, F. Lignières, and L. Petitde-

сжимаемые низкочастотные волны магнито-Россби.

mange, Geophys. Astrophys. Fluid Dynam. 114, 336

В приближении нестандартной β-плоскости

(2020).

могут взаимодействовать две сжимаемые магнит-

8. J. M. Stone, J. F. Hawley, C. F. Gammie, and

ные инерционно-гравитационные волны с частотой

S. A. Balbus, Astrophys. J. 463, 656 (1996).

ω_mig′ и волна магнито-Россби, две волны магнито-

9. K. Batygin, S. Stanley, and D. J. Stevenson, Astro-

Россби и сжимаемая магнитная инерционно-

phys. J. 776, 53 (2013).

гравитационная волна с частотой ω_mig′ , две сжи-

маемые магнитные инерционно-гравитационные

10. V. G. A. Böning, H. Hu, and L. Gizon, Astron. Astro-

волны с частотой ωmigβ и сжимаемая магнитостро-

phys. 629, A26 (2019).

1213

М. А. Федотова, А. С. Петросян

ЖЭТФ, том 158, вып. 6 (12), 2020

11.

B. Loeptien, L. Gizon, A. C. Birch et al., Nature

32.

M. A. Calkins, K. Julien, and P. Marti, Proc. Roy.

Astron. 2, 568 (2018).

Soc. London A 471, 20140689 (2015).

12.

M. Dikpati, B. Belucz, P. A. Gilman, and S. W. McIn-

33.

S. Paolucci, Sandia Nat. Lab. Rep. SAND82-8277

tosh, Astrophys. J. 862, 159 (2018).

Livermore, CA, USA (1982).

34.

N. Botta, R. Klein, and A. Almgren, Summary Rep.

13.

S. W. McIntosh, W. J. Cramer, M. P. Marcano, and

No 55, Potsdam Inst. for Climate Impact Research

R. J. Leamon, Nature Astron. 1, 0086 (2017).

(1999).

14.

T. V. Zaqarashvili and E. Gurgenashvili, Front.

35.

R. Klein, N. Botta, T. Schneider et al., J. Eng. Math.

Astron. Space Sci. 6, 7 (2018).

39, 261 (2001).

15.

L. Gizon, D. Fournier, and M. Albekioni, https://

36.

S. I. Braginsky and P. H. Roberts, Geophys. Astro-

arxiv.org/abs/2008.02185v1.

phys. Fluid Dyn. 79, 1 (1995).

16.

Д. А. Климачков, А. С. Петросян, ЖЭТФ 152, 705

37.

G. A. Glatzmaier and P. H. Roberts, Physica D 97,

(2017).

81 (1996).

17.

M. A. Fedotova, D. A. Klimachkov, and A. S. Petro-

38.

P. Olson and U. R. Christensen, Earth and Planetary

syan, Plasma Phys. Rep. 46, 50 (2020).

Sci. Lett. 250, 561 (2006).

18.

М. А. Федотова, А. С. Петросян, ЖЭТФ 158, 374

39.

C. A. Jones, K. M. Kuzanyan, and R. H. Mitchell, J.

(2020).

Fluid Mech. 634, 291 (2009).

40.

P. A. Gilman and G. A. Glatzmaier, Astrophys. J.

19.

M. Dikpati, P. S. Cally, S. W. McIntosh et al., Sci.

Suppl. Ser. 45, 335 (1981).

Rep. 7, 14750 (2017).

41.

R. K. Yadav and J. Bloxham, PNAS https://doi.org/

20.

M. Dikpati and S. W. McIntosh, Space Weather 18,

10.1073/pnas.2000317117 (2020).

e2018SW002109 (2020).

42.

G. A. Glatzmaier, J. Comput. Phys. 55, 461 (1984).

21.

В. И. Петвиашвили, О. А. Похотелов, Уединенные

волны в плазме и атмосфере, Энергоатомиздат,

43.

S. R. Lantz and Y. Fan, Astrophys. J. Suppl.

Москва (1989).

Ser. 121, 247 (1999).

22.

О. Г. Онищенко, О. А. Похотелов, Н. М. Астафье-

44.

M. S. Miesch, J. R. Elliott, J. Toomre et al., Astro-

phys. J. 532, 593 (2000).

ва, УФН 178, 605 (2008).

45.

A. S. Brun, M. S. Miesch, and J. Toomre, Astrophys.

23.

D. A. Klimachkov and A. S. Petrosyan, Phys. Lett.

J. 614, 1073 (2004).

A 381, 106 (2017).

46.

B. P. Brown, M. K. Browning, A. S. Brun et al.,

24.

A. S. Petrosyan, D. A. Klimachkov, M. A. Fedotova,

Astrophys. J. 689, 1354 (2008).

and T. A. Zinyakov, Atmosphere 11, 314 (2020).

47.

B. P. Brown, M. S. Miesch, M. K. Browning et al.,

25.

G. K. Vallis, Atmospheric and Oceanic Fluid Dy-

Astrophys. J. 731, 69 (2011).

namics: Fundamentals and Large-Scale Circulation,

48.

P. K. Smolarkiewicz and P. Charbonneau, J. Comput.

Cambridge Univ. Press (2006).

Phys. 236, 608 (2013).

49.

J. Goldstein, R. H. D. Townsend, and E. G. Zweibel,

26.

B. P. Brown, G. M. Vasil, and E. G. Zweibel, Astro-

Astrophys. J. 881, 66 (2019).

phys. J. 756, 109 (2012).

50.

D. J. Raymond, Physics 589 — Geophysical Fluid

27.

A. S. Almgrenet, J. B. Bell, A. Nonaka, and M. Zin-

Dynamics. Wave Modes of a Resting Atmosphere.

gale, Comp. Sci. Eng. 11(2), 24 (2009).

Ch. 3: Sound, Inertia-Gravity Waves, and Lamb

Waves, Physics Internal Website, http://kestrel.

28.

G. K. Batchelor, Quart. J. Roy. Meteor. Soc. 79(340),

nmt.edu/raymond/classes/ph589/notes/ssmodes/

224 (1953).

ssmodes.pdf.

29.

J. G. Charney and Y. Ogura, J. Meteor. Soc. Jpn

51.

J. I. Yano, J. Fluid Mech. 810, 475 (2017).

Ser. II 38(6), 19a (1960).

52.

G . Falkovich,Fluid Mechanics: a Short Course for

30.

D. O. Gough, J. Atmosph. Sci. 26, 448 (1969).

Physicists, Cambridge Univ. Press (2011).

53.

Д. А. Климачков, А. С. Петросян, ЖЭТФ 149, 965

31.

P. R. Bannon, J. Atmosph. Sci. 53, 3618 (1996).

(2016).

1214