ЖУРНАЛ ОБЩЕЙ ХИМИИ, 2023, том 93, № 4, с. 644-653
К 300-летию со дня основания Санкт-Петербургского государственного университета
УДК 541.49;546.6
СТРУКТУРА И УСТОЙЧИВОСТЬ ВОДОРОДНЫХ
СОЕДИНЕНИЙ ЭЛЕМЕНТОВ 13/15 ГРУПП,
СТАБИЛИЗИРОВАННЫХ КИСЛОТАМИ И
ОСНОВАНИЯМИ ЛЬЮИСА
© 2023 г. А. В. Помогаева1, А. С. Лисовенко1, А. Ю. Тимошкин1,*
1 Санкт-Петербургский государственный университет, Университетская наб. 7-9, Санкт-Петербург, 199034 Россия
*e-mail: a.y.timoshkin@spbu.ru
Поступило в редакцию 21 марта 2023 г.
После доработки 27 марта 2023 г.
Принято к печати 28 марта 2023 г.
Квантово-химическим методом B3LYP-D3/def2-TZVP рассчитаны структурные и термодинамические
характеристики донорно-акцепторных комплексов LA·E′H2EH2·LB (E = B, Al, Ga; E’ = P, As, Sb; LB = SMe2,
NMe3); LA - кислоты Льюиса на основе элементов 13 группы ER3 (E = B, Al, Ga; R = H, Me, F, Cl, Br, I, C6F5) и
карбонилы переходных металлов Fe(CO)4, M(CO)5, (M = Cr, Mo, W), CpMn(CO)2. Показано, что отрыв
основания Льюиса менее эндотермичен, чем кислоты Льюиса. Выявлены ряды изменения устойчивости
комплексов в зависимости от природы элементов 13 и 15 групп и кислоты Льюиса. Наибольший стаби-
лизирующий эффект оказывает W(CO)5.
Ключевые слова: водородные соединения элементов 13/15 групп, кислоты Льюиса, основания Льюиса,
донорно-акцепторная связь, квантово-химические расчеты
DOI: 10.31857/S0044460X23040170, EDN: AWMBFJ
Валентно-изоэлектронные аналоги этилена на
иса (LB) [3]. Действительно, разработаны мето-
основе элементов 13-15 групп являются перспек-
дики, позволяющие синтезировать донорно-ста-
тивными прекурсорами для синтеза материалов
билизированный фосфанилборан PH2BH2·NMe3
для микроэлектроники и функциональных поли-
в заметных количествах (порядка 1 г) [4], что
меров [1]. Ввиду того, что мономерные водород-
позволило изучить процесс его термического раз-
ные соединения E‘H2EH2, где E и E′ элементы 13
ложения [5]. Известны также тяжелые аналоги
и 15 групп, отличаются низкой устойчивостью по
фосфанилборана E′H2EH2·LB, для стабилизации
отношению к процессам олигомеризации, актив-
которых используются более сильные основания
но разрабатываются экспериментальные подходы,
Льюиса, такие как N-гетероциклические карбены
позволяющие стабилизировать такие соединения
[6]. Напротив, стабилизация E′H2EH2 исключи-
за счет донорно-акцепторного взаимодействия с
тельно за счет комплексообразования с кислотой
кислотами и основаниями Льюиса [2].
Льюиса (LA) на настоящий момент еще не реа-
Результаты квантово-химических расчетов по-
лизована на практике. Как показали квантово-хи-
казывают принципиальную возможность стабили-
мические расчеты комплексов LA·E′H2EH2 [7], в
зации неорганических аналогов этилена E′H2EH2
таких соединениях проявляются дополнительные
за счет взаимодействия только с основанием Лью-
взаимодействия атомов водорода или атомов эле-
644
СТРУКТУР
А И УСТОЙЧИВОСТЬ ВОДОРОДНЫХ СОЕДИНЕНИЙ
645
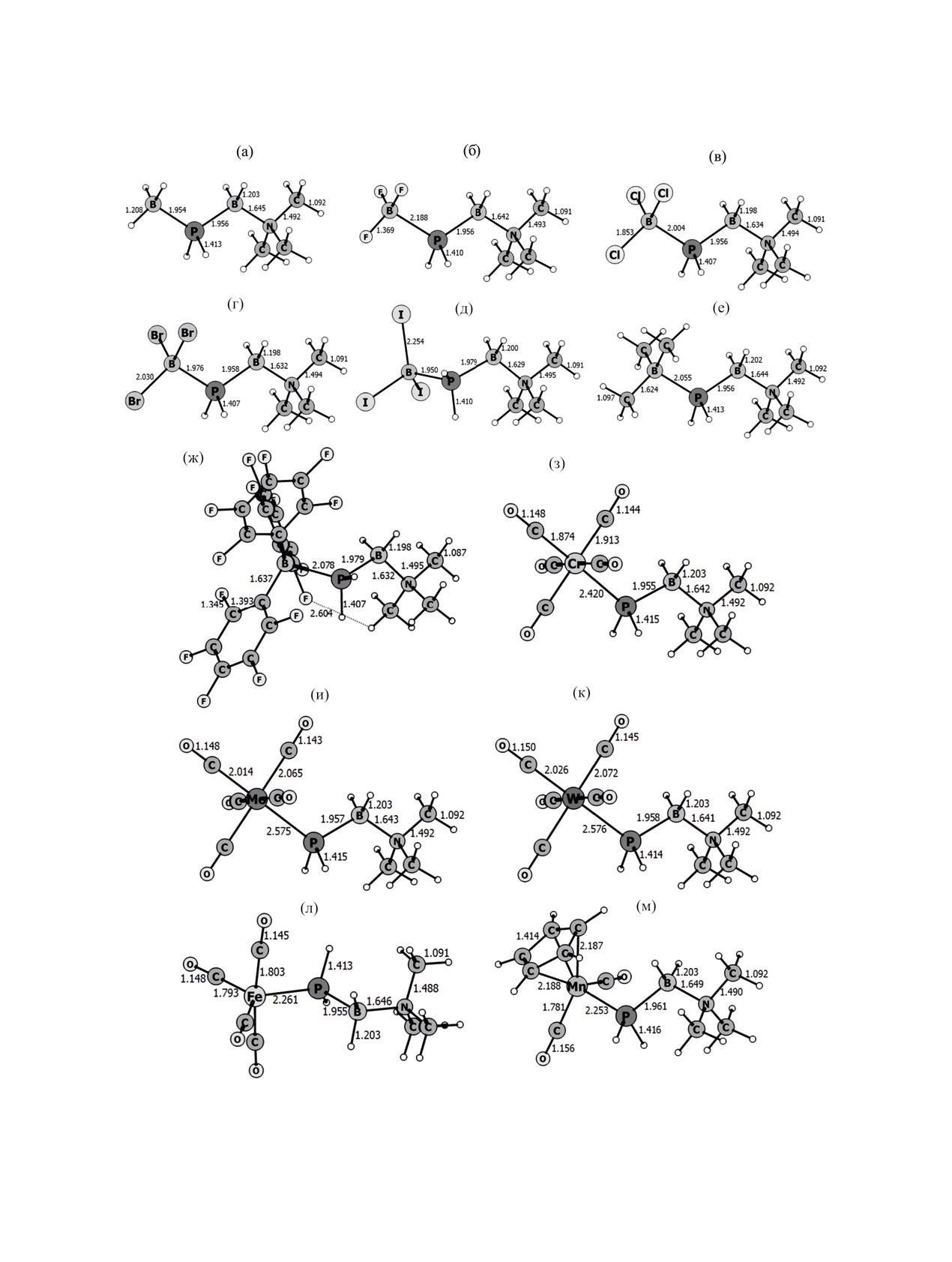
Рис. 1. Оптимизированные геометрии комплексов LA·PH2BH2·NMe3. Межъядерные расстояния даны в Å. Уровень теории
B3LYP-D3/def2-TZVP.
ЖУРНАЛ ОБЩЕЙ ХИМИИ том 93 № 4 2023
646
ПОМОГАЕВА и др.
Таблица 1. Свободные энергии Гиббса Δ(1)G°298 (кДж/моль) для процесса газофазной диссоциации комплекса
LA·E′H2EH2·NMe3 с отрывом кислоты Льюиса
E′E
LA
PB
AsB
SbB
PAl
AsAl
SbAl
PGa
AsGa
SbGa
BMe3
-33.9
-47.7
-a
-44.9
-29.8
-30.7
-44.3
-28.6
-30.1
BH3
73.7
46.4
25.7
58.8
35.4
18.1
59.2
34.2
16.3
BF3
-6.5
-9.4
-13.5
-16.3
-10.5
-13.3
-16.9
-14.1
-15.0
BCl3
22.4
-9.4
-34.0
27.4
1.9
-27.5
23.5
-3.1
-33.5
BBr3
41.9
34.3
1.7
50.8
23.3
-6.8
46.9
18.2
-12.7
BI3
64.9
48.5
17.6
65.9
37.5
8.3
62.0
32.5
2.2
B(C6F5)3
41.6
21.1
-19.9
35.0
15.5
-13.6
34.3
12.3
-14.9
AlMe3
15.1
-5.3
-9.7
-3.2
-11.0
-15.9
6.2
-2.5
-17.0
AlH3
49.3
36.8
21.1
39.8
29.0
15.3
38.8
27.1
12.8
AlF3
90.7
75.7
54.4
79.5
65.5
45.8
78.4
64.8
43.6
AlCl3
85.5
70.4
48.3
93.0
78.6
53.3
88.6
72.7
48.0
AlBr3
88.4
74.6
50.9
94.6
80.5
56.2
90.6
75.5
51.5
AlI3
86.5
74.6
48.8
90.0
76.6
54.3
85.9
71.7
48.8
Al(C6F5)3
101.1
86.4
58.4
90.7
78.0
51.0
89.7
75.4
52.5
GaMe3
1.9
-16.0
-18.3
-14.9
-20.2
-24.0
-10.4
-12.0
-24.8
GaH3
38.7
28.2
16.3
29.6
21.0
10.8
28.8
19.6
8.8
GaF3
104.0
89.8
70.7
95.3
81.6
63.7
90.4
77.7
59.9
GaCl3
83.0
69.5
50.6
92.7
80.4
59.4
88.0
74.9
54.5
GaBr3
81.1
69.1
49.4
89.0
77.1
58.3
84.8
71.9
51.3
GaI3
74.6
58.9
40.5
78.4
67.4
49.8
74.3
62.4
43.9
Ga(C6F5)3
90.1
77.1
53.3
79.3
68.5
45.7
77.9
65.7
43.1
Cr(CO)5
106.7
91.6
81.6
96.4
82.6
69.5
98.4
82.7
68.7
Mo(CO)5
116.6
98.9
85.9
101.6
88.3
74.0
102.4
87.6
72.6
W(CO)5
131.2
117.3
102.1
119.0
104.4
89.5
120.6
104.3
87.9
Fe(CO)4
109.9
91.3
80.0
100.5
83.3
70.6
101.1
82.4
71.3
CpMn(CO)2
120.3
99.9
86.0
108.3
89.3
73.5
110.9
89.0
76.3
a При оптимизации геометрии комплекс диссоциирует на свободные фрагменты.
мента 13 группы с терминальными атомами LA,
тельных блоков для синтеза полиэлементных оли-
что в конечном итоге приводит к образованию
гомеров [12].
циклических соединений или обмену атомов водо-
В настоящей работе нами предпринято систе-
рода на атомы галогена.
матическое квантово-химическое исследование
Наиболее энергетически выгодной является
влияния природы атомов элементов 13 и 15 групп,
стабилизация E′H2EH2 посредством комплексо-
кислоты Льюиса и основания Льюиса на измене-
образования как с кислотой, так и с основанием
ние структурных и термодинамических характе-
Льюиса. Донорно-акцепторно стабилизирован-
ристик комплексов LA·E′H2EH2·LB (E = B, Al, Ga;
ные соединения LA·E′H2EH2·LB синтезированы и
E′ = P, As, Sb; LB = SMe2, NMe3; LA = ER3 (R = H, Me,
структурно охарактеризованы в системах EE′ = BP,
F, Cl, Br, I, C6F5), Fe(CO)4, M(CO)5 (M = Cr, Mo, W),
AlP, GaP, BAs, AlAs [8-11]. В качестве кислот Лью-
CpMn(CO)2; LB = NMe3, SMe2.
иса использовались M(CO)5 (M = Cr, W), E(C6F5)3,
Оптимизированные геометрии комплексов
EX3 (E = B, Ga). Следует отметить, что соединения
LA·E′H2EH2·NMe3 представлены на рис. 1 на
LA·E′H2EH2·LB могут служить в качестве строи-
примере соединений с E = B, E′ = P. Большинство
ЖУРНАЛ ОБЩЕЙ ХИМИИ том 93 № 4 2023
СТРУКТУР
А И УСТОЙЧИВОСТЬ ВОДОРОДНЫХ СОЕДИНЕНИЙ
647
Таблица 2. Свободные энергии Гиббса, Δ(1)G°298 (кДж/моль) для процесса газофазной диссоциации комплекса
LA·E′H2EH2·SMe2 с отрывом кислоты Льюиса
E′E
LA
PB
AsB
SbB
PAl
AsAl
SbAl
PGa
AsGa
SbGa
BMe3
-30.4
-19.9
-a
-47.2
-28.9
-27.1
-46.2
-28.2
-28.5
BH3
76.7
50.0
31.0
56.1
33.7
19.1
57.2
33.8
17.5
BF3
-3.9
-2.3
-3.7
-18.9
-11.5
-10.8
-18.8
-12.0
-11.9
BCl3
41.1
10.8
-30.1
22.1
-3.0
-30.0
20.5
-5.6
-34.1
BBr3
65.1
32.8
0.4
46.5
19.2
-8.9
29.2
16.7
-13.4
BI3
80.9
47.4
15.9
62.3
34.2
7.0
60.9
31.4
2.3
B(C6F5)3
41.9
16.6
-4.9
29.1
8.7
-11.9
29.5
9.7
-13.5
AlMe3
17.1
8.3
-6.3
3.6
-3.8
-14.0
5.2
-4.0
-15.0
AlH3
51.4
39.6
25.3
36.6
27.2
16.0
36.5
26.5
13.6
AlF3
90.7
75.1
56.6
76.2
65.1
45.5
75.6
62.2
42.6
AlCl3
83.9
69.7
52.2
85.7
72.2
37.8
83.4
72.1
39.9
AlBr3
88.1
71.2
50.8
87.9
74.7
54.0
85.8
71.9
49.7
AlI3
96.1
81.3
59.3
83.8
71.7
52.0
81.8
68.2
47.6
Al(C6F5)3
99.7
85.8
60.0
87.4
76.7
55.2
85.8
77.4
51.4
GaMe3
4.6
-1.6
-12.1
-8.6
-13.2
-19.9
-6.2
-13.5
-21.4
GaH3
41.3
31.4
20.9
26.6
19.4
11.8
26.3
18.6
9.4
GaF3
103.7
88.7
71.5
125.5
76.9
81.0
86.7
95.4
59.5
GaCl3
81.1
68.1
63.7
84.9
73.3
55.8
82.3
69.9
51.0
GaBr3
79.1
81.2
62.1
81.7
70.9
54.5
79.4
67.9
49.9
GaI3
84.6
71.7
53.9
71.9
61.6
46.6
69.6
58.7
42.0
Ga(C6F5)3
88.7
76.4
53.7
76.5
66.7
50.2
74.2
68.6
46.1
Cr(CO)5
110.4
97.4
82.9
93.6
81.2
70.4
94.6
81.1
70.3
Mo(CO)5
114.6
102.3
87.2
98.9
86.6
78.0
101.9
86.7
73.9
W(CO)5
134.6
120.2
103.3
115.8
102.8
91.8
118.8
102.6
89.7
Fe(CO)4
114.4
92.0
83.7
96.3
80.3
71.6
99.5
81.6
70.4
CpMn(CO)2
125.0
103.8
89.6
105.8
89.2
74.2
109.5
88.6
77.8
a При оптимизации геометрии комплекс диссоциирует на свободные фрагменты.
соединений принимают «зигзагообразную» кон-
стояние H···F 2.37 Å реализуется в комплексе
формацию, в которой торсионный угол LAE′EN
B(C6F5)3·PH2AlH2·NMe3, максимальное 3.02 Å в
близок к 180° (рис. 1). В некоторых комплексах c
комплексе Ga(C6F5)3·PH2BH2·NMe3. Оптимизиро-
кислотами Льюиса EX3 (X = Cl, Br, I) наблюдается
ванные геометрии (декартовы координаты атомов)
искажение (торсионный угол 30-50°) за счет сла-
для всех исследованных соединений и их термоди-
бых водородных связей H···X (межъядерные рас-
намические характеристики приведены в Допол-
стояния 2.7-3.2 Å).
нительных материалах.
В оптимизированных структурах всех комплек-
Изменения стандартной энергии Гиббса про-
сов с E(C6F5)3 присутствуют короткие контакты
цесса газофазной диссоциации комплексов по
между атомами водорода NMe3 или SMe2 групп
уравнению (1) Δ(1)G°298 представлены в табл. 1 для
и атомами фтора LA (рис. 1ж) с межъядерным
комплексов с LB = NMe3 и табл. 2 для комплексов
расстоянием H···F больше суммы ван-дер-ва-
с SMe2.
альсовых радиусов атомов фтора
(1.20 Å)
и водорода
(1.47 Å)
[13]. Минимальное рас-
LA·E′H2EH2·LB = LA + E′H2EH2·LB.
(1)
ЖУРНАЛ ОБЩЕЙ ХИМИИ том 93 № 4 2023
648
ПОМОГАЕВА и др.
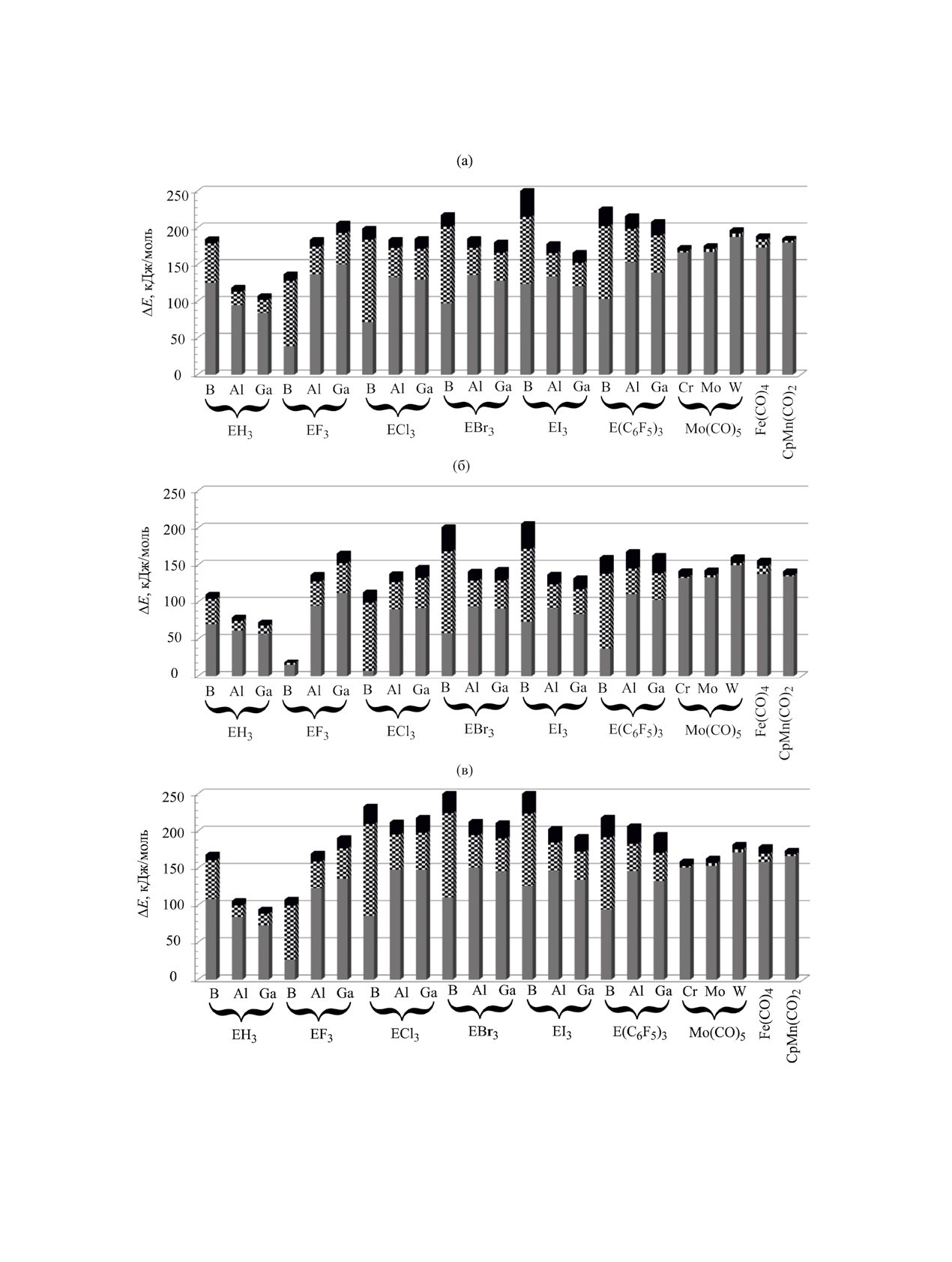
Рис. 2. Энергии донорно-акцепторного связи LA-E′ и ее составляющие (кДж/моль): энергии диссоциации Δ(1)E (серый),
энергии перестройки фрагментов ΔreorgE(LA) (шахматный) и ΔreorgE(E′H2EH2·LB) (черный) для комплексов LA·E′H2EH2·LB.
(a) E′E = PB, (б) E′E = SbB (в) E′E = PAl. Уровень теории B3LYP-D3/def2-TZVP.
ЖУРНАЛ ОБЩЕЙ ХИМИИ том 93 № 4 2023
СТРУКТУР
А И УСТОЙЧИВОСТЬ ВОДОРОДНЫХ СОЕДИНЕНИЙ
649
борсодержащих кислот Льюиса наибольшие, то
энергия донорно-акцепторного связи ЕDA оказы-
вается максимальной для комплексов с BI3 и BBr3
(рис. 2).
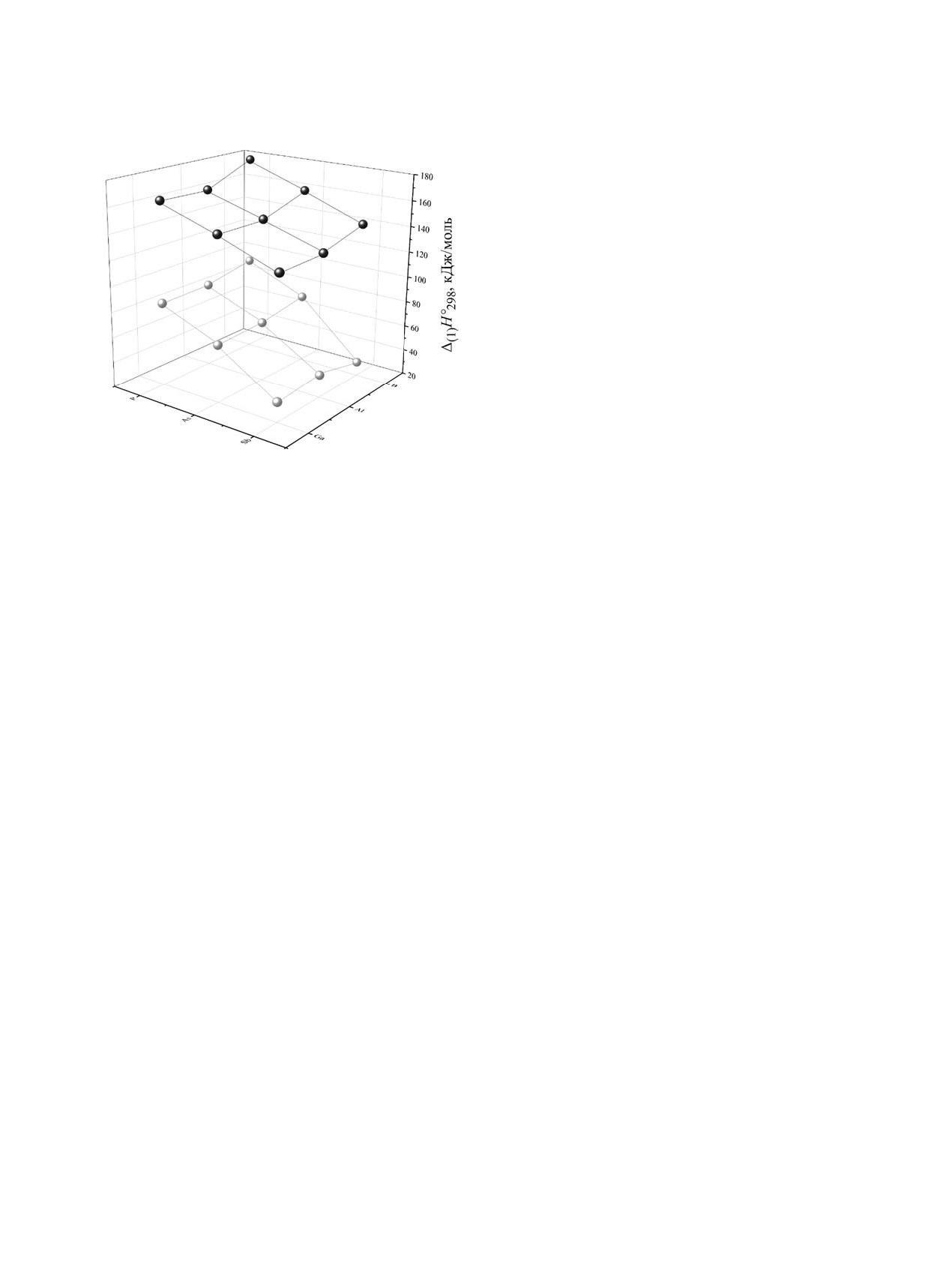
Энергии диссоциации [процесс (1)] для всех
рассмотренных комплексов уменьшаются в ряду
P > As > Sb (рис. 3), причем комплексы, содержа-
щие сурьму и борсодержащие кислоты Льюиса
BH3, BCl3, BBr3 и B(C6F5)3, наименее стабильны.
При этом Δ(1)G°298 оказывается отрицательной или
близкой к нулю для всех борсодержащих кислот
Льюиса, кроме BH3.
Природа элемента 13 группы в E′H2EH2·LB
оказывает небольшое влияние на значения Δ(1)H°298
(рис. 3), для всех рассмотренных комплексов раз-
Рис. 3. Стандартные энтальпиии диссоциации [процесс
личие между алюминий и галлий-содержащими
(1)] для LA·E’H2EH2·NMe3 с LA = B(C6F5)3
(белые
E′H2EH2·LB не превышает 7 кДж/моль. Разница
(черные шарики). Уровень теории
шарики) и W(CO)5
в значениях Δ(1)Н°298 между бор и алюминийсо-
B3LYP-D3/def2-TZVP.
держащими E′H2EH2·LB достигает 20 кДж/моль в
случае, если LA = ER3, X= H, F, Cl, Br, I.
Самыми слабыми, с точки зрения стабилизации
Величины Δ(1)G°298 для комплексов с тримети-
E′H2EH2·LB, оказываются кислоты Льюиса BF3 и
ламином и диметилсульфидом схожи между собой
EMe3. Следует отметить, что процессы диссоциа-
(для большинства комплексов различие не превы-
ции с отрывом BF3 и BMe3 экзергонны (табл. 1).
шает 7 кДж/моль), что свидетельствует о малом
BF3 образует слабый донорно-акцепторного ком-
влиянии основания Льюиса. Лишь для некоторых
плекс с E′H2EH2·LB в случае E′ = P, а для E′ = As,
комплексов, когда есть существенная разница в
Sb донорно-акцепторного комплекс не образует-
значениях торсионных углов LAE′EN, максималь-
ся, взаимодействие между фрагментами является
ное различие в Δ(1)G°298 достигает 20-30 кДж/моль.
ван-дер-ваальсовым. Наибольший стабилизиру-
Интересно проследить влияние природы кис-
ющий эффект оказывают карбонилы переходных
лоты Льюиса LA на энергию донорно-акцептор-
металлов, значения Δ(1)Н°298 увеличиваются от 113
ной связи EDA, рассчитанной по уравнению (2).
для Cr(CO)5·SbH2GaH2·NMe3 до 181 кДж/моль для
W(CO)5·PH2BH2·SMe.
EDA = Δ(1)E + ΔreorgE(LA) + ΔreorgE(E′H2EH2·LB),
(2)
в целом слабо зависят от при-
Значения Δ(1)Н°298
где Δ(1)E - энергия диссоциации донорно-акцеп-
роды LB, разница между комплексами с SMe2 и
торного комплекса на LA и E′H2EH2·LB [процесс
NMe3 в среднем составляет всего 3.5 кДж/моль.
(1)], ΔreorgE(LA) и ΔreorgE(E′H2EH2·LB) - энергии
Ожидается, что комплексообразование с более
перестройки акцепторного и донорного фрагмен-
сильным основанием Льюиса NMe3 будет боль-
тов при образовании комплекса.
ше стабилизировать донорно-акцепторного связь
Полученные данные для некоторых соединений
LA-E′, чем комплексообразование с SMe2. Од-
представлены на рис. 2 (данные для всех соедине-
нако внутримолекулярные взаимодействия су-
ний приведены в Дополнительных материалах).
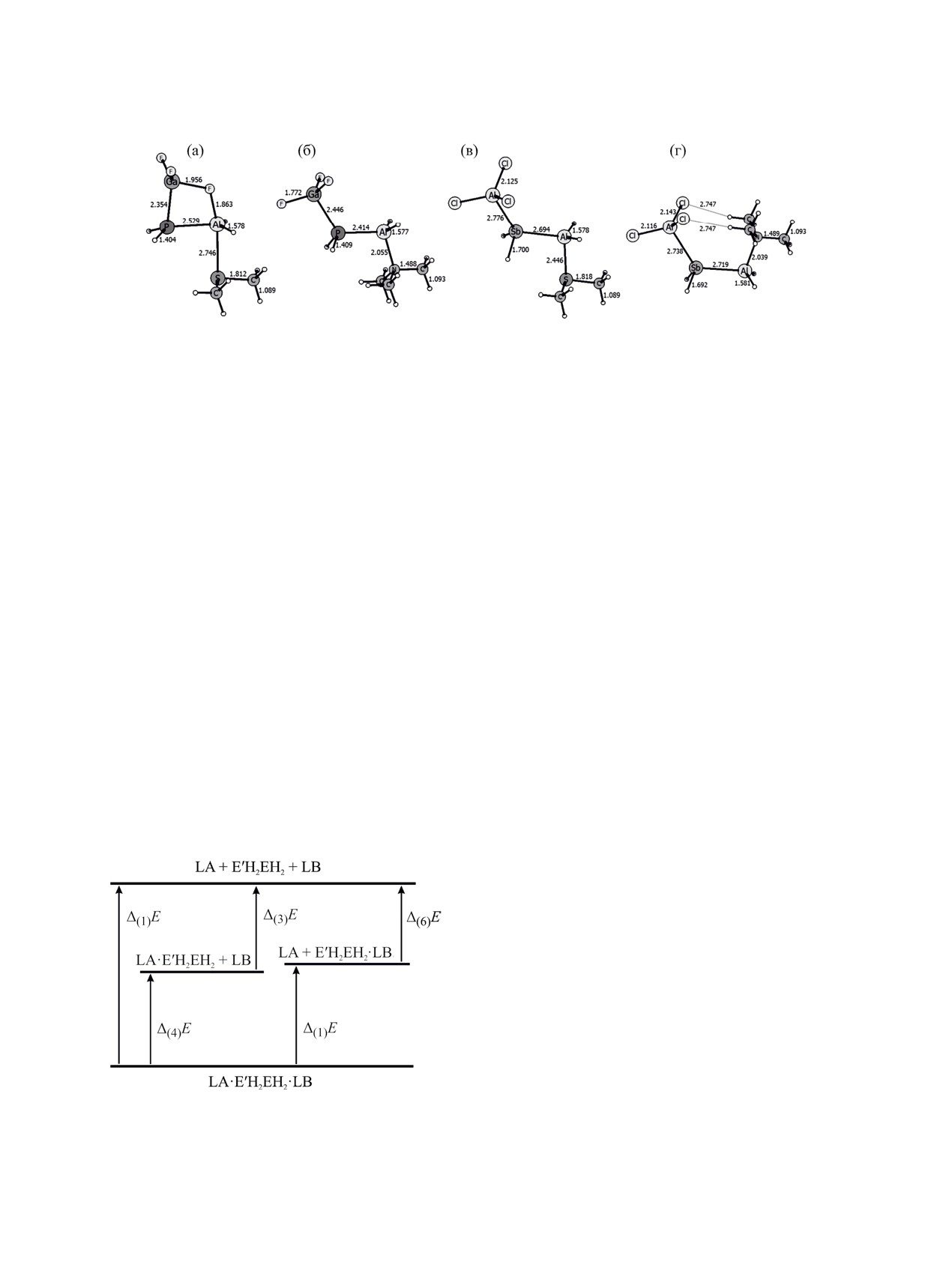
щественно меняют ситуацию: так, в соединении
Среди комплексов с кислотами Льюиса на осно-
GaF3·PH2AlH2·SMe2 (рис. 4а) один из атомов фто-
ве элементов 13 группы самыми прочными явля-
ра GaF3 занимает мостиковое положение меж-
ются комплексы с Al(C6F5)3, Ga(C6F5)3, AlF3, GaF3
ду атомами Al и Ga, что приводит к тому, что
(энтальпии диссоциации Δ(1)Н°298 от
81 до
Δ(1)Н°298 такого соединения на
43 кДж/моль
145 кДж/моль). Поскольку энергии перестройки
больше, чем аналогичного комплекса с NMe3
ЖУРНАЛ ОБЩЕЙ ХИМИИ том 93 № 4 2023
650
ПОМОГАЕВА и др.
Рис. 4. Оптимизированные геометрии GaF3·PH2AlH2·SMe2 (a), GaF3·PH2AlH2·NMe3 (б), AlCl3·SbH2AlH2·SMe2 (в),
AlCl3·SbH2AlH2·NMe3 (г). Уровень теории B3LYP-D3/def2-TZVP.
(рис. 4б), в котором сдвига атома фтора не проис-
Процесс (1) существенно (на 52-70 кДж/моль)
ходит. Наоборот, для системы AlCl3·SbH2AlH2·LB
более экзотермичен, чем процесс (3) для E = B; для
в случае LB = SMe2 (рис. 4в) значение Δ(1)Н°298 на
E = Al разница между процессами (1) и (3) неве-
23 кДж/моль меньше, чем для LB = NMe3 (рис. 4г),
лика: в диапазоне от -2 до 26 кДж/моль для всех
что обусловлено дополнительными взаимодей-
E(C6F5)3 и M(CO)5. Энергетическая диаграмма
ствиями между атомами водорода триметиламина
процессов представлена на рис. 5.
и атомами хлора AlCl3. Подобные взаимодействия
В табл. 3 для наиболее сильной из рассмотрен-
отмечены Кетковым с соавторами [14] для ком-
ных кислот Льюиса W(CO)5 представлены энер-
плексов сурьмы с основаниями Льюиса.
гии диссоциации для процессов (4) и (5).
Представляет интерес влияние комплексо-
образования с основанием Льюиса на энергетику
LA·E′H2EH2·LB = LA·E′H2EH2 + LB,
(4)
процесса отрыва LA от LA·E′H2EH2·LB [процесс
LA·E′H2EH2·LB = LA + E′H2EH2 + LB.
(5)
(1)] по сравнению с диссоциацией комплексов,
стабилизированных только кислотой Льюиса
Оптимизированные геометрии комплексов
LA·E′H2EH2 [процесс (3)], исследованных в рабо-
W(CO)5·E′H2EH2 представлены на рис. 6. На рис.
те [7].
6а представлена структура комплекса без допол-
нительных взаимодействий, на рис. 6б-г - струк-
LA·E′H2EH2 = LA + E′H2EH2.
(3)
туры, в которых происходит дополнительное вза-
имодействие элемента 13 группы с одной из СО
групп пентакарбонила вольфрама.
Сила основания Льюиса мало влияет на энер-
гию отрыва кислоты Льюиса [процесс (1)], но су-
щественна для диссоциации LA·E′H2EH2·LB на
свободные компоненты [процесс (5)]. Отрыв кис-
лоты Льюиса [процесс (1)] более эндотермичен,
чем отрыв основания Льюиса [процесс (4)].
Представляет интерес сравнить сумму про-
цессов диссоциации с отрывом кислоты Льюиса
[процесс (1)] и основания Льюиса [процесс (4)]
c диссоциацией LA·E′H2EH2·LB сразу на сво-
бодные компоненты [процесс (5)]. Разность ΔΔE,
Рис. 5. Энергетическая диаграмма процессов диссоци-
рассчитанная по формуле (6), определяет величи-
ации комплексов LA·E′H2EH2·LB.
ну синергетического эффекта при стабилизации
ЖУРНАЛ ОБЩЕЙ ХИМИИ том 93 № 4 2023
СТРУКТУР
А И УСТОЙЧИВОСТЬ ВОДОРОДНЫХ СОЕДИНЕНИЙ
651
Таблица 3. Энергии диссоциации комплексов W(CO)5·E′H2EH2·LB [процессы (1), (4), (5)], энергии донорно-акцеп-
торного связи с кислотой EDA(LA) и основанием EDA(LB) Льюиса и разности ΔΔE и ΔΔEDA (кДж/моль)
LB
EE′
Δ(1)E
EDA(LA)
Δ(4)E
EDA(LB)
Δ(5)E
EDA(LA+LB)
ΔΔE
ΔΔEDA
NMe3
BP
187.6
196.7
152.9
256.4
314.2
398.7
26.3
54.4
NMe3
BAs
169.0
179.2
171.2
266.9
311.4
393.1
28.8
53.0
NMe3
BSb
149.8
160.5
190.5
274.5
305.9
386.0
34.4
49.0
NMe3
AlP
171.3
181.5
143.6
181.6
301.2
334.4
13.7
28.7
NMe3
AlAs
155.9
167.5
156.4
185.6
289.5
322.9
22.8
30.2
NMe3
AlSb
139.0
150.2
132.9
187.3
275.4
308.2
-3.5
29.3
NMe3
GaP
172.3
182.8
124.0
146.5
275.1
302.2
21.2
27.1
NMe3
GaAs
155.8
167.8
127.4
150.3
262.1
290.0
21.1
28.1
NMe3
GaSb
137.6
149.5
127.3
151.5
246.7
274.6
18.2
26.4
SMe2
BP
189.6
190.4
102.3
179.4
263.6
321.1
28.3
48.7
SMe2
BAs
171.3
171.7
120.2
189.1
260.5
315.2
31.0
45.6
SMe2
BSb
154.1
152.8
143.4
200.4
258.7
312.7
38.8
40.5
SMe2
AlP
167.9
177.8
96.8
122.7
254.4
275.1
10.3
25.4
SMe2
AlAs
153.9
163.4
109.4
126.1
242.4
263.4
20.9
26.1
SMe2
AlSb
140.5
146.7
87.6
128.4
230.1
250.4
-2.0
24.7
SMe2
GaP
170.1
180.0
90.8
105.0
241.9
260.3
19.0
24.7
SMe2
GaAs
154.8
164.6
94.0
108.3
228.7
247.8
20.1
25.1
SMe2
GaSb
139.8
147.0
95.6
110.4
215.0
234.1
20.4
23.3
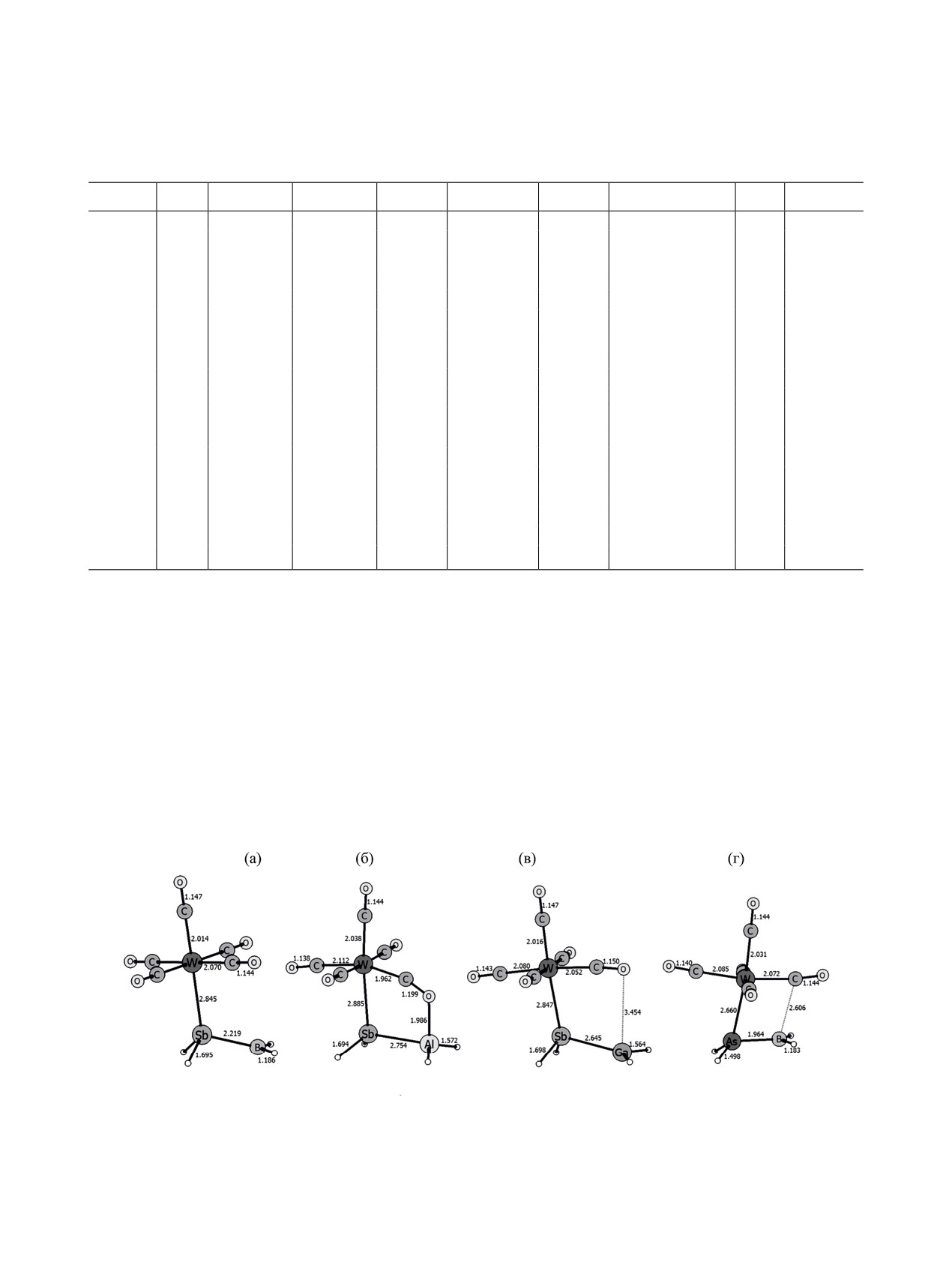
E′H2EH2 одновременно и кислотой, и основанием
атомом алюминия в W(CO)5·SbH2AlH2 (рис. 6б).
Льюиса.
Аналогичная разность энергий донорно-акцептор-
ного связей (7) всегда положительна и принимает
ΔΔE = Δ(1)E + Δ(4)E - Δ(5)E.
(6)
значения от 23 до 54 кДж/моль, что свидетельству-
Разность ΔΔE, как правило, положительна
ет о заметном синергетическом эффекте при одно-
(табл. 3), за исключением систем с SbH2AlH2,
временной стабилизации водородных соединений
где наблюдается сильное взаимодействие между
элементов 13/15 групп и кислотой, и основанием
терминальным атомом кислорода СО группы с
Льюиса для всех изученных систем.
Рис. 6. Оптимизированные геометрии W(CO)5·SbH2BH2 (a), W(CO)5·SbH2AlH2 (б), W(CO)5·SbH2GaH2 (в), W(CO)5·AsH2BH2
(г). Уровень теории B3LYP-D3/def2-TZVP.
ЖУРНАЛ ОБЩЕЙ ХИМИИ том 93 № 4 2023
652
ПОМОГАЕВА и др.
ΔΔE(DA) = EDA(LA) + EDA(LB) - EDA(LA+LB).
(7)
Работа выполнена при финансовой поддержке
Российского научного фонда (грант DFG 21-43-
Для стабилизации комплексов водородных со-
04404) с использованием оборудования Вычисли-
единений с тяжелыми пниктогенами, особенно
тельного центра Санкт-Петербургского государ-
сурьмой, требуются достаточно сильные кислоты
ственного университета.
Льюиса, как например пентакарбонилвольфрама.
Таким образом, на основании квантово-хими-
КОНФЛИКТ ИНТЕРЕСОВ
ческих расчетов показано наличие синергетиче-
Авторы заявляют об отсутствии конфликта
ского эффекта при совместной донорно-акцеп-
интересов.
торного стабилизации мономерных водородных
соединений элементов 13/15 групп и кислотой, и
ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ
основанием Льюиса.
Дополнительные материалы для этой статьи
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
доступны по doi
10.31857/S0044460X23040170
для авторизованных пользователей.
Квантово-химические расчеты в газовой фазе
выполнены с использованием стандартного пакета
СПИСОК ЛИТЕРАТУРЫ
программ Gaussian 16 [15] в рамках теории функ-
1.
Staubitz A., Robertson A.P.M., Sloan M.E., Man-
ционала плотности методом B3LYP-D3 [16-18]
ners I. // Chem. Rev. 2010. Vol. 110. P. 4023. doi
c def2-TZVP [19] базисным набором. Структуры
10.1021/cr100105a
всех соединений в газовой фазе полностью опти-
2.
Vogel U., Timoshkin A.Y., Scheer M. // Angew.
мизированы с последующим колебательным ана-
Chem. Int. Ed. 2001. Vol. 40. P. 4409. doi
лизом и отвечают минимуму на поверхности по-
10.1002/1521-3773(20011203)40:23<4409::AID-
тенциальной энергии. В единичных случаях для
ANIE4409>3.0.CO;2-F
оптимизированных структур наблюдались малые
3.
Schwan K.-C., Timoshkin A.Y., Zabel M., Scheer M. //
(менее 20i см-1) мнимые колебательные частоты,
Chem.-Eur. J. 2006, Vol. 12. P. 4900. doi 10.1002/
обусловленные недостатками модели гармониче-
chem.200600185
4.
Marquardt C., Adolf A., Stauber A., Bodensteiner M.,
ского осциллятора для свободной энергии [20].
Virovets A.V., Timoshkin A.Y., Scheer M. // Chem.-Eur.
Для таких комплексов термическую поправку кор-
J. 2013. Vol. 19. P. 11887. doi 10.1002/chem.201302110
ректировали путем удвоения вклада от нижней
5.
Butlak A.V., Kazakov I.V., Stauber A., Hegen O.,
действительной колебательной моды. Энергию
Scheer M., Pomogaeva A.V., Timoshkin A.Y. // Eur.
донорно-акцепторной связи рассчитывали, как
J. Inorg. Chem. 2019. Vol. 35. P. 3885. doi 10.1002/
сумму энергии диссоциации комплекса и энер-
ejic.201900817
гий перестройки акцепторного (LA) и донорного
6.
Marquardt C., Hegen O., Hautmann M., Balazs G.,
(E′H2EH2·LB) и фрагментов. Энергия перестройки
Bodensteiner M., Virovets A.V., Timoshkin A.Y.,
фрагмента - та энергия, которую необходимо за-
Scheer M. // Angew. Chem. Int. Ed. 2015. Vol. 54.
тратить на переход от оптимизированной геоме-
P. 13122. doi 10.1002/anie.201505773
7.
Pomogaeva A.V., Lisovenko A.S., Zavgorodnii A.S.,
трии молекулы в газовой фазе в геометрию, кото-
Timoshkin A.Y. // J. Comput. Chem. 2023. Vol. 44. N 3.
рую она принимает в составе комплекса.
P. 218. doi 10.1002/jcc.26867
ИНФОРМАЦИЯ ОБ АВТОРАХ
8.
Vogel U., Hoemensch P., Schwan K.-C., Timoshkin A.Y.,
Scheer M. // Chem.-Eur. J. 2003. Vol. 9. P. 515. doi
Помогаева Анна Владимировна, ORCID: https://
10.1002/chem.200390054
orcid.org/0000-0002-5131-4240
9.
Vogel U., Timoshkin A.Y., Schwan K.-C., Bodensteiner M.,
Scheer M. // J. Organomet. Chem. 2006. Vol. 691.
Лисовенко Анна Сергеевна, ORCID: https://
P. 4556. doi 10.1016/j.jorganchem.2006.04.014
orcid.org/0000-0001-7443-0124
10.
Schwan K.-C., Adolf A., Thoms C., Zabel M., Timosh-
Тимошкин Алексей Юрьевич, ORCID: https://
kin A.Y., Scheer M. // Dalton Trans. 2008. P. 5054. doi
orcid.org/0000-0002-1932-6647
10.1039/B809773A
ФИНАНСОВАЯ ПОДДЕРЖКА
ЖУРНАЛ ОБЩЕЙ ХИМИИ том 93 № 4 2023
СТРУКТУР
А И УСТОЙЧИВОСТЬ ВОДОРОДНЫХ СОЕДИНЕНИЙ
653
11. Marquardt C., Kahoun T., Baumann J., Timoshkin
Honda Y., Kitao O., Nakai H., Vreven T., Throssell K.,
A.Y., Scheer M. // Z. anorg. allg. Chem. 2017. Vol. 643.
Montgomery J.A., Peralta J.E., Ogliaro F., Bear-
P. 1326. doi 10.1002/zaac.201700219
park M.J., Heyd J.J., Brothers E.N., Kudin K.N.,
12. Hegen O., Marquardt C., Timoshkin A.Y., Scheer M. //
Staroverov V.N., Keith T.A., Kobayashi R., Normand J.,
Angew. Chem. Int. Ed. 2017. Vol. 56. P. 12783. doi
Raghavachari K., Ren- dell A.P., Burant J.C.,
10.1002/anie.201707436
Iyengar S.S., Tomasi J., Cossi M., Millam J.M., Klene M.,
13. Rowland R.S., Taylor R. // J. Phys. Chem. 1996.
Adamo C., Cammi R., Ochter- ski J.W., Martin R.L.,
Vol. 100. P. 7384. doi 10.1021/jp953141+
Morokuma K., Farkas O., Foresman J.B., Fox D.J. //
14. Ketkov S., Rychagova E., Kather R., Beckmann J. //
Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford,
J. Organomet. Chem. 2021. Vol. 949. P. 121944. doi
CT. 2016.
10.1016/j.jorganchem.2021.121944
16. Becke A.D. // J. Chem. Phys. 1993. Vol. 98. P. 1372. doi
15. Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E.,
10.1063/1.464304
Robb M.A., Cheeseman J.R., Scalmani G., Barone V.,
17. Lee C., Yang W., Parr R.G. // Phys. Rev. (B). 1988.
Petersson G.A., Nakatsuji H., Li X., Caricato M.,
Vol. 37. P. 785. doi 10.1103/PhysRevB.37.785
Marenich A.V., Bloino J., Janesko B.G., Gomperts R.,
18. Grimme S., Antony J., Ehrlich S., Krieg H. // J. Chem.
Mennucci B., Hratchian H.P., Ortiz J.V., Izmaylov A.F.,
Phys. 2010. Vol. 132. P. 154104. doi 10.1063/1.3382344
Sonnenberg J.L.,Williams-Young D.,Ding F.,Lipparini F.,
19. Weigend F., Ahlrichs R. // Phys Chem. Chem. Phys.
Egidi F., Goings J., Peng B., Petrone A., Henderson T.,
2005. Vol. 7. P. 3297. doi 10.1039/B508541A.
Ranasinghe D., Zakrzewski V.G., Gao J., Rega N.,
20. Cramer C.J. Essentials of Computational Chemistry:
Zheng G., Liang W., Hada M., Ehara M., Toyota K.,
Theories and Models. Chichester: John Wiley and Sons,
Fukuda R., Hasegawa J., Ishida M., Nakajima T.,
2004, Р. 357.
Structure and Stability of Group 13/15 Hydrides Stabilized
by Lewis Acids and Lewis Bases
A. V. Pomogaevaa, A. S. Lisovenkoa, and A. Y. Timoshkina,*
a St. Petersburg State University, St. Petersburg, 199034 Russia
*e-mail: a.y.timoshkin@spbu.ru
Received March 21, 2023; revised March 27, 2023; accepted March 28, 2023
Structural and thermodynamic characteristics of donor-acceptor complexes LA·E′H2EH2·LB (E = B, Al, Ga; E′ =
P, As, Sb; LB = SMe2, NMe3); LA - Lewis acids of group 13 elements ER3 (E = B, Al, Ga; R = H, Me, F, Cl, Br, I, C6F5)
and transition metal carbonyls Fe(CO)4, M(CO)5, (M = Cr, Mo, W), CpMn(CO)2 were computed by quantum
chemical B3LYP-D3/def2-TZVP method. It is shown that removal of the Lewis base is less endothermic than
removal of Lewis acid. Stability trends of the complexes depending on group 13/15 elements and Lewis acids
were established. Tungsten pentacarbonyl has the highest stabilization effect.
Keywords: group 13/15 element hydrides, Lewis acids, Lewis bases, donor-acceptor bond, quantum chemical
calculations
ЖУРНАЛ ОБЩЕЙ ХИМИИ том 93 № 4 2023