Известия РАН. Механика твердого тела, 2023, № 3, стр. 99-105

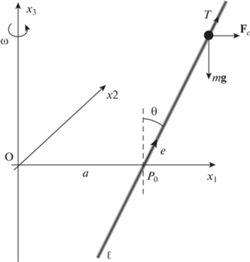
1. Постановка задачи. Пусть шероховатая прямолинейная спица $\ell $ совершает равномерное вращение с постоянной угловой скоростью $\omega > 0$ вокруг вертикальной оси, отстоящей от спицы на расстоянии a. Предположим, что на спицу нанизана тяжелая бусинка P. Требуется найти положения равновесия бусинки относительно спицы в предположении о том, что коэффициент сухого трения равен $\mu = {\text{tg}}\alpha $, где $0 \leqslant \alpha < \pi {\text{/}}2$ – угол трения. Ускорение силы тяжести считается равным g. Предполагается, что спица образует с восходящей вертикалью угол $0 \leqslant \theta \leqslant \pi {\text{/}}2$, см. рис. 1.

2. Общие условия существования относительных равновесий. В равномерно вращающейся вместе со спицей системе отсчета бусинка будет находиться в равновесии под действием (рис. 1) силы тяжести $m{\mathbf{g}}$, центробежной силы ${{{\mathbf{F}}}_{c}} = m{{{\mathbf{g}}}_{c}}$, а также реакции связи, состоящей из нормальной компоненты ${\mathbf{N}}$ (не изображена на рисунке) и силы трения ${\mathbf{T}} = T{\mathbf{e}}$, где ${\mathbf{e}}$ – единичный вектор, направленный вверх вдоль спицы. Пусть масса бусинки принята за единицу. Тогда, если ${\mathbf{f}} = {{{\mathbf{g}}}_{c}} + {\mathbf{g}}$, то условие равновесия запишется в виде

Согласно закону Кулона–Амонтона величины нормальной реакции и силы трения стеснены неравенством

Домножая левую и правую части последнего неравенства на неотрицательную¹¹ величину ${\text{|}}{\mathbf{T}}{\text{|}} + \mu {\text{|}}{\mathbf{N}}{\text{|}}$, получим

Здесь и далее (·, ·) – скалярное произведение. Принимая во внимание ортогональность векторов ${\mathbf{T}}$ и ${\mathbf{N}}$, последнее из неравенств запишем в виде

Из уравнения (2.1) находим

и неравенство (2.2) может быть записано как

Далее, путем скалярного умножения левой и правой частей уравнения (2.1) на ${\mathbf{e}}$ и дальнейших преобразований, находим величину $T$:

Так как

то и неравенство (2.3) приобретает вид

Это неравенство составляет основной предмет дальнейших исследований.

3. Зависимость относительных равновесий от параметров. Пусть $O{{P}_{0}}$ – общий перпендикуляр к оси вращения и спице, причем точка O принадлежит оси вращения, а точка ${{P}_{0}}$ – спице. Введем вращающуюся вместе со спицей систему отсчета $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, ось $O{{x}_{3}}$ которой направлена вдоль оси вращения, ось $O{{x}_{1}}$ – вдоль общего перпендикуляра, а ось $O{{x}_{2}}$ дополняет их до правой тройки. При этом ${{\overleftarrow {OP} }_{0}} = (a{{,0,0)}^{T}}$, e = (0, sinθ, ${\text{cos}}\theta {{)}^{T}}$, ${\mathbf{g}} = (0,0, - g{{)}^{T}}$. Вводя параметр $p \in {\mathbf{R}}$, отвечающий за удаление бусинки P от точки ${{P}_{0}}$ на прямой, зададим ее положение вектором

Тогда ${{{\mathbf{g}}}_{c}} = {{\omega }^{2}}{{(a,p\sin \theta ,0)}^{T}},$ ${\mathbf{f}} = ({{\omega }^{2}}a,{{\omega }^{2}}p\sin \theta , - g{{)}^{T}},$

и неравенство (2.4) сводится к неравенству приводимому к виду

Введение безразмерной координаты $p{\kern 1pt} '{\text{:}}$ $p = ap{\kern 1pt} '$ и дальнейшее отбрасывание штриха позволяют представить это неравенство в виде

Решения неравенства (3.1) относительно p определяют на спице $\ell $ области, заполненные относительными равновесиями (ОЗОР). Зависимость этих областей от безразмерного параметра ${{\unicode{230} }}$ и от углов α и θ составляет предмет дальнейших исследований.

а) Если $A = 0$ при ${{\unicode{230} }} = 0$, т.е. спица не вращается или пересекается с осью вращения, то неравенство (3.1) записывается как

Неравенство выполнено при $\pi {\text{/}}2 - \theta \leqslant \alpha $ и не выполнено в противном случае. Это классический результат, иллюстрирующий смысл угла трения α [1] (см. также [2]). б) Если $A = 0$ при $\theta = 0$, т.е. спица вертикальна, то неравенство (3.1) приводится к виду

которое выполнено при $0\; \leqslant {\text{tg}}\alpha \leqslant {{{{\unicode{230} }}}^{{ - 1}}}$.

в) Если $A = 0$ при ${{\cos }^{2}}\alpha - {{\cos }^{2}}\theta = 0$, то неравенство (3.1) приводится к виду

Тогда, так как $0 \leqslant \alpha < \pi {\text{/}}2$, то и $0 \leqslant \theta < \pi {\text{/}}2$, и $\cos \theta \ne 0$. Случай θ = 0 разобран выше, поэтому решение неравенства (3.4) имеет вид

Граничная точка ${{P}_{ \star }}$, определяемая значением $p = {{p}_{ \star }}$,

• совпадает с точкой P₀ при $\sin \theta = s$,

• располагается выше точки P₀ при $\sin \theta \in (0;s)$,

• располагается ниже точки P₀ при $\sin \theta \in \left( {s,1} \right]$.

г) Если $A < 0$, т.е. ${{\cos }^{2}}\alpha - {{\cos }^{2}}\theta < 0$, то в левой части неравенства (3.1) стоит квадратный трехчлен относительно p, дискриминант которого имеет вид

Неравенство (3.1) при этом приводится к виду

Величины ${{p}_{ \pm }}$ вещественны если

Если K ≥ 1, то угол θ < α, если $K < 1$, то используя обозначение $\beta = \arccos K$, имеем

В этом случае относительные равновесия занимают область, отвечающую значениям параметра

т.е. располагаются вне интервала $({{p}_{ - }};{{p}_{ + }})$.

При $D < 0$ вещественных корней нет, а с учетом $A < 0$, неравенство (3.1) выполнено при любых значениях $p$, т.е. ОЗОР – все точки спицы.

д) При выполнении условия $A > 0$, т.е. ${{\cos }^{2}}\alpha - {{\cos }^{2}}\theta > 0$, неравенство (3.1) имеет вид

Относительные равновесия занимают область, отвечающую значениям параметра

Поскольку ${{\cos }^{2}}\alpha - {{\cos }^{2}}\theta > 0$, то $D \geqslant 0$ и величины ${{p}_{ \pm }}$ вещественны.

4. Графическое представление зависимости относительных равновесий от параметров. Для иллюстрации различных случаев расположения ОЗОР на плоскости (θ, α) изобразим три кривые. Кривая ${{\Gamma }_{1}}$: $D = 0$ отделяющую область, в которой изучаемый квадратный трехчлен имеет два вещественных корня, от области, в которой вещественных корней нет. ${{\Gamma }_{2}}$: $C = 0$, разделяет области, где эти корни одного или разных знаков и, наконец, ${{\Gamma }_{3}}$: $A = 0$, разделяет области, где ветви изображающей трехчлен параболы направлены вниз или вверх. Кривые ${{\Gamma }_{1}}$, ${{\Gamma }_{2}}$ и ${{\Gamma }_{3}}$ разбивают квадрат S = {0 ≤ θ ≤ π/2, $0 \leqslant \alpha \leqslant \pi {\text{/}}2\} $ на пять областей $I.$–$V.$ При этом

Для ${{\unicode{230} }} = 1{\text{/}}2$ эти области изображены на рис. 2.

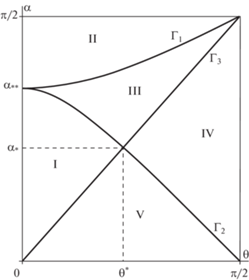
При неограниченном увеличении параметра ${{\unicode{230} }}$, области $I.$, $III.$ и $V.$ (см. рис. 2) уменьшаются, исчезая в пределе. При этом кривая ${{\Gamma }_{2}}$ сливается с граничным отрезком α = 0, а кривая ${{\Gamma }_{1}}$ приближается к диагонали α = θ. В предельном случае, оставшиеся области $II.$ и $IV.$ разбивают квадрат S на равные треугольники с общим основанием на диагонали квадрата S, соответствующей кривой ${{\Gamma }_{3}}$.

При неограниченном уменьшении параметра ${{\unicode{230} }}$ до нуля область $II.$ уменьшается и сливается с граничным отрезком $\alpha = \pi {\text{/}}2$. При этом кривая ${{\Gamma }_{2}}$ приближается к диагонали $\alpha = \pi {\text{/}}2 - \theta $. В пределе, при ${{\unicode{230} }} = 0$, т.е. в случае а), области $I.$, $III.$, $IV.$ и $V.$ разбивают квадрат S на равные треугольники с общей вершиной и основаниями, противоположными этой вершине, на сторонах квадрата S. При этих условиях неравенство (3.2) выполнено в точках диагонали $\alpha = \pi {\text{/}}2 - \theta $.

В случае б) неравенство (3.3) выполнено в точках отрезка θ = 0, $\alpha \in [0,{{\alpha }_{{ \star \star }}}]$.

В случае в) неравенство (3.4) выполнено в точках кривой ${{\Gamma }_{3}}$.

Случаю г) отвечают области $I.$–$III.$

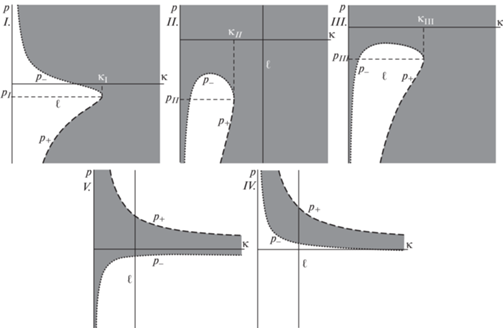
На рис. 3 серым закрашены области, где существуют ОЗОР. Области построены для случае ${{\unicode{230} }} = 0.5$, на рисунках схематично изображена спица $\ell $, что позволяет проиллюстрировать области ОЗОР. Пунктирной линией отмечены точки границы при ${{p}_{ - }}({{\unicode{230} }})$ = 0, штриховой линией отмечены точки границы при ${{p}_{ + }}({{\unicode{230} }}) = 0$. Точки $({{{{\unicode{230} }}}_{i}},{{p}_{i}})$, $i = I,II$, III отвечают случаям, когда ${{p}_{ - }}({{\unicode{230} }}) = {{p}_{ + }}({{\unicode{230} }})$. Для области $I.$ ОЗОР представляется в виде объединения двух лучей, направленных вверх и вниз по спице, при этом начало верхнего луча лежит выше точки ${{P}_{0}}$, начало нижнего луча лежит ниже точки ${{P}_{0}}$. Для области $II.$ вся спица заполнена ОЗОР. Для области $III.$ ОЗОР опять представляется в виде объединения двух лучей, направленных вверх и вниз по спице, но при этом начала обоих лучей лежат ниже точки ${{P}_{0}}$, т.е. сама точка ${{P}_{0}}$ принадлежит ОЗОР.

Случаю д) отвечают области $IV.$ и $V.$, см. рис. 3. Для области $IV.$ ОЗОР представляется в виде отрезка, концы которого лежат по разные стороны от точки P₀, и точка P₀ принадлежит ОЗОР. Для области V., ОЗОР также является отрезком, но целиком лежащим выше точки P₀.

5. Выводы. Рассмотренная в учебнике А. Зоммерфельда ([1], стр. 73) задача о тяжелой бусинке на вращающейся спице представляет собой замечательный пример системы, в которой при прохождении параметра, например, коэффициента трения, через определенное значение, множество неизолированных относительных равновесий, заполняющее целую прямую, исчезает²². Как показало настоящее исследование, выполненное в продолжение ряда исследований по существованию, устойчивости и бифуркациям равновесий в системах с трением (см., например, [4–13]), в рамках несложного обобщения задачи А. Зоммерфельда обнаруживается достаточно богатая (с точки зрения динамических эффектов) картина бифуркаций относительных равновесий.