Известия РАН. Механика твердого тела, 2023, № 3, стр. 36-57
АСИМПТОТИЧЕСКОЕ ИССЛЕДОВАНИЕ ИЗГИБА ПЛАСТИНЫ ДЛЯ СИЛЬНО ОРТОТРОПНОГО МАТЕРИАЛА
С. В. Шешенин a, *, Р. Р. Мурадханов a, **
a Московский государственный университет им. М.В. Ломоносова
Москва, Россия
* E-mail: sergey.sheshenin@mail.ru
** E-mail: mrdhnv@yandex.ru
Поступила в редакцию 01.02.2022
После доработки 28.07.2022
Принята к публикации 31.07.2022
- EDN: FTLVUA
- DOI: 10.31857/S0572329922600608
Аннотация
Методика асимптотического осреднения была развита для трехмерных уравнений в частных производных с быстро осциллирующими коэффициентами. Например, для уравнений теории упругости. Затем была модифицирована и применялась к тонким телам в виде пластин (однородных или неоднородных, с ровными лицевыми поверхностями или нет), описываемых трехмерной теорией упругости. В этих случаях асимптотические решения строились относительно одного малого параметра, обычно являющегося отношением толщины пластины к характерному размеру в плане. Методика осреднения в таком случае также понижает размерности задачи, т.е. сводит трехмерную краевую задачу к некоторой двумерной.
В данной работе приводится обоснование применения метода к задаче с двумя малыми параметрами в случае однородной тонкой сильно ортотропной пластины, изгибаемой поверхностной нагрузкой без учета массовых сил. Вторым малым параметром является отношение поперечных модулей упругости к модулям в плане пластины. Показано, что сильная ортотропия эквивалентна увеличению толщины эквивалентной пластины.
Описана процедура получения распределения напряжений по толщине пластины для трех приближений. Первое приближение дает классическую теорию Кирхгофа, называемую также теорией Кирхгофа–Лява, а третье приближение совпадает с теорией Амбарцумяна и позволяет находить поперечные сдвиговые и нормальное напряжения. Рассмотрение цилиндрического изгиба дает возможность найти решения в рамках классических теорий пластин в виде формул, так же как и три приближения асимптотической теории, что упрощает сравнение. Рассмотрены примеры, когда осредненные ортотропные модули взяты для однослойного волокнистого композита.
1. Введение. Известно, что сильно ортотропные пластины не описываются теорией Кирхгофа (К). Например, в [1] это показано численными расчетами. В данной работе проводится асимптотическое исследование частного случая сильной ортотропии.
Методика асимптотического осреднения (метод многих масштабов) была первоначально создана для случая трехмерной периодической среды (cм. [2, 3] и др.) и, в частности, для теории упругости [4, 5]. Затем она была модифицирована [6] и применялась к тонким телам в виде неоднородных гофрированных пластин, описываемых трехмерной теорией упругости, как в математической литературе [7, 8] так и в работах по механике [9–13]. Обзор литературы можно найти в [7]. В [14] метод применен в первом приближении для анализа пластического деформирования пластины. В [9] достаточно детально проанализированы первые три приближения в случае упругости. В данной работе приводится обоснование применения метода в задаче упругости с двумя малыми параметрами в случае однородной тонкой сильно ортотропной пластины, и также анализируются три первых приближения. Малыми параметрами являются отношение толщины пластины к характерному размеру в плане и отношение поперечных модулей упругости к модулям в плане пластины. Метод осреднения в таком случае состоит в понижении размерности задачи, также как и все теории пластин и оболочек [15]. Это делается чисто математически и приводит к последовательности двумерных задач в области пластины и одномерных задач в поперечном направлении. Показано, что сильно ортотропная пластина эквивалентна пластине увеличенной толщины с измененными жесткостями.
Отметим, что в приведенной литературе рассматривается обычная линейная теория упругости. Понижение размерности для моментной теории упругости предложено в [16].
Необходимо отметить, что независимо от работ этого направления асимптотический подход применялся к однородным плоским пластинам в первом приближении в ранней работе [17] и ряде последующих работ [18, 19], а также в работах процитированных в [19]. Техника асимптотического исследования, используемая в этих разных циклах работ, разная, но результаты, касающиеся первого приближения и наличия пограничного слоя одинаковы. Применяемый нами асимптотический метод позволяет получить уравнения в области в трех первых приближениях, но не дает граничные условия с тем же асимптотическим приближением. Его достоинство состоит в том, что он дает распределение перемещений и напряжений в поперечном направлении, которое можно использовать при построении конечных элементов не только для однородных пластин, но и для неоднородных, например, слоистых. Три асимптотических приближения не заменяют классические теории пластин, но сравнение представляется интересным, особенно для сильно ортотропных пластин. В частности, сравнение распределения напряжений в поперечном направлении.
Асимптотический метод, конечно, не заменяет другие подходы построения теорий пластин и оболочек, что поясняется в работах В.В. Васильева [20–23] и других авторов, в которых весьма интересно и поучительно описаны история развития теорий пластин, их сравнение и современное состояние.
Если вернуться к данной работе, то следует начать с краткого описания, к чему приводит асимптотический метод. Первое приближение дает классическую теорию Кирхгофа (Кирхгофа–Лява) и приводит к существенной погрешности в случае сильной ортотропии. Второе приближение позволяет находить поперечные сдвиговые деформации и напряжения, а третье – и поперечное нормальное напряжение. Третье приближение аналогично теории третьего порядка [24]. Второе приближение относительно распределения напряжений в поперечном направлении похоже на теории Тимошенко [25] и Рейсснера [26].
В качестве задачи сравнения рассматривается цилиндрический изгиб сильно ортотропной пластины постоянной толщины под действием равномерно-распределенной или сосредоточенной нагрузки. Использование цилиндрического изгиба для сравнения вызвано стремлением найти решения для указанных теорий в виде формул, также как и в трех приближениях асимптотической теории. Результаты численных решений будут получены позже.
Для сравнения рассмотрены примеры, когда модули осредненного материала пластины получены для однослойного волокнистого композита. Дается сравнение решений по рассмотренным теориям между собой и с конечно-элементным решением трехмерной задачи на мелкой сетке.
2. Применения асимптотического метода в задаче с двумя малыми параметрами. Рассмотрим дифференциальные уравнения равновесия трехмерной теории упругости для ортотропного материала, первые две оси ортотропии которого параллельны первым двум декартовым осям:
(2.1)
$\begin{gathered} {{C}_{{IJKL}}}{{u}_{{K,LJ}}} + {{C}_{{I3K3}}}{{u}_{{K,33}}} + {{C}_{{IJ33}}}{{u}_{{3,3J}}} = 0 \\ {{C}_{{3J3L}}}{{u}_{{3,JL}}} + {{C}_{{33KL}}}{{u}_{{K,3L}}} + {{C}_{{3333}}}{{u}_{{3,33}}} = 0 \\ \end{gathered} $Здесь и далее малые индексы $i,j,k,l$ принимают значения 1, 2, 3, а большие $I,J,K,L$ – значения 1, 2. Все величины предполагаются безразмерными, если не оговорено обратное. Поскольку мы рассматриваем случай сильно ортотропной пластины, то упругие модули в плоскости пластины существенно превышают упругие модули в поперечном направлении. Введем малый параметр δ – параметр, задающий сильную ортотропию. Пусть ${{\tilde {C}}_{{ijkl}}}$ – безразмерные модули одного порядка. Тогда для упругих модулей исходной задачи можно записать:
Сделаем замену: ${{x}_{I}} = {{\tilde {x}}_{I}},{{x}_{3}} = \sqrt \delta \cdot {{\tilde {x}}_{3}};{{u}_{I}} = {{\tilde {u}}_{I}},{{u}_{3}} = {{\tilde {u}}_{3}}{\text{/}}\sqrt \delta $. Пусть также все $C_{{ijkl}}^{*}$ = ${{\tilde {C}}_{{ijkl}}}$ за исключением $C_{{3333}}^{*} = {{\widetilde C}_{{3333}}}{\text{/}}\delta $. После подстановки в систему (2.1) и тождественных преобразований получим систему в координатах ${{\tilde {x}}_{i}}$:
(2.2)
$\begin{gathered} C_{{IJKL}}^{*}{{{\tilde {u}}}_{{K,LJ}}} + C_{{I3K3}}^{*}{{{\tilde {u}}}_{{K,33}}} + C_{{IJ33}}^{*}{{{\tilde {u}}}_{{3,3J}}} = 0 \\ C_{{3J3L}}^{*}{{{\tilde {u}}}_{{3,JL}}} + C_{{33KL}}^{*}{{{\tilde {u}}}_{{K,3L}}} + C_{{3333}}^{*}{{{\tilde {u}}}_{{3,33}}} = 0 \\ \end{gathered} $Поскольку ${{x}_{I}} \in [0,1]$, ${{x}_{3}} \in [ - h{\text{/}}2,{\kern 1pt} h{\text{/}}2]$ и в рамках задачи $\varepsilon = h{\text{/}}l$ (рассматривается пластина длины l = 1), следовательно в соответствии со сделанной ранее заменой ${{\tilde {x}}_{I}} \in [0,1]$ и ${{\tilde {x}}_{3}} \in \left[ { - {\mathbf{\tilde {\varepsilon }}}{\text{/}}2,{\mathbf{\tilde {\varepsilon }}}{\text{/}}2} \right]$, где $\tilde {\varepsilon } = \varepsilon {\text{/}}\sqrt \delta $. Таким образом, систему (2.2), записанную в координатах ${{\tilde {x}}_{i}}$, можно рассматривать как уравнения для пластины большей приведенной толщины $\tilde {\varepsilon }$ с модулями $C_{{ijkl}}^{*}$ одного порядка за исключением модуля $C_{{3333}}^{*}\, = \,{{\tilde {C}}_{{3333}}}$/δ.
Представляется, что решение системы (2.2) слабо зависит от модуля $C_{{3333}}^{*}$: при значительном изменении данного модуля решение изменяется незначительно. Это приводит к идее применить асимптотический метод к системе (2.2) с модулем $C_{{3333}}^{*}$ и выяснить поведение асимптотического решения при $\delta \to 0$.
3. Асимптотическое разложение. В этой секции мы проверим, применимо ли стандартное асимптотическое разложение перемещений к (2.2) при стремлении второго параметра δ к нулю. При этом для упрощения письма опустим знаки тильды и звездочки, помня, что речь идет о системе (2.2), содержащей малый параметр δ. Как обычно, введем быструю координату ${{{\mathbf{\xi }}}_{3}} = {{x}_{3}}{\text{/}}\varepsilon $. Далее запятой обозначается производная как по координатам xi, так и по координате ${{{\mathbf{\xi }}}_{3}}$ в зависимости от контекста. Решение задачи в перемещениях ищется в виде:
Здесь $N_{i}^{{P{{Q}_{0}} \ldots {{Q}_{k}}}} = N_{i}^{{P{{Q}_{0}} \ldots {{Q}_{k}}}}({{{\mathbf{\xi }}}_{3}})$ – функции жесткости, $w = w({{x}_{1}},{{x}_{2}})$ – гладкая составляющая прогиба приведенной пластины, ui – компоненты перемещений приведенной пластины. Введем функции:
Все формулы написаны в декартовой системе координат, поэтому индексы написаны вверху или внизу только для удобства различения их смысла. Штрих означает производную по ξ3. Подставив общую формулу для трех компонент перемещений в закон Гука, получим:
Далее подставим полученное выражение в уравнение равновесия (2.2), тогда получим:
(3.1)
$(P_{{i3}}^{{P{{Q}_{0}}}}){{w}_{{,P{{Q}_{0}}}}} + \sum\limits_{m = 1}^M {{\varepsilon }^{m}}[P_{{i{{Q}_{m}}}}^{{P{{Q}_{0}}..{{Q}_{{m - 1}}}}} + (P_{{i3}}^{{P{{Q}_{0}}..{{Q}_{{m - 1}}}{{Q}_{m}}}})]{{w}_{{,P{{Q}_{0}}..{{Q}_{{m - 1}}}{{Q}_{m}}}}} = 0$Чтобы удовлетворить уравнение (3.1), учитывая разный порядок членов относительно ε, приравняем члены при производных прогиба к нулю. Получим задачи для нахождения локальных функций P и N. В первом приближении имеем:
(3.2)
$\begin{gathered} (P_{{i3}}^{{P{{Q}_{0}}}})' = 0,\quad {{{\mathbf{\xi }}}_{{\text{3}}}} \in {\text{[}} - {\text{0}}{\text{.5,0}}{\text{.5]}} \\ P_{{ij}}^{{P{{Q}_{0}}}}{{n}_{j}} = 0;\quad {{{\mathbf{\xi }}}_{{\text{3}}}} = - {\text{0}}{\text{.5,0}}{\text{.5}} \\ \end{gathered} $Решая систему (3.2), получим ненулевые функции [10, 12]:
Ключевым моментом здесь является стремление $N_{3}^{{P{{Q}_{0}}}}$ к конечному пределу, а именно – к нулю при стремлении δ к нулю. Производная имеет вид $(N_{3}^{{P{{Q}_{0}}}}){\kern 1pt} '\, = \,{{C}_{{33P{{Q}_{0}}}}}{{{\mathbf{\xi }}}_{3}}{\text{/}}{{C}_{{3333}}}$. Поэтому $P_{{ij}}^{{P{{Q}_{0}}}}({{{\mathbf{\xi }}}_{3}}) \to - {{C}_{{ijP{{Q}_{0}}}}}{{{\mathbf{\xi }}}_{3}}$ при $\delta \to 0$. С учетом того, что локальная функция $N_{3}^{{P{{Q}_{0}}}}$ найдена, можно найти функции $P_{{ij}}^{{P{{Q}_{0}}}}$. Решение этой задачи позволяет получить выражения для нахождения компонент σ11, σ12 и σ22.
Во втором приближении имеем:
(3.3)
$\begin{gathered} P_{{i{{Q}_{1}}}}^{{P{{Q}_{0}}}} + (P_{{i3}}^{{P{{Q}_{0}}{{Q}_{1}}}})' = 0,\quad {{{\mathbf{\xi }}}_{{\text{3}}}} \in {\text{[}} - {\text{0}}{\text{.5,0}}{\text{.5]}} \\ P_{{ij}}^{{P{{Q}_{0}}{{Q}_{1}}}}{{n}_{j}} = 0;\quad {{{\mathbf{\xi }}}_{{\text{3}}}} = - {\text{0}}{\text{.5,0}}{\text{.5}} \\ \end{gathered} $Решая систему (3.3), получим:
Константа C находится из соотношения $\langle N_{I}^{{P{{Q}_{0}}{{Q}_{1}}}}\rangle = 0$, где $\langle \Phi ({\mathbf{\zeta }})\rangle = \int\limits_{ - \frac{1}{2}}^{\frac{1}{2}} \Phi ({\mathbf{\zeta }})d{\mathbf{\zeta }}$. Таким образом, через функцию $N_{I}^{{P{{Q}_{0}}{{Q}_{1}}}}$ можно найти функции $P_{{ij}}^{{P{{Q}_{0}}{{Q}_{1}}}}$, которые позволяют получить выражения для компонент σ13 и σ23. Из предыдущей формулы видно, что для локальных функций второго приближения существуют конечные пределы при стремлении δ к нулю. Интересно заметить, что во втором приближении основные напряжения σ11, σ12, σ22 сохраняют линейное распределение, свойственное теории Рейсснера.
Аналогично можно рассмотреть третье приближение:
(3.4)
$\begin{gathered} P_{{i{{Q}_{2}}}}^{{P{{Q}_{0}}{{Q}_{1}}}} + (P_{{i3}}^{{P{{Q}_{0}}{{Q}_{1}}{{Q}_{2}}}}) = 0,\quad {{{\mathbf{\xi }}}_{{\text{3}}}} \in {\text{[}}{\kern 1pt} - {\kern 1pt} {\text{0}}{\text{.5,0}}{\text{.5]}} \\ P_{{ij}}^{{P{{Q}_{0}}{{Q}_{1}}{{Q}_{2}}}}{{n}_{j}} = 0,\quad {{{\mathbf{\xi }}}_{{\text{3}}}} = - {\text{0}}{\text{.5}} \\ P_{{ij}}^{{P{{Q}_{0}}{{Q}_{1}}{{Q}_{2}}}}{{n}_{j}} = {{D}_{{P{{Q}_{0}}{{Q}_{1}}{{Q}_{2}}}}}{\text{/}}{{\varepsilon }^{3}};\quad {{{\mathbf{\xi }}}_{{\text{3}}}} = {\text{0}}{\text{.5}} \\ \end{gathered} $Решая систему (3.4), получим:
Константа C снова находится из условия $\left\langle {N_{I}^{{P{{Q}_{0}}{{Q}_{1}}{{Q}_{2}}}}} \right\rangle = 0$, означающее что w является средним по толщине прогибом. Так же как в первом приближении функция $N_{3}^{{P{{Q}_{0}}{{Q}_{1}}{{Q}_{2}}}}$ стремится к нулю при стремлении к нулю параметра δ. Через функцию $N_{I}^{{P{{Q}_{0}}{{Q}_{1}}{{Q}_{2}}}}$ можно найти функции $P_{{ij}}^{{P{{Q}_{0}}{{Q}_{1}}{{Q}_{2}}}}$, которые позволят получить выражения для компоненты σ33, а также уточнения компонент σ11, σ12, σ22. Таким образом, в третьем приближении основные напряжения распределены в поперечном направлении нелинейно, так же как в теории [24].
Так что же меняется для сильно ортотропной пластине при δ → 0? Кроме увеличения толщины пластины согласно $\tilde {\varepsilon } = \varepsilon {\text{/}}\sqrt \delta $ изменяются модули, входящие в изгибные жесткости $D_{{IJ}}^{{PQ}}$. Вместо модулей ${{E}_{1}}{\text{/}}(1 - {{\nu }_{{12}}}{{\nu }_{{21}}}),{{E}_{2}}{\text{/}}(1 - {{\nu }_{{12}}}{{\nu }_{{21}}}),{{E}_{2}}{{\nu }_{{12}}}{\text{/}}(1 - {{\nu }_{{12}}}{{\nu }_{{21}}})$, входящих в закон Гука для плоского напряженного состояния, в пределе при δ → 0 получаем модули ${{C}_{{1111}}},\;{{C}_{{2222}}},\;{{C}_{{1122}}}$, входящие в двумерный закон Гука при плоском деформированном состоянии. Таким образом, сильно ортотропная пластина эквивалентна более толстой пластине с измененными жесткостями.
4. Моменты и перерезывающие силы. В предыдущей секции с помощью асимптотического разложения удалось удовлетворить уравнениям равновесия с точностью до $O({{{\mathbf{\varepsilon }}}^{3}})$. Разрешающее уравнение для прогиба w можно получить из граничного условия на верхней поверхности пластины, где приложена поперечная нагрузка [11]. Однако можно рассмотреть интегральные уравнения равновесия (см., например, [9, 10])) относительно поперечных сил ${{Q}_{I}} = \int\limits_{ - \frac{h}{2}}^{\frac{h}{2}} {{\sigma }_{{I3}}}{\kern 1pt} d{{x}_{3}}$ и моментов ${{M}_{{IJ}}} = \int\limits_{ - \frac{h}{2}}^{\frac{h}{2}} {{\sigma }_{{IJ}}}{\kern 1pt} {{x}_{3}}{\kern 1pt} d{{x}_{3}}$:
Представим прогиб в n-м приближении в виде: $w = {{w}^{0}} + \varepsilon {\kern 1pt} {{w}^{1}} + {{\varepsilon }^{2}}{\kern 1pt} {{w}^{2}} + \ldots + {{\varepsilon }^{n}}{\kern 1pt} {{w}^{n}}$. В первом приближении получаем ${{\sigma }_{{IJ}}} = \varepsilon {\kern 1pt} P_{{IJ}}^{{PQ}}{\kern 1pt} w_{{,PQ}}^{0}$. Домножив на ${{x}_{3}}$ и проинтегрировав по толщине пластины, получим:
Обозначим $D_{{IJ}}^{{P{{Q}_{0}} \ldots {{Q}_{m}}}} = \left\langle {{{{\mathbf{\xi }}}_{3}} \cdot P_{{IJ}}^{{P{{Q}_{0}} \ldots {{Q}_{m}}}}} \right\rangle $ – тензор изгибных жесткостей. Тогда:
(4.2)
$D_{{IJ}}^{{PQ}}{\kern 1pt} w_{{,IJPQ}}^{0} = \frac{1}{{{{e}^{3}}}}{{M}_{{IJ,JI}}} = - \frac{q}{{{{{\mathbf{\varepsilon }}}^{3}}}}$Поэтому в дальнейшем нагрузку q заменим на $p{{\varepsilon }^{3}}$.
Во втором приближении имеем:
Домножив на x3 и проинтегрировав по толщине пластины, получим:
Откуда с учетом уравнения, полученного в первом приближении, получим
(4.3)
$D_{{IJ}}^{{PQ}}{\kern 1pt} w_{{,IJPQ}}^{1} + D_{{IJ}}^{{PQ{{Q}_{1}}}}{\kern 1pt} w_{{,IJPQ{{Q}_{1}}}}^{0} = 0$Аналогично, в третьем приближении получаем разложение:
Домножив на x3 и проинтегрировав по толщине пластины, получим:
Отсюда с учетом уравнений, полученных в первых двух приближениях, получим:
(4.4)
$D_{{IJ}}^{{PQ}}{\kern 1pt} w_{{,IJPQ}}^{2} + D_{{IJ}}^{{PQ{{Q}_{1}}}}{\kern 1pt} w_{{,IJPQ{{Q}_{1}}}}^{1} + D_{{IJ}}^{{PQ{{Q}_{1}}{{Q}_{2}}}}{\kern 1pt} w_{{,IJPQ{{Q}_{1}}{{Q}_{2}}}}^{0} = 0$Таким образом прогиб пластины в третьем приближении ищется в виде w = w0 = = $\varepsilon {{w}^{1}} + {{\varepsilon }^{2}}{{w}^{2}}$, где функции wi в соответствии с (4.2), (4.3), (4.4) удовлетворяют дифференциальным уравнениям:
5. Классические теории изгиба пластины. Классическая теория пластин и оболочек, называемая теорией Кирхгофа (К) или Кирхгофа–Лява, соответствует первому приближению асимптотического разложения. Далее для упрощения записи принято: ${{x}_{1}} = x,\;{{x}_{2}} = y,\;{{x}_{3}} = z$. На основании предположений поле перемещений в рамках данной теории представляется в виде ${{u}_{1}} = - z\frac{{\partial w}}{{\partial x}}$, ${{u}_{2}} = - z\frac{{\partial w}}{{\partial y}}$, ${{u}_{3}} = w(x,y)$. Используется закон Гука для плоско-напряженного состояния:
(5.1)
$\begin{gathered} {{\sigma }_{{11}}} = \frac{1}{{1 - {{\nu }_{{12}}}{{\nu }_{{21}}}}}\left[ {{{E}_{1}}{{\varepsilon }_{{11}}} + {{E}_{2}}{{\nu }_{{12}}}{{\varepsilon }_{{22}}}} \right] \\ {{\sigma }_{{22}}} = \frac{1}{{1 - {{\nu }_{{12}}}{{\nu }_{{21}}}}}\left[ {{{E}_{2}}{{\varepsilon }_{{22}}} + {{E}_{1}}{{\nu }_{{21}}}{{\varepsilon }_{{11}}}} \right] \\ {{\sigma }_{{12}}} = {{G}_{{12}}}{{\gamma }_{{12}}} \\ \end{gathered} $В результате получается окончательное уравнение
(5.2)
${{D}_{1}}\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} + 2\left( {{{D}_{3}} + 2{{D}_{{12}}}} \right)\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{2}}\partial {{y}^{2}}}} + {{D}_{2}}\frac{{{{\partial }^{4}}w}}{{\partial {{y}^{4}}}} = q$Здесь использованы обозначения:
Асимптотическое исследование, приведенное выше, показывает, что сильная ортотропия пластины эквивалентна увеличению ее толщины. Поэтому теория К-Л не обеспечивает достаточную точность расчетов и целесообразно использовать теории более высокого порядка точности относительно параметра ε. Более точной теорией является теория Рейсснера. Уравнения данной теории построены на менее “жестком” предположении о поведении нормали, которая не остается нормальной к деформированной срединной поверхности, а поворачивается на некоторый угол: ${{u}_{1}} = - z{\kern 1pt} {{\varphi }_{1}}$, ${{u}_{2}} = - z{\kern 1pt} {{\varphi }_{2}}$, ${{u}_{3}} = w(x,y)$. Распределение напряжений ${{\sigma }_{{IJ}}}$ по толщине пластины остается линейным: ${{\sigma }_{{IJ}}} = \alpha \cdot z$, где $\alpha = {{M}_{{IJ}}}{\text{/}}{{h}^{3}}$. Это предположение позволяет в явном виде выписать выражения для компонент напряжений ${{\sigma }_{{i3}}}$. Из уравнений равновесия ${{\sigma }_{{IJ,J}}} + {{\sigma }_{{I3,3}}} = 0$, ${{\sigma }_{{I3,I}}} + {{\sigma }_{{33,3}}} = 0$ следует:
(5.3)
${{\sigma }_{{I3}}} = \frac{{3{{Q}_{I}}}}{{2h}}\left[ {1 - {{{\left( {\frac{{2z}}{h}} \right)}}^{2}}} \right],\quad {{\sigma }_{{33}}} = \frac{{3q}}{4}\left[ {\frac{2}{3} + \frac{{2z}}{h} - \frac{1}{3}{{{\left( {\frac{{2z}}{h}} \right)}}^{3}}} \right]$В рамках теории Рейсснера вводится сдвиговой корректирующий коэффициент $\kappa $:
(5.4)
${{Q}_{1}} = \kappa {{G}_{{13}}}h\left( { - {{\varphi }_{1}} + \frac{{\partial w}}{{\partial x}}} \right),\quad {{Q}_{2}} = \kappa {{G}_{{23}}}h\left( { - {{\varphi }_{2}} + \frac{{\partial w}}{{\partial y}}} \right)$Сдвиговой коэффициент зависит от формы поперечного сечения и коэффициента Пуассона. Было предложено множество инвариантов для выражения данного коэффициента. В статье [27] приводится обзор результатов расчета сдвигового коэффициента для балок с прямоугольным и круглым поперечным сечением различных авторов, который частично приведен в табл. 1 . В статье [28], в которой рассматривается третье приближение, приводится следующий результат для сдвигового коэффициента, исходя из асимптотического разложения: $\kappa = \frac{5}{6} + \frac{{29}}{6}\frac{\nu }{{12 - 7\nu }}$. В данной работе используется значение κ = 5/6, типичное для оригинальных работ Тимошенко, Рейсснера.
Для получения дифференциального уравнения изгиба пластины можно использовать закон Гука как для плоско-напряженного, так и для трехмерного состояния. Используя закон Гука для плоско-напряженного состояния (5.1), получим: M11 = = $\int\limits_{ - \frac{h}{2}}^{\frac{h}{2}} {{\sigma }_{{11}}} \cdot zdz = - {{D}_{1}}{\kern 1pt} {{\varphi }_{{1,1}}}\, - \,{{D}_{3}}{\kern 1pt} {{\varphi }_{{2,2}}},$ M22 = $\int\limits_{ - \frac{h}{2}}^{\frac{h}{2}} {{\sigma }_{{22}}} \cdot z\;dz = - {{D}_{2}}{{\varphi }_{{2,2}}} - {{D}_{3}}{{\varphi }_{{1,1}}},$ M12 = $\int\limits_{ - \frac{h}{2}}^{\frac{h}{2}} {{\sigma }_{{12}}} \cdot z\;dz$ = = –D12(φ1, 2 + φ2, 1). На основании (4.1) и (5.4) выражения для моментов имеют вид:
(5.5)
$\begin{gathered} {{M}_{{11}}} = - {{D}_{1}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} - {{D}_{3}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} + \frac{6}{{5h}}\left[ {\frac{{{{D}_{1}}}}{{{{G}_{{13}}}}} - \frac{{{{D}_{3}}}}{{{{G}_{{23}}}}}} \right]{{Q}_{{1,1}}} - \frac{{6{{D}_{3}}}}{{5{{G}_{{23}}}h}}q \\ {{M}_{{22}}} = - {{D}_{2}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} - {{D}_{3}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \frac{6}{{5h}}\left[ {\frac{{{{D}_{2}}}}{{{{G}_{{23}}}}} - \frac{{{{D}_{3}}}}{{{{G}_{{13}}}}}} \right]{{Q}_{{2,2}}} - \frac{{6{{D}_{3}}}}{{5{{G}_{{13}}}h}}q \\ {{M}_{{12}}} = - 2{{D}_{{12}}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial x\partial y}} + \;\frac{{6{{D}_{{12}}}}}{{5h}}\left( {\frac{1}{{{{G}_{{13}}}}}{\kern 1pt} {{Q}_{{1,2}}} + \frac{1}{{{{G}_{{23}}}}}{\kern 1pt} {{Q}_{{2,1}}}} \right) \\ \end{gathered} $Как следует из уравнений (4.1):
Подставив в данное уравнение (5.6) выражения для моментов системы (5.5), запишем дифференциальное уравнение изгиба ортотропной пластины относительно прогиба и перерезывающих сил в рамках теории Рейсснера (приняв гипотезу плоско-напряженного состояния):
Теперь используем закон Гука для трехмерного состояния: ε11 = (σ11 – ν12σ22 – ‒ ${{\nu }_{{13}}}{{\sigma }_{{33}}}){\text{/}}{{E}_{1}}$, ${{\varepsilon }_{{22}}} = ({{\sigma }_{{22}}} - {{\nu }_{{23}}}{{\sigma }_{{33}}} - {{\nu }_{{21}}}{{\sigma }_{{11}}}{\text{/}}{{E}_{2}}$, ${{\gamma }_{{12}}} = {{\sigma }_{{12}}}{\text{/}}{{G}_{{12}}}$. Поскольку распределение компонент напряжений σi3 по толщине пластины известно, то выразим из записанных выше соотношений компоненты σ11, σ12 и σ22 через ε11, ε22, γ12 и σ33:
Домножим каждое уравнение на z и проинтегрируем по толщине пластины:
Далее используем уравнения (5.4), связывающие функции φI и ${{w}_{{,I}}}$. Выражая из них φI через ${{w}_{{,I}}}$, с использованием первой группы уравнений (4.1) получим соотношения относительно прогиба и перерезывающих сил:
(5.7)
$\begin{gathered} {{M}_{{11}}} = - {{D}_{1}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} - {{D}_{3}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} + \frac{6}{{5h}}\left[ {\frac{{{{D}_{1}}}}{{{{G}_{{13}}}}} - \frac{{{{D}_{3}}}}{{{{G}_{{23}}}}}} \right]{{Q}_{{1,1}}} + \left[ {\frac{{{{h}^{2}}\left( {{{\nu }_{{13}}} + {{\nu }_{{12}}}{{\nu }_{{23}}}} \right)}}{{10\left( {1 - {{\nu }_{{12}}}{{\nu }_{{21}}}} \right)}} - \frac{{6{{D}_{3}}}}{{5{{G}_{{23}}}h}}} \right]q \\ {{M}_{{22}}} = - {{D}_{2}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} - {{D}_{3}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \frac{6}{{5h}}\left[ {\frac{{{{D}_{2}}}}{{{{G}_{{23}}}}} - \frac{{{{D}_{3}}}}{{{{G}_{{13}}}}}} \right]{{Q}_{{2,2}}} + \left[ {\frac{{{{h}^{2}}\left( {{{\nu }_{{23}}} + {{\nu }_{{13}}}{{\nu }_{{21}}}} \right)}}{{10\left( {1 - {{\nu }_{{12}}}{{\nu }_{{21}}}} \right)}} - \frac{{6{{D}_{3}}}}{{5{{G}_{{13}}}h}}} \right]q \\ {{M}_{{12}}} = - 2{{D}_{{12}}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial x\partial y}} + \;\frac{{6{{D}_{{12}}}}}{{5h}}\left( {\frac{1}{{{{G}_{{13}}}}}{\kern 1pt} {{Q}_{{1,2}}} + \frac{1}{{{{G}_{{23}}}}}{\kern 1pt} {{Q}_{{2,1}}}} \right) \\ \end{gathered} $Теперь подставив в уравнение (5.6) выражения для моментов системы (5.7), получим дифференциальное уравнение изгиба пластины относительно прогиба и перерезывающих сил в рамках теории Рейсснера с использованием закона Гука для трехмерного состояния:
Поскольку выполняется ${{Q}_{{1,111}}} + {{Q}_{{2,222}}} + {{Q}_{{1,212}}} + {{Q}_{{2,112}}} = \Delta \left( {{{Q}_{{1,1}}} + {{Q}_{{2,2}}}} \right) = - \Delta q$, то в рамках изотропного случая ${{D}_{1}} = {{D}_{2}} = {{D}_{3}} + 2{{D}_{{12}}} = D$, следовательно:
Конечно, последнее уравнение имеет смысл, если распределение поверхностной нагрузки достаточно гладкое.
В теории Рейсснера распределение напряжений σIJ по толщине пластины полагается линейным. Однако с ростом ортотропии линейность нарушается. Теории третьего порядка, в частности, описывают это. В соответствии [24], в рамках данной теории поле перемещений представляется в виде: ${{u}_{1}} = - z{{\varphi }_{1}} - \frac{{4{{z}^{3}}}}{{3{{h}^{2}}}}\left( { - {{\varphi }_{1}} + \frac{{\partial w}}{{\partial x}}} \right)$, u2 = –zφ2 – $\frac{{4{{z}^{3}}}}{{3{{h}^{2}}}}\left( { - {{\varphi }_{2}} + \frac{{\partial w}}{{\partial y}}} \right)$, ${{u}_{3}} = w(x,y)$.
Как и в теории Рейсснера, при получении дифференциального уравнения изгиба пластины в рамках теории третьего порядка можно использовать закон Гука как для плоско-напряженного состояния, так и для трехмерного. Компоненты εIJ записываются следующим образом:
Сначала используем закон Гука для плоско-напряженного состояния (5.1), получим соотношения:
Далее необходимо получить уравнения, связывающие функции φI и ${{w}_{{,I}}}$.
(5.8)
${{Q}_{I}} = {{G}_{{I3}}}\int\limits_{ - \frac{h}{2}}^{\frac{h}{2}} {{\gamma }_{{I3}}}{\kern 1pt} dz = {{G}_{{I3}}}\left( { - {{\varphi }_{I}} + {{w}_{{,I}}}} \right)\int\limits_{ - \frac{h}{2}}^{\frac{h}{2}} \left[ {1 - \frac{{4{{z}^{2}}}}{{{{h}^{2}}}}} \right]{\kern 1pt} dz = \frac{{2{{G}_{{I3}}}h}}{3}\left( { - {{\varphi }_{I}} + {{w}_{{,I}}}} \right)$Выражая из (5.8) функции φI через ${{w}_{{,I}}}$ и подставляя в систему, с использованием первой группы уравнений (4.1) получим выражения моментов через прогиб и перерезывающие силы:
(5.9)
$\begin{gathered} {{M}_{{11}}} = - {{D}_{1}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} - {{D}_{3}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} + \frac{6}{{5h}}\left[ {\frac{{{{D}_{1}}}}{{{{G}_{{13}}}}} - \frac{{{{D}_{3}}}}{{{{G}_{{23}}}}}} \right]{{Q}_{{1,1}}} - \frac{{6{{D}_{3}}}}{{5{{G}_{{23}}}h}}q \\ {{M}_{{22}}} = - {{D}_{2}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} - {{D}_{3}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \frac{6}{{5h}}\left[ {\frac{{{{D}_{2}}}}{{{{G}_{{23}}}}} - \frac{{{{D}_{3}}}}{{{{G}_{{13}}}}}} \right]{{Q}_{{2,2}}} - \frac{{6{{D}_{3}}}}{{5{{G}_{{13}}}h}}q \\ {{M}_{{12}}} = - 2{{D}_{{12}}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial x\partial y}} + \;\frac{{6{{D}_{{12}}}}}{{5h}}\left( {\frac{1}{{{{G}_{{13}}}}}{\kern 1pt} {{Q}_{{1,2}}} + \frac{1}{{{{G}_{{23}}}}}{\kern 1pt} {{Q}_{{2,1}}}} \right) \\ \end{gathered} $Подставив в уравнение (5.6) выражения для моментов системы (5.9), получим дифференциальное уравнение изгиба пластины, записанное относительно прогиба и перерезывающих сил, в рамках теории третьего порядка для плоско-напряженного состояния:
Видно, что уравнение получается таким же, как и для теории Рейсснера (для плоско-напряженного состояния).
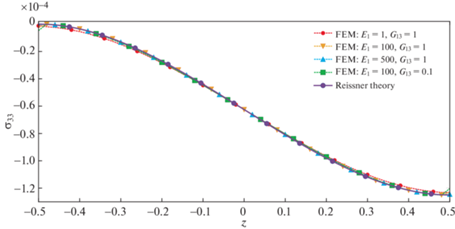
Теперь будем использовать закон Гука для трехмерного состояния. Использование распределения (5.3) для компоненты σ33 для теорий Рейсснера и теории третьего порядка обосновано сравнением с конечно-элементным решением. На рис. 1 сравниваются графики σ33. Видно хорошее совпадение. Для всех рассматриваемых примеров ${{E}_{2}} = {{E}_{3}} = 1$ ГПа, ${{\nu }_{{12}}} = {{\nu }_{{13}}} = {{\nu }_{{23}}} = 1{\text{/}}4$, ${{G}_{{12}}} = {{G}_{{23}}} = 1$ ГПа. Поскольку расчеты в рамках МКЭ производились на мелкой сетке, то это решение можно считать точным.
Используя распределение компоненты σ33 по толщине пластины, выразим из закона Гука компоненты σ11, σ12, σ22 через ε11, ε22, γ12 и σ33 и далее получим выражения для моментов:
(5.10)
$\begin{gathered} {{M}_{{11}}} = - {{D}_{1}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} - {{D}_{3}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} + \frac{6}{{5h}}\left[ {\frac{{{{D}_{1}}}}{{{{G}_{{13}}}}} - \frac{{{{D}_{3}}}}{{{{G}_{{23}}}}}} \right]{{Q}_{{1,1}}} + \left[ {\frac{{{{h}^{2}}\left( {{{\nu }_{{13}}} + {{\nu }_{{12}}}{{\nu }_{{23}}}} \right)}}{{10\left( {1 - {{\nu }_{{12}}}{{\nu }_{{21}}}} \right)}} - \frac{{6{{D}_{3}}}}{{5{{G}_{{23}}}h}}} \right]q \\ {{M}_{{22}}} = - {{D}_{2}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} - {{D}_{3}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \frac{6}{{5h}}\left[ {\frac{{{{D}_{2}}}}{{{{G}_{{23}}}}} - \frac{{{{D}_{3}}}}{{{{G}_{{13}}}}}} \right]{{Q}_{{2,2}}} + \left[ {\frac{{{{h}^{2}}\left( {{{\nu }_{{23}}} + {{\nu }_{{13}}}{{\nu }_{{21}}}} \right)}}{{10\left( {1 - {{\nu }_{{12}}}{{\nu }_{{21}}}} \right)}} - \frac{{6{{D}_{3}}}}{{5{{G}_{{13}}}h}}} \right]q \\ {{M}_{{12}}} = - 2{{D}_{{12}}}{\kern 1pt} \frac{{{{\partial }^{2}}w}}{{\partial x\partial y}} + \frac{{6{{D}_{{12}}}}}{{5h}}\left( {\frac{1}{{{{G}_{{13}}}}}{\kern 1pt} {{Q}_{{1,2}}} + \frac{1}{{{{G}_{{23}}}}}{\kern 1pt} {{Q}_{{2,1}}}} \right) \\ \end{gathered} $Подставив в уравнение (5.6) выражения для моментов системы (5.10), получим дифференциальное уравнение изгиба пластины в рамках теории третьего порядка, совпадающее с аналогичным уравнением в теории Рейсснера.
6. Вычислительные примеры. Цилиндрический изгиб пластины В декартовой системе координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ рассматривается цилиндрический изгиб ортотропной пластины постоянной толщины h, закрепленной шарнирно. На верхней поверхности пластины ${{x}_{3}} = h{\text{/}}2$ действует нагрузка $q({{x}_{1}})$ (рис. 2). Размеры задачи представлены безразмерными, поэтому h фактически есть $h{\text{/}}{{l}_{1}}$. Рассмотренные задачи являются статически определимыми.
Равномерно-распределенная нагрузка. Для $q(x) = - p{{h}^{3}} = {\text{const}}$, из уравнений равновесия имеем:
Расмотриваемые примеры есть статически определимые, что при нахождении прогиба позволяет использовать распределение поперечной силы и момента. Безусловно, это ограничивает общность рассмотрения.
Рассматривая последовательно первые три приближения и решая уравнения (4.2), (4.3), (4.4), получим прогиб пластины под действием равномерно-распределенной нагрузки в рамках асимптотической теории в третьем приближении:
Прогибы в рамках классических теорий выражаются следующими формулами.
По теории К:
По теории Рейсснера и теории третьего порядка в плоско-напряженном состоянии:
По теориям Рейсснера и теории третьего порядка в трехмерном состоянии:
Сосредоточенная нагрузка. Рассмотрим сосредоточенную нагрузку q(x1) = $P{{h}^{3}}{\kern 1pt} \delta ({{x}_{1}}$ – 1/2), где в качестве $\delta ({{x}_{1}} - 1{\text{/}}2)$ обозначена дельта-функция. Из условия равновесия получаем перерезывающую силу и изгибающий момент:
Обозначим за ${{w}^{ - }}$ – прогиб пластины $w(x)$ на отрезке $x \in [0;0.5]$, ${{w}^{ + }}$ – прогиб пластины w(x) на отрезке $x \in [0.5;1]$. Решая уравнения (4.2), (4.3), (4.4), получим прогиб пластины под действием сосредоточенной нагрузки в рамках асимптотической теории в третьем приближении:
Прогиб по теории К–Л имеет вид:
В рамках теории Рейсснера при гипотезе плоско-напряженного состояния следует последовательно найти сначала функцию φ1, а затем и прогиб w(x). Таким образом, получаем
Аналогично рассматривается трехмерное состояние. Оказывается, что функции φ1(x) для плоско-напряженного и трехмерного состояния совпадают, откуда следует совпадение прогиба пластины в рамках теории Рейсснера для трехмерного и плоско-напряженного состояний. А поскольку дифференциальное уравнение в рамках теории Рейсснера идентично теории третьего порядка, то решение в плоско-напряженном и трехмерном состоянии в рамках теории третьего порядка записывается аналогичным образом.
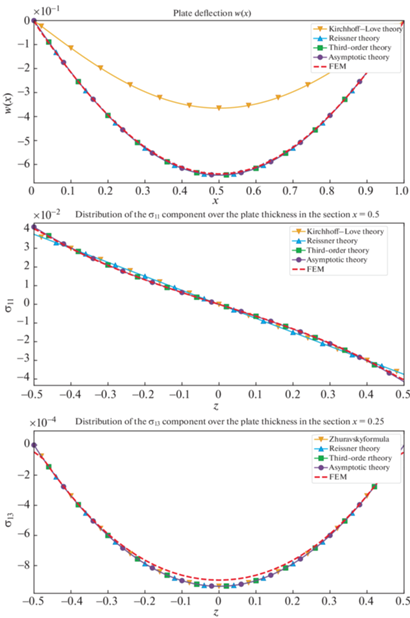
7. Сравнение теорий на примере однослойного волокнистого композита. Рассмотрим однонаправленный волокнистый резинокордный композит [29]. Простейшие формулы для эффективных свойств взяты из [30]:
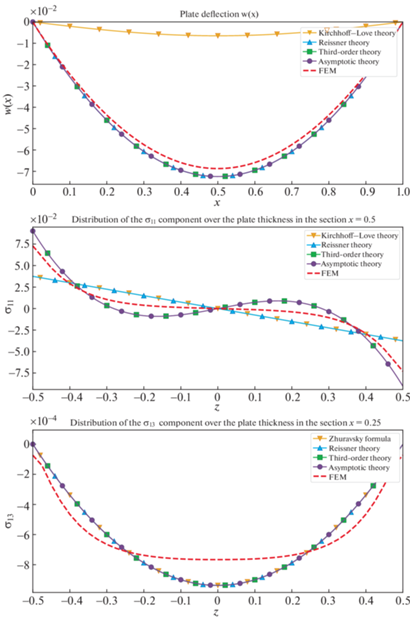
В соответствии с [30], принято, что ${{G}_{{13}}} = {{G}_{{12}}}$. Далее приводятся результаты расчетов для пластины толщины h = 1/20 под действием равномерно-распределенной нагрузки плотностью $q = - {{h}^{3}}$ и сосредоточенной нагрузки $P = {{h}^{3}}$. Материалом матрицы является резина с модулями Er = 0.015 Гпа, ${{\nu }_{r}} = 0.499$, в качестве корда используется текстильный корд или сталь. Для резинокордного слоя приведенные выше формулы признаются достаточными по точности. Эффективные свойства волокнистого композита для данных материалов корда представлены в табл. 2 .
Поскольку в рамках теории Кирхгофа поиск касательного напряжения σ13 не представляется возможным, то используется формула Журавского.
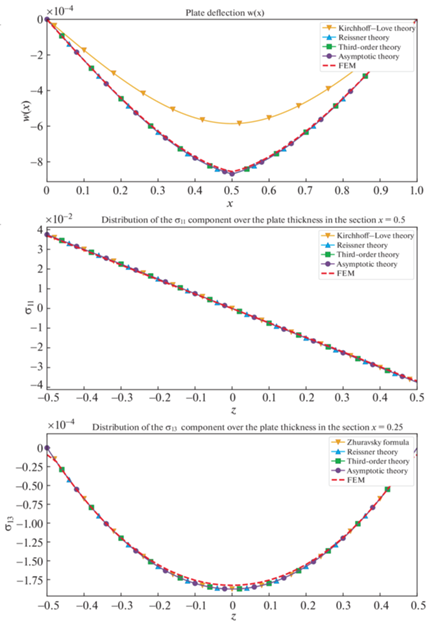
Расчеты, показанные на рис. 3, 4 показывают, что решение по теории третьего порядка совпадает с асимптотическим решением. Прогиб по теории Рейсснера также совпадает с прогибом по отмеченным теориям.
Материал резинокорда с текстильным кордом обладает умеренно большой ортотропией. Он используется в качестве каркаса радиальной шины. Как видно теории высшего порядка дают хорошее приближение. Однако прогиб по теории Кирхгофа получается совсем неточным. Зато изгибающее напряжение совпадает с напряжением по теории Рейсснера.
Однако картина распределения напряжений меняется при переходе к резинокордному материалу со стальным кордом, используемым в качестве брекера. Из рис. 4 видно, что прогибы, полученные по теориям 2-го и 3-го порядка близки друг к другу и к точному решению. Прогиб по теории Кирхгофа совершенно неточен. Но больший интерес вызывает распределение в поперечном направлении нормального изгибающего напряжения. Распределение по теориям Кирхгофа и Рейсснера совпадают и, конечно, линейные. Они сильно отличаются от распределения по теории третьего порядка и асимптотической теории. Последние совпадают между собой, но отличаются от точного решения. Более того, обе теории демонстрируют нефизичные перегибы графика. Распределение поперечного касательного напряжения одинаково для всех теорий высшего порядка и снова существенно отличается от точного распределения, полученного МКЭ.
Таким образом, можно сделать вывод, что для пластины из сильно ортотропного материала, такой как резинокорд брекера, точное решение целесообразно находить МКЭ, используя кусочно-линейную аппроксимацию в поперечном направлении.
Граница применимости теории. Как видно из продемонстрированных расчетов, при сильно выраженной ортотропии, когда отношение модулей ${{E}_{1}}$ и ${{G}_{{13}}}$ велико, теории могут проявлять нефизичное поведение компоненты напряжений σ11. Также неприемлемым оказывается асимптотическое приближение. Для цилиндрического изгиба выясним, когда наступает подобный эффект. Для этого запишем явное выражение для компоненты σ11 в рамках, например, теории третьего порядка.
Рассматривается цилиндрический изгиб пластины в рамках плоско-напряженного состояния, поэтому $w = w(x)$.
В соответствии с формулами (5.8), $ - {{\varphi }_{1}} + {{w}_{{,1}}} = 3{{Q}_{1}}{\text{/}}(2{{G}_{{13}}}h)$, откуда
Также из системы (5.9) следует:
В таком случае:
Поскольку ${{E}_{1}}{\text{/}}\left( {1 - {{\nu }_{{12}}}{{\nu }_{{21}}}} \right) = 12{{D}_{1}}{\text{/}}{{h}^{3}}$, то:
Таким образом компонента σ11 как функция от z имеет вид: $f(z) = a{\kern 1pt} z + b{\kern 1pt} {{z}^{3}}$, где:
Для того, чтобы функция $f(z) = az + b{{z}^{3}}$ была монотонной и не имела перегибов, необходимо выполнение условия: $a{\text{/}}b > 0$. Действительно, поскольку $f_{{}}^{'}(z) = a + 3b{{z}^{2}}$ и f ''(z) = 6bz, то если существует точка, отличная от нуля, в которой производная функции $f(z)$ принимает значение 0, то это точка локального минимума/максимума. А такие точки существуют, когда подкоренное выражение при решении уравнения $f_{{}}^{'}(z) = 0$ положительно, т.е. $ - a{\text{/}}3b > 0$. Таким образом получаем:
Поскольку ${{\nu }_{{21}}} = {{E}_{2}}{{\nu }_{{12}}}{\text{/}}{{E}_{1}}$, тогда окончательно:
В большинстве рассматриваемых случаев ${{E}_{1}} \gg {{E}_{2}}$, поэтому последнее неравенство принимает вид:
Таким образом, как показывает условие (7.1) отношение продольного модуля Юнга к поперечному модулю сдвига должно быть ограничено сверху, чтобы не возникало нефизичного распределения изгибающего напряжения.
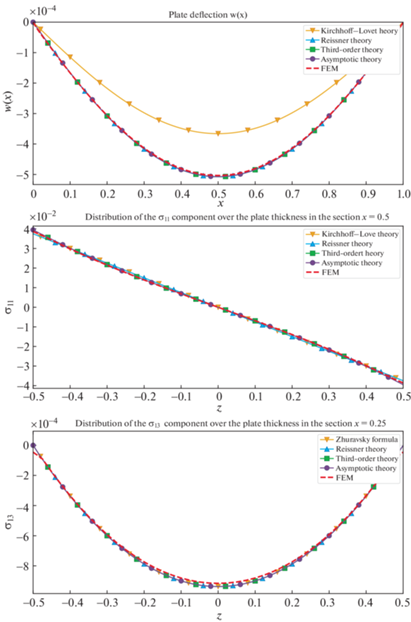
8. Пример полимерно-волокнистого композита. Рассмотрим еще один пример ортотропного материала, эффективные свойства которого соответствуют однонаправленному полимерно-волокнистому композиту (ПВК), волокна которого направлены вдоль оси 1. Эффективные свойства возьмем по формулам из [31]:
Рассмотрим композит с матрицей в виде эпоксидной смолы и углеродными волокнами. В табл. 3 в соответствии с [30] приводятся упругие модули, используемые при расчете эффективных свойств полидисперсной среды. Эффективные модули ПВК в соответствии с ранее определенными формулами приведены в табл. 4 . Далее приводятся результаты расчетов для равномерно-распределенной нагрузки плотностью $q = - p{{h}^{3}}$ и сосредоточенной нагрузки $q({{x}_{1}}) = P{{h}^{3}}\delta ({{x}_{1}} - 1{\text{/}}2)$, где в качестве $\delta ({{x}_{1}} - 1{\text{/}}2)$ обозначена дельта-функция.
9. Заключение. Предложено развитие асимптотической теории пластин до третьего порядка точности на случай сильно ортотропного материала. В этом случае в задаче имеется два малых параметра. В частном случае зависимости между параметрами исходную задачу с сильной ортотропией удалось свести к задаче для более толстой пластины, для которой метод асимптотического разложения применим в стандартном виде.
Асимптотическая теория сравнивается с классическими теориями Кирхгофа, Рейсснера и теорией третьего порядка. Показано, что для теории Рейсснера при сдвиговом коэффициенте κ = 5/6 и теории третьего порядка дифференциальные уравнения прогиба пластины принимают одинаковый вид. Следует отметить, что для однородной пластины используемое асимптотическое представление в первом приближении приводит к дифференциальным уравнениям, аналогичным теории Кирхгофа, а в третьем – теории третьего порядка Амбарцумяна. Теория Рейсснера находится как бы между ними, поскольку использует другое распределение основных напряжений по толщине пластины, чем третье приближение асимптотической теории и теории третьего порядка. Именно, распределение компонент ${{\sigma }_{{IJ}}}$ по толщине пластины для теории Рейсснера являются линейными, а для асимптотической теории и теории третьего порядка изменяются по кубическому закону.
Сравнение теорий проводилось для задачи цилиндрического изгиба для пластины под действием равномерно–распределенной или сосредоточенной нагрузок. Для верификации расчетов использовалось конечно–элементное решение на мелкой сетке.
Показано, что для резинокордного слоя брекера все рассмотренные теории не обеспечивают достаточной точности. При этом теория третьего порядка и асимптотическая теория приводят к нефизичному результату. Таким образом, существует граница применения данных теорий. Для столь сильно ортотропного материала целесообразно использовать кусочно-линейную аппроксимацию перемещений и основных напряжений в поперечном направлении.
Работа выполнена при поддержке Междисциплинарной научно-образовательной школы Московского университета “Фундаментальные и прикладные исследования космоса”.
Tаблица 1. Сдвиговой коэффициент $\kappa $
| Автор | Год | Прямоугольное сечение | Круглое сечение |
|---|---|---|---|
| Timoshenko | 1921 | 2/3 | – |
| Timoshenko | 1922 | $(5 + 5\nu ){\text{/}}(6 + 5\nu )$ | $(6 + 12\nu + 6{{\nu }^{2}}){\text{/}}(7 + 12\nu + 4{{\nu }^{2}})$ |
| Goens | 1931 | 5/6 | 9/10 |
| Olsson | 1934 | $(20 + 20\nu ){\text{/}}(24 + 15\nu )$ | – |
| Cowper | 1966 | $(10 + 10\nu ){\text{/}}(12 + 11\nu )$ | $(6 + 6\nu ){\text{/}}(7 + 6\nu )$ |
| Tanji et al | 1972 | $ \approx (6 + 12\nu + 6{{\nu }^{2}}){\text{/}}(7 + 12\nu + 4{{\nu }^{2}})$ | $ \approx (6 + 12\nu + 6{{\nu }^{2}}){\text{/}}(7 + 12\nu + 4{{\nu }^{2}})$ |
Tаблица 2. Эффективные свойства волокнистого композита для различных материалов корда
| Материал корда | γc | ${{E}_{c}}$ (GPa) | νc | ${{G}_{c}}$ (GPa) | ${{E}_{1}}$ | ${{E}_{2}}$ | ν12 | ${{G}_{{12}}}$ |
|---|---|---|---|---|---|---|---|---|
| Текстиль | 0.25 | 1.7 | 0 | 0.85 | 0.43 | 0.0053 | 0.37 | 0.0013 |
| Сталь | 0.12 | 200 | 0.25 | 80 | 24.0 | 0.023 | 0.47 | 0.0057 |
Список литературы
Янковский А.П. Применения явного по времени метода центральных разностей для численного моделирования динамического поведения упругопластически деформируемых гибких армированных пластин // Вычислительная механика сплошных сред. 2016. Т. 9. № 3. С. 279–297. https://doi.org/10.7242/1999-6691/2016.9.3.24
Sanchez-Palencia E. Non-homogeneous media and vibration theory. Berlin: Springer Berlin Heidelberg. 1980. 398 p. https://doi.org/10.1007/3-540-10000-8
Бахвалов Н.С., Панасенко Г.П. Осреднение процессов в периодических средах. Математические задачи механики композиционных материалов. М.: Наука. 1984. 352 с.
Победря Б.Е. Механика композиционных материалов. М.: Изд-во Моск. ун-та. 1984. 336 с.
Аннин Б.Д., Каламкаров А.Л., Колпаков А.Г., Партон B.З. Расчет и проектирование композиционных материалов и элементов конструкций. Новосибирск: Наука: Сиб. издат. 1993. 256 с.
Kohn R.V., Vogelius M. A new model of thin plates with rapidly varying thickness // Int. J. Solids Struct. 1984. V. 20. № 4. P. 333–350. https://doi.org/10.1016/0020-7683(84)90044-1
Levinski T., Telega J.J. Plates, laminates and shells. New York: World Scientific. 2000. https://doi.org/10.1142/3539
Панасенко Г.П., Резцов М.В. Осреднение трехмерной задачи теории упругости в неоднородной пластине // Докл. АН СССР. 1987. Т. 294. № 5. С. 1061–1065.
Шешенин С.В. Асимптотический анализ периодических в плане пластин // Изв. РАН. МТТ. 2006. № 6. С. 71–79.
Шешенин С.В. Применение метода осреднения к пластинам, периодическим в плане // Вестн. Моск. ун-та. Матем. Механ. 2006. С. 47–51.
Шешенин С.В., Скопцов К.А. Теория пластин, основанная на методе асимптотических разложений. // Мат. модел. числ. мет. 2014. № 2. С. 49–61.
Скопцов К.А., Шешенин С.В. Асимптотической анализ слоистых пластин и пологих оболочек // Изв. РАН. МТТ. 2011. № 1. С. 161–171.
Димитриенко Ю.И., Яковлев Д.О. Сравнительный анализ решений асимтотической теории многослойных тонких пластин и трехмерной теории упругости // Инженерный журнал: наука и инноваций. 2013. Т. 7. № 19. С. 17. https://doi.org/10.18698/2308-6033-2013-7-899
Шешенин С.В., Савенкова М.И. Осреднение нелинейных задач в механике композитов // Вестн. Моск. ун-та. Матем. Механ. 2012. № 5. С. 58–61.
Гольденвейзер А.Л. Теория тонких упругих оболочек. М.: Наука. 1976. 512 с.
Назаров А.А. Основы теории и методы расчета пологих оболочек. М.: Стройиздат. 1966. 304 с.
Гольденвейзер А.Л. Построение приближенной теории изгиба пластины методом асимптотического интегрирования уравнений теории упругости // ПММ. 1962. Т. 26. № 4. С. 668–686.
Гольденвейзер А.Л. О приближенных методах расчета тонких упругих оболочек и пластин // Изв. АН. МТТ. 1997. № 3. С. 134–149.
Гольденвейзер А.Л. Замечания о статье В.В. Васильева “Об асимптотическом методе обоснования теории пластин” // Изв. АН. МТТ. 1997. № 4. С. 150–157.
Васильев В.В. О теории тонких пластин // Изв. АН. МТТ. 1992. № 3. С. 26–47.
Васильев В.В. К дискуссии по классической теории пластин // Изв. АН. МТТ. 1995. № 4. С. 140–149.
Васильев В.В. Об асимптотическом методе обоснования теории пластин // Изв. АН. МТТ. 1997. № 3. С. 150–155.
Васильев В.В. Классическая теория пластин – история и современный анализ // Изв. АН. МТТ. 1998. № 3. С. 46–58.
Амбарцумян С.А. Общая теория анизотропных оболочек. М.: Наука. 1974. 448 p.
Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки. М.: Наука. 1966. 636 с.
Reissner E. The effect of transverse shear deformation on the bending of elastic plates // J. Appl. Mech. 1945. V. 12. № 2. P. A69–A77. https://doi.org/10.1115/1.4009435
Kaneko T. On Timoshenko’s correction for shear in vibrating beams // J. Phys. D: Appl. Phys. 1975. V. 8. № 16. P. 1927–1936. https://doi.org/10.1088/0022-3727/8/16/003
Шешенин С.В. Модуль механики композитов для пакета FYDESIS // Чебышевский сборник. 2017. Т. 18. № 3. С. 506–523. https://doi.org/10.22405/2226-8383-2017-18-3-506-523
Sheshenin S.V., Du Y. Homogenization of rubber-cord layers at moderately large deformations // Mech. Compos. Mater. 2021. V. 57. 3. P. 275–286. https://doi.org/10.1007/s11029-021-09953-2
Vasiliev V.V., Morozov E.V. Mechanics and analysis of composite materials. Oxford: Elsevier Science Techn. 2001. 424 p.
Кристенсен Р.М. Введение в механику композитов. М.: Мир. 1982. 336 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела