Известия РАН. Механика твердого тела, 2023, № 3, стр. 135-151

МОДЕЛЬ МИКРОМЕХАНИЧЕСКОГО МОДАЛЬНО-ЛОКАЛИЗОВАННОГО АКСЕЛЕРОМЕТРА С ЧУВСТВИТЕЛЬНЫМ ЭЛЕМЕНТОМ В ВИДЕ БАЛКИ С НАЧАЛЬНОЙ ПОГИБЬЮ

Д. А. Индейцев^a, b, Н. В. Можгова^b, *, А. В. Лукин^b, **, И. А. Попов^b, ***

^a Институт проблем машиноведения Российской академии наук
Санкт-Петербург, Россия

^b Санкт-Петербургский политехнический университет Петра Великого
Санкт-Петербург, Россия

^* E-mail: nmojgova@yandex.ru
^** E-mail: lukin_av@spbstu.ru
^*** E-mail: popov_ia@spbstu.ru

Поступила в редакцию 19.08.2022
После доработки 07.09.2022
Принята к публикации 08.09.2022

EDN: JLSWBB
DOI: 10.31857/S0572329922600645

Полный текст (PDF)

Аннотация

Настоящее исследование посвящено математическому моделированию предложенной новой архитектуры микроэлектромеханического модально-локализованного датчика ускорений (МЭМС-акселерометра/гравиметра) с чувствительным элементом в виде защемленной с двух концов микробалки с начальной погибью, выполненной по форме первой несимметричной моды свободных колебаний. В работе показано, что при несимметричной форме начальной погиби в области положительных осевых усилий существуют зоны близости частотных ветвей, соответствующих второй симметричной и первой несимметричной формам колебаний. При конструкционном обеспечении требуемого значения осевого растягивающего усилия в микробалке этот эффект может быть использован, в частности, для измерения осевой компоненты переносного ускорения по принципу амплитудной модальной локализации. Предусмотренная в компоновке датчика возможность нагрева чувствительного элемента с помощью протекающего по микробалке электрического тока позволяет управлять рабочей точкой режима колебаний и, таким образом, в весьма широких пределах варьировать диапазон измеряемых ускорений и степень чувствительности датчика. Предложенная в статье конфигурация электродов возбуждения колебаний и съема выходного сигнала позволяет, с помощью контура обратной связи, стабилизировать на требуемом уровне амплитуду колебаний по рабочей (третьей) симметричной форме и, при этом, измерять связанную с изменением величины измеряемой компоненты переносного ускорения амплитуду колебаний по несимметричной форме. Таким образом, в работе предложена и исследована математическая модель оригинального модально-локализованного акселерометра (гравиметра), содержащего единственный чувствительный микробалочный элемент и задействующего эффект обмена энергией между различными его формами колебаний.

Ключевые слова: МЭМС, балка с начальной погибью, бистабильность, акселерометр, модальная локализация колебаний, близость частот

1. Введение. Все большее распространение в современной индустрии нано- микроэлектромеханических систем (Н/МЭМС) находит использование существенно нелинейных характеристик проектируемых механических архитектур и принципов генерации колебаний, а также коллективных динамических свойств подвижных элементов устройств, что позволяет на порядки повысить точность и стабильность измерений для широкого класса датчиков физических величин [1]. Интенсивное развитие получают исследования и прикладные разработки в области применения особенностей модального взаимодействия в нелинейных и слабосвязанных колебательных системах с двумя и более степенями свободы.

Одной из приоритетных задач индустрии МЭМС является создание вибрационно и температурно устойчивых высокочувствительных элементов микромеханических систем инерциальной навигации (акселерометров, гравиметров, гироскопов). В части МЭМС-акселерометров и МЭМС-гравиметров, наряду с классическими амплитудно-модулированными схемами (см., например, [2]), интенсивно развивается направление разработки резонансных и модально-локализованных датчиков [3–6]. Основным принципом работы таких систем является влияние измеряемой компоненты ускорения подвижного объекта на рабочую частоту или вид собственной формы колебаний микромеханической архитектуры. В большом числе современных работ (см., к примеру, [7]) сообщается о том, что для модально-локализованных систем с контуром обратной связи по амплитуде может быть достигнута на порядки более высокая чувствительность, чем для датчиков с частотным выходом.

Значительный научный и практический интерес представляет изучение уникальных спектральных (модальных и резонансных) свойств микромеханических систем с проектируемыми возмущениями геометрии (начальной погибью балочных, пластинчатых и иных конструкций) и использование этих свойств для высокоточных измерений. Известен целый ряд работ, в которых демонстрируются возможности успешного практического использования подобных механических архитектур для задач высокоточных измерений: силы или переносного ускорения [8, 9], перемещений [10], скорости [11] и градиента скорости потока жидкости [12], газовых сенсоров [13, 14]. Известны также работы по использованию систем с начальной погибью в качестве актуаторов [15] и логических элементов перспективных вычислительных устройств [16]. На настоящий момент в большинстве созданных устройств в качестве чувствительного элемента применяется микробалка с начальной погибью, обладающая свойством бистабильности при действии постоянного электрического поля в межэлектродном зазоре.

Математическое моделирование и проектирование механических конструкций рассматриваемого класса требует использования весьма сложных геометрически и физически нелинейных моделей упругого деформирования континуальных систем. Этой группе вопросов посвящена обширная литература (см., к примеру, [17–29]). Отдельное интенсивно развивающееся направление исследований составляют задачи нелинейной статики и динамики микромеханических конструкций с проектируемыми возмущениями геометрии, действующих в электрических полях различных конфигураций. А именно, значительное число работ посвящено изучению вопросов ветвления, бифуркаций, нарушения симмметрии положений равновесия и режимов переключения между ними для микробалок с начальной погибью [30–39]. Особенности спектральных и нелинейных динамических характеристик таких конструкций также являются предметом обширной группы исследований [40–53]. Известны работы, посвященные вопросам синтеза алгоритмов управления колебаниями подобных систем и обработки выходных сигналов [54–56]. Активно развивается направление проектирования микромеханических датчиков с проектируемыми возмущениями геометрии более сложной формы: мембран и пластинок [57–64].

Эффект локализации колебаний между симметричной и несимметричной формами колебаний микробалки с начальной погибью изучается в работе [52]. В работе рассматривается симметричная форма начальной погиби и несколько видов электростатического нагружения, в том числе несимметричным полем, при котором наблюдается эффект локализации колебаний по указанным формам. В настоящей работе локализация колебаний возникает при возбуждении колебаний симметричным полем, но используется несимметричная форма начальной погиби микробалки.

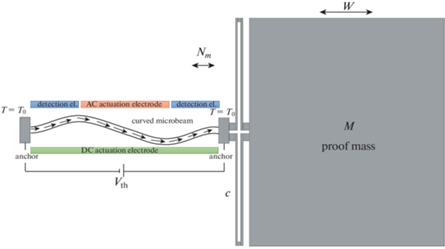
2. Предлагаемая модель акселерометра. Модель акселерометра, принцип действия которого основан на локализации колебаний, изображена на рис. 1. В качестве чувствительного элемента выступает начально изогнутая балка, защемленная с двух сторон, которая находится в поле действия одного неподвижного электрода возбуждения колебаний и двух неподвижных электродов съема колебаний. Электрическое напряжение, сообщенное концам балки, позволяет менять собственные частоты чувствительного элемента и настраиваться на рабочий режим. Подвижная масса M упруго прикреплена к микробалке с помощью системы подвесов. Внешнее ускорение приводит массу в движение и возникает распорное усилие N_m, действующее на микробалку. Рабочий режим возбуждается центральным электродом и представляет собой колебания по третьей (второй симметричной) собственной форме балки. При наличии внешнего ускорения распорное усилие изменяет значения собственных частот балки и при правильном выборе параметров системы наблюдается эффект близости частот между второй (первой несимметричной) и третьей (второй симметричной) формами колебаний чувствительного элемента. Происходит обмен энергией между указанными формами, и колебания по второй собственной форме детектируются боковыми электродами.

Рис. 1.

Модель модально-локализованного акселерометра.

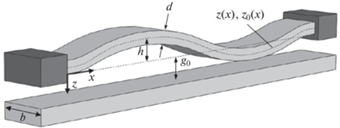
3. Математическая модель чувствительного элемента. Рассматривается изначально изогнутая микробалка длины $L$, заделанная с двух сторон и имеющая прямоугольное поперечное сечение с толщиной $d$ и шириной $b$ (рис. 2).

Рис. 2.

Начально изогнутая микробалка в поле одного электрода.

Балка изготовлена из однородного изотропного упругого материала с модулем Юнга E. Начальная форма балки описывается функцией ${{\hat {z}}_{0}}(\hat {x}) = \hat {h} \cdot {{w}_{0}}(\hat {x})$, где $\hat {h}$ – начальное отклонение верхней точки балки от средней линии в неискривленном положении и ${{w}_{0}}(\hat {x})$ – безразмерная функция, для которой выполняется условие $\mathop {\max }\limits_{\hat {x} \in [0,L]} {\text{|}}{{w}_{0}}(\hat {x}){\text{|}} = 1$. Балка находится в поле одного неподвижного электрода, находящегося на расстоянии ${{g}_{0}}$. Предполагается, что $d \ll L$ и что прогиб умеренно велик по сравнению с толщиной балки, поэтому имеется необходимость учета растяжения средней плоскости.

Уравнение динамики системы имеет вид:

(3.1)

$\begin{array}{*{20}{l}} {EI(\hat {z}{\kern 1pt} '{\kern 1pt} '{\kern 1pt} '{\kern 1pt} '\, - \hat {z}_{0}^{{''''}}) + \rho A\frac{{{{\partial }^{2}}\hat {z}}}{{\partial {{{\hat {t}}}^{2}}}} + c\frac{{\partial{ \hat {z}}}}{{\partial{ \hat {t}}}} = \left( {N + \frac{{EA}}{{2L}}\int\limits_0^L {(\hat {z}{\kern 1pt} {{'}^{2}}\, - \hat {z}_{0}^{{'2}})d\hat {x}} } \right)\hat {z}{\kern 1pt} '{\kern 1pt} '\, + F} \end{array}$

где $\hat {z}(\hat {x})$ – функция прогиба, $I = b{{d}^{3}}{\text{/}}12$ – момент инерции сечения балки, $\rho $ – плотность материала балки, c – коэффициент трения, N – распорное усилие, $A = bd$ – площадь поперечного сечения балки, $(){\kern 1pt} '$ – производная по координате $d{\text{/}}d\hat {x}$, $F$ – электростатическая сила, которая описывается следующим выражением:

(3.2)

$\begin{array}{*{20}{l}} {F = - \frac{1}{2}\frac{{\varepsilon bV_{{DC}}^{2}}}{{{{{({{g}_{0}} + \hat {z})}}^{2}}}}} \end{array}$

где $\varepsilon $ – относительная диэлектрическая проницаемость среды в зазоре, $b$ – ширина балки, ${{V}_{{DC}}}$ – амплитуда постоянной компоненты напряжения.

Распорное усилие N вызвано тремя факторами:

1. (${{N}_{{th}}}$) эффектом Джоуля, возникающим из-за протекающего тока вдоль балки,

2. (${{N}_{m}}$) инерционной силой, вызванной ускорением внешней массы M,

3. (${{N}_{0}}$) механическим усилием, вызванным преднапряженным состоянием балки (может быть как растягивающим, так и сжимающим):

(3.3)

$\begin{array}{*{20}{l}} {N = {{N}_{{th}}} + {{N}_{m}} + {{N}_{0}}} \end{array}$

Инерционная сила связана с ускорением массы следующим образом:

(3.4)

$\begin{array}{*{20}{l}} {{{N}_{m}} = MW} \end{array}$

где W – ускорение корпуса.

Уравнение теплопроводности в объеме балочного резонатора имеет вид:

(3.5)

$\begin{array}{*{20}{l}} { - \frac{d}{{d\hat {x}}}\left( {k\frac{{dT}}{{d\hat {x}}}} \right) = {{J}^{2}}{{\rho }_{e}}} \end{array}$

где $k$ – коэффициент теплопроводности материала балки, J – плотность тока, ${{\rho }_{e}}$ – удельное сопротивление материала балки. Предполагается, что свойства материала балки не зависят от температуры.

Плотность тока можно выразить через напряжение, прикладываемое на разные концы балки ${{V}_{{th}}}$:

$J = \frac{{{{V}_{{th}}}}}{{{{\rho }_{e}}L}}$

Тогда уравнение теплопроводности примет вид

(3.6)

$\begin{array}{*{20}{l}} { - k\frac{{{{d}^{2}}T}}{{d{{{\hat {x}}}^{2}}}} = \frac{{V_{{th}}^{2}}}{{{{\rho }_{e}}{{L}^{2}}}}} \end{array}$

Решением уравнения (3.6) является

(3.7)

$\begin{array}{*{20}{l}} {T(\hat {x}) = - \frac{{V_{{th}}^{2}}}{{k{{\rho }_{e}}{{L}^{2}}}}({{x}^{2}} + {{C}_{1}}x + {{C}_{2}})} \end{array}$

где константы интегрирования ${{C}_{1}},\;{{C}_{2}}$ определяются из граничных условий первого рода на торцах балки, там поддерживается температура окружающей среды ${{T}_{0}}$:

(3.8)

$\begin{array}{*{20}{l}} {T(0) = {{T}_{0}},\quad T(L) = {{T}_{0}}} \end{array}$

откуда

(3.9)

$\begin{array}{*{20}{l}} {{{C}_{1}} = - L,\quad {{C}_{2}} = - \frac{{{{T}_{0}}k{{\rho }_{e}}{{L}^{2}}}}{{V_{{th}}^{2}}}} \end{array}$

Таким образом, температура вдоль оси балки определяется выражением:

(3.10)

$\begin{array}{*{20}{l}} {T(\hat {x}) = - \frac{{V_{{th}}^{2}}}{{k{{\rho }_{e}}{{L}^{2}}}}({{x}^{2}} - Lx) + {{T}_{0}}} \end{array}$

Распорное усилие, вызванное эффектом Джоуля, зависит от температуры следующим образом:

(3.11)

$\begin{array}{*{20}{l}} {{{N}_{{th}}} = - \frac{{EA}}{L}\int\limits_0^L {\alpha (T[\hat {x}] - {{T}_{0}})d\hat {x}} = - \frac{{EAV_{{th}}^{2}\alpha }}{{6k{{\rho }_{e}}}}} \end{array}$

где α – коэффициент температурного расширения материала балки, ${{T}_{0}}$ – начальная температура балки, знак – означает, что усилие сжимающее.

Таким образом, уравнение движения начально изогнутой балки в поле одного неподвижного электрода с протекающим по ней током имеет вид:

(3.12)

$\begin{gathered} EI(\hat {z}{\kern 1pt} '{\kern 1pt} '{\kern 1pt} '{\kern 1pt} '\, - \hat {z}_{0}^{{''''}}) + \rho A\frac{{{{\partial }^{2}}\hat {z}}}{{\partial {{{\hat {t}}}^{2}}}} + c\frac{{\partial{ \hat {z}}}}{{\partial{ \hat {t}}}} = \\ \, = \left( {{{N}_{{th}}} + {{N}_{m}} + {{N}_{0}} + \frac{{EA}}{{2L}}\int\limits_0^L {(\hat {z}{\kern 1pt} {{'}^{2}}\, - \hat {z}_{0}^{{'2}})d\hat {x}} } \right)\hat {z}{\kern 1pt} '{\kern 1pt} '\, - \frac{1}{2}\frac{{\varepsilon bV_{{DC}}^{2}}}{{{{{({{g}_{0}} + \hat {z})}}^{2}}}} \\ \end{gathered} $

После введения безразмерных параметров

$z = \frac{{\hat {z}}}{{{{g}_{0}}}},\quad x = \frac{{\hat {x}}}{L},\quad t = \frac{{\hat {t}}}{T}$

где $T = \sqrt {\rho bd{{L}^{4}}{\text{/}}EI} $ – масштаб времени,

${{\alpha }_{1}} = 6{{\left( {\frac{{{{g}_{0}}}}{d}} \right)}^{2}},\quad {{c}_{{non}}} = \frac{{12c{{L}^{4}}}}{{ETb{{d}^{3}}}},\quad {{\alpha }_{2}} = \frac{{6\varepsilon {{L}^{4}}}}{{Eg_{0}^{3}{{d}^{3}}}},\quad \lambda = {{\alpha }_{2}}V_{{DC}}^{2}$

${{N}_{{non,th}}} = \frac{{12{{L}^{2}}}}{{Eb{{d}^{3}}}}{{N}_{{th}}},\quad {{N}_{{non,m}}} = \frac{{12{{L}^{2}}}}{{Eb{{d}^{3}}}}{{N}_{m}},\quad {{N}_{{non,0}}} = \frac{{12{{L}^{2}}}}{{Eb{{d}^{3}}}}{{N}_{0}}$

может быть получено уравнение в безразмерном виде:

(3.13)

$\begin{gathered} \frac{{{{\partial }^{4}}z}}{{\partial {{x}^{4}}}} - \frac{{{{\partial }^{4}}{{z}_{0}}}}{{\partial {{x}^{4}}}} + \ddot {z} + {{c}_{{non}}}\dot {z} = \\ \, = \left[ {{{\alpha }_{1}}\int\limits_0^0 {(z{\kern 1pt} {{'}^{2}}\; - z_{0}^{{'2}})dx} + {{N}_{{non,th}}} + {{N}_{{non,m}}} + {{N}_{{non,0}}}} \right]\frac{{{{\partial }^{2}}z}}{{\partial {{x}^{2}}}} - \frac{{{{\alpha }_{2}}V_{{DC}}^{2}}}{{{{{(1 + z)}}^{2}}}} \\ \end{gathered} $

где $(\mathop {}\limits^. )$ – производная по безразмерному времени d/dt.

В настоящей работе будет рассмотрена нелинейная задача о статическом равновесии, а также спектральная задача вблизи положений равновесия, найденных на первом этапе.

3.1. Уравнение статического равновесия системы. Уравнение статического равновесия в безразмерном виде:

(3.14)

$\begin{array}{*{20}{l}} {z{\kern 1pt} '{\kern 1pt} '{\kern 1pt} '{\kern 1pt} '\; - z_{0}^{{''''}} = \left[ {{{\alpha }_{1}}\int\limits_0^1 {(z{\kern 1pt} {{'}^{2}}\; - z_{0}^{{'2}})dx} + {{N}_{{non,th}}} + {{N}_{{non,m}}} + {{N}_{{non,0}}}} \right]z{\kern 1pt} '{\kern 1pt} '\; - \frac{{{{\alpha }_{2}}V_{{DC}}^{2}}}{{{{{(1 + z)}}^{2}}}}} \end{array}$

где $()'$ – производная по безразмерной координате d/dx.

Для получения модели пониженного порядка применяется метод Галеркина, то есть ищется приближенное решение уравнения (3.14) в виде:

(3.15)

$\begin{array}{*{20}{l}} {z(x) = {{\phi }_{0}}(x) + \sum\limits_{i = 1}^n {{C}_{i}}{{\phi }_{i}}} \end{array}$

где ${{\phi }_{0}}(x) = 0$, так как граничные условия задачи однородны.

Разложение (3.15) выполняется по ортогональным собственным формам прямой балки, удовлетворящим уравнению (3.16):

(3.16)

$\begin{array}{*{20}{l}} {\phi _{i}^{4} = \omega _{{non,i}}^{2}{{\phi }_{i}},\quad i = 1,2,...,n} \end{array}$

где $\omega _{{non,i}}^{2}$ – квадрат безразмерной собственной частоты.

С учетом разложения в ряд по собственным формам и граничных условий, уравнение статического равновесия приобретает вид

(3.17)

$\begin{gathered} \int\limits_0^1 {{{\phi }_{j}}} {{\left( {1 - \sum\limits_{l = 1}^n {{C}_{l}}{{\phi }_{l}}} \right)}^{2}}\left( {\sum\limits_{i = 1}^n {{C}_{i}}\omega _{{non,i}}^{2}{{\phi }_{i}}} \right)dx + \lambda \int\limits_0^1 {{{\phi }_{j}}dx} - \\ \, - {{\alpha }_{1}}\int\limits_0^1 {{{\phi }_{j}}} {{\left( {1 - \sum\limits_{l = 1}^n {{C}_{l}}{{\phi }_{l}}} \right)}^{2}}\left[ {\sum\limits_{i = 1}^n {{C}_{i}}\phi _{i}^{{''}}{{{\int\limits_0^1 {\left( {\sum\limits_{k = 1}^n {{C}_{k}}{{\phi }_{k}}} \right)} }}^{2}}} \right]dx = 0 \\ \end{gathered} $

где ${{\phi }_{i}}$ и C_i – собственные формы и коэффициенты при них соответственно.

Полученное алгебраическое уравнение относительно коэффициентов C_i разложения функции прогиба по собственным формам решается с помощью методов теории бифуркаций в программном комплексе MATLAB MATCONT [65].

3.2. Уравнение малых колебаний в окрестности положения равновесия. Уравнение динамики системы имеет вид

(3.18)

$\begin{array}{*{20}{l}} {{{z}^{{IV}}} - z_{0}^{{IV}} + \ddot {z} + {{c}_{{non}}}\dot {z} = \left[ {{{\alpha }_{1}}\int\limits_0^1 {(z{\kern 1pt} {{'}^{2}}\; - z_{0}^{{'2}})dx} + {{N}_{{non,th}}} + {{N}_{{non,m}}} + {{N}_{{non,0}}}} \right]z{\kern 1pt} '{\kern 1pt} '\; - \frac{\lambda }{{{{{(1 + z)}}^{2}}}}} \end{array}$

Безразмерную функцию прогиба $z(x,t)$ можно разложить на статическую часть ${{z}_{s}}$ (найденную из уравнения статического равновесия (3.14)) и динамическую компоненту, зависящую от времени z_d:

(3.19)

$\begin{array}{*{20}{l}} {z(x,t) = {{z}_{s}}(x) + {{z}_{d}}(x,t)} \end{array}$

Подстановка данного разложения в уравнение динамики приводит к уравнению относительно динамической составляющей функции прогиба:

(3.20)

$\begin{gathered} z_{s}^{{IV}} + z_{d}^{{IV}} - z_{0}^{{IV}} + {{{\ddot {z}}}_{d}} + {{c}_{{non}}}{{{\dot {z}}}_{d}} = \\ \, = \left[ {{{\alpha }_{1}}\int\limits_0^1 {((z_{s}^{'} + z_{d}^{'}{{)}^{2}} - z_{0}^{{'2}})dx} + {{N}_{{non,th}}} + {{N}_{{non,m}}} + {{N}_{{non,0}}}} \right]\frac{{{{\partial }^{2}}({{z}_{s}} + {{z}_{d}})}}{{\partial {{x}^{2}}}} - \frac{\lambda }{{{{{(1 + {{z}_{s}} + {{z}_{d}})}}^{2}}}} \\ \end{gathered} $

После раскрытия скобок, разложения члена электростатической силы в ряд Тейлора по функции ${{z}_{d}}$ и пренебрежения членами второго и более высоких порядков малости уравнение примет следующий вид:

(3.21)

$\begin{gathered} z_{s}^{{IV}} + z_{d}^{{IV}} - z_{0}^{{IV}} + {{{\ddot {z}}}_{d}} + {{c}_{{non}}}{{{\dot {z}}}_{d}} = {{\alpha }_{1}}\int\limits_0^1 {(z_{s}^{{'2}} - z_{0}^{{'2}})dxz_{s}^{{''}}} + {{\alpha }_{1}}\int\limits_0^1 {(z_{s}^{{'2}} - z_{0}^{{'2}})dxz_{d}^{{''}}} + \\ \, + 2{{\alpha }_{1}}\int\limits_0^1 {z_{s}^{'}z_{d}^{'}dxz_{s}^{{''}}} + ({{N}_{{non,th}}} + {{N}_{{non,m}}} + {{N}_{{non,0}}})(z_{s}^{{''}} + z_{d}^{{''}}) - \frac{\lambda }{{{{{(1 + {{z}_{s}})}}^{2}}}} + \frac{{2\lambda {{z}_{d}}}}{{{{{(1 + {{z}_{s}})}}^{3}}}} \\ \end{gathered} $

Часть слагаемых, составляющих уравнение статического равновесия, взаимно компенсируются. В предположении отсутствия диссипации ${{c}_{{non}}} = 0$ малые свободные колебания около статического равновесия определяются уравнением

(3.22)

$\begin{array}{*{20}{l}} \begin{gathered} z_{d}^{{IV}} + {{{\ddot {z}}}_{d}} = \left[ {{{\alpha }_{1}}\int_0^1 (z_{{s{\kern 1pt} }}^{{'2}} - z_{0}^{{'2}})dx + {{N}_{{non,th}}} + {{N}_{{non,m}}} + {{N}_{{non,0}}}} \right]z_{d}^{{''}} + \\ \, + 2{{\alpha }_{1}}\int\limits_0^1 {z_{s}^{'}z_{d}^{'}dxz_{s}^{{''}}} + \frac{{2\lambda {{z}_{d}}}}{{{{{(1 + {{z}_{s}})}}^{3}}}} \\ \end{gathered} \end{array}$

Аналогично уравнению статики, динамическая компонента функции прогиба также может быть разложена в ряд по собственным формам прямой балки:

(3.23)

$\begin{array}{*{20}{l}} {{{z}_{d}}(x,t) = \sum\limits_{i = 1}^n {{u}_{i}}(t){{\phi }_{i}}(x)} \end{array}$

Далее разложение подставляется в уравнение (3.22), четвертая производная заменится на соответствующее ей слагаемое согласно уравнению (3.16), а также все уравнение умножается на собственную форму ${{\phi }_{j}}$ и интегрируется от 0 до 1. В результате этих действий получена следующая система линейных ОДУ:

(3.24)

$\begin{gathered} {{{\ddot {u}}}_{j}} + \omega _{{non,j}}^{2}{{u}_{j}} = \left[ {{{\alpha }_{1}}\int\limits_0^1 {(z_{s}^{{'2}} - z_{0}^{{'2}})dx} + {{N}_{{non,th}}} + {{N}_{{non,m}}} + {{N}_{{non,0}}}} \right]\int\limits_0^1 {{{\phi }_{j}}} \sum\limits_{i = 1}^n {{u}_{i}}\phi _{i}^{{''}}dx + \\ \, + 2{{\alpha }_{1}}\int\limits_0^1 {{{\phi }_{j}}z_{s}^{{''}}} \left( {\int_0^1 z_{s}^{'}\sum\limits_{i = 1}^n dx} \right)dx + \int\limits_0^1 {{{\phi }_{j}}\frac{{2\lambda }}{{{{{(1 + {{z}_{s}})}}^{3}}}}} \sum\limits_{i = 1}^n {{u}_{i}}{{\phi }_{i}}dx,\quad j = 1,2,...,n \\ \end{gathered} $

Уравнение (3.24) представляет собой систему линейно связанных обыкновенных дифференциальных уравнений относительно модальных координат u_j. Решение задачи на собственные значения данной системы уравнений дает первые n собственных частот балки.

4. Диаграммы статического равновесия. В настоящем пункте приведены статические диаграммы положений равновесия, полученные путем продолжения по параметру постоянного электрического напряжения λ в уравнении (3.11).

Ниже на рисунке 3,b приведена зависимость прогиба в центре балки и в точках, соответствующих $\frac{1}{4}$ и $\frac{3}{4}$ длины балки от параметра статического напряжения. Маркерами отображены точки, в которых на рисунке 3,a изображены соответствующие им функции прогиба балки в процессе движения по бифуркационной диаграмме.

Рис. 3.

Диаграмма статического равновесия и функция прогиба микробалки. (a) – эволюция функции прогиба при движении по бифуркационной диаграмме, (b) – диаграмма равновесия (${{\alpha }_{1}} = 150,$ $h = 0.3,$ ${{N}_{{non}}} = 0$).

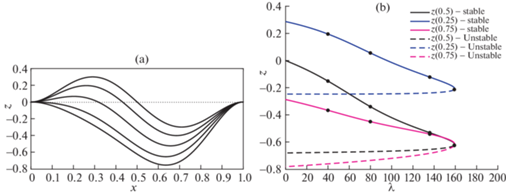
При несимметричной форме начальной погиби микробалка не обладает свойством бистабильности – существования двух различных устойчивых положений равновесия при одном значении электростатического напряжения.

5. Анализ малых колебаний в окрестности положения равновесия. Приведем результаты исследования частот и амплитуд малых колебаний вблизи положений равновесия, найденных ранее в п. 4. Ниже представлены результаты исследования зависимости собственных частот и форм изгибных колебаний балки при варьировании параметров электростатического напряжения $\lambda $ и распорного усилия N. Следует отметить, что при решении задачи на собственные значения для каждого значения указанных параметров использовалась функция статического прогиба ${{z}_{s}}$, найденная из уравнения (3.14) при текущих значениях параметров. На рис. 4 изображены зависимости первых трех частот изгибных колебаний балки при увеличении параметра статического напряжения.

Рис. 4.

Зависимость первых трех собственных частот микробалки от параметра статического напряжения $\lambda ,N = 0$.

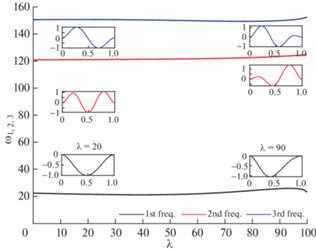
На рис. 5 изображены зависимости первых трех частот изгибных колебаний балки при варьировании параметра распорного усилия. Согласно уравнению (3.3), распорное усилие складывается из усилия механической природы, вызванного преднапряженным состоянием чувствительного элемента, нагрева вследствие эффекта Джоуля при протекании тока через балку, а также усилия, вызванного ускорением подвижной массы, что является полезным выходным сигналом прибора.

Рис. 5.

Зависимость первых трех собственных частот микробалки от параметра распорного усилия $N,\lambda = 0.$

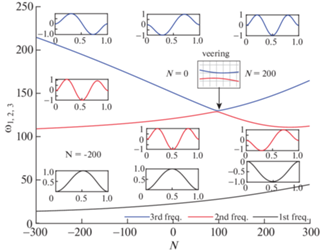
В положительной области по параметру N на рис. 5, то есть в области растяжения, наблюдается эффект близости частотных ветвей, соответствующих второй (первой несимметричной) и третьей (второй симметричной) собственным формам. Вид функции прогиба при значениях параметра N до и после области близости показывает, что частотные ветви также меняются местами после прохождения этой зоны. Аналогичный эффект близости указанных частотных ветвей наблюдается в работе [52] при возбуждении начально изогнутой микробалки несимметричным электростатическим полем.

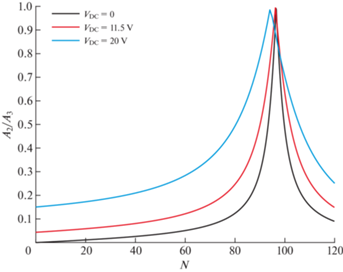
Для обнаружения эффекта локализации колебаний в данной зоне была построена зависимость отношения амплитуд колебаний на указанных частотных ветвях от параметра N, изображенная на рис. 6. Анализ данного графика показывает, что в системе наблюдается эффект локализации колебаний и обмена энергией между второй и третьей формами изгибных колебаний. Однако, эффект наблюдается в области растяжения чувствительного элемента, а настройка на рабочий режим происходит путем приложения разности потенциалов к торцам балки, что приводит к сжатию. Таким образом, необходимое значение параметра N₀, соответствующего начальному преднапряженному состоянию, равно примерно 110 безразмерных единиц.

Рис. 6.

Амплитудное отношение колебаний на второй и третьей собственных частотах.

Далее представлены зависимости частотных ветвей второй и третьей собственных форм в размерном виде и отношение амплитуд колебаний по данным формам относительно величины напряжения ${{V}_{{th}}}$ с учетом преднапряженного состояния ${{N}_{0}}$. Используемые числовые значения параметров системы приведены в таблице 1 (материал балки – изотропный кремний).

Таблица 1.

Числовые значения параметров системы

Величина	Значение	Величина	Значение
Длина балки	1000 мкм	Модуль Юнга кремния	170 ГПа
Толщина балки	2 мкм	Плотность кремния	2329 кг/м³
Ширина балки	25 мкм	Коэффициент теплопроводности кремния	130 Вт/(м · К)
Межэлектродный зазор	8 мкм	Удельная теплоемкость кремния	700 Дж/(кг · К)
Амплитуда начальной погиби	2.6 мкм	КЛТР кремния	2.6 × 10^–6 1/К
Осевое усилие N₀	2.5 × 10^–4 Н	Относительная диэлектрическая проницаемость воздуха	1

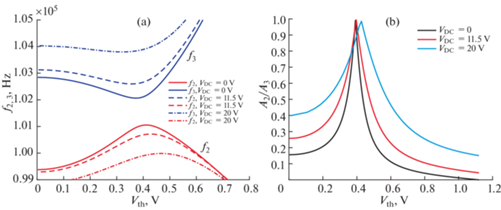
Из рис. 7 можно сделать вывод, что для сдвига рабочей точки прибора в нужном диапазоне требуется относительно небольшое значение управляющего напряжения – меньше 1 В.

Рис. 7.

Зависимость второй и третьей собственных частот и их амплитудного отношения от разности потенциалов на концах балки. (a) – зависимость частотных ветвей от ${{V}_{{th}}}$, (b) – зависимость отношения амплитуд от ${{V}_{{th}}}$.

Заключительным этапом данной работы является анализ чувствительности акселерометра в зависимости от выбора рабочей точки и соотношения масс чувствительного элемента и подвижной массы. Результаты исследования представлены в таблице 2, а также на рис. 8 представлены зависимости отношения амплитуд от величины внешнего измеряемого ускорения.

Таблица 2.

Сравнение выходных характеристик датчика при разных соотношениях масс и выборе рабочей точки

Отношение масс M/m	Рабочая точка, V	Частота f₃, кГц	Чувствительность $(A)$, млн^–1/g
100	${{V}_{{th}}} = 0.4$	102.1	8107
	${{V}_{{th}}} = 0.43$	102.3	4290
	${{V}_{{th}}} = 0.46$	102.6	2227
300	${{V}_{{th}}} = 0.4$	102.1	24 321
	${{V}_{{th}}} = 0.43$	102.3	12 869
	${{V}_{{th}}} = 0.46$	102.6	6682
500	${{V}_{{th}}} = 0.4$	102.1	40 535
	${{V}_{{th}}} = 0.43$	102.3	21 449
	${{V}_{{th}}} = 0.46$	102.6	11 137
1000	${{V}_{{th}}} = 0.4$	102.1	81 071
	${{V}_{{th}}} = 0.43$	102.3	42 898
	${{V}_{{th}}} = 0.46$	102.6	22 274

Рис. 8.

Зависимость отношения амплитуд колебаний по второй и третьей собственным формам от величины внешнего ускорения, ${{V}_{{th}}} = 0.43V$.

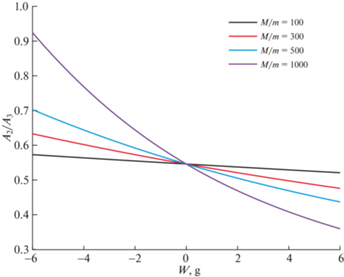
Исходя из результатов, представленных в таблице 2, можно сделать вывод о том, что при отношении массы подвижной части прибора к массе чувствительного элемента (балки) в диапазоне $M{\text{/}}m = [100,\,\,1000]$ чувствительность амплитудного выхода модально-локализованного акселерометра, описанного в данной работе, достигает величин порядка 80000 ppm/g. Величина относительной чувствительности акселерометра с амплитудным выходом сопоставима с характеристиками известных модально-локализованных акселерометров [66–68].

Заключение. В настоящей работе выполнено параметрическое исследование нелинейных задач статики и динамики малых колебаний для изначально искривленной микробалки как перспективного чувствительного элемента высокоточных резонансных датчиков различных физических величин. Изучен фактор формы начальной погиби микробалки. Показано, что при несимметричной форме начальной погиби в области положительных осевых усилий существуют зоны близости частотных ветвей, соответствующих второй симметричной и первой несимметричной формам колебаний. При конструкционном обеспечении требуемого значения осевого растягивающего усилия в микробалке этот эффект может быть использован, в частности, для измерения осевой компоненты переносного ускорения по принципу амплитудной модальной локализации. Предусмотренная в компоновке датчика возможность нагрева чувствительного элемента с помощью протекающего по микробалке электрического тока позволяет управлять рабочей точкой режима колебаний и, таким образом, в весьма широких пределах варьировать диапазон измеряемых ускорений и степень чувствительности датчика. Предложенная в статье конфигурация электродов возбуждения колебаний и съема выходного сигнала позволяет, с помощью контура обратной связи, стабилизировать на требуемом уровне амплитуду колебаний по рабочей (третьей) симметричной форме и, при этом, измерять связанную с изменением величины измеряемой компоненты переносного ускорения амплитуду колебаний по несимметричной форме. Таким образом, в работе предложена и исследована математическая модель оригинального модально-локализованного акселерометра (гравиметра), содержащего единственный чувствительный микробалочный элемент и задействующего эффект обмена энергией между различными его формами колебаний.

Поддержка. Исследование выполнено за счет гранта Российского научного фонда № 21-71-10009, https://rscf.ru/project/21-71-10009/.

Список литературы

Hajjaj A.Z., Jaber N., Ilyas S. et al. Linear and nonlinear dynamics of micro and nanoresonators: Review of recent advances // Int. J. Non-Lin. Mech. 2019. V. 119. https://doi.org/10.1016/j.ijnonlinmec.2019.103328
Belyaev Ya.V., Belogurov A.A., Bocharov A.N. et al. Design of a micromechanical accelerometer. // 25th Saint Petersburg Int. Conference on Integrated Navigation Systems (ICINS). IEEE, 2018. P. 1–7. https://doi.org/10.23919/ICINS.2018.8405921
Wang C., Chen F., Wang Y. et al. Micromachined Accelerometers with Sub-μg/Hz Noise Floor: A Review // Sensors. 2020. V. 20. P. 4054. https://doi.org/10.3390/s20144054
Morozov N.F., Indeitsev D.A., Igumnova V.S. et al. Nonlinear dynamics of mode-localized MEMS accelerometer with two electrostatically coupled microbeam sensing elements // Int. J. Non-Lin. Mech. 2022. V. 138. P. 103852. https://doi.org/10.1016/j.ijnonlinmec.2021.103852
Morozov N.F., Indeitsev D.A., Igumnova V.S. et al. A novel model of a mode-localized MEMS accelerometer // Dokl. Phys. 2020. V. 65. P. 371–375.
Morozov N.F., Indeitsev D.A., Igumnova V.S. et al. Effect of Nonlinearity on Mode Localization Phenomena in Dynamics of MEMS Resonant Sensor with Two Electrostatically Coupled Microbeams // Vest. St. Petersburg Univ. Math. 2021. V. 54. № 2. P. 135–144. https://doi.org/10.1134/S1063454121020072
Yang J., Zhong J., Chang H. A Closed-Loop Mode-Localized Accelerometer // J. Microelectromech. Syst. 2018. V. 27. № 2. P. 210–217. https://doi.org/10.1109/JMEMS.2017.2787544
Benjamin E., Lullinsky S., Krylov S. Bistable force/acceleration sensor based on pull-in voltage monitoring // 2016 IEEE International Symposium on Inertial Sensors and Systems. IEEE, 2016. P. 109–112. https://doi.org/10.1109/ISISS.2016.7435557
Benjamin E., Lullinsky S., Krylov S. Design and Implementation of a Bistable Force/Acceleration Sensing Device Considering Fabrication Tolerances // J. Microelectromech. Syst. 2018. V. 27. No. 5. P. 854–865. https://doi.org/10.1109/JMEMS.2018.2852621
Krakover N., Ilic B., Krylov S. Displacement Sensing Based on Resonant Frequency Monitoring of Electrostatically Actuated Curved Micro Beams // J. Micromech. Microeng. 2016. V. 26. P. 115006. https://doi.org/10.1088/0960-1317/26/11/115006
Kessler Y., Ilic B., Krylov S., Liberzon A. Flow Sensor Based on the Snap-Through Detection of a Curved Micromechanical Beam // J. Microelectromech. Syst. 2018. V. 27. № 6. P. 945–947. https://doi.org/10.1109/JMEMS.2018.2868776
Kessler Y., Liberzon A., Krylov S. Flow Velocity Gradient Sensing Using a Single Curved Bistable Microbeam // J. Microelectromech. Syst. 2020. V. 29. № 5. P. 1020–1025. https://doi.org/10.1109/JMEMS.2020.3012690
Hajjaj A., Jaber N., Alcheikh N., Younis M. A Resonant Gas Sensor Based on Multimode Excitation of a Buckled Microbeam // IEEE Sensors J. 2019. V. 20. № 4. P. 1778–1785. https://doi.org/10.1109/JSEN.2019.2950495
Najar F., Ghommem M., Abdel-Rahman E. Arch microbeam bifurcation gas sensors // Nonlin. Dyn. 2021. V. 104. P. 923–940. https://doi.org/10.1007/s11071-021-06319-0
Zhu R., Wallrabe U., Woias P. et al. Semi-rigid ring-shaped electrode dielectric electroactive polymer membrane as buckling actuator // J. Micromech. Microeng. 2019. V. 29. P. 055001. https://doi.org/10.1088/1361-6439/ab078d
Tella S., Younis M.I. Toward cascadable MEMS logic device based on mode localization // Sens. Actuators, A. 2020. V. 315. P. 112367. https://doi.org/10.1016/j.sna.2020.112367
Rega G., Lacarbonara W., Nayfeh A. Reduction Methods for Nonlinear Vibrations of Spatially Continuous Systems with Initial Curvature// IUTAM Symposium on Recent Developments in Non-linear Oscillations of Mechanical Systems. Solid Mechanics and Its Applications. Vol. 77 / Ed. by N.Van Dao, E.J.Kreuzer Dordrecht: Springer, 2000. P. 235–246. https://doi.org/10.1007/978-94-011-4150-5_24.
Cao D.Q., Liu D., Wang C. Nonlinear dynamic modelling for MEMS components via the Cosserat rod element approach // J. Micromech. Microeng. 2005. V. 15. P. 1334. https://doi.org/10.1088/0960-1317/15/6/027
Lacarbonara W., Yabuno H. Refined models of elastic beams undergoing large in-plane motions: Theory and experiment // Int. J. Solids Struct. 2005. V. 43. № 17. P. 5066–5084. https://doi.org/10.1016/j.ijsolstr.2005.07.018
Srinil N., Rega G., Chucheepsakul S. Two-to-one resonant multi-modal dynamics of horizontal/inclined cables. Part I: Theoretical formulation and model validation // Nonlin. Dyn. 2007. V. 48. P. 231–252. https://doi.org/10.1007/s11071-006-9086-0
Srinil N., Rega G. Two-to-one resonant multi-modal dynamics of horizontal/inclined cables. Part II: Internal resonance activation, reduced-order models and nonlinear normal modes // Nonlin. Dyn. 2007. V. 48. P. 253–274. https://doi.org/10.1007/s11071-006-9087-z
Cao D.Q., Tucker R. Nonlinear dynamics of elastic rods using the Cosserat theory: Modelling and simulation // J. Solids Struct. 2008. V. 45. P. 460–477. https://doi.org/10.1016/j.ijsolstr.2007.08.016
Luo A.C.J. On a nonlinear theory of thin rods // Communications in Nonlinear Science and Numerical Simulation. 2010. V. 15. № 12. P. 4181–4197. https://doi.org/10.1016/j.cnsns.2010.01.043
Vlajic N., Fitzgerald T., Nguyen V., Balachandran B. Geometrically exact planar beams with initial pre-stress and large curvature: Static configurations, natural frequencies, and mode shapes // Int. J. Solids Struct. 2014. V. 51. P. 3361–3371. https://doi.org/10.1016/j.ijsolstr.2014.05.026
Lembo M. Exact solutions for post-buckling deformations of nanorods // Acta Mech. 2017. V. 228. P. 2283–2298. https://doi.org/10.1007/s00707-017-1834-3
Zhou Y., Yi Z., Stanciulescu I. Nonlinear Buckling and Postbuckling of Shallow Arches With Vertical Elastic Supports // J. Appl. Mech. 2019. V. 86. № 6. P. 0610011. https://doi.org/10.1115/1.4042572
Nicoletti R. On the natural frequencies of simply supported beams curved in mode shapes // J. Sound Vibr. 2020. V. 485. P. 115597. https://doi.org/10.1016/j.jsv.2020.115597
Pandurangi S., Elliott R., Healey T., Triantafyllidis N. Stable Spatially Localized Configurations in a Simple Structure – A Global Symmetry-Breaking Approach // J. Elasticity. 2020. V. 142. P. 163–199. https://doi.org/10.1007/s10659-020-09794-5
Emam S., Lacarbonara W. Buckling and postbuckling of extensible, shear-deformable beams: Some exact solutions and new insights // Int. J. Non-Lin. Mech. 2021. V. 129. P. 103667. https://doi.org/10.1016/j.ijnonlinmec.2021.103667
Medina L., Gilat R., Krylov S. Symmetry breaking in an initially curved micro beam loaded by a distributed electrostatic force // Int. J. Solids Struct. 2012. V. 49. P. 1864–1876. https://doi.org/10.1016/j.ijsolstr.2012.03.040
Medina L., Gilat R., Krylov S. Symmetry breaking in an initially curved pre-stressed micro beam loaded by a distributed electrostatic force // Int. J. Solids Struct. 2014. V. 51. P. 2047. https://doi.org/10.1016/j.ijsolstr.2014.02.010
Shojaeian M., Beni T.Y., Ataei H. Size-dependent snap-through and pull-in instabilities of initially curved pre-stressed electrostatic nano-bridges // J. Phys. D: Appl. Phys. 2016. V. 49. P. 295303. https://doi.org/10.1088/0022-3727/49/29/295303
Medina L., Gilat R., Krylov S. Latching in bistable electrostatically actuated curved micro beams // Int. J. Eng. Sci. 2017. V. 110. P. 15–34. https://doi.org/10.1016/j.ijengsci.2016.10.001
Medina L., Gilat R., Krylov S. Bow Actuator: Low Voltage Switching in Electrostatically Actuated Bistable Beams // Proc. of the ASME 2018 Int. Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 4: 23rd Design for Manufacturing and the Life Cycle Conference; 12th International Conference on Micro- and Nanosystems. ASME, 2018. P.V004T08A009.https://doi.org/10.1115/DETC2018-85534
Sharma A., Godara R.K., Joglekar M. Static and DC dynamic pull-in analysis of curled microcantilevers with a compliant support // Microsyst. Technol. 2019. V. 25. P. 965–975. https://doi.org/10.1007/s00542-018-4046-4
Medina L., Gilat R., Krylov S. Dynamic release condition in latched curved micro beams // Commun. Nonlin. Sci. Numeric. Simulat. 2019. V. 73. P. 291–306. https://doi.org/10.1016/j.cnsns.2019.01.022
Medina L., Seshia A. Bistability and simultaneous mode actuation in electrostatically actuated initially curved coupled micro beams // Int. J. Non-Lin. Mech. 2020. V. 126. P. 103549. https://doi.org/10.1016/j.ijnonlinmec.2020.103549
Medina L., Seshia A. Tristable properties and limit point behaviour in electrostatically actuated initially curved coupled micro beams // Int. J. Mech. Sci. 2021. V. 204. P. 106543. https://doi.org/10.1016/j.ijmecsci.2021.106543
Medina L., Gilat R., Ilic B., Krylov S. Single Electrode Bidirectional Switching of Latchable Prestressed Bistable Micromechanical Beams // IEEE Sens. J. 2021. V. 21. № 19, P. 21349–21358. https://doi.org/10.1109/JSEN.2021.3103265
Lacarbonara W., Arafat H., Nayfeh A. Non-linear interactions in imperfect beams at veering // Int. J. Non-Lin. Mech. 2005. V. 40. P. 987–1003. https://doi.org/10.1016/j.ijnonlinmec.2004.10.006
Alkharabsheh S., Younis M. Statics and Dynamics of MEMS Arches Under Axial Forces // J. Vibr. Acoust. 2013. V. 135. P. 021007. https://doi.org/10.1115/1.4023055
Hajjaj A., Alcheikh N., Younis M. The static and dynamic behavior of MEMS arch resonators near veering and the impact of initial shapes // Int. J. Non-Lin. Mech. 2017. V. 95. P. 277–286 https://doi.org/10.1016/j.ijnonlinmec.2017.07.002
Alqasimi E.J., Ouakad M.H. Vibrational Response of Initially Deformed Bi-stable Microbeams Under the Combined Effect of Mechanical Shock Loads and Electrostatic Forces // J. Vibr. Acoust. 2017. V. 140. № 2. P. 021013. https://doi.org/10.1115/1.4038107
Ghayesh M., Farokhi H. Bistable nonlinear response of MEMS resonators // Nonlin. Dyn. 2017. V. 90. P. 1627–1645. https://doi.org/10.1007/s11071-017-3753-1
Alfosail K.F., Hajjaj Z.A., Younis I.M. Theoretical and Experimental Investigation of Two-to-One Internal Resonance in MEMS Arch Resonators // J. Computat. Nonlin. Dyn. 2018. V. 14. P. 011001. https://doi.org/10.1115/1.4041771
Tausiff M., Ouakad H.M., Alqahtani H., Alofi A. Local nonlinear dynamics of MEMS arches actuated by fringing-field electrostatic actuation // Nonlin. Dyn. 2019. V. 95. https://doi.org/10.1007/s11071-018-4731-y
Ouakad M.H., Najar F. Nonlinear Dynamics of MEMS Arches Assuming Out-of-Plane Actuation Arrangement // J. Vibr. Acoust. 2019. V. 141. № 4. P. 041010. https://doi.org/10.1115/1.4043064
Hajjaj A., Alfosail F., Jaber N. et al. Theoretical and experimental investigations of the crossover phenomenon in micromachined arch resonator: part I – linear problem // Nonlin. Dyn. 2020. V. 99, P. 393–405.https://doi.org/10.1007/s11071-019-05251-8
Hajjaj A., Alfosail F., Jaber N. et al. Theoretical and experimental investigations of the crossover phenomenon in micromachined arch resonator: part II – simultaneous 1:1 and 2:1 internal resonances // Nonlin. Dyn. 2020. V. 99. P. 407–432. https://doi.org/10.1007/s11071-019-05242-9
Alneamy A.M., Khater M.E., Al-Ghamdi M.S. et al. Large Oscillation of Electrostatically Actuated Curved Beams // J. Micromech. Microeng. 2020. V. 30. P. 095005. https://doi.org/10.1088/1361-6439/ab94d1
Alcheikh N., Ouakad H.M., Ben Mbarek S., Younis M.I. Investigations Into the Linear Coupling Between Symmetric and Anti-Symmetric Modes of V-Shaped MEMS Resonators Under Electrostatic Perturbation. // Proceedings of the ASME 2021 International Mechanical Engineering Congress and Exposition. Volume 7A: Dynamics, Vibration, and Control. ASME, 2021. P. V07AT07A029.https://doi.org/10.1115/IMECE2021-73535
Alcheikh N., Ouakad H.M., Ben Mbarek S., Younis M.I. Crossover/Veering in V-Shaped MEMS Resonators // J. Microelectromech. Syst. 2021. V. 31. № 1. P. 74–86. https://doi.org/10.1109/JMEMS.2021.3126551
Rosenberg S., Shoshani O. Zero-dispersion point in curved micro-mechanical beams // Nonlin. Dyn. 2022. V. 107. P. 1–14. https://doi.org/10.1007/s11071-021-07015-9
Medina L., Gilat R., Ilic R., Krylov S. Open Loop, Self-Excitation in a Bistable Micromechanical Beam Actuated By a DC Electrostatic Load // Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 4: 22nd Design for Manufacturing and the Life Cycle Conference; 11th International Conference on Micro- and Nanosystems. ASME, 2017. P. V004T09A006.https://doi.org/10.1109/MEMSYS.2017.7863525
Rajaei A., Vahidi-Moghaddam A., Ayati M., Baghani M. Integral sliding mode control for nonlinear damped model of arch microbeams // Microsyst. Technol. 2019. V. 25. P. 57–68. https://doi.org/10.1007/s00542-018-3931-1
Kessler Y., Liberzon A., Krylov S. On Sampling Rate Limits in Bistable Microbeam Sensors // J. Microelectromech. Syst. 2021. V. 6. P. 980–989.https://doi.org/10.1109/JMEMS.2021.3117838
Medina L., Gilat R., Krylov S. Bistable behavior of electrostatically actuated initially curved micro plate // Sens. Actuat. A: Phys. 2016. V. 248. https://doi.org/10.1016/j.sna.2016.07.027
Saghir S., Bellaredj M.L., Ramini A., Younis M.I. Initially curved microplates under electrostatic actuation: Theory and experiment // J. Micromech. Microeng. 2016. V. 26. https://doi.org/10.1088/0960-1317/26/9/095004
Medina L., Gilat R., Krylov S. On The Usage of Berger’s Model for Electrostatically Actuated Circular Curved Micro Plates. // Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 4: 22nd Design for Manufacturing and the Life Cycle Conference; 11th International Conference on Micro- and Nanosystems. ASME, 2017. P.V004T09A006. https://doi.org/10.1115/DETC2017-67523
Medina L., Gilat R., Krylov S. Bistability criterion for electrostatically actuated initially curved micro plates // Int. J. Eng. Sci. 2018. V. 130. P. 75–92. https://doi.org/10.1016/j.ijengsci.2018.05.006
Saghir S., Younis I.M. An investigation of the mechanical behavior of initially curved microplates under electrostatic actuation // Acta Mech. 2018. V. 229. P. 2909–2922. V. 229. https://doi.org/10.1007/s00707-018-2141-3
Ghayesh H.M., Farokhi H. Nonlinear behaviour of electrically actuated microplate-based MEMS resonators // Mech. Syst. Signal Proc. 2018. V. 109. P. 220–234. https://doi.org/10.1016/j.ymssp.2017.11.043
Dorfmeister M., Kossl B., Schneider M. et al. Switching performance of bistable membranes activated with integrated piezoelectric thin film transducers // J. Micromech. Microeng. 2019. V. 29. P. 105008. https://doi.org/10.1088/1361-6439/ab3185
Asher A., Benjamin E., Medina L. et al. Bistable Micro Caps Fabricated by Sheet Metal Forming // J. Micromech. Microeng. 2020. V. 30. P. 065002. https://doi.org/10.1088/1361-6439/ab7f52
Dhooge A., Govaerts W., Kuznetsov A. Y. MATCONT: a MATLAB package for numerical bifurcation analysis of ODEs // ACM Transactions on Mathematical Software (TOMS). 2003. V. 29. № 2. P. 141–164.
Guo X., Yang B., Li C., Liang Z. Enhancing output linearity of weakly coupled resonators by simple algebraic operations // Sens. Actuat. A: Phys. 2021. V. 325. P. 112696.
Kang H., Yang J., Chang H. A closed-loop accelerometer based on three degree-of-freedom weakly coupled resonator with self-elimination of feedthrough signal // IEEE Sensors J. 2018. V. 18. № 10. P. 3960–3967.
Zhang H.M., Yuan W.Z., Li B.Y. et al. A novel resonant accelerometer based on mode localization of weakly coupled resonators // Transducers-2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS). IEEE, 2015. P. 1073–1076.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал