1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 3, 2023

Известия РАН. Механика твердого тела, 2023, № 3, стр. 152-162

ОБ ОЦЕНКЕ ЧУВСТВИТЕЛЬНОСТИ КОЭФФИЦИЕНТОВ МОДЕЛЕЙ ДЛЯ НЕОДНОРОДНЫХ ТЕЛ

А. О. Ватульян a, *, В. О. Юров a, b, **

a Южный федеральный университет
Ростов-на-Дону, Россия

b Южный математический институт – филиал ВНЦ РАН
Владикавказ, Россия

* E-mail: aovatulyan@sfedu.ru
** E-mail: vitja.jurov@yandex.ru

Поступила в редакцию 26.11.2022
После доработки 05.12.2022
Принята к публикации 06.12.2022

Полный текст (PDF)

Аннотация

Рассмотрена задача об определении характеристик чувствительности неоднородных изотропных упругих тел по отношению к трем функциям, характеризующим неоднородность – коэффициентам Ламе и плотности. Сформулированы соответствующие краевые задачи, получены формулы для определения чувствительности. Представлен пример для цилиндрического стержня при анализе продольных и изгибных колебаний, проанализирована чувствительность к изменению модуля Юнга и плотности. При помощи итерационного алгоритма и метода регуляризации А.Н. Тихонова решен ряд обратных задач по определению этих характеристик для монотонных и немонотонных законов их изменения, представлены результаты вычислительных экспериментов. Проанализирована норма разности точного и восстановленного решений. Даны рекомендации по выбору частотного диапазона для зондирования, наиболее эффективного с точки зрения реконструкции.

Ключевые слова: чувствительность, неоднородность, цилиндр, стержень, обратная задача, слабая постановка, производные по Фреше

Введение. В последние годы при решении многих задач механики деформируемого твердого тела, особенно при изучении идентификации параметров новых моделей интерес вызывает исследование чувствительности решений по отношению к параметрам модели – модулям упругости, параметрам вязкоупругих и пороупругих операторов, пьезомодулей, коэффициентам теплопроводности и другим характеристикам. Это связано с интенсивным исследованием по меньшей мере двух важных классов задач для однородных или неоднородных деформируемых тел.

Первый класс задач связан с нахождением некоторых оптимальных параметров или законов изменения характеристик, доставляющих экстремум некоторого функционала качества [1], характеризующего деформативность, минимум веса при сохранении прочности, армирование, критические значения в задачах устойчивости, резонансные частоты и др.

Второй класс связан с решением ряда обратных задач по реконструкции постоянных или переменных свойств тел при наличии дополнительной информации о решении в виде компонент граничных полей, амплитудно-частотных характеристик, резонансных частот [2–9]. При этом отметим, что наиболее адекватными постановками являются такие, когда дополнительная информация в обратной задаче задана на границе изучаемого тела, что при решении обратных задач приводит к изучению нелинейных операторных уравнений (или систем) с компактными операторами. Другая постановка, которая стала достаточно интенсивно изучаться в последнее время, опирается на дополнительную информацию, заданную в виде компонент полей смещений, заданных (измеренных) внутри тела. Эта постановка, опирающаяся на измерительные ресурсы эластографии, и реализующаяся для идентификации мягких тканей в биомеханике, приводит к линейным операторным уравнениям, которые стали предметом исследований относительно недавно [10–13].

Выявление параметров задачи, которые наиболее сильно (или слабо) влияют на исследуемые функции или функционалы, важные для дальнейшего анализа соответствующей проблемы, составляет суть анализа чувствительности.

В ряде случаев, когда изучаемые характеристики постоянны, такой анализ даже по отношению к целому комплексу характеристик осуществляется на базе стандартной схемы – при помощи вычисления частных производных измеряемой (заданной) функции или функционала по параметрам, относительно которых такой анализ осуществляется. Приравнивание их нулю приводит к базовой системе уравнений для определения параметров. Соответственно численная процедура анализа чувствительности производится следующим образом: фиксируются все параметры, кроме одного, и анализируются зависимости наблюдаемой характеристики от этого параметра. К сожалению, анализ чувствительности не может быть осуществлен в рамках такой схемы, если анализируемые параметры переменны, что часто встречается в последнее время при анализе и оптимизации свойств функционально-градиентных материалов, и требует более тонких подходов. Заметим, что при этом чувствительность определяется не только параметрами или функциями, характеризующими физические свойства объекта, но и способом нагружения.

Так, статья [6] посвящена некоторым статическим и динамическим обратным задачам, возникающим для моделей линейной упругости для трехмерных упругих сред и тонких упругих пластин, а именно идентификации распределений модулей упругости, параметров модели или скрытых объектов, таких как трещины. Представлены формулы для определения параметрической или геометрической чувствительности.

В [14] разработан анализ чувствительности первого и второго порядка задачи на собственные значения обобщенных несимметричных матриц с использованием теории возмущений. Затем эти результаты применяются для анализа чувствительности при изучении распространения волн в конструкциях. Введены характеристики чувствительности по отношению к системным параметрам волновых чисел и форм волновых мод. Приведены выражения для групповой скорости. Для демонстрации предлагаемого подхода используются численные результаты для тонкой балки и слоистой панели.

Наиболее простыми и подробно изученными являются задачи для функционально-градиентных стержней и слоистых балочных структур [9, 15, 16].

В качестве примера приведем задачу об идентификации законов изменения модуля упругости и плотности неоднородного изотропного цилиндрического стержня, один торец которого закреплен [16], при анализе продольных и изгибных колебаний. При этом можно возбуждать колебания различного типа под воздействием разного типа нагрузок (продольные, изгибные, крутильные). Отметим, что параметр Ляме $\lambda $ не входит в задачу о крутильных колебаниях, соответственно чувствительность тангенциального смещения к этому параметру (функции) равна нулю. Возникает вопрос – каким образом необходимо нагружать объект (и выбирать частотный отрезок нагружения или несколько таких отрезков), чтобы соответствующий отклик был чувствителен к искомой характеристике и таким образом создавать процедуру идентификации, близкую к оптимальной.

Отметим, что имеются следующие возможности при анализе заданных (измеренных) характеристик смещений.

1. Для функций, которые параметризуются конечным набором числовых параметров (полиномы, тригонометрические полиномы, линейные комбинации экспонент) – это нахождение частных производных, либо, как описано выше, осуществление вычислительных экспериментов при фиксации всех параметров, исследование зависимости базового функционала от каждого параметра.

2. В случае, когда идентифицируемые характеристики переменны, возможно для оценочных прикидочных расчетов использовать верхние и нижние оценки для функций, которые часто известны.

3. Ввести соответствующие характеристики чувствительности средствами функционального анализа, используя производные соответствующих операторов по Фреше [17], составить и анализировать краевые задачи относительно таких производных.

Таким образом, целью настоящей работы является обсуждение и формулировка критериев чувствительности для неоднородных материалов и элементов конструкций из них. Отметим, что в ряде ситуаций возможно указать такие режимы нагружения объекта, при которых чувствительность объекта по отношению к какой-либо характеристике равна нулю. Например, помимо приведенного выше примера для крутильных колебаний, таковым является модуль сдвига при возбуждении в образце цилиндрической формы продольных или изгибных колебаний.

1. Постановка задачи, введение основных характеристик чувствительности для неоднородных упругих тел. Рассмотрим соответствующую проблему чувствительности для оператора теории упругости. Пусть краевая задача об установившихся колебаниях неоднородного упругого тела описывается в рамках следующей постановки.

Рассмотрим установившиеся колебания ограниченной области V с кусочно-гладкой границей $S = {{S}_{u}} \cup {{S}_{{{\sigma }}}}$, а nj – компоненты единичного вектора внешней нормали к S. Сформулируем постановку коэффициентных обратных задач для определения зависящих от координат материальных характеристик материала в случае задания дополнительной информации на границе объекта.

Уравнения установившихся колебаний имеют вид:

(1.1)
${{\sigma }}_{{ij,j}}^{{}} + {{\rho }}{{{{\omega }}}^{2}}u_{i}^{{}} = 0\quad i = 1,2,3$

Определяющие соотношения представляют собой закон Гука для анизотропного упругого тела

(1.2)
${{{{\sigma }}}_{{ij}}} = {{c}_{{ijkl}}}{{u}_{{k,l}}}$

Соотношения (1.1), (1.2) позволяют записать систему дифференциальных уравнений второго порядка, которая наиболее часто используется для анализа колебаний однородных и неоднородных тел. Для формулировки краевой задачи необходимо задать граничные условия, будем считать, что в общей ситуации они представляют собой условия смешанного типа

(1.3)
${{\left. {{{u}_{i}}} \right|}_{{{{S}_{u}}}}} = 0,\quad {{\left. {{{{{\sigma }}}_{{ij}}}{{n}_{j}}} \right|}_{{{{S}_{\sigma }}}}} = {{p}_{i}}$

Здесь ${{c}_{{ijkl}}}$ – компоненты тензора упругих модулей, являющиеся кусочно-непрерывными функциями координат, которые удовлетворяют обычным условиям симметрии и положительной определенности, ${{\rho }}$ – плотность среды.

Сформулируем задачу определения коэффициентов дифференциального оператора теории упругости по дополнительной информации

(1.4)
${{\left. {{{u}_{i}}} \right|}_{{{{S}_{{{\sigma }}}}}}} = {{f}_{i}}\left( {x,{{\omega }}} \right),\quad {{\omega }} \in \left[ {{{{{\omega }}}_{1}},{{{{\omega }}}_{2}}} \right]$

Такая постановка соответствует измерению поля перемещений на части границы ${{S}_{{{\sigma }}}}$, на которой осуществляется нагружение, в некотором диапазоне частот. Отметим, что в такой общей постановке задача является нелинейной и построение решения осуществляется на основе построения некоторого итерационного процесса, который достаточно подробно описан в [9, 16, 17]. Приведем постановку в случае изотропного тела, для которого закон Гука (2) имеет вид

(1.5)
${{\sigma }}_{{ij}}^{{}} = {{\lambda }}{{u}_{{k,k}}}{{{{\delta }}}_{{ij}}} + {{\mu }}\left( {{{u}_{{i,j}}} + {{u}_{{j,i}}}} \right)$
где ${{\lambda }},{{\mu }}$ – параметры Ляме, являющиеся положительными функциями координат.

Для упругих тел можно пользоваться обобщенным соотношением взаимности и полученным на его основе операторным соотношением [9]. При исследовании коэффициентных обратных задач, состоящих в определении функций, характеризующих неоднородность, для общих линейных моделей механики сплошной среды также можно опираться на слабую формулировку, которая весьма часто используется и для исследования прямых задач.

При формулировке слабой постановки спроектируем уравнение движения (1.1) на элемент ${{\nu }}$, представляющий собой вектор-функцию с дифференцируемыми компонентами и удовлетворяющую граничным условиям на ${{S}_{u}}$ (далее будем считать, что ${{\nu }}\, \in \,{{H}_{0}}(V)$). Используя теорему Гаусса–Остроградского и учитывая граничные условия в (1.3), приведем это равенство к виду $А(a,u,{{\nu }}) = b({{\nu }})$, где $А(a,u,{{\nu }})$ есть трилинейная форма (линейная по каждому аргументу) переменных $a,u,{{\nu }}$, $b({{\nu }})$ – линейная форма.

Так, слабая постановка для анизотропной теории упругости состоит в нахождении компонент вектора смещений, причем для трилинейной и линейной форм имеем соответственно

(1.6)
$\begin{gathered} А(a,u,{{\nu }}) = \int\limits_V {2L({{u}_{i}},{{{{\nu }}}_{i}},{{C}_{{ijkl}}},{{\rho }})dV} ,\quad b({{\nu }}) = \int\limits_{{{S}_{\sigma }}} {{{p}_{i}}{{{{\nu }}}_{i}}dS} ,{{\omega }} \in \left[ {{{{{\omega }}}_{1}},{{{{\omega }}}_{2}}} \right] \\ 2L({{u}_{i}},{{{{\nu }}}_{i}},{{C}_{{ijkl}}},{{\rho }}) = {{C}_{{ijkl}}}{{u}_{{k,l}}}{{{{\nu }}}_{{i,j}}} - {{\rho }}{{{{\omega }}}^{2}}{{u}_{i}}{{{{\nu }}}_{i}} \\ \end{gathered} $

Для решения обратной задачи по восстановлению трех переменных характеристик ${{\lambda }},{{\mu }},{{\rho }}$ используется несколько подходов, в основе которых лежит итерационный метод типа Ньютона [9–16] и его модификации. Сформулируем соответствующие операторные уравнения. Для нахождения трех характеристик будем использовать три режима зондирования, которые характеризуются как разными областями приложения нагрузки, так и способом ее приложения. Обозначим эти нагрузки через $p_{i}^{{(m)}},\;m = 1{\text{,}}2,3$; соответствующие им поля смещений будем обозначать через $u_{i}^{{(m)}}$.

В изотропном случае для определяющих соотношений вида (5) из слабой постановки (1.6), полагая ${{{{\nu }}}_{i}} = u_{i}^{{(m)}}$, имеем следующую систему нелинейных интегральных уравнений типа Урысона

(1.7)
$\begin{gathered} \int\limits_V {[{{\lambda }}{{{(u_{{k,k}}^{{(m)}})}}^{2}} + {{\mu }}(u_{{i,j}}^{{(m)}} + u_{{j,i}}^{{(m)}})(u_{{i,j}}^{{(m)}} + u_{{j,i}}^{{(m)}}) - {{\rho }}{{{{\omega }}}^{2}}u_{i}^{{(m)}}u_{i}^{{(m)}}]dV} = \int\limits_{{{S}_{{{\sigma }}}}} {p_{i}^{{(m)}}f_{i}^{{(m)}}dS} \\ m = 1,2,3 \\ \end{gathered} $

Особенностью этой системы, состоящей из 3 нелинейных интегральных уравнений, является знакоопределенность ядер, зависящих от компонент смещений и их градиентов, при неизвестных функциях ${{\lambda }},{{\mu }},{{\rho }}$. Возможное нарушение знакоопределенности в зависимости от компонент тензора деформаций имеется в случае использования модели несжимаемого материала, а также при таком виде нагружения, когда шаровая часть тензора деформаций обращается в ноль (что приводит к обращению в ноль ядра при ${{\lambda }}$, что отмечено выше). Заметим попутно, что ядра при ${{\mu }}$ и ${{\rho }}$ в ноль не обращаются. Обычно система нелинейных операторных уравнений вида (1.7) исследуется на основе операторного метода Ньютона, при этом требуется нахождение производных по Фреше от основного оператора и выбор начального приближения.

Начальное приближение для реализации итерационного процесса отыскивается обычно в некотором узком классе функций – постоянных, линейных или кусочно-линейных путем минимизации функционала невязки

(1.8)
${{J}_{0}} = \sqrt {\int\limits_{{{{{\omega }}}_{1}}}^{{{{{\omega }}}_{2}}} {\int\limits_{{{S}_{{{\sigma }}}}} {{{{(f - {{u}^{{(0)}}})}}^{2}}dS} } d{{\omega }}} $
и на каждом шаге итерационного процесса необходимо формировать и решать линейную систему интегральных уравнений Фредгольма первого рода с гладкими ядрами, позволяющую находить поправки к некоторому приближению. Далее будем считать, что ${{g}_{1}}$ характеризует поправки для ${{\lambda }}$, ${{g}_{2}}$ характеризует поправки для параметра ${{\mu }}$, а ${{g}_{3}}$ характеризует поправки для плотности, гладкие ядра в (1.7) ${{K}_{{1m}}},{{K}_{{2m}}}$ неотрицательны, ${{K}_{{3m}}}$ – отрицательны. Решение таких интегральных уравнений и систем представляет собой некорректную задачу [2] и может быть построено лишь на основе сужения пространства поиска до компактного или конечномерного множества, причем регуляризованные решения строятся на базе метода А.Н. Тихонова. Особенностью ситуации, когда определяется несколько функций, является то обстоятельство, что ядра системы в силу различной чувствительности в равномерной норме могут различаться на порядок и более друг от друга, что приводит к сильному вырождению линейных систем при численной реализации. Это подтверждают результаты вычислительных экспериментов, осуществленные при решении обратных задач для цилиндрической области [17–20]. В вычислительных экспериментах по определению трех функций, зависящих от радиальной координаты, показано, что законы изменения ${{\mu }}$ и ${{\rho }}$ находятся с приемлемой точностью, а ${{\lambda }}$ – с весьма невысокой, что связано с разным порядком ядер в интегральных уравнениях типа (1.7).

Вернемся к операторному уравнению, в описание которого помимо полевых переменных входят коэффициенты, образующие вектор $a = \{ {{a}_{1}},{{a}_{2}},{{a}_{3}}\} = \{ {{\lambda }},{{\mu }},{{\rho }}\} $.

Для оценки чувствительности введем в рассмотрение следующие характеристики чувствительности относительно величин напряжений и смещений, где производные понимаются в смысле Фреше [21]

(1.9)
$\frac{{\partial {{{{\sigma }}}_{{ij}}}}}{{\partial {{а}_{k}}}} = {{\xi }}_{{ij}}^{{(k)}},\quad \frac{{\partial {{u}_{i}}}}{{\partial {{a}_{k}}}} = {{\zeta }}_{i}^{{(k)}}$

Осуществляя необходимые построения и формируя соответствующие краевые задачи для введенных производных, получим связанную систему краевых задач. При этом, используя соответствующие соотношения взаимности, для произвольной нагрузки для введенных характеристик получены следующие соотношения

(1.10)
$\begin{gathered} \int\limits_{{{S}_{{{\sigma }}}}} {{{p}_{i}}{{\zeta }}_{i}^{{(1)}}dS} + \int\limits_V {{{{({{u}_{{i,i}}})}}^{2}}dV} = 0 \\ \int\limits_{{{S}_{{{\sigma }}}}} {{{p}_{i}}{{\zeta }}_{i}^{{(2)}}dS} + 1{\text{/}}2\int\limits_V {({{u}_{{i,j}}} + {{u}_{{j,i}}})({{u}_{{i,j}}} + {{u}_{{j,i}}})dV} = 0 \\ \int\limits_{{{S}_{{{\sigma }}}}} {{{p}_{i}}{{\zeta }}_{i}^{{(3)}}dS} - {{{{\omega }}}^{2}}\int\limits_V {{{u}_{i}}{{u}_{i}}dV} = 0 \\ \end{gathered} $

Отметим, что для оценки чувствительности в некоторой точке поверхности тела следует осуществить зондирование с помощью сосредоточенных нагрузок. При этом соотношения (1.10) дают

(1.11)
$\begin{gathered} p_{i}^{{(1)}}{{\zeta }}_{i}^{{(1)}}\left( {{{x}_{{01}}}} \right) + \int\limits_V {{{{({{u}_{{i,i}}})}}^{2}}dV} = 0 \\ p_{i}^{{(2)}}{{\zeta }}_{i}^{{(2)}}\left( {{{x}_{{02}}}} \right) + 1{\text{/}}2\int\limits_V {\left( {{{u}_{{i,j}}} + {{u}_{{j,i}}}} \right)\left( {{{u}_{{i,j}}} + {{u}_{{j,i}}}} \right)dV} = 0 \\ p_{i}^{{(3)}}{{\zeta }}_{i}^{{(3)}}\left( {{{x}_{{03}}}} \right) - {{{{\omega }}}^{2}}\int\limits_V {{{u}_{i}}{{u}_{i}}dV} = 0, \\ \end{gathered} $
которые позволяют определять чувствительность тела по отношению к различным видам воздействий и сравнивать отклики для различных законов неоднородности.

2. Пример оценки чувствительности для цилиндрического стержня. В качестве примера оценки чувствительности рассмотрим частную обратную задачу об определении двух функций $g\left( x \right)$ и $r\left( x \right)$ соответственно безразмерного модуля Юнга и безразмерной плотности для консольно-закрепленного стержня, в котором возбуждаются а) продольные колебания за счет приложения продольной силы единичной амплитуды на конце, б) изгибные колебания за счет приложения единичного момента на конце. В качестве дополнительной информации в обратной задаче будем считать, что заданы амплитудно-частотные характеристики о смещении и угле поворота на конце в зависимости от частоты колебаний.

(2.1)
$u\left( {1,{{\tau }}} \right) = f({{\tau }}),\quad {{\tau }} \in \left[ {0,{{{{\tau }}}_{1}}} \right]$
(2.2)
$w{\kern 1pt} '\left( {1,{{\tau }}} \right) = {{\varphi }}({{\tau }}),\quad {{\tau }} \in \left[ {0,{{{{\tau }}}_{2}}} \right]$

В работе [16] построены интегральные уравнения вида (1.7) для стержня, в котором возбуждаются продольные или изгибные колебания. Эти уравнения имеют вид

(2.3)
$f({{\tau }}) = \int\limits_0^1 {g({{\xi }})u{\kern 1pt} {{'}^{2}}({{\xi }},{{\tau }})d{{\xi }}} - {{\tau }}\int\limits_0^1 {r({{\xi }}){{u}^{2}}({{\xi }},{{\tau }})d{{\xi }}} ,{{\tau }} \in [0,{{{{\tau }}}_{1}}]$
(2.4)
${{\varphi }}({{\tau }}) = \int\limits_0^1 {g({{\xi }})w_{{}}^{{''2}}({{\xi }},{{\tau }})d{{\xi }}} - {{\gamma \tau }}\int\limits_0^1 {r({{\xi }}){{w}^{2}}({{\xi }},{{\tau }})d{{\xi }}} ,{{\tau }} \in [0,{{{{\tau }}}_{2}}]$
соответственно ядра интегральных операторов обладают свойствами знакоопределенности, отмеченными выше. Здесь $u$ и $w$ – соответственно амплитуды продольных и изгибных перемещений стержня, которые, вообще говоря, являются нелинейными операторами от искомых функций g(x) и r(x); введены безразмерные параметры: ${{\tau = }}{{{{\kappa }}}^{2}} = {{{{\rho }}}_{0}}{{{{\omega }}}^{2}}{{l}^{2}}{\text{/}}{{E}_{0}}$, ${{\gamma }} = 4{{l}^{2}}{\text{/}}{{a}^{2}}$ (для кругового стержня радиуса $a$), ${{{{\rho }}}_{0}},{{E}_{0}}$ – характерные значения плотности и модуля Юнга.

Итерационный процесс, описанный выше, приводит на n-й итерации к последовательному решению задач для стержней с известными переменными характеристиками и нахождению поправок из системы интегральных уравнений вида [16]. Собственно чувствительность для этого объекта отражают операторные зависимости $f({{\tau }}),$ ${{\varphi }}({{\tau }})$ от материальных характеристик стержня. Если ввести соответствующие производные, отражающие чувствительность $\frac{{\partial u}}{{\partial g}}(g,r,x)$, $\frac{{\partial w}}{{\partial g}}(g,r,x)$, $\frac{{\partial u}}{{\partial r}}(g,r,x)$, $\frac{{\partial w}}{{\partial r}}(g,r,x)$ и оператор

$\begin{gathered} A{\text{:}}\,{\text{G}} \to {\text{F}} \\ {\text{G}}\left( {g,r} \right) = {\text{M[}}{{g}_{ - }}{\text{, }}{{g}_{ + }}{\text{]}} \times {\text{M[}}{{r}_{ - }}{\text{, }}{{r}_{ + }}{\text{],}}\quad {\text{F}}\left( {f,{{\varphi }}} \right) = {{{\text{C}}}^{\infty }}[{{{{\tau }}}_{ - }},{{{{\tau }}}_{ + }}] \times {{{\text{C}}}^{\infty }}[{{{{\tau }}}_{ - }},{{{{\tau }}}_{ + }}] \\ \end{gathered} $
$\begin{gathered} A = A\left( {u,w,g,r} \right) \to \left( {f,{{\varphi }}} \right) \\ {{{{\theta }}}_{{\text{1}}}} = {{f}_{{,g}}}\quad {{{{\theta }}}_{{\text{2}}}} = {{f}_{{,r}}}\quad {{{{\theta }}}_{{\text{3}}}} = {{{{\varphi }}}_{{,g}}}\quad {{{{\theta }}}_{{\text{4}}}} = {{{{\varphi }}}_{{,r}}} \\ \end{gathered} $
то нетрудно построить операторные уравнения для этих функций, а также установить некоторые соотношения для расчетов и соответствующие неравенства

$\frac{{df}}{{dg}} = - \int\limits_0^1 {{{{\left( {u{\kern 1pt} '} \right)}}^{2}}dx} < 0,\quad \frac{{df}}{{dr}} = {{\tau }}\int\limits_0^1 {{{u}^{2}}dx} > 0$
$\frac{{d{{\varphi }}}}{{dg}} = - \int\limits_0^1 {{{{(w_{{}}^{{''}})}}^{2}}dx} < 0,\quad \frac{{d{{\varphi }}}}{{dr}} = {{\gamma \tau }}\int\limits_0^1 {{{w}^{2}}dx} > 0$

Из этих неравенств следуют следующие выводы, которые аналогичны теоремам сравнения Штурма.

1. Увеличение модуля упругости для неоднородного стержня приводит к уменьшению амплитуды продольного смещения и угла поворота.

2. Увеличение плотности для неоднородного стержня приводит к увеличению амплитуды колебаний продольного смещения и угла поворота.

3. Характеристики чувствительности сильно возрастают при приближении к резонансным значениям для соответствующих операторов, частотный анализ позволит выделить области, наиболее благоприятные для реконструкции неоднородных характеристик.

Замечания. 1. Отметим, что эти выводы относятся к тем сравнениям характеристик, когда неравенства выполняются всюду в области, занятой стержнем.

2. Важным также является сравнительный анализ разнородных характеристик чувствительности и выявление частотных областей, в которых они имеют одинаковый порядок.

Исследования в рамках предлагаемого подхода могут быть использованы при анализе колебаний кругового цилиндра и волновода [20] и решении КОЗ при общих двумерных и трехмерных законах неоднородности, а также при анализе влияния компонент предварительных напряжений.

3. Вычислительный эксперимент. При помощи методов пристрелки вычислим чувствительности для балки, материальные свойства которой описываются функциями $g\left( x \right) = 1.33 - 2\left( {1 - x} \right)x$, $r\left( x \right) = 0.67 + 2\left( {1 - x} \right)x$, примем, что ${{\gamma }} = 100$.

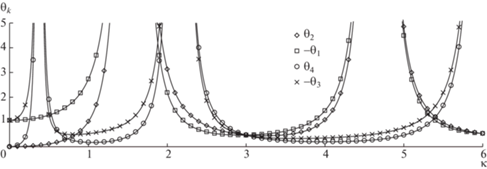
На рис. 1 изображены зависимости функций $ - {{{{\theta }}}_{{\text{1}}}},{{{{\theta }}}_{{\text{2}}}}, - {{{{\theta }}}_{{\text{3}}}},{{{{\theta }}}_{{\text{4}}}}$ от параметра ${{\kappa }}$. Они являются знакоопределенными. Структура этих функций такова. Они бесконечно дифференцируемы, имеются разрывы второго рода, соответствующие резонансам (изгибным ${{\kappa }} = \left\{ {0.34,2.2,7.84, \ldots } \right\}$ и продольным ${{\kappa }} = \left\{ {1.57,\,4.71, \ldots } \right\}$) и антирезонансы (на них амплитуды соответствующих перемещений обращаются в ноль). Были проведены масштабные вычислительные эксперименты, приведем результаты некоторых из них.

Рис. 1.

Зависимость $\left| {{{{{\theta }}}_{j}}} \right|,\,\,j = 1,2,3,4$ от параметра ${{\kappa }}$.

Рассмотрим задачу по восстановлению функций $g\left( x \right) = 1.33 - 0.67x$, r(x) = 0.67 + x2. Построим АЧХ задач продольных и изгибных колебаний $f({{\tau }}),{{\varphi }}({{\tau }})$. Рассмотрим два набора частот.

1. Точки первого набора ${{\kappa }} = \left\{ {0.25,0.4,0.6,1.0,1.1,1.2,1.3,1.4,1.6,1.7} \right\}$. В качестве точек первого набора выбраны такие точки, которые были бы близки к резонансным частотам и удалены от нуля и частот антирезонанса. Введем следующие характеристики

(3.1)
$J_{j}^{f} = \sqrt {\sum\limits_s {{{{(f\left( {{{{{\kappa }}}_{s}}} \right) - {{u}^{{(j)}}}\left( {1,{{{{\kappa }}}_{s}}} \right))}}^{2}}} + \sum\limits_s {{{{({{\varphi }}\left( {{{{{\kappa }}}_{s}}} \right) - w{\kern 1pt} {{'}^{{(j)}}}\left( {1,{{{{\kappa }}}_{s}}} \right))}}^{2}}} } $
(3.2)
$J_{j}^{g} = \sqrt {\int\limits_0^1 {{{{\left( {g\left( x \right) - {{g}_{j}}\left( x \right)} \right)}}^{2}}} dx} ,\quad J_{j}^{r} = \sqrt {\int\limits_0^1 {{{{\left( {r\left( x \right) - {{r}_{j}}\left( x \right)} \right)}}^{2}}} dx} $

На основе точек первого набора вычисляется функционал невязки в соответствии с (3.1). Путем его минимизации найдено начальное приближение ${{g}_{0}}\left( x \right) = 0.97$, r0(x) = = $0.67 + 0.58x$. На основе метода регуляризации А.Н. Тихонова с автоматическим выбором параметра регуляризации реализован итерационный процесс и найдены искомые функции.

В табл. 1 сравнение АЧХ выполнено в евклидовой метрике (3.1) (так как в используемом частотном диапазоне содержатся и резонансы), а сравнение точных функций g(x), r(x) с результатами реконструкции в метрике ${{L}_{2}}$ (3.2). Для использования невязки (3.2) и перехода к следующей итерации используются кусочно-линейные аппроксимации. Нулевая итерация соответствует начальному приближению. Заметим, что существенное снижение невязки в решении происходит уже при первой итерации.

Таблица 1.

Сравнительный анализ невязок на итерациях

№ итерации $J_{j}^{f}$ $J_{j}^{g}$ $J_{j}^{r}$
0 0.28 0.038 0.022
1 1.00 0.0064 0.0080
2 0.15 0.0070 0.0057
3 0.055 0.0069 0.0055

2. Аналогичный вычислительный эксперимент выполним для второго набора частот ${{\kappa }} = \left\{ {0.1,0.2,0.4,0.6,0.7,0.8,0.9,1.0,1.75,1.85} \right\}$. Путем минимизации функционала невязки найдено начальное приближение ${{g}_{0}}\left( x \right) = 1.0$, ${{r}_{0}}\left( x \right) = 0.67 + 0.6x$.

В табл. 2 представлены невязки для второго диапазона частот. Отметим, что они также значительно уменьшаются уже после первой итерации. При том, что невязка по АЧХ оказалась меньше, чем в предыдущем случае, невязки в реконструкции функций g(x) и r(x) оказались выше. Таким образом, можно считать этот частотный набор менее удачным.

Таблица 2.

Сравнительный анализ невязок на итерациях

№ итерации $J_{j}^{f}$ $J_{j}^{g}$ $J_{j}^{r}$
0 0.185 0.038 0.021
1 0.098 0.0098 0.012
2 0.033 0.0082 0.011
3 0.030 0.0078 0.010

Рассмотрим также задачу по восстановлению немонотонных функций с одинаковым среднеинтегральным значением $g\left( x \right) = 1.33 - 2\left( {1 - x} \right)x$, $r\left( x \right) = 0.67 + 2\left( {1 - x} \right)x$. Зададим третий частотный набор ${{\kappa }} = \left\{ {0.42,0.52,0.7,0.8,0.9,1.0,1.1,1.2,1.3,1.4} \right\}$. Путем минимизации функционала невязки найдено начальное приближение ${{g}_{0}}\left( x \right) = 0.8$, ${{r}_{0}}\left( x \right) = 0.67 + 0.1x$.

Из табл. 3 видно, что невязки, отвечающие начальному приближению достаточно велики. Оказалось, что $g\left( x \right) > {{g}_{0}}\left( x \right)$ на всем интервале и $r\left( x \right) > {{r}_{0}}\left( x \right)$ при $x < 0.95$. Наблюдение за решением на итерациях позволило выявить, что после 2 итерации не происходит его существенных изменений.

Таблица 3.

Сравнительный анализ невязок на итерациях

№ итерации $J_{j}^{f}$ $J_{j}^{g}$ $J_{j}^{r}$
0 0.905 0.062 0.103
1 0.661 0.0038 0.0013
2 0.125 0.0015 0.0013
3 0.063 0.0016 0.00095
4 0.050 0.0017 0.0012

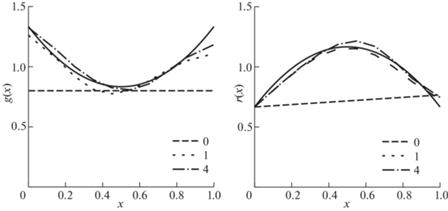
На рис. 2 сплошными линиями изображены точные решения обратной задачи: g(x) слева и r(x) справа. Пунктирной линией (номер 0) изображено начальное приближение g0(x) и ${{r}_{0}}\left( x \right)$. Под номерами 1 и 4 изображены, соответственно, результаты реконструкции на первой и четвертой (последней) итерациях.

Рис. 2.

Результаты реконструкции на 1 и 4 итерациях.

Результаты вычислительных экспериментов позволили сформулировать следующие рекомендации при решении коэффициентных ОЗ для стержневых структур при выборе частотного диапазона:

1. Не использовать узкий частотный диапазон для съема АЧХ.

2. Оптимально в качестве частотного диапазона использовать частоты в окрестности первого и второго резонанса, поскольку в окрестности нуля практически отсутствует чувствительность к изменению плотности, а после второго резонанса ядра интегральных уравнений начинают достаточно сильно осциллировать, обращаясь в ноль в наборе точек, что негативно влияет на обусловленность матрицы получаемой алгебраической системы и в целом на процесс реконструкции.

3. Так как ядро при поправке к плотности обращается в нуль на закрепленном конце стержня, то для получения приемлемых результатов реконструкции нужно задать значение плотности в этой точке.

Заключение. Обсуждены некоторые аспекты исследования обратных задач по нахождению переменных характеристик для моделей теории упругости. На основе производных по Фреше введены характеристики чувствительности для модели неоднородной линейной теории упругости, построены общие соотношения, позволяющие вычислять характеристики чувствительности при установившихся воздействиях. Представлен пример для неоднородного стержня, найдены соответствующие характеристики чувствительности.

Благодарности. Исследование выполнено за счет гранта Российского научного фонда № 22-11-00265, https://rscf.ru/project/22-11-00265/, Южный федеральный университет.

Список литературы

  1. Баничук Н.В., Кобелев В.В., Рикардс Р.Б. Оптимизация элементов конструкций из композиционных материалов М.: Машиностроение, 1988. 224 с.

  2. Кабанихин С.И. Обратные и некорректные задачи. Новосибирск: Сибирское научное издательство, 2009. 458 с.

  3. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1986. 288 с.

  4. Bui H.D. Inverse Problems in the Mechanic of Materials: An Introduction. Boca Raton: CRC Press, 1994. 224 p.

  5. Isakov V. Inverse problems for PDE. Springer-Verlag, 2005. 284 p.

  6. Bonnet M., Constantinescu A. Inverse problems in elasticity // Inverse Probl. 2005. № 21. P. 1–50. https://doi.org/10.1088/0266-5611/21/2/R01

  7. Глэдвелл Г.М.Л. Обратные задачи теории колебаний. М.-Ижевск: Регулярная и хаотическая динамика. Институт компьютерных исследований, 2008. 608 с.

  8. Neto F.D.M., Neto A.J.S. An Introduction to Inverse Problems with Applications. Berlin: Springer, 2013. 255 p.

  9. Ватульян А.О. Коэффициентные обратные задачи механики. М.: Физматлит, 2019. 272 с.

  10. Sinkus R., Lorenzen J., Schrader D., Lorenzen M., Dargatz M., Holz D. High-resolution tensor MR elastography for breast tumour detection // Phys. Med. Biol. 2000. V. 45. P. 1649–1664. https://doi.org/10.1088/0031-9155/45/6/317

  11. Manduca A., Oliphant T.E., Dresner M.A., Mahowald J.L., Kruse S.A., Amromin E., Felmlee J.P., Greenleaf J.F., Ehman R.L. Magnetic resonance elastography: Non-invasive mapping of tissue elasticity // Medical Image Analysis. 2001. V. 5. № 4. P. 237–254. https://doi.org/10.1016/S1361-8415(00)00039-6

  12. Сарвазян А.П., Руденко О.В., Свенсон С.Д., Фаулкс Ю.Б., Емельянов С.Ю. Упругая визуализация сдвиговых волн: новая ультразвуковая технология медицинской диагностики // УЗИ Мед. Биол. 1998. Т. 24. С. 1419–1435.

  13. Arani A., Manduca A., Ehman R.L., Huston Ill.J. Harnessing brain waves: a review of brain magnetic resonance elastography for clinicians and scientists entering the field // Br. J. Radiol. 2021. V. 94. № 1119. P. 20200265. https://doi.org/10.1259/bjr.20200265

  14. Cicirello A., Mace B.R., Kingan M.J., Yang Y. Sensitivity analysis of generalised eigenproblems and application to wave and finite element models // J. Sound Vibr. 2020. V. 478. P. 115345. https://doi.org/10.1016/j.jsv.2020.115345

  15. Perkowski Z., Czabak M. Description of behaviour of timber-concrete composite beams includinginterlayer slip, uplift, and long-term effects: Formulation of the model and coefficient inverse problem // Eng. Struct. 2019. 194. P. 230–250. https://doi.org/10.1016/j.engstruct.2019.05.058

  16. Ватульян А.О., Юров В.О. Об определении механических характеристик стержневых элементов из функционально-градиентных материалов // Изв. РАН. МТТ. 2021. № 4. С. 52–63. https://doi.org/10.31857/S0572329921040139

  17. Vatulyan A.O., Dudarev V.V., Mnukhin R.M. Identification of characteristics of a functionally graded isotropic cylinder // Int. J. Mech. Mater.Des. 2021. V. 17. № 2. P. 321–332. https://doi.org/10.1007/s10999-020-09527-5

  18. Vatulyan A.O., Dudarev V.V., Mnukhin R.M., Nedin R.D. Identification of the Lamé parameters of an inhomogeneous pipe based on the displacement field data // Eur. J. Mech. A/Solids. 2020. V. 81. P. 103939. https://doi.org/10.1016/j.euromechsol.2019.103939

  19. Dudarev V.V., Vatulyan A.O., Mnukhin R.M., Nedin R.D. Concerning an approach to identifying the Lamé parameters of an elastic functionally graded cylinder // Math. Meth. Appl. Sci. 2020. V. 43. № 11. P. 6861–6870. https://doi.org/10.1002/mma.6428

  20. Vatulyan A.O., Yurov V.O. On the reconstruction of material properties of a radially inhomogeneous cylindrical waveguide // Math. Meth. Appl. Sci. 2021. V. 44. № 6. P. 4756–4769. https://doi.org/10.1002/mma.7067

  21. Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. М.: Мир, 1983. 432 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал