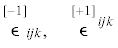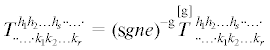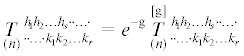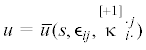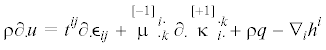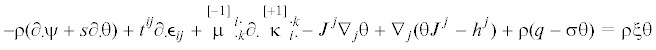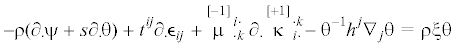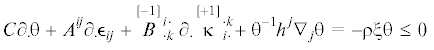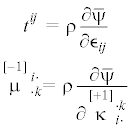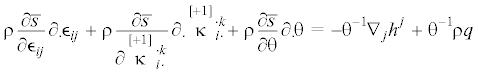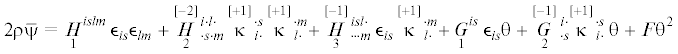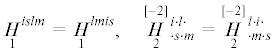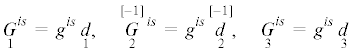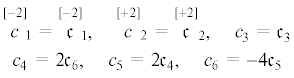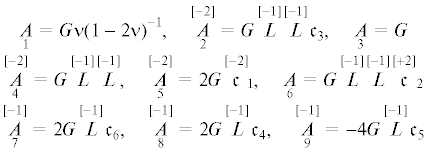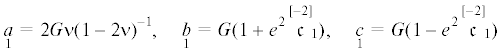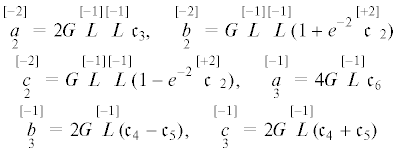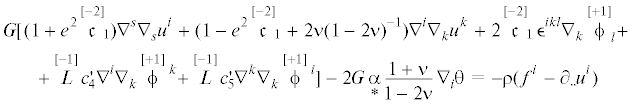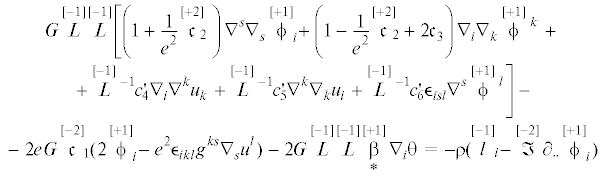Известия РАН. Механика твердого тела, 2023, № 3, стр. 163-176
СВЯЗАННАЯ ТЕРМОУПРУГОСТЬ ГЕМИТРОПНЫХ СРЕД. ПСЕВДОТЕНЗОРНАЯ ФОРМУЛИРОВКА
Е. В. Мурашкин a, *, Ю. Н. Радаев a, **
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: evmurashkin@gmail.com
** E-mail: radayev@ipmnet.ru
Поступила в редакцию 15.01.2023
После доработки 22.01.2023
Принята к публикации 23.01.2023
- EDN: JMQVBJ
- DOI: 10.31857/S0572329922600876
Аннотация
В статье рассматривается проблема вывода определяющих уравнений для микрополярного термоупругого континуума GN-I в специфике стандартного псевдотензорного формализма. Псевдотензорный подход в большинстве случаев оправдан при моделировании гемитропных микрополярных тел, термомеханические свойства которых чувствительны к зеркальным отражениям трехмерного пространства. Приводятся минимально необходимые для понимания сведения из теории псевдотензоров. Привлекаются общие термодинамические подходы, обсуждаются уравнения баланса энтропии и различные формы баланса внутренней и свободной энергии Гельмгольца. Устанавливаются веса основных термомеханических псевдотензоров. В линейном приближении выводятся определяющие уравнения гемитропного микрополярного термоупругого континуума (GN-I) первого типа. В линейном приближении получена связанная система дифференциальных уравнений теплопроводности и динамических уравнений микрополярного термоупругого континуума GN-I.
1. Введение. Изучение термомеханических свойств современных конструкционных материалов и метаматериалов [1–6] оказывается возможным в результате синтеза аппарата современной термодинамики [7–9] и микроструктурных представлений [10–12]. Большинство биоматериалов и метаматериалов с точки зрения их термомеханических свойств чувствительны к преобразованиям, изменяющим ориентацию пространства11, например, зеркальным отражениям и инверсиям пространства22. Однако, следует понимать, что определяющие тензоры и определяющие постоянные линейных изотропных микрополярных сред не проявляют чувствительность к указанным преобразованиям. Наиболее простой моделью, с определяющими псевдоскалярами, чувствительными к упомянутым преобразованиям пространства, оказывается гемитропная микрополярная среда, задающаяся девятью определяющими псевдоскалярами.
Термодинамические процессы, протекающие в термодинамических системах, с точки зрения математической модели определяются эволюцией параметров состояния33, составляющих термодинамический базис. Термодинамические процессы можно условно разделить на равновесные и неравновесные. Равновесным называется такой термодинамический процесс, при котором все состояния, через которые последовательно эволюционирует система, с достаточной степенью точности являются равновесными состояниями, т.е. когда все термодинамические характеристики чрезвычайно близки к своим средним значениям44. К таким процессам можно отнести медленно протекающие процессы, когда время релаксации достаточно мало, по сравнению с характерным временем перехода между двумя соседними равновесными состояниями. В этом случае процессы чаще всего рассматриваются как квазистатические, поскольку для динамических процессов высказанные условия в большинстве случаев нарушаются.
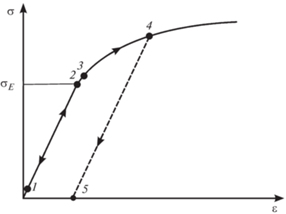
Кроме того, термодинамические процессы, можно разделить на обратимые и необратимые. Обратимым называется такой термодинамический процесс, для любых двух состояний которого фактически реализуются термодинамические процессы как в прямом, так и в обратном направлениях. Поясним сказанное на двух простых примерах. Рассмотрим в качестве примера модель атермической деформации цилиндрического упругопластического образца до и за пределом упругости (см. рис. 1). При значениях силовой нагрузки, ниже предела упругости ${{\sigma }_{E}}$, что на рисунке соответствует точкам кривой между состояниями 1 и 2, термодинамический процесс будет обратимым и разгрузка образца вернет процесс к начальному состоянию 1 [17]. При нагружении образца выше предела текучести (состояния 3 и 4) образец начнет проявлять неупругие свойства и процесс разгрузки пойдет по пути 4–5, а не вернется в состояние 1 по траектории $4 - 3 - 2 - 1$, что означает необратимость процесса 1–4. В термодинамически необратимых процессах наблюдается неконтролируемое (неуправляемое, самопроизвольное) производство энтропии (uncontrollable entropy production).
Для описания состояния термодинамической системы используются функции, функционально зависящие от базиса термодинамических переменных (параметров состояния: энтропия, деформация, температура), и термодинамические потенциалы состояния (внутренняя энергия, свободная энергия Гельмгольца и другие энергетические формы).
Термодинамический подход к исследованию процессов деформирования микрополярных материалов использовался, например, в работах [10–12] и работах авторов [6, 18, 19], где проводится построение определяющих уравнений для упругих микрополярных материалов в терминах абсолютных тензоров. Однако, построение определяющих уравнений и термодинамических потенциалов для гемитропных микрополярных термоупругих сред на корректной основе требует привлечения аппарата алгебры псевдотензоров (см., например, [14, 20, 21]).
В настоящей работе обсуждаются вопросы вывода определяющих соотношений для микрополярного термоупругого континуума GN-I в терминах псевдотензоров. Приводятся (правда, в минимальной степени) основные понятия алгебры и анализа псевдотензоров [22–28]. Обсуждаются уравнения баланса энтропии и различные формы баланса внутренней и свободной энергии Гельмгольца. Вычисляются веса основных термомеханических величин. В линейном приближении выводятся определяющие уравнения гемитропного микрополярного связанного термоупругого континуума GN-I.
2. Псевдотензоры в трехмерном евклидовом пространстве. Рассмотрим трехмерное евклидово пространство55. Выберем в пространстве криволинейную систему координат ${{x}^{k}}{\kern 1pt} {\kern 1pt} (k = 1,2,3)$. Метрика пространства задается квадратом линейного элемента длины согласно
где ${{g}_{{ij}}}$ – компоненты метрического тензора. Компоненты фундаментального тензора gij связаны с метрическим тензором соотношениемИ метрический, и фундаментальный тензоры являются абсолютными (истинными) тензорами. То же самое относится к символу Кронекера $\delta _{k}^{i}$.
Введем в рассмотрение локальные базисные триэдры, связанные с выбранной координатной системой в трехмерном пространстве: $\mathop \imath \limits_\mathfrak{a} $ ($\mathfrak{a} = 1,2,3$) – локальный ковариантный базис; $\mathop \imath \limits^\mathfrak{b} $ ($\mathfrak{b} = 1,2,3$) – локальный контравариантный (взаимный) базис.
Базисные векторы и взаимные базисные векторы удовлетворяют следующему соотношению:
Метаиндексы $\mathfrak{a}$ и $\mathfrak{b}$ (в отличие от тензорных индексов) записываются шрифтом “fraktur”.
С ориентацией локальных базисов связан фундаментальный объект псевдотензорной алгебры и многомерной геометрии – символы перестановок [23–25], которые не являются абсолютными тензорами и определяются согласно соотношениям:
(2.3)
${{\epsilon }_{{ijk}}} = {{\epsilon }^{{ijk}}} = \left\{ \begin{gathered} + 1,\quad {\text{для}}\;{\text{троек}}\;(1,2,3),\;(2,3,1),\;(3,1,2) \hfill \\ - 1,\quad {\text{для}}\;{\text{троек}}\;(3,2,1),\;(1,3,2),\;(2,1,3) \hfill \\ - 0,\quad {\text{во}}\;{\text{всех}}\;{\text{остальных}}\,\,{\text{случаях}} \hfill \\ \end{gathered} \right.$Заметим, что $\epsilon $-символы нарушают основные привила тензорного формализма, что видно уже по (2.3). Символы перестановок ${{\epsilon }_{{ijk}}}$ и ${{\epsilon }^{{ijk}}}$ являются относительными ковариантными тензорами (псевдотензорами) веса –1 (${\text{w}}{\text{.g}}{\text{.t}}. = - 1$) и одновременно – относительными контравариантными тензорами веса +1 (${\text{w}}{\text{.g}}{\text{.t}}. = + 1$), поэтому было бы корректно использовать для них следующие обозначения:
Далее сверху корневого символа относительного тензора в квадратных скобках будем отмечать его вес. Нулевой вес, присущий абсолютным тензорам, не отражается нами в обозначениях.
Введем в рассмотрение ориентирующий трехмерное пространство псевдоскаляр (относительный скаляр веса +1 (${\text{w}}{\text{.g}}{\text{.t}}. = + 1$)), представляющий собой смешанное произведение базисных векторов:
(2.4)
$e = \mathop e\limits^{[ + 1]} = (\mathop \imath \limits_1 \; \times \mathop \imath \limits_2 ) \cdot \mathop \imath \limits_3 {\kern 1pt} $(2.5)
$\frac{1}{e} = \mathop e\limits^{[ - 1]} {{\,}^{{ - 1}}} = (\mathop \imath \limits^1 \; \times \mathop \imath \limits^2 ) \cdot \mathop \imath \limits^3 $Обратим внимание, что псевдоскаляр (2.4) с точностью до знака совпадает с объемом параллелепипеда, построенного на базисных векторах $\mathop \imath \limits_\mathfrak{a} $. Нетрудно показать, что в евклидовом пространстве справедливо равенство
где g – детерминант метрического тензора. Условие $g = 1$ (${\text{|}}e{\text{|}} = 1$) является фундаментальным для развития общей теории относительности [29] и, например, математической теории пластичности [30]. Важно отметить, что в этом случае абсолютные тензоры совпадают с псевдотензорами с точностью до знака, учитывая уравнение (2.8) получимОткуда следует, что псевдотензоры меняют свой знак на противоположный при изменении ориентации координатного репера если их вес нечетный. Подчеркнем, что e > 0 для правоориентированной координатной системы, e < 0 для левоориентированной координатной системы.
Псевдотензор 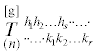 веса g ранга $n = s + r$ с помощью степеней фундаментального ориентирующего псевдоскаляра можно преобразовать
к абсолютному тензору того же ранга согласно
веса g ранга $n = s + r$ с помощью степеней фундаментального ориентирующего псевдоскаляра можно преобразовать
к абсолютному тензору того же ранга согласно
В дальнейшем изложении у фундаментальных символов, таких как e и g, указание на их вес будем опускать.
Ковариантная производная псевдотензорного поля 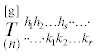 была введена О. Вебленом [26, 27] и вычисляется согласно [14, 24]:
была введена О. Вебленом [26, 27] и вычисляется согласно [14, 24]:
(2.9)
$\begin{gathered} {{\nabla }_{p}}\mathop {\mathop T\limits^{[{\text{g}}]} }\limits_{(n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot {{k}_{1}}{{k}_{2}} \ldots {{k}_{r}}}}^{{{{h}_{1}}{{h}_{2}} \ldots {{h}_{s}} \cdot \cdot \ldots \cdot }} = {{\partial }_{p}}\mathop {\mathop T\limits^{[{\text{g}}]} }\limits_{(n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot {{k}_{1}}{{k}_{2}} \ldots {{k}_{r}}}}^{{{{h}_{1}}{{h}_{2}} \ldots {{h}_{s}} \cdot \cdot \ldots \cdot }} + \Gamma _{{qp}}^{{{{h}_{1}}}}\mathop {\mathop T\limits^{[{\text{g}}]} }\limits_{(n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot {{k}_{1}}{{k}_{2}} \ldots {{k}_{r}}}}^{{q{{h}_{2}} \ldots {{h}_{s}} \cdot \cdot \ldots \cdot }} + \cdots + \Gamma _{{qp}}^{{{{h}_{s}}}}\mathop {\mathop T\limits^{[{\text{g}}]} }\limits_{(n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot {{k}_{1}}{{k}_{2}} \ldots {{k}_{r}}}}^{{{{h}_{1}}{{h}_{2}} \ldots q \cdot \cdot \ldots \cdot }}\, - \\ \, - \Gamma _{{{{k}_{1}}p}}^{q}\mathop {\mathop T\limits^{[{\text{g}}]} }\limits_{(n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot q{{k}_{2}} \ldots {{k}_{r}}}}^{{{{h}_{1}}{{h}_{2}} \ldots {{h}_{s}} \cdot \cdot \ldots \cdot }} - \cdots - \Gamma _{{{{k}_{r}}p}}^{q}\mathop {\mathop T\limits^{[{\text{g}}]} }\limits_{(n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot {{k}_{1}}{{k}_{2}} \ldots q}}^{{{{h}_{1}}{{h}_{2}} \ldots {{h}_{s}} \cdot \cdot \ldots \cdot }} - {\text{g}}\mathop {\mathop T\limits^{[{\text{g}}]} }\limits_{(n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot {{k}_{1}}{{k}_{2}} \ldots {{k}_{r}}}}^{{{{h}_{1}}{{h}_{2}} \ldots {{h}_{s}} \cdot \cdot \ldots \cdot }}\Gamma _{{qp}}^{q} \\ \end{gathered} $В частности, для псевдоскаляра ковариантная производная, независимо от веса ${\text{g}}$, примет вид
(2.10)
${{\nabla }_{p}}\mathop T\limits^{[{\text{g}}]} = {{\partial }_{p}}\mathop T\limits^{[{\text{g}}]} - {\text{g}}\mathop T\limits^{[{\text{g}}]} \Gamma _{{sp}}^{s}$Учитывая свойства символов Кристоффеля $\Gamma _{{sp}}^{s}$ и соотношение (2.6), получим выражение для ковариантной производной (2.10)
(2.11)
${{\nabla }_{p}}\mathop T\limits^{[{\text{g}}]} = {{\partial }_{p}}\mathop T\limits^{[{\text{g}}]} - {{e}^{{ - 1}}}{\text{g}}\mathop T\limits^{[{\text{g}}]} {{\partial }_{p}}e$Однако, существуют альтернативные подходы реализации ковариантного дифференцирования псевдотензора. Определим ковариантную производную псевдотензора произвольного ранга и целого веса ${\text{g}}$ с помощью соотношения:
(2.12)
${{\nabla }_{p}}\mathop {\mathop T\limits^{[{\text{g}}]} }\limits_{(n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot {{k}_{1}}{{k}_{2}} \ldots {{k}_{r}}}}^{{{{h}_{1}}{{h}_{2}} \ldots {{h}_{s}} \cdot \cdot \ldots \cdot }} = {{e}^{{\text{g}}}}{{\nabla }_{p}}({{e}^{{ - {\text{g}}}}}\mathop {\mathop T\limits^{[{\text{g}}]} }\limits_{(n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot {{k}_{1}}{{k}_{2}} \ldots {{k}_{r}}}}^{{{{h}_{1}}{{h}_{2}} \ldots {{h}_{s}} \cdot \cdot \ldots \cdot }}){\kern 1pt} $Кроме того, реализовать ковариантное дифференцирование псевдотензора с целым положительным весом (${\text{g}} > 0$) можно с помощью символов перестановок согласно правилу66
(2.13)
$\begin{gathered} {{\nabla }_{p}}\mathop {\mathop T\limits^{[{\text{g}}]} }\limits_{(n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot {{k}_{1}}{{k}_{2}} \ldots {{k}_{r}}}}^{{{{h}_{1}}{{h}_{2}} \ldots {{h}_{s}} \cdot \cdot \ldots \cdot }} = (N{{!)}^{{ - {\text{g}}}}}\underbrace {\mathop \epsilon \limits^{[ + 1]} {{{\kern 1pt} }^{{{{k}_{{r + 1}}} \ldots {{k}_{{r + N}}}}}} \cdots \mathop \epsilon \limits^{[ + 1]} {{{\kern 1pt} }^{{{{k}_{{r + ({\text{g}} - 1)N + 1}}} \ldots {{k}_{{r + N{\text{g}}}}}}}}}_{\text{g}} \times \\ \, \times {{\nabla }_{p}}(\mathop {\mathop T\limits^{[{\text{g}}]} }\limits_{(n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot {{k}_{1}}{{k}_{2}} \ldots {{k}_{r}}}}^{{{{h}_{1}}{{h}_{2}} \ldots {{h}_{s}} \cdot \cdot \ldots \cdot }}\underbrace {{{{\mathop \epsilon \limits^{[ - 1]} }}_{{{{k}_{{r + 1}}} \ldots {{k}_{{r + N}}}}}} \cdots {{{\mathop \epsilon \limits^{[ - 1]} }}_{{{{k}_{{r + ({\text{g}} - 1)N + 1}}} \ldots {{k}_{{r + N{\text{g}}}}}}}}}_{\text{g}}){\kern 1pt} \\ \end{gathered} $Все три вида реализации ковариантной производной (2.9), (2.12) и (2.13) являются эквивалентными, что было продемонстрировано в работе [31].
3. Термодинамические потенциалы состояния для гемитропных микрополярных термоупругих сред GN-I. Введем в рассмотрение внутреннюю энергию u в расчете на единицу массы. Понятие внутренней энергии, как физической величины, характеризующей элементарную термодинамическую систему, подробно обсуждается в классической монографии [16, С. 25–28]. Стандартное статистическое определение внутренней энергии элементарной термодинамической системы можно найти там же [16, c. 103–105]. В статистической физике во внутреннюю энергию системы включают энергию разных видов движения и взаимодействия входящих в систему частей: энергию поступательного, вращательного и колебательного движений атомов и молекул, энергию внутри- и межмолекулярного взаимодействия, энергию электронных оболочек атомов и др. В этом случае внутренняя энергия трактуется как физическая величина.
Помимо трактовки u как физической величины, связанной с элементарной термодинамической системой, в механике континуума ее приходится рассматривать как непрерывное физическое поле (physical field), поскольку континуум является объединением элементарных термодинамических систем. В механике континуума значение u как физической величины не представляет интереса ни в теоретическом, ни в прикладном плане. Подлинный интерес представляет трактовка внутренней энергии как термодинамического потенциала состояния, т.е. как однозначной, непрерывной и ограниченной снизу функции базиса термодинамических переменных (параметров состояния). Чертой сверху будем в дальнейшем обозначать потенциалы состояния. Например $\bar {u}$ означает, что внутренняя энергия u рассматривается как термодинамический потенциал состояния, зависящий от некоторого конечного набора базисных термодинамических переменных (параметров состояния). В термомеханике микрополярных континуумов имеем:
• s – энтропия в расчете на единицу массы (абсолютный скаляр);
• 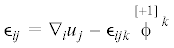 – асимметричный тензор деформации;
– асимметричный тензор деформации;
• 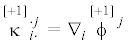 – псевдотензор деформации изгиба–кручения.
– псевдотензор деформации изгиба–кручения.
Поворот ϕj может трактоваться двояко: либо как ковариантный псевдовектор отрицательного веса
${{\mathop \phi \limits^{[ - 1]} }_{{j}}}$, либо как контравариантный псевдовектор положительного веса 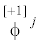 . В настоящей работе в качестве псевдовектора поворота мы будем использовать контравариантный
псевдовектор положительного веса
. В настоящей работе в качестве псевдовектора поворота мы будем использовать контравариантный
псевдовектор положительного веса 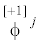 . Перечисленные выше переменные мы считаем образующими термодинамический базис в случае
микрополярного термоупругого континуума GN-I.
. Перечисленные выше переменные мы считаем образующими термодинамический базис в случае
микрополярного термоупругого континуума GN-I.
Все сказанное выше можно выразить следующим уравнением:
Фундаментальным утверждением (3.1) постулируется равенство физического значения внутренней энергии $u$ (абсолютного скаляра, не зависящего от зеркальных отражений и инверсий трехмерного пространства) и значения функциональной зависимости $\bar {u}$.
Сопряженной к энтропии величиной в термодинамике выступает термодинамическая температура (абсолютная температура). Термодинамическая температура может вводиться статистически, как модуль канонического распределения Гиббса [16, c. 104–105]. В термомеханике континуума абсолютная температура $\theta $ (абсолютный скаляр) определяется как функция параметров термодинамического состояния и вычисляется как частная производная потенциальной функции (3.1) по энтропии s, т.е.
(3.2)
$\theta = \frac{{\partial{ \bar {u}}(s,{{\epsilon }_{{ij}}},\mathop \kappa \limits^{[ + 1]} \,_{{i \cdot }}^{{ \cdot j}})}}{{\partial s}}$Формула (3.2) наглядно демонстрирует отличие $u$ от $\bar {u}$. В работах некоторых авторов [8, 7 ] приоритет отдается обратной к температуре величине $\frac{1}{\theta }$ – холодности (coldness).
Уравнение баланса внутренней энергии для линейных микрополярных теорий, как хорошо известно, имеет следующий вид
Здесь ${{\partial }_{ \cdot }}$ – производная по времени при фиксированных координатах xk, ${{t}^{{ik}}}$ – тензор силовых напряжений, $\rho $ – массовая плотность (абсолютный скаляр), 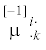 – псевдотензор моментных напряжений, q – лучистое тепло (абсолютный скаляр), ${{h}^{i}}$ – абсолютный вектор потока тепла. В приближении малых деформаций мы считаем $\dot {a} = {{\partial }_{ \cdot }}a$.
– псевдотензор моментных напряжений, q – лучистое тепло (абсолютный скаляр), ${{h}^{i}}$ – абсолютный вектор потока тепла. В приближении малых деформаций мы считаем $\dot {a} = {{\partial }_{ \cdot }}a$.
В конвенциональном виде уравнение баланса энтропии примем
где ${{J}^{j}}$ – абсолютный вектор потока энтропии, $\xi $ – неконтролируемое производство энтропии77 (в единицу времени в расчете на единицу массы), $\sigma $ – контролируемое производство энтропии (в единицу времени в расчете на единицу массы). Отметим, что $\xi $ и $\sigma $ являются абсолютными скалярами.В термомеханике широко используется еще один термодинамический потенциал – свободная энергия Гельмгольца. Минуя статистический смысл свободной энергии, приписывая ей отрицательный знак, введем с помощью преобразования Лежандра внутренней энергии
(3.5)
$ - \bar {\psi }(\theta ,{{\epsilon }_{{ij}}},\mathop \kappa \limits^{[ + 1]} \,_{{i \cdot }}^{{ \cdot j}}) = \theta s - \bar {u}(s,{{\epsilon }_{{ij}}},\mathop \kappa \limits^{[ + 1]} \,_{{i \cdot }}^{{ \cdot j}}),\quad \theta = \frac{{\partial{ \bar {u}}}}{{\partial s}}$Преобразование Лежандра и его основные свойства подробно обсуждаются в монографии [30, c. 155–157].
На основания инволютивности преобразования Лежандра, получим
(3.6)
$\bar {u}(s,{{\epsilon }_{{ij}}},\mathop \kappa \limits^{[ + 1]} \,_{{i \cdot }}^{{ \cdot j}}) = \theta s - ( - \bar {\psi }(\theta ,{{\epsilon }_{{ij}}},\mathop \kappa \limits^{[ + 1]} \,_{{i \cdot }}^{{ \cdot j}})),\quad s = - \frac{{\partial{ \bar {\psi }}}}{{\partial \theta }}$(3.7)
$s = \bar {s}(\theta ,{{\epsilon }_{{ij}}},\mathop \kappa \limits^{[ + 1]} \,_{{i \cdot }}^{{ \cdot j}}),\quad \bar {s} = - \frac{{\partial{ \bar {\psi }}}}{{\partial \theta }}$4. Определяющие уравнения гемитропного микрополярного термоупругого континуума GN-I. Уравнение баланса свободной энергии можно получить подстановкой соотношений (3.4) и (3.5) в уравнение (3.3). В результате несложных преобразований получим
В предположении
уравнение (4.1) преобразуется к одной из приведенных формДля необратимых термодинамических процессов справедливо следующее фундаментальное неравенство:
где(4.5)
${{A}^{{ij}}} = \rho \frac{{\partial{ \bar {\psi }}}}{{\partial {{\epsilon }_{{ij}}}}} - {{t}^{{ij}}}$Откуда следуют определяющие соотношения
Для неконтролируемого производства энтропии справедливо уравнение
(4.7)
$\rho \xi = - {{\theta }^{{ - 2}}}{{h}^{j}}{{\nabla }_{j}}\theta = - {{\theta }^{{ - 1}}}{{J}^{j}}{{\nabla }_{j}}\theta = - {{\overline J }^{j}}({{\nabla }_{k}}\ln \theta ){{\nabla }_{j}}\ln \theta ,\quad \inf \theta > 0$На основании уравнения баланса энтропии (3.4) при учете (4.6) получаем нелинейное уравнение теплопроводности
Линеаризованную по базисным термодинамическим переменным, свободную энергию для микрополярного термоупругого континуума GN-I можно принять в форме
Здесь ${{\mathop H\limits_1 }^{{islm}}}$, 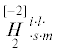 ,
, 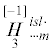 , ${{\mathop G\limits_1 }^{{is}}}$,
, ${{\mathop G\limits_1 }^{{is}}}$, 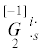 , $F$ – определяющие тензоры и псевдотензоры микрополярного термоупругого континуума GN-I,
$\theta \to \theta - {{\theta }_{0}}$ – малый температурный инкремент (считается малой первого порядка), θ0 – референциальная температура. Веса определяющих псевдотензоров сведены в таблицу
1. Отметим, что
, $F$ – определяющие тензоры и псевдотензоры микрополярного термоупругого континуума GN-I,
$\theta \to \theta - {{\theta }_{0}}$ – малый температурный инкремент (считается малой первого порядка), θ0 – референциальная температура. Веса определяющих псевдотензоров сведены в таблицу
1. Отметим, что 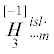 и
и 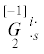 являются определяющими псевдотензорами, чувствительными к преобразованиям зеркального
отражения трехмерного пространства.
являются определяющими псевдотензорами, чувствительными к преобразованиям зеркального
отражения трехмерного пространства.
Для определяющих псевдотензоров ${{\mathop H\limits_1 }^{{islm}}}$, 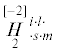 справедливы условия симметрии
справедливы условия симметрии
Воспользовавшись определяющими соотношениями (4.6), в итоге получим
(4.10)
$\begin{gathered} {{t}^{{is}}} = {{\mathop H\limits_1 }^{{islm}}}{{\epsilon }_{{lm}}} + \frac{1}{2}\mathop {\mathop H\limits_3 }\limits^{[ - 1]} {\kern 1pt} _{{ \cdot \cdot \cdot m}}^{{isl \cdot }}\mathop \kappa \limits^{[ + 1]} {\kern 1pt} _{{l \cdot }}^{{ \cdot m}}\, + \frac{1}{2}{{\mathop G\limits_1 }^{{is}}}\theta {\kern 1pt} \\ \mathop \mu \limits^{[ - 1]} {\kern 1pt} _{{ \cdot s}}^{{i \cdot }}\, = \mathop {\mathop H\limits_2 }\limits^{[ - 2]} {\kern 1pt} _{{ \cdot s \cdot m}}^{{i \cdot l \cdot }}\mathop \kappa \limits^{[ + 1]} {\kern 1pt} _{{l \cdot }}^{{ \cdot m}} + \frac{1}{2}\mathop {\mathop H\limits_3 }\limits^{[ - 1]} {\kern 1pt} _{{ \cdot \cdot \cdot s}}^{{lmi \cdot }}{{\epsilon }_{{lm}}} + \frac{1}{2}\mathop {\mathop G\limits_2 }\limits^{[ - 1]} {\kern 1pt} _{{ \cdot s}}^{{i \cdot }}\theta {\kern 1pt} \\ 2\rho \bar {s} = - {{\mathop G\limits_1 }^{{is}}}{{\epsilon }_{{is}}} - \mathop {\mathop G\limits_2 }\limits^{[ - 1]} {\kern 1pt} _{{ \cdot s}}^{{i \cdot }}\mathop \kappa \limits^{[ + 1]} {\kern 1pt} _{{i \cdot }}^{{ \cdot s}} - 2F\theta {\kern 1pt} \\ {{h}^{i}} = - {{\mathop G\limits_3 }^{{is}}}{{\nabla }_{s}}\theta \\ \end{gathered} $5. Линейный гемитропный микрополярный термоупругий континуум. Полученная энергетическая форма (4.9) используется, как правило, при построении моделей гемитропных микрополярных упругих континуумов. Определяющие тензоры и псевдотензоры для линейного гемитропного микрополярного упругого континуума нечувствительны к поворотам координатного репера, поэтому для них будут справедливы следующие координатные представления88
(5.1)
$\begin{gathered} \mathop {\mathop H\limits_2 }\limits^{[ - 2]} {{{\kern 1pt} }^{{islm}}}\; = \mathop {\mathop a\limits_2 }\limits^{[ - 2]} {{g}^{{is}}}{{g}^{{lm}}} + \mathop {\mathop b\limits_2 }\limits^{[ - 2]} {{g}^{{il}}}{{g}^{{sm}}} + \mathop {\mathop c\limits_2 }\limits^{[ - 2]} {{g}^{{im}}}{{g}^{{sl}}}{\kern 1pt} \\ \mathop {\mathop H\limits_3 }\limits^{[ - 1]} {{{\kern 1pt} }^{{islm}}}\; = \mathop {\mathop a\limits_3 }\limits^{[ - 1]} {{g}^{{is}}}{{g}^{{lm}}} + \mathop {\mathop b\limits_3 }\limits^{[ - 1]} {{g}^{{il}}}{{g}^{{sm}}} + \mathop {\mathop c\limits_3 }\limits^{[ - 1]} {{g}^{{im}}}{{g}^{{sl}}}{\kern 1pt} \\ \end{gathered} $Здесь $\mathop {\mathop a\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, $\mathop {\mathop b\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, $\mathop {\mathop c\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, $\mathop {\mathop d\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $ ($\mathfrak{a} = 1,2,3;$ ${\text{g}} = 0, - 1, - 2$) – двенадцать определяющих псевдоскаляры гемитропного микрополярного термоупругого тела GN-I. Метаиндекс $\mathfrak{a}$ – нумерует определяющие псевдоскаляры. С точки зрения тензорной алгебры $\mathop {\mathop a\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, $\mathop {\mathop b\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, $\mathop {\mathop c\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, $\mathop {\mathop d\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, как минимум, являются полуизотропными инвариантами.
Подставив координатные представления (5.1) в определяющие соотношения (4.10), получим
(5.2)
$\begin{gathered} {{\mathop \mu \limits^{[ - 1]} }^{{is}}} = (\mathop {\mathop a\limits_2 }\limits^{[ - 2]} {{g}^{{is}}}{{g}^{{lm}}} + \mathop {\mathop b\limits_2 }\limits^{[ - 2]} {{g}^{{il}}}{{g}^{{sm}}} + \mathop {\mathop c\limits_2 }\limits^{[ - 2]} {{g}^{{im}}}{{g}^{{sl}}}){{\mathop \kappa \limits^{[ + 1]} }_{{lm}}} + \\ \, + \frac{1}{2}(\mathop {\mathop a\limits_3 }\limits^{[ - 1]} {{g}^{{is}}}{{g}^{{lm}}} + \mathop {\mathop b\limits_3 }\limits^{[ - 1]} {{g}^{{il}}}{{g}^{{sm}}} + \mathop {\mathop c\limits_3 }\limits^{[ - 1]} {{g}^{{im}}}{{g}^{{sl}}}){{\epsilon }_{{lm}}} + \frac{1}{2}\mathop {\mathop d\limits_2 }\limits^{[ - 1]} \theta {{g}^{{is}}} \\ \end{gathered} $Вместо определяющих псевдоскаляров $\mathop {\mathop a\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, $\mathop {\mathop b\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, $\mathop {\mathop c\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, $\mathop {\mathop d\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $ можно перейти к конвенциональным определяющим псевдоскалярам, таким как: G – модуль сдвига; $\nu $ – коэффициент Пуассона; $\mathop L\limits^{[ - 1]} $ – характерная микродлина; 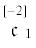 ,
, 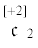 , ${{\mathfrak{c}}_{3}}$, ${{\mathfrak{c}}_{4}}$, ${{\mathfrak{c}}_{5}}$, ${{\mathfrak{c}}_{6}}$ – не имеющие физической размерности псевдоскаляры; $\mathop \alpha \limits_* $ – коэффициент линейного теплового расширения; $\mathop {\mathop \beta \limits_* }\limits^{[ + 1]} $ – коэффициент теплового изгиба–кручения; λ – коэффициент теплопроводности; c – теплоемкость на единицу массы при ${{\epsilon }_{{is}}} = 0$ (см. [36, 37]). В этом случае характерная микродлина $L$ будет псевдоскаляром отрицательного веса –1.
, ${{\mathfrak{c}}_{3}}$, ${{\mathfrak{c}}_{4}}$, ${{\mathfrak{c}}_{5}}$, ${{\mathfrak{c}}_{6}}$ – не имеющие физической размерности псевдоскаляры; $\mathop \alpha \limits_* $ – коэффициент линейного теплового расширения; $\mathop {\mathop \beta \limits_* }\limits^{[ + 1]} $ – коэффициент теплового изгиба–кручения; λ – коэффициент теплопроводности; c – теплоемкость на единицу массы при ${{\epsilon }_{{is}}} = 0$ (см. [36, 37]). В этом случае характерная микродлина $L$ будет псевдоскаляром отрицательного веса –1.
Сравнивая (5.2) с аналогичными формулами в [37, формулы (2.12)]:
(5.3)
$\begin{gathered} \mathop A\limits_1 = G\nu {{(1 - 2\nu )}^{{ - 1}}},\quad \mathop {\mathop A\limits_2 }\limits^{[ - 2]} = G\mathop L\limits^{[ - 1]} \mathop L\limits^{[ - 1]} {{c}_{3}},\quad \mathop A\limits_3 = G \\ \mathop {\mathop A\limits_4 }\limits^{[ - 2]} = G\mathop L\limits^{[ - 1]} \mathop L\limits^{[ - 1]} ,\quad \mathop {\mathop A\limits_5 }\limits^{[ - 2]} = 2G{{\mathop c\limits^{[ - 2]} }_{{1}}},\quad \mathop A\limits_6 = 2G\mathop L\limits^{[ - 1]} \mathop L\limits^{[ - 1]} {{\mathop c\limits^{[ + 2]} }_{{2}}} \\ \mathop {\mathop A\limits_7 }\limits^{[ - 1]} = G\mathop L\limits^{[ - 1]} {{c}_{4}},\quad \mathop {\mathop A\limits_8 }\limits^{[ - 1]} = G\mathop L\limits^{[ - 1]} {{c}_{5}},\quad \mathop {\mathop A\limits_9 }\limits^{[ - 1]} = G\mathop L\limits^{[ - 1]} {{c}_{6}} \\ \end{gathered} $Подставляя (5.4) в (5.3), получим
откуда, учитывая определяющие уравнения (5.2), можно установить(5.6)
$\begin{gathered} \mathop a\limits_1 = 2\mathop A\limits_1 ,\quad \mathop b\limits_1 \; + \mathop c\limits_1 = 2\mathop A\limits_3 ,\quad \mathop b\limits_1 \; - \mathop c\limits_1 = {{e}^{2}}\mathop {\mathop A\limits_5 }\limits^{[ - 2]} \\ \mathop {\mathop a\limits_2 }\limits^{[ - 2]} = 2\mathop {\mathop A\limits_2 }\limits^{[ - 2]} ,\quad \mathop {\mathop b\limits_2 }\limits^{[ - 2]} + \mathop {\mathop c\limits_2 }\limits^{[ - 2]} = 2\mathop {\mathop A\limits_4 }\limits^{[ - 2]} ,\quad \mathop {\mathop b\limits_2 }\limits^{[ - 2]} - \mathop {\mathop c\limits_2 }\limits^{[ - 2]} = {{e}^{{ - 2}}}\mathop A\limits_6 \\ \mathop {\mathop a\limits_3 }\limits^{[ - 1]} = 2\mathop {\mathop A\limits_7 }\limits^{[ - 1]} ,\quad \mathop {\mathop b\limits_3 }\limits^{[ - 1]} + \mathop {\mathop c\limits_3 }\limits^{[ - 1]} = 2\mathop {\mathop A\limits_8 }\limits^{[ - 1]} ,\quad \mathop {\mathop b\limits_3 }\limits^{[ - 1]} - \mathop {\mathop c\limits_3 }\limits^{[ - 1]} = - \mathop {\mathop A\limits_9 }\limits^{[ - 1]} \\ \end{gathered} $Подставляя (5.5) в (5.6) и выражая $\mathop {\mathop a\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, $\mathop {\mathop b\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, $\mathop {\mathop c\limits_\mathfrak{a} }\limits^{[{\text{g}}]} $, в итоге получим
Принимая обозначения для определяющих постоянных
(5.8)
$c_{4}^{'} = {{c}_{4}} + \frac{1}{2}{{c}_{5}} + \frac{1}{4}{{c}_{6}},\quad c_{5}^{'} = \frac{1}{2}{{c}_{5}} - \frac{1}{4}{{c}_{6}},\quad c_{6}^{'} = - {{c}_{6}}$(5.9)
$c_{4}^{'} = 2{{\mathfrak{c}}_{6}} + {{\mathfrak{c}}_{4}} - {{\mathfrak{c}}_{5}},\quad c_{5}^{'} = {{\mathfrak{c}}_{4}} + {{\mathfrak{c}}_{5}},\quad c_{6}^{'} = 4{{\mathfrak{c}}_{5}}$Заключение. В настоящей статье рассмотрен сравнительно новый подход к математическому моделированию связанной термоупругой гемитропной среды.
1. Предложены новые подходы к построению энергетических форм и уравнений механики микрополярной термоупругости.
2. Получены уравнение теплопроводности и динамические уравнения гемитропного микрополярного термоупругого GN-I континуума в пседотензорной формулировке.
3. Использовались общие термодинамические принципы неравновесной термодинамики.
4. Анизотропные определяющие псевдотензоры в представлении квадратичной энергетической формы включают: 3 псевдотензора четвертого ранга, 3 псевдотензора второго ранга и один абсолютный скаляр.
5. Анизотропная энергетическая форма редуцировалась к гемитропной с помощью специальных координатных представлений для определяющих псевдотензоров.
6. Рассмотрены различные варианты определяющих скаляров и псевдоскаляров, в том числе, конвенционально используемые материальные псевдоскаляры: модуль сдвига, коэффициент Пуассона, характерная микродлина (являющаяся псевдоскаляром отрицательного веса, чувствительным к отражениям трехмерного пространства), коэффициент линейного теплового расширения; коэффициент теплового искажения, коэффициент теплопроводности, теплоемкость на единицу массы и псевдоскаляры, не имеющие физической размерности.
Благодарности. Исследование выполнено за счет гранта Российского научного фонда (проект № 23-21-00262).
Таблица 1.
Веса определяющих тензоров и псевдотензоров связанной термоупругой гемитропной среды
| Терминологическое обозначение | Символьное обозначение | Вес | Преобразование к абсолютному тензору |
|---|---|---|---|
| определяющий тензор i (first constitutive tensor) | ${{\mathop H\limits_1 }^{{islm}}}$ | 0 | |
| определяющий псевдотензор ii (second constitutive pseudotensor) | 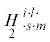 |
–2 | 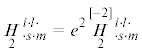 |
| определяющий псевдотензор iii (third constitutive pseudotensor) | 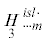 |
–1 | 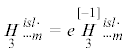 |
| определяющий тензор iv (firth constitutive tensor) | ${{\mathop G\limits_1 }^{{is}}}$ | 0 | |
| определяющий псевдотензор v (fifth constitutive pseudotensor) |
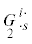 |
–1 | 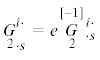 |
| определяющий скаляр vi (sixth constitutive scalar) |
Список литературы
Turpin J.P., Bossard J.A., Morgan K.L. et al. Reconfigurable and tunable metamaterials: a review of the theory and applications // Int. J. Antennas Propag. 2014. V. 2014. P. 429837. https://doi.org/10.1155/2014/429837
Giorgio I., Hild F., Gerami E. et al. Experimental verification of 2D cosserat chirality with stretch-micro-rotation coupling in orthotropic metamaterials with granular motif // Mech. Res. Commun. 2022. P. 104020. https://doi.org/10.1016/j.mechrescom.2022.104020
Reasa D.R., Lakes R.S. Nonclassical Chiral Elasticity of the Gyroid Lattice // Phys. Rev. Lett. 2020. V. 125. P. 205502. https://doi.org/10.1103/PhysRevLett.125.205502
Askari M., Hutchins D.A., Thomas P.J. et al. Additive manufacturing of metamaterials: A review // Addit. Manuf. 2020. V. 36. P. 101562. https://doi.org/10.1016/j.addma.2020.101562
Kovalev V.A., Murashkin E.V., Radayev Yu.N. Metamaterial models of continuum multiphysics // Труды международной школы-конференции молодых ученых “Механика 2016”. Цахкадзор, Армения, 03–07 октября 2016. Ереван: Национальный университет архитектуры и строительства Армении, 2016. С. 160–163.
Ковалев В.А., Мурашкин Е.В. О принципе термомеханической ортогональности в проблемах моделирования сложных сред и метаматериалов // Вестн. Чувашского гос. пед. ун-та им. И.Я. Яковлева. Сер.: Мех. пред. сост. 2019. № 1(49). P. 20–31. https://doi.org/10.26293/chgpu.2019.39.1.003
Müller I., Ruggeri T. Rational extended thermodynamics. Berlin: Springer Science & Business Media, 2013. 411 p.
Truesdell C. Rational thermodynamics: a course of lectures on selected topics. New York: McGraw-Hill, 1969. 208+ix p.
Truesdell C., Toupin R. The classical field theories // Principles of Classical Mechanics and Field Theory / Ed. by S. Flügge. Berlin, Heidelberg: Springer, 1960. P. 226–858. https://doi.org/10.1007/978-3-642-45943-6_2
Besdo D. Ein beitrag zur nichtlinearen theorie des Cosserat-kontinuums // Acta Mech. 1974. V. 20. № 1. P. 105–131. https://doi.org/10.1007/BF01374965
Nowacki W. Theory of micropolar elasticity. Springer, 1972. 286 p. https://doi.org/10.1007/978-3-7091-2720-9
Nowacki W. Theory of asymmetric elasticity. Oxford: Pergamon Press, 1986. 383 p.
Розенфельд Б.А. Многомерные пространства. М.: Наука, 1966. 668 с.
Радаев Ю.Н., Мурашкин Е.В. Псевдотензорная формулировка механики гемитропных микрополярных сред // Проблемы прочности и пластичности. 2020. Т. 82. № 4. С. 399–412. https://doi.org/10.32326/1814-9146-2020-82-4-399-412
Седов Л.И. Введение в механику сплошной среды. М.: Физматгиз, 1962. 592 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 5. Статистическая физика. Часть 1. М.: Физматлит, 2001. 616 с.
Радаев Ю.Н. Задачи и теоремы по курсу “Математическая теория пластичности”. Самара: Самарский гос. ун-т, 1996. 80 с.
Ковалев В.А., Радаев Ю.Н. Волновые задачи теории поля и термомеханика. Саратов: Изд-во Сарат. ун-та, 2010. 328 с.
Ковалев В.А., Радаев Ю.Н. Элементы теории поля: вариационные симметрии и геометрические инварианты. М.: Физматлит, 2009. 156 с.
Murashkin E.V., Radayev Yu.N. On a micropolar theory of growing solids // Вестн. Сам. гос. техн. ун-та. Сер. физ.-мат. науки. 2020. Т. 24. № 3. С. 424–444. https://doi.org/10.14498/vsgtu1792
Kovalev V.A., Murashkin E.V., Radayev Yu.N. On the Neuber theory of micropolar elasticity. A pseudotensor formulation // Вестн. Сам. гос. техн. ун-та. Сер. физ.-мат. науки. 2020. Т. 24. № 4. С. 752–761. https://doi.org/10.14498/vsgtu1799
Гуревич Г.Б. Основы теории алгебраических инвариантов. М., Л.: ГИТТЛ, 1948. 408 с.
Schouten J.A. Tensor Analysis for Physicist. Oxford: Clarendon Press, 1965. 434 p.
Sokolnikoff I. Tensor Analysis: Theoryand Applications to Geometry and Mechanics of Continua. New York: John Wiley & Sons Inc., 1964. 361 p.
Synge J.L., Schild A. Tensor Calculus. Toronto: Toronto University Press, 1949. 334 p.
Veblen O., Thomas T.Y. Extensions of relative tensors // Trans. Am. Math. Society. 1924. V. 26. P. 373–377.
Veblen O. Invariants of Quadratic Differential Forms. Cambridge: The University Press, 1933. 102 p.
Мак-Коннел А.Дж. Введение в тензорный анализ: С приложениями к геометрии, механике и физике. М.: Физматгиз, 1963. 411 с.
Копф А. Основы теории относительности Эйнштейна. М.: ГТТИ, 1933. 175 с.
Радаев Ю.Н. Пространственная задача математической теории пластичности. Самара: Самар. гос. ун-т, 2006. 340 p.
Мурашкин Е.В., Радаев Ю.Н. Алгебраический алгоритм систематического приведения одноточечных псевдотензоров к абсолютным тензорам // Вестн. Чувашского гос. пед. ун-та им. И.Я. Яковлева. Сер.: Мех. пред. сост. 2022. № 1(51). P. 17–26. https://doi.org/10.37972/chgpu.2022.51.1.002
Jeffreys H. Cartesian Tensors. Cambridge: Cambridge University Press, 1931. 101 p.
Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980. 512 p.
Мурашкин Е.В., Радаев Ю.Н. Ковариантно постоянные тензоры в пространствах Евклида. Элементы теории // Вестн. Чувашского гос. пед. ун-та им. И.Я. Яковлева. Сер.: Мех. пред. сост. 2022. № 2(52). P. 106–115. https://doi.org/10.37972/chgpu.2022.51.1.002
Мурашкин Е.В., Радаев Ю.Н. Ковариантно постоянные тензоры в пространствах Евклида. Приложения к механике континуума // Вестн. Чувашского гос. пед. ун-та им. И.Я. Яковлева. Сер.: Мех. пред. сост. 2022. № 2(52). P. 118–127. https://doi.org/10.37972/chgpu.2022.51.1.002
Радаев Ю.Н. Правило множителей в ковариантных формулировках микрополярных теорий механики континуума // Вестн. Сам. гос. техн. ун-та. Сер. физ.-мат. науки. 2018. V. 22. № 3. P. 504–517. https://doi.org/10.14498/vsgtu1635
Мурашкин Е.В., Радаев Ю.Н. Об определяющих псевдоскалярах гемитропных микрополярных сред в инверсных координатных системах // Вестн. Сам. гос. техн. ун-та. Сер. физ.-мат. науки. 2021. Т. 25. № 3. С. 457–474. https://doi.org/10.14498/vsgtu1870
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела