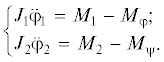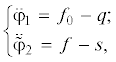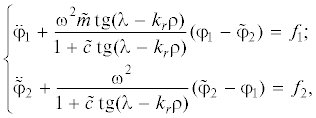Проблемы машиностроения и надежности машин, 2019, № 3, стр. 10-18

Введение. Одним из необходимых элементов электромеханического привода машин различного отраслевого назначения является система передаточных механизмов, предназначенная для согласования механических характеристик двигателей и рабочих машин. В качестве передаточных механизмов в настоящее время продолжают широко использоваться червячные передачи, несмотря на их недостатки и все возрастающую конкуренцию со стороны более современных механизмов – планетарных и волновых передач. Червячные редукторы входят в состав привода роторных технологических машин и автоматических роторных линий машиностроительных, пищевых и фармацевтических производств [1, 2]. Стремление компенсировать недостатки червячных передач и расширить область их применения приводит к совершенствованию конструкций известных схем [3], разработке новых схем [4] и необходимости тщательного анализа динамических процессов в машинах с такими передачами.

Наличие больших сил трения в червячных передачах приводит к существенной нелинейности математических моделей, описывающих динамику привода, может являться причиной ряда явлений, принципиально невозможных в линейных системах, что требует особого подхода к составлению и исследованию этих моделей. Работы в этом направлении можно разделить на три группы.

1. Работы, посвященные обобщению общих принципов механики на системы с трением и исследованию свойств нелинейных систем дифференциальных уравнений, описывающих такие системы. У истоков этих работ стоял известный французский ученый П. Пэнлеве. Далее этим вопросом продолжает заниматься большой ряд зарубежных и отечественных ученых [5–7].

2. Работы, связанные с исследованием самоторможения, возникающего в таких системах, и его использованием в машинах [8, 9].

3. Работы, посвященные анализу динамики технологических машин, роботов, манипуляторов и других устройств с электромеханическим приводом, в состав которого входят червячные редукторы [10–13]. В большинстве этих работ основное внимание уделяется исследованию переходных режимов движения, в которых нелинейные свойства червячной передачи проявляются наиболее ярко. Влияние процессов в электродвигателе на динамику привода не учитывалось или учитывалось с помощью статической характеристики.

В роторных технологических машинах основным режимом движения является режим установившегося движения. Колебания в этом режиме приводят к появлению значительных динамических нагрузок, могут привести к нарушению технологического процесса и зависят не только от свойств передаточного механизма, но и от электромагнитных процессов, протекающих в электродвигателе. Целью настоящей статьи является исследование вынужденных колебаний, возникающих в электромеханическом приводе с червячным редуктором роторных технологических машин под действием периодической технологической нагрузки с учетом свойств приводного асинхронного электродвигателя.

Постановка задачи. Известно, что протекание колебательных процессов в электроприводе с асинхронными электродвигателями определяется не только инерционными и упругими характеристиками механической части системы, но и переходными электромагнитными процессами в самом электродвигателе, которые с достаточной точностью описываются его динамической характеристикой. Причем для сравнительно тихоходных машин, к которым можно отнести и технологические роторные машины с червячным приводом, большее влияние на характеристики колебаний могут оказывать электромагнитные процессы в двигателе, а не упругость звеньев. Поэтому анализ вынужденных колебаний будем проводить в два этапа: 1) исследование вынужденных колебаний для модели с жесткими звеньями при учете динамической характеристики электродвигателя; 2) исследование вынужденных колебаний для модели с упругими звеньями при учете динамической характеристики электродвигателя. Такой подход позволяет выявить свойства динамических процессов в приводе, определяемые применяемым электродвигателем, и определить область применимости результатов, получаемых при использовании более простой модели, не учитывающей упругость звеньев.

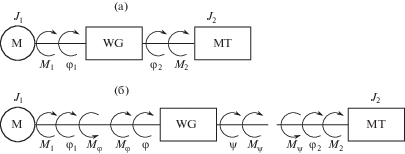
Исследование вынужденных колебаний в приводе на основе расчетной модели с жесткими звеньями. Рассматриваемая роторная технологическая машина состоит из электромеханического привода, включающего в себя асинхронный электродвигатель M и червячный редуктор WG, а также рабочей машины роторного типа MT (рис. 1а). На схеме обозначены: ${{J}_{1}}$, ${{J}_{2}}$ – моменты инерции ротора двигателя и рабочей машины, соответственно, включающие приведенные к ним моменты инерции промежуточных деталей; ${{M}_{1}}$ – крутящий момент на валу двигателя; ${{M}_{2}}$ – момент сил сопротивления, приложенный к рабочей машине, являющийся известной периодической функцией времени; ${{\varphi }_{1}}$, ${{\varphi }_{2}}$ – угловые координаты валов двигателя и рабочей машины соответственно; $\varphi $, $\psi $, ${{M}_{\varphi }}$, ${{M}_{\psi }}$ – угловые координаты и моменты на входе и выходе червячной кинематической пары.

Червячный редуктор описывается известным кинематическим соотношением

и силовым передаточным отношением [14] где $u$ – передаточное число редуктора; $\lambda $ – делительный угол подъема линии витка червяка; $\rho $ – приведенный угол трения; ${{k}_{r}}$ – коэффициент режима работы червячной пары, зависящий от направлений вращения элементов пары и внутренних сил в зацеплении, При записи (2) принято, что в рассматриваемом режиме скорость скольжения в зацеплении не меняется и можно принять $\rho = const$.

При работе асинхронного электродвигателя в установившемся режиме связь между угловой скоростью ротора и моментом, развиваемым электродвигателем, с достаточной точностью можно представить его динамической характеристикой в виде [14]

где ${{T}_{e}}$ – электромагнитная постоянная времени электродвигателя; ${{M}_{{10}}}$, $k$ – параметры статической механической характеристики.

Разделяя расчетную схему на две подсистемы, связанные с помощью червячного редуктора (рис. 1б), причем ${{\varphi }_{1}} = \varphi $, ${{\varphi }_{2}} = \psi $, записывая их уравнения движения и выполняя необходимые преобразования с учетом (1)–(4), получим математическую модель системы в виде дифференциального уравнения второго порядка относительно момента двигателя

где ${{T}_{1}} = {{J}_{1}}{\text{/}}k$, ${{T}_{2}} = (\mu {{J}_{2}}){\text{/}}({{u}^{2}}k)$ – механические постоянные времени электродвигателя и рабочей машины; $\mu = \mu ({{k}_{r}})$ – вспомогательная кусочно-линейная функция, определяемая зависимостью

Если предположить, что в режиме установившегося движения коэффициент режима не меняется, то уравнение (5) будет линейным, решение которого хорошо известно, и тогда частота собственных колебаний системы

При $4{{T}_{e}} < {{T}_{1}} + {{T}_{2}}$ собственное движение системы будет апериодическим. Для анализа зависимости собственной частоты (6) от параметров привода введем безразмерные постоянные времени, Для асинхронных электродвигателей серии 4А по ГОСТ 19523-81 мощностью от 1 до 30 кВт и синхронной частотой вращения 1500 и 3000 об/мин относительная постоянная времени ${{\tau }_{1}}$ находится в пределах от 1.6 до 9.1. Значение относительной постоянной времени рабочей машины ${{\tau }_{2}}$ зависит от вида машины и режима движения. Для рассматриваемого класса машин ${{\tau }_{2}} = 1{\kern 1pt} - {\kern 1pt} 3$ при ${{k}_{r}} = - 1$ и ${{\tau }_{2}} = - 1{\kern 1pt} - {\kern 1pt} 1$ при ${{k}_{r}} = + 1$. Вводя безразмерную частоту $\tilde {\chi } = \chi {\text{/}}{{\chi }_{0}}$, где ${{\chi }_{0}} = {{\left[ {{{T}_{e}}({{T}_{1}} + {{T}_{2}})} \right]}^{{ - 1/2}}}$ – собственная частота недемпфированной системы, и используя (7), получим Для определенных областей значений относительных постоянных времени $1 + {{\tau }_{2}}$ < < 4τ₁, собственное движение привода будет колебательным.

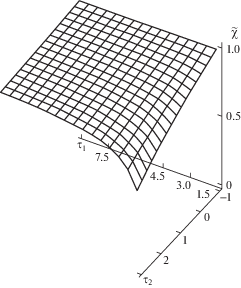
На рис. 2 представлена зависимость относительной собственной частоты привода $\tilde {\chi }$ от безразмерных постоянных времени ${{\tau }_{1}}$ и ${{\tau }_{2}}$, построенная на основании (8). Видно, что $\tilde {\chi }$ монотонно возрастает при увеличении ${{\tau }_{1}}$ и уменьшении ${{\tau }_{2}}$, находясь в пределах от 0.577 до 1.

При исследовании вынужденных колебаний будем предполагать, что в режиме установившегося движения коэффициент режима ${{k}_{r}}$ не меняется. Это позволяет использовать принцип суперпозиции и ограничиться определением реакции системы на моногармоническое воздействие вида

где ${{M}_{{20}}}$ – постоянная составляющая момента сил сопротивления (${{M}_{{20}}} < 0$); ${{M}_{{2a}}}$ – амплитуда переменной составляющей; $\Omega $ – частота колебаний момента сил сопротивления.

Переходя в уравнении (5) с учетом (1)–(4) к операторной форме записи, а затем к комплексной переменной $p = j\Omega $, и используя (1)–(4) получим амплитудно-частные характеристики (АЧХ) момента ${{M}_{\psi }}$

Реакцию системы на воздействие (9) можно записать в виде

В работе [15] было показано, что изменение коэффициента режима приводит к скачкообразному изменению производных внутренних сил и моментов и резкому возрастанию динамических нагрузок. Следовательно, переключение элементов червячной кинематической пары является нежелательным, а в технологических машинах в режиме установившегося движения вообще недопустимым.

Необходимое и достаточное условие постоянства знака момента ${{M}_{\psi }}(t)$, определяющего режим работы червячной пары,

одновременно является условием линейности исходной системы уравнений и, следовательно, определяет область применимости найденного решения.

Для решения вопроса о возможности выполнения этого условия в реальных приводах исследуем зависимость наибольшего значения АЧХ ${{A}_{{{{M}_{\psi }}}}}(\Omega )$ от значений параметров системы. Для упрощения анализа приведем рассматриваемую характеристику к безразмерным переменным

где безразмерная частота внешнего воздействия принята в виде $\tilde {\Omega } = \Omega \sqrt {{{T}_{e}}({{T}_{1}} + {{T}_{2}})} $.

На рис. 3 представлены графики уровня функции $\mathop {\max }\limits_\Omega {{A}_{{{{M}_{\psi }}}}}(\tilde {\Omega })$ от значений относительных постоянных времени при ${{k}_{r}} = - 1$. Видно, что в заданном диапазоне изменения относительных постоянных времени наибольшее значение АЧХ при ${{k}_{r}} = - 1$ не превышает 1.35. Условие (10) в этом случае выполняется, если отношение амплитуды переменной составляющей момента сил сопротивления к постоянной составляющей не превышает 74%. Если колебания в системе начинаются при ${{k}_{r}} = + 1$, то рассматриваемая АЧХ для значений относительной постоянной времени рабочей машины ${{\tau }_{2}}$, близких k – 1, может достигать очень больших значений. В этом случае, даже при незначительных колебаниях момента сил сопротивления, условие (10) не будет выполняться. Это приведет к изменению режима движения и возникновению дополнительных динамических нагрузок.

Исследование вынужденных колебаний в приводе с учетом упругости звеньев. Наибольшую податливость в приводе имеют участки валопровода между электродвигателем и входом червячного редуктора, а также выходом червячного редуктора и рабочей технологической машиной. Поэтому расчетную схему привода с учетом упругости звеньев представим в виде двухмассной системы (рис. 4). Жесткости соответствующих участков валов обозначим ${{c}_{1}}$, ${{c}_{2}}$.

Для составления математической модели системы разобьем ее на отдельные подсистемы (рис. 4), уравнения движения которых имеют вид

Деформации валов будут определяться зависимостями

Вводя относительные величины

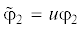приведем дифференциальные уравнения (11) к виду где – угловая координата ротора, приведенная к валу двигателя.

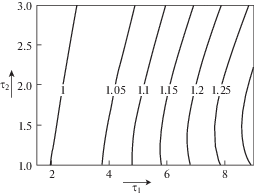
Решая систему уравнений (11), с учетом (1)–(3) относительно моментов на входе и выходе червячной передачи ${{M}_{\varphi }}$, ${{M}_{\psi }}$ и угловой координаты $\varphi $ и выполняя затем необходимые преобразования, придем к системе двух дифференциальных уравнений второго порядка, относительно угловых координат ротора электродвигателя и рабочей машины

где $\tilde {m} = {{J}_{2}}{\text{/}}({{J}_{1}}\operatorname{tg} \lambda {{u}^{2}})$; $\tilde {c} = {{c}_{2}}{\text{/}}{{c}_{1}} \cdot \operatorname{tg} \lambda {{u}^{2}}$, $\omega = \sqrt {{{c}_{2}}{\text{/}}{{J}_{2}}} $.

Для рассматриваемого класса машин значения относительных параметров $\tilde {m}$ и $\tilde {c}$находятся в пределах $4 \leqslant \tilde {m} \leqslant 16$, $0.02 \leqslant \tilde {c} \leqslant 0.1$.

Уравнение динамической характеристики электродвигателя (4) также приводим к относительным величинам

где $f_{0}^{{}} = M_{{10}}^{{}}{\text{/}}{{J}_{1}}$ – некоторая постоянная величина.

В силу соотношения (3) полученная математическая модель привода является кусочно-линейной. Однако, если предположить, что при установившемся движении привода коэффициент режима не меняется, то система (12) становится линейной и для ее исследования можно использовать обычные методы.

Характеристическое уравнение системы будет иметь вид

Нулевой корень этого уравнения соответствует установившемуся движению системы с постоянной скоростью, а остальные характеристические показатели определяются из решения соответствующего уравнения четвертой степени.

При исследовании вынужденных колебаний используем известный метод операторных передаточных функций. Относительную возмущающую силу ${{f}_{2}}$ представим в виде

где ${{f}_{{20}}}$ – постоянная составляющая силы; ${{f}_{{2a}}}$ – амплитуда переменной составляющей.

Переходя к операторной форме записи в дифференциальных уравнениях (12), (13), а затем к комплексному аргументу $p = i\Omega $ получим передаточные функции системы, определяющие ее реакцию на переменную составляющую возмущающей силы (14), и далее по аналогии с предыдущим, АЧХ для кинематических и силовых параметров. Окончательные выражения для АЧХ из-за их громоздкости здесь не приводятся. Анализ корней характеристического уравнения и АЧХ в общем виде невозможен, поэтому на основе полученных зависимостей был выполнен ряд расчетов, охватывающих всю область значений исходных параметров системы для рассматриваемого класса машин.

Анализ результатов расчета на основе модели с учетом упругости звеньев и сравнение их с результатами, полученными на основе модели с жесткими звеньями, позволил сделать следующие выводы: изменение параметра $\tilde {c}$ в принятом диапазоне практически не влияет на значения характеристических показателей, вид и численные значения АЧХ; изменение параметра $\tilde {m}$ в принятом диапазоне приводит к соизмеримому изменению как действительной, так и мнимой частей характеристических показателей и, не меняя принципиально вид зависимости амплитуды вынужденных колебаний от частоты возмущающей силы, приводит к значительному изменению амплитуды колебаний; для самотормозящейся и несамотормозящейся передач при движении в режиме ${{k}_{r}} = - 1$ вторая собственная частота, определяемая упругостью звеньев привода, примерно на порядок больше первой собственной частоты, определяемой динамическими свойствами приводного асинхронного электродвигателя. Первая собственная частота с достаточной точностью определяется на основании модели с жесткими звеньями. Вторая собственная частота значительно больше возможной частоты возмущающей силы для машин рассматриваемого класса, следовательно, в этом случае для исследования вынужденных колебаний в приводе можно использовать модель с жесткими звеньями; для самотормозящихся передач при движении в режиме ${{k}_{r}} = + 1$ вторая собственная частота уменьшается и становится соизмеримой с первой. Действительная часть характеристических показателей ${{\xi }_{{3,4}}}$ положительна, что указывает на неустойчивость движения в этом режиме. Амплитуда колебаний будет возрастать и в определенный момент времени произойдет переключение червячной передачи в другой режим ${{k}_{r}} = - 1$, соответствующий устойчивым колебаниям. Применение модели с жесткими звеньями в этом случае приводит не только к значительным количественным ошибкам, но и качественно неверному описанию динамических процессов, происходящих в системе.

Информация о финансовой поддержке. Результаты исследований опубликованы при финансовой поддержке ТулГУ в рамках научного проекта № 2017-37ПУБЛ.

Конфликт интересов: Авторы заявляют, что у них нет конфликта интересов.