Проблемы машиностроения и надежности машин, 2023, № 3, стр. 3-16

Для решения серьезных задач, стоящих перед отечественным машиностроением [1, 2] весьма важны механизмы параллельной структуры, отличающиеся высокими функциональными характеристиками [3, 4]. Данные механизмы явились темой исследований, представленных во многих работах, в частности, многочисленные публикации посвящены особым положениям этих устройств, в которых механизм либо теряет одну или несколько степеней свободы, либо теряет управляемость [5–7]. Следует отметить, что подобного рода механизмы можно получить объединением двух манипуляторов последовательной структуры, которые связаны через объект манипулирования, однако в данном случае каждая кинематическая пара снабжена приводом [8].

Многие публикации посвящены синтезу механизмов параллельной структуры, обладающих специфическими свойствами. Это необходимо для решения некоторых конкретных технических задач. В частности, речь идет о механизмах, обладающих свойством изоморфности, т.е. постоянством передаточных отношений между приводами и выходным звеном [9]. Также большое внимание было уделено механизмам с постоянной точкой ввода выходного звена в рабочую зону [10]. В ряде случае важным является обеспечение свойства динамической развязки [11].

В последнее время много внимания уделяется механизмам, выходное звено которых приводится в движение с помощью тросов [12], а также механизмам, входные звенья которых перемещаются по круговой направляющей [13, 14]. Неизменно актуальной является задача построения механизмов, обладающих повышенной точностью (повторяемостью). При этом применяются изгибные упругие кинематические пары [15].

Одним из наиболее известных используемых механизмов является механизм робота Delta [16–19]. В данном устройстве, обеспечивающем поступательные движения выходного звена, имеют место три кинематические цепи, в каждой из которых содержится привод и шарнирный параллелограмм.

В настоящей статье ставится задача определения плюккеровых координат силовых винтов, передаваемых на выходное звено механизма типа Delta. На этой основе можно найти взаимосвязь между повторяемостью позиционирования приводов и повторяемостью положений выходного звена. Поэтому требуется решить задачу о положениях и задачу о скоростях. При этом решение задачи о скоростях можно использовать для анализа точности (повторяемости). Важно уяснить, какова взаимосвязь между повторяемостью положений выходного звена и близостью к особым положениям.

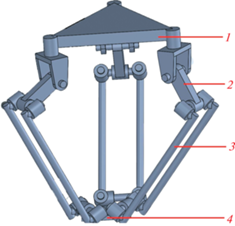
Рассматриваемый механизм (рис. 1) содержит основание 1, три кинематические цепи, в каждой из которых имеется входное звено 2, шарнирный параллелограмм 3, сопряженный с выходным звеном 4. Механизм имеет три степени свободы, обеспечивающие поступательные движения выходного звена.

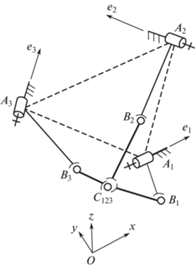
Для решения обратной задачи о положениях используем замещающую схему (рис. 2).

Эта схема получена путем “сдвигания” трех кинематических цепей к центру, так, чтобы оси вращательных пар, расположенных на выходном звене, пересеклись бы в одной точке. В данном случае точки А₁, А₂, А₃ – это центры, через которые проходят оси приводных вращательных пар, единичные векторы которых – е₁, е₂, е₃. Точки В₁, В₂, В₃ соответствуют серединам начальных звеньев шарнирных параллелограммов, точка С₁₂₃ соответствует совмещенным центрам конечных звеньев шарнирных параллелограммов. Все точки можно представить их координатами в системе Oxyz.

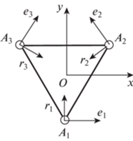
Если плоскость xOy проходит через точки А₁, А₂, А₃, то взаимное положение основания механизма и системы координат (рис. 3) определяет векторы r₁, r₂, r₃, перпендикулярные векторам е₁, е₂, е₃ и проходящие через точки А₁, А₂, А₃ (в дальнейшем для исключения сложных индексов номера элементов механизмов будем записывать в строчку).

Представим векторы, характеризующие положения осей кинематических пар и радиус-векторы точек, выражающих конфигурацию звеньев механизма. Единичные векторы осей входных кинематических пар и радиус-векторы центров этих пар

Кроме того, представим радиус-векторы центров входных кинематических пар и центр выходного звена, обозначив соответствующие точки

Найдем обобщенную координату θ₁ для первой кинематической цепи. Имеют место векторные и скалярные соотношения

где А1С – это вектор, проведенный из точки А1 в точку С; С1 – точка основания перпендикуляра, опущенного из точки С на плоскость, перпендикулярную вектору Е1 и проходящую через точку А1; ${{L}_{{{\mathbf{CC1}}}}}$ – расстояние между точками С и С1. Иначе соотношение можно переписать в виде

Вектор СС1 можно представить следующим образом:

где все элементы относятся к координатам соответствующих векторов.

Радиус-вектор точки С1 записывается следующим образом:

что можно представить в координатной форме в виде

Здесь все элементы соответствуют координатам упомянутых ранее векторов. В соответствии с изложенным вектор А1С1 будет иметь координаты

Расстояния между точками А1 и С1, В1 и С1 выражаются как

Исходя из теоремы косинусов, имеем

Кроме того, из геометрических соотношений имеем

Первая обобщенная координата имеет значение

Таким образом, обратная задача о положениях для первой кинематической цепи решена. Аналогичное решение имеем для второй и третьей кинематических цепей.

Переходим к численному примеру, в котором будет учтено то, что точки С1, С2, С3 будут разнесены в соответствии с конструкцией механизма. При исходном, “совмещенном”, положении кинематических цепей имели место соотношения

В случае, когда все точки расположения входных кинематических пар и точки центров шарниров, соединяющих кинематические цепи и выходное звено, “разнесены” на 0.1 м

где ${\mathbf{A1}}{\kern 1pt} '$, ${\mathbf{A2}}{\kern 1pt} '$, ${\mathbf{A3}}{\kern 1pt} '$ – это новые радиус-векторы точек крепления входных вращательных кинематических пар; С11, С22, С33 – новые радиус-векторы точек крепления выходных пар всех кинематических цепей.

Новые положения радиус-векторов точек крепления входных вращательных кинематических пар, м

Геометрические свойства остаются прежними

Приведем пример нахождения угла ${{{{\theta }}}_{1}}$ в первой кинематической цепи. Пусть центр выходного звена расположен на оси z на расстоянии 1.2 м от центра координат. В этом случае вектор, проведенный из точки $A1{\kern 1pt} '$ до точки С11 имеет координаты

Радиус-вектор точки С1, являющийся проекцией точки С11 на плоскость, проходящую через точку A1′ и перпендикулярную вектору е1, выражается следующим образом:

Вектор, соединяющий точки A1′ и С1, имеет координаты

Расстояние между точками A1′ и С1, а также точками B1′ и С1 равны

Исходя из теоремы косинусов, имеем

Кроме того, нужно учесть угол ${{{{\psi }}}_{1}}$ между вектором ${\mathbf{A1}}{\kern 1pt} '{\kern 1pt} {\mathbf{C1}}$ и радиус-вектором A1′

Находим обобщенные координаты

Для второй и третьей кинематических цепей порядок решения и результат аналогичен.

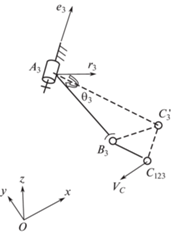
На основе решения задачи о положениях рассмотрим далее задачу о скоростях. Пусть для примера скорость точки С (рис. 4) имеет координаты, м/с

Приведем соотношения для третьей кинематической цепи. Вектор, соединяющий точки A3′ и B3′, выражается следующим образом:

Радиус-вектор точки B3′

Вектор, соединяющий точки B3′ и C33 (точка B3′ принадлежит входному звену и смещена относительно точки В3 на 1 м, точка С33 принадлежит выходному звену), выражается следующим образом:

Проекция скорости Vc на вектор B3C

Учтем, что точка B3′ вращается вокруг вектора е3

Проекция VB3 на вектор B3C при ${{{{\omega }}}_{3}} = 1$ рад/с

Реальная угловая скорость равна

Аналогичные результаты имеем для других кинематических цепей.

Далее рассмотрим плюккеровы координаты ортов осей кинематических пар, силовых винтов, передаваемых с кинематических цепей на выходное звено, а также кинематического винта выходного звена. Главные (векторные) части ортов осей входных кинематических пар были рассмотрены ранее. Моментные части этих ортов представим в виде

Следовательно, плюккеровы координаты единичных векторов осей входных кинематических пар будут иметь значения

Для определения плюккеровых координат силовых винтов, передаваемых на выходное звено со стороны кинематических цепей, будем иметь в виду единичный вектор (для первой кинематической цепи q1) и момент этого вектора (для первой кинематической цепи tc1) силового винта ЕС1, расположенного вдоль оси промежуточного звена шарнирного параллелограмма

Для остальных кинематических цепей выражения аналогичны.

Для каждой кинематической цепи имеет место силовой винт, препятствующий вращению выходного звена вокруг одной оси. Этот силовой винт ${\mathbf{EB1}}$ перпендикулярен плоскости соответствующего шарнирного параллелограмма. Для его определения используем соотношения

где ${\mathbf{B1}}{\kern 1pt} '{\kern 1pt} {\mathbf{C11}}$ – вектор, соединяющий центры промежуточной и конечной кинематических пар первой кинематической цепи; ${\mathbf{tb1}}$ – моментная часть рассматриваемого силового винта.

Итак, будем иметь матрицу плюккеровых координат силовых винтов

для конкретного положения определитель равен: $\left| {\mathbf{E}} \right| = - 0.051$.

Кинематический винт выходного звена обозначим как

Относительные моменты силовых винтов и кинематического винта выходного звена

Второе, четвертое и шестое уравнения включают в себя только угловые скорости, это относительные моменты с силовыми винтами, препятствующими вращению выходного звена.

Найдем относительные моменты силовых винтов и кинематических винтов во входных парах, будем иметь (в данном случае относительные моменты формально обозначаем как скалярные произведения)

Выпишем данные уравнения в матричной форме

Исходя из этого уравнения, угловые скорости должны равняться нулю, либо должен равняться нулю определитель матрицы коэффициентов.

Зададим скорости в приводах и определим скорость выходного звена, решив систему уравнений

Согласно рассматриваемому примеру

Решив данную систему уравнений, получим

решение получено в размерности линейной скорости, м/с.

Далее рассмотрим вопрос точности (повторяемости) данного механизма в зависимости от близости к особым положениям, в которых определитель матрицы плюккеровых координат силовых винтов равен нулю. В данном случае особые положения будут иметь место в том случае, когда все шарнирные параллелограммы расположатся в одной плоскости.

Чем ближе к особому положению, тем меньше должен быть по модулю определитель матрицы, составленный из плюккеровых координат силовых винтов и тем больше должно быть отклонение положения выходного звена при одинаковых ошибках в приводах.

Зададим погрешность в приводах, равной Δ₁ = Δ₂ = Δ₃ = Δ для конкретного положения выходного звена z = –l.2 м (в частности, пусть Δ = 0.00001 рад). Будем иметь соотношения

где Δ_x, Δ_y, Δ_z – ошибки положения выходного звена. Для конкретного случая получим

При проведении аналогичной операции для положения z = –1.1 м

То есть имеем соотношение полученных результатов

Это соотношение показывает, что при приближении к особому положению повторяемость ухудшается. Проверим это утверждение экспериментально. Для этого использовался серийный робот типа Delta и различное измерительное оборудование. Эксперимент предполагал подход к двум точкам, расположенным на разных расстояниях от особого положения. Было проведено два раза по сто испытаний, в простейшем случае использовался стрелочный индикатор, цена деления которого составляла 1 мк (рис. 5). Гистограммы (рис. 6), показывают, что в положении, более близком к особому (представлены косой штриховкой), повторяемость ухудшается.

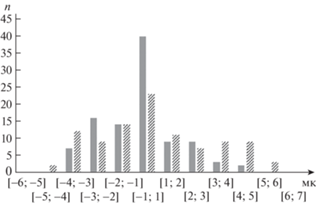
Заключение. Таким образом, в настоящей статье решена задача определения плюккеровых координат силовых винтов, передаваемых на выходное звено механизма типа Delta. Найдена взаимосвязь между повторяемостью позиционирования приводов и повторяемостью положений выходного звена указанного механизма. При этом приведено решение задачи о положениях и задачи о скоростях. Решение задачи о скоростях использовано для анализа повторяемости. Установлено, что при удалении от особых положений повторяемость улучшается.

Исследования проводились с использованием оборудования Центра коллективного пользования ИМАШ РАН – промышленного робота Fanuc M-1iA/0.5A, измерительной лазерной системы CHOTEST SJ6000, координатно-измерительной машины Hexagon Absolute Arm 8312, 6 осей.