Проблемы машиностроения и надежности машин, 2023, № 3, стр. 48-57

Двухслойная балка в условиях ползучести и роста поврежденности при трехточечном нагружении

К. А. Хвостунков^1, 2, *, К. А. Федотов^1, 2

¹ Московский государственный университет им. М.В. Ломоносова
Москва, Россия

² Институт структурной макрокинетики и проблем материаловедения РАН им. А.Г. Мержанова
Черноголовка, Московская область, Россия

^* E-mail: khvostunkov@gmail.com

Поступила в редакцию 25.10.2022
После доработки 09.02.2023
Принята к публикации 20.02.2023

EDN: PQIHHN
DOI: 10.31857/S0235711923030082

Полный текст (PDF)

Аннотация

Проблема замедленного разрушения и длительной прочности многослойных композитов представляет не только фундаментальный, но и прикладной интерес. Предложенное решение позволяет оценить влияние геометрии, структуры и соотношения свойств слоистого композита на его долговечность. Время до разрушения двухслойной металлической балки прямоугольного сечения определяется в зависимости от отношения толщин слоев и их модулей Юнга.

Ключевые слова: поврежденность двухслойной балки, время до разрушения двухслойной балки

На сегодняшний день в промышленности активно расширяется область применения многослойных композитов для решения конкретных технических задач. При их дизайне и проектировании учитываются как геометрические размеры, так и физико-механические свойства каждого слоя, что позволяет создать композиционный материал с заданными эксплуатационными характеристиками и дать качественный и количественные прогнозы по его работе в конкретных условиях. Особое внимание уделяется многослойным металлокерамическим композиционным материалам, свойства которых, зачастую, превосходят высоколегированные стали и твердые сплавы [1–5]. Однако существует сложность в дизайне таких материалов, так как керамика, имеет высокую хрупкость и различные коэффициенты термического расширения по сравнению с металлами.

Представляется интересным определить насколько сильно пропорции толщин слоев и их модули Юнга могут влиять на время до разрушения, коль скоро они влияют на напряженное состояние балки. Время до разрушения при постоянном нагружении определяется видом кинетического уравнения для меры поврежденности материала. Есть ряд классических решений задачи о времени до разрушения нагруженной балки из однородного материала. Характерным для всех этих решений является применение гипотезы плоских сечений. Обычно вид кинетического уравнения берется в форме, аналогичной закону установившейся ползучести Нортона. В решении Работнова–Милейко [6] продольные напряжения в поперечном сечении балки предполагаются постоянными по координате, ортогональной нейтральной оси, аналогично распределению в идеально пластическом шарнире. Вариант с линейным распределением продольных напряжений по упругому закону рассмотрен в работах Локощенко–Печениной–Шестерикова [7] и в работе Кулагина–Локощенко [7], где форма кинетического уравнения взята на основе дробно-линейного закона установившейся ползучести Шестерикова–Юмашевой.

Авторы настоящей статьи оценивают время до разрушения двухслойной балки при трехточечном изгибе в зависимости от параметра γ равного отношению модулей Юнга и параметра η, задающего отношение толщины слоя, противоположного стороне приложения нагрузки, ко всей толщине балки. Такое теоретическое решение варианта классической задачи механики поврежденности для кусочно-постоянных свойств материала балки является подготовительным этапом для планирования последующей серии экспериментов по прочности и долговечности слоистых композитов, получаемых методами самораспространяющегося высокотемпературного синтеза.

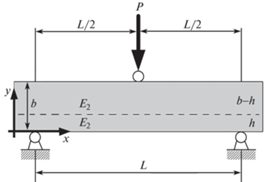
Постановка задачи. Рассмотрим двухслойную балку из упругих материалов. Направим ось x горизонтально вдоль оси балки, а y – ортогонально оси x, вверх по высоте. Ось z направлена ортогонально плоскости ху по ширине балки (рис. 1), L – расстояние между опорами при трехточечном нагружении, b – высота балки, a – ширина, $h$ – высота нижнего слоя, (b–h) – высота верхнего слоя.

Рис. 1.

Схема балки.

Отношения длины балки к ее высоте и ширине полагаются достаточно большими, чтобы можно было не учитывать влияние касательных напряжений.

К краю центрального сечения балки на внешней плоскости верхнего слоя приложена постоянная нагрузка P, равномерно распределенная по ширине балки.

Оба слоя балки находятся в условиях установившейся ползучести, описываемой уравнением Нортона, где ${{\zeta }_{i}}$ – константы сопротивления ползучести для i-го слоя

$\dot {\varepsilon } = {{\zeta }_{i}}{{\sigma }^{n}}\left( {x,y} \right),\quad {{\zeta }_{i}} = {{{{{{\varepsilon }_{{ni}}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{{ni}}}} {\left( {{{\sigma }_{{ni}}}} \right)}}} \right. \kern-0em} {\left( {{{\sigma }_{{ni}}}} \right)}}}^{n}}.$

Мера поврежденности вводится как параметр, характеризующий долю несплошности и характеризуемый самым простым вариантом кинетического уравнения Работнова–Качанова, где ${{B}_{i}}$ – константы кинетического уравнения для i-го слоя

$\dot {\omega }\left( {x,y,t} \right) = {{B}_{i}}{{\sigma }^{m}}\left( {x,y} \right).$

Скорость изменения кривизны нейтральной оси балки в центральном сечении предполагается величиной постоянной

$\dot {\kappa }\left( {\frac{L}{2},t} \right) = Q = \frac{2}{b}\zeta {{\left( {\frac{{\left( {2n + 1} \right)}}{{2n}}} \right)}^{n}}{{\left( {\frac{P}{{2{{E}_{2}}ab}}} \right)}^{n}}{{\left( {\frac{L}{b}} \right)}^{n}}{{\left( {2{{E}_{2}}} \right)}^{n}}.$

Требуется определить время до разрушения и исследовать его зависимость от отношения толщин слоев в балке и их модулей Юнга.

Критерием разрушения является условие достижения единицы в значении параметра поврежденности на нижнем крае балки.

Упругий случай. Рассмотрим упругий случай, соответствующий начальному моменту нагружения. Здесь мы найдем зависимость максимума растягивающего напряжения и взаимное расположение нейтральной оси и границы раздела слоев.

В соответствии с гипотезой плоских сечений в заданной системе координат имеем распределение упругих напряжений по сечению в виде

(1)

$\sigma \left( {x,y} \right) = \kappa (x)E\left( y \right)\left( {{{y}_{0}} - y} \right),\quad E\left( y \right) = \left\{ \begin{gathered} {{E}_{1}},\quad y \in [0,h], \hfill \\ {{E}_{2}},\quad y \in (h,b], \hfill \\ \end{gathered} \right.$

где ${{y}_{0}}$ – координата нейтральной оси; $\kappa (x)$ – ее кривизна; $E\left( y \right)$ – модуль Юнга материала. Изменением напряжений по координате z пренебрегаем.

Запишем уравнения равновесия в силах и моментах

$\left\{ \begin{gathered} \int\limits_0^b {\sigma \left( {x,y} \right)dy} = 0, \hfill \\ a\int\limits_0^b {\sigma \left( {x,y} \right)\left( {{{y}_{0}} - y} \right)dy} = M(x), \hfill \\ \end{gathered} \right.\quad M(x) = \left\{ \begin{gathered} \frac{P}{2}x,\quad x \in [0,{L \mathord{\left/ {\vphantom {L {2],}}} \right. \kern-0em} {2],}} \hfill \\ \frac{P}{2}\left( {L - x} \right),\quad x \in [{L \mathord{\left/ {\vphantom {L {2,L].}}} \right. \kern-0em} {2,L].}} \hfill \\ \end{gathered} \right.$

Введем безразмерные координаты и параметры

$\begin{gathered} \bar {x} = \frac{x}{L},\quad \bar {y} = \frac{y}{b},\quad {{{\bar {y}}}_{0}} = \frac{{{{y}_{0}}}}{b},\quad \eta = \frac{h}{b},\quad \gamma = \frac{{{{E}_{1}}}}{{{{E}_{2}}}}, \\ l = \frac{L}{b},\quad p = \frac{P}{{2{{E}_{2}}ab}},\quad \bar {\kappa }\left( {\bar {x}} \right) = b\kappa \left( x \right). \\ \end{gathered} $

Запишем систему уравнений равновесия продольных сил и моментов для $\bar {x} \in [0,\;1{\text{/}}2]$

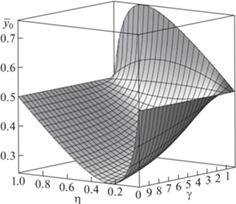
$\left\{ \begin{gathered} \int\limits_0^\eta {\gamma \left( {{{{\bar {y}}}_{0}} - \bar {y}} \right)d\bar {y}} + \int\limits_\eta ^1 {\left( {{{{\bar {y}}}_{0}} - \bar {y}} \right)d\bar {y}} = 0, \hfill \\ \int\limits_0^\eta {\gamma {{{\left( {{{{\bar {y}}}_{0}} - \bar {y}} \right)}}^{2}}d\bar {y}} + \int\limits_\eta ^1 {{{{\left( {{{{\bar {y}}}_{0}} - \bar {y}} \right)}}^{2}}d\bar {y}} = pl\bar {x}{{\left( {\bar {\kappa }\left( {\bar {x}} \right)} \right)}^{{ - 1}}}. \hfill \\ \end{gathered} \right.$

Из уравнения равновесия сил получаем координату нейтральной оси ${{\bar {y}}_{0}}\left( {\gamma ,\eta } \right)$ (рис. 2)

(2)

${{\bar {y}}_{0}}\left( {\gamma ,\eta } \right) = \frac{1}{2}\left( {1 + {{\eta }^{2}}\left( {\gamma - 1} \right)} \right){{\left( {1 + \eta \left( {\gamma - 1} \right)} \right)}^{{ - 1}}}.$

Рис. 2.

Зависимость положения нейтральной оси от толщины нижнего слоя $\eta = h{\text{/}}b$ и от отношения модулей Юнга слоев $\gamma = {{{{E}_{1}}} \mathord{\left/ {\vphantom {{{{E}_{1}}} {{{E}_{2}}}}} \right. \kern-0em} {{{E}_{2}}}}.$

Из уравнения равновесия моментов выражаем кривизну ${{\bar {\kappa }}_{0}}\left( {\bar {x}} \right)$

${{\bar {\kappa }}_{0}}\left( {\bar {x}} \right) = 12pl\left( {1 + \eta \left( {\gamma - 1} \right)} \right){{\left( {\left( {\gamma - 1} \right)\left( {\gamma {{\eta }^{4}} - {{{\left( {\eta - 1} \right)}}^{4}}} \right) + \gamma } \right)}^{{ - 1}}}\bar {x},\quad \bar {x} \in [0,\;1{\text{/}}2].$

Подставляя (2) в (1), получаем для $\bar {x} \in [0,\;1{\text{/}}2]$

$\sigma \left( {\bar {x},\bar {y}} \right) = \left\{ \begin{gathered} 12pl\left( {1 + \eta \left( {\gamma - 1} \right)} \right){{\left( {\left( {\gamma - 1} \right)\left( {\gamma {{\eta }^{4}} - {{{\left( {\eta - 1} \right)}}^{4}}} \right) + \gamma } \right)}^{{ - 1}}}\gamma \left( {{{{\bar {y}}}_{0}} - \bar {y}} \right)\bar {x},\quad \bar {y} \in [0,\eta ], \hfill \\ 12pl\left( {1 + \eta \left( {\gamma - 1} \right)} \right){{\left( {\left( {\gamma - 1} \right)\left( {\gamma {{\eta }^{4}} - {{{\left( {\eta - 1} \right)}}^{4}}} \right) + \gamma } \right)}^{{ - 1}}}\left( {{{{\bar {y}}}_{0}} - \bar {y}} \right)\bar {x},\quad \bar {y} \in (\eta ,1]. \hfill \\ \end{gathered} \right.$

В силу линейного распределения, максимум растягивающих напряжений будет достигнут на нижнем крае поперечного сечения при $\bar {y} = 0$, $\bar {x} = 1{\text{/}}2$

$\sigma \left( {\gamma ,\eta } \right) = 3pl\left( {1 + {{\eta }^{2}}\left( {\gamma - 1} \right)} \right){{\left( {1 + \frac{{\left( {\gamma - 1} \right)}}{\gamma }\left( {\gamma {{\eta }^{4}} - {{{\left( {\eta - 1} \right)}}^{4}}} \right)} \right)}^{{ - 1}}}.$

Рассмотрим производную напряжения на краю по $\eta $ при постоянной γ

$\frac{{\partial \sigma \left( {\gamma ,\eta } \right)}}{{\partial \eta }} = - lp\frac{{6\left( {\gamma - 1} \right)\left( {\left( {\gamma - 1} \right){{\eta }^{3}} + 3\eta - 2} \right)\gamma \left( {\left( {\gamma - 1} \right){{\eta }^{2}} + 2\eta - 1} \right)}}{{{{{\left( {{{{\left( {\gamma - 1} \right)}}^{2}}{{\eta }^{4}} + 4\left( {\gamma - 1} \right){{\eta }^{3}} - 6\left( {\gamma - 1} \right){{\eta }^{2}} + 4\left( {\gamma - 1} \right)\eta + 1} \right)}}^{2}}}}.$

Из условия стационарности получаем условия экстремума по η и с учетом ограничения $\eta \in [0,\;1]$ получаем координаты локальных экстремумов (рис. 3).

Рис. 3.

Графики зависимости напряжений на нижнем крае центрального сечения балки от отношения толщин слоев при различных отношениях модулей Юнга γ.

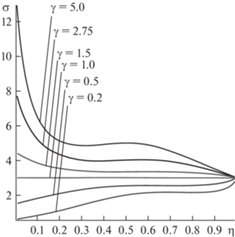
Для $0 < \gamma < 1$: локальный максимум ${{\eta }_{1}} = {{\left( {1 + \sqrt \gamma } \right)}^{{ - 1}}}$, локальный минимум

${{\eta }_{2}} = \left[ {\sqrt 3 \cos \left( {\frac{1}{3}\arctan \left( {\frac{{\sqrt \gamma }}{{\sqrt {1 - \gamma } }}} \right) + \frac{\pi }{6}} \right) - \sin \left( {\frac{1}{3}\arctan \left( {\frac{{\sqrt \gamma }}{{\sqrt {1 - \gamma } }}} \right) + \frac{\pi }{6}} \right)} \right]{{\left( {1 - \gamma } \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$

Для $\gamma > 1$: локальный минимум ${{\eta }_{1}} = 1 + \sqrt \gamma $, локальный максимум

${{\eta }_{3}} = {{\left( {1 + \sqrt {{\gamma \mathord{\left/ {\vphantom {\gamma {\left( {\gamma - 1} \right)}}} \right. \kern-0em} {\left( {\gamma - 1} \right)}}} } \right)}^{{\frac{1}{3}}}}{{\left( {\gamma - 1} \right)}^{{ - \frac{1}{3}}}} - {{\left( {1 + \sqrt {{\gamma \mathord{\left/ {\vphantom {\gamma {\left( {\gamma - 1} \right)}}} \right. \kern-0em} {\left( {\gamma - 1} \right)}}} } \right)}^{{ - \frac{1}{3}}}}{{\left( {\gamma - 1} \right)}^{{ - \frac{2}{3}}}}.$

В случае равенства упругих свойств обоих слоев $\gamma = 1$ мы получаем расположение нейтральной оси посередине сечения и классическую зависимость кривизны от жесткости балки и изгибающего момента

${{\bar {y}}_{0}} = \frac{1}{2},\quad {{\bar {\kappa }}_{0}} = 6\frac{{pl}}{{Eb}} = 3\frac{{PL}}{{a{{b}^{3}}E}} = \frac{M}{{EJ}},\quad M = \frac{{PL}}{4},\quad J = \frac{1}{{12}}a{{b}^{3}}.$

Учет поврежденности. Рассмотрим скалярную меру поврежденности [1] как отношение разрушенной площади ${{S}_{d}}$ поперечного сечения некоего эталонного стержня ко всей начальной площади $S$: $\omega = {{{{S}_{d}}} \mathord{\left/ {\vphantom {{{{S}_{d}}} S}} \right. \kern-0em} S}$. Видимая связь приложенной силы и исходного поперечного сечения в виде выводимой на графике зависимости напряжения от деформации будет описываться модулем Юнга, учитывающим внутреннюю поврежденность $\sigma $ = ${F \mathord{\left/ {\vphantom {F S}} \right. \kern-0em} S}$ = $E\left( \omega \right)\varepsilon $. На самом деле реальные напряжения ${{\sigma }_{{{\text{real}}}}}$ в неразрушенных областях сечения будут связаны с деформациями на основании исходного модуля Юнга Е: ${{\sigma }_{{{\text{real}}}}}$ = ${F \mathord{\left/ {\vphantom {F {\left( {S - {{S}_{d}}} \right)}}} \right. \kern-0em} {\left( {S - {{S}_{d}}} \right)}}$ = $E\varepsilon $. Откуда, согласно принципу эквивалентности деформаций, приравнивая их, получаем $E\left( \omega \right)$ = $E{{\left( {S - {{S}_{d}}} \right)} \mathord{\left/ {\vphantom {{\left( {S - {{S}_{d}}} \right)} S}} \right. \kern-0em} S}$ = $E\left( {1 - \omega } \right)$.

Переходя к нашей балке, считаем, что в зоне положительных компонент тензора напряжений происходит повреждение материала, и мы вводим меньший, чем исходный модуль Юнга $E\left( \omega \right)$, снижающий его суммарную силу сопротивления изгибу и приводящий к смещению нейтральной оси в координату ${{y}_{0}}\left( {x,t} \right)$. В итоге в растягиваемой зоне напряжение в точке будет задаваться уменьшенным значением

$\sigma \left( {x,y,t} \right) = E\left( {1 - \omega \left( {x,y,t} \right)} \right)\kappa \left( {x,t} \right)\left( {{{y}_{0}}\left( {x,t} \right) - y} \right),$

где зависимость переменного параметра поврежденности от времени определяется кинетическим уравнением вида

$\dot {\omega }\left( {x,y,t} \right) = {{A}_{i}}{{\dot {\kappa }}^{{{{\lambda }_{i}}}}}\left( {x,t} \right){{\left( {{{y}_{0}}\left( {x,t} \right) - y} \right)}^{{{{\lambda }_{i}}}}},\quad {{A}_{i}} = {{B}_{i}}\zeta _{i}^{{ - {{\lambda }_{i}}}},\quad {{\lambda }_{i}} = {{{{m}_{i}}} \mathord{\left/ {\vphantom {{{{m}_{i}}} {{{n}_{i}}}}} \right. \kern-0em} {{{n}_{i}}}}.$

Уравнения равновесия продольных сил и моментов для произвольного поперечного сечения двуслойной балки, скомпоновав слагаемые с поврежденностью отдельно, перейдя снова к безразмерным координатам, запишем в виде

$\left\{ \begin{gathered} \int\limits_0^1 {E\left( {\bar {y}} \right)\left( {{{{\bar {y}}}_{0}}\left( {\bar {x},t} \right) - \bar {y}} \right)d\bar {y}} = \int\limits_0^{{{{\bar {y}}}_{0}}} {E\left( {\bar {y}} \right)\left( {{{{\bar {y}}}_{0}}\left( {\bar {x},t} \right) - \bar {y}} \right)\omega \left( {\bar {x},\bar {y},t} \right)d\bar {y},} \hfill \\ {\kern 1pt} \int\limits_0^1 {E\left( {\bar {y}} \right){{{\left( {{{{\bar {y}}}_{0}}\left( {\bar {x},t} \right) - \bar {y}} \right)}}^{2}}d\bar {y}} = \int\limits_0^{{{{\bar {y}}}_{0}}} {E\left( {\bar {y}} \right){{{\left( {{{{\bar {y}}}_{0}}\left( {\bar {x},t} \right) - \bar {y}} \right)}}^{2}}\omega \left( {\bar {x},\bar {y},t} \right)d\bar {y}} + {{{{E}_{2}}pl\bar {x}} \mathord{\left/ {\vphantom {{{{E}_{2}}pl\bar {x}} {\bar {\kappa }\left( {\bar {x},t} \right).}}} \right. \kern-0em} {\bar {\kappa }\left( {\bar {x},t} \right).}} \hfill \\ \end{gathered} \right.$

Положим далее для простоты ${{\lambda }_{i}} = 1$, $i = 1,\;2$ и проинтегрируем кинетическое уравнение для поврежденности по времени

$\omega \left( {\bar {x},\bar {y},t} \right) = A\left( {\bar {y}} \right)Q\left( {\varphi \left( {\bar {x},t} \right) - \bar {y}t} \right),\quad \varphi = \int\limits_0^t {{{{\bar {y}}}_{0}}(\bar {x},t)dt} .$

В критический момент времени ${{t}_{*}}$

$\begin{gathered} \omega \left( {\bar {x},\bar {y},{{t}_{*}}} \right) = A\left( {\bar {y}} \right)Q\left( {\varphi \left( {1{\text{/}}2,{{t}_{*}}} \right) - \bar {y}{{t}_{*}}} \right), \\ \omega \left( {\bar {x} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},\bar {y} = 0,{{t}_{*}}} \right) = {{A}_{1}}Q\left( {\varphi \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},{{t}_{*}}} \right)} \right) = 1 \Rightarrow \left( {\varphi \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},{{t}_{*}}} \right)} \right) = {{\left( {{{A}_{1}}Q} \right)}^{{ - 1}}}, \\ \Rightarrow \quad \omega \left( {\bar {x},\bar {y},{{t}_{*}}} \right) = {{A\left( {\bar {y}} \right)} \mathord{\left/ {\vphantom {{A\left( {\bar {y}} \right)} {{{A}_{1}}}}} \right. \kern-0em} {{{A}_{1}}}} - QA\left( {\bar {y}} \right)\bar {y}{{t}_{*}}. \\ \end{gathered} $

Тогда система уравнений равновесия в середине стержня примет вид

(3)

$\left\{ \begin{gathered} \int\limits_0^1 {E\left( {\bar {y}} \right)\left( {\bar {y}_{0}^{*} - \bar {y}} \right)d\psi } = \int\limits_0^{\bar {y}_{0}^{*}} {E\left( {\bar {y}} \right)\left( {\bar {y}_{0}^{*} - \bar {y}} \right)\left( {\frac{{A\left( {\bar {y}} \right)}}{{{{A}_{1}}}} - QA\left( {\bar {y}} \right)\bar {y}{{t}_{*}}} \right)d\bar {y},} \hfill \\ \int\limits_0^1 {E\left( {\bar {y}} \right){{{\left( {\bar {y}_{0}^{*} - \bar {y}} \right)}}^{2}}d\psi } = \int\limits_0^{\bar {y}_{0}^{*}} {E\left( {\bar {y}} \right){{{\left( {\bar {y}_{0}^{*} - \bar {y}} \right)}}^{2}}\left( {\frac{{A\left( {\bar {y}} \right)}}{{{{A}_{1}}}} - QA\left( {\bar {y}} \right)\bar {y}{{t}_{*}}} \right)d\bar {y}} + \frac{{{{E}_{2}}pl\bar {x}}}{{\bar {\kappa }\left( {\bar {x},t} \right)}}. \hfill \\ \end{gathered} \right.$

В случае двуслойной балки, зависимость модуля Юнга и коэффициента кинетического уравнения от координаты поперечного сечения

$\begin{gathered} E\left( {\bar {y}} \right) = {{E}_{1}},\quad \bar {y} \in [0,\eta ],\quad E\left( {\bar {y}} \right) = {{E}_{2}},\quad \bar {y} \in \left( {\eta ,1} \right], \\ A\left( {\bar {y}} \right) = {{A}_{1}},\quad \bar {y} \in [0,\eta ],\quad A\left( {\bar {y}} \right) = {{A}_{2}},\quad \bar {y} \in \left( {\eta ,1} \right]. \\ \end{gathered} $

Для простоты далее мы положим ${{A}_{1}} = {{A}_{2}} = A = B{{\zeta }^{{ - 1}}}$. Тогда в безразмерных координатах $\dot {\bar {\kappa }}$ = $2{{\left( {1 + 1{\text{/}}\left( {2n} \right)} \right)}^{n}}\zeta {{\left( {2{{E}_{2}}pl} \right)}^{n}}$ = Q, и мы получаем приведенное время

$\tau = AQt = 2{{\left( {1 + 1{\text{/}}\left( {2n} \right)} \right)}^{n}}B{{\left( {2{{E}_{2}}pl} \right)}^{n}}t = 2{{\left( {1 + 1{\text{/}}\left( {2n} \right)} \right)}^{n}}B\sigma _{0}^{n}t,\quad {{\sigma }_{0}} = 2{{E}_{2}}pl.$

Расположение нейтральной оси. Рассмотрим, как расположена нейтральная ось относительно границы слоев. Это повлияет на вид уравнений равновесия.

Случай, когда нейтральная ось совпадает в начальный момент времени с границей, разделяющей слои $\eta \in [0,\;1]$, ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{{\eta }^{2}}\left( {\gamma - 1} \right){{\left( {1 + \eta \left( {\gamma - 1} \right)} \right)}^{{ - 1}}}$ = η.

Мы получили условие на толщину слоев относительно модулей упругости, когда нейтральная ось находится на границе их раздела $\eta = {{\left( {1 + \sqrt \gamma } \right)}^{{ - 1}}}$.

Случай А. Нейтральная ось в момент разрушения находится в верхнем слое $\bar {y}_{0}^{*} > \eta $.

В этом случае ненулевая поврежденность заполняет весь нижний слой и частично верхний. Тогда, проинтегрировав по $\bar {y}$ (3), получаем уравнение на зависимость координаты нейтральной оси и выражение для времени через нее.

В критический момент $\bar {x} = 1{\text{/}}2$, $t = {{t}_{*}}$, ${{\bar {y}}_{0}} = \bar {y}_{0}^{*}$. Далее звездочку не пишем.

При оценке значения Apl уравнения равновесия преобразуются в замкнутую систему относительно координаты нейтральной оси в момент разрушения ${{\bar {y}}_{0}}$ и временем до разрушения $t$

(4)

$\left\{ \begin{gathered} \frac{{{{{\left( {{{{\bar {y}}}_{0}} - 1} \right)}}^{2}}}}{{\left( {\bar {y}_{0}^{3} + \left( {\gamma - 1} \right){{\eta }^{2}}\left( {3{{{\bar {y}}}_{0}} - 2\eta } \right)} \right)}} + \frac{{2Apl\left( {1 + \eta \left( {\gamma - 1} \right)} \right)}}{{\left( {\gamma + \left( {\gamma - 1} \right)\left( {\gamma {{\eta }^{4}} - {{{\left( {\eta - 1} \right)}}^{4}}} \right)} \right)}} + \hfill \\ + \;\frac{{2Apl}}{{{{{\left( {{{{\bar {y}}}_{0}} - 1} \right)}}^{2}}}}\frac{{\left( {\bar {y}_{0}^{3} + \left( {\gamma - 1} \right){{\eta }^{2}}\left( {3{{{\bar {y}}}_{0}} - 2\eta } \right)} \right)}}{{\left( {\bar {y}_{0}^{3}\left( {{{{\bar {y}}}_{0}} - 4} \right) - \left( {\gamma - 1} \right){{\eta }^{2}}\left( {9{{\eta }^{2}} - 16\eta \left( {{{{\bar {y}}}_{0}} + \frac{1}{2}} \right) + 6{{{\bar {y}}}_{0}}\left( {{{{\bar {y}}}_{0}} + 2} \right)} \right)} \right)}} = 0, \hfill \\ AQt = 2B{{\left( {1 + 1{\text{/}}\left( {2n} \right)} \right)}^{n}}{{\left( {2{{E}_{2}}pl} \right)}^{n}}t = 3{{\left( {{{{\bar {y}}}_{0}} - 1} \right)}^{2}}{{\left( {\bar {y}_{0}^{3} + \left( {\gamma - 1} \right){{\eta }^{2}}\left( {3{{{\bar {y}}}_{0}} - 2\eta } \right)} \right)}^{{ - 1}}}. \hfill \\ \end{gathered} \right.$

Случай В. Нейтральная ось в момент разрушения находится в нижнем слое $\bar {y}_{0}^{*} < \eta $.

Проинтегрируем также по $\bar {y}$ систему (3) и получим систему для определения времени разрушения в случае B в серединном сечении ($\bar {x} = 1{\text{/}}2$), учитывая, что в этот момент $AQ\varphi = 1$

(5)

$\left\{ \begin{gathered} \frac{{\left( {\gamma - 1} \right){{{\left( {{{{\bar {y}}}_{0}} - \eta } \right)}}^{2}} + {{{\left( {{{{\bar {y}}}_{0}} - 1} \right)}}^{2}}}}{{\gamma \bar {y}_{0}^{3}}} + 2Apl\frac{{\left( {1 + \eta \left( {\gamma - 1} \right)} \right)}}{{\left( {\gamma - 1} \right)\left( {\gamma {{\eta }^{4}} - {{{\left( {\eta - 1} \right)}}^{4}}} \right) + \gamma }} - \hfill \\ - \;2Apl\frac{1}{{\left( {\gamma - 1} \right){{{\left( {{{{\bar {y}}}_{0}} - \eta } \right)}}^{2}}\left( {4\eta - {{{\bar {y}}}_{0}}} \right) + {{{\left( {{{{\bar {y}}}_{0}} - 1} \right)}}^{2}}\left( {4 - {{{\bar {y}}}_{0}}} \right)}} = 0, \hfill \\ AQt = \frac{{3\left( {\gamma - 1} \right){{{\left( {{{{\bar {y}}}_{0}} - \eta } \right)}}^{2}} + 3{{{\left( {{{{\bar {y}}}_{0}} - 1} \right)}}^{2}}}}{{\gamma \bar {y}_{0}^{3}}}. \hfill \\ \end{gathered} \right.$

Рассмотрим предельный случай, при каких $\eta $ и $\gamma $ в момент равенства единице параметра поврежденности на внешнем крае серединного сечения координата нейтральной оси достигает границы раздела слоев ${{\bar {y}}_{0}} = {{\eta }_{*}}$, $\omega \left( {\bar {x} = 1{\text{/}}2,\;\bar {y} = 0,\;{{t}_{0}}} \right)$ = $AQ{{\varphi }_{0}}$ = 1, ${{\varphi }_{0}}$ = $\int_0^{{{t}_{0}}} {{{{\bar {y}}}_{0}}\left( {1{\text{/}}2,t} \right)dt} $

$\left\{ \begin{gathered} \hfill \\ 2Apl\eta _{*}^{7}{{\gamma }^{3}} - \eta _{*}^{4}\left( {1 - {{\eta }_{*}}} \right)\left[ {{{{\left( {1 - {{\eta }_{*}}} \right)}}^{3}}\left( {4 - {{\eta }_{*}}} \right) - 2Apl\left( {3\eta _{*}^{2} - 7{{\eta }_{*}} + 8} \right)} \right]{{\gamma }^{2}} - \hfill \\ - \;{{\eta }_{*}}{{\left( {1 - {{\eta }_{*}}} \right)}^{3}}\left[ {2{{{\left( {1 - {{\eta }_{*}}} \right)}}^{2}}\left( {4 - {{\eta }_{*}}} \right)\left( {\eta _{*}^{2} - {{\eta }_{*}} + 2} \right) - 2Apl\eta _{*}^{2}\left( {5 - 2{{\eta }_{*}}} \right)} \right]\gamma - \hfill \\ - \;\left( {4 - {{\eta }_{*}}} \right){{\left( {1 - {{\eta }_{*}}} \right)}^{8}} = 0,\quad AQ{{t}_{0}} = \frac{{3{{{\left( {1 - {{\eta }_{*}}} \right)}}^{2}}}}{{\gamma \eta _{*}^{3}}}. \hfill \\ \end{gathered} \right.$

При заданных параметрах $\gamma $ и $Apl$ из второго уравнения получаем ${{\eta }_{*}}$ (рис. 4).

Рис. 4.

Границы областей расположения нейтральной оси в момент разрушения при Apl = $2.8 \times {{10}^{{ - 4}}}$.

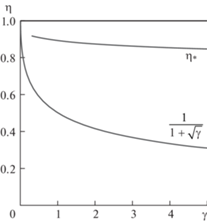
Для $0 \leqslant \eta < {{\left( {1 + \sqrt \gamma } \right)}^{{ - 1}}}$ в начальный момент времени нейтральная ось уже находится в верхнем слое и к моменту разрушения она лишь выше поднимается к верхней границе балки.

Для ${{\left( {1 + \sqrt \gamma } \right)}^{{ - 1}}} < \eta < {{\eta }_{*}}$ в начальный момент времени нейтральная ось находится в нижнем слое, но к моменту разрушения она уже располагается в верхнем слое.

Для ${{\eta }_{*}} < \eta < 1$ в начальный момент времени нейтральная ось находится в нижнем слое и к моменту времени разрушения не успевает достичь границы раздела слоев.

Время до разрушения. При значениях параметров (табл. 1), получаем зависимость начального положения нейтральной оси ${{\bar {y}}_{0}} = {{\bar {y}}_{0}}\left( {\eta ,\gamma } \right)$ и по формулам (4) и (5) вычисляем время до разрушения для $0 < \eta < 1$.

Таблица 1.

Используемые коэффициенты

Описание	Обозначение	Значение
Безразмерная нагрузка	$p = \frac{P}{{2ab{{E}_{2}}}}$	$p = \frac{{5.3 \times {{{10}}^{3}}}}{{2 \times 5 \times {{{10}}^{{ - 3}}} \times 3.8 \times {{{10}}^{{ - 3}}} \times 2 \times {{{10}}^{{11}}}}} = 7 \times {{10}^{{ - 4}}}$
Безразмерная длина	$l = \frac{L}{b}$	$l = \frac{L}{b} = \frac{{38 \times {{{10}}^{{ - 3}}}}}{{3.8 \times {{{10}}^{{ - 3}}}}} = 10$
Отношение коэффициентов сопротивления поврежден- ности и ползучести	$A = \frac{B}{\zeta }$	$A = \frac{B}{\zeta } = 0.04$
Сочетание реологических, геометрических и силовых параметров системы	Apl	$2.8 \times {{10}^{{ - 4}}}$

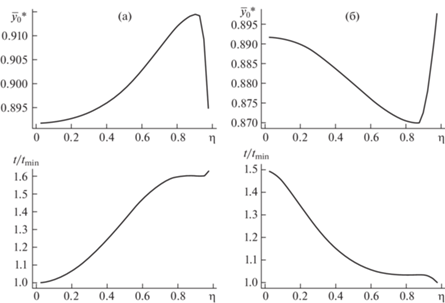
Для примера на рис. 5 приведены графики зависимости положения нейтральной оси в момент разрушения и соответствующего времени до разрушения при значениях пропорции модулей Юнга слоев $\gamma = {{{{E}_{1}}} \mathord{\left/ {\vphantom {{{{E}_{1}}} {{{E}_{2}}}}} \right. \kern-0em} {{{E}_{2}}}}$.

Рис. 5.

Положение нейтральной оси в момент разрушения и соответствующее время при ${{\lambda }_{i}} = 1$ для отношений модулей Юнга слоев: (а) – $\gamma = 0.36$; (б) – $\gamma = 2.25$.

В случае одинаковых слоев, при $\gamma = 1$ обе системы (4) и (5), с учетом замены $2Apl$ = $B{{\sigma }_{0}}{{\left( {\zeta E} \right)}^{{ - 1}}}$, $AQt$ = $2{{\left( {1 + 1{\text{/}}\left( {2n} \right)} \right)}^{n}}B{{\sigma }_{0}}^{n}t$ сводятся к системе

$\left\{ \begin{gathered} \frac{{{{{\left( {{{{\bar {y}}}_{0}} - 1} \right)}}^{2}}}}{{\bar {y}_{0}^{3}}} = \frac{B}{\zeta }\frac{{{{\sigma }_{0}}}}{E}\left( {\frac{1}{{\left( {4 - {{{\bar {y}}}_{0}}} \right){{{\left( {{{{\bar {y}}}_{0}} - 1} \right)}}^{2}}}} - 1} \right), \hfill \\ B\sigma _{0}^{n}t = 3{{\left[ {2{{{\left( {1 + 1{\text{/}}\left( {2n} \right)} \right)}}^{n}}} \right]}^{{ - 1}}}\frac{{{{{\left( {{{{\bar {y}}}_{0}} - 1} \right)}}^{2}}}}{{\bar {y}_{0}^{3}}}, \hfill \\ t = \frac{1}{{\zeta \sigma _{0}^{{n - 1}}E}}\left( {\frac{1}{{\left( {4 - {{{\bar {y}}}_{0}}} \right){{{\left( {{{{\bar {y}}}_{0}} - 1} \right)}}^{2}}}} - 1} \right). \hfill \\ \end{gathered} \right.$

Первое уравнение – это пересечение двух гипербол с переменным коэффициентом. Из второго уравнения итоговой системы мы получаем зависимость константы кинетического уравнения от времени до разрушения и положения нейтральной оси в этот момент

$B = 3\frac{{{{{\left( {{{{\bar {y}}}_{0}} - 1} \right)}}^{2}}}}{{\bar {y}_{0}^{3}}}{{\left( {2{{{\left( {2 + 1{\text{/}}n} \right)}}^{n}}{{p}^{n}}{{l}^{n}}{{E}^{n}}t} \right)}^{{ - 1}}}.$

Выводы. В результате анализа полученных данных, мы можем сказать, что время до разрушения существенно зависит от отношения толщин слоев балки и различие времен до разрушения может составлять более 50%. Такой результат может являться дополнительным условием выбора пропорций толщин слоев и соотношения их модулей при проектировании новых двуслойных материалов, получаемых на основе самораспространяющегося высокотемпературного синтеза.

Полученные зависимости максимального растягивающего напряжения от пропорций упругих свойств и толщин слоев будут использованы в анализе данных по хрупкому разрушению эталонных образцов разрабатываемого материала на основе керамических (TiB₂) и интерметаллидных (TiAl₃) слоев.

Список литературы

Bazhin P.M., Konstantinov A.S., Chizhikov A.P., Pazniak A.I., Kostitsyna E.V., Prokopets A.D., Stolin A.M. Laminated cermet composite materials: The main production methods, structural features and properties (review) // Ceramics Int. 2021. V. 47. Iss. 2. P. 1513.
Bazhina A., Konstantinov A., Chizhikov A., Bazhin P., Stolin A., Avdeeva V. Structure and mechanical characteristics of a layered composite material based on TiB/TiAl/Ti // Ceramics Int. 2022. V. 48. Iss. 10. P. 14295.
Prokopets A.D., Bazhin P.M., Konstantinov A.S., Chizhikov A.P., Antipov M.S., Avdeeva V.V. Structural features of layered composite material TiB2/TiAl/Ti6Al4V obtained by unrestricted SHS-compression // Materials Letters. 2021. 130165.
Прокопец А.Д., Константинов А.С., Чижиков А.П., Бажин П.М., Столин А.М. Закономерности формирования структуры градиентных композиционных материалов на основе МАХ-фазы Ti3AlC2 на титане // Неорганические материалы. 2020. Т. 56. № 10. С. 1145.
Бажин П.М., Столин А.М., Константинов А.С., Чижиков А.П., Прокопец А.Д., Алымов М.И. Особенности строения слоистых композиционных материалов на основе боридов титана, полученных методом свободного СВС-сжатия // Доклады академии наук. 2019. Т. 488. № 3. С. 263.
Работнов Ю.Н., Милейко С.Т. Кратковременная ползучесть. М.: Наука, 1970. 224 с.
Локощенко А.М., Печенина Н.Е., Шестериков С.А. Долговечность цилиндрического бруса при чистом изгибе // Известия высших учебных заведений. Машиностроение. 1988. № 9. С. 9.
Kulagin D., Lokoshchenko A. Analysis of the influence of aggressive environment on creep and creep rupture of rod under pure bending // Archive of Applied Mechanics. 2005. V. 74 (8). P. 518.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал