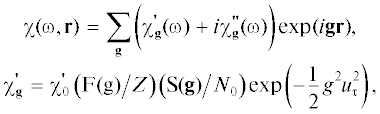Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2023, № 5, стр. 73-79
Влияние многократного рассеяния на спектрально-угловую плотность дифрагированного переходного излучения
С. В. Блажевич a, А. С. Горлов b, А. В. Носков a, b, *, А. Э. Федосеев a
a Белгородский государственный национальный исследовательский университет
308015 Белгород, Россия
b Белгородский государственный технологический университет им. В.Г. Шухова
308012 Белгород, Россия
* E-mail: noskovbupk@mail.ru
Поступила в редакцию 10.07.2022
После доработки 14.10.2022
Принята к публикации 14.10.2022
- EDN: ALIMQZ
- DOI: 10.31857/S1028096023050035
Аннотация
В работе исследуется дифрагированное переходное излучение релятивистского электрона пересекающего монокристаллическую пластинку в геометрии рассеяния Брэгга. Получены выражения, описывающие спектрально-угловую плотность дифрагированного переходного излучения с учетом и без учета многократного рассеяния релятивистского электрона в монокристаллической пластинке. Показано влияние многократного рассеяния на спектр дифрагированного переходного излучения релятивистского электрона.
1. ВВЕДЕНИЕ
При пересечении заряженной частицей границы раздела двух сред возникает переходное излучение (ПИ) [1, 2]. Влияние многократного рассеяния заряженной частицы атомами среды на спектрально-угловую плотность ПИ в аморфной среде обсуждалось в работах [3–5]. В работах [3, 4] влияние многократного рассеяния, соответственно, на спектр и угловую плотность ПИ рассматривалось на качественном уровне, а в работе [5] – с использованием строгого кинетического подхода к усреднению спектрально-угловой плотности ПИ по всем возможным траекториям движения электрона в веществе.
Переходное излучение, возникающие на передней границе монокристаллической мишени, дифрагирует на системе параллельных атомных плоскостей кристалла, образуя в направлении близком к направлению рассеяния Брэгга в узком спектральном диапазоне дифрагированное переходное излучение (ДПИ) [6–8]. Важно отметить, что в рентгеновском диапазоне частот экспериментально может быть обнаружено и исследовано ДПИ от одной границы мишени, в отличие от ПИ, которое можно наблюдать только от двух границ, т.е. в условиях значительного влияния на спектрально-угловую плотность излучения интерференции волн ПИ от разных границ и фотопоглощения волн материалом мишени. При этом ПИ имеет еще и очень широкий спектр, что значительно снижает возможности исследования влияния многократного рассеяния релятивистских электронов на спектрально-угловую плотность ПИ. ДПИ имеет очень узкий частотный диапазон, является по сути переходным излучением только от одной границы, поэтому, по мнению авторов, является важным и удобным объектом для исследования влияния многократного рассеяния излучающих релятивистских электронов на угловую плотность ПИ.
В работах [9–11] влияние расходимости электронного пучка на спектрально-угловые характеристики ДПИ и параметрического рентгеновского излучение (ПРИ) исследовалось в геометрии рассеяния Лауэ.
Настоящая работа посвящена исследованию ДПИ, возбуждаемого пучком релятивистских электронов, пересекающих монокристаллическую пластинку произвольной толщины в геометрии рассеяния Брэгга с учетом многократного рассеяния пучка релятивистских электронах на атомах мишени. Для учета многократного рассеяния используется традиционный метод усреднения спектрально-угловой и угловой плотностей излучений по расширяющемуся пучку прямолинейных траекторий электронов.
2. ГЕОМЕТРИЯ ПРОЦЕССА ИЗЛУЧЕНИЯ
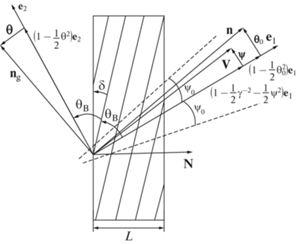
Рассмотрим пучок релятивистских электронов, пересекающих монокристалл в геометрии рассеяния Брэгга (рис. 1). Введем угловые переменные ${\mathbf{\psi }}{\text{,}}$ ${\mathbf{\theta }}$ и ${{{\mathbf{\theta }}}_{0}}$ в соответствии с определениями скорости выделенного в пучке релятивистского электрона ${\mathbf{V}}$ и единичных векторов: ${\mathbf{n}}$ – в направлении импульса фотона, излученного вблизи направления вектора скорости электрона, и ${{{\mathbf{n}}}_{{\mathbf{g}}}}$ – в направлении рассеяния Брэгга:
(1)
$\begin{gathered} {\mathbf{V}} = \left( {1 - \frac{1}{2}{{\gamma }^{{ - 2}}} - \frac{1}{2}{{\psi }^{2}}} \right){{{\mathbf{e}}}_{1}} + {\mathbf{\psi }},\,\,\,\,{{{\mathbf{e}}}_{1}}{\mathbf{\psi }} = 0, \\ {\mathbf{n}} = \left( {1 - \frac{1}{2}\theta _{0}^{2}} \right){{{\mathbf{e}}}_{1}} + {{{\mathbf{\theta }}}_{0}},\,\,\,\,{{{\mathbf{e}}}_{1}}{{{\mathbf{\theta }}}_{0}} = 0, \\ {{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}} = \cos 2{{\theta }_{{\text{B}}}},\,\,\,\,{{{\mathbf{n}}}_{{\mathbf{g}}}} = \left( {1 - \frac{1}{2}{{\theta }^{2}}} \right){{{\mathbf{e}}}_{2}} + {\mathbf{\theta }},\,\,\,\,{{{\mathbf{e}}}_{2}}{\mathbf{\theta }} = 0, \\ \end{gathered} $3. СПЕКТРАЛЬНО-УГЛОВАЯ И УГЛОВАЯ ПЛОТНОСТИ ИЗЛУЧЕНИЯ
В работе [12] в рамках двухволнового приближения динамической теории дифракции была развита теория когерентного рентгеновского излучения, возбуждаемого в монокристалле в геометрии рассеяния Брэгга пучком релятивистских электронов в направлении n (рис. 1) близком к направлению ${{{\mathbf{e}}}_{1}}$ оси пучка. Были получены выражения, описывающие амплитуды напряженностей электрических полей волн параметрического рентгеновского излучение вблизи направления скорости релятивистского электрона (ПРИВ) и переходного излучения (ПИ). На их основе были получены и исследованы выражения, описывающие спектрально-угловые характеристики ПРИВ, ПИ и их интерференционное слагаемое.
Используя обозначения и рассуждения аналогичные проведенным в работе [11], в настоящей работе мы получили выражение для амплитуды напряженности когерентного рентгеновского излучения $E_{{Rad}}^{{(s)}},$ возбуждаемого в тонкой непоглощающей монокристаллической мишени релятивистским электроном, движущегося в пучке под углом ${\mathbf{\psi }}({{\psi }_{\parallel }},{{\psi }_{ \bot }})$ к оси пучка ${{{\mathbf{e}}}_{1}}.$ Амплитуда поля излучения была представлена в виде суммы полей, одно из которых соответствует вкладу механизма ПРИ $\left( {E_{{{\text{PXR}}}}^{{(s)}}} \right),$ а другое вкладу ДПИ $\left( {E_{{{\text{DTR}}}}^{{{\text{(}}s{\text{)}}}}} \right).$ Амплитуда поля ДПИ имеет вид:
(2)
$\begin{gathered} E_{{{\text{ДПИ}}}}^{{(s)}} = \frac{{8{{\pi }^{2}}ieV{{\Omega }^{{(s)}}}}}{\omega }\frac{{{{\omega }^{2}}{{\chi }_{{\mathbf{g}}}}{{C}^{{(s,\tau )}}}}}{{2\omega \Delta }} \times \\ \times \,\,\left[ {\frac{1}{{\frac{{{{\gamma }_{0}}}}{{\left| {{{\gamma }_{{\mathbf{g}}}}} \right|}}\left( { - {{\chi }_{0}}(\omega ) - \frac{2}{\omega }\frac{{{{\gamma }_{0}}}}{{{{\gamma }_{{\mathbf{g}}}}}}\lambda _{{\mathbf{g}}}^{ * } + \beta \frac{{{{\gamma }_{0}}}}{{{{\gamma }_{{\mathbf{g}}}}}}} \right)}} + \frac{\omega }{{2\frac{{{{\gamma }_{0}}}}{{\left| {{{\gamma }_{{\mathbf{g}}}}} \right|}}\lambda _{0}^{ * }}}} \right] \times \\ \times \,\,\left( {{{\Delta }^{{(2)}}} - {{\Delta }^{{(1)}}}} \right), \\ \end{gathered} $(3)
$\begin{gathered} \Delta = \lambda _{{\mathbf{g}}}^{{(2)}}\exp \left( {i\frac{{\lambda _{{\mathbf{g}}}^{*} - \lambda _{{\mathbf{g}}}^{{(2)}}}}{{{{\gamma }_{{\mathbf{g}}}}}}L} \right) - \lambda _{{\mathbf{g}}}^{{(1)}}\exp \left( {i\frac{{\lambda _{{\mathbf{g}}}^{*} - \lambda _{{\mathbf{g}}}^{{(1)}}}}{{{{\gamma }_{{\mathbf{g}}}}}}L} \right), \\ {{\Delta }^{{(2)}}} = \exp \left( {i\frac{{\lambda _{{\mathbf{g}}}^{*} - \lambda _{{\mathbf{g}}}^{{(2)}}}}{{{{\gamma }_{{\mathbf{g}}}}}}L} \right),\,\,\,\,{{\Delta }^{{(1)}}} = \exp \left( {i\frac{{\lambda _{{\mathbf{g}}}^{*} - \lambda _{{\mathbf{g}}}^{{(1)}}}}{{{{\gamma }_{{\mathbf{g}}}}}}L} \right), \\ {{C}^{{(s,\tau )}}} = {{( - 1)}^{\tau }}{{C}^{{(s)}}},\,\,\,\,{{С}^{{(1)}}} = 1,\,\,\,\,{{С}^{{(2)}}} = \left| {\cos 2{{\theta }_{{\text{B}}}}} \right|, \\ {\text{T}}\lambda _{{\mathbf{g}}}^{{(1,2)}} = \frac{{\omega \left| {\chi _{{\mathbf{g}}}^{'}{{C}^{{(s)}}}} \right|}}{2}\left( {{{\xi }^{{(s)}}}} \right.\left. { \pm \sqrt {{{\xi }^{{(s)}}}^{2} - \varepsilon } } \right), \\ \lambda _{{\mathbf{g}}}^{ * } = \frac{{\omega \left| {\chi _{{\mathbf{g}}}^{'}{{C}^{{(s)}}}} \right|}}{2}\left( {2{{\xi }^{{(s)}}} - \varepsilon {{\sigma }^{{(s)}}}} \right), \\ {{\xi }^{{(s)}}}\left( \omega \right) = {{\eta }^{{(s)}}}(\omega ) + \frac{{1 + \varepsilon }}{{2{{\nu }^{{(s)}}}}}, \\ {{\sigma }^{{(s)}}} = \frac{1}{{\left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}}{\kern 1pt} {\kern 1pt} \left( {{{\gamma }^{{ - 2}}} + {{{({{\theta }_{ \bot }} - {{\psi }_{ \bot }})}}^{2}} + {{{({{\theta }_{\parallel }} + {{\psi }_{\parallel }})}}^{2}} - \chi _{0}^{'}} \right){\kern 1pt} , \\ {{\eta }^{{(s)}}}(\omega ) = \frac{{2{{{\sin }}^{2}}{{\theta }_{{\text{B}}}}}}{{{{V}^{2}}\left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}}\left( {1 - \frac{{\omega (1 - {{\theta }_{{||}}}{\text{ctg}}{{\theta }_{{\text{B}}}})}}{{{{\omega }_{{\text{B}}}}}}} \right), \\ {{\nu }^{{(s)}}} = \frac{{\chi _{{\mathbf{g}}}^{'}{{C}^{{(s)}}}}}{{\chi _{0}^{'}}},\,\,\,\,\varepsilon = \frac{{\sin ({{\theta }_{{\text{B}}}} - \delta )}}{{\sin ({{\theta }_{{\text{B}}}} + \delta )}}, \\ \end{gathered} $Так как в области рентгеновских частот выполняется неравенство $\frac{{2{{{\sin }}^{2}}{{\theta }_{{\text{B}}}}}}{{{{V}^{2}}\left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}} \gg 1,$ то ${{\eta }^{{(s)}}}(\omega )$ является быстрой функцией от частоты $\omega {\kern 1pt} .$ Для дальнейшего анализа спектров ПРИ и ДПИ удобно рассматривать ${{\eta }^{{(s)}}}(\omega )$ (или ${{\xi }^{{(s)}}}\left( \omega \right)$) в качестве спектральной переменной, характеризующей частоту $\omega {\kern 1pt} .$
Параметр ${{\nu }^{{(s)}}},$ принимающий значения в промежутке $0 \leqslant {{\nu }^{{(s)}}} \leqslant 1,$ определяет степень отражения поля волны излучения от рассматриваемой системы параллельных атомных плоскостей монокристалла, которая обусловливается характером интерференции волн, отраженных от разных плоскостей. Параметр $\varepsilon $ для фиксированного значения ${{\theta }_{{\text{B}}}}$ определяет ориентацию входной поверхности мишени относительно отражающей системы параллельных атомных плоскостей монокристалла.
Подставляя (2) в известное выражение для спектрально-угловой плотности рентгеновского излучения:
(4)
$\omega \frac{{{{d}^{2}}N_{{{\text{ДПИ}}}}^{{(s)}}}}{{d\omega d\Omega }} = {{\omega }^{2}}{{(2\pi )}^{{ - 6}}}\sum\limits_{s\,{\kern 1pt} = \,{\kern 1pt} 1}^2 {{{{\left| {E_{{{\text{ДПИ}}}}^{{(s)}}} \right|}}^{2}}} ,$(5а)
$\begin{gathered} \omega \frac{{{{d}^{2}}N_{{{\text{ДПИ}}}}^{{(s)}}}}{{d\omega d\Omega }} = \\ = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}{{\left( {\frac{{{{\Omega }^{{(s)}}}}}{{\Delta ({{\theta }_{ \bot }},{{\theta }_{{||}}},{{\psi }_{ \bot }},{{\psi }_{{||}}})}} - \frac{{{{\Omega }^{{(s)}}}}}{{\Delta ({{\theta }_{ \bot }},{{\theta }_{{||}}},{{\psi }_{ \bot }},{{\psi }_{{||}}}) - \chi _{0}^{'}}}} \right)}^{2}}{\kern 1pt} R_{{{\text{ДПИ}}}}^{{(s)}}, \\ \end{gathered} $(5б)
$R_{{{\text{ДПИ}}}}^{{(s)}} = \frac{{{{\varepsilon }^{2}}}}{{{{\xi }^{{{{{(s)}}^{2}}}}} - ({{\xi }^{{{{{(s)}}^{2}}}}} - \varepsilon ){{{\operatorname{cth} }}^{2}}\left( {\frac{{{{b}^{{(s)}}}\sqrt {\varepsilon - {{\xi }^{{(s)}}}^{2}} }}{\varepsilon }} \right)}},$(6)
$\begin{gathered} \Delta ({{\theta }_{ \bot }},{{\theta }_{{||}}},{{\psi }_{ \bot }},{{\psi }_{{||}}}) = \\ = {{\gamma }^{{ - 2}}} + {{({{\theta }_{ \bot }} - {{\psi }_{ \bot }})}^{2}} + {{({{\theta }_{{||}}} + {{\psi }_{{||}}})}^{2}}, \\ {{\Omega }^{{(1)}}} = {{\theta }_{ \bot }} - {{\psi }_{ \bot }},\,\,\,\,{{\Omega }^{{(2)}}} = {{\theta }_{{||}}} + {{\psi }_{{||}}}, \\ {{b}^{{(s)}}} = \frac{1}{{2\sin ({{\theta }_{{\text{B}}}} + \delta )}}\frac{L}{{L_{{{\text{ext}}}}^{{(s)}}}},\,\,\,\,L_{{{\text{ext}}}}^{{(s)}} = {1 \mathord{\left/ {\vphantom {1 {\omega \left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}}} \right. \kern-0em} {\omega \left| {\chi _{{\mathbf{g}}}^{'}} \right|{{C}^{{(s)}}}}}. \\ \end{gathered} $4. УЧЕТ МНОГОКРАТНОГО РАССЕЯНИЯ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ В МОНОКРИСТАЛЛЕ
Рассмотрим один электрон, движущийся в составе падающего на монокристаллическую мишень пучка электронов под углом ${\mathbf{\psi }}$ относительно оси пучка ${{{\mathbf{e}}}_{1}}.$ В результате многократного рассеяния на атомах мишени направление его движения по отношению к оси пучка будет изменяться как функция пройденного в мишени пути $t{\text{:}}$ ${\mathbf{\psi }} \to {\mathbf{\psi }} + \Delta {\mathbf{\psi }}(t).$
Компоненты $\Delta {{\psi }_{ \bot }},$ $\Delta {{\psi }_{\parallel }}$ угла рассеяния $\Delta {\mathbf{\psi }}$ будем описывать функцией Гаусса, меняющейся с длиной пути прохождения в мишени $t{\text{:}}$
(7)
$f(\Delta {{\psi }_{ \bot }},\Delta {{\psi }_{\parallel }},t) = \frac{1}{{\pi \left( {\psi _{0}^{2} + \psi _{s}^{2}t} \right)}}{{e}^{{ - {\kern 1pt} \frac{{\Delta \psi _{ \bot }^{2}{\kern 1pt} + {\kern 1pt} \Delta \psi _{\parallel }^{2}}}{{\psi _{0}^{2}{\kern 1pt} + {\kern 1pt} \psi _{s}^{2}t}}}}},$$\psi _{s}^{2} = \frac{{E_{s}^{2}}}{{{{m}^{2}}{{\gamma }^{2}}}}\frac{1}{{{{L}_{R}}}}{{\left( {1 + 0.038{\text{ln}}\left( {\frac{t}{{{{L}_{R}}}}} \right)} \right)}^{2}}$ – средний квадрат угла многократного рассеяния электрона на единице длины как функция пути $t,$ пройденного электроном в монокристаллической мишени [13], ${{E}_{s}} \approx 21\,\,{\text{МэВ}}.$
В результате усреднения выражения (5) для спектрально-угловой плотности ДПИ одного электрона, полагая ${{\psi }_{0}} = 0$ в (7), получим:
(8)
$\begin{gathered} {{\left\langle {\omega \frac{{{{d}^{2}}N_{{{\text{ДПИ}}}}^{{(s)}}}}{{d\omega d\Omega }}} \right\rangle }_{{\Delta {\mathbf{\psi }}}}} = \\ = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}\frac{1}{{{{L}_{e}}}}\int\limits_0^{{{L}_{e}}} {\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{{\left( {\frac{{{{\Omega }^{{(s)}}}}}{\Delta } - \frac{{{{\Omega }^{{(s)}}}}}{{\Delta {\text{*}} - \chi _{0}^{'}}}} \right)}}^{2}}R_{{{\text{ДПИ}}}}^{{(s)}}\frac{1}{{\pi \psi _{s}^{2}t}}} } } \times \\ \times \,\,{{e}^{{ - {\kern 1pt} \frac{{\Delta \psi _{ \bot }^{2}{\kern 1pt} + {\kern 1pt} \Delta \psi _{\parallel }^{2}}}{{\psi _{s}^{2}t}}}}}d\Delta {{\psi }_{ \bot }}d\Delta {{\psi }_{\parallel }}dt, \\ \end{gathered} $По величине $t,$ которая представляет путь, пройденный электроном в мишени, мы проводим интегрирование в пределах от нуля до полной длины пути электрона в мишени ${{L}_{e}}.$
Проанализируем влияние многократного рассеяния электронов атомами среды на спектрально-угловую плотность дифрагированного переходного излучения для различных значений энергии электрона, которая определяется Лоренц-фактором $\gamma .$ Угловая плотность ПИ на передней границе мишени, согласно (5а) пропорционально следующему выражению:
(9)
$\begin{gathered} {{\left( {\frac{{{{\Omega }^{{(s)}}}}}{\Delta } - \frac{{{{\Omega }^{{(s)}}}}}{{\Delta {\text{*}} - \chi _{0}^{'}}}} \right)}^{2}} = \\ = \left( {\frac{{{{\Omega }^{{(s)}}}}}{{{{\gamma }^{{ - 2}}} + {{{({{\theta }_{ \bot }} - {{\psi }_{ \bot }})}}^{2}} + {{{({{\theta }_{{||}}} + {{\psi }_{\parallel }})}}^{2}}}}} \right. - \\ {{\left. { - \,\,\frac{{{{\Omega }^{{(s)}}}}}{{{{\gamma }^{{ - 2}}} + {{{({{\theta }_{ \bot }} - {{\psi }_{ \bot }})}}^{2}} + {{{({{\theta }_{{||}}} + {{\psi }_{\parallel }})}}^{2}} - \chi _{0}^{'}}}} \right)}^{2}}. \\ \end{gathered} $В случае же малых энергий электронов $\left( {{{\gamma }^{{ - 2}}} \geqslant \left| {\chi _{0}^{'}} \right|} \right),$ в выражении (9) второе слагаемое по величине будет сопоставимо с первым, что приведет практически к отсутствию ДПИ (и ПИ). Многократное рассеяние может существенно повлиять на угловую плотность ДПИ (и ПИ), поскольку приведет к уменьшению второго слагаемого в (9) и ослаблению компенсации первого слагаемого вторым. Таким образом, многократное рассеяние при малых энергиях релятивистского электрон $\left( {{{\gamma }^{{ - 2}}} \gg \left| {\chi _{0}^{'}} \right|} \right)$ может на порядки увеличить угловую плотность ДПИ. Данный эффект многократного рассеяния в угловой плотности ДПИ (и ПИ) ранее никем не заявлялся и не исследовался ни теоретически, ни экспериментально.
Переходное излучение формируется в виде разности между полем электрона, которое он имел при влете в мишень, и экранированным полем электрона в среде. Многократное рассеяние может влиять только на составляющую поля волны переходного излучения, которая формируется при движении электрона в веществе мишени. В этой связи в выражении для спектрально-угловой плотности ДПИ (8), учитывающем многократное рассеяние электрона, мы ввели замену $\Delta \to \Delta {\text{*}}$ только во втором слагаемом, описывающем поле электрона в материале мишени.
Усредняя выражение (8) по всем возможным начальным прямолинейным траекториям электрона в пучке, получим выражение, описывающее спектрально-угловую плотность ДПИ пучка релятивистских электронов, с учетом многократного рассеяния в монокристалле, нормированную на один электрон:
(10)
$\begin{gathered} {{\left\langle {\omega \frac{{{{d}^{2}}N_{{{\text{ДПИ}}}}^{{(s)}}}}{{d\omega d\Omega }}} \right\rangle }_{{\Delta {\mathbf{\psi }}}}} = \frac{{{{e}^{2}}}}{{{{\pi }^{2}}}}\frac{1}{{{{L}_{e}}}}\frac{1}{{\pi \psi _{0}^{2}}} \times \\ \times \,\,\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\left[ {\int\limits_0^{{{L}_{e}}} {\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{{\left( {\frac{{{{\Omega }^{{(s)}}}}}{\Delta } - \frac{{{{\Omega }^{{(s)}}}}}{{\Delta {\text{*}} - \chi _{0}^{'}}}} \right)}}^{2}}R_{{{\text{ДПИ}}}}^{{(s)}}} } } } \right.} } \times \\ \left. { \times \,\,\frac{1}{{\pi \left( {\psi _{0}^{2} + \psi _{s}^{2}t} \right)}}{{e}^{{ - {\kern 1pt} \frac{{\Delta \psi _{ \bot }^{2}{\kern 1pt} + {\kern 1pt} \Delta \psi _{\parallel }^{2}}}{{\psi _{0}^{2}{\kern 1pt} + {\kern 1pt} \psi _{s}^{2}t}}}}}d\Delta {{\psi }_{ \bot }}d\Delta {{\psi }_{\parallel }}dt} \right] \times \\ \times \,\,{{e}^{{ - {\kern 1pt} \frac{{\psi _{ \bot }^{2}{\kern 1pt} + {\kern 1pt} \psi _{\parallel }^{2}}}{{\psi _{0}^{2}}}}}}d{{\psi }_{ \bot }}d{{\psi }_{\parallel }}. \\ \end{gathered} $Поскольку электроны в пучке возбуждают излучение не когерентно, то мы можем рассматривать влияние многократного рассеяния на угловую плотность ДПИ на примере одного излучающего электрона, пересекающего переднюю границу монокристаллической мишени вдоль оси ${{{\mathbf{e}}}_{1}}$ (${\mathbf{\psi }} = 0$). Численные расчеты спектрально-угловой плотности ДПИ без учета многократного рассеяния проведем по формуле (5), а с учетом по формуле (8). Будем рассматривать релятивистский электрон с энергией $\gamma = 100,$ пересекающий монокристалл углерода $С(111),$ с параметрами процесса: ${{\theta }_{{\text{B}}}} = 16.2^\circ ,$ ${{\omega }_{{\text{B}}}} = 10{\kern 1pt} 900\,\,{\text{эВ}},$ $\varepsilon = 1.$
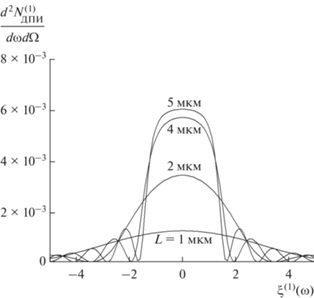
На рис. 2 представлены кривые, построенные по формуле (5), описывающие спектрально-угловую плотность ДПИ при фиксированном угле наблюдения без учета многократного рассеяния. Рисунок демонстрирует рост амплитуды спектра ДПИ при увеличении толщины мишени и насыщении роста приблизительно при $L = 5\,\,мкм.$ Рассматриваемые условия показали, что такая толщина монокристалла является предельной для генерации ДПИ.
Рис. 2.
Спектрально-угловые плотности ДПИ для различной толщины монокристалла при фиксированных углах наблюдения: ${{\theta }_{ \bot }} = 10,$ ${{\theta }_{\parallel }} = 0.$ $\gamma = 100.$
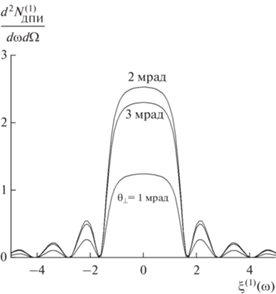
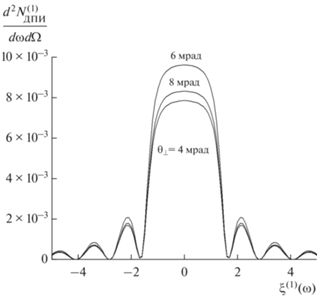
На рис. 3 представлены кривые, описывающие спектрально-угловые плотности ДПИ для различных углов наблюдения ${{\theta }_{ \bot }},$ при ${{\theta }_{\parallel }} = 0.$ Из рисунка видно, что спектрально-угловая плотность максимальна при угле приближенном ${{\theta }_{ \bot }} = 6\,\,{\text{мрад}}{\text{.}}$
Рис. 3.
Спектрально-угловые плотности ДПИ для различных углов наблюдения ${{\theta }_{ \bot }},$ ${{\theta }_{{||}}} = 0.$ $\gamma = 100.$
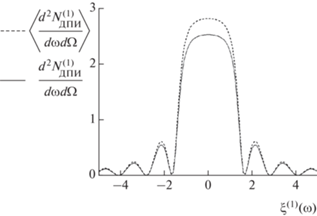
На рис. 4 представлены кривые, построенные по формулам (5) и (8), которые описывают спектр ДПИ с учетом (пунктирная кривая) и без учета (сплошная кривая) многократного рассеяния электрона на атомах мишени толщиной $L = 5\,\,мкм$ и угле наблюдения ${{\theta }_{ \bot }} = 6\,\,{\text{мрад,}}$ ${{\theta }_{\parallel }} = 0.$ Из рисунка следует, что в рассматриваемых условиях учет многократного рассеяния дает приблизительно пятикратное увеличение амплитуды спектрально-угловой плотности ДПИ по сравнению с расчетом без учета многократного рассеяния. Кривые на рис. 2–4 построены для энергии электрона, соответствующей Лоренц-фактору ($\gamma = 100$). Аналогичные кривые на рис. 5–7 построены для большей энергии электрона ($\gamma = 300$). При такой энергии электрона (рис. 7) влияние многократного рассеяния электронов на атомах среды на спектрально-угловую плотность излучения становится значительно более слабым. В случае увеличения энергии электронов $\gamma > 300$ влияние многократного рассеяния на спектрально-угловую плотность ДПИ будет пренебрежимо малым.
Рис. 4.
Спектрально-угловые плотности ДПИ с учетом (пунктирная кривая) и без учета (сплошная кривая) многократного рассеяния: $\gamma = 100,$ $L = 5\,\,мкм,$ ${{\theta }_{ \bot }} = 6\,\,{\text{мрад}}{\text{.}}$
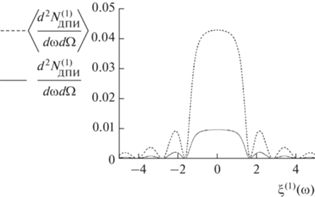
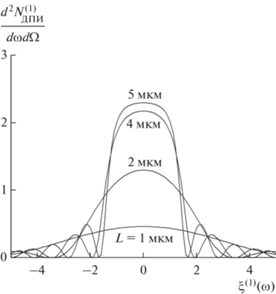
Рис. 5.
Спектрально-угловые плотности ДПИ для различной толщины монокристалла при фиксированных углах наблюдения: ${{\theta }_{ \bot }} = 3\,\,{\text{мрад,}}$ ${{\theta }_{{||}}} = 0.$ $\gamma = 300.$
ЗАКЛЮЧЕНИЕ
В работе развита динамическая теория дифрагированного переходного излучения, генерируемого пучком релятивистских электронов в монокристаллической пластине в геометрии рассеяния Брэгга в условиях многократного рассеяния падающих частиц. Получены выражения, описывающие спектрально-угловую плотность ДПИ как с учетом, так и без учета многократного рассеяния электронов пучка атомами мишени. Исследовано влияние многократного рассеяния электрона на спектрально-угловую плотность ДПИ. Расчеты угловой спектрально-угловой плотности ДПИ демонстрируют рост угловой плотности ДПИ при увеличении толщины мишени. Главным новым результатом работы является установление факта значительного роста спектрально-угловой плотности дифрагированного переходного излучения в условиях многократного рассеяния излучающих электронов на атомах монокристаллической мишени.
Результаты данной работы могут быть полезными при постановке новых экспериментов по исследованию свойств ПРИ и ДПИ и интерпретации результатов экспериментов при небольших энергиях электронов ($\gamma \leqslant 100$), в которых принципиально важно правильно учитывать вклад ДПИ.
Список литературы
Гинзбург В.Л., Франк И.М. // ЖЭТФ. 1946. Т. 16. С. 15.
Гинзбург В.Л., Цытович В.Н. // Переходное излучение и переходное рассеяние. М.: Наука, 1984.
Пафомов В.Е. // Докл. АН СССР. 1960. Т. 133. № 6. С. 1315.
Болотовский Б.М. // Труды ФИАН. 1982. Т. 140. С. 95.
Гарибян Г.М. // ЖЭТФ. 1960. Т. 39. Вып. 2. С. 332.
Caticha A. // Phys. Rev. A. 1989. T. 40. C. 4322.
Baryshevsky V. // Nucl. Instrum. Methods. Phys. Res. A. 1997. T. 122. C. 13.
Nasonov N. // Phys. Lett. A. 1998. T. 246. C. 148.
Блажевич С.В., Носков А.В. // ЖЭТФ. 2015. Т. 147. С. 875.
Блажевич С.В., Носков А.В. // ЖЭТФ. 2016. Т. 150. С. 643.
Блажевич С.В., Бронникова М.В., Носков А.В. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2020. № 9. С. 66.
Блажевич С.В., Люшина К.С., Носков А.В. // ЖЭТФ. 2019. Т. 155. С. 242.
Partic1e Data Group, Barnett R.M. et al. //Phys. Rev. D. 1996. V. 54. P. 1.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования