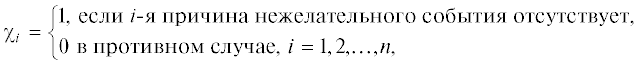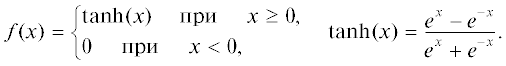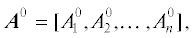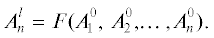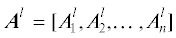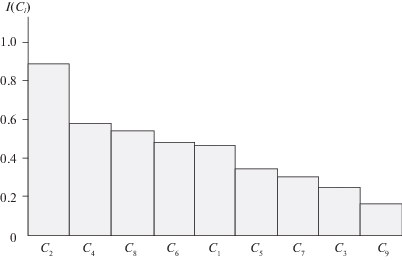Известия РАН. Теория и системы управления, 2019, № 2, стр. 47-57
АНАЛИЗ РИСКА: НЕЧЕТКАЯ КОГНИТИВНАЯ КАРТА КАК АЛЬТЕРНАТИВА ДЕРЕВУ ОТКАЗОВ
А. П. Ротштейн *
Иерусалимский политехнический ин-т (Махон Лев)
Иерусалим, Израиль
* E-mail: rothstei@g.jct.ac.il
Поступила в редакцию 18.10.2018
После доработки 19.11.2018
Принята к публикации 26.11.2018
Аннотация
Анализируются ограничения метода деревьев отказов в задачах анализа риска. Как альтернатива этому методу рассматривается возможность применения нечетких когнитивных карт – нового аппарата моделирования, не получившего достаточного распространения в теории надежности. На основе нечетких когнитивных карт предлагается метод ранжирования факторов риска, который иллюстрируется на примере человеко-машинной системы.
Введение. Понятие риска связано с вероятностью некоторого нежелательного события, ведущего к потерям: техническим, финансовым, военными и т.д. Для специалиста по надежности понятие “нежелательное событие” ассоциируется с понятием “отказ” – основным в теории надежности [1]. Поэтому метод дерева событий, который принято называть методом дерева отказов [2] (см. также [1]), получил широкoe распространение в моделировании безопасности и риска в технических, экономических, социальных и других системах [3–6].
В статье анализируются ограничения логико-вероятностной методологии анализа риска и как альтернатива рассматривается возможность применения нечетких когнитивных карт (НКК) – нового аппарата моделирования, не получившего достаточного распространения в теории надежности. На основе НКК предлагается метод ранжирования факторов риска, который иллюстрируется на примере системы “водитель–автомобиль–дорога”.
1. Дерево отказов и его ограничения. Дерево отказов – это наглядное иерархическое представление логической функции (в теории надежности [1] ее принято называть структурной функцией):
которая отражает причинно-следственную связь между выходным условием χs возникновения нежелательного события (отказ системы, авария, финансовые потери и др.) и входными условиями χi возникновения его причин (отказы элементов, неправильное обслуживание, политические санкции и др.), где:Универсального способа выбора множества входных условий χi, т.е. факторов риска, не существует. В решении этой проблемы может быть полезен опыт отбора факторов, влияющих на функцию отклика, из теории планирования эксперимента [7] или диаграмма Исикавы (“рыбья кость”) из методов управления качеством [8].
Переход от логической функции (1.1) к вероятностной функции
позволяет оценивать вероятность Ps отсутствия нежелательного события (риска) по известным вероятностям Pi отсутствия его причин, где(1.3)
${{P}_{s}} = {\text{Prob(}}{{\chi }_{s}} = 1{\text{)}},\quad {{P}_{i}} = {\text{Prob(}}{{\chi }_{i}} = 1{\text{)}}{\text{.}}$Математической основой перехода от (1.1) к (1.2) является логико-вероятностное исчисление И.А. Рябинина [3]. С помощью вероятностной функции (1.2) решается важная для проектирования задача ранжирования (упорядочения) элементов системы в соответствии с их важностью в смысле влияния на вероятность отказа системы. Представим функцию (1.2) в виде ряда:
(1.4)
$\quad{{P}_{s}} = {{b}_{0}} + \mathop \sum \limits_{i = 1}^n {{b}_{i}}{{P}_{i}} + \quad\mathop \sum \limits_{i = 1}^n {{b}_{{ij}}}{{P}_{i}}{{P}_{j}} + \ldots .$(1.5)
${{b}_{i}} = \frac{{\partial {{P}_{s}}}}{{\partial {{P}_{i}}}},\quad {{b}_{{ij}}} = \frac{{{{\partial }^{2}}{{P}_{s}}}}{{\partial {{P}_{i}}\partial {{P}_{j}}}}\quad.$(1.6)
${{I}_{i}} = \frac{{\partial {{P}_{s}}}}{{\partial {{P}_{i}}}} = {{P}_{s}}({{P}_{1}},\quad \ldots \quad,{{P}_{{i - 1}}},\quad1,\quad{{P}_{{i + 1}}},\quad \ldots \quad,\quad{{P}_{n}}) - \quad{{P}_{s}}({{P}_{1}},\quad \ldots \quad,{{P}_{{i - 1}}},\quad0,\quad{{P}_{{i + 1}}},\quad \ldots \quad,\quad{{P}_{n}}).$Ограничения метода деревьев отказов [2] и логико-вероятностных моделей анализа безопасности и риска [3–5] состоят в следующем.
А. Бинарная концепция нарушений (1 – нет отказа, 0 – есть отказ) затрудняет моделирование промежуточных состояний элементов, которые лишь снижают эффективность работы системы, но не приводят к ее полному отказу. Применение бинарной концепции вполне оправдано для технических систем с хорошо определенной структурой (например, электрические схемы), элементы которых допускают повторение опытов в одинаковых условиях, что необходимо для корректного получения вероятностей (1.3). Поэтому в моделях (1.2) и (1.6) могут использоваться справочные данные об интенсивностях отказов элементов системы.
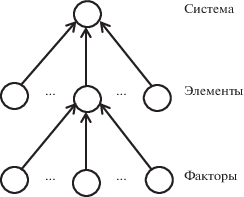
Б. Для человеко-машинных систем [11] на дереве отказов необходимо учитывать не только структурные и функциональные элементы системы, но и влияющие друг на друга факторы, связанные с человеком, техникой и внешней средой (рис. 1). В системах с повышенной опасностью (транспорт, энергетика, химическая промышленность) причиной многих аварий и катастроф являются ошибки человека. На вероятность ошибочных действий человека влияют такие факторы, как его мотивация, внимательность, ответственность, утомление и др. Отсутствие четких границ между правильными (1) и неправильными (0) значениями этих факторов затрудняет их бинарную оценку и проведение опытов в одинаковых условиях, что необходимо для корректного применения логико-вероятностных моделей (1.1)–(1.6). Это ограничение снимается средствами нечеткой логики [12]. Здесь вместо бинарного индикатора χ = 1 (успех) или 0 (неуспех) используется функция принадлежности μ(x) ∈ [0, 1], с помощью которой оценивается уровень соответствия значения х некоторого фактора к нечеткому терму “успех”.
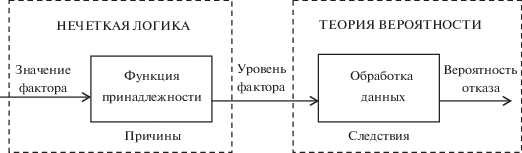
Взаимосвязь нечеткой логики и теории вероятности в моделях надежности (рис. 2) подобна взаимосвязи логической функции (1.1) и ее вероятностного аналога (1.2): нечеткая логика моделирует поведение системы в пространстве причин отказов, т.е. факторов, влияющих на надежность системы; вероятностные модели используют информацию о свершившихся событиях, т.е. об отказах как следствиях критических значений влияющих факторов.
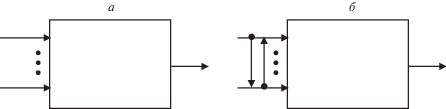
Удобным средством моделирования многофакторных зависимостей на основе экспертной информации являются нечеткие правила “если – то” [12], которые находят широкое применение в анализе надежности [13–15]. Ограничением нечетких правил служит допущение о независимости входных переменных, т.е. влияющих факторов (рис. 3а). Этого ограничения лишены НКК [16], которые еще не получили распространения в теории надежности. Здесь входные переменные влияют не только на выход, но и друг на друга (рис. 3б).
Ниже предлагается метод ранжирования взаимосвязанных факторов риска на основе НКК. Для иллюстрации метода используется система “водитель–автомобиль–дорога”.
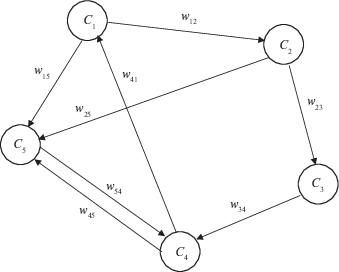
2. Основные понятия и соотношения. 2.1. Общие замечания. НКК введены Б. Коско [16] как обобщение бинарных когнитивных карт Р. Аксельрода [17], предназначенных для моделирования динамики причинно-следственных связей в социально-политических системах. НКК представляет собой ориентированный граф со взвешенными дугами, пример которого показан на рис. 4. Вершины графа Ci, называемые концептами, соответствуют входным и выходным переменным, которые учитываются в модели. Взвешенные дуги графа отражают силу влияния wij изменения одной переменной Ci на изменение другой переменной Cj.
Термин “когнитивный” говорит о том, что исходными данными для моделирования служат субъективные мнения эксперта, выраженные словами типа “повышается” или “понижается”, например: “повышение Ci приводит к понижению Cj”. В бинарных когнитивных картах [17] “повышение” оценивается как “+1”, а “понижение” – как “–1”.
Термин “нечеткие” говорит о том, НКК [16] используют различные уровни “повышения” и “понижения”. Они задаются числами из интервалов [0,1] и [0,–1], что соответствует термам “слабо”, “средне”, “сильно” и др. из теории нечетких множеств [12].
С точки зрения теории идентификации [18, 19], которая занимается восстановлением закономерностей по экспериментальным данным, НКК – это аппроксиматор зависимости “входы–выход” с взаимодействующими входами. Как и любой аппроксиматор, например регрессия, нечеткие правила, нейронная сеть и др., НКК содержит настраиваемые параметры, которые должны оцениваться путем минимизации невязки между модельными и экспериментальными значениями выхода. Если экспериментальные данные “входы–выход” отсутствуют, то качество модели целиком зависит от квалификации эксперта. Искусство моделирования состоит в том, чтобы компенсировать недостающие экспериментальные данные за счет высокого качества экспертных оценок.
Уместно сопоставить НКК и марковские цепи (процессы), привычные специалистам по надежности. Оба вида моделей – это взвешенные ориентированные графы. В основе различия НКК от марковских моделей надежности лежит принципиальное различие нечеткой логики (причин) и теории вероятности (следствий), показанное на рис. 2: марковские модели отражают динамику вероятностей состояний системы с учетом отказов и восстановлений; НКК моделируют динамику изменения уровней взаимодействующих факторов, которые являются причинами отказов и влияют на вероятность их возникновения.
2.2. К о н ц е п т ы. Пусть C = {C1, C2, …, Cn} – известное множество концептов, т.е. переменных, используемых в модели. Согласно [16], каждый концепт Ci ∈ C оценивается величиной Ai ∈ ∈ [0, 1], которая определяет уровень концепта и задается экспертно. Для получения величины Ai предлагается такой способ.
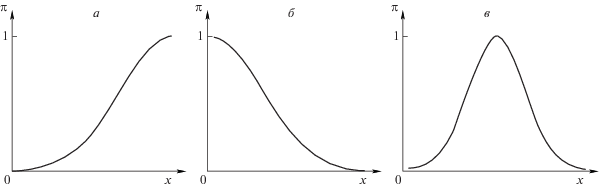
Каждый концепт Ci ∈ C будем считать лингвистической переменной [12], которая оценивается величиной xi на универсальном множестве – интервале [${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i}}$, ${{\bar {x}}_{i}}$], где ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_{i}}$(${{\bar {x}}_{i}}$) – нижняя (верхняя) граница. Для оценки концепта Ci ∈ C будем использовать нечеткий терм “перфектность концепта Ci”, который обозначается PCi и представляет собой нечеткое множество
а) “неперфектно” (0) – перфектно (1)”,
б) “перфектно (1) – неперфектно (0)”,
в) “неперфектно (0) – перфектно (1) – неперфектно (0).
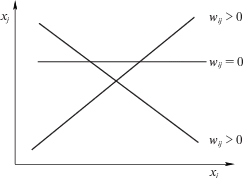
2.3. Связи между концептами. Вес wij дуги, соединяющей концепты Ci и Cj, указывает на силу влияния Ci на Cj. Пусть концепты Ci и Cj характеризуются переменными xi и xj, а в результате эксперимента удается построить зависимость xj = φ(xi). Тогда вес wij определяется как производная wij = dxj/dxi, которая может быть трех видов (рис. 6):
wij > 0, если повышение (понижение) величины xi приводит к повышению (понижению) величины xj (положительное влияние Ci на Cj);
wij < 0, если повышение (понижение) величины xi приводит к понижению (повышению) величины xj (отрицательное влияние Ci на Cj);
wij = 0, если значение xj не зависит от значения xi (отсутствие влияния Ci на Cj).
В случае экспертной оценки величины wij используется 9-балльная шкала силы влияния:
wij = {–1 (отрицательное очень сильное), –0.75 (отрицательное сильное), –0.5 (отрицательное среднее), –0.25 (отрицательное слабое), 0 (отсутствует), 0.25 (положительное слабое), 0.5 (положительное среднее), 0.75 (положительное сильное), 1 (положительное очень сильное)}. Возможны промежуточные значения.
Для получения экспертных оценок можно воспользоваться методом наименьшего влияния, предложенным в [21].
2.4. Рекуррентные соотношения. Согласно [16, 22], динамика изменения величины концептов в НКК определяется соотношением
(2.1)
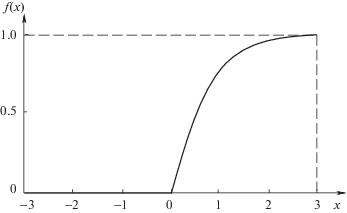
$A_{i}^{{k + 1}} = f\left( {\mathop \sum \limits_{\begin{array}{*{20}{c}} {j = 1} \\ {j \ne i} \end{array}}^n A_{j}^{k}{{w}_{{ji}}} + cA_{i}^{k}} \right),\quad k = 0,1,2,\quad \ldots ,$В этой работе предполагается, что c = 1, а в качестве пороговой функции используется положительная часть гиперболического тангенса (рис. 7):
2.5. Матричная модель. Рекуррентное соотношение (2.1) можно представить в матричной форме
где Ak = [$A_{1}^{k}$, $A_{2}^{k}$, …, $A_{n}^{k}$] – (1 × n) – вектор состояния НКК, элементы которого задают значения концептов на шаге k,(2.3)
${{W}_{0}} = \left[ {\begin{array}{*{20}{c}} 0&{{{w}_{{12}}}}& \cdots &{{{w}_{{1n}}}} \\ {{{w}_{{21}}}}&0& \cdots &{{{w}_{{2n}}}} \\ \cdot & \cdot & \cdots & \cdot \\ {{{w}_{{n1}}}\quad}&{{{w}_{{n2}}}}& \cdots &0 \end{array}} \right]$Если вместо матрицы (2.3) использовать (n × n)-матрицу
(2.4)
$W = \left[ {\begin{array}{*{20}{c}} c&{{{w}_{{12}}}}& \cdots &{{{w}_{{1n}}}} \\ {{{w}_{{21}}}}&c& \cdots &{{{w}_{{2n}}}} \\ \cdot & \cdot & \cdots & \cdot \\ {{{w}_{{n1}}}}&{{{w}_{{n2}}}}& \cdots &c \end{array}} \right]\quad,$Начальное состояние НКК определяется вектором
элементы которого отражают значения концептов на шаге k = 0. В результате взаимодействия между концептами НКК входит в стационарный режим, который соответствует одному из видов устойчивости [23]: устойчивый фокус, предельный цикл (орбита) или хаотический аттрактор.3. Ранжирование концептов. При распределении ресурсов на обеспечение надежности системы используются количественные оценки (ранги) важности ее элементов. В статистической теории надежности [1] наибольшее распространение получил индекс важности элемента по Бирнбауму [2], который имеет смысл чувствительности функции надежности системы к изменению надежности элементов и вычисляется по формуле (2.6). В нашем случае элементами модели являются входные концепты – факторы, влияющие на выходной уровень риска. Поэтому возникает необходимость вычисления индексов важности концептов НКК.
3.1. Определение индексов важности. Во множестве концептов {C1, C2, …, Cn} будем предполагать следующее:
Cn – выходной концепт, который определяет уровень риска в системе и оценивается числом An ∈ [0, 1],
C1, C2, …, Cn – 1 – входные концепты, соответствующие взаимосвязанным факторам, которые влияют на уровень риска в системе и оцениваются уровнями Ai ∈ [0, 1], i = 1, 2, …, n – 1.
Значение концепта Cn на l-м шаге является функцией от элементов вектора (2.6), т.е.
Предполагается, что $A_{n}^{l}$ – значение Cn в стационарном режиме, т.е. на таком шаге l, когда $A_{n}^{l}$ близко к $A_{n}^{{l - 1}}$. Зависимость (3.1) является аналогом (1.2), что позволяет перейти к определению рангов концептов на основе производных (1.5).Пусть I(Cj) – индекс важности концепта Cj, а I(Cj, Ck) индекс совместный важности концептов Cj и Ck. Следуя (1.5), определим эти индексы важности следующим образом:
(3.2)
$I({{C}_{j}}) = \frac{{\partial A_{n}^{l}}}{{\partial {{A}_{j}}}} = \frac{{F({{1}_{j}},{\mathbf{0}}) - F({\mathbf{0}})}}{{1 - 0}} = F({{1}_{j}},{\mathbf{0}}),\quad$(3.3)
$I({{C}_{j}},{{C}_{k}}) = \frac{{{{\partial }^{2}}A_{n}^{l}}}{{\partial {{A}_{j}}\partial {{A}_{k}}}} = \frac{{F({{1}_{j}},{{1}_{k}},{\mathbf{0}}) - F({\mathbf{0}})}}{{(1 - 0)(1 - 0)}} = F({{1}_{j}},{{1}_{k}},{\mathbf{0}}),$З а м е ч а н и е. Нулевые значения входных концептов (кроме одного в (3.2) и двух в (3.3), равных единице) выбраны для того, чтобы исключить возможность их влияния на выходной концепт за счет транзитивных связей.
3.2. Алгоритм вычисления индексов важности.
Шаг 1. Задать начальный вектор (2.6). Для индекса важности I(Cj) начальный вектор задается как
а для индекса важности I(Cj, Ck) в видеШаг 2. Пользуясь рекуррентным соотношением (2.5), найти вектор состояния НКК
в установившемся режиме, т.е. на таком шаге l, при котором |$A_{i}^{{l + 1}}$ – $A_{i}^{l}$| < ε, где ε – малое положительное число, i = 1,2, …, n.Шаг 3. Индексами важности I(Cj) и I(Cj, Ck) считать элементы $A_{n}^{l}$ вектора (3.6), полученные при начальных векторах (3.4) и (3.5) соответственно.
4. Системы “водитель–автомобиль–дорога”. 4.1. Концепты и влияния.
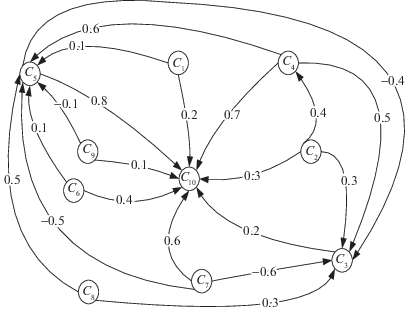
Нечеткая когнитивная карта системы приведена на рис. 8, где концепты имеют следующее содержание: C1 – квалификация водителя, C2 – дорожные условия, C3 – удельные затраты на эксплуатацию, C4 – условия эксплуатации, C5 – периодичность технического обслуживания, C6 – качество технического обслуживания и ремонта, C7 – качество конструкции автомобиля, C8 – качество эксплуатационных материалов и запасных частей, C9 – условия хранения, C10 – надежность и безопасность автомобиля.
Матрица W (2.4) с экспертными оценками силы влияний, в которой принималось c =1, имеет вид
4.2. Индексы важности концептов. Таблица 1 содержит девять пар векторов, связанных с вычислением индексов важности концептов C1, …, C9. Каждая пара содержит начальный вектор (3.4) и вектор (3.6) в установившемся режиме. Последний элемент второго вектора в каждой паре соответствует индексу важности концепта, например I(C1) = 0.686. Пошаговое изменение уровня выходного концепта (C10 – надежность и безопасность автомобиля) при вычислении индексов важности входных концептов (влияющих факторов) представлено на рис. 9. Диаграмма индексов важности концептов показана на рис. 10. Результаты вычисления индексов важности совместного влияния концептов сведены в табл. 2, например I(C1, C2) = 0.949.
Таблица 1.
Значения концептов в стационарном состоянии для различных начальных векторов
| Шаг | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 3040 | 0.022 | 0.000 | 0.000 | 0.000 | 0.187 | 0.000 | 0.000 | 0.000 | 0.000 | 0.68579 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 774 | 0.000 | 0.044 | 0.000 | 0.365 | 0.747 | 0.000 | 0.000 | 0.000 | 0.000 | 0.94834 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 3717 | 0.000 | 0.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.22707 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 3014 | 0.000 | 0.000 | 0.000 | 0.022 | 0.335 | 0.000 | 0.000 | 0.000 | 0.000 | 0.79115 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 5324 | 0.000 | 0.000 | 0.000 | 0.000 | 0.017 | 0.000 | 0.000 | 0.000 | 0.000 | 0.33491 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 3196 | 0.000 | 0.000 | 0.000 | 0.000 | 0.186 | 0.022 | 0.000 | 0.000 | 0.000 | 0.68912 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 4953 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.017 | 0.000 | 0.000 | 0.30912 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 2742 | 0.000 | 0.000 | 0.000 | 0.000 | 0.321 | 0.000 | 0.000 | 0.023 | 0.000 | 0.77418 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 3086 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.022 | 0.18667 |
Рис. 9.
Пошаговое изменение уровня надежности и безопасности системы при вычислении индексов важности влияющих факторов
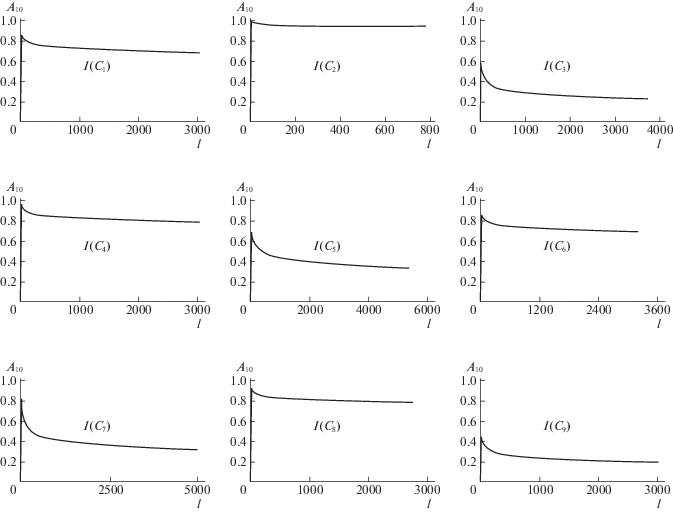
Таблица 2.
Индексы важности совместного влияния факторов
| Концепты | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|
| C1 | 0.949 | 0.686 | 0.801 | 0.686 | 0.730 | 0.335 | 0.786 | 0.255 |
| C2 | 0.948 | 0.948 | 0.948 | 0.950 | 0.949 | 0.950 | 0.948 | |
| C3 | 0.791 | 0.335 | 0.689 | 0.309 | 0.774 | 0.254 | ||
| C4 | 0.791 | 0.803 | 0.703 | 0.823 | 0.782 | |||
| C5 | 0.689 | 0.309 | 0.774 | 0.187 | ||||
| C6 | 0.356 | 0.788 | 0.294 | |||||
| C7 | 0.309 | 0.323 | ||||||
| C8 | 0.763 |
Заключение. Предложен метод ранжирования факторов риска с использованием НКК – нового и пока еще мало исследованного аппарата моделирования, который может найти применение в задачах анализа надежности и безопасности сложных систем со слабо определенной структурой: технических, экономических, военных и др. Иллюстрация метода выполнена на примере системы “водитель–автомобиль–дорога”.
В сравнении с деревьями отказов и логико-вероятностными моделями, получившими наибольшее распространение в анализе риска, предложенный подход обладает рядом преимуществ.
1. Отсутствуют ограничения бинарности событий (есть/нет) и независимости причин риска, связанных с отказами элементов и влияющими факторами.
2. Не требуется знание вероятностей событий, вместо которых можно использовать экспертную информацию об уровнях работоспособности элементов и уровнях влияния факторов риска, взаимодействующих между собой.
3. Построение НКК и ее корректировка гораздо проще, чем построение дерева отказов. Удобство состоит в том, что на основе единого ориентированного графа удается отобразить разнородные причины, приводящие к риску из-за ненадежности системы: человеческий фактор, качество техники и ее обслуживания, условия внешней среды и др.
Список литературы
Барлоу Р., Прошан Ф. Статистическая теория надежности и испытания на безотказность. М.: Наука, 1984.
Haasl D.F. Advanced Concepts in Fault tree Analysis. Proceedings of the System Safety Symposium. Seattle: The Boeing Company, 1965.
Рябинин И.А. Надежность и безопасность структурно-сложных систем. СПб.: Изд-во С.-Петерб. ун-та, 2007.
Соложенцев Е.Д. Сценарное логико-вероятностное управление риском в бизнесе и технике. СПб.: ИД “Бизнес-пресса”, 2004.
Соложенцев Е.Д. Управление риском и эффективностью в экономике. Логико-вероятностный подход. СПб.: Изд-во С.-Петерб. ун-та, 2009.
Белов П.Г. Моделирование опасных процессов в техносфере. М.: Изд-во Академии гражданской защиты МЧС РФ, 1999.
Адлер Ю.П., Маркова Е.В., Грановский Ю.П. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976.
Ishikawa K. Guide to Quality Control. London: Chapman and Hall, 1991.
Birnbaum Z.W. On the Importance of Different Components in a Multicomponent System // Multivariate analysis – 2 / Ed P.R. Krishnaiah. N.Y.: Acad. Press, 1969. P. 581–592.
Hong J.S., Lie C.H. Joint Reliability Importance of two Edges in undirected Network // IEEE Transaction on Reliability. 1993. V. 2. № 1. P. 17–23.
Губинский А.И. Надежность и качество функционирования эргатических систем. Л.: Наука, 1982.
Заде Л. Понятие лингвистической переменной и ее применение к принятию приближенных решений. М.: Мир, 1976.
Cai K.Y. Introduction on Fuzzy Reliability. Boston: Kluwer Acad. Publ., 1996.
Ротштейн А.П., Штовба С.Д. Нечеткая надежность алгоритмических процессов. Винница: Континент – ПРИМ, 1997.
Уткин Л.В., Шубинский И.Б. Нетрадиционные методы анализа надежности информационных систем. СПб.: Любавич, 1998.
Kosko B. Fuzzy Cognitive Maps // Intern. J. Man-Machine Studies. 1986. V. 24. P. 65–75.
Axelrod R. Structure of Decision: The Cognitive Maps of Political Elites. Princeton University Press, 1976.
Цыпкин Я.З. Основы информационной теории идентификации. М.: Наука, 1984.
Rotshtein A., Rakytyanska H. Fuzzy Evidence in Identification, Forecasting and Diagnosis. Berlin: Springer, 2012.
Ротштейн А.П. Выбор условий деятельности человека на основе нечеткой перфектности // Изв. РАН. ТиСУ. 2018. № 6.
Ротштейн А.П. Ранжирование элементов системы на основе нечеткого отношения влияния и транзитивного замыкания // Кибернетика и системный анализ. 2017. № 1. С. 68–78.
Kosko B. Neural Network and Fuzzy Systems. Englewood Cliffs. N.Y.: Prentice – Hall, 1992.
Бутенин Н.В., Неймарк Ю.И., Фуфаев Н.А. Введение в теорию нелинейных колебаний. М.: Наука, 1987.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления