Агрохимия, 2020, № 7, стр. 90-96

ВВЕДЕНИЕ

Динамику составляющих агроценоз процессов ранее изучали в рамках комплекса агрономических наук (почвоведение, агрохимия, растениеводство, защита растений) [1–3]. Соответствующие представления оставались на качественном (описательном) уровне, что частично тогда объясняли сложностью изучаемых процессов, недостатком экспериментальных сведений о распределениях элементов питания растений, недостатком сведений о физике почв, физиологии и биохимии растений, в том числе и ограниченностью математических моделей, которые были бы способны к решению подобного рода задач. В результате этого наукоемкие технологические рекомендации, позволяющие воссоздать цикл процессов, также в большинстве случаев носили качественный характер. Отдельные количественные указания (например, применение рекомендуемых доз внесения удобрений или оросительных норм) часто приводили даже к отрицательным или к непрогнозируемым результатам.

Доступность высокопроизводительной компьютерной техники и экспериментального репрезентативного выборочного материала, новые сведения о процессах в ризосфере и развитие информационных технологий создали базу для качественного перехода к использованию методов математического моделирования,

Цель создания таких моделей состоит в создании аппарата для расчета пространственно-временнóй динамики биомассы растений и элементов их питания как минерального, так и органического происхождения. При его построении следует учитывать влияние почвенных и метеорологических условий на продукционный процесс, рост растений, их развитие и формирование конечного урожая. В большей степени отмеченные качества реализованы в работах [4–6].

Наличие репрезентативной выборки данных только отдельных характеристик (температуры, влажности, содержания питательных веществ и др.) обусловлено трудоемкостью проведения опытов в полевых условиях. Поэтому для задачи моделирования было важно синтезировать имеющийся экспериментальный материал, найти взаимосвязи между разрозненными фактами, выявить основные факторы, наиболее важные для самого процесса моделирования [7].

Для оценки целесообразности применения того или иного математического аппарата следует выполнить классификацию/типизацию математических моделей, которая определяется уровнем детализации рассматриваемых явлений, способами их формального представления [8]. Разделение моделей развития растений на решения теоретических и практических задач предложено в работе [9]. Отсутствие грани между ними обусловливает неуместность такой классификации. Разделение моделей на основании различий процессов метаболизма растений и процессов их регуляции выполнено в работе [10]. Поскольку оба разделения используют однотипные уравнения, то такая классификация видится не вполне приемлемой. Естественной видится типизация на основе различий сущностей соответствующих математических аппаратов, в данном случае – статистических и динамических моделей [11–15].

СТАТИСТИЧЕСКИЕ МОДЕЛИ

Статистические модели применяют при допущении, что рассматриваемые процессы определяются преобладающей регулярной и существенно в меньшей степени – случайной составляющей. Совокупность этих моделей охватывает такие области, как эмпирические модели, корреляционный и факторный анализы, анализ временных рядов и др. [2, 16, 17]. Запись уравнения множественной регрессии имеет вид

где $Y$ – зависимая переменная, которая определяется линейной комбинацией независимых переменных (так называемых предикторов) {${{X}_{i}}$, $i = 1{\kern 1pt} - {\kern 1pt} n$}; {${{\beta }_{i}}$, $i = 0{\kern 1pt} - {\kern 1pt} n$} регрессионные коэффициенты (оцениваются на основании выборочных данных); $\varepsilon $ характеризует случайную ошибку модели (1) (как правило, принимается ее нормальное распределение с нулевым математическим ожиданием определенной дисперсией).

Модели (1) широко применяют во всех областях изучения агроэкосистем. В работе [18] их использовали для изучения влияния радиации на растительный покров, в [19] – динамики органического углерода пахотных почв Нечерноземной зоны России, в [20] – выделения углерода из материнской луковицы тюльпана в его развивающуюся надземную часть и в луковицу-детку в период от появления всходов до отмирания листьев. Воздействия метеорологических условий среды южного чернозема на урожай зеленой массы кукурузы также изучали при помощи модели (1) [21].

Область применения регрессионных моделей ограничена случаем их функционального представления (1). При этом в качестве предикторов могут выступать некоторыми функциями наблюдаемых независимых переменных.

ДИНАМИЧЕСКИЕ МОДЕЛИ

Динамические модели характеризуют процесс, где изменение времени полагается непрерывным. В их основе лежат детальные представления о механизмах рассматриваемых явлений.

Модели локальной динамики биомассы растений. Указанный тип моделей следует допущению о гомогенном пространственном распределении растений, и биомасса (показатель роста, длина и т.д.) растений – непрерывно дифференцируемая функция. При их построении полагают, что относительная/удельная динамика такого показателя пропорциональна определенной функции:

где левая часть – это удельная скорость изменения $Y~$ в единицу времени, а правая часть – удельная или относительная скорость изменения в пересчете на единицу биомассы. Аргументами этой функции может выступать некоторая совокупность показателей для других видов растений, что отражает межвидовые отношения растений.

Уместно заметить, что размерность правой части обратна размерности времени. Поэтому показателем динамики системы может выступать не только биомасса растения, но и его длина, площадь сечения и т.п. Но в каждом отдельном случае правая часть имеет соответствующую динамике этого показателя характерную для него структуру. Тогда балансовое уравнение для локальной динамики принимает вид

где i указывает вид растения, G_i и H_i – функции рождаемости и смертности. Если в агроценозе участвуют несколько видов растений, то при наличии между ними межвидовых отношений (конкуренции, кооперации и т.п.) эти функции, кроме различных ${{Y}_{i}}$, могут зависеть от показателей для других видов. При этом они могут также зависеть от ряда показателей, которые определяют состояние среды (например, температурный и водный режим ризосферы). Поскольку при росте биомассы растет конкуренция растений за ограниченный ресурс и, стало быть, смертность/деградация растений, то ${{H}_{i}}$ – монотонно возрастающая функция ${{Y}_{i}}$. Во многих случаях ${{G}_{i}}$ определяется физиологическими пределами рождаемости [22] и не зависит от текущего ${{Y}_{i}}$, так что ${{G}_{i}}\sim {{Y}_{{\max ,i}}}$. Суммируя перечисленное, уравнение для локальной динамики растений принимает вид где ${{\mu }_{i}}$ и ${{\beta }_{i}}$ – некоторые динамические функции параметров состояния среды (в этом случае – температуры T и влажности W). Характер изменения этой функции хорошо известен [22]: в естественных условиях среды кривая ${{Y}_{i}}\left( t \right)$ в начальный период своего изменения линейна, далее следует ее перегиб, за которым идет нелинейный участок с выходом на ее максимальную величину. Модификации этого уравнения относятся к типу так называемого уравнения Ферхюльста [11], а сама кривая именуется логистической кривой.

Для представления динамики линейного размера нескольких типов культур (гречихи, просо, тюльпана) в работе [23] использовано подобное (3) уравнение (для простоты изложения нижний индекс опущен):

где l – текущая высота растения (см), ${{l}_{{\max }}}$ – теоретическая максимальная высота (см), которую может достигнуть растение по окончанию роста, ${\mu \;}$ –константа, T = T(t) – текущая температура, T_min = = 10°C и T_max = 30°C (согласно наблюдениям). В модели принимается, что вне рамок этого диапазона температур растение прекращает свой рост, а не погибает. В этот период температура хорошо аппроксимируется выражением где ω – частота колебаний. В модели полагается, что где ${{T}_{{{\text{mid}}}}} = \left( {{{T}_{{\min }}} + {{T}_{{\max }}}} \right){\text{/}}2$. Параметры $\mu $ и ${{l}_{{\max }}}$ оценивали на основании 13-летней выборки экспериментальных наблюдений. Сопоставление выборочных и модельных распределений показывало их высокое согласие (коэффициент корреляции между ними >0.9).

Модель скорости поглощения растением элементов минерального питания обычно строится на основании уравнения Михаэлиса–Ментена, которое характеризует динамику потребления субстрата. При его использовании принимается допущение, что образование продукта реакции идет быстро и необратимо. Его запись принимает вид

где ${{{v}}_{N}}(k)$ – скорость поглощения питательного минерального субстрата единичной поглощающей поверхностью корней растения из слоя k, ${{V}_{{\max }}}$ – максимальная скорость поглощения (мг/см²/сут). В этом случае ${{K}_{N}}$ – видоспецифическая константа, численно равная концентрации субстрата, при которой скорость роста равна половине максимальной (константа полунасыщения или константа Михаэлиса–Ментена) [24]; ${{C}_{N}}(k)$ – концентрация субстрата в k-слое почвы. В работе (4) полагают пропорциональность поглощения элементов минерального питания их содержанию в ризосфере. Для оценки суммарной скорости применяют сумму скоростей по всей поглощающей поверхности корней по слоям почвы: где ${{B}_{R}}(k)$ – биомасса корней в k-м слое почвы, ${{K}_{R}}$ – поглощающая поверхность единицы биомассы корней, ${{{v}}_{{{\text{SUM}}}}}$ – суммарное количество элементов питания, поглощенного всей корневой системой растений за 1 сут (кг/га/сут), N – число слоев почвы, занятых корнями.

Модели сообщества микроорганизмов. Присутствие в ризосфере сообществ микроорганизмов обусловлено выделениями корневой системы растений питательных для них субстанций. Например, стебли и листья выделяют углеводы и органические кислоты. Микроорганизмы также поселяются на поверхности различных органов растений, образуя эпифитные сообщества, внедряясь в ткани растений [25]. Примером такой системы выступает модель динамики биомассы микроорганизмов-аммонификаторов, которые выполняют основную роль в минерализации органического вещества почвы [26]:

где ${{V}_{g}}$ – скорость роста микробной массы ${{M}_{b}}$ и ${{V}_{d}}$ – скорости выделения C в почву; ${{C}_{a}}$ – баланс C, выделенного в воздушное пространство; $\rho $ – коэффициент утилизации; ${{V}_{\Gamma }}$ – скорость минерализации гумуса в углеродных единицах; ${{N}_{{\min }}}$ – общий баланс азота; ${{R}_{\Gamma }}$ – соотношение C : N в гумусе; ${{R}_{{mb}}}$ – отношение C : N в клетках бактерии. Первые 2 уравнения определяют баланс C при минерализации органического вещества в почве: первое из них описывает изменение биомассы микроорганизмов через их рост и отмирание, а второе – баланс C, выделенного в воздушное пространство через минерализацию гумуса и отмирание органики. Третье уравнение определяет баланс N при разложении органики, которое пропорционально скорости минерализации гумуса, скорости роста микробной массы и отмирания бактерий.

Поскольку скорость ${{V}_{\Gamma }}$ возрастает с ростом ${{M}_{b}}$, то естественно полагать их пропорциональность, т.е. ${{V}_{{\Gamma }}} = \alpha {{M}_{b}}$. Cмертность бактерий определяются емкостью жизненного цикла популяции. Тогда уравнение динамики биомассы в углеродных единицах ${{M}_{b}}$ принимает вид

где $\beta $ – константа, а ${{C}_{\Gamma }}$ – баланс органического C. Согласно этому уравнению, в начальный период следует плавный рост ${{M}_{b}}$, затем нелинейный участок перегиба и далее ее рост до своей предельной величины ${{C}_{\Gamma }}{\text{/}}\beta $.

В представлении этой модели питательным субстратом выступает преимущественно гумус, хотя это справедливо для любого попадающего в почву органического субстрата, в том числе растительным остаткам и органическим удобрениям. В момент внесения их в почву равновесие нарушается, и начинается переходный процесс. Повышенная концентрация C приводит к росту биомассы бактерий. Как правило, рост сопровождается иммобилизацией (созданием определенной неподвижности) N из минерального пула (сообщества). Но этот процесс кратковременный: согласно уравнению Ферхюльста, вскоре следует новое равновесное состояние, где биомасса бактерий стабилизируется на более высоком уровне, и соответственно увеличивается содержание в ней C и N.

Модели агроценозов. Для построения модели агроценоза суммируют представленные выше сведения и допущения. В частности, динамика биомассы следует модификации уравнения Ферхюльста, где функция рождаемости ${{G}_{i}}$ из уравнения (2) – возрастающая функция субстрата. Его динамика определяется содержанием в ризосфере соответствующих минеральных элементов. В случае включения в рассмотрение микроорганизмов, как звена трансформации минералов в элементы питания растений, в систему следует добавить соответствующее уравнение их динамики.

Модель динамики биомассы растения на примере динамики проточной системы приведена в работе [27]:

где ${{Y}_{i}}$ – биомасса i-го вида из общего сообщества m-видов; n – группы сходных элементов минерального питания (азота, фосфора, калия, кремния и т.п.),  j – элемент этой группы; ${{Z}_{j}}$ – содержание минеральных веществ в среде; ${{{v}}_{{ij}}}({{Z}_{j}},{{q}_{{ij}}})$ – удельная скорость потребления микроорганизмами питательных элементов; ${{\mu }_{{ij}}}({{q}_{{ij}}})$ – удельная скорость роста биомассы в зависимости от содержания питательных элементов в этих клетках ${{q}_{{ij}}}$; ${{\mu }_{i}}\left( {{{Q}_{i}}} \right)$ определяется по принципу “узкого места” Либиха по формуле ${{\mu }_{i}}\left( {{{Q}_{i}}} \right)$ = $\min {{\mu }_{{ij}}}\left( {{{Q}_{{ij}}}} \right)$; D – скорость протока вещества в системе через ${{z}_{0}}$ – содержание минеральных веществ во входящем потоке.

Первое уравнение определяет динамику биомассы проточной системы, которая пропорциональна содержанию в клетках питательных элементов. Эти элементы выступают основным фактором роста популяции микроорганизмов, тогда как уменьшение биомассы происходит за счет ее естественной убыли $D$. Второе уравнение определяет динамику содержания в среде минеральных веществ, которая зависит от разницы их начального содержания и естественной убыли, а также их потребления микроорганизмами из этой среды. Последнее уравнение определяет динамику содержания в клетках питательных веществ. Согласно этим уравнениям, изменение стратегии поведения изучаемого объекта определяется не только окружающей средой, но и состоянием самого объекта. Важную роль играет скорость протока вещества. Недостаток этого подхода заключается в том, что в качестве одного из основных факторов исключен блок отмершей органики. Решение подобной задачи было выполнено в работе [1], где была построена замкнутая модель динамики массы фитопланктона, минеральных веществ и отмершей органики.

Концептуальная модель системы, динамическими компонентами которой выступают растения, сообщества микроорганизмов, элементы минерального питания подвижной и неподвижной форм, органическое вещество почвы приведена в работе [29]. Поскольку в настоящее время отсутствует соответствующий экспериментальный материал, то в этом случае далее рассмотрен ее отдельный блок кинетики минерального питания и роста растения. Соответствующий экспериментальный материал с разрешения автора заимствован из работы [30].

При построении модели принимали такие допущения:

1 – динамика биомассы определяется ее естественной скоростью роста и влиянием элементов минерального питания, а также действием подобного в модели Ферхюльста фактора ее самолимитирования;

2 – относительная скорость изменения содержания элементов минерального питания в растении на единицу его биомассы пропорциональна содержанию этого элемента в ризосфере, которое растение в дальнейшем может утилизировать;

3 – ограниченность объема тела растения обусловливает его определенную “емкость” элементов питания, которое растение может утилизировать из ризосферы (больше, чем некоторое количество элементов питания растение не может содержать в своем теле);

4 – в самом растении учитывают также взаимодействия между элементами как объектами химического происхождения (конкуренция, симбиоз и т.п.).

Следуя этим допущениям, модель динамики системы почва–удобрение–растение в этом случае можно записать уравнениями

где $B = B\left( {t,k} \right)$ – биомасса растения в момент времени t для почв с k-м содержанием ${{{\text{K}}}_{2}}{\text{O}}$; ${{p}_{0}}$ характеризует естественный прирост биомассы; ${{p}_{1}}$, ${{p}_{2}}$, ${{p}_{3}}$ – коэффициенты при слагаемых, которые характеризуют прирост биомассы вследствие влияния элементов минерального питания; ${{p}_{4}}$ – коэффициент при члене, который характеризует самолимитирование роста биомассы; ${{C}_{i}}$ – содержание i-го элемента в надземной части растения, i = 1–3 (последовательно: калий, фосфор и азот, единицами измерения которых выступают весовые доли ${{{\text{K}}}_{{\text{2}}}}{\text{O}}$, P₂O₅ и N); ${{C}_{{0,i}}}$ – начальное содержание i-го элемента в ризосфере; ${{q}_{{i,0}}}$ – коэффициент пропорциональности (пункт 2 допущений), он определяет ту долю содержания элементов питания в ризосфере, которая может быть утилизирована растением; ${{q}_{{i.i}}}$ характеризует предельную “емкость” содержания элементов питания в теле растения; ${{q}_{{i.j}}}$  j ≠ i – коэффициенты пропорциональности при членах, посредством которых в самом растении учитывают взаимодействия между собой элементов минерального питания.

Первое уравнение системы соответствует модификации уравнения Ферхюльста: в рамках этого уравнения сумма первых 4-х членов характеризует прирост биомассы вследствие естественного прироста и воздействия на динамику растения элементов его питания.

Оценка предельного содержания в растении i‑го вида элементов минерального питания следует из приравнивания к нулю правой части 2-го уравнения. В первом приближении допускается, что предельные содержания определяются системой линейно алгебраических уравнений, определяющей стационарное состояние системы. Тогда, следуя методике нелинейного оценивания параметров [31], на основе статистических данных [30], были подсчитаны коэффициенты модели и построены соответствующие распределения.

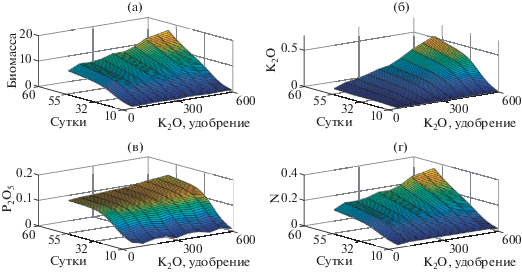
На рис. 1 представлены модельные распределения биомассы растений и содержания в ней элементов минерального питания. Анализ распределений показывает существенное превышение среди остальных соответствующего азоту ${{{\text{С}}}_{3}}~$ коэффициента ${{p}_{3}}$, что указывает на его ведущую роль в процессе обеспечения роста биомассы растения, что тем самым согласуется с установившейся закономерностью накопления питательных веществ в процесса роста растения [2]. Тот факт, что растение выносит в пересчете на сухую массу от 0.5 до 2% почвенного азота, около 0.2% фосфора и 0.9% калия, подтверждается взаимным соотношением коэффициентов друг с другом ${{p}_{1}}{\text{/}}{{p}_{2}}{\text{/}}{{p}_{3}}$ [1]. Повышение содержания ${{{\text{K}}}_{2}}{\text{O}}$ также способствует росту содержания рассмотренных в данной работе остальных элементов минерального питания.

ЗАКЛЮЧЕНИЕ

Выполнен анализ моделей динамики биомассы растений, где элементами их питания могут выступать продукты трансформации ризосферными микроорганизмами соответствующих минералов. Выбор объектов для обзора обусловлен их характерной направленностью. В этих моделях не учитывают свойственную практическим ситуациям пространственную неоднородность, что является типичным для рассмотренной области исследований. В частности, не учитывают факт направленности следования микроорганизмов ризосферы по градиенту распределения биомасс. Кроме того, не учитывают разделения минерального питания на элементы растворимых и нерастворимых форм, взаимные переходы этих элементов из одной формы в другую. Отмеченные вопросы составляют предмет последующих исследований.