Агрохимия, 2020, № 8, стр. 86-93

ВВЕДЕНИЕ

В работе [1] представлена концепция управления агротехнологиями в системах точного земледелия (ТЗ), которая определяет 4 уровня управления связанных между собой задач. Верхний уровень является стратегическим и реализуется в годовом масштабе времени, охватывая севообороты. Второй уровень, реализуемый в одном интервале вегетации в суточном масштабе времени, является программным и разрешает компромисс между конечным результатом и затрачиваемым на его получение ресурсом. Два нижних уровня управления, реализуемые в реальном времени, отрабатывают оптимальные решения, полученные на верхних уровнях с учетом меняющихся условий вегетации и технических особенностей исполнительных технологических машин и устройств.

В работах [2, 3] была рассмотрена задача управления параметрами химического состояния почвы на стратегическом уровне, в которой синтезировались оптимальные стратегии внесения минеральных удобрений и мелиорантов во все годы используемого севооборота. В настоящей работе рассмотрен программный уровень, где управление заключается в выборе оптимальной последовательности технологических операций, определении их размера в заданное время выполнения в течение одного вегетационного периода. Такими операциями является внесение минеральных удобрений и поливы, обеспечивающие доступность элементов питания растениями в посеве возделываемой культуры. В работах [2, 3] эту задачу решали на модельной культуре, в качестве которой были исследованы многолетние травы, идущие на приготовление грубых волокнистых кормов для молочного скота. Цель работы – дальнейшее развитие теоретической базы программного управления параметрами почв под культурами, претерпевающими в период вегетации несколько фенологических фаз развития. Таковой культурой в этом случае служила яровая пшеница.

МЕТОДИКА ИССЛЕДОВАНИЯ

Фундаментальной основой для решения задач программного управления являются математические модели, описывающие динамику параметров состояния объекта управления (ОУ), в нашем случае – это сельскохозяйственное поле под посевом яровой пшеницы. При этом рассматриваемый ОУ характеризуется как континуальными параметрами состояния, к которым могут быть отнесены параметры состояния биомассы самого посева и почвенной среды, так и структурными состояниями, к которым могут быть отнесены фенофазы. Несмотря на то, что наступление фенофаз зависит от многих условий, при решении задачи программного управления удобно воспользоваться временными шкалами. Существует несколько таких шкал для определения времени наступления фенофаз злаковых культур: Фикеша (1954), Келлера и Баггиолини (1954), Задокса, Чанга и Конзака (1974) и др. В настоящей работе использовали шкалу Задокса, которая для яровой пшеницы имеет следующий вид в суточном времени t:

Весь период вегетации в зависимости от структуры биомассы посева может быть разделен на 2 интервала времени: со 2-й по 9-ю и с 9-й по 13‑ю фенофазы.

Для первого интервала времени для фенофаз со 2-й по 9-ю модель динамики параметров структуры биомассы посева имеет следующий вид [4]:

где приняты следующие обозначения: x_1m – средняя для площади поля плотность общей биомассы посева, включающая сухое вещество и сырую массу (влагу), ц/га; x_2m – средняя для площади поля плотность сырой массы посева, ц/га; внешними возмущениями в обоих блоках являются  f₁ – среднесуточная температура воздушной среды, °C;   f₂ – среднесуточный уровень радиации, Вт/(м² ч); f₃ – среднесуточная интенсивность осадков, мм; параметры химического состояния почвы: ${{v}_{{\text{N}}}}$ – содержание азота в почве, ${{v}_{{\text{K}}}}$ – содержание калия в почве, ${{v}_{{\text{P}}}}$ – содержание фосфора в почве; ${{v}_{{{\text{Mg}}}}}$ – содержание магния в почве; ${{v}_{5}}$ – влагозапас в почве, мм.

Модель (1) для удобства дальнейшего применения удобно представить в канонической символьной векторно-матричной форме, где все переменные объединены в векторы, а параметр – в соответствующие матрицы

Для 2-го интервала времени для фенофаз с 9-й по 13-ю модель динамики параметров структуры биомассы посева имеет следующий вид:

В этом блоке структуры биомассы параметрами состояния являются: x_1u – средняя для площади поля плотность общей биомассы посева, включающей в себя массу колосьев и стеблей, ц/га; x_2u – средняя для площади поля плотность сырой массы посева, ц/га; x_3u – средняя для площади поля плотность массы колосьев, включающей в себя массу стержня колоса, зерна, остьев, колосовых чешуек, ц/га; внешними возмущениями в обоих блоках являются: f₁ – среднесуточная температура воздушной среды, °C; f₂ – среднесуточный уровень радиации, Вт/(м² ч); f₃ – среднесуточная интенсивность осадков, мм; параметры химического состояния почвы: ${{{v}}_{{\text{N}}}}$ – содержание азота в почве, ${{{v}}_{{\text{K}}}}$ – содержание калия в почве, ${{{v}}_{{\text{P}}}}$ – содержание фосфора в почве; ${{{v}}_{{{\text{Mg}}}}}$ – содержание магния в почве; ${{{v}}_{5}}$ – влагозапас в почве, мм.

Каноническая символьная векторно-матричная форма модели (3) имеет вид:

Модель динамики параметров состояния почвы для фенофаз со 2-й по 9-ю имеет следующий вид:

или в компактной символьной форме

Модель параметров химического состояния почвы для фенофаз со 9-й по 13-ю:

где ${{d}_{{\text{P}}}}(t)$, ${{d}_{{\text{K}}}}(t)$, ${{d}_{{\text{N}}}}(t)$ ${{d}_{W}}(t)$ – дозы внесения элементов питания, соответственно фосфора – P, калия – K, мелиоранта – Ca, азота – N, магния – Mg, кг/га и норма полива, мм; ${{a}_{{11}}}$–${{a}_{{33}}}$, ${{b}_{2}}$–${{b}_{3}}$, ${{c}_{1}}$–${{c}_{3}}$ – параметры модели, оцениваемые по экспериментальным данным; t – суточное время.

В моделях (5), (7) введены параметры m_ij – связи показателей химического состояния почвы и состояния биомассы посева, которые учитывают вынос элементов питания и влаги из почвы. В моделях (6), (8) эти параметры объединены в матрицы M₂₉, M_9,13.

Модель (7) в компактной символьной векторно-матричной форме имеет вид:

В соответствии с разработанной концепцией управления агротехнологиями рассматриваемая задача решается в 2 этапа [1]. На первом этапе в качестве управляющих переменных применяют параметры состояния почвы, и находят программу их изменения во всем временнóм интервале вегетации, обеспечивающую достижение поставленной цели управления. На 2-м этапе находят последовательность технологических операций, обеспечивающих минимальное отклонение параметров почвы от оптимальной программы, полученной на первом этапе. Такая декомпозиция задачи программного управления существенно упрощает синтез оптимальных программ управления, учитывая тот факт, что почва, как среда, через которую реализуется управление, представляет собой самостоятельную сложную многомерную динамическую систему. Кроме того, результаты оптимизации на первом этапе представляют самостоятельный интерес, т.к. позволяют оценить потенциальный уровень урожайности культуры.

В соответствии с методикой динамического программирования [6], задача первого этапа решается от конца вегетационного периода к его началу. Поэтому и целью управления в этой задаче является получение заданной урожайности культуры в конце интервала вегетации, при выполнении условия получения заданной структуры всего биологического урожая, а именно, требуемого соотношения между массой стеблей (соломы) и колоса (зерна и мякины), а также достижение требуемой влажности зерна.

В обозначенных параметрах состояния формально цель управления выглядит следующим образом:

где: U* – заданная урожайность зерна, ц/га.

Критерий оптимальности для межвегетационного периода с 9-й по 13-ю фенофазу, отвечающий поставленной цели, имеет следующий вид:

где $\operatorname{X} _{U}^{{\rm T}} = \left[ {\begin{array}{*{20}{c}} {{\text{1}}{\text{.1}}U}&{{\text{0}}{\text{.15}}U}&U \end{array}} \right]$ – вектор, компонентами которого являются: общая биомасса, сырая масса, масса зерна (урожай); ${{G}_{u}} = {{\left[ {\begin{array}{*{20}{c}} {{{g}_{{11}}}}&0&0 \\ 0&{{{g}_{{22}}}}&0 \\ 0&0&{{{g}_{{33}}}} \end{array}} \right]}_{u}}$ – весовая матрица массовых и качественных составляющих критерия.

Критерий (9) представляет собой взвешенную сумму квадратов отклонения прогнозных величин в конце периода вегетации вектора ${{\operatorname{X} }_{u}}({{T}_{{13}}})$ от заданной величины $\operatorname{X} _{u}^{{\text{*}}}$. Формируемая программа управления должна обеспечивать минимум этого критерия.

Результатом решения задачи управления является программа оптимального изменения параметров состояния почвы, а также начальные условия параметров состояния посева перед началом фазы колошения, которые являются терминальными показателями для параметров состояния предшествующей фенологической фазы.

В соответствии со схемой принципа максимума [6], гамильтониан для системы (4) и критерия оптимальности (9) имеет вид:

где Ψ_u – вектор сопряженных переменных, являющийся решением следующей динамической системы:

С учетом введенных обозначений пошаговый алгоритм решения задачи представляет собой следующую последовательность операций.

Шаг 0. Устанавливают календарное время начала T₉ и конца T₁₃ межфазового периода формирования урожая, чем задают интервал времени решения задачи. Задают начальные условия: вектор параметров состояния посева X_u(T₉) и начальную программу управления V(t) = V₀. Принимают средние многолетние величины вектора климатических возмущений $\operatorname{F} ({{T}_{9}},{{T}_{{15}}})$. Задают минимальную величину критерия оптимальности (9), при котором алгоритм останавливается. Принимают циклическую переменную алгоритма i = 0.

Шаг 1. Решают систему ${{\dot {X}}_{{ui}}} = {{A}_{u}}{{\operatorname{X} }_{{ui}}}(t)$ + B_uV_i(t) + + C_uF(t) в прямом времени в интервале $t \in ({{T}_{9}},{{T}_{{15}}})$, в результате чего получают векторный массив X_ui(t).

Шаг 2. Решают систему

в обратном времени в интервале $t \in ({{T}_{{15}}},{{T}_{9}})$, в результате чего получают векторный массив Ψ_ui(–t), который разворачивается во времени Ψ_ui(t).

Шаг 3. Находят очередное приближение программы управления вектором параметров химического состояния почвы:

Шаг 4. Находят очередное приближение начальных условий на границе фенофаз

Шаг 5. Принимают циклическую переменную i = i + 1, осуществляют переход к шагу 1, вплоть до выполнения условия

Теперь подобную задачу решают и в интервале, предшествующем фазе колошения.

Шаг 6. Принимают конечные условия для межвегетационного периода $t \in ({{T}_{1}},{{T}_{9}})$ ${{\operatorname{X} }_{m}}({{T}_{9}})$ = = $\operatorname{H} \operatorname{X} _{{ui + 1}}^{*}({{T}_{9}})$, где $\operatorname{H} = \left[ {\begin{array}{*{20}{c}} 1&{\begin{array}{*{20}{c}} 0&0 \end{array}} \\ 0&{\begin{array}{*{20}{c}} 1&0 \end{array}} \end{array}} \right]$ – матрица связи.

Шаг 7. Принимают критерий оптимальности для межвегетационного периода с первой по 9-ю фенофазы:

Критерий (12) имеет такой же смысл и форму, как и критерий (9), с той лишь разницей, что его определяют для 9-й фенофазы.

Шаг 8. Устанавливают календарное время начала T₁ и конца T₉ межфазового периода формирования урожая. Задают начальные условия: вектор параметров состояния посева X_m(T₁) и начальную программу управления V(t) = V₀. Принимают средние многолетние величины вектора климатических возмущений $\operatorname{F} ({{T}_{1}},{{T}_{9}})$. Принимают циклическую переменную i=0.

Шаг 9. Решают систему ${{{\dot {X}}}_{{mi}}} = {{{\text{A}}}_{m}}{{{\text{X}}}_{{mi}}}(t)$ + + B_mV_i(t) + C_mF(t) в прямом времени в интервале $t \in ({{T}_{1}},{{T}_{9}})$, в результате чего получают векторный массив X_mi(t).

Шаг 10. Решают систему

в обратном времени в интервале $t \in ({{T}_{9}},{{T}_{1}})$, в результате чего получают векторный массив Ψ_mi(–t), который разворачивается во времени Ψ_mi(t).

Шаг 11. Находят очередное приближение программы управления вектором параметров химического состояния почвы:

Шаг 12. Принимают циклическую переменную i = i + 1, осуществляют переход к шагу 1, вплоть до выполнения условия

В результате решения задачи первого этапа формируется оптимальная программа изменения параметров состояния почвы $\operatorname{V} {\text{*}}(t)$ во всем интервале вегетации, а также программа потенциального развития посева $\operatorname{X} {\text{*}}(t)$, которая получается при подстановке оптимальной программы изменения параметров состояния почвы в модели параметров состояния посевов (2), (4).

Достижимой целью управления на 2-м этапе общего решения задачи является: “обеспечение наиболее близкого приближения к оптимальной программе изменения содержания элементов питания и влагосодержания в почве, полученной на первом этапе за счет независимого выбора размеров подкормок и поливов”. При этом внесение удобрений и поливы проводят в фиксированные моменты времени наступления следующих фенологических фаз: s = 3 (кущение), s = 9 (колошение), s = 10 (цветение), s = 11 (молочная спелость).

В свою очередь задача управления на этом этапе решается в 2-х интервалах времени: с 1-й по 9-ю и с 9-й по 13-ю фенофазу. Она заключается в нахождении последовательности векторов доз внесения удобрений и поливов, доставляющих минимум следующим критериям:

где ${{\operatorname{C} }_{D}}$ – вектор стоимостей единиц управления.

Гамильтонианы систем моделей (6), (8) и критериев (13), (14) имеют следующий вид:

Алгоритм нахождения этих последовательностей имеет следующий вид.

Шаг 1. Задают циклическую переменную i = 0, начальное приближение последовательностей ${\text{D}}_{{0,1,9i}}^{*}(t)$ = {D_0i(t₃), D_0i(t₉)}, ${\text{D}}_{{0,10,11i}}^{*}(t)$ = {D_0i(t₁₀), D_0i(t₁₁)}, средние многолетние величины климатических параметров F(t), минимальную величину критериев оптимальности δ, при которой алгоритм останавливается.

Шаг 2. Для программы потенциального развития посева $\operatorname{X} _{m}^{*}(t)$, полученной на первом этапе, в прямом времени в интервале $t \in ({{T}_{1}},{{T}_{9}})$, ${{\operatorname{V} }_{{1,9,i}}}({{T}_{2}})$ = = V_1,9,i0 решают систему:

в результате чего получают векторный массив ${{\operatorname{V} }_{{1,9,i}}}(t)$.

Вычисляют критерий (13) и если ${{J}_{{1,9,i}}}$ < δ, то останавливаюся, иначе происходит переход к шагу 5.

Шаг 3. Для программы потенциального развития посева ${\text{X*}}(t)$, полученной на первом этапе, в прямом времени в интервале $t \in ({{T}_{9}},{{T}_{{13}}})$, ${{\operatorname{V} }_{{9,13,i}}}({{T}_{2}})$ = V_9,13,i0 решают систему:

в результате чего получают векторный массив ${{\operatorname{V} }_{{9,13,i}}}(t)$.

Вычисляют критерий (14) и если ${{J}_{{9,13,i}}}$ < δ, то останавливаются, иначе происходит переход к шагу 4.

Шаг 4. Решают системы для сопряженных переменных:

в обратном времени в интервале $t \in ({{T}_{9}},{{T}_{1}})$, ${{\Psi }_{{1,9,i}}}({{T}_{9}}) = 0$, в результате чего получают векторный массив Ψ_1,9,i(–t), который разворачивается во времени Ψ_1,9,i(t); в обратном времени в интервале $t \in ({{T}_{{13}}},{{T}_{9}})$, ${{\Psi }_{{9,13,i}}}({{T}_{{13}}}) = 0$, в результате чего получают векторный массив Ψ_9,13,i(–t), который разворачивается во времени Ψ_9,13,i(t).

Шаг 5. Находят очередные приближения векторов доз внесения удобрений и поливов D*(t)_i+1:

вычисляют критерий оптимальности J_1,9, если условие J_1,9,i ≤ δ не выполняется, то циклическую переменную принимают равной i = i + 1 и осуществляют переход к шагу 2, вплоть до выполнения условия J_1,9 ≤ δ: вычисляют критерий оптимальности J_9,13, если условие J_9,13 ≤ δ не выполняется, то циклическую переменную принимают равной i = i + 1 и осуществляют переход к шагу 3, вплоть до выполнения условия J_9,13,i ≤ δ.

АПРОБАЦИЯ

Для апробации предложенной теории использовали экспериментальные данные опытного полигона Агрофизического НИИ за период 2012–2017 гг., по которым строили базовые математические модели. В отсутствии на этом полигоне систем орошения эти данные дополнили результатами, полученными путем генерации посредством базовых моделей, в которых учитывали поливы во всех фенофазах посева яровой пшеницы.

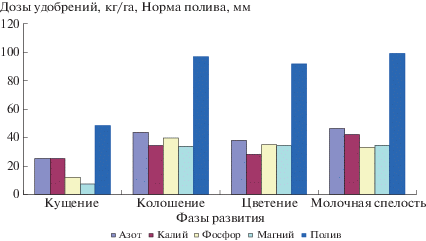
На графиках (рис. 1) представлена динамика посева яровой пшеницы во всем интервале вегетации при формировании оптимальной последовательности доз внесения удобрений и поливов для заданного урожая 50 ц/га во всех выбранных фенофазах (рис. 2). Эффективность управления оценивали величинами критерия оптимальности (12) в фенофазы: s = 3 (кущение) – J₃ = 1.69 (ц/га)², s = 9 (колошение) – J₉ = 1.33 (ц/га)², s = 10 (цветение) – J₁₀ = 1.3 (ц/га)², s = 11 (молочная спелость) – J₁₁ = 1.2 (ц/га)². Тенденция к уменьшению величины критерия отражала увеличение точности воспроизводства оптимальной программы изменения параметров почвы, полученной на первом этапе решения общей задачи управления. Полученные результаты соответствовали используемым экспериментальным данным и выбранной последовательности фенофаз. Для других данных и другой последовательности фенофаз результаты будут иными. Сравнение эффективности таких вариантов является предметом самостоятельного исследования. В задачу данной работы входил только анализ работоспособности предложенной теории и алгоритмов управления.

ЗАКЛЮЧЕНИЕ

Предложена новая теория и алгоритм программного управления состоянием посевов яровой пшеницы, апробированная по экспериментальным данным. Их основная особенность заключается в том, что общую задачу управления решают в 2 этапа, на первом из которых синтезируют оптимальную программу изменения параметров почвы, обеспечивающую достижение заданного результата, на втором этапе находят оптимальную последовательность технологических операций по внесению удобрений и поливов, выполняемую по заранее выбранным фенологическим фазам развития культуры. Указанная последовательность обеспечивает достижение заданной урожайности культуры и структуры биомассы посева. Разработанный на основе предложенной теории программно-технический комплекс может стать эффективным цифровым инструментарием для современного агронома.