Акустический журнал, 2019, T. 65, № 1, стр. 10-21
Восстановление параметров морского дна при когерентном сейсмоакустическом зондировании. III. Накопление сигналов и подавление шумов
В. И. Калинина a, b, И. П. Смирнов b, А. И. Хилько a, b, А. А. Хилько a, *
a Нижегородский государственный университет им. Н.И. Лобачевского
603950 Нижний, Новгород, пр. Гагарина 23, Россия
b Институт прикладной физики РАН
603950 Нижний, Новгород, ул. Ульянова 46, Россия
* E-mail: anton.khilko@gmail.com
Поступила в редакцию 12.12.2017
После доработки 28.08.2018
Принята к публикации 15.07.2018
Аннотация
Исследуются методы и алгоритмы накопления сигналов и подавления шумов, позволяющие повысить точность и устойчивость реконструкции геоакустических параметров при послойной реконструкции донных слоев с использованием параметрических моделей формирования сигналов, отраженных от упругого слоистого полупространства при когерентном импульсном зондировании дна морского шельфа. Приводятся результаты анализа эффективности предлагаемых алгоритмов, выполненного методом численного стохастического моделирования.
ВВЕДЕНИЕ
В работах [1–3] были исследованы методы оптимизации решающих правил и повышения устойчивости к шумам при когерентной сейсмоакустической (СА) реконструкции геоакустических параметров морского дна. Особенностью этого метода является когерентное накопление отраженных от донных слоев СА-импульсов на фоне шумов и помех и последующее оценивание значений толщин, плотностей, скоростей продольных и поперечных волн, декрементов затухания в донных слоях путем максимизации значений целевых функций при принятии решений с требуемой достоверностью. В исследуемом методе СА-реконструкции для генерации зондирующих СА-импульсов используются когерентные излучатели, которые вместе с приемными решетками на небольшой глубине буксируются научно-исследовательским судном (НИС) в подводном положении [4–7]. В такой схеме СА-наблюдения основным источником акустических шумов и помех является шумы НИС-буксировщика, которые совместно с аддитивными шумами океана и реверберационными помехами маскируют полезные сигналы и мешают реконструкции параметров дна. Метод когерентной СА‑реконструкции геоакустических параметров морского дна является одним из методов решения задачи СА-инверсии, применяемых при поиске морских месторождений полезных ископаемых [8–11]. Развиваемый метод и другие методы СА‑инверсии являются обратной задачей реконструкции строения морского дна, решаемой на основе использования априорных данных, в том числе в виде моделей формирования СА-сигналов [1–3].
Устойчивость и точность решения задачи СА-наблюдения зависят от адекватности моделей сигналов и шумов и оптимальности методов поиска и принятия решений. Развитая в [1–3, 7] в рамках приближения геометрической акустики физико-математическая модель позволяет использовать взаимосвязь параметров отдельных донных слоев для сужения интервала поиска решения в многомерном пространстве параметров при их послойной реконструкции. При этом ошибки оценивания параметров верхних донных слоев понижают качество оценок параметров более глубоких слоев. Для повышения устойчивости алгоритмов реконструкции параметров морского дна правила принятия решений должны быть оптимизированы с учетом статистических характеристик шумов [12–18]. В случае гауссовых шумов в качестве решающих правил используют процессоры, в частности определяемые корреляционными характеристиками шумов и сигналов [18].
В настоящей работе методами численного стохастического моделирования исследуются особенности накопления сигналов и подавления шумов, позволяющие повысить точность и робастность реконструкции геоакустических параметров при послойной реконструкции морского дна в случае использования априорной информации в виде параметрических моделей формирования сигналов, отраженных от упругого слоистого полупространства при когерентном импульсном зондировании. В дополнение к исследованиям возможностей реконструкции параметров дна в виде жидких слоев, выполненным в [1, 2], в настоящей работе анализируются особенности реконструкции морского дна в виде упругих слоев.
1. МОДЕЛЬ ФОРМИРОВАНИЯ ОТРАЖЕННЫХ ОТ МОРСКОГО ДНА СА-ИМПУЛЬСОВ
Используемые в настоящее время методы решения обратной задачи морской сейсморазведки (инверсии) обсуждаются в [8–14]. В алгоритмах инверсии, вектор восстановленных значений геоакустических параметров донных слоев $\varphi $ соответствует экстремуму выходной мощности процессора. Поиск экстремума осуществляется в определяемой априорной информацией области Ξ. При этом методы прямого перебора гипотез малоэффективны вследствие высокой размерности пространства поиска и овражного характера целевой функции. В этом случае следует использовать методы упорядоченного поиска, учитывающие специфику задачи. Одним из вариантов подобных методов являются методы последовательной релаксации, состоящие в последовательной максимизации сформированного функционала по отдельным параметрам (группам параметров) при фиксированных значениях прочих параметров. Эффективность подобных методов зависит главным образом от различных аспектов стратегии поиска, в частности от удачности выбора начальных значений, а также выбора последовательности оценок значений определяемых параметров. Выбор оптимальной последовательности оценок наблюдаемых параметров может основываться на использовании модели формирования отраженных от слоистого дна СА-импульсов. Такая модель, объединяя большой объем априорной информации, позволяет использовать зависимости между наблюдаемыми параметрами.
В задаче восстановления параметров упругого слоистого дна вектор ${\mathbf{\varphi }}$ имеет следующие компоненты: толщины слоев, плотности их грунтов, скорости продольных волн, скорости поперечных волн, их декременты затухания; соответственно, размерность пространства параметров равна $L = 6\left( {N + 1} \right),$ где N – число слоев (толщина нижнего слоя ${{h}_{N}}$ считается бесконечной). Рассматриваемая задача имеет ряд особенностей, связанных со структурой измеряемых спектральных компонент СА-поля. В число таких компонент входят прямое поле g от источника, а также отраженное морской поверхностью поле ${{g}^{{(V)}}},$ которые не зависят от донных параметров ${\mathbf{\varphi }}$ и являются помехами при реконструкции дна. Другой особенностью является то, что поле ${{g}^{{(0)}}},$ отраженное верхней границей первого донного слоя, зависит только от параметров этого верхнего слоя. Кроме этого, заметим, что поле ${{g}^{{(1)}}},$ отраженное верхней границей второго донного слоя, зависит только от параметров первых двух слоев. Аналогичные особенности имеют место и для границ остальных слоев. Наконец, отраженное верхней границей слоя N поле ${{g}^{{(N)}}}$ зависит от всех компонентов вектора φ. Для морского дна в виде жидкого слоистого полупространства амплитуды компонентов $g,{{g}^{{(V)}}},{{g}^{{(0)}}}, \ldots ,{{g}^{{(N)}}}$ чаще всего монотонно убывают (мощность первых двух на 10–20 дБ превосходит мощности прочих), а времена прихода соответствующих компонентов полей на антенну монотонно возрастают [1, 2]. Если донные слои достаточно толстые, а зондирование дна осуществляется достаточно короткими СА-импульсами, волновые компоненты, соответствующие различным слоям, не пересекаются и не интерферируют. В случае дна в виде упругих слоев зависимости спадания амплитуд и нарастания задержек импульсов, отраженных от донных слоев компонент, имеют более сложную структуру. Это связано прежде всего с тем, что структура отраженных от упругого слоистого дна импульсов формируется не только продольными, но и поперечными, а также обменными волновыми компонентами. В общем случае отраженные от каждой границы сигналы представляют собою наборы распределенных по оси задержек СА-импульсов. При этом суммарный, отраженный от дна сигнал имеет сложную интерференционную структуру. По мере заглубления границы число отраженных от нее СА-импульсов быстро нарастает, их амплитуды уменьшаются, и они распределяются все в большем интервале задержек. Число принимаемых приемником отраженных СА-импульсов достигает величины $M = 1 + \sum\nolimits_{i = 1}^N {{{4}^{i}}} .$ Результирующее отраженное от слоистого упругого дна СА-поле может выглядеть сильно изрезанным, приобретая хаотический вид. Идентификация волн в таких условиях возможна лишь с помощью априорной информации в виде модели. При этом реконструкцию можно осуществлять только последовательно, начиная от самого верхнего слоя, продвигаясь к нижележащим слоям [1, 2]. В любом случае оптимизация поиска решений в многомерном пространстве параметров возможна лишь при использовании закономерностей формирования СА-сигналов и связей всех параметров.
Исследуем зондирование дна когерентными сложно модулированными импульсами, обеспечивающими эффективную селекцию сигналов по временам прихода [3–5]. Рассмотрим модель океанического волновода в виде однородного слоя жидкости $0 < z < H$ с плотностью жидкости ${{\rho }_{0}},$ скоростью распространения звука ${{c}_{0}}$ и декрементом затухания ${{\delta }_{0}}.$ Дно, согласно рассматриваемому приближению, будем представлять последовательностью из N упругих слоев $H + {{h}_{k}}$ < $ < z < H + {{h}_{{k + 1}}},$ $k = 1 \ldots N;$ нижний упругий слой считаем бесконечно глубоким: ${{h}_{{N + 1}}} = \infty .$ Полученные после выполнения инверсии оценки значений совокупности из L геометрических и геофизических параметров морского дна представляют собою изображение морского дна. Из-за влияния помех и шумов, затухания зондирующих акустических волн, а также использования ограниченных пространственно-частотных апертур излучающих и приемных систем изображение будет отличаться от истинного морского дна. Точность реконструкции донных слоев с увеличением глубины наблюдения будет падать. Как показано в [2, 3], глубина и точность реконструкции зависят от объема априорной информации, а также от уровня и структуры шумов и помех. Будем рассматривать помещенную в океанический волновод систему наблюдения, состоящую из совокупности S ненаправленных независимых друг от друга когерентных излучателей звука ${{S}_{i}}$, размещенных в точках множества $\left\{ {r_{i}^{{\left( S \right)}}} \right. = \left( {x_{i}^{{\left( S \right)}},y_{i}^{{\left( S \right)}},z_{i}^{{\left( S \right)}}} \right),$ $\left. {i = 1 \ldots K_{S}^{{}}} \right\}$ (излучающая антенна), и расположенной на относительно небольшом горизонтальном расстоянии от излучателя системы R ненаправленных гидрофонов ${{R}_{j}},$ расположенных в точках множества $\left\{ {r_{j}^{{\left( R \right)}} = \left( {x_{j}^{{\left( R \right)}},y_{j}^{{\left( R \right)}},z_{j}^{{\left( R \right)}}} \right),\,j = 1 \ldots {{K}_{R}}} \right\}$ (приемная антенна) (рис. 1а). Излучателем ${{S}_{i}}$ возбуждается импульсный сигнал ${{g}_{i}}(\omega ) = {{C}_{i}}(\omega ){{g}_{S}}(\omega ),$ где ${{g}_{S}}(\omega )$ – спектральная плотность импульса, ${{С }_{i}}(\omega )$ – комплексная амплитуда возбуждения i-го излучателя.
Рис. 1.
Формирование отраженных импульсов от слоистого дна. (а) Траектория импульса при однократном отражении от нижней границы n-го слоя, (б) отражение и преломление продольных (слева) и поперечных (справа) волн на границах упругих слоев.
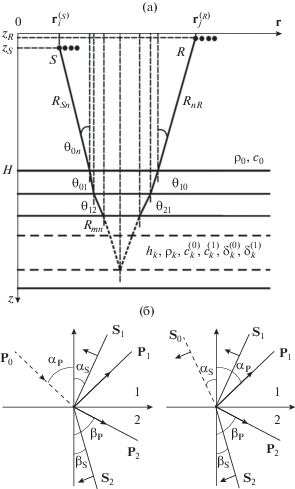
Рассмотрим полное поле, отраженное от дна, состоящего из упругих слоев, в которых плотности – ${{\rho }_{k}},$ скорости продольных и поперечных волн в слое $k$ – $c_{k}^{{(0)}}$ и $c_{k}^{{(1)}}$ соответственно, декременты затухания – $\delta _{k}^{{(0)}}$ и $\delta _{k}^{{(1)}},$ волновые числа – $k_{k}^{{(0)}} = {\omega \mathord{\left/ {\vphantom {\omega {c_{k}^{{(0)}}}}} \right. \kern-0em} {c_{k}^{{(0)}}}}$ и $k_{k}^{{(1)}} = {\omega \mathord{\left/ {\vphantom {\omega {c_{k}^{{(1)}}}}} \right. \kern-0em} {c_{k}^{{(1)}}}}.$ Рассмотрим точку приема R, расположенную внутри волновода на горизонтальном расстоянии ${{r}_{{SR}}}$ от источника S. Пренебрегая волнами, испытывающими более чем двукратное прохождение через отдельные слои, представим спектральную амплитуду полного импульса в точке приема суммой волн, отраженных от нижних границ донных слоев: $\hat {g}(\omega ) = \sum\nolimits_{n = 1}^N {{{{\hat {g}}}_{n}}(\omega )} ,$ где ${{\hat {g}}_{n}}(\omega )$ – сумма волн, отраженных от нижней границы слоя $n = 1, \ldots ,N\,:$ ${{\hat {g}}_{n}}(\omega ) = \sum\nolimits_{k = 0}^{{{2}^{n}} - 1} {\hat {g}_{n}^{{\left( k \right)}}(\omega )} .$ Каждая из приходящих в приемник волн $\hat {g}_{n}^{{\left( k \right)}},$ отраженных от нижней границы слоя n, может быть однозначно представлена своим номером k, записанным в двоичном коде $k = {{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}} \ldots {{z}_{1}}} \right)}_{2}},$ где ${{s}_{i}},{{z}_{i}} \in \left\{ {0,1} \right\},$ $i = 1, \ldots ,\,n$ – двоичные знаки, показывающие тип волны при ее прохождении через слой i: 0 – продольная, 1 – поперечная. При этом волны, которые распространяются вниз, нумеруются первыми n индексами ${{s}_{1}},{{s}_{2}},...{{s}_{n}},$ а волны, идущие вверх, – индексами ${{z}_{n}}, \ldots {{z}_{1}}.$ Например, волны, приходящие в приемник от нижней границы первого слоя, имеют следующие двоичные номера: ${{(00)}_{2}}$ – продольная вниз и продольная вверх волны, ${{(01)}_{2}}$ – продольная вниз и поперечная вверх волны, ${{(10)}_{2}}$ – поперечная вниз и продольная вверх волны, ${{(11)}_{2}}$ – поперечная вниз и поперечная вверх волны. Поэтому $\hat {g}(\omega ) = \sum\nolimits_{n = 1}^N {{{{\hat {g}}}_{n}}(\omega )} $ = $\sum\nolimits_{n = 1}^N {\sum\nolimits_{k = 0}^{{{2}^{n}} - 1} {\hat {g}_{n}^{{\left( k \right)}}} (\omega )} $ = $ = \sum\nolimits_{n = 1}^N {\sum\nolimits_{{{s}_{1}} = 0}^1 \cdots } \sum\nolimits_{{{s}_{n}} = 0}^1 {\sum\nolimits_{{{z}_{n}} = 0}^1 \cdots } \sum\nolimits_{{{z}_{1}} = 0}^1 {\hat {g}_{n}^{{{{{\left( {{{s}_{1}} \ldots {{s}_{n}}{{z}_{n}} \ldots {{z}_{1}}} \right)}}_{2}}}}(\omega )} .$ Полагая для удобства ${{s}_{0}} = {{z}_{0}} = 0$ (волна в жидкости всегда продольная), представим каждое из полей $\hat {g}_{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}(\omega )$ в малоугловом приближении в виде
(1)
$\begin{gathered} \hat {g}_{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}(\omega ) = \frac{{{{g}_{S}}(\omega ){{e}^{{ - i\varphi _{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}} - \Delta _{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}}}}}}{{R_{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}}} \times \\ \times \,\,\prod\limits_{m = 0}^{n - 1} {W_{{m,m + 1}}^{{\left( {{{s}_{m}}{{s}_{{m + 1}}}} \right)}}\left( {\theta _{{mn}}^{{\left( {{{s}_{m}}} \right)}}} \right)} V_{n}^{{\left( {{{s}_{n}}{{z}_{n}}} \right)}}\left( {\theta _{{nn}}^{{\left( {{{s}_{n}}} \right)}}} \right) \times \\ \times \,\,\prod\limits_{m = n}^1 {W_{{m,m - 1}}^{{\left( {{{z}_{m}}{{z}_{{m - 1}}}} \right)}}\left( {\theta _{{mn}}^{{\left( {{{z}_{m}}} \right)}}} \right).} \\ \end{gathered} $Здесь $R_{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}} \ldots {{z}_{1}}} \right)}}_{2}}}} = {{R}_{{Sn}}}$ + $\sum\nolimits_{m = 1}^n {R_{{mn}}^{{\left( {{{s}_{m}}} \right)}}} $ + $ + \,\,\sum\nolimits_{m = n}^1 {R_{{mn}}^{{\left( {{{z}_{m}}} \right)}}} + {{R}_{{nR}}}$ – полное расстояние, которое проходит волна, $\varphi _{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}} \ldots {{z}_{1}}} \right)}}_{2}}}}(\omega ) = {{k}_{0}}\left( {{{R}_{{Sn}}} + {{R}_{{nR}}}} \right)$ + $ + \,\,\sum\nolimits_{m = 1}^n {k_{m}^{{\left( {{{s}_{m}}} \right)}}R_{{mn}}^{{\left( {{{s}_{m}}} \right)}}} + \sum\nolimits_{m = n}^1 {k_{m}^{{\left( {{{z}_{m}}} \right)}}} R_{{mn}}^{{\left( {{{z}_{m}}} \right)}}$ – полный фазовый набег волноводной компоненты, $\Delta _{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}} \ldots {{z}_{1}}} \right)}}_{2}}}}(\omega ) = \left( {{{R}_{{Sn}}} + {{R}_{{nR}}}} \right){{\delta }_{0}}(\omega ) + \sum\nolimits_{m = 1}^n {R_{{mn}}^{{\left( {{{s}_{m}}} \right)}}} $ × $ \times \,\,\delta _{m}^{{\left( {{{s}_{m}}} \right)}}(\omega )$ + $\sum\nolimits_{m = n}^1 {R_{{mn}}^{{\left( {{{z}_{m}}} \right)}}\delta _{m}^{{\left( {{{z}_{m}}} \right)}}(\omega )} $ – полный коэффициент затухания. Для волны типа ${{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}} \ldots {{z}_{1}}} \right)}_{2}},$ приходящей от источника S в приемник R, начальный угол падения на дно приближенно равен ${{\theta }^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}} \ldots {{z}_{1}}} \right)}}_{2}}}}}$ = ${{r}_{{SR}}}\left( {2H - {{z}_{R}} - {{z}_{S}} + \frac{1}{{{{c}_{0}}}}} \right.$$\sum\nolimits_{m = 1}^n {c_{m}^{{\left( {{{s}_{m}}} \right)}}{{h}_{m}}} $ + $ + \,\,{{\left. {\frac{1}{{{{c}_{0}}}}\sum\nolimits_{m = n}^1 {c_{m}^{{\left( {{{z}_{m}}} \right)}}{{h}_{m}}} } \right)}^{{ - 1}}}.$ Угол падения этой волны $\theta _{{mn}}^{{({{s}_{m}},{{z}_{m}})}}$ на слой m задается по начальному углу падения $\theta _{{mn}}^{{({{s}_{1}}...{{s}_{n}},{{z}_{n}}...{{z}_{1}})}}$ законами преломления Снеллиуса, а расстояние, которое она проходит в этом слое (рис. 1б), $R_{{mn}}^{{\left( {{{s}_{m}},{{z}_{m}}} \right)}}$ = ${{h}_{m}}\sqrt {1 + {{{\left( {\frac{{c_{m}^{{\left( {{{s}_{m}},{{z}_{m}}} \right)}}}}{{{{c}_{0}}}}\theta _{{mn}}^{{\left( {{{s}_{m}},{{z}_{m}}} \right)}}} \right)}}^{2}}} .$ Далее, $W_{{m,\,m + 1}}^{{\left( {{{s}_{m}}{{s}_{{m + 1}}}} \right)}}(\theta )$ – коэффициент преломления волны типа ${{s}_{m}}$ в волну типа ${{s}_{{m + 1}}}$ при переходе ее из слоя m в слой $m + 1$ под углом падения θ на нижнюю границу слоя m, $W_{{m,\,m - 1}}^{{\left( {{{z}_{m}}{{z}_{{m - 1}}}} \right)}}\left( \theta \right)$ – коэффициент преломления волны типа ${{z}_{m}}$ в волну типа ${{z}_{{m - 1}}}$ при переходе ее из слоя m в слой $m - 1$ под углом падения θ, $V_{n}^{{\left( {{{s}_{n}}{{z}_{n}}} \right)}}\left( \theta \right)$ – коэффициент отражения волны типа ${{s}_{n}}$ в волну типа ${{z}_{n}}$ от нижней границы слоя n под углом падения на нее θ. Коэффициенты отражения и преломления для волн всех типов,
падающих из слоя 1 на границу со слоем 2 (см. рис. 1), определяются формулами Цёппритца (под углом падения ${{\alpha }_{P}},$ $V_{n}^{{\left( {{{s}_{n}}{{z}_{n}}} \right)}}\left( \theta \right)$ и $V_{P}^{P},$ и $m = \frac{{{{\rho }_{2}}v_{2}^{{(0)}}}}{{{{\rho }_{1}}v_{1}^{{(0)}}}}$ угол ${{\beta }_{S}}$ 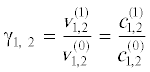 ):
):
где ${{\gamma }_{{1,2}}} = \frac{{v_{{1,2}}^{{(1)}}}}{{v_{{1,2}}^{{(0)}}}},$ $m = \frac{{{{\rho }_{2}}v_{2}^{{(0)}}}}{{{{\rho }_{1}}v_{1}^{{(0)}}}},$ $\frac{{\sin {{\alpha }_{p}}}}{{v_{1}^{{(0)}}}}$ = $\frac{{\sin {{\alpha }_{s}}}}{{v_{1}^{{\left( 1 \right)}}}}$ = $ = \,\,\frac{{\sin {{\beta }_{p}}}}{{v_{2}^{{(0)}}}} = $ $\frac{{\sin {{\beta }_{s}}}}{{v_{2}^{{(1)}}}}$ (закон Снеллиуса),
В используемом геометроакустическом приближении параметры отраженных от границ слоев волн зависят от частоты: $\hat {g}_{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}(\omega )$ = $ = A_{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}{{g}_{S}}(\omega ){{e}^{{ - i\omega \tau _{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}}}},$ где $A_{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}$ = $ = \frac{1}{{R_{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}}}$ $\prod\nolimits_{m = 0}^{n - 1} {W_{{m,m + 1}}^{{\left( {{{s}_{m}}{{s}_{{m + 1}}}} \right)}}\left( {\theta _{{mn}}^{{\left( {{{s}_{m}}} \right)}}} \right)} $ $V_{n}^{{\left( {{{s}_{n}}{{z}_{n}}} \right)}}\left( {\theta _{{nn}}^{{\left( {{{s}_{n}}} \right)}}} \right)$ × $ \times \,\,\prod\nolimits_{m = n}^1 {W_{{m,m - 1}}^{{\left( {{{z}_{m}}{{z}_{{m - 1}}}} \right)}}} \left( {\theta _{{mn}}^{{\left( {{{z}_{m}}} \right)}}} \right){{e}^{{ - \Delta _{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}\left( {{{\omega }_{0}}} \right)}}},$ $\Delta _{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}({{\omega }_{0}}) - $ коэффициент затухания на центральной частоте импульса. Поэтому суммарная спектральная амплитуда принимаемого импульса будет определяться следующим образом:
Будем осуществлять фильтрацию поступившего на приемную систему сигнала с помощью согласованного фильтра $G(\tau ) = \int_{ - \infty }^\infty {{{g}_{R}}(t)} g_{S}^{ * }\left( {t - \tau } \right)dt.$ С учетом принятых выше определений сигнал с выхода согласованного фильтра будет определяться как $G(\tau ) = \sum\nolimits_{n = 1}^N {\sum\nolimits_{{{s}_{1}} = 0}^1 \cdots } $$\sum\nolimits_{{{z}_{1}} = 0}^1 {A_{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}} $ × $ \times \,\,{{F}_{S}}\left( {\tau - \tau _{n}^{{{{{\left( {{{s}_{1}}...{{s}_{n}}{{z}_{n}}...{{z}_{1}}} \right)}}_{2}}}}} \right),$ где τ – параметр фильтра, ${{F}_{S}}(\tau )$ – функция неопределенности импульсного сигнала ${{F}_{S}}(\tau ) = \int_{ - \infty }^\infty {{{g}_{S}}} \left( t \right)g_{S}^{ * }\left( {t - \tau } \right)dt.$
При СА-зондировании морского дна во всем диапазоне частот и задержек при измерении полезные сигналы маскируются мультипликативными реверберационными помехами, возникающими за счет рассеяния зондирующих импульсов на всех случайных граничных и объемных неоднородностях водной толщи и дна. Как показывают оценки, наибольший вклад в реверберационную помеху вносит рассеяние на донной поверхности. Спектральная плотность мощности такого рода донной реверберации от источника ${{S}_{i}}$ на приемник ${{R}_{j}}$ может быть найдена интегрированием углового спектра по полному телесному углу ${{\Omega }_{R}}$ лучей, приходящих на гидрофон $g_{{ij}}^{{\left( r \right)}}(\omega )$ = $ = \iint_{{{\Omega }_{R}}} {{{N}_{{ij}}}}\left( {{{e}_{R}},\omega } \right)d\Omega \left( {{{e}_{R}}} \right).$ При этом в качестве простейшей модели рассеяния можно использовать модель, в которой угловой спектр определяется выражением ${{N}_{{ij}}}\left( {{{e}_{R}},\omega } \right)$ = ${{\left| {V\left( {{{e}_{R}}} \right)} \right|}^{2}}m\left( {{{e}_{{{{S}_{i}}Q}}},{{e}_{{{{R}_{j}}Q}}}} \right)$ × × ${{\left| {\left\langle {n,{{e}_{{{{R}_{j}}Q}}}} \right\rangle } \right|}^{{ - 1}}}I_{{ij}}^{{\left( S \right)}}\left( {Q,\omega } \right),$ где $I_{{ij}}^{{\left( S \right)}}\left( {Q,\omega } \right)$ = $ = {{\left| {{{{\hat {C}}}_{i}}(\omega )g(\omega )} \right|}^{2}}r_{{{{S}_{i}}Q}}^{{ - 2}},$ $V\left( {{{e}_{R}}} \right)$ = $\exp \left[ { - {{\delta }_{0}}\left( {{{r}_{{{{S}_{i}}Q}}} + {{r}_{{Q{{R}_{j}}}}}} \right)} \right],$ а $m\left( {{{e}_{1}},{{e}_{2}}} \right)$ = ${{m}_{{\max }}}\sin {{\chi }_{1}}\sin {{\chi }_{2}}$ – коэффициент рассеяния в точке дна $Q = Q\left( {{{e}_{R}}} \right),$ ${{\chi }_{1}}\;{\text{и }}\;{{\chi }_{2}}$ – углы скольжения падающей и рассеянной волны относительно донной поверхности, ${{e}_{{1,\,2}}}$ – направления лучей в точке Q падения их на дно, n – нормаль в этой точке. При импульсном зондировании реверберационные сигналы распределяются вдоль оси задержек в виде откликов согласованного фильтра, соответствующих рассеянию в имеющих форму эллиптических колец импульсных объемах [5]. Кроме реверберационных помех полезные СА-сигналы маскируются и аддитивными шумами. Как показывают эксперименты, наибольший вклад в шумы при СА-зондировании морского дна в большинстве случаев вносит шум судна-буксировщика. Такие шумы часто не являются гауссовыми [4, 5].
2. СТРУКТУРА ОТРАЖЕННЫХ ОТ МОРСКОГО ДНА СА-ИМПУЛЬСОВ
Развитая выше модель позволяет исследовать взаимосвязь основных параметров задачи и на этой основе оптимизировать решающие правила, обеспечивающие максимальное накопление полезных сигналов, и снизить требования к априорным данным, то есть найти наилучшую процедуру поиска решения обратной задачи. Согласно используемой модели, спектральная плотность отраженных от упругого слоистого дна сигналов зависит от взаимного положения источника S и точки приема R, параметров зондирующих импульсов, а также геоакустических параметров и толщины слоев. Рассмотрим структуру СА-импульсов, отраженных от морского дна, имеющего типичное для условий морского шельфа строение в виде полупространства из упругих слоев (рис. 2а). Для такой модели зависимости модуля коэффициентов отражения продольной и поперечной волны от углов для границ характеризуются многочисленными особенностями, в частности, имеют место критические углы, при которых наблюдается полное внутреннее отражение, а также возбуждение граничных волн. Кроме того, фаза отраженной волны может существенно меняться. На структуру отраженного от слоистого полупространства акустического поля существенно влияет частотно-зависимое затухание, которое наиболее сильно сказывается при критических углах возбуждения граничных волн Рэлея. Указанные выше эффекты обычно проявляются при углах падения и наблюдения, превышающих 20°–30°. Для принятой в рамках настоящего исследования модели СА-наблюдения углы падения и наблюдения обычно не превышают десяти градусов. На рис. 2б показаны результаты расчетов структуры СА-импульсов с выхода согласованного фильтра, отраженных от рассматриваемой модели дна в виде семи упругих слоев. Зондирующие ЛЧМ-импульсы возбуждались в полосе частот $\Delta f$ от 150 до 250 Гц источником с мощностью 300 Вт. Видно, что отраженные от разных границ импульсы, соответствующие различным волновым компонентам, пересекаются. При их интерференции формируется сложная структура, интерпретация которой, в частности идентификация компонент, затрудняется. В целом видно, что уровни различных волновых компонент, отраженных от слоистого полупространства, различаются на 2–4 порядка, причем средние их значения быстро спадают с глубиной. Волновые компоненты, связанные с переизлучением энергии в поперечные волны, в целом относительно малы, так, что их измерение возможно лишь при высоком уровне излучения и слабых помехах и шумах. Из сравнения уровней рассчитанных сигналов и помех в типичных условиях наблюдения (табл. 1) можно приближенно оценить возможность реконструкции параметров слоев с достаточно контрастными границами при их залегании на глубинах порядка 200–300 м. Существует возможность улучшения ситуации путем наращивания мощности зондирующих импульсов, а также подавления шумов и помех буксировщика. Однако такие возможности требуют преодоления многочисленных технических трудностей и повышают требования к экспериментальному оборудованию. Кроме того, остается требование минимизации экологического урона, что накладывает предел увеличению мощности зондирующих сигналов.
Рис. 2.
Структура дна (а) и компоненты ЛЧМ-импульса, отраженного от морского дна в виде шести упругих слоев на полупространстве (б).
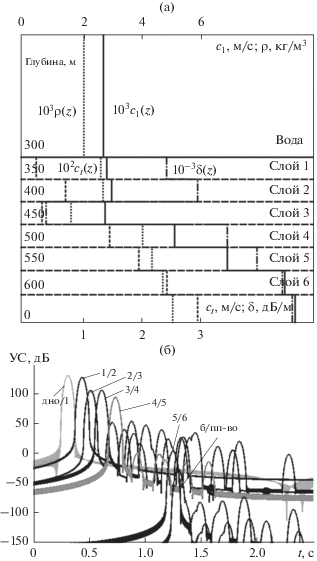
Таблица 1
| S-излучатель | ${{F}_{S}}(0),$ Вт | $\Delta f,$ Гц | ${{T}_{S}},$ с | $x_{1}^{{\left( S \right)}},$ м | $z_{1}^{{\left( S \right)}},$ м | $x_{i}^{{\left( S \right)}} - x_{{i + 1}}^{{\left( S \right)}},$ м |
|---|---|---|---|---|---|---|
| 300 | 150–250 | 0.125 | 0 | 120 | – | |
| R-приемник из n = 20 гидрофонов | – | $\Delta f$, Гц | – | $x_{1}^{{\left( R \right)}},$ м | $z_{1}^{{\left( R \right)}},$ м | $x_{j}^{{\left( R \right)}} - x_{{j + 1}}^{{\left( R \right)}},$ м |
| – | 150–250 | – | 10 | 36.875 | 3.6875 | |
| Истинные значения параметров волновода | ||||||
| Слои, k | ${{\rho }_{k}},$ кг/м3 | $c_{k}^{{\left( 0 \right)}},$ м/с | $c_{k}^{{(1)}},$ м/с | $\delta _{k}^{{(0)}},$ дБ/м | $\delta _{k}^{{(1)}},$ дБ/м | ${{h}_{k}},$ м |
| 0 | 1040 | 1450 | – | 0 | – | 300 |
| 1 | 1500 | 1600 | 400 | 0 | 0 | 100 |
| 2 | 1800 | 1900 | 700 | 0 | 0 | ∞ |
| Диапазон поиска, определяемый из априорных данных | ||||||
| Слои, k | ${{\rho }_{k}},$ кг/м3 | $c_{k}^{{\left( 0 \right)}},$ м/с | $c_{k}^{{(1)}},$ м/с | $\delta _{k}^{{(0)}},$ дБ/м | $\delta _{k}^{{(1)}},$ дБ/м | ${{h}_{k}},$ м |
| 0 | 1040 | 1450 | – | 0 | – | 300 |
| 1 | 1480–1520 | 1580–1600 | 380–420 | 0 | 0 | 80–120 |
| 2 | 1780–1820 | 1880–1920 | 680–720 | 0 | 0 | ∞ |
3. ВОССТАНОВЛЕНИЕ ПАРАМЕТРОВ ДОННЫХ СЛОЕВ
Простейшим методом реконструкции параметров морского дна является сравнение измеренных в пределах входной апертуры (t, ${{{\mathbf{r}}}_{R}}$) данных с аналогичными данными, рассчитанными с помощью модели. Однако в этом случае уровень шумов будет максимальным, и глубина и точность реконструкции параметров дна будут невелики. Максимизация точности и глубины СА-реконструкции дна с учетом упомянутых ограничений может быть обеспечена оптимизацией решающих правил, реализующихся на основе накопления полезных сигналов и подавления шумов и помех. Выполнение указанных операций возможно лишь с использованием априорной информации. Рассмотрим особенности такого рода алгоритма для случая, когда прием СА-сигналов осуществляется горизонтальной антенной с гидрофонами, размещенными в точках ${{{\mathbf{r}}}_{R}}.$ Зондирующие СА-ЛЧМ-импульсы возбуждаются точечным СА-излучателем. При выполнении реконструкции геофизических параметров дна измеряемые данные подвергаются инверсии, выполняемой алгоритмом поиска и принятия решений.
На первом этапе инверсии отраженные от дна импульсы вместе с помехами и шумами подвергаются согласованной фильтрации. При этом используются априорные данные о структуре зондирующих импульсов. Такая операция обеспечивает частотное накопление сигналов в полосе работы излучателя, в частности, отношение сигнала к гауссовскому шуму вырастет в $\sqrt {\Delta f\Delta T} $ раз, где $\Delta T$ – длина импульса.
На втором этапе инверсии выполняется операция пространственного накопления импульсов в пределах пространственной апертуры решетки гидрофонов. Такое накопление осуществляется вдоль годографа, определяющего траекторию времен прихода импульсов на гидрофоны решетки. Положение годографа находится с помощью алгоритма, основывающегося на использовании гипотез о значениях геофизических параметров. Полученный подобным образом выборочный вектор измеряемых данных после накопления ${{{\mathbf{x}}}_{l}}$ используется для составления выборочной корреляционной матрицы [1–3]: ${{\hat {\Gamma }}_{x}}(\tau ) = \sum\nolimits_{l = 1}^L {{{{{x}_{l}}x_{l}^{'}} \mathord{\left/ {\vphantom {{{{x}_{l}}x_{l}^{'}} L}} \right. \kern-0em} L}} ,$ где L – число реализаций (число излученных импульсов).
Следующим, третьим этапом инверсии является определение параметров дна, при котором используется проекционный процессор (MUSIC, а также другие процессоры и их обобщения). В качестве оценок параметров выбираются те их значения, которые максимизируют мощность процессора, работающего с корреляционной матрицей. В частности, мощность процессора MUSIC, отвечающая пробному набору параметров ϕ, вычисляется по формуле ${{P}_{{{\text{MUSIC}}}}}(\phi )$ = $\frac{1}{{e_{0}^{ + }(\phi ){{{\hat {\Pi }}}_{n}}{{e}_{0}}(\phi )}},$ где ${{e}_{0}}\left( \phi \right)$ – нормированный сигнальный вектор; ${{\hat {\Pi }}_{{\text{n}}}} \equiv {{\hat {\Psi }}_{{\text{n}}}}\hat {\Psi }_{{\text{n}}}^{ + },$ ${{\hat {\Psi }}_{{\text{n}}}} = [{{\hat {\psi }}_{{J + 1}}}, \cdots ,{{\hat {\psi }}_{N}}]$ – матрица, сформированная из собственных векторов корреляционной матрицы; J – число старших собственных значений (параметр процессора). Адаптивный процессор AMUSIC допускает контролируемое отклонение сигнального вектора от ${{e}_{0}}\,:$ отвечающий пробному вектору ${{e}_{0}}\left( \phi \right)$ робастный вектор $e(\phi ,\varepsilon )$ находится из решения задачи $e(\phi ,\varepsilon ) = \arg {{\min }_{e}}$ × $ \times \,\,\left\{ {{{e}^{ + }}{{{\hat {\Pi }}}_{{\text{n}}}}e:{{{\left\| {e - {{e}_{0}}(\phi )} \right\|}}^{2}} \leqslant \varepsilon ,{{{\left\| e \right\|}}^{2}} = 1} \right\},$ при этом выходная мощность адаптивного процессора определяется формулой $P(\varepsilon ,\phi ) = \frac{1}{{{{e}^{ + }}(\phi ,\varepsilon ){{{\hat {\Pi }}}_{{\text{n}}}}e(\phi ,\varepsilon )}}.$ Параметр согласованных фильтров $\tau $ для каждого из гидрофонов выступает при этом как управляющий параметр метода. Он позволяет усилить значения сигналов, поступающих от заданного слоя при одновременном подавлении шумов и сигналов от других слоев [3]. Для этого достаточно для каждого из гидрофонов с учетом априорных данных выбрать параметры согласованного фильтра равными временам прихода сигналов от соответствующей границы. Другим эффективным процессором, который широко используется при решении задач сейсмоакустической инверсии, является L2‑норма [7, 9, 12]. Накопление полезных сигналов при использовании такого рода процессора, как отмечалось выше, повышает устойчивость алгоритмов инверсии.
Рассмотрим этот эффект на примере часто встречающейся в практике ситуации, когда морское дно состоит из упругого слоя, лежащего на упругом полупространстве. Параметры модели, описывающей дно указанной формы, приведены в табл. 1. На рис. 3. показана структура отраженных от слоистого дна в виде упругого слоя на упругом полупространстве ЛЧМ-импульсов с выхода согласованного фильтра. Суммарный сигнал состоит из импульса, отраженного от донной поверхности, а также из группы импульсов, которые отразились от нижней границы верхнего упругого слоя (рис. 3). На рисунке показан результат интерференции всех отраженных от дна импульсных компонент. В общем случае, когда донные слои имеют относительно малую толщину, отраженные от донных границ импульсы могут пересекаться и маскировать друг друга. В рассматриваемом случае, когда верхний упругий слой имеет достаточно большую толщину, импульсы не пересекаются. С выхода приемной решетки формируется годограф – совокупность отраженных от дна импульсов, выстраивающихся в плоскости {$x_{1}^{{\left( R \right)}}$ – $\tau $} набора траекторий (см. рис. 3). Как видно из расчетов, уровни поперечных и обменных компонент существенно меньше продольных компонент. В случае относительно маломощных источников и высоких уровней шумов измерения параметров поперечных и обменных компонент не могут быть осуществлены с необходимой точностью. С учетом указанных обстоятельств ограничимся при инверсии использованием лишь данных, соответствующих продольным компонентам, в частности волне, отраженной от донной поверхности. При рассматриваемой модели расчетов эта волновая компонента локализуется в области задержек 0.3 с (рис. 3). Один из часто используемых вариантов инверсии заключается в применении в качестве решающего правила L2-нормы – квадрата невязки между измеряемыми данными и результатами 1модельных расчетов [7, 9, 12]. Однако, как уже отмечалось, учет параметрической зависимости характеристик модели позволяет реализовать алгоритмы накопления, что делает метод инверсии более устойчивым (робастным). В рассматриваемом случае в качестве алгоритма накопления сигналов используем когерентное накопление отраженных от донных границ сигналов, расположенных вдоль траекторий, формирующихся на годографе с выхода приемной антенны. В частности, такой траекторией является криволинейная траектория в плоскости {$x_{{}}^{{\left( R \right)}}$ – τ}, соответствующая продольной компоненте, отраженной от донной поверхности (импульс 1, на рис. 3). При согласованной фильтрации и таком пространственном накоплении антенной длиной $\Delta {{L}_{n}} = x_{n}^{{\left( R \right)}} - x_{1}^{{\left( R \right)}},$ когда модельные сигналы полностью совпадают с наблюдаемыми (измеряемыми) сигналами, отношение сигнала с выхода антенны к гауссовскому шуму вырастет в $\sqrt {\Delta f\Delta T\Delta L} $ раз. Поскольку при инверсии значения параметров донных слоев считаются неизвестными, необходимо осуществлять поиск решения, который соответствует минимуму величины L2-нормы. Поиск следует осуществлять в интервале значений параметров донного слоя, который определяется априорной информацией. Воспользуемся проекционным методом и рассмотрим структур с выхода L2-процессора в плоскости параметров $\left\{ {c_{1}^{{(0)}},{{\rho }_{1}}} \right\},$ полагая остальные параметры задачи заданными приближенно из априорных данных (табл. 1). На рис. 4 показана структура сигналов с выхода процессора в виде L2‑нормы в области расположения истинных значений параметров $\left\{ {c_{1}^{{(0)}},{{\rho }_{1}}} \right\},$ размер которой также выбирается из априорных данных. При расчетах выходных сигналов процессора полагалось, что шумы полностью отсутствуют. Из анализа структуры сигнала L2-процессора в плоскости $\left\{ {c_{1}^{{(0)}},{{\rho }_{1}}} \right\}$ после когерентного накопления в плоскости {$x_{{}}^{{\left( R \right)}}$ – τ} отраженной от донной поверхности продольной компоненты (рис. 4а) видно, что относительный экстремум находится в овраге, что связано с относительно слабой зависимостью сигнала процессора от ${{\rho }_{1}}.$ Экстремум локализован в малой области, что обеспечивает большую точность и устойчивость при оценке параметров $\left\{ {c_{1}^{{(0)}},{{\rho }_{1}}} \right\}.$ На рис. 4б показан сигнал с такого же процессора для случая, когда накопление не используется. В этом случае экстремум менее выражен и не так глубок, что снижает точность и устойчивость оценивания. Можно полагать, что указанный эффект обуславливается тем, что в отсутствие накопления рассматриваемый локальный экстремум зависит от сразу всех параметров морского дна, тогда как в первом случае зависимость сигнала процессора от других параметров дна слабее. При наличии шумов точность оценивания падает. Однако очевидно, что при накоплении сигналов и подавлении шумов скорость спадания точности оценивания много меньше. На рис. 5 показаны реализации зависимостей выходных сигналов L2-процессора в присутствии гауссовского шума, при котором отношение сигнала к шуму (С/Ш) на входе приемных гидрофонов составляло приблизительно 10 дБ. При этом для случая, рассмотренного при численных экспериментах, выходное отношение С/Ш оценивается как 30 дБ. Из представленных результатов видно, что при таком уровне шумов положение экстремума (рис. 5а) смещено от истинных значений параметров, несмотря на использование алгоритма накопления. В то же время в случае, когда накопление не использовалось, глубина экстремума существенно уменьшилась (рис. 5б), а области расположения оценочных значений для различных реализаций шума стали располагаться в более широком интервале значений. Для более устойчивой оценки ошибок при оценивании решений в присутствии шума рассмотрим усредненные характеристики ошибок по большому интервалу реализаций шума. На рис. 6 показаны зависимости средних оценок $\left\langle {\delta c_{1}^{{(0)}}} \right\rangle $ (рис. 6а), $\left\langle {\delta \rho _{1}^{{}}} \right\rangle $ (рис. 6б) и дисперсий $\sigma \left( {\delta c_{1}^{{(0)}}} \right)$ (рис. 6в), $\sigma \left( {\delta \rho _{1}^{{}}} \right)$ (рис. 6г) смещений параметров $\delta c_{1}^{{(0)}} = \left| {\tilde {c}_{1}^{{(0)}} - c_{1}^{{(0)}}} \right|$ и $\delta {{\rho }_{1}} = \left| {{{{\tilde {\rho }}}_{1}} - {{\rho }_{1}}} \right|$ в зависимости от входного отношения С/Ш для случая использования накопления (кривые с номером 1) и для случая его отсутствия (кривые с номером 2). Представленные зависимости получены при усреднении по 103 реализациям шума. Из представленных зависимостей видно, что присутствие шума приводит к среднему смещению оценок и их разбросу, которые нарастают по мере увеличения уровня шума. Видно также, что точность оценивания плотности верхнего упругого слоя заметно меньше, чем точность восстановления значения скорости продольной волны. Это обусловлено тем, что параметры отраженного сигнала от упругого слоя относительно слабо зависят от плотности слоя по сравнению с зависимостью от скорости продольной волны, что в частности проявляется в овражной форме структуры мощности процессора в исследуемой плоскости параметров. Как видно из графиков, показанных на рис. 6, использование алгоритма накопления сигналов позволило существенно повысить устойчивость оценки параметров донного слоя, что следует из сравнения кривых 1 и 2. Как уже упоминалось ранее, повышение устойчивости решений в рассматриваемом случае обуславливается накоплением сигналов и ослаблением шумов. Дальнейшие этапы реконструкции параметров упругого слоя должны основываться на измерениях волновых компонент, отраженных от нижней границы верхнего упругого слоя, в том числе и поперечной волны. Это позволяет оценить скорость такой волны и толщину верхнего упругого слоя. При этом полученные на предыдущих этапах оценки плотности слоя и скорости продольной волны будут использоваться как уточненные по сравнению с априорными данными значения. После оценки скорости поперечной волны и толщины слоя можно вернуться к оценке продольной волны и плотности. Итерационный процесс уточнения чаще всего сходится. Полученные оценки параметров верхнего упругого слоя используются при оценке нижнего упругого слоя. Такая реконструкция является послойной. Поскольку оценки параметров верхнего слоя могут быть получены лишь с ограниченной точностью, которая зависит от отношения сигнала к шуму, а также ширины полосы частот зондирующих импульсов и размеров приемной антенны, точность оценивания параметров нижних слоев будет меньше. По мере реконструкции более глубоких слоев ошибки будут накапливаться, так что начиная с некоторой глубины реконструкция параметров донных слоев перестанет удовлетворять заданным требованиям.
Рис. 3.
Структура отраженных от слоистого дна в виде упругого слоя на упругом полупространстве ЛЧМ-импульсов с выхода согласованного фильтра в пределах апертуры приемной решетки из 20 гидрофонов (годограф), где 1 – импульс, отраженный от донной поверхности, 2 – группа импульсов, отраженных от нижней границы верхнего слоя.
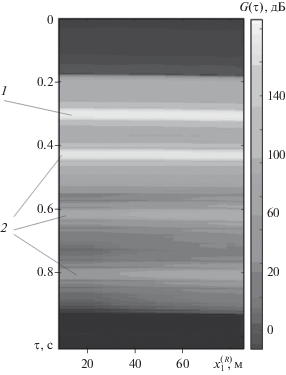
Рис. 4.
Мощность в логарифмическом масштабе L2-процессора в плоскости $\left\{ {c_{1}^{{(0)}},\,\,{{\rho }_{1}}} \right\}$ в отсутствие шумов при когерентном накоплении в плоскости {$x_{{}}^{{\left( R \right)}}$ – τ} отраженной от донной поверхности продольной компоненты (а), а также сигнал такого же процессора для случая, когда накопление не используется (б).
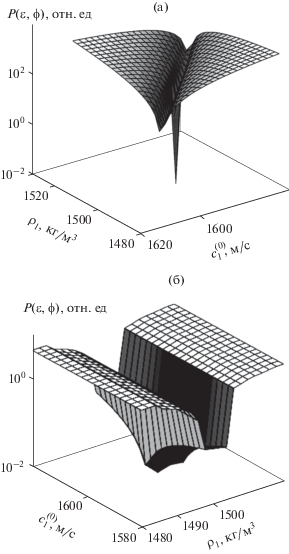
Рис. 5.
Структура мощности в логарифмическом масштабе L2-процессора в плоскости (${{\rho }_{1}}$, $c_{1}^{{(0)}}$) при заданных из априорных данных $c_{1}^{{(1)}} = 400$ м/с, ${{h}_{1}}$ = 100 м, уровне излучения УИ = 76 дБ, уровне аддитивного шума УШ = 68 дБ и отношении сигнала к шуму на входе приемной решетки С/Ш = 10 дБ, при использовании накопления (а) и для случая его отсутствия (б).
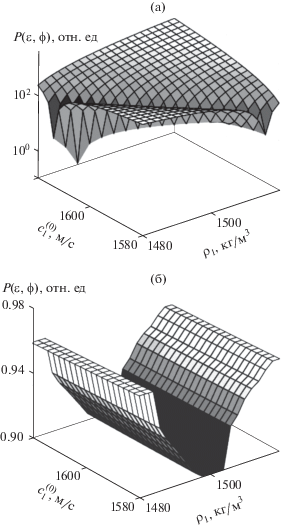
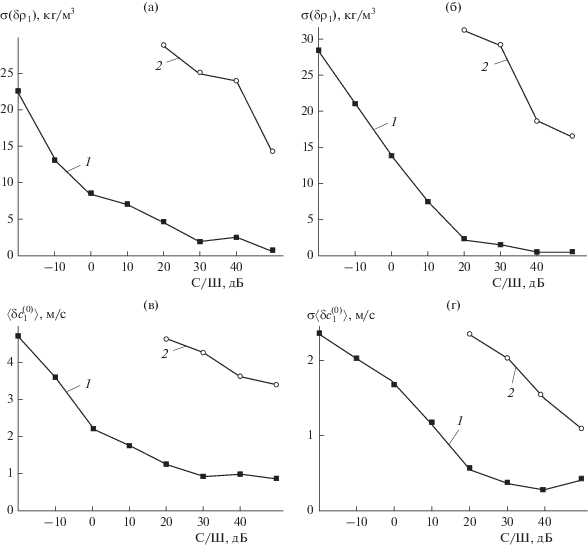
Рис. 6.
Зависимость усредненных по 103 реализациям шума оценок $\left\langle {\delta c_{1}^{{(0)}}} \right\rangle $ (а), $\left\langle {\delta \rho _{1}^{{}}} \right\rangle $ (б) и дисперсий $\sigma \left( {\delta c_{1}^{{(0)}}} \right)$ (в), $\sigma \left( {\delta \rho _{1}^{{}}} \right)$ (г) смещений параметров $\delta c_{1}^{{(0)}} = \left| {\tilde {c}_{1}^{{(0)}} - c_{1}^{{(0)}}} \right|$ и $\delta {{\rho }_{1}} = \left| {{{{\tilde {\rho }}}_{1}} - {{\rho }_{1}}} \right|$ в зависимости от входного отношения сигнала к шуму (С/Ш) для случая использования накопления сигналов (1) и его отсутствия (2).
ЗАКЛЮЧЕНИЕ
В работе исследованы методы и алгоритмы накопления сигналов и подавления шумов, позволяющие повысить точность и устойчивость реконструкции геоакустических параметров при послойной реконструкции донных слоев. Алгоритмы основаны на использовании параметрической модели формирования сигналов, отраженных от упругого слоистого полупространства при когерентном импульсном зондировании дна морского шельфа. Такая модель разработана в геометроакустическом приближении с использованием формул Цёппритца. Заметим, что в предыдущих работах авторов [1, 2], рассматривалась такого рода модель лишь для дна в виде жидких слоев. В настоящей же работе параметрическая модель формирования сигналов при сейсмоакустическом зондировании усложнена, поскольку рассматривается дно в виде упругих слоев. В этом случае структура отраженных от упругого слоистого дна импульсов существенно усложняется. Установлено, что при отражении от упругого слоистого дна импульсных СА-сигналов от каждой границы отражается набор импульсов, которые распределены в пространстве задержек. Все элементы такой группы импульсов несут информацию о границе и могут быть использованы при реконструкции ее параметров. Алгоритм накопления измеренных сигналов заключается в совместной обработке такой группы. Предложен метод, основанный на разделении в структуре регистрируемых импульсов вкладов различных границ морского дна. Для ослабления взаимных помех от различных донных границ выполняется послойная реконструкция, когда сначала определяются параметры верхних слоев, а на дальнейших этапах такие оценки используются для реконструкции более глубоких слоев. Исследована эффективность предлагаемых алгоритмов методом численного стохастического моделирования. Показано, что последовательное выделение и накопление полезных СА-сигналов для отдельных донных слоев позволяет максимизировать устойчивость алгоритмов реконструкции параметров дна при когерентном СА-зондировании.
Работа выполнена в рамках базовой части государственного задания (проект 3.5672.2017/БЧ), а также частично, в части численных экспериментов, при поддержке РФФИ (проект № 16-29-02081).
Список литературы
Смирнов И.П., Калинина В.И., Хилько А.И. Восстановление параметров морского дна при когерентном сейсмоакустическом зондировании. I. Решающие правила // Акуст. журн. 2018. Т. 64. № 1. С. 46–55.
Смирнов И.П., Калинина В.И., Хилько А.И. Восстановление параметров морского дна при когерентном сейсмоакустическом зондировании. II. Анализ робастности // Акуст. журн. 2018. Т. 64. № 2. С. 207–216.
Калинина В.И., Смирнов И.П., Хилько А.И. Оптимизация алгоритмов решения обратной задачи при реконструкции геоакустических параметров слоев дна морского шельфа с помощью зондирования когерентными сейсмоакустическими импульсами // Ученые записки физического факультета Московского университета. 2017. № 5. С. 1750131.
Калинина В.И., Смирнов И.П., Малеханов А.И., Хилько А.И. Когерентная морская сейсмоакустика: новые подходы к реконструкции структуры донных слоев в шельфовых акваториях // Изв. РАН. Серия Физическая. 2017. Т. 81. № 8. С. 1020−1027.
Лазарев В.А., Малеханов А.И., Мерклин Л.Р., Романова В.И., Стромков А.А., Таланов В.И., Хилько А.И. Экспериментальное исследование возможностей сейсмоакустического зондирования морского дна когерентными импульсными сигналами // Акуст. журн. 2012. Т. 58. № 2. С. 227–236.
Лазарев В.А., Малеханов А.И., Мерклин Л.Р., Романова В.И., Таланов В.И., Хилько А.И. Когерентное сейсмоакустическое профилирование морского дна с использованием широкополосных сигналов // Океанология. 2013. Т. 53. № 6. С. 843−850.
Романова В.И., Хилько А.И., Смирнов И.П. Использование модели отражения импульсов от упругого слоистого дна для реконструкции параметров слоев при буксировке когерентного акустического излучателя в мелком море / Сб. трудов XХV сессии Российского акустического общества и сессии Научного совета по акустике РАН. Т. 2. М.: ГЕОС, 2012. С. 280–285.
Денисов М.С. Сейсмическая миграция: анализ постановки задачи, способов ее решения и ограничений метода // Технологии сейсморазведки. 2013. № 4. С. 56–61.
Ампилов Ю.П., Барков А.Ю., Яковлев И.В., Филиппова К.Е., Приезжев И.И. Почти все о сейсмической инверсии. Часть 1 // Технологии сейсморазведки. 2009. № 4. С. 3–16.
Яковлев И.В., Ампилов Ю.П., Филиппова К.Е. Почти все о сейсмической инверсии. Ч. 2 // Технологии сейсморазведки. 2011. № 1. С. 5–15.
Алексеев А.С. Обратные динамические задачи сейсмики / В кн. “Некоторые методы и алгоритмы интерпретации геофизических данных”. М.: Наука, 1967. С. 9−84.
Jianyong Bai, David Yingst, Synchronous inversion of speed and density in time area using an inversion method taking into account the full form of an impulse / 84th Annual International Meeting, SEG, Expanded Abstracts. 2014. P. 962–966.
Oldendurg D.W., Sheuer T., Levy S. Recovery of the acoustic impedance form reflection seismograms // Geophysics. 1983. V. 48. P. 1318–1337.
Jackson D.R., Odom R.I., Boyd M.L., Ivakin A.N. A Geoacoustic Bottom Interaction Model (GABIM) // IEEE J. Ocean. Eng. 2010. V. 35. № 3. P. 603–617.
Rice J.K., White J.S. Norms for smoothing and estimation // SIAM Rev. 1964. V. 6. P. 243–256.
Claerbout J.F., Muir F. Robust modeling of erratic data // Geophysics. 1973. V. 38. P. 826–844.
Nadu G. Classification algorithms in pattern recognition // IEEE Trans. on Audio and Electroacoust. 1968. V. AO-16. № 2. P. 345.
Коваленко В.В., Хилько А.И., Романова В.И. Адаптивное оценивание параметров движущегося источника звука по данным от акустических сенсоров // Труды Всероссийской конференции “Нелинейная динамика в когнитивных системах”. Н. Новгород: ИПФ РАН, 2011. С. 93–97.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал


