Акустический журнал, 2019, T. 65, № 1, стр. 3-9

ВВЕДЕНИЕ

Интегро-дифференциальные уравнения вида

имеют весьма общий смысл и широкую область применимости [1]. Здесь $K\left( s \right)$ – ядро интегрального члена уравнения (1), а $f\left( V \right)$ – нелинейный член, который может соответствовать степенной (квадратичной Q, кубичной C) или неаналитической (модульной M, квадратично-кубичной $QC$) нелинейности. Член $f\left( V \right)$ может представлять также любую линейную комбинацию перечисленных выше нелинейностей. Обозначения $Q,\,\,С ,\,\,М ,\,\,QC$ для краткости будут использованы в дальнейшем изложении. Смысл остальных обозначений таков: V – акустическое давление, нормированное на характерную величину (исходную амплитуду волны); θ – время в сопровождающей системе координат, нормированное на исходную частоту; z – пройденное волной расстояние, отнесенное к характерной нелинейной длине.

Для вырожденных ядер $K\left( s \right),$ представляющих собой комбинацию дельта-функции и ее производных, из (1) получаются уравнения типа Хохлова–Заболотской, Кадомцева–Петвиашвили, Хохлова–Заболотской–Кузнецова и другие подобные уравнения для пучков, а в случае одномерных волн – уравнения типа Хопфа, Бюргерса и аналогичные эволюционные уравнения с высшими производными. Дифференциальные уравнения следуют из (1) и для некоторых других ядер [2]. Наиболее известны уравнения с экспоненциальным ядром:

которое следует из релаксационной модели Мандельштама–Леонтовича [3]. В этом случае для плоских волн из (1) получается

Это уравнение в форме (3) выведено в работе [4], а в интегральной форме – в работе [5].

Разнообразные формы ядер, полезные для приложений, обсуждаются в статье [6]. В частности, степенные зависимости коэффициента затухания волны от частоты с дробными показателями степени, типичные для биологических тканей и геофизических структур, принципиально требуют интегро-дифференциального описания. То же относится к средам со сложной внутренней динамикой релаксационного типа.

Как находится ядро$K\left( s \right)$ в каждом конкретном случае? Частотные зависимости дисперсии и поглощения (действительной и мнимой части волнового числа 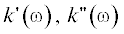) измеряются или определяются из физической модели типа Мандельштама–Леонтовича. Затем решается обратная задача, и ядро реконструируется стандартными методами, использующими принцип причинности и соотношения типа Крамерса–Кронига [7].

Например, показатель степени в частотной зависимости затухания в биотканях изменяется от 2.1 (кости черепа) до 1.1 (скелет) и 0.6 (кожа) [8]. Чаще всего в диапазоне единиц мегагерц (медицинский ультразвук) 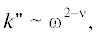$0 < \nu < 1.$ Для такой зависимости нетрудно показать, что $K(s)\sim {{s}^{{\nu - 1}}}.$ Особенность при $s = 0$ часто оказывается несущественной, поскольку уравнение содержит “свертку” сингулярного ядра с осциллирующей функцией, описывающей поле волны.

Точных решений для уравнений (1) известно немного. Найдены, например, стационарные решения для сред с Q- и QC-нелинейностями (в работах [3] и [9] соответственно) и экспоненциальной релаксацией.

Если интересоваться не конкретной средой, а общими свойствами нелинейных волн, удобен прием, сводящий интегро-дифференциальное уравнение к дифференциально-разностной модели или даже к простому отображению. Этот переход [6, 9] эффективен для ядер, отличных от нуля на конечном интервале. Простейший случай соответствует среде с постоянной “памятью”, для которой

Иными словами, до момента $s = {{\theta }_{{{\text{rel}}}}}$ среда “все помнит”, а в этот момент “все забывает”. При наличии такого ядра уравнение (2) принимает вид

Для стационарной волны (5) превращается в разностное соотношение:

Отображение (6) $V\left( \theta \right) \to V\left( {\theta - {{\theta }_{{{\text{rel}}}}}} \right)$ описывает фронт ударной волны с шириной, растущей с увеличением числа D. Константа C определяется из условия на бесконечности. Например, если $V\left( {\theta \to \infty } \right) \to {{V}_{0}},\,$ то $С = f\left( {{{V}_{0}}} \right).$

ИМПУЛЬСЫ В СРЕДАХ С ЧЕТНЫМИ НЕЛИНЕЙНОСТЯМИ

Рассмотрим процессы эволюции импульсных сигналов в релаксирующих средах с конечным временем памяти, обладающих нелинейностями четного типа – квадратичной Q или модульной M. Положим в уравнении (5) соответственно

Для обеих нелинейностей ${{f}_{Q}},\,{{f}_{M}}$ имеем $f\left( { - V} \right) = f\left( V \right).$ Однако решение уравнения (5) этой симметрией обладать не будет.

В первом случае для степенной Q-нелинейности уравнение (5) примет вид

Пусть на границе $z = 0$ исходная форма сигнала дается функцией $V\left( {z = 0,\theta } \right) = \sin \theta ,$ отличной от нуля в области $ - 2\pi < \theta < 2\pi .$ Иными словами, импульс представляет собой отрезок синусоиды, содержащий два ее периода. С точки зрения авторов, выбранная форма позволяет наглядно продемонстрировать основные проявления нелинейных и релаксационных эффектов.

Процесс эволюции такого импульса показан на рис. 1 для значений параметров $D = 0.1,{{\theta }_{{{\text{rel}}}}} = 1.$ Наблюдается формирование ударных фронтов сжатия. Положительные и отрицательные области профиля искажаются неодинаково, как и должно быть в среде с релаксацией (см. [10–12]). В целом импульс уширяется из-за “разбегания” ударных фронтов, занимавших исходное положение в точках $\theta = \pm 2\pi .$ Этот процесс приводит на больших расстояниях к превращению исходного сигнала в двуполярный импульс типа N-волны.

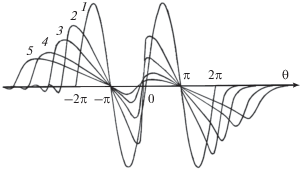
Напротив, другие точки $\theta = \pm \pi $ остаются “закрепленными” и не меняют своего положения в процессе распространения волны. Между ними при $\theta = 0$ образуется ударный фронт сжатия, после чего область $ - \pi < \theta < \pi $ начинает интенсивно затухать. Профиль в этой области ведет себя подобно волне S-типа.

Напомним, что Q-нелинейность является основной в нелинейной акустике жидких и газообразных сред [10]. Она возникает в силу двух обстоятельств. Во-первых, в уравнениях механики сплошных сред присутствуют нелинейные члены (пример – конвективный член $\left( {{\mathbf{u}}\nabla } \right)\,{\mathbf{u}}$ в уравнении движения Эйлера или Навье–Стокса). Эту нелинейность обычно называют “геометрической”. Во-вторых, имеется “физическая” нелинейность, связанная с нелинейным характером процесса деформирования среды и в конечном итоге – с нелинейностью сил межмолекулярного взаимодействия. Математически она дается квадратичным членом разложения в степенной ряд возмущения плотности среды по малым возмущениям акустического давления.

Рассмотрим теперь неаналитическую четную нелинейность M-типа, для которой уравнение (5) примет вид

Как и в предыдущем случае, считаем, что на границе $z = 0$ исходная форма сигнала дается функцией $V\left( {z = 0,\theta } \right) = \sin \theta ,$ отличной от нуля в области $ - 2\pi < \theta < 2\pi .$ Процесс эволюции сигнала при его распространении в среде иллюстрирован на рис. 2. Значения параметров $D = 0.2,{{\theta }_{{{\text{rel}}}}} = 1.$

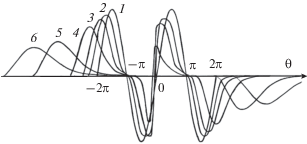
Аналогично случаю, показанному на рис. 1, здесь область $ - \pi < \theta < \pi $ также вырождается в результате нелинейного затухания, причем еще быстрее, чем для Q‑нелинейной среды. Для кривых 5 и 6 на рис. 2 ($z = 5,\,\,10$) волновое возмущение в пределах $ - \pi < \theta < \pi $ практически неотличимо от нуля. В этой области профиль волны описывается асимптотическими формулами, полученными в работе [13]. На расстояниях $z = 5,\,\,10$ полный профиль волны представляет собой два удаляющихся друг от друга импульса разной полярности.

Напомним, что M-нелинейность встречается в твердых телах, имеющих различные модули упругости по отношению к деформациям сжатия и растяжения. Обычно она встречается в средах с дефектами их надмолекулярной структуры и связана с так называемой “структурной” нелинейностью. Модульная M-нелинейность дает линейную зависимость амплитуды второй гармоники от амплитуды первой $\left( {{{A}_{2}}\sim {{A}_{1}}} \right),$ в то время как квадратичная или Q-нелинейность дает иную зависимость $\left( {{{A}_{2}}\sim A_{1}^{2}} \right).$ В общем случае, когда существенны обе нелинейности, показатель степени в зависимости $\,{{A}_{2}} = KA_{1}^{m}\,$ лежит в области от 1 до 2 [14]. Это явление наблюдалось в эксперименте [15]. Предприняты попытки создания элементов с M-нелинейностью [16, 17] для включения их в матрицу метаматериала.

ИМПУЛЬСЫ В СРЕДАХ С НЕЧЕТНЫМИ НЕЛИНЕЙНОСТЯМИ

Перейдем теперь к изучению импульсных сигналов в релаксирующих средах с конечным временем памяти, обладающих нелинейностями нечетного типа – кубичной C или квадратично-кубичной QC. Положим в уравнении (5) соответственно

Для степенной нелинейности C-типа уравнение (5) примет вид

Поведение решения уравнения (11) изображено на рис. 3 для тех же значений параметров и той же исходной формы импульса, что и на рис. 1.

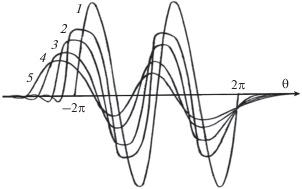
Основное различие в поведении волн в средах с Q- и C-нелинейностями, как видно из сравнения рисунков, состоит в следующем. В Q-среде с положительным знаком нелинейности, в которой локальная скорость распространения увеличивается с ростом возмущения, могут образовываться только ударные фронты сжатия. Поэтому при достаточно слабой диссипации и дисперсии (малые числа D) волна превращается в последовательность импульсов треугольной формы с ударными передними фронтами. В средах же с нечетными нелинейностями форма импульсов в последовательности иная – она близка к трапециевидной (кривые 2 и 3 на рис. 3).

Трапециевидные структуры в профиле волны более четко выражены на рис. 4, кривые 3–5. Эти профили построены для значения параметра $D = 0.02,$ меньшего, чем для кривых на рис. 2, где $D = 0.2.$ Поэтому здесь диссипативное сглаживание ударных фронтов выражено слабее.

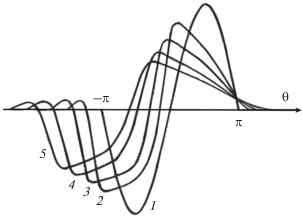
Формирование нелинейных структур трапециевидной формы происходит потому, что в C-среде могут существовать как ударные волны сжатия, так и ударные волны разрежения [11].

Напомним, что C-нелинейность является основным видом нелинейности для поперечных упругих волн в бездефектных изотропных твердых телах. Большой интерес к C-нелинейным волнам возник в связи с использованием интенсивного ультразвука для возбуждения сдвиговых волн в мягких биологических тканях.

Обсудим теперь поведение волны в квадратично-кубичной QC-среде с релаксацией. Эволюцию профиля волны будем описывать уравнением

Поскольку, как уже было указано (10), неаналитическая QC-нелинейность является нечетной, поведение импульса на рис. 5 качественно похоже на поведение такого же импульса в C-нелинейной среде (рис. 3). Здесь тоже образуются ударные волны как сжатия, так и разрежения, а также трапециевидные нелинейные структуры.

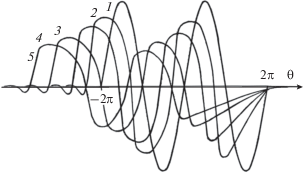
Заметим, что нечетные нелинейности (10) изменяют скорость распространения сигнала. Этот “эффект самовоздействия” приводит к сдвигу профиля волны вперед (см. рис. 3–5), а в случае пучков, ограниченных в поперечном сечении – к их самофокусировке или, напротив, к саморефракции.

Следует указать, что QC-модели применимы к описанию нескольких физических объектов. Экспериментально показано [19], что при больших интенсивностях звука отверстие в пластинке обнаруживает нелинейный отклик. При этом связь акустического давления с колебательной скоростью дается приближенно формулой $p{\text{'}} = \varsigma u\left| u \right|.$ Аналогичный член появляется в интеграле Коши–Лагранжа при осциллирующем движении среды. Таблицы коэффициентов $\varsigma $ для различных форм обтекаемых препятствий даны в справочнике [20]. Добавляя нелинейный член такого вида в уравнения гидродинамики, нетрудно с помощью стандартных упрощений вывести эволюционное QC-уравнение. Метаматериал с QC-нелинейностью можно изготовить, размещая обтекаемые элементы в объеме жидкости. Эффект QC‑нелинейности проявляется, в частности, в горле резонаторов Гельмгольца с волокнистым наполнителем, которые используются для поглощения интенсивного звука [21].

Еще один пример связан со спектральными измерениями. Если на входе QC‑среды задан монохроматический сигнал, то в среде рождаются гармоники, низшая из которых – третья. На малых расстояниях она пропорциональна квадрату амплитуды волны основной частоты ($ \sim \,p_{0}^{{'2}}$) и растет с расстоянием как ${{z}^{1}}.$ Однако в обычной Q‑среде эти зависимости имеют другой вид: $\sim \,p_{0}^{{'3}}$ и $\sim \,{{z}^{2}}.$ Часто наблюдают отклонения от них. Например, в поликристаллах сплава алюминия отклонения от законов $\sim \,p_{0}^{{'3}}$ и $\sim \,{{z}^{2}}$ объяснялись нелинейным трением на межзеренных границах [22]. Поведение QC-типа описано также для сдвиговых волн (например, в мягких биотканях), симметрия которых не допускает Q-эффектов. В любом случае зависимости третьей гармоники от расстояния $\sim \,{{z}^{m}},(1 < m < 2)$ и от амплитуды $\sim \,p_{0}^{{'k}}\,\,(2 < k < 3)$ свидетельствуют о наличии QC-элементов в объеме среды. Другие приложения и эксперимент описаны в обзоре [23].

ВЛИЯНИЕ ВРЕМЕНИ РЕЛАКСАЦИИ

В предыдущих расчетах всюду полагалось ${{\theta }_{{{\text{rel}}}}} = 1.$ Таким образом, безразмерные параметры – характерная частота исходного сигнала и время релаксации – оказались связанными. Теперь для лучшего понимания влияния релаксационных процессов на трансформацию профиля волны нужно варьировать параметр ${{\theta }_{{{\text{rel}}}}}.$

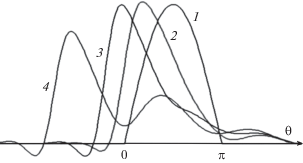
Эффекты релаксации хорошо проявляются при рассмотрении однополярных импульсов. На рис. 6 изображен процесс эволюции положительного импульса, исходная форма которого дается половиной периода синусоиды. Наряду с нелинейным увеличением крутизны переднего фронта волны здесь отчетливо выражены эффекты, связанные с релаксацией. Во-первых, это затухание, уменьшающее максимальное пиковое значение возмущения с ростом пройденного волной расстояния. Во-вторых, это дисперсионное увеличение скорости движения переднего фронта. Наконец, это “затягивание” заднего фронта волны, также связанное с дисперсией.

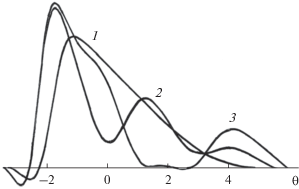
Перейдем теперь к сравнению профилей положительного однополярного импульса (рис. 6), прошедшего одинаковое расстояние, но в средах с разным временем релаксации. Такие профили представлены на рис. 7 для расстояния $z = 5.$ Кривые 1–3 построены для разных времен релаксации ${{\theta }_{{{\text{rel}}}}} = 0.5,\,\,2,\,\,3.$ Видно, что дисперсионные эффекты, о которых говорилось при обсуждении рис. 6, с ростом ${{\theta }_{{{\text{rel}}}}}$ заметно усиливаются.

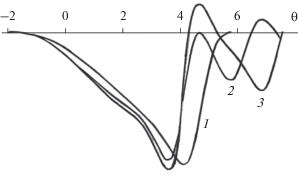
Сравним теперь профили отрицательного однополярного импульса (рис. 8), прошедшего одинаковое расстояние в средах с разным временем релаксации. Кривые на рис. 8 построены для тех же значений параметров, что и на рис. 7 для положительного импульса. Кривые 1, 2 и 3 отвечают последовательно увеличивающимся значениям ${{\theta }_{{{\text{rel}}}}}.$ Видно, что с усилением релаксации затягивание заднего фронта усиливается, в то время как передний фронт искажается заметно слабее, вне зависимости от ${{\theta }_{{{\text{rel}}}}}.$

ДРУГИЕ УПРОЩЕННЫЕ МОДЕЛИ И ЗАКОНЫ ДИСПЕРСИИ

Найдем закон дисперсии для модели (5). Запишем это уравнение в линеаризованной форме, положив $f\left( V \right) \equiv 0\,:$

Ищем решение в виде

Подставляя (14) в (13), получим

Дополнительный член к мнимой части в показателе экспоненты (пропорциональный D) описывает добавку к скорости распространения волны, зависящую от частоты. Действительная часть показателя описывает затухание (при $\omega {{\theta }_{{{\text{rel}}}}} < \pi $).

Очевидно, модель (5), (13) допускает обобщение. Реальное ядро $K\left( s \right)$ можно кусочно аппроксимировать не двумя константами, как в формуле (4), а несколькими постоянными (в пределах нескольких ограниченных интервалов) значениями. При этом в правой части уравнений (5), (13) появится сумма членов со “сдвинутыми” аргументами.

Еще одна упрощенная модель получается с использованием ядра со следующей линейно убывающей “памятью”:

При этом вместо (5) получается такое дифференциально-разностное уравнение:

К удобным для численного анализа уравнениям приводит комбинация представлений (4) и (16), то есть произвольная кусочно-линейная аппроксимация, приближающая ядро $K\left( s \right)$ с нужной нам точностью.

ЗАКЛЮЧЕНИЕ

При численном исследовании сформулированных в этой работе задач использовались разностные схемы третьего порядка точности сквозного расчета разрывов, описанные в работах [12, 24].

На наш взгляд, исследования нелинейных процессов в нелинейных средах с модельными типами ядер следует продолжить, поскольку прямое интегрирование интегро-дифференциальных уравнений (1) представляет собой гораздо более сложную проблему. При этом целесообразно начать с модели (17) и других аналогичных упрощенных дифференциально-разностных уравнений.

Работа поддержана грантом РНФ № 14-22-00042.