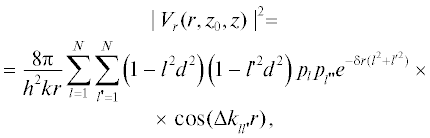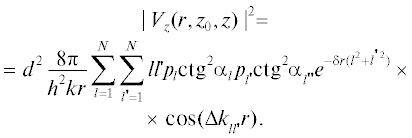Акустический журнал, 2019, T. 65, № 2, стр. 203-213
Закономерности ослабления векторно-скалярных звуковых полей в зонах интерференционных максимумов
Г. Н. Кузнецов a, *, А. Н. Степанов a, b
a Институт общей физики им. А.М. Прохорова РАН
119991 Москва, ул. Вавилова 38, Россия
b Самарский национальный исследовательский университет имени академика С.П. Королева
443086 Самара, Московское шоссe 34, Россия
* E-mail: skbmortex@mail.ru
Поступила в редакцию 18.04.2018
После доработки 14.09.2018
Принята к публикации 12.09.2018
Аннотация
Получены и исследуются численные и аналитические зависимости, определяющие связанные с увеличением расстояния закономерности ослабления звукового давления и ортогональных проекций вектора колебательной скорости низкочастотных сигналов, формируемых в волноводе в зонах интерференционных максимумов. Применительно к волноводу Пекериса и ненаправленному монопольному источнику найдены удобные аппроксимирующие выражения, которые хорошо согласуются с точными законами спадания различных составляющих векторно-скалярного поля в этих зонах.
1. ВВЕДЕНИЕ
Основы методов приближенной аппроксимации законов спадания усредненной – регулярной составляющей поля звукового давления (ЗД), создаваемого монопольным излучателем в волноводе, заложены в [1]. Позднее эта задача применительно к волноводу Пекериса–Бреховских рассматривалась в целом ряде работ, обзор и анализ которых, а также обобщение законов спадания на векторно-скалярные поля и мультипольные источники выполнены в [2]. Вместе с тем из простых физических соображений следует, что кроме затухания усредненного поля представляют интерес законы спадания звуковой энергии в зонах интерференционных максимумов амплитуды (ИМА) – особенно для дискретных составляющих, на которых интерференция проявляется наиболее ярко.
В этих зонах, во-первых, наблюдается наибольшее отношение сигнал/помеха [3]. Во-вторых, при расположении приемной или излучающей антенны в зоне ИМА наблюдаются сравнительно гладкие и предсказуемые градиенты фазы [4, 5], что позволяет накапливать звуковую энергию на апертуре антенны и повышать помехоустойчивость обнаружения [6]. Одновременно из-за “гладкости” и предсказуемости градиентов фазы в зонах ИМА в результате фазирования сигналов на апертуре антенны имеется возможность достаточно точного пеленгования источников звуковых сигналов [6, 7].
Большой интерес к зонам ИМА связан также с особыми свойствами интерференционной структуры звукового поля [8]. В частности, с возможностью построения и анализа динамических инвариантов [9, 10]. С использованием этих “особых” характеристик интерференционной структуры связывают возможность исследования влияния динамики внутренних волн и других неоднородностей [11, 12], возможность устойчивого пеленгования широкополосных сигналов [6, 7], а также ставят и решают задачу эффективного обнаружения слабых сигналов на фоне помех [13–15]. Не меньший интерес представляет возможность обнаружения и одновременно оценки расстояния до источника и радиальной скорости его движения [16].
Соотношения, необходимые для анализа поля в зонах ИМА, можно получить с помощью предложенного в [1] способа приближенного аналитического решения дисперсионного уравнения в волноводе Пекериса, ${\text{ctg}}x = \frac{i}{{\tilde {m}x}}\sqrt {{{x}^{2}} - {{{(kh\nu )}}^{2}}} ,$ где $i$ – мнимая единица, $\tilde {m} = {{{{\rho }_{1}}} \mathord{\left/ {\vphantom {{{{\rho }_{1}}} {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}},$ ${{\rho }_{0}}$ – плотность среды в волноводе, ${{\rho }_{1}}$ – плотность среды в подстилающем полупространстве, $k = {\omega \mathord{\left/ {\vphantom {\omega {{{с }_{0}}}}} \right. \kern-0em} {{{с }_{0}}}}$ – волновое число, $\omega $ – круговая частота источника звука, ${{c}_{0}}$ – скорость звука в волноводе, $h$ – толщина волновода, ${{\nu }^{2}} = 1 - {{\tilde {n}}^{2}},$ $\tilde {n} = {{n}_{0}}(1 + i\beta ),$ ${{n}_{0}} = {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} {{{c}_{1}} < 1}}} \right. \kern-0em} {{{c}_{1}} < 1}},$ ${{c}_{1}}$ – скорость звука в подстилающем полупространстве, $\beta \geqslant 0$ – коэффициент поглощения звука в грунте. Найденные приближенные значения корней дисперсионного уравнения имеют вид ${{x}_{l}} \approx {{l\pi h} \mathord{\left/ {\vphantom {{l\pi h} H}} \right. \kern-0em} H},$ $l = 1,\;2,\;...;$ $H = {{h + \tilde {m}} \mathord{\left/ {\vphantom {{h + \tilde {m}} {k{{\nu }_{0}}}}} \right. \kern-0em} {k{{\nu }_{0}}}}$ – эффективная толщина волновода Пекериса, $\nu _{0}^{2} = 1 - n_{0}^{2}.$ Это решение дает возможность записать выражение для потенциала $\psi $ звукового поля монопольного излучателя в волноводе Пекериса в виде суммы нормальных волн [1]:
(1)
$\psi (r,{{z}_{0}},z) = \frac{{2\pi }}{{kh}}\sum\limits_{l = 1}^N {{{A}_{l}}H_{0}^{{(1)}}({{\xi }_{l}}r)} ,$(2)
$\begin{gathered} |P(r,{{z}_{0}},z){{|}^{2}} = \frac{{8\pi {{\omega }^{2}}\rho _{0}^{2}}}{{{{k}^{3}}{{h}^{2}}r}}\left[ {\sum\limits_{l = 1}^N {p{}_{l}^{2}} {{e}^{{ - 2\delta r{{l}^{2}}}}} + } \right. \\ + \,\,\left. {\sum\limits_{l = 1}^N {\sum\limits_{l' \ne l}^N {{{p}_{l}}{{p}_{{l'}}}{{e}^{{ - \delta r({{l}^{2}} + {{{l'}}^{2}})}}}\cos (\Delta {{k}_{{ll'}}}r} } )} \right], \\ \end{gathered} $Если проанализировать выражение (2), то можно заметить различие величин коэффициентов, стоящих под знаком экспоненты. Как следствие, можно предположить, что зависимости от расстояния r регулярной (R) и интерференционной (I) составляющих окажутся разными. Для упрощенного и предварительного анализа запишем выражения для R и I в предположении, что в волноводе 1распространяются, например, две моды, $N = 2{\text{:}}$
Видно, что для любых коэффициентов возбуждения ${{p}_{1}}$ и ${{p}_{2}}$ значение выражения $2{{p}_{1}}{{p}_{2}}{{e}^{{ - 5\delta r}}}$ меньше, чем сумма $p_{1}^{2}{{e}^{{ - 2\delta r}}} + p_{2}^{2}{{e}^{{ - 8\delta r}}}.$ Увеличение в (2) количества нормальных волн принципиальных изменений в рассуждения не вносит, и это свойство несложно по индукции доказать для любого количества нормальных волн N. Отсюда следует, что интерференционная часть $I$ спадает – уменьшается с увеличением расстояния – быстрее, чем регулярная $R$.
Однако представляет интерес не только качественная, но и количественная оценка скорости спадания интерференционной части выражения (2). Эта задача поставлена и частично решена в [17], но анализ выполнен только для скалярного поля (звукового давления) и для ограниченного интервала расстояний между приемником и излучателем. Кроме того, в [17] характеристики поля исследуются только в предельных случаях – для приемников или источников, расположенных непосредственно в середине волновода или вблизи поверхностей раздела – у свободной поверхности или у дна. Несмотря на указанные ограничения, для этих трех зон ИМА в [17] выявлено существенное различие законов ослабления интенсивности звука в зависимости от глубин расположения z и z0 (что представляется интересным и важным с практической точки зрения результатом). Но обнаружена и общая закономерность – во всех случаях уменьшение или увеличение интенсивности в зонах ИМА происходит при изменении расстояния приблизительно в $\sqrt r $ быстрее, чем изменение величины регулярной составляющей в сопоставимых условиях.
Представляет интерес обобщение полученных в [17] результатов на различные глубины источника ${{z}_{0}}$ и приемника $z$ и произвольные расстояния $r$ между монопольным источником и приемником, а также распространение задачи на векторно-скалярные поля, т.е. на горизонтальные и вертикальные проекции вектора колебательной скорости (ГПКС и ВПКС). Полученные зависимости могут быть использованы для упрощенного, но с достаточной точностью, расчета зависимостей от расстояния ЗД, ГПКС и ВПКС, а при необходимости – и проекций вектора потока мощности.
2. ПОВЕРХНОСТИ ИНТЕРФЕРЕНЦИОННЫХ МАКСИМУМОВ
Можно показать, и путем расчетов в этом не сложно убедиться, что для различных расстояний $r$ и глубин ${{z}_{0}}$ и $z$ интерференционные кривые $|P(r,{{z}_{0}},z){{|}^{2}}$ ограничены сверху функцией ${{G}^{P}}(r,{{z}_{0}},z):$
(3)
$\begin{gathered} |P(r,{{z}_{0}},z){{|}^{2}} \leqslant {{G}^{P}}(r,{{z}_{0}},z) = \\ = \frac{{{{A}^{P}}}}{r}{{\left( {\sum\limits_{l = 1}^N {|\sin l{{\alpha }_{1}}\sin l{{\alpha }_{2}}|} {{e}^{{ - {\delta }r{{l}^{2}}}}}} \right)}^{2}}, \\ \end{gathered} $Дополнительно к описанию поля ЗД получим для монопольного источника выражения для ГПКС и ВПКС. Эти выражения имеют вид сумм, аналогичных сумме нормальных волн поля для ЗД (1) и исследуются в [18, 19]. Их можно упростить, если учесть, что корни дисперсионного уравнения равны ${{{{x}_{l}} \approx l{\pi }h} \mathord{\left/ {\vphantom {{{{x}_{l}} \approx l{\pi }h} H}} \right. \kern-0em} H}.$ Тогда ${{{{x}_{l}}} \mathord{\left/ {\vphantom {{{{x}_{l}}} {{{kh \approx l{\pi }} \mathord{\left/ {\vphantom {{kh \approx l{\pi }} {kH = ld}}} \right. \kern-0em} {kH = ld}}}}} \right. \kern-0em} {{{kh \approx l{\pi }} \mathord{\left/ {\vphantom {{kh \approx l{\pi }} {kH = ld}}} \right. \kern-0em} {kH = ld}}}},$ где ${{{{d = {\pi }} \mathord{\left/ {\vphantom {{d = {\pi }} {kH = {\lambda }}}} \right. \kern-0em} {kH = {\lambda }}}} \mathord{\left/ {\vphantom {{{{d = {\pi }} \mathord{\left/ {\vphantom {{d = {\pi }} {kH = {\lambda }}}} \right. \kern-0em} {kH = {\lambda }}}} {2H}}} \right. \kern-0em} {2H}}$ – безразмерный параметр, равный отношению длины волны к удвоенной эффективной толщине волновода. В результате получим ${{V}_{r}}(r,{{z}_{0}},z)$ = $\frac{{2{\pi }}}{h}\sum\nolimits_{l = 1}^N {\sqrt {1 - {{l}^{2}}{{d}^{2}}} {{p}_{l}}H_{1}^{{(1)}}({{{\xi }}_{l}}r)} ,$ ${{V}_{z}}(r,{{z}_{0}},z)$ = = $d\frac{{2{\pi }}}{h}\sum\nolimits_{l = 1}^N {l{{p}_{l}}{\text{ctg}}{{{\alpha }}_{l}}H_{0}^{{(1)}}({{{\xi }}_{l}}r)} .$ Соответственно, квадраты модулей ГПКС и ВПКС в том же приближении имеют вид
Полагая далее функции $\cos (\Delta {{k}_{{ll'}}}r)$ для всех $l$ и $l{\text{'}}$ равными единице и введя обозначение ${{A}^{V}} = {{8{\pi }} \mathord{\left/ {\vphantom {{8{\pi }} {k{{h}^{2}}}}} \right. \kern-0em} {k{{h}^{2}}}},$ получим функции
(4)
$\begin{gathered} {{G}^{{Vr}}}(r,{{z}_{0}},z) = \\ = \frac{{{{A}^{V}}}}{r}{{\left( {\sum\limits_{l = 1}^N {\sqrt {1 - {{l}^{2}}{{d}^{2}}} \left| {\sin l{{{\alpha }}_{1}}\sin l{{\alpha }_{2}}} \right|{{e}^{{ - {\delta }r{{l}^{2}}}}}} } \right)}^{2}}, \\ \end{gathered} $(5)
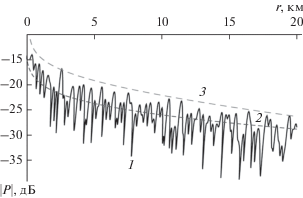
$\begin{gathered} {{G}^{{Vz}}}(r,{{z}_{0}},z) = \\ = {{d}^{2}}\frac{{{{A}^{V}}}}{r}{{\left( {\sum\limits_{l = 1}^N {l\left| {\sin l{{{\alpha }}_{1}}\cos l{{{\alpha }}_{2}}} \right|{{e}^{{ - {\delta }r{{l}^{2}}}}}} } \right)}^{2}}, \\ \end{gathered} $На рис. 1 приведены три зависимости ЗД в децибелах от расстояния: интерференционная кривая 1, рассчитанная по (1), кривая 2 – регулярная составляющая интенсивности [2] и кривая 3 – функция $\sqrt {{{G}^{P}}(r,{{z}_{0}},z)} ,$ рассчитанная по (3). Расчеты выполнены для погруженного на глубину ${{z}_{0}}$ = = 100 м источника с частотой 50 Гц и приемника, находящегося у дна: $z$ = 200 м. Горизонтальное расстояние между источником и приемником изменяется от 100 м до 20 км. Толщина волновода $h = $ 200 м, скорость звука в воде 1500 м/с, параметры дна $\tilde {m} = 2.7,$ $\tilde {n} = 0.83$, коэффициент поглощения в дне 0.15. Видно, что интерференционная составляющая амплитуды ЗД и сигналы, рассчитанные в зонах ИМА, спадают существенно быстрее, чем регулярная составляющая, определяющая средний уровень ЗД.
Рис. 1.
Интерференционная кривая 1, регулярная составляющая 2 и кривая максимумов амплитуды звукового давления 3 на расстояниях между источником и приемником до 20 км.
Значительно более общую и наглядную картину можно получить, зафиксировав в соотношениях (2)–(5) глубину источника ${{z}_{0}}$ и варьируя глубину приемника z и расстояние r от источника до приемника (можно наоборот). На рис. 2 в координатах $(r,z)$ представлены рассчитанная по выражению (1) интерференционная поверхность $\left| {P(r,z)} \right|$ (стрелка 1) и ограничивающая ее сверху поверхность интерференционных максимумов $\sqrt {{{G}^{P}}(r,z)} $ (стрелка 2), вычисленные при вариации расстояния и глубины приемника для погруженного на глубину ${{z}_{0}}$ = 100 м источника звука. Расчеты произведены для тех же характеристик волновода, но для частоты 25 Гц.
Рис. 2.
Интерференционная поверхность (стрелки 1) (а) и поверхность максимумов (стрелка 2), ограничивающая интерференционную поверхность (б), частота 25 Гц.

На рис. 3 приведены изображения ПИМ амплитуды ЗД (а) и ВПКС (б) от монополя с частотой 50 Гц, находящегося на глубине 100 м в волноводе с указанными выше параметрами. Глубина приемника, как и на рис. 2, изменяется от 0 до 200 м, горизонтальное расстояние – от 100 м до 10 км. Вид ПИМ для ГПКС не приводится, так как она практически полностью совпадает с ПИМ для ЗД.
Рис. 3.
Поверхности интерференционных максимумов амплитуды давления (а) и вертикальной проекции колебательной скорости (б). Частота 50 Гц.
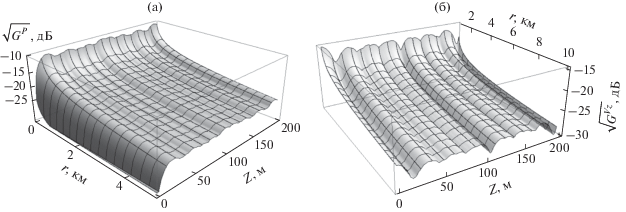
Приведенные на рис. 2б и 3 поверхности отчетливо отображают не заслоненные мелкомасштабными интерференционными колебаниями основные закономерности спадания полей с расстоянием и их изменения с глубиной приемника. В частности, видно, что спадание ЗД и ВПКС в зонах ИМА при увеличении расстояния внешне похоже на спадание регулярных составляющих: на нулевой глубине приемника давление равно нулю, а ВПКС отлична от нуля; на середине эквивалентной глубины волновода ЗД имеет локальный максимум, а колебательная скорость – минимум; обе поверхности симметричны относительно середины эквивалентной глубины волновода. Но ослабление поля при увеличении расстояния r происходит быстрее, чем для регулярной составляющей, а изменение поверхностей при увеличении глубины приемника носит ярко выраженный колебательный характер, зависящий от интерференции мод.
3. АППРОКСИМИРУЮЩИЕ СООТНОШЕНИЯ ДЛЯ ОПИСАНИЯ ПОВЕРХНОСТЕЙ ИНТЕРФЕРЕНЦИОННЫХ МАКСИМУМОВ
Для практических целей целесообразно иметь удобные приближенные аналитические соотношения, которыми по аналогии с оценками для спадания регулярных составляющих [2] можно аппроксимировать выражения (3)–(5) для функций, определяющих ПИМ давления и колебательной скорости. Отметим, что в [2] при аппроксимации соотношений, которые описывают регулярные составляющие квадратов модулей амплитуд давления, суммы приближенно заменялись интегралами. Однако напрямую использовать этот способ для аппроксимации функций, описывающих структуру ПИМ, нельзя, так как наличие модуля произведения тригонометрических функций под знаком интеграла приводит к невозможности вычислить его аналитически. Кроме того, как следует из рис. 2 и 3, форма поверхностей ИМА на малых глубинах или вблизи дна изменяется очень резко. Имеются также зоны интерференционных минимумов, где исследуемые зависимости изменяются непредсказуемым образом. Поэтому подобрать одну общую аппроксимацию ПИМ для всех глубин, по нашему мнению, невозможно.
В связи с указанными обстоятельствами 1область изменения глубин $0 \leqslant z,{{z}_{0}} \leqslant h$ разбивается на три подобласти, в каждой из которых можно индивидуальным способом освободиться от знака модуля и/или подобрать подходящую аппроксимацию. Такими подобластями могут быть интервалы приповерхностных, придонных и средних глубин. В дальнейшем для краткости будем называть “приграничными” приповерхностные глубины источника и излучателя, которые удовлетворяют условиям ${{0 \leqslant z,{{z}_{0}} \leqslant H} \mathord{\left/ {\vphantom {{0 \leqslant z,{{z}_{0}} \leqslant H} N}} \right. \kern-0em} N},$ а также, с учетом симметрии относительно середины эффективной толщины ${H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0em} 2}$ аргументов у функции, описывающей ПИМ, и придонные глубины ${{H - H} \mathord{\left/ {\vphantom {{H - H} {N \leqslant z,{{z}_{0}} \leqslant h}}} \right. \kern-0em} {N \leqslant z,{{z}_{0}} \leqslant h}}.$ Глубины, не удовлетворяющие этим условиям, т.е. относящиеся к средней части волновода – глубины ${H \mathord{\left/ {\vphantom {H {N \leqslant z,{{z}_{0}}}}} \right. \kern-0em} {N \leqslant z,{{z}_{0}}}}$ ≤ $H - {H \mathord{\left/ {\vphantom {H N}} \right. \kern-0em} N},$ условно назовем “средними”.
Для приграничных глубин $\left( {{{0 \leqslant z,{{z}_{0}} \leqslant H} \mathord{\left/ {\vphantom {{0 \leqslant z,{{z}_{0}} \leqslant H} N}} \right. \kern-0em} N}} \right)$ ∨ ∨ $\left( {{{H - H} \mathord{\left/ {\vphantom {{H - H} {N \leqslant z,{{z}_{0}} \leqslant h}}} \right. \kern-0em} {N \leqslant z,{{z}_{0}} \leqslant h}}} \right)$ знак модуля в (3) можно опустить. После чего можно применить способ, использованный в [2], и получить для малых расстояний, на которых $\delta r \ll 1,$ аппроксимирующее (3) выражение
Если учесть, что ${{E}_{c}}(x)$ = $\sum\nolimits_{l = 1}^N {\cos lх } $ = = $\cos (N + 1)$ $\frac{x}{2}\sin N\frac{x}{2}{{\sin }^{{ - 1}}}\frac{x}{2}$ [20], то на малых расстояниях приближенное соотношение ${{G}^{{*P}}}(r,{{z}_{0}},z)$ для функции ${{G}^{P}}(r,{{z}_{0}},z)$, может быть записано в виде ${{G}^{{*P}}}(r,{{z}_{0}},z)$ = $\frac{{{{A}^{p}}}}{{4r}}{{\left( {{{E}_{с }}({{b}_{1}}) - {{E}_{с }}({{b}_{2}})} \right)}^{2}}.$ А для больших расстояний, когда экспоненциальным сомножителем $\exp ( - \delta r{{l}^{2}})$ пренебречь невозможно, функцию, аппроксимирующую ПИМ ЗД, запишем так:
Здесь учтено, что
В случае, когда приграничным является источник ${{0 \leqslant {{z}_{0}} \leqslant H} \mathord{\left/ {\vphantom {{0 \leqslant {{z}_{0}} \leqslant H} N}} \right. \kern-0em} N}$ или ${{H - H} \mathord{\left/ {\vphantom {{H - H} {N \leqslant {{z}_{0}} \leqslant h}}} \right. \kern-0em} {N \leqslant {{z}_{0}} \leqslant h}},$ а глубина приемника находится в диапазоне ${H \mathord{\left/ {\vphantom {H N}} \right. \kern-0em} N} < z$ < $H - {H \mathord{\left/ {\vphantom {H N}} \right. \kern-0em} N},$ в соотношении (3) из-под знака модуля можно вынести только первый положительный сомножитель $\sin {{а }_{1}}l$. Для получения искомой аппроксимации остающийся в сумме (3) знакопеременный сомножитель $\sin {{a}_{2}}l$ заменяется средним по полупериоду значением: ${{|\sin {{a}_{2}}l| \approx 2} \mathord{\left/ {\vphantom {{|\sin {{a}_{2}}l| \approx 2} \pi }} \right. \kern-0em} \pi }.$ Тогда ${{G}^{p}}(r,{{z}_{0}},z)$ = $\frac{{{{A}^{p}}}}{r}$ ${{\left( {\sum\nolimits_{l = 1}^N {\left| {\sin l{{a}_{1}}\sin l{{a}_{2}}} \right|} {{e}^{{ - {\delta }r{{l}^{2}}}}}} \right)}^{2}}$ ≈ ≈ $\frac{{4{{A}^{p}}}}{{{{\pi }^{2}}r}}{{\left( {\sum\limits_{l = 1}^N {\sin l{{a}_{1}}{{e}^{{ - {\delta }r{{l}^{2}}}}}} } \right)}^{2}},$ ${{G}^{p}}(r,{{z}_{0}},z)$ ≈ $\frac{{4{{A}^{p}}}}{{{{\pi }^{2}}r}}$ × × ${{\left( {\sum\nolimits_{l = 1}^N {\sin l{{a}_{1}}} } \right)}^{2}},$ и для малых расстояний при $\delta r \ll 1$ аппроксимирующую зависимость для ПИМ ЗД запишем в виде ${{G}^{{*p}}}(r,{{z}_{0}},z)$ = = $\frac{{4{{A}^{p}}}}{{{{\pi }^{2}}r}}E_{s}^{2}({{a}_{1}}),$ где ${{E}_{s}}(x)$ = $\sum\nolimits_{l = 1}^N {\sin lх } .$ Для больших расстояний при аппроксимации описания ПИМ для ЗД сумму заменим интегралом: $\sum\nolimits_{l = 1}^N {\sin l{{a}_{1}}{{e}^{{ - \delta r{{l}^{2}}}}}} $ ≈ $\int_0^N {\sin {{a}_{1}}x{{e}^{{ - {\text{ }}\delta r{{x}^{2}}}}}} dx.$ Тогда аппроксимирующая зависимость для ПИМ ЗД представляется в следующем виде:
Аналогичные результаты можно получить и в случае, когда условию приграничности удовлетворяет глубина приемника ${{0 \leqslant z \leqslant H} \mathord{\left/ {\vphantom {{0 \leqslant z \leqslant H} N}} \right. \kern-0em} N}$ или ${{H - H} \mathord{\left/ {\vphantom {{H - H} {N \leqslant z \leqslant h}}} \right. \kern-0em} {N \leqslant z \leqslant h}},$ а источник находится на глубине ${H \mathord{\left/ {\vphantom {H {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}}} \right. \kern-0em} {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}}.$ Средняя подобласть характеризуется тем, что обе глубины ${{z}_{0}}$ и $z$ не удовлетворяют условиям приграничности ${H \mathord{\left/ {\vphantom {H {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}}} \right. \kern-0em} {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}},$ ${H \mathord{\left/ {\vphantom {H {{{N < z < H - H} \mathord{\left/ {\vphantom {{N < z < H - H} N}} \right. \kern-0em} N}}}} \right. \kern-0em} {{{N < z < H - H} \mathord{\left/ {\vphantom {{N < z < H - H} N}} \right. \kern-0em} N}}}$ и в сумме (3) оба тригонометрических сомножителя являются знакопеременными. Для получения приближенных зависимостей они заменяются средними по полупериоду гармонической функции значениями: ${{|\sin {{a}_{1}}l|\, \approx 2} \mathord{\left/ {\vphantom {{|\sin {{a}_{1}}l|\, \approx 2} \pi }} \right. \kern-0em} \pi }$ и ${{|\sin {{a}_{2}}l|\, \approx 2} \mathord{\left/ {\vphantom {{|\sin {{a}_{2}}l|\, \approx 2} \pi }} \right. \kern-0em} \pi }.$ Полученные в результате предлагаемого подхода аппроксимирующие выражения для разных глубин источника и приемника и для различных расстояний для функций ${{G}^{P}}(r,{{z}_{0}},z),$ описывающей ПИМ звукового давления, приведены в табл. 1. В этой таблице для каждого варианта сочетания глубин источника и приемника в третьем столбце вверху приведено соотношение для малых расстояний, а внизу – для больших.
Таблица 1.
Аппроксимирующие соотношения функции ПИМ ЗД монополя
| Ограничения на ${{z}_{0}}$ | Ограничения на $z$ | Аппроксимирующее соотношение |
|---|---|---|
| ${{0 \leqslant {{z}_{0}} \leqslant H} \mathord{\left/ {\vphantom {{0 \leqslant {{z}_{0}} \leqslant H} N}} \right. \kern-0em} N},$${{H - H} \mathord{\left/ {\vphantom {{H - H} {N \leqslant {{z}_{0}} \leqslant h}}} \right. \kern-0em} {N \leqslant {{z}_{0}} \leqslant h}}$ | ${{0 \leqslant z \leqslant H} \mathord{\left/ {\vphantom {{0 \leqslant z \leqslant H} N}} \right. \kern-0em} N},$${{H - H} \mathord{\left/ {\vphantom {{H - H} {N \leqslant z \leqslant h}}} \right. \kern-0em} {N \leqslant z \leqslant h}}$ | $G_{{}}^{p} \approx \frac{{{{A}^{p}}}}{{4r}}{{\left( {{{E}_{с }}({{b}_{1}}) - {{E}_{с }}({{b}_{2}})} \right)}^{2}}$ |
| $G_{{}}^{p} \approx \frac{{{{A}^{p}}\pi }}{{16\delta {{r}^{2}}}}{{\left( {S({{b}_{1}}) - S({{b}_{2}})} \right)}^{2}}$ | ||
| ${{0 \leqslant {{z}_{0}} \leqslant H} \mathord{\left/ {\vphantom {{0 \leqslant {{z}_{0}} \leqslant H} N}} \right. \kern-0em} N},$${{H - H} \mathord{\left/ {\vphantom {{H - H} {N \leqslant {{z}_{0}} \leqslant h}}} \right. \kern-0em} {N \leqslant {{z}_{0}} \leqslant h}}$ | ${H \mathord{\left/ {\vphantom {H {{{N < z < H - H} \mathord{\left/ {\vphantom {{N < z < H - H} N}} \right. \kern-0em} N}}}} \right. \kern-0em} {{{N < z < H - H} \mathord{\left/ {\vphantom {{N < z < H - H} N}} \right. \kern-0em} N}}}$ | $G_{{}}^{p} \approx \frac{{4{{A}^{p}}}}{{{{\pi }^{2}}r}}E_{S}^{2}({{a}_{1}})$ |
| $G_{{}}^{p} \approx \frac{{{{A}^{p}}}}{{\pi \delta {{r}^{2}}}}\exp \left( { - 2t_{1}^{2}} \right){{\operatorname{Im} }^{2}}\left( {{\text{erf}}\left( {i{{t}_{1}}} \right) - {\text{erf}}\left( {N\sqrt {\delta r} + i{{t}_{1}}} \right)} \right)$ | ||
| ${H \mathord{\left/ {\vphantom {H {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}}} \right. \kern-0em} {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}}$ | ${{0 \leqslant z \leqslant H} \mathord{\left/ {\vphantom {{0 \leqslant z \leqslant H} N}} \right. \kern-0em} N},$${{H - H} \mathord{\left/ {\vphantom {{H - H} {N \leqslant z \leqslant h}}} \right. \kern-0em} {N \leqslant z \leqslant h}}$ | $G_{{}}^{p} \approx \frac{{4{{A}^{p}}}}{{{{\pi }^{2}}r}}E_{s}^{2}({{a}_{2}})$ |
| $G_{{}}^{p} \approx \frac{{{{A}^{p}}}}{{\pi \delta {{r}^{2}}}}\exp \left( { - 2t_{2}^{2}} \right){{\operatorname{Im} }^{2}}\left( {{\text{erf}}\left( {i{{t}_{2}}} \right) - {\text{erf}}\left( {N\sqrt {\delta r} + i{{t}_{2}}} \right)} \right)$ | ||
| ${H \mathord{\left/ {\vphantom {H {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}}} \right. \kern-0em} {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}}$ | ${H \mathord{\left/ {\vphantom {H {{{N < z < H - H} \mathord{\left/ {\vphantom {{N < z < H - H} N}} \right. \kern-0em} N}}}} \right. \kern-0em} {{{N < z < H - H} \mathord{\left/ {\vphantom {{N < z < H - H} N}} \right. \kern-0em} N}}}$ | $G_{{}}^{p} \approx \frac{{4{{A}^{P}}}}{{{{\pi }^{3}}\delta {{r}^{2}}}}{\text{er}}{{{\text{f}}}^{2}}\left( {N\sqrt {\delta r} } \right)$ |
Выражение (4) для функции ${{G}^{{Vr}}}(r,{{z}_{0}},z),$ которая описывает поверхность, ограничивающую интерференционную поверхность ГПКС, отличается от (3) для функции ${{G}^{p}}(r,{{z}_{0}},z),$ ограничивающей интерференционную поверхность ЗД, только наличием под знаком суммы сомножителя $\sqrt {1 - {{l}^{2}}{{d}^{2}}} .$ Учитывая малость значений параметра $d < 1,$ для любых номеров $l$ нормальных волн справедливо $\sqrt {1 - {{l}^{2}}{{d}^{2}}} \leqslant \sqrt {1 - {{d}^{2}}} .$ Поэтому аппроксимации интерференционной поверхности ГПКС для всех сочетаний глубин и расстояний находятся умножением на полином $1 - {{d}^{2}}$ соответствующих соотношений для ЗД из табл. 1.
В соотношении (5), определяющем ПИМ для ВПКС, функция ${{\cos l{{a}_{2}} = \cos l\pi z} \mathord{\left/ {\vphantom {{\cos l{{a}_{2}} = \cos l\pi z} H}} \right. \kern-0em} H}$ остается положительной для любых номеров l, если удовлетворяется неравенство ${{\pi zN} \mathord{\left/ {\vphantom {{\pi zN} {{{H \leqslant \pi } \mathord{\left/ {\vphantom {{H \leqslant \pi } 2}} \right. \kern-0em} 2}}}} \right. \kern-0em} {{{H \leqslant \pi } \mathord{\left/ {\vphantom {{H \leqslant \pi } 2}} \right. \kern-0em} 2}}}.$ Значит, для ВПКС “приграничными” следует считать приповерхностные ${{0 \leqslant z \leqslant 0.5H} \mathord{\left/ {\vphantom {{0 \leqslant z \leqslant 0.5H} N}} \right. \kern-0em} N}$ и придонные ${{H - 0.5H} \mathord{\left/ {\vphantom {{H - 0.5H} N}} \right. \kern-0em} N}$ ≤ $z \leqslant h$ глубины. Соответственно, для глубины приемника изменяется понятие “средней” глубины: ${{0.5H} \mathord{\left/ {\vphantom {{0.5H} N}} \right. \kern-0em} N} \leqslant z$ ≤ $H - {{0.5H} \mathord{\left/ {\vphantom {{0.5H} N}} \right. \kern-0em} N}.$ Глубина источника ${{z}_{0}}$ по-прежнему связана с функцией синус, и ограничения для подобластей глубин источника не изменяются. Полученные с учетом указанной особенности аппроксимирующие соотношения для функции ПИМ ВПКС монополя (5) приведены в табл. 2.
Таблица 2.
Аппроксимирующие соотношения функции ПИМ ВПКС монополя
| Ограничения на ${{z}_{0}}$ | Ограничения на $z$ | Аппроксимирующее соотношение |
|---|---|---|
| ${{0 \leqslant {{z}_{0}} \leqslant H} \mathord{\left/ {\vphantom {{0 \leqslant {{z}_{0}} \leqslant H} N}} \right. \kern-0em} N},$${{H - H} \mathord{\left/ {\vphantom {{H - H} {N \leqslant {{z}_{0}} \leqslant h}}} \right. \kern-0em} {N \leqslant {{z}_{0}} \leqslant h}}$ | ${{0 \leqslant z \leqslant 0.5H} \mathord{\left/ {\vphantom {{0 \leqslant z \leqslant 0.5H} N}} \right. \kern-0em} N},$${{H - 0.5H} \mathord{\left/ {\vphantom {{H - 0.5H} {N \leqslant z \leqslant h}}} \right. \kern-0em} {N \leqslant z \leqslant h}}$ | |
| ${{G}^{{Vz}}} \approx {{d}^{2}}\frac{{{{A}^{V}}}}{{16{{\delta }^{2}}{{r}^{3}}}}(0.5\sqrt {{\pi \mathord{\left/ {\vphantom {\pi {\delta r}}} \right. \kern-0em} {\delta r}}} \left( {{{b}_{1}}S({{b}_{1}}) + {{b}_{2}}S({{b}_{2}})} \right) - $ $ - \,\,{{e}^{{ - \delta r{{N}^{2}}}}}{{\left( {\sin N{{b}_{1}} + \sin N{{b}_{2}})} \right)}^{2}}$ |
||
| ${{0 \leqslant {{z}_{0}} \leqslant H} \mathord{\left/ {\vphantom {{0 \leqslant {{z}_{0}} \leqslant H} N}} \right. \kern-0em} N},$${{H - H} \mathord{\left/ {\vphantom {{H - H} {N \leqslant {{z}_{0}} \leqslant h}}} \right. \kern-0em} {N \leqslant {{z}_{0}} \leqslant h}}$ | $\begin{gathered} {{0.5H} \mathord{\left/ {\vphantom {{0.5H} {N \leqslant z \leqslant }}} \right. \kern-0em} {N \leqslant z \leqslant }} \hfill \\ {{ \leqslant H - 0.5H} \mathord{\left/ {\vphantom {{ \leqslant H - 0.5H} N}} \right. \kern-0em} N} \hfill \\ \end{gathered} $ | ${{G}^{{Vz}}} \approx {{d}^{2}}\frac{{4{{A}^{V}}}}{{{{\pi }^{2}}r}}E_{s}^{{'2}}({{a}_{1}})$ |
| ${{G}^{{Vz}}} \approx {{d}^{2}}\frac{{{{A}^{V}}}}{{{{\pi }^{2}}{{\delta }^{2}}{{r}^{3}}}}{{\left( {\frac{1}{2}\sqrt {\frac{\pi }{{\delta r}}} {{a}_{1}}S({{a}_{1}}) - {{e}^{{ - \delta r{{N}^{2}}}}}\sin N{{a}_{1}}} \right)}^{2}}$ | ||
| ${H \mathord{\left/ {\vphantom {H {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}}} \right. \kern-0em} {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}}$ | ${{0 \leqslant z \leqslant 0.5H} \mathord{\left/ {\vphantom {{0 \leqslant z \leqslant 0.5H} N}} \right. \kern-0em} N},$${{H - 0.5H} \mathord{\left/ {\vphantom {{H - 0.5H} {N \leqslant z \leqslant h}}} \right. \kern-0em} {N \leqslant z \leqslant h}}$ | ${{G}^{{Vz}}} \approx {{d}^{2}}\frac{{4{{A}^{V}}}}{{{{\pi }^{2}}r}}E_{с }^{{'2}}({{a}_{2}})$ |
| ${{G}^{{Vz}}} \approx {{d}^{2}}\frac{{{{A}^{V}}}}{{{{\pi }^{2}}{{\delta }^{2}}{{r}^{3}}}}\left( {1 - {{e}^{{ - \delta r{{N}^{2}}}}}\cos {{a}_{2}}N} \right.{{\left. { - \frac{{{{a}_{2}}}}{{{{{(\delta r)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left( {{\text{DasonF}}(t) - {{e}^{{ - \delta r{{N}^{2}}}}}V} \right)} \right)}^{2}}$ | ||
| ${H \mathord{\left/ {\vphantom {H {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}}} \right. \kern-0em} {{{N < {{z}_{0}} < H - H} \mathord{\left/ {\vphantom {{N < {{z}_{0}} < H - H} N}} \right. \kern-0em} N}}}$ | $\begin{gathered} {{0.5H} \mathord{\left/ {\vphantom {{0.5H} {N \leqslant z \leqslant }}} \right. \kern-0em} {N \leqslant z \leqslant }} \hfill \\ {{ \leqslant H - 0.5H} \mathord{\left/ {\vphantom {{ \leqslant H - 0.5H} N}} \right. \kern-0em} N} \hfill \\ \end{gathered} $ | ${{G}^{{Vz}}} \approx {{d}^{2}}\frac{{4{{A}^{V}}}}{{{{\pi }^{4}}{{\delta }^{2}}{{r}^{3}}}}{{\left( {1 - {{e}^{{ - \delta r{{N}^{2}}}}}} \right)}^{2}}$ |
В таблицах обозначено: $E_{s}^{'}(x) = \sum\nolimits_{l = 1}^N {l\sin lx} ,$ $E_{c}^{'}(x)$ = $\sum\nolimits_{l = 1}^N {l\cos lх } ,$ $V = \operatorname{Re} (U)\cos {{a}_{2}}N$ – $\operatorname{Im} (U)\sin {{a}_{2}}N,$ $U = {\text{DasonF}}({{t}_{2}} + iN\sqrt {\delta r} ),$ ${\text{DasonF}}(z)$ = $i\sqrt {\frac{\pi }{2}} {{e}^{{ - {{z}^{2}}}}}$ × × ${\text{erf}}( - iz).$
Сравнивая приведенные в табл. 1 и 2 соотношения с аппроксимирующими зависимостями для регулярных составляющих [2, 19], делаем вывод, что во всех рассмотренных случаях величины ЗД, ГПКС и ВПКС в зонах ИМА убывают в $\sqrt r $ раз быстрее, но законы спадания для ВПКС существенно отличаются от законов ослабления ЗД и ГПКС. Это свойство характерно как для регулярных составляющих поля, так и для полей в зонах ИМА.
4. ЧИСЛЕННЫЙ АНАЛИЗ ПОГРЕШНОСТИ АППРОКСИМАЦИИ ИССЛЕДУЕМЫХ ХАРАКТЕРИСТИК СИГНАЛОВ
Рассмотрим результаты численного моделирования. На рис. 4 приведены вычисленные с использованием соотношений (3)–(5) зависимости ПИМ от расстояния и глубины приемника (рис. 4а, 4в), а также аппроксимирующие поверхности (рис 4б, 4г). Излучатель располагался на глубине 5 м. Частота звука 25 Гц. Для этих условий максимальные погрешности аппроксимации оказались менее 1.4 дБ для ЗД и ГПКС и 2.1 дБ для ВПКС.
Рис. 4.
Поверхности интерференционных максимумов ЗД (а) и ВПКС (в), а также поверхности их аппроксимаций (б) и (г). Источник на глубине ${{z}_{0}}$ = 5 м, частота 25 Гц.
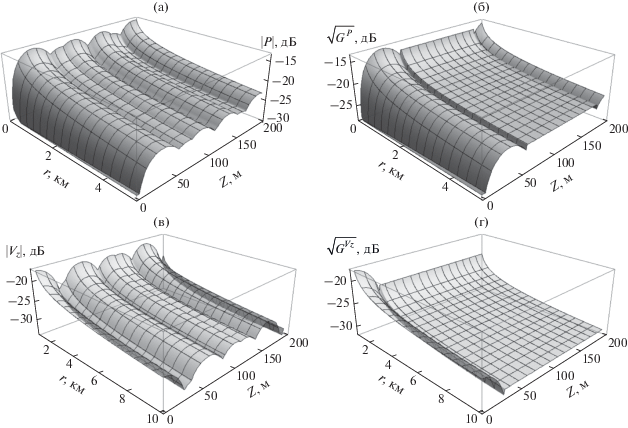
На рис. 4 хорошо видно, как резко изменяется величина как ЗД, так и ВПКС при приближении источника или приемника к свободной поверхности. Заметен также “провал” в зоне “стыка” двух типов аппроксимации (рис. 4б). Существенно, что такие провалы можно сделать меньше, но тогда увеличивается общая погрешность либо в приграничной, либо в срединной зонах. Необходим выбор компромиссного варианта.
Следует также обратить внимание, что на аппроксимирующих поверхностях в зоне средних глубин интерференционная структура “вырождается”, но сохраняет при увеличении расстояния “генеральный” наклон рельефа. Причина в том, что при аппроксимации в этой зоне синусоидальные зависимости от глубины заменялись средними по полупериоду гармонической функции значениями ${{|\sin {{{\alpha }}_{1}}l|\, \approx 2} \mathord{\left/ {\vphantom {{|\sin {{{\alpha }}_{1}}l|\, \approx 2} {\pi }}} \right. \kern-0em} {\pi }}$ и ${{|\cos {{{\alpha }}_{2}}l|\, \approx 2} \mathord{\left/ {\vphantom {{|\cos {{{\alpha }}_{2}}l|\, \approx 2} {\pi }}} \right. \kern-0em} {\pi }}.$ Поэтому понятие “погрешность” следует понимать в определенном смысле условно. В действительности это не погрешность, а “отклонение” усредненной по глубине величины от интерферирующей. Однако видно, что и в этом случае характеристики поля вблизи границ раздела в полной мере учитывают их влияние.
На рис. 5 изображены некоторые сечения поверхностей ИМА и их аппроксимаций, представленных на рис. 4 – кривые для ИМА (сплошные линии) и их аппроксимации (пунктирные линии). Видно, что точное решение и аппроксимация достаточно хорошо согласуются между собой – максимальные погрешности аппроксимации составляют 1.4 дБ для звукового давления и ГПКС и 1.8 дБ для ВПКС.
Рис. 5.
Кривые для описания максимумов ЗД (а, б) и максимумов ВПКС (в, г), а также их аппроксимации для глубин: источника ${{z}_{0}}$ = 5 м, приемника $z$ = 80 м. Частота 25 Гц.

Для выявления общих свойств полученных аппроксимирующих соотношений проведены численные эксперименты, при которых рассчитывались абсолютные величины разностей ${{\Delta }^{p}}(r,{{z}_{0}},z)$ = = $\left| {\sqrt {{{G}^{p}}(r,{{z}_{0}},z)} } \right.$ – $\left. {\sqrt {{{G}^{{*p}}}(r,{{z}_{0}},z)} } \right|,$ ${{\Delta }^{{Vr}}}(r,{{z}_{0}},z)$ = = $\left| {\sqrt {{{G}^{{Vr}}}(r,{{z}_{0}},z)} } \right.$ – $\left. {\sqrt {{{G}^{{*Vr}}}(r,{{z}_{0}},z)} } \right|$ и ${{\Delta }^{{Vz}}}(r,{{z}_{0}},z)$ = = $\left| {\sqrt {{{G}^{{Vz}}}(r,{{z}_{0}},z)} } \right.$ – $\left. {\sqrt {{{G}^{{*Vz}}}(r,{{z}_{0}},z)} } \right|$ между функциями интерференционных максимумов ${{G}^{p}},$ ${{G}^{{Vr}}},$ ${{G}^{{Vz}}}$ и зависящими от подобласти и зоны расстояний соответствующими аппроксимациями ${{G}^{{*p}}},$ ${{G}^{{*Vr}}}$ и ${{G}^{{*Vz}}}.$ В проведенных расчетах частота изменялась от 25 до 200 Гц, а коэффициент поглощения дна принимал значения 0.001, 0.01, 0.05, 0.1 и 0.2.
Расчеты, выполненные для волновода Пекериса, показали, что наиболее значимыми факторами, которые влияют на величину погрешности аппроксимации, являются частота источника и коэффициент поглощения дна. Увеличение частоты источника вследствие увеличения количества нормальных волн и сглаживания рельефа естественным образом приводит к уменьшению погрешности аппроксимаций, которые получены заменой сумм интегралами. Увеличение коэффициента поглощения в дне влияет на показатель $\delta r$ в находящихся под знаком сумм экспонентах, что приводит к быстрому затуханию мод с высокими номерами и усилению интерференции, а это в свою очередь приводит к ухудшению аппроксимирующих свойств полученных соотношений.
На рис. 6 приведены поверхности погрешностей (отклонений) аппроксимаций, рассчитанные при вариации глубин источника и приемника. Представлены максимальные значения функций ${{\Delta }^{P}},$ ${{\Delta }^{{Vr}}}$ и ${{\Delta }^{{Vz}}}$ при изменении расстояний в диапазоне от 100 до 5000 м: ${{\Delta }^{P}}({{z}_{0}},z)$ = $\mathop {\max }\limits_{100\,\, \leqslant \,\,r\,\, \leqslant \,\,5000} {{\Delta }^{P}}(r,{{z}_{0}},z),$ ${{\Delta }^{{Vr}}}({{z}_{0}},z)$ = $\mathop {\max }\limits_{100\,\, \leqslant \,\,r\,\, \leqslant \,\,5000} {{\Delta }^{{Vr}}}(r,{{z}_{0}},z)$ и ${{\Delta }^{{Vz}}}({{z}_{0}},z)$ = = $\mathop {\max }\limits_{100\,\, \leqslant \,\,r\,\, \leqslant \,\,5000} {{\Delta }^{{Vz}}}(r,{{z}_{0}},z).$ В этих расчетах частота была равна 50 Гц, а коэффициент поглощения в дне – 0.05.
Рис. 6.
Поверхности погрешностей аппроксимации в зависимости от глубин приемника и источника: (а) ЗД и (б) ВПКС. Частота 50 Гц.
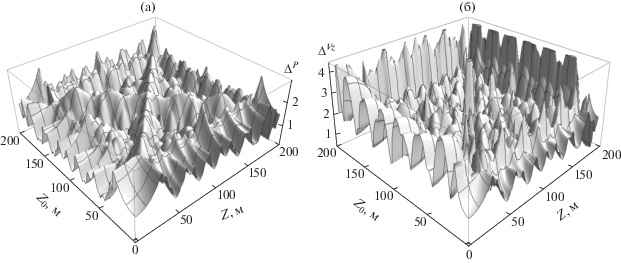
В указанном выше диапазоне изменения частот, коэффициентов поглощения дна, а также горизонтальных расстояний между источником и приемником максимальная погрешность аппроксимации функций максимумов ЗД и ГПКС – не превышает 3.2 дБ. Аппроксимация функции максимумов ВПКС осуществляется с более высокой максимальной погрешностью – до 8 дБ. Но эти погрешности, особенно для ВПКС, локализуются в основном при расположении источника или приемника в зонах интерференционных минимумов и вблизи свободной поверхности или у дна, т.е. в “приграничных” зонах. Отклонения усредненных величин от значений в зонах ИМА в несколько раз меньше. Иными словами, погрешность аппроксимации существенно возрастает в зонах с большими и непредсказуемыми градиентами амплитуды и фазы, что представляется естественным. Большие погрешности в зонах интерференционных минимумов объясняются также тем, что при описании поля в этих зонах динамики амплитуды, и особенно фазы, практически не предсказуемы и не контролируются, особенно при наличии помех.
Установлено также, что большие значения погрешности наблюдаются на границах “склеивания” различных вариантов аппроксимации. А для ВПКС максимальные погрешности связаны еще и с положением приемника (или излучателя) вблизи середины эффективной толщины волновода, так как при их нахождении на этой глубине вертикальная проекция колебательной скорости обращается в нуль. Соответственно, вблизи этой глубины наблюдается зона минимума поля ВПКС и максимальные погрешности аппроксимаций. Вне указанных глубин погрешности аппроксимации функций максимумов ЗД и ГПКС не превышают 2 дБ, а для функции максимумов ВПКС – 4 дБ.
ЗАКЛЮЧЕНИЕ
Характер зависимостей ЗД и проекций КС в зонах ИМА от расстояния существенно различается для малых и больших расстояний между источником и приемником и в среднем заметно различается для разных глубин расположения приемников и излучателя. При их расположении вблизи свободной поверхности или у дна спадание всех составляющих поля в зонах ИМА происходит еще быстрее, чем поля в срединной части волновода. Но аппроксимирующие зависимости для всех расстояний и выбранных глубин дают достаточно точный прогноз вырождения интерференционной структуры поля как для ЗД, так и для проекций КС. Это позволяет выполнять в зонах ИМА оценку законов спадания характеристик всех составляющих поля, не прибегая к сложным полевым расчетам.
Введение ПИМ позволяет дать укрупненное описание пространственно-частотной структуры зон ИМА при изменении расстояния и частоты звука. Этот результат может использоваться при выборе и обосновании алгоритмов обнаружения и оценки параметров источников, учитывающих интерференционную структуру звукового поля [13–16]. Согласие зависимостей от расстояния или частоты характеристик ПИМ для ЗД и ГПКС свидетельствует о высокой корреляции огибающих этих зависимостей [21] и возможности увеличения помехоустойчивости обнаружения векторно-скалярными приемниками, совместно использующими звуковую энергию ЗД и ГПКС [14]. Зависимости от расстояния ВПКС существенно отличаются от аналогичных зависимостей для ЗД и ГПКС. Это подтверждается уменьшением корреляции между ВПКС и ЗД (ГПКС) [21].
В результате выполненных аппроксимаций поля удается дать достаточно точное описание зависимостей ЗД, ГПКС и ВПКС от расстояния не только регулярной составляющей [2], но и их интерференционной структуры в зонах ИМА. Зависимости от расстояния максимальных значений горизонтальных проекций вектора колебательной скорости практически совпадают с аналогичными зависимостями для ЗД. Максимальные значения вертикальных проекций КС ослабляются при увеличении расстояния еще быстрее, чем регулярные составляющие для этой проекции или ЗД и ГПКС в зонах ИМА. Иными словами, основной вывод, полученный в [17] только для поля ЗД в ограниченном интервале расстояний и на предельных глубинах – ускоренный спад ЗД в зонах ИМА – может быть распространен на все глубины и все, т.е. малые и большие расстояния, а также применим не только для ЗД, но и для векторных проекций – ГПКС и ВПКС.
При распространении сигналов на большие расстояния дополнительно проявляются волнение свободной поверхности и расчлененность поверхности грунта. Влияет также неоднородность гидрологических характеристик в водном слое. Это приведет к уменьшению когерентности однотипных и разнотипных мод и дополнительному ускорению спадания величины сигналов в зонах интерференционных максимумов по сравнению с полученными в статье зависимостями. Эта проблема требует дополнительного рассмотрения.
Работа выполнена при финансовой поддержке программы “Акустика мелкого моря, нелинейная акустическая диагностика, нелинейная динамика волн” (номер гос. регистрации AAAA-A18-118021390174-1).
Список литературы
Бреховских Л.М. Волны в слоистых средах. М.: Изд-во АН СССР, 1957. 502 с.
Кузнецов Г.Н., Степанов А.Н. Аппроксимирующие модели регулярной составляющей инфразвукового поля мультипольных источников в плоском волноводе // Акуст. журн. 2013. Т. 59. № 3. С. 378–390.
Урик Р.Дж. Основы гидроакустики. Л.: Судостроение, 1978. 448 с.
Грачев Г.А., Кузнецов Г.Н. О средней скорости изменения фазы акустического поля вдоль плоского волновода // Акуст. журн. 1985. Т. 31. № 2. С. 266–268.
Kuznetsov G.N., Stepanov A.N. Interference and phase structure of the low-frequency vector-scalar field in shallow water for variable reception or transmission depths // Phys. Wave Phenom. 2015. V. 23. № 4. P. 279–291.
Kuznetsov G.N., Lebedev O.V. The use of effective phase velocity to decrease the direction finding error for a low-frequency signal in a waveguide // Phys. Wave Phenom. 2012. V. 20. № 1. P. 58–66.
Кузнецов Г.Н., Степанов А.Н. Амплитудно-фазовая структура векторно-скалярного низкочастотного поля в мелком море // Гидроакустика. 2016. Т. 27(3). С. 23–37.
Орлов Е.Ф., Шаронов Г.А. Интерференция звуковых волн в океане. Владивосток: Дальнаука, 1998. 196 с.
Чупров С.Д. Интерференционная структура звукового поля в слоистом океане / Акустика океана. Современное состояние. М.: Наука, 1982. C. 71–82.
Касаткин Б.А. Инвариантные характеристики звукового поля в слоистом океане // Докл. АН СССР. 1986. Т. 291. № 6. С. 1483–1487.
Кузькин В.М., Лин Й.-Т., Луньков А.А., Линч Дж.Ф., Петников В.Г. Частотные смещения интерференционной структуры звукового поля в летний период времени на океанском шельфе // Акуст. журн. 2011. Т. 57. № 3. С. 387–397.
Kuz’kin V.M., Lyakhov G.A., Pereselkov S.A. Method for measuring the frequency shifts of interference maxima in monitoring of dispersion media: theory, implementation, and prospects // Phys. Wave Phenom. 2010. V. 18. № 3. P. 196−222.
Каришнев Н.С., Кузнецов Г.Н., Луньков А.А. Анализ надводной обстановки с использованием векторно-скалярной цилиндрической антенны // Гидроакустика. 2015. Т. 23(3). С. 27–40.
Казначеев И.В., Кузнецов Г.Н., Кузькин В.М., Переселков С.А. Интерферометрический метод обнаружения движущегося источника звука векторно-скалярным приемником // Акуст. журн. 2018. Т. 64. № 1. С. 33−45.
Кузнецов Г.Н., Кузькин В.М., Переселков С.А., Просовецкий Д.Ю. Помехоустойчивость интерферометрического метода оценки скорости источника звука в мелком море // Акуст. журн. 2016. Т. 62. № 5. С. 556−572.
Кузнецов Г.Н., Кузькин В.М., Переселков С.А. Спектрограмма и локализация источника звука в мелком море // Акуст. журн. 2017. Т. 63. № 4. С. 406–418.
Грачев Г.А., Кузнецов Г.Н. Ослабление интерференционных максимумов акустического поля в мелком море // Акуст. журн. 1985. Т. 31. № 5. С. 675–678.
Kuznetsov G.N., Stepanov A.N. Laws approximating the decay of the vector fields of the vibration velocity and intensity for a monopole source in a waveguide // Phys. Wave Phenom. 2016. V. 24. № 4. P. 324–332.
Кузнецов Г.Н., Степанов А.Н. Приближенные аналитические представления законов спадания векторно-скалярных полей мультипольных источников в волноводе Пекериса // Акуст. журн. 2017. Т. 63. № 6. С. 623–636.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. 4‑е изд. М.: Физматгиз, 1963. 1100 с.
Белов А.И., Кузнецов Г.Н. Пеленгование и подавление векторно-скалярных звуковых сигналов в мелком море с учетом их корреляционной и модовой структуры // Акуст. журн. 2016. Т. 62. № 3. С. 308–317.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал