Акустический журнал, 2019, T. 65, № 2, стр. 197-202

Для задач акустической томографии океана необходимо развитие теоретических моделей как зондирующих сигналов, так и акустических помех естественного происхождения. Одной из таких помех, постоянно наблюдаемых в натурных условиях, является динамический шум, генерируемый ветровым волнением. Основной сложностью построения адекватной модели динамических шумов океана является учет всех факторов волноводного распространения шумового поля, поскольку процесс его генерации исследован относительно хорошо. В подавляющем большинстве работ рассматривалось формирование динамического шума в плоскослоистом волноводе [1]. Позднее были предприняты попытки учесть эффекты многократного рассеяния шумового поля в волноводе с флуктуирующими параметрами [2–4]. В океанических волноводах, открытых к поверхности, основным источником таких флуктуаций является ветровое волнение, т.е. шумовое поле не только генерируется ветровым волнением, но и испытывает многократное рассеяние на взволнованной морской поверхности.

При рассмотрении этих эффектов основные результаты были получены для идеализированной модели изотропного ветрового волнения [3] и предварительные – для упрощенной модели его частотно-углового спектра [4]. В данной работе рассматривается влияние ветрового волнения на формирование динамического шума для адекватной модели морского волнения с эмпирическим частотно-угловым спектром. Основное внимание уделяется горизонтальной анизотропии динамического шума, которая возникает в открытом море, вдали от берегового шельфа и исключительно вследствие эффектов многократного рассеяния. Проведено численное моделирование углового спектра (в горизонтальной плоскости) низкочастотного динамического шума для типичной гидрологии зимнего типа как в мелком море, так и в глубоком океане.

Рассмотрим акустическое поле, генерируемое дипольными источниками [1] ветрового шума, однородно распределенными на свободной поверхности океанического волновода. Волновод предполагается плоскослоистым с профилем скорости звука $с \left( z \right)$ и, вообще говоря, многослойным дном. Свободная граница описывается уравнением $z = \zeta \left( {{\mathbf{r}},t} \right),$ где случайные вертикальные смещения $\zeta \left( {{\mathbf{r}},t} \right)$ со средним, равным нулю, обусловлены ветровым волнением. Для акустики мелкого моря наибольший интерес представляет низкочастотный диапазон с верхней границей $f* \leqslant 300\;{\text{Г ц }}{\text{.}}$ При этом для типичных скоростей ветра $V < 15\;{\text{м /с }}$ среднеквадратичная амплитуда $\sqrt {\left\langle {{{\zeta }^{2}}} \right\rangle } $ и частота $\omega *,$ как правило, удовлетворяют условию малости параметра Рэлея:

где ${{\theta }_{{{\text{crit}}}}}$ – критический угол волновода. В случае модового описания поля это условие означает малость эффектов однократного рассеяния мод, локализованных в волноводе, но позволяет описывать не малые эффекты многократного рассеяния. Исходным для анализа является стационарное уравнение переноса для интенсивности мод в волноводе с нерегулярной границей [3], описывающее совместные эффекты генерации мод дипольными источниками и рассеяние их на взволнованной морской поверхности. В случае статистически однородного и стационарного шумового поля это уравнение имеет вид где ${{N}_{n}}$ – интенсивность моды, ${{W}_{{mn}}}$ – вероятность перехода энергии между модами дискретного спектра, ${{\gamma }_{n}}$ – декремент затухания когерентной компоненты вследствие рассеяние моды на нерегулярной границе, $\operatorname{Im} {{k}_{n}}$ – мнимая часть волнового числа, обусловленная затуханием моды в донном грунте и водной среде, ${{Q}_{n}}$ – дипольный источник шума для моды с индексом n.

При произвольном значении частоты спектра шума и скорости ветра система уравнений (2) может быть решена лишь численными методами, но в интересующем нас диапазоне частот $f \leqslant 300\;{\text{Г ц }}$ и скоростей ветра $V < 15\;{\text{м /с }}$ можно использовать приближенное решение. Действительно, по определению, декремент ${{\gamma }_{n}}$ имеет вид

где второе слагаемое описывает рассеяние n-й моды во все моды сплошного спектра, т.е. излучение ее из волновода. Таким образом, параметр

всегда меньше единицы. Более того, как показывают оценки, при типичных значениях ${{\theta }_{{{\text{crit}}}}}\sim 0.2 \ldots 0.3$ и с учетом $f \leqslant 300\;{\text{Г ц }}$, $V < 15\;{\text{м /с }}$ параметр ${{\varepsilon }_{n}} \ll 1,$ а значит, и решение уравнения (2) можно искать в виде разложения по этому малому параметру. Ограничиваясь главным членом этого разложения, получим, что

При этом дипольный источник шума ${{Q}_{n}}$ имеет вид

где ${{\rho }_{0}}$ – плотность воды, $s\left( {{{k}_{x}},{{k}_{y}}} \right)$ – спектр дипольного момента давления на свободной поверхности. Декремент ${{\gamma }_{n}}$ может быть выражен через частотно-угловой спектр ветрового волнения $B\left( {\Omega ,\theta } \right)$ в виде где g – ускорение свободного падения, ${{k}_{0}} = {\omega \mathord{\left/ {\vphantom {\omega {c\left( 0 \right)}}} \right. \kern-0em} {c\left( 0 \right)}}.$ Заметим, что приведенная формула для ${{\gamma }_{n}}$ учитывает как рассеяние n-й моды во все моды дискретного спектра, так и рассеяние ее в моды сплошного спектра. Эмпирические спектры ветрового волнения обычно приводят в виде произведения частотного спектра $S\left( \Omega \right)$ и нормированного углового спектра $Q\left( {\Omega ,\theta } \right),$ т.е.

В дальнейшем для частотного спектра $S\left( \Omega \right)$ мы будем использовать общепринятую модель JONSWAP, а для углового спектра $Q\left( {\Omega ,\theta } \right)$ – эмпирический спектр, полученный в серии натурных экспериментов на разных стадиях развития ветрового волнения [5]:

Здесь α – направление ветра, ${{\Omega }_{m}}$ – частота спектрального максимума, причем для развитого волнения ${{\Omega }_{m}} = {{0.8g} \mathord{\left/ {\vphantom {{0.8g} V}} \right. \kern-0em} V},$ а для неразвитого значение ${{\Omega }_{m}}$ зависит от времени (дистанции) развития волнения. Для эмпирических констант β и γ выберем средние значения $\beta = 8 \times {{10}^{{ - 3}}},$ $\gamma = 3.3.$ В дальнейшем нас будет интересовать угловое распределение в горизонтальной плоскости энергии динамического шума для акустических мод с различными номерами. При этом можно сделать ряд замечаний общего характера, т.е. не зависящих от конкретного вида звукового канала и параметров задачи. Из физических соображений очевидно, что угловой спектр шума симметричен относительно направления ветра и поэтому в ¹дальнейшем будет анализироваться в диапазоне углов $0 \leqslant \alpha \leqslant \pi .$ При этом, как это следует из формул (7)−(12), в этом диапазоне углов он также симметричен относительно направления, перпендикулярного ветру, т.е. угла $\alpha = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$ Из формул (5) также очевидно, что степень горизонтальной анизотропии шумового поля зависит от соотношения эффектов рассеяния и объемных потерь в волноводе, т.е. величин ${{\gamma }_{n}}$ и $\left. {\left| {\operatorname{Im} {{k}_{n}}} \right.} \right|.$ Существенной анизотропии можно ожидать лишь при условии ${{\gamma }_{n}} \geqslant \left| {\operatorname{Im} \left. {{{k}_{n}}} \right|} \right..$ Это условие, однако, не является достаточным, поскольку в некоторых ситуациях декремент ${{\gamma }_{n}}$ может также обладать слабой угловой зависимостью. Анализ формул (7)–(9) показывает, что угловая зависимость ${{\gamma }_{n}}$ наиболее выражена для низших мод с волновыми числами ${{k}_{n}},$ удовлетворяющих условию ${{{{k}_{0}} - {{k}_{n}} \ll \Omega _{m}^{2}} \mathord{\left/ {\vphantom {{{{k}_{0}} - {{k}_{n}} \ll \Omega _{m}^{2}} g}} \right. \kern-0em} g}$ (напомним, что ${{\Omega }_{m}}$ – частота спектрального максимума ветрового волнения). С ростом номера моды угловая зависимость ${{\gamma }_{n}}$ становится более слабой, и для мод, удовлетворяющих условию ${{{{k}_{0}} - {{k}_{n}} \gg \Omega _{m}^{2}} \mathord{\left/ {\vphantom {{{{k}_{0}} - {{k}_{n}} \gg \Omega _{m}^{2}} g}} \right. \kern-0em} g}$ (если они существуют), декремент ${{\gamma }_{n}}$ практически изотропен. Таким образом, можно утверждать, что степень горизонтальной анизотропии шумового поля максимальна для мод с низкими номерами и уменьшается (хотя и не всегда монотонно) для мод с высокими номерами. При малых значениях критического угла волновода условие сильной анизотропии ${{{{k}_{0}} - {{k}_{n}} \ll \Omega _{m}^{2}} \mathord{\left/ {\vphantom {{{{k}_{0}} - {{k}_{n}} \ll \Omega _{m}^{2}} g}} \right. \kern-0em} g}$ может выполняться для всех мод, локализованных в волноводе.

Приведем результаты расчетов углового спектра динамического шума в мелком море и глубоком океане. Очевидно, что интересующие нас эффекты в первую очередь значимы для гидрологии зимнего типа, когда ось звукового канала находится на поверхности либо на сравнительно небольшой глубине. В противном случае акустические моды локализованы вдали от поверхности, и эффекты рассеяния для них экспоненциально малы. Формально это выражается в малости производных $\left( {{{d{{\varphi }_{n}}} \mathord{\left/ {\vphantom {{d{{\varphi }_{n}}} {dz}}} \right. \kern-0em} {dz}}} \right),$ фигурирующих в выражениях для декремента ${{\gamma }_{n}}.$

Вначале приведем результаты численных расчетов углового спектра шума для мелководного волновода с линейным профилем $c\left( z \right),$ открытым к поверхности, и параметрами, типичными для Баренцева моря: глубина $H = 200\;{\text{м ,}}$ $c\left( 0 \right)$ = 1490 м/с, $c\left( H \right) = 1500\;{\text{м /с }},$ дно жидкое со скоростью звука ${{c}_{1}} = 2300\;{\text{м /с ,}}$ плотностью ${{\rho }_{1}} = 2\;{\text{г /с }}{{{\text{м }}}^{{\text{3}}}}$ и коэффициентом затухания $\delta = 0.1\;{{{\text{д Б }}} \mathord{\left/ {\vphantom {{{\text{д Б }}} {{\text{м }}\;{\text{к Г ц }}}}} \right. \kern-0em} {{\text{м }}\;{\text{к Г ц }}}}.$ На рис. 1 приведены для частоты $f = 250\;{\text{Г ц }}$ нормированные угловые спектры ${{{{N}_{n}}\left( \theta \right)} \mathord{\left/ {\vphantom {{{{N}_{n}}\left( \theta \right)} {N_{n}^{{\left( 0 \right)}}}}} \right. \kern-0em} {N_{n}^{{\left( 0 \right)}}}},$ где $N_{n}^{{\left( 0 \right)}}$ соответствует отсутствию эффектов рассеяния (${{\gamma }_{n}} = 0,$) и угол θ отсчитывается от направления скорости ветра. Для сравнения приведены результаты расчетов для первой моды (n = 1), одной из высших мод (n = 50) и мод с промежуточными номерами (n = 10, 20, 30) при трех значениях скорости ветра – V = 5, 8 и 12 м/с. Видно, что для мод с низкими номерами n = 1…10 анизотропия углового спектра порядка 3 дБ при слабом ветре V = 5 м/с и достигает 5 дБ при умеренном ветре (V = 8…12 м/с). Для мод с промежуточными номерами n = 20…30 анизотропия углового спектра меняется в пределах 0.5–3 дБ. Для высших мод n ~ 50 угловой спектр шума практически изотропен при всех скоростях ветра. Для низших мод волновода, не проникающих в дно, анизотропия спектра шума слабо зависит от величины δ, поэтому приведенные результаты расчетов, по сути, имеют универсальный характер. Для высших мод спектр шума изотропен также при любых значениях коэффициента затухания в дне. Вместе с тем для мод с промежуточными номерами степень анизотропии шума может существенно зависеть от соотношения эффектов рассеяния и затухания в дне (значений ${{\gamma }_{n}}$ и δ).

Рассмотрим теперь результаты численных расчетов для глубокого моря. В качестве примера мы выбрали приповерхностный звуковой канал зимнего типа с профилем скорости звука, характерным для Тихого океана в камчатском регионе (рис. 2).

В расчетах предполагалось, что глубина океана H = 2000 м, скорость звука в грунте ${{c}_{l}}$ = 1500 м/с, плотность грунта ρ = 2 г/см³. Для акустических мод, локализованных в таком волноводе, основные потери при распространении связаны не с затуханием в данном грунте, а с объемным затуханием в воде. Для коэффициента объемного затухания в воде β мы использовали обобщенную формулу Терпа, которая в диапазоне $f \leqslant \;1\;{\text{к Г ц }}$ имеет вид

где частота измеряется в герцах, β – в неперах на метр.

Расчеты были проведены для частоты $f$ = 250 Гц и для тех же трех типичных значений скорости ветра V = 5, 8 и 12 м/с. На рис. 3 показаны результаты расчетов нормированного углового спектра мод с номерами n = 1, 10, 20, 30, 80 (всего в волноводе локализованы 83 моды). Видно, что при слабом ветре 5 м/с анизотропия углового спектра меняется в пределах 1.5–3 дБ и максимальна для мод с номерами n = 1…10. При умеренной скорости ветра (V = 8…12 м/с) анизотропия спектра увеличивается и достигает величин 2.5–4 дБ. При этом интересно отметить близость угловых спектров для мод с номерами n = 20…80. Этот эффект связан с их локализацией в той области волновода, где профиль звука близок к линейному, а для линейного канала эффекты ветрового рассеяния слабо зависят от номера моды. Заметим также, что в данном примере не наблюдается изотропизации шума для высших мод из-за малого значения критического угла волновода.

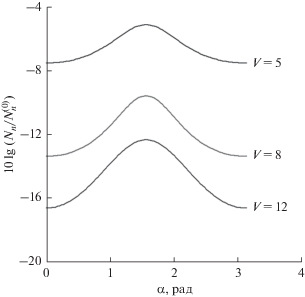
Наряду с рассмотрением анизотропии шумового поля для отдельных мод представляет практический интерес и исследование анизотропии динамического шума, просуммированного по всем модам, локализованным в волноводе (например, для расчета характеристик горизонтальной антенны). В случае антенны, расположенной на глубине z_A, суммарный угловой спектр шума $N(\alpha )$ имеет вид

Расчеты $N(\alpha )$ были проделаны для тех же параметров задачи и условий распространения в предположении, что приемные элементы расположены на глубине ${{z}_{A}} = 10\;{\text{м }}.$ На рис. 4 приведены результаты нормированной величины ${{N(\alpha )} \mathord{\left/ {\vphantom {{N(\alpha )} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}}$ (${{N}_{0}}$ соответствует отсутствию эффектов рассеяния, т.е. ${{\gamma }_{p}} = 0$) для мелкого моря. Аналогичные зависимости для глубокого моря приведены на рис. 5. По этим результатам можно сделать вывод, что отмеченные выше закономерности имеют место и для суммарного углового спектра. При этом степень анизотропии суммарного шумового поля в зависимости от скорости ветра меняется в пределах 2–4 дБ.

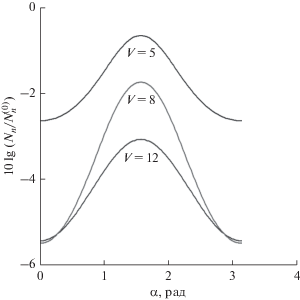
Следует также отметить, что эффекты рассеяния шумового поля на ветровом волнении могут существенно влиять и на уровень динамического шума. Приведенные выше результаты расчетов нормированной интенсивности позволяют наглядно увидеть ослабление энергии шумового поля по сравнению с моделью распространения шума в плоскослоистом волноводе. Например, для суммарного по модам шума в мелком море этот эффект достигает 13 дБ (см. рис. 4).

Что касается несомненно важного вопроса об абсолютном уровне динамических шумов, то он требует привлечения эмпирических данных и теоретических моделей для дипольных источников шума, т.е. обсуждения механизмов генерации шумов ветрового происхождения. При этом следует заметить, что в низкочастотном диапазоне $f \leqslant 500\;{\text{Г ц }}$ по существующим представлениям имеется несколько конкурентных механизмов генерации шума (турбулентные пульсации ветра, обрушение гребней ветровых волн и др.). Эти вопросы являются предметом дальнейших исследований.

В заключение кратко сформулируем основные результаты. Проанализирован механизм формирования горизонтальной анизотропии шумов ветрового происхождения, обусловленный их рассеянием на анизотропном ветровом волнении. В отличие от работы [4], где использовался модельный спектр ветрового волнения, проведено численное моделирование углового спектра шума для эмпирического спектра ветровых волн. Кроме того, обсуждается анизотропия шумового поля в более широкой постановке для различных натурных ситуаций (мелкого и глубокого моря), для селектированных по модам шумов и без модовой селекции. Проанализированы вариации анизотропии и уровня шума в зависимости от скорости ветра.

В целом, из результатов численных расчетов можно сделать вывод о том, что анизотропия динамического шума в открытом море может иметь существенную величину и представляет интерес для задач прикладной акустики.

Работа выполнена при частичной поддержке РФФИ по гранту № 16-02-00929.