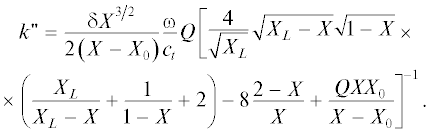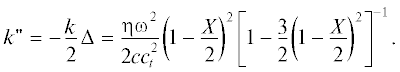Акустический журнал, 2019, T. 65, № 2, стр. 166-181
Поля радиационных сил и акустические течения в жидком слое на твердом полупространстве
В. А. Гусев a, *, О. В. Руденко a, b, c
a Московский государственный университет им. М.В. Ломоносова, физический факультет
119991 Москва, ГСП-1, Ленинские горы, Россия
b Институт общей физики им. А.М. Прохорова РАН
119991 Москва, ул. Вавилова 38, Россия
c Институт физики Земли им. О.Ю. Шмидта РАН
123242 Москва, Б. Грузинская ул. 10, стр. 1, Россия
* E-mail: vgusev@bk.ru
Поступила в редакцию 28.12.2018
После доработки 28.12.2018
Принята к публикации 16.01.2019
Аннотация
Рассчитаны акустическое поле и поле радиационных сил в жидком слое на твердой подложке, формирующиеся при распространении поверхностной волны вдоль границы раздела. Учтено влияние поверхностного натяжения, вязких напряжений на границе и затухания в объеме жидкости на характеристики полей. Найдены дисперсионные уравнения и скорости распространения волны. Рассчитаны радиационные силы, действующие на элемент объема жидкости в стоячей волне. Изучена структура течений. Обсуждается их воздействие на частицы малого размера и возможности формирования упорядоченных структур из этих частиц.
ВВЕДЕНИЕ
Наблюдается рост числа публикаций по акустическому воздействию на капли микронных размеров и возбуждаемым в них течениям. Разрабатываются устройства (микро-платформы, микрочипы), реализующие перемещение капель поверхностными акустическими волнами (ПАВ) [1–10]. Обычно ПАВ возбуждаются на подложке из пьезоэлектрического материала. После первых экспериментов [11], как известно, появилось множество работ, сформировавших важное научно-прикладное направление – акустоэлектронику [12]. Современные исследования здесь стимулируются запросами биологии, цитологии, химии, а в последнее время – развитием нанотехнологий. Одной из задач является воздействие на содержимое капли, в частности, его перемешивание течениями, индуцируемыми ПАВ. Используется воздействие ПАВ на каплю и для ее дробления – “микроатомизации” за счет генерации капиллярных волн.
Важное применение – формирование на подложке структур заданной морфологии при высыхании в поле волны пленки жидкости, содержащей взвешенные частицы. Сегодня широко используются технологии формирования структур за счет самосборки наночастиц в процессе испарения раствора. Акустическое воздействие не только создает новый механизм упорядочения, но и позволяет управлять параметрами формируемой структуры.
Большинство работ по данной проблеме – экспериментальные. Это связано с потребностями технологий. Очевидно, что теоретическое сопровождение должно помочь в понимании физики процессов, а также в оптимизации параметров системы и акустического воздействия. Для создания теории нужно рассчитать акустические поля, затем радиационные силы, акустические микропотоки и, наконец, их воздействие на частицы.
Ниже рассмотрена следующая система. На твердую подложку помещен слой жидкости толщиной h. Бегущими вдоль поверхности раздела встречными ПАВ формируется стоячая волна, проникающая как в твердое полупространство, так и в жидкий слой. Поле в жидкости воздействует на взвешенные в ней частицы, способствуя формированию периодической структуры.
АКУСТИЧЕСКИЕ ПОЛЯ В ЖИДКОМ СЛОЕ И В ПОДЛОЖКЕ
Исходные уравнения
Вначале рассмотрим задачу в базовой постановке [13]. Плоскость $(x,\,\,y)$ декартовых координат совпадает с границей $z = 0$ твердое тело– жидкий слой. Ось z направлена вертикально вниз. Верхняя граница жидкого слоя – это плоскость $z = - h.$ Акустические поля в такой системе рассматривались ранее и описаны, например, И.А. Викторовым [13]. Однако для новых приложений требуется некоторое развитие теории. Здесь нужно кратко повторить основные известные результаты, чтобы затем их обобщить.
Смещение U элемента твердой среды выражается через скалярный $\Phi $ и векторный ${\mathbf{\Psi }}$ потенциалы:
При этом для двумерной задачи (в которой смещение вдоль координаты y отсутствует, а потенциалы от y не зависят) отлична от нуля только одна y-компонента векторного потенциала ${\mathbf{\Psi }} = \left( {0,\Psi ,0} \right)$ и смещения по осям x и z имеют вид:(1)
$\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right)\left( {\begin{array}{*{20}{c}} \Phi \\ \Psi \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {k_{l}^{2}\Phi } \\ {k_{t}^{2}\Psi } \end{array}} \right) = 0.$Решения уравнений (1) отыскиваются в виде плоских волн, бегущих вдоль горизонтальной оси x и убывающих с координатой z:
(2)
$\left( {\begin{array}{*{20}{c}} \Phi \\ \Psi \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {A\exp \left( { - qz} \right)} \\ {B\exp \left( { - sz} \right)} \end{array}} \right)\exp \left( { - i\omega t + ikx} \right).$Рассмотрим теперь поле в жидком слое $ - h < z < 0.$ Вначале считаем жидкость идеальной и пользуемся линеаризованными уравнениями Эйлера и непрерывности:
(3)
${{\rho }_{0}}\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \nabla p{\text{'}} = 0,\,\,\,\,\frac{{\partial p{\text{'}}}}{{\partial t}} + c_{0}^{2}{{\rho }_{0}}div{\mathbf{u}} = 0.$Для жидкости тоже удобно ввести скалярный потенциал φ. Соответствующие выражения для акустических переменных и волновое уравнение, получаемые из (3), имеют вид:
(4)
${\mathbf{u}} = \nabla \varphi ,\,\,\,\,p{\text{'}} = - {{\rho }_{0}}\frac{{\partial \varphi }}{{\partial t}},\,\,\,\,\frac{{{{\partial }^{2}}\varphi }}{{\partial {{t}^{2}}}} - c_{0}^{2}\Delta \varphi = 0.$(5)
$\begin{gathered} \varphi = \left( {{{C}_{1}}{{e}^{{irz}}} + {{C}_{2}}{{e}^{{ - irz}}}} \right)\exp \left( { - i\omega t + ikx} \right), \\ r = \sqrt {k_{0}^{2} - {{k}^{2}}} . \\ \end{gathered} $Нужно удовлетворить следующим условиям.
1. На границе раздела $z = 0$ равны смещения по вертикали, то есть
В дальнейшем экспоненциальный множитель, отмечающий распространение волны вдоль границы раздела, будем опускать.
2. На границе $z = 0$ равны нормальные напряжения: ${{\sigma }_{{zz}}} = - p.$ Нормальное напряжение в твердом теле:
(7)
$\begin{gathered} \left( { - \lambda {{k}^{2}} + \lambda {{q}^{2}} + 2\mu {{q}^{2}}} \right)A - 2i\mu ksB = \\ = - i\omega {{\rho }_{0}}\left( {{{C}_{1}} + {{C}_{2}}} \right). \\ \end{gathered} $3. На границе $z = 0$ касательные напряжения в твердом теле равны нулю, поскольку жидкость считается идеальной. Касательное напряжение:
4. На свободной поверхности жидкости – верхней границе жидкого слоя $z = - h$ – акустическое давление $p{\text{'}}$ равно нулю:
Итак, есть четыре однородных уравнения (6)–(9) для определения неизвестных амплитуд A, B, ${{C}_{1}},$ ${{C}_{2}}$ и волнового числа k. Дисперсионное уравнение находится из условия равенства нулю детерминанта этой системы:
(10)
$4{{k}^{2}}qs - {{\left( {{{k}^{2}} + {{s}^{2}}} \right)}^{2}} = \frac{{{{\rho }_{0}}}}{\rho }qk_{t}^{4}\left\{ {\begin{array}{*{20}{c}} {{{r}^{{ - 1}}}\operatorname{tg} \left( {rh} \right),} \\ {r_{ * }^{{ - 1}}\operatorname{th} \left( {r{\text{*}}h} \right).} \end{array}} \right.$Заметим, что уравнение (10) отличается от дисперсионного уравнения (1.58) в книге [13]. Если в (10) плотность жидкости ${{\rho }_{0}}$ или толщину слоя h положить равными нулю, получается обычное дисперсионное уравнение для рэлеевских волн, бегущих вдоль границы твердое тело–вакуум. Правая часть (10) учитывает влияние жидкого слоя.
Верхняя строка в правой части (10) соответствует такому решению этого уравнения, при котором скорость волны в системе больше скорости звука в жидкости, но меньше скоростей продольной и поперечной волн в твердом теле: ${{c}_{0}} < c < {{c}_{t}} < {{c}_{l}}.$ Нижняя строка в правой части (10) соответствует скорости волны, меньшей скорости звука в жидкости: $c < {{c}_{0}}.$ При этом $r = ir*,$ $r* = \sqrt {{{k}^{2}} - k_{0}^{2}} .$
Дисперсионные зависимости
Подставляя в (10) выражения $k = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c},$ ${{k}_{l}} = {\omega \mathord{\left/ {\vphantom {\omega {{{c}_{l}}}}} \right. \kern-0em} {{{c}_{l}}}},$ ${{k}_{t}} = {\omega \mathord{\left/ {\vphantom {\omega {{{c}_{t}}}}} \right. \kern-0em} {{{c}_{t}}}},$ q = $\omega \sqrt {{{c}^{{ - 2}}} - c_{l}^{{ - 2}}} ,$ s = $\omega \sqrt {{{c}^{{ - 2}}} - c_{t}^{{ - 2}}} ,$ $r = \omega \sqrt {c_{0}^{{ - 2}} - {{c}^{{ - 2}}}} ,$ запишем дисперсионное уравнение (10) в виде:
(11)
$\begin{gathered} \sqrt {1 - \frac{{{{c}^{2}}}}{{c_{l}^{2}}}} \sqrt {1 - \frac{{{{c}^{2}}}}{{c_{t}^{2}}}} - {{\left( {1 - \frac{{{{c}^{2}}}}{{2c_{t}^{2}}}} \right)}^{2}} = \\ = \frac{1}{4}\frac{{{{\rho }_{0}}}}{\rho }{{\left( {\frac{c}{{{{c}_{t}}}}} \right)}^{4}}\sqrt {1 - \frac{{{{c}^{2}}}}{{c_{l}^{2}}}} \times \\ \times \,\,\left\{ {\begin{array}{*{20}{c}} {{{{\left( {\frac{{{{c}^{2}}}}{{c_{0}^{2}}} - 1} \right)}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}\operatorname{tg} \left( {H\frac{{{{c}_{0}}}}{c}\sqrt {\frac{{{{c}^{2}}}}{{c_{0}^{2}}} - 1} } \right),\,\,\,\,c > {{c}_{0}},} \\ {{{{\left( {1 - \frac{{{{c}^{2}}}}{{c_{0}^{2}}}} \right)}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}\operatorname{th} \left( {H\frac{{{{c}_{0}}}}{c}\sqrt {1 - \frac{{{{c}^{2}}}}{{c_{0}^{2}}}} } \right),\,\,\,\,c < {{c}_{0}}.} \end{array}} \right. \\ \end{gathered} $Анализ уравнения (11) удобно провести, нормируя все скорости в формуле (11) на скорость поперечной волны ${{c}_{t}}.$ Чтобы избежать неточных утверждений, имеющихся в литературе [13], рассмотрим вначале простой частный случай, положив ${{c_{l}^{2}} \mathord{\left/ {\vphantom {{c_{l}^{2}} {c_{t}^{2}}}} \right. \kern-0em} {c_{t}^{2}}} = 2.$ В этом случае корень дисперсионного уравнения, отвечающий рэлеевской волне (бегущей вдоль границы твердого полупространства с вакуумом), находится аналитически: ${{c_{R}^{2}} \mathord{\left/ {\vphantom {{c_{R}^{2}} {c_{t}^{2}}}} \right. \kern-0em} {c_{t}^{2}}}$ ≡ XR = $3 - \sqrt 5 \approx 0.764.$ Дисперсионное уравнение (11) при этом упрощается. Явное выражение для волновой толщины слоя имеет вид
(12)
$\begin{gathered} H = \sqrt {\frac{{2X}}{{1 - 2X}}} \times \\ \times \,\,\operatorname{arth} \left[ {\frac{{4\rho }}{{{{\rho }_{0}}}}\frac{{\sqrt {1 - 2X} }}{{{{X}^{2}}}}\left( {\sqrt {1 - X} - {{{\left( {1 - \frac{X}{2}} \right)}}^{{3/2}}}} \right)} \right], \\ {{X}_{S}} = 0.442 < X < {{X}_{0}} = \frac{1}{2}, \\ H = \sqrt {\frac{{2X}}{{2X - 1}}} \times \\ \times \,\,\left\{ {\pi n + \operatorname{arctg} \left[ {\frac{{4\rho }}{{{{\rho }_{0}}}}\frac{{\sqrt {2X - 1} }}{{{{X}^{2}}}}\left( {\sqrt {1 - X} - {{{\left( {1 - \frac{X}{2}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right)} \right]} \right\}, \\ {{X}_{0}} < X < 1. \\ \end{gathered} $Здесь мы обозначили $X = {{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {c_{t}^{2}}}} \right. \kern-0em} {c_{t}^{2}}}$ и положили для определенности ${{c_{0}^{2}} \mathord{\left/ {\vphantom {{c_{0}^{2}} {c_{t}^{2}}}} \right. \kern-0em} {c_{t}^{2}}} \equiv {{X}_{0}} = 0.5.$ Величина ${{X}_{S}} \approx 0.442$ равна значению X, при котором аргумент гиперболического арктангенса в (12) обращается в единицу. Соответствующая скорость волны оказывается равной скорости волны Стоунли ${{c}_{S}}$ на границе твердого и жидкого полупространств. Она, как известно [13], несколько меньше, чем скорость волны в неограниченной жидкости (${{c}_{S}} < {{c}_{0}}$), для которой $X = {{X}_{0}} = 0.5$ в формуле (12). Точка ${{X}_{0}} = 0.5$ разделяет области применимости первой и второй формул (12). Значение $\,n = 0$ отвечает нулевой моде, а $\,n = 1,\,2,...$ – модам с более высокими номерами.
Дисперсионные кривые, рассчитанные по формулам (12), построены на рис. 1 для мод с номерами 0, 1 и 2. Нужно обратить внимание, что скорости распространения высших мод при увеличении толщины слоя H стремятся к скорости звука в жидкости, в то время как для нулевой моды скорость стремится к скорости волны Стоунли.
Рис. 1.
Иллюстрация к дисперсионному соотношению (12). По вертикали отложена волновая толщина $H = {{{{\omega \,h} \mathord{\left/ {\vphantom {{\omega \,h} c}} \right. \kern-0em} c}}_{0}}$ жидкого слоя. По горизонтали – нормированный квадрат скорости распространения волны в структуре $X = {{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {c_{t}^{2}}}} \right. \kern-0em} {c_{t}^{2}}}.$ Принято значение ${{4\rho } \mathord{\left/ {\vphantom {{4\rho } {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}} = 10$ и следующие соотношения скоростей: ${{c_{l}^{2}} \mathord{\left/ {\vphantom {{c_{l}^{2}} {c_{t}^{2}}}} \right. \kern-0em} {c_{t}^{2}}} = 2,$ ${{X}_{0}} = {{c_{0}^{2}} \mathord{\left/ {\vphantom {{c_{0}^{2}} {c_{t}^{2}}}} \right. \kern-0em} {c_{t}^{2}}} = 0.5.$ При этом для рэлеевской волны получается ${{X}_{R}} = {{c_{R}^{2}} \mathord{\left/ {\vphantom {{c_{R}^{2}} {c_{t}^{2}}}} \right. \kern-0em} {c_{t}^{2}}} \approx 0.764,$ а для волны Стоунли ${{X}_{S}} = {{c_{S}^{2}} \mathord{\left/ {\vphantom {{c_{S}^{2}} {c_{t}^{2}}}} \right. \kern-0em} {c_{t}^{2}}} \approx 0.442.$

На рис. 2 иллюстрирована дисперсионная зависимость для использованной в экспериментах [14] системы: пленка водного раствора на подложке из ниобата лития. Заданы следующие параметры. Жидкость (вода): плотность ${{\rho }_{0}} = 1$ г/см3, скорость звука ${{c}_{0}} = 1500$ м/с. Подложка (ниобат лития): плотность $\rho = 4.7$ г/см3, скорость продольных волн ${{c}_{l}} = 7250$ м/с, скорость поперечных волн ${{c}_{t}} = 3750$ м/с, скорость рэлеевской волны ${{c}_{R}} = 3480$ м/с. Частота волны 15 МГц. Изображена зависимость от толщины жидкого слоя H относительного отклонения скорости волны c от скорости рэлеевской волны ${{c}_{R}}.$ При малых H для основной моды эти скорости различаются слабо. При увеличении H скорость c уменьшается, и при больших толщинах стремится к скорости волны Стоунли ${{c}_{S}},$ которая для заданных параметров очень близка к скорости звука в жидкости ${{c}_{0}}.$ Наряду с этим, при увеличении H возникает следующая (первая) мода, ее скорость при $H \to \infty $ стремится к скорости звука в жидкости. В точке рождения первой моды ее скорость равна скорости поперечных волн в подложке ${{c}_{t}}.$ Обычно в экспериментах толщина слоя оказывается много меньшей длины волны ($H \ll 1$), и скорость $c$ мало отличается от скорости рэлеевской волны ${{c}_{R}}.$ Таким образом, можно ожидать, что период образующейся структуры из наночастиц будет равен примерно половине длины рэлеевской волны.
Учет поверхностного натяжения
На характер действующих на взвешенные частицы радиационных сил и особенности формирующихся упорядоченных структур могут повлиять дополнительные факторы, обычно не учитываемые при расчете поверхностных волн. Один из таких факторов – поверхностное натяжение жидкого слоя. При его учете в базовой задаче изменится условие 4 (формула (9)) на свободной поверхности жидкости. Остальные граничные условия (формулы (6)–(8)) останутся прежними. Новое условие – давление на свободной границе $z = - h$ при наличии поверхностного натяжения – определяется формулой Лапласа:
(13)
$p - {{p}_{0}} = \sigma \left( {\frac{{{{\partial }^{2}}\xi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\xi }}{{\partial {{y}^{2}}}}} \right).$(14)
${{\left. {\left( {{{\rho }_{0}}\frac{{{{\partial }^{2}}\varphi }}{{\partial {{t}^{2}}}} + \sigma \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}\frac{{\partial \varphi }}{{\partial z}}} \right)} \right|}_{{z = - h}}} = 0.$(15)
$\begin{gathered} {{C}_{2}} = - {{C}_{1}}\frac{{1 + i\Sigma }}{{1 - i\Sigma }}\exp \left( { - 2irh} \right) = \\ = - {{C}_{1}}\exp \left( { - 2ir{{h}_{{{\text{eff}}}}}} \right), \\ \end{gathered} $(16)
$\Sigma = {{\sigma {{k}^{2}}r} \mathord{\left/ {\vphantom {{\sigma {{k}^{2}}r} {{{\rho }_{0}}{{\omega }^{2}}}}} \right. \kern-0em} {{{\rho }_{0}}{{\omega }^{2}}}}.$Выражение (17) показывает, что поверхностное натяжение приводит к уменьшению действующей высоты жидкого слоя. Проанализируем возможные эффекты, вызванные поверхностным натяжением. Учитывая выражение для волнового числа r, перепишем величину $\Sigma $ через параметры задачи $\Sigma = \frac{\sigma }{{{{\rho }_{0}}{{c}^{2}}}}\frac{{2\pi f}}{{{{c}_{0}}}}\sqrt {1 - {{c_{0}^{2}} \mathord{\left/ {\vphantom {{c_{0}^{2}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} .$ Переходя к безразмерным величинам, использованным при записи выражения (12), получим:
(18)
$\Sigma = 2\pi \frac{{f\sigma }}{{{{\rho }_{0}}c_{0}^{3}}}\frac{{{{X}_{0}}}}{X}\sqrt {\frac{{X - {{X}_{0}}}}{X}} ,\,\,\,\,X > {{X}_{0}}.$При $X < {{X}_{0}}$ по аналогии с (12) нужно изменить знак подкоренного выражения в (18) и заменить в (17) функцию arctg на arth. Порядок величины $\Sigma $ определяется первым множителем в (18). Зададим следующие значения параметров, характерные для эксперимента [14]: частота волны $f = 15$ МГц, жидкость – вода с плотностью ${{\rho }_{0}} = 1000$ кг/м3 и скоростью звука ${{c}_{0}} = 1500$ м/с. Коэффициент поверхностного натяжения для воды при температуре 20°С равен $\sigma = 0.72$ Н/м. Тогда оказывается $\Sigma \sim {{10}^{{ - 5}}}.$ Заменяя в этом случае $arctg\Sigma $ значением его аргумента, получим выражение для эффективной высоты жидкого слоя ${{h}_{{{\text{eff}}}}} \approx h - {\Sigma \mathord{\left/ {\vphantom {\Sigma r}} \right. \kern-0em} r}$ = $h - \frac{\sigma }{{{{\rho }_{0}}c_{0}^{2}}}\frac{{{{X}_{0}}}}{X}.$ Поправка на высоту жидкого слоя в этом случае уже не зависит от частоты, а ее характерное значение для выбранных параметров задачи составляет $\delta h = {\sigma \mathord{\left/ {\vphantom {\sigma {{{\rho }_{0}}{{c}^{2}}}}} \right. \kern-0em} {{{\rho }_{0}}{{c}^{2}}}}\sim {{10}^{{ - 9}}}$ м. Наибольшие характерные значения коэффициента поверхностного натяжения для классических материалов составляют порядка 5 Н/м (ртуть при 25°С, жидкое олово при 400°С), что увеличивает величину эффекта приблизительно на порядок, однако и в этом случае поверхностное натяжение оказывает несущественное влияние. Согласно (18) для достижения максимально возможного проявления влияния поверхностного натяжения нужно, помимо увеличения соответствующего коэффициента σ, увеличивать частоту, например, переходить к гиперзвуку, уменьшать плотность и скорость звука в жидком слое. Все это обеспечивает максимальное значение арктангенса, равное только ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},$ так что максимальное изменение действующей высоты жидкого слоя определяется величиной r : ${{h}_{{{\text{eff}}}}} = h - {{r}^{{ - 1}}}\operatorname{arctg} \Sigma \to h - {\pi \mathord{\left/ {\vphantom {\pi {2r}}} \right. \kern-0em} {2r}},$ ${\pi \mathord{\left/ {\vphantom {\pi {2r}}} \right. \kern-0em} {2r}} = {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} {4f}}} \right. \kern-0em} {4f}}\sqrt {1 - {{{{X}_{0}}} \mathord{\left/ {\vphantom {{{{X}_{0}}} X}} \right. \kern-0em} X}} $ и для параметров задачи ${\pi \mathord{\left/ {\vphantom {\pi {2r}}} \right. \kern-0em} {2r}}\sim {{10}^{{ - 4}}}$ м. Таким образом, влиянием поверхностного натяжения на динамику процессов в жидком слое действительно можно пренебречь. Однако в особых случаях, например, когда при высыхании раствора взвешенные частицы образуют полимерную пленку малой толщины, а эффективный коэффициент поверхностного натяжения может существенно возрастать, учет натяжения может представить интерес и влиять на характеристики формирующейся структуры.
Влияние диссипации звука в жидкости
Еще одним фактором, способным влиять на структуру полей в рассматриваемой системе, является затухание звука в жидкости, обусловленное ее вязкостью. Для точного расчета полей с учетом вязкости необходимо рассматривать расширенную по сравнению с рассмотренной выше системой (3) систему уравнений гидродинамики, включающую уравнение Навье–Стокса. В этом случае полное акустическое поле в жидком слое будет также складываться как из потенциальной, так и вихревой компонент, как и в твердой подложке. Отличие только в том, что сдвиговые компоненты акустического поля в жидкости обусловлены вязкостью и поэтому быстро затухают. Однако наличие вязкости и вихревой компоненты изменяет граничные условия и их количество. А именно, появляется ненулевая правая часть в условии равенства касательных напряжений на границе твердая подложка–жидкий слой, а также добавляются два новых условия – равенства касательных смещений на границе подложка–жидкий слой и равенства нулю касательных напряжений на верхней границе жидкого слоя. В результате для нахождения дисперсионного уравнения получается детерминант размером не 4 × 4, как выше, а уже 6 × 6. Нахождение скорости поверхностной волны в этом случае требует использования упрощающих предположений или численных методов.
Расчет полей ПАВ на границе вязкой жидкости в более простой постановке – на границе двух полупространств и для волн Лэмба – проведен в ряде работ, в частности [15–17]. В этих работах показано, что, во-первых, для слабовязких жидкостей, например воды, изменение дисперсионных характеристик, скоростей ПАВ при наличии вязкости незначительно. Это означает, что при расчете амплитуд акустического поля для прикладных целей можно пользоваться упрощенными моделями, две из которых будут рассмотрены ниже. С другой стороны, учет вихревых компонент приводит к значительному возрастанию затухания ПАВ, что важно при рассмотрении волновых процессов в протяженных системах.
Модель 1. Учет затухания звука в объеме жидкого слоя
При наличии затухания в объеме жидкости в уравнении движения (3) появится дополнительное слагаемое, содержащее b – эффективный коэффициент вязкости. Волновое уравнение (4) примет вид:
(19)
$\frac{{{{\partial }^{2}}\varphi }}{{\partial {{t}^{2}}}} - c_{0}^{2}\Delta \varphi - \frac{b}{{{{\rho }_{0}}}}\Delta \frac{{\partial \varphi }}{{\partial t}} = 0.$Изменится также и связь между акустическим давлением и потенциалом скорости: $p{\text{'}} = - {{\rho }_{0}}\frac{{\partial \varphi }}{{\partial t}} + b\Delta \varphi .$ Соответственно, вместо граничного условия на свободной поверхности жидкости, приводящего к (9), получим ${{\left. {p{\text{'}}} \right|}_{{z = - h}}} = {{\left. {\left( {i\omega {{\rho }_{0}}\varphi + b\Delta \varphi } \right)} \right|}_{{z = - h}}} = 0.$
Решение уравнения (19) имеет форму (5), однако вместо параметра r в нем следует положить ${{r}_{1}} = \sqrt {k_{1}^{2} - {{k}^{2}}} ,$ где $k_{1}^{2} = k_{0}^{2}{{\left( {1 - i\delta } \right)}^{{ - 1}}}$ – комплексное волновое число в жидкости. Такую же замену $r \to {{r}_{1}}$ следует произвести и в дисперсионном уравнении (10). Параметр $\delta = {{\omega \,b} \mathord{\left/ {\vphantom {{\omega \,b} {{{\rho }_{0}}c_{0}^{2}}}} \right. \kern-0em} {{{\rho }_{0}}c_{0}^{2}}}$ мал, если поглощение в жидкости на расстояниях порядка длины волны можно считать слабым. Например, для жидкого слоя $b \approx {{10}^{{ - 3}}}$ Па с и при характерных мегагерцовых частотах получаем $\delta \sim {{10}^{{ - 4}}}.$ Таким образом, применение упрощенной модели в данном случае обосновано.
Поскольку основной интерес представляет тонкий слой – высыхающая пленка жидкости, ограничимся рассмотрением нулевой моды в дисперсионном уравнении (10), (11). Разлагая $\operatorname{tg} \left( {{{r}_{1}}h} \right)$ при малых толщинах слоя в ряд и полагая значения параметров теми же, что и в формуле (12), получим упрощенное дисперсионное соотношение
(20)
$\begin{gathered} \sqrt {1 - X} - {{\left( {1 - \frac{X}{2}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} = \\ = \frac{H}{{4\sqrt 2 }}\frac{{{{\rho }_{0}}}}{\rho }{{X}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\left( {1 + \frac{{{{H}^{2}}}}{3}\frac{{2X - 1}}{{2X}} - i\delta \frac{{{{H}^{2}}}}{3}} \right). \\ \end{gathered} $Видно, что единственный мнимый член в правой части (19) пропорционален не только малому параметру δ, но и кубу малой волновой толщины слоя H. Такую же зависимость от параметров δ и H будут иметь мнимые добавки к $X,\,\,c$ и волновому числу. Это означает, что при высыхании жидкой пленки затухание быстро уменьшается и становится пренебрежимо малым. Очевидно, что затухание в системе во всех случаях меньше, чем в неограниченной жидкости, поскольку основная часть волновой энергии сосредоточена в идеальной среде – твердом полупространстве.
Найдем приближенное выражение для коэффициента затухания волны при произвольной толщине
жидкого слоя. Представим волновое число в виде 
 и подставим его в уравнение (10), считая, что действительная часть $k{\text{'}}$ удовлетворяет уравнению (10) без диссипации. После вычислений получаем выражение для мнимой части волнового числа:
и подставим его в уравнение (10), считая, что действительная часть $k{\text{'}}$ удовлетворяет уравнению (10) без диссипации. После вычислений получаем выражение для мнимой части волнового числа:
При малых H величина Q стремится к нулю со стороны положительных значений. Это означает, что мнимая добавка
к волновому числу положительна и при записи фазового множителя в виде $\exp \left( { - i\omega t + ikx} \right)$ = 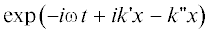 определяет затухание волны по мере распространения.
определяет затухание волны по мере распространения.
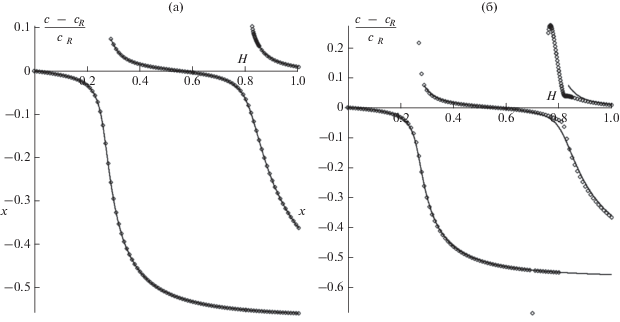
На рис. 3 изображены рассчитанные по точной формуле (10) с учетом замены $r \to {{r}_{1}}$ дисперсионные кривые (зависимости скорости звука от толщины слоя) при наличии затухания
в жидкости для двух значений δ. По оси абсцисс отложена нормированная высота жидкого
слоя H, по оси ординат – относительное отклонение скорости граничной волны от скорости рэлеевской
волны (на границе твердого тела и вакуума) ${{\left( {c - {{c}_{R}}} \right)} \mathord{\left/ {\vphantom {{\left( {c - {{c}_{R}}} \right)} {{{c}_{r}}}}} \right. \kern-0em} {{{c}_{r}}}}.$ Сплошная линия – дисперсионные кривые для идеальной жидкости, квадратики – для вязкой
жидкости. Видно, что при $\delta = 0.01$ дисперсионные кривые практически не изменились, а при $\delta = 0.05$ наиболее заметно изменяются зависимости для высших мод. Нулевая мода практически
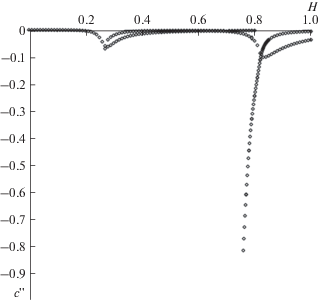
не изменилась. На рис. 4 изображена зависимость мнимой добавки к скорости c", ответственной за затухание и вводимой в соответствии с выражением 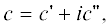 от толщины жидкого слоя. На всех графиках видны три моды. Таким образом, затухание
в жидкости сильнее сказывается на высших модах, и практически не сказывается на дисперсионной
кривой первой моды, затухание высших мод также оказывается более значительным.
от толщины жидкого слоя. На всех графиках видны три моды. Таким образом, затухание
в жидкости сильнее сказывается на высших модах, и практически не сказывается на дисперсионной
кривой первой моды, затухание высших мод также оказывается более значительным.
Модель 2. Учет вязких напряжений на границе жидкого слоя и подложки
Сдвиговая вязкость создает дополнительный механизм взаимодействия волн на границе жидкого слоя и подложки. Нужно отметить, что при предельном переходе к среде с нулевым сдвиговым модулем или нулевой вязкостью первым выпадает условие равенства касательных смещений на границе. Поэтому основные эффекты содержатся в граничном условии равенства касательных напряжений при $z = 0.$ При учете вязких сдвиговых напряжений вместо уравнения (8) получим:
После подстановки в эту формулу выражений (2), (5) для потенциалов и использования первого граничного условия (6) удается получить связь
(21)
$B = - 2ikq\frac{{1 + i\beta }}{{{{k}^{2}} + {{s}^{2}} + 2i\beta {{k}^{2}}}}A,\,\,\,\,\beta = \omega \frac{\eta }{\mu }.$(22)
$\begin{gathered} 4{{k}^{2}}qs\left( {1 + i\beta } \right) - {{\left( {{{k}^{2}} + {{s}^{2}}} \right)}^{2}} \times \\ \times \,\,\left( {1 + i\beta \frac{{2{{k}^{2}}}}{{{{k}^{2}} + {{s}^{2}}}}} \right) = \frac{{{{\rho }_{0}}}}{\rho }qk_{t}^{4}\frac{{tgrh}}{r}. \\ \end{gathered} $Вклад касательных напряжений содержится в левой части (22) и определяется параметром $\beta $, который обычно мал. Оценим его характерное значение. Для воды коэффициент вязкости $\eta \sim {{10}^{{ - 3}}}$ Па с, сдвиговый модуль твердой подложки $\mu = \rho c_{t}^{2}$ и для ниобата лития $\mu \approx 4.7 \times {{10}^{3}} \times {{3.8}^{2}} \times {{10}^{6}} \approx 6.8 \times {{10}^{{10}}}$ Па. На частоте $f = 15$ МГц получаем $\beta \sim {{10}^{{ - 6}}}.$ С учетом малости β и волновой толщины H жидкого слоя получается дисперсионное соотношение, аналогичное (19):
(23)
$\begin{gathered} \sqrt {1 - X} - {{\left( {1 - \frac{X}{2}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} + \\ + \,\,i\beta \left( {\sqrt {1 - X} - \sqrt {1 - \frac{X}{2}} } \right) = \frac{H}{{4\sqrt 2 }}\frac{{{{\rho }_{0}}}}{\rho }{{X}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $Заменим в соотношении (23) X на $X\left( {1 + i\Delta } \right),$ где Δ – малая добавка. После вычисления Δ удается рассчитать коэффициент затухания – мнимую часть волнового числа:
Видно, что при малой толщине жидкого слоя волна затухает примерно так, как затухала бы сдвиговая волна в твердом теле с вязкостью, равной вязкости жидкости.Для произвольных значений толщины жидкого слоя можно получить следующее выражение для коэффициента затухания:
где нужно подставить волновое число k, найденное из уравнения (10).Таким образом, во всех случаях коэффициент затухания оказывается достаточно малым, что позволяет для практических расчетов использовать упрощенные подходы для его расчета, не привлекая полную схему с учетом вихревых компонент акустического поля в вязкой жидкости.
Акустическое поле в жидком слое
Поскольку потенциал дается выражением (5), определив константы ${{C}_{1}}$ и ${{C}_{2}},$ можно записать:
(24)
$\varphi = - i\omega A\frac{q}{r}\frac{{k_{t}^{2}}}{{{{k}^{2}} + {{s}^{2}}}}\frac{{\sin r\left( {z + h} \right)}}{{\cos rh}}{{e}^{{ - i\left( {\omega t - kx} \right)}}}.$Стоячая волна в жидком слое
Пусть теперь по подложке распространяются две встречные волны. Потенциал волны, бегущей в положительном направлении оси x, определяется выражением (24). Волну, распространяющуюся в отрицательном направлении $( - x),$ можно получить, произведя в (24) формальную замену $k \to - k.$ Суммарный потенциал равен:
(25)
$\begin{gathered} \varphi = {{\varphi }_{1}} + {{\varphi }_{2}} = 2D\left( z \right)\cos kx{{e}^{{ - i\omega t}}} = \\ = - i\omega A\frac{{2q}}{r}\frac{{k_{t}^{2}}}{{{{k}^{2}} + {{s}^{2}}}}\frac{{\sin r\left( {z + h} \right)}}{{\cos rh}}\cos kx{{e}^{{ - i\omega t}}}. \\ \end{gathered} $Из формулы (25) находятся действительные компоненты колебательной скорости и акустическое давление:
(26)
$\begin{gathered} {{u}_{x}} = \frac{k}{r}{{U}_{0}}\sin r\left( {z + h} \right)\sin kx\sin \omega t, \\ {{u}_{z}} = - {{U}_{0}}\cos r\left( {z + h} \right)\cos kx\sin \omega t, \\ p{\text{'}} = - \frac{{{{\rho }_{0}}\omega }}{r}{{U}_{0}}\sin r\left( {z + h} \right)\cos kx\cos \omega t. \\ \end{gathered} $Затухание приведет к изменению волновых чисел k и r, каждое из которых получает мнимую добавку. Полученные выше выражения для комплексных
амплитуд при учете только объемного затухания сохранятся, однако при переходе к действительным
величинам необходимо явно выписать все мнимые добавки. В общем случае величина $D\left( z \right)$ получит мнимую добавку $i\Delta D,$ а профиль амплитуды вдоль горизонтальной оси будет определяться выражением  =
= 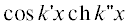 –
– 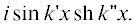 В результате для потенциала по аналогии с (25) можно записать выражение
В результате для потенциала по аналогии с (25) можно записать выражение
Таким образом, затухание приводит к появлению второй гармонической составляющей, т.е. к появлению зависящего от координаты сдвига фазы. Это может повлиять на характер формирования пространственной структуры.
РАДИАЦИОННОЕ ДАВЛЕНИЕ АКУСТИЧЕСКОЙ ВОЛНЫ И ПОТОКИ ЖИДКОСТИ В СЛОЕ
В предыдущем разделе рассчитаны характеристики поля в жидком слое, изменяющиеся во времени по гармоническому закону. Средние значения от них равны нулю. Поэтому усредненная по периоду акустических колебаний сила, действующая на элемент объема жидкости и на взвешенные в жидкости частицы, также должна быть равной нулю. Ожидаемого формирования структур в этом приближении происходить не должно. Ненулевые средние значения появятся при учете квадратично нелинейных членов в исходных уравнениях гидродинамики. Поскольку средние от квадратичных комбинаций осциллирующих переменных не обращаются тождественно в ноль, появится отличная от нуля усредненная сила, приводящая к структурированию ансамбля частиц.
Характер движения частиц малого размера в жидкости
Радиационное давление звука описано во многих обзорах (см., например, [18]). Давление, действующее со стороны акустического поля произвольной конфигурации на взвешенную частицу, рассчитано в работе [19]. Причиной появления радиационной силы [19] является реакция частицы на рассеяние падающей волны. Однако для частиц малого размера такой механизм, видимо, не является основным. Как известно, доля рассеянной частицей волновой энергии пропорциональна ${{\left( {kR} \right)}^{4}}$, где R – радиус частицы (см., например, [20]). Например, для частиц полистирола с радиусом 100 нм, облучаемых волной на частоте 15 МГц [14], этот параметр имеет порядок 10–9. Поэтому преобладающим оказывается следующий механизм: частицы, ввиду их малого размера, могут полностью увлекаться акустическим течением в жидкости и перемещаться вместе с ней.
Рассмотрим частицу малого размера в колеблющейся жидкости. Уравнение движения имеет вид (см., например, [21]):
(27)
$m\frac{{{{d}^{2}}}}{{d{{t}^{2}}}}\left( {{{X}_{S}} - \xi } \right) = - m{\text{'}}\frac{{{{d}^{2}}\xi }}{{d{{t}^{2}}}} + {{F}_{{{\text{diss}}}}} + F.$Переходя в (27) к скоростям частицы $v = {{d{{X}_{S}}} \mathord{\left/ {\vphantom {{d{{X}_{S}}} {dt}}} \right. \kern-0em} {dt}}$ и жидкости $u = {{d\xi } \mathord{\left/ {\vphantom {{d\xi } {dt}}} \right. \kern-0em} {dt}}$ и конкретизируя выражение для диссипативной силы [21], получим уравнение:
(28)
$\begin{gathered} \frac{4}{3}\pi {{R}^{3}}\left( {{{\rho }_{S}} + \frac{{{{\rho }_{0}}}}{2}} \right)\frac{d}{{dt}}\left( {v - u} \right) = - \frac{4}{3}\pi {{R}^{3}}\left( {{{\rho }_{S}} - {{\rho }_{0}}} \right)\frac{{du}}{{dt}} - \\ - \,\,6\pi \eta R\left( {1 + R\sqrt {\frac{{{{\rho }_{0}}\omega }}{{2\eta }}} } \right)\left( {v - u} \right) - \\ - \,\,3\pi {{R}^{2}}\sqrt {\frac{{2\eta {{\rho }_{0}}}}{\omega }} \left( {1 + \frac{{2R}}{9}\sqrt {\frac{{{{\rho }_{0}}\omega }}{{2\eta }}} } \right)\frac{d}{{dt}}\left( {v - u} \right) + F. \\ \end{gathered} $Рассмотрим задачу в отсутствие радиационной силы. Тогда сила в правой части состоит из трех частей. Первое слагаемое является источником вынужденного движения частицы. Второе слагаемое отвечает за затухание относительного движения частицы, третье представляет добавку к инерционному члену. При учете только первого слагаемого скорость частицы получает дополнительную поправку по сравнению со скоростью частиц среды, пропорциональную разности плотностей. При учете диссипативной силы решение имеет структуру вида
Отсюда видно, что собственное движение частицы на больших временах затухает. Для случая изменения скорости жидкости по гармоническому закону ${{u}_{0}}{{e}^{{i\omega t}}}$ коэффициент перед вынужденным решением равен $\gamma = {{i{{\omega }_{0}}{{t}_{0}}{{u}_{0}}m{\text{'}}} \mathord{\left/ {\vphantom {{i{{\omega }_{0}}{{t}_{0}}{{u}_{0}}m{\text{'}}} {\left( {1 - i{{\omega }_{0}}{{t}_{0}}} \right)}}} \right. \kern-0em} {\left( {1 - i{{\omega }_{0}}{{t}_{0}}} \right)}}.$ Если ${{\omega }_{0}}{{t}_{0}} \ll 1,$ то $\gamma \approx i{{\omega }_{0}}{{t}_{0}}{{u}_{0}}m{\text{'}}$ – малая поправка к скорости движения частицы относительно жидкости. В противоположном случае ${{\omega }_{0}}{{t}_{0}} \gg 1,$ т.е. высокочастотного по сравнению с релаксационными процессами воздействия, $\gamma \approx i{{u}_{0}}m{\text{'}}$ и движение определяется только внешним акустическим воздействием и не зависит от характеристик среды.
Оценим характерные значения параметров, определяющих поведение наночастицы в акустическом поле. В первом слагаемом для времени затухания величина ${{2{{\rho }_{0}}{{R}^{2}}} \mathord{\left/ {\vphantom {{2{{\rho }_{0}}{{R}^{2}}} {9\eta }}} \right. \kern-0em} {9\eta }}$ для частиц полистирола оказывается равной $\sim {{10}^{{ - 8}}} - {{10}^{{ - 9}}}$ с, поправка, связанная с частотой, оказывается незначительной (~0.1, вплоть до ~1) и не влияет на порядок величины. Второе слагаемое имеет приблизительно такой же порядок $\sim {{10}^{{ - 8}}}$ с. Такие времена соответствуют частотам порядка сотен мегагерц. Соответственно, для частот порядка десятков мегагерц параметр ${{\omega }_{0}}{{t}_{0}}$ является малой величиной. Это означает, что при воздействии акустических полей с частотами порядка десятков мегагерц и ниже можно пренебречь собственным движением частиц малого размера и считать, что частицы полностью увлекаются жидкостью. При воздействии высокочастотных акустических полей (порядка сотен мегагерц) собственные движения могут оказать влияние на конечную конфигурацию частиц, однако, как уже указывалось, радиационное давление, связанное с рассеянным частицами малого размера полем, в любом случае оказывается малым по сравнению с радиационным давлением на элемент объема жидкости. Поэтому при расчете радиационного давления на частицы следует использовать формулы для давления на элемент объема жидкости, содержащий взвешенные наночастицы.
В стационарном потоке, когда скорости ${{v}_{{st}}},\,\,{{u}_{{st}}}$ от времени не зависят, их разность будет определяться только действием радиационной силы F и силы Стокса. Первая стремится увеличить скорость частиц относительно течения, вторая, напротив, уменьшает ее. Используя формулу Горькова для радиационного давления на частицу в поле стоячей волны [19], приведем уравнение (28) к следующему виду:
Радиационное давление на жидкость
Радиационная сила ${{F}_{i}}$ выражается через тензор радиационных напряжений ${{\Pi }_{{ik}}}$ [22]:
(29)
${{F}_{i}} = - \frac{\partial }{{\partial {{x}_{k}}}}{{\Pi }_{{ik}}},\,\,\,\,{{\Pi }_{{ik}}} = \frac{\varepsilon }{{{{\rho }_{0}}c_{0}^{2}}}\left\langle {{{p}^{{'2}}}} \right\rangle {{\delta }_{{ik}}} + {{\rho }_{0}}\left\langle {{{u}_{i}}{{u}_{k}}} \right\rangle .$Вычислим теперь компоненты радиационной силы:
(30)
$\begin{gathered} - {{F}_{x}} = \frac{{\partial {{\Pi }_{{xx}}}}}{{\partial x}} + \frac{{\partial {{\Pi }_{{xz}}}}}{{\partial z}} = \frac{{{{\rho }_{0}}kU_{0}^{2}}}{4}\sin 2kx \times \\ \times \,\,\left( {\left( {\varepsilon - 1} \right)\frac{{k_{0}^{2}}}{{{{r}^{2}}}}\cos 2r\left( {z + h} \right) - \left( {\left( {\varepsilon - 1} \right)\frac{{k_{0}^{2}}}{{{{r}^{2}}}} + 1} \right)} \right), \\ \end{gathered} $(31)
$\begin{gathered} - {{F}_{z}} = \frac{{\partial {{\Pi }_{{zz}}}}}{{\partial z}} + \frac{{\partial {{\Pi }_{{zx}}}}}{{\partial x}} = \frac{{{{\rho }_{0}}rU_{0}^{2}}}{4}\sin 2r\left( {z + h} \right) \times \\ \times \,\,\left( {\left( {\varepsilon - 1} \right)\frac{{k_{0}^{2}}}{{{{r}^{2}}}}\cos 2kx + \frac{{\left( {\varepsilon - 1} \right)k_{0}^{2} + {{k}^{2}}}}{{{{r}^{2}}}}} \right). \\ \end{gathered} $Выражения (30), (31) удобны для анализа радиационных сил в жидком слое малой толщины, когда скорость поверхностной волны больше скорости звука в жидкости, поскольку в этом случае все коэффициенты положительны и можно легко определить знаки входящих в формулы слагаемых. Множитель в скобках для горизонтальной силы ${{F}_{x}}$ всегда отрицателен для всех значений z, так что направление ${{F}_{x}}$ определяется только горизонтальной координатой $x$. Поскольку зависимость по $x$ периодическая, то образуются максимумы силы и минимумы, в которых сила равна нулю. По-видимому, в этих областях в основном группируются взвешенные частицы. Аналогичный множитель в скобках для вертикальной силы положителен для всех значений x, так что направление вертикальной компоненты силы не зависит от горизонтальной координаты x и определяется только координатой z. Анализ дисперсионных кривых показал, что параметр $rh$ может меняться в пределах от нуля до ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ с дальнейшим периодическим сдвигом на $\pi n$, n – целое. Это означает, что множитель $\sin 2r\left( {z + h} \right)$ положителен, и вертикальная компонента радиационной силы стремится собрать взвешенные частицы на свободной поверхности жидкости. Это значит, что при уменьшении толщины испаряющегося слоя сгруппированные частицы оседают на поверхность подложки.
Поскольку радиационные силы квадратичны по акустическому полю, то период пространственной структуры, возникающей под их воздействием в горизонтальном направлении, равен не длине акустической волны, а ее половине, так как $2k = 2 \times {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda } = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {\left( {{\lambda \mathord{\left/ {\vphantom {\lambda 2}} \right. \kern-0em} 2}} \right)}}} \right. \kern-0em} {\left( {{\lambda \mathord{\left/ {\vphantom {\lambda 2}} \right. \kern-0em} 2}} \right)}}.$
Потенциал радиационного давления
Радиационное давление в общем случае является тензорной величиной, однако в данной задаче $rot{\mathbf{F}} = 0,$ т.е. силу радиационного давления можно представить в виде градиента некоторого потенциала ${\mathbf{F}} = - gradV.$ Найдем этот потенциал, используя выражения (30)–(31):
Акустические течения, вызванные радиационным давлением
Радиационное давление приводит жидкость в движение, вынуждая ее течь. Структура установившихся течений при малых гидродинамических числах Рейнольдса рассчитывается на основе системы уравнений [23]:
(32)
$ - \eta \Delta {{{\mathbf{U}}}_{{\text{т }}}} = - \nabla P + {\mathbf{F}},\,\,\,\,div{{{\mathbf{U}}}_{{\text{т }}}} = 0.$(33)
$\Delta \Delta \Psi = 0,\,\,\,\,{{U}_{{{\text{т }}x}}} = {{\partial \Psi } \mathord{\left/ {\vphantom {{\partial \Psi } {\partial z}}} \right. \kern-0em} {\partial z}},\,\,\,\,{{U}_{{{\text{т }}z}}} = - {{\partial \Psi } \mathord{\left/ {\vphantom {{\partial \Psi } {\partial x}}} \right. \kern-0em} {\partial x}}.$К уравнениям необходимо добавить следующие граничные условия. На границе $z = 0$ с твердым полупространством скорость течения равна нулю (${{U}_{{{\text{т }}x}}} = {{U}_{{{\text{т }}z}}} = 0$); на свободной границе жидкости $z = - h$ отсутствуют вертикальный поток (${{U}_{{{\text{т }}z}}} = 0$) и давление на поверхность ($P = 0$).
Учитывая структуру рассчитанного поля радиационных сил, ищем решение со следующей зависимостью от горизонтальной координаты:
(34)
$\begin{gathered} \Psi = {{\Psi }_{0}}\left( z \right)\sin (2kx),\,\,\,\,{{U}_{x}} = A\left( z \right)\sin (2kx), \\ {{U}_{z}} = B\left( z \right)\cos (2kx). \\ \end{gathered} $Из формул (34), определяющих функцию тока, следует, что существуют связи $A = \Psi _{0}^{'},$ $B = - 2k{{\Psi }_{0}},$ $B{\text{'}} = - 2kA.$ Интегрируя уравнение для линий тока ${{dx} \mathord{\left/ {\vphantom {{dx} {{{U}_{{{\text{т }}x}}} = {{dz} \mathord{\left/ {\vphantom {{dz} {{{U}_{{{\text{т }}z}}}}}} \right. \kern-0em} {{{U}_{{{\text{т }}z}}}}}}}} \right. \kern-0em} {{{U}_{{{\text{т }}x}}} = {{dz} \mathord{\left/ {\vphantom {{dz} {{{U}_{{{\text{т }}z}}}}}} \right. \kern-0em} {{{U}_{{{\text{т }}z}}}}}}},$ с учетом этих связей получаем уравнение ${{\Psi }_{0}}\sin (2kx) = {\text{const}}{\text{.}}$ Видим, что на прямых $x = {{\pi n} \mathord{\left/ {\vphantom {{\pi n} {2k}}} \right. \kern-0em} {2k}}$ в плоскости $(x,\,z)$ скорость течения обращается в ноль. Эти прямые разделяют на плоскости $(x,\,z)$ области с противоположно направленными скоростями (см. рис. 6).
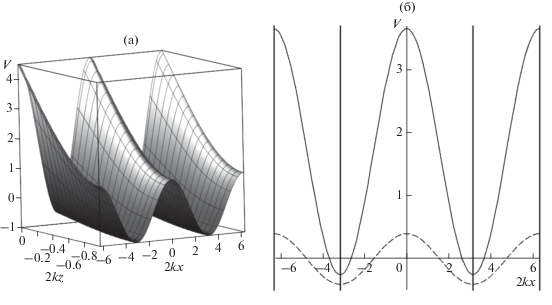
Рис. 6.
Линии тока акустического течения. По оси абсцисс отложена величина $X = 2kx,$ по оси ординат $Z = 2kz.$

Этот качественный результат подтверждается результатом расчета линий тока. Из бигармонического уравнения (33) получается обыкновенное дифференциальное уравнение для функции ${{\Psi }_{0}}(z),$ которое затем решается:
Окончательное решение для функции тока имеет вид:
Это выражение использовано для построения линий тока акустического течения. Как видно из рис.6, линии тока гуще расположены в окрестностях линий $2kx = \pi n.$ Это означает, что при наличии сил взаимодействия между частицами, которые могут быть как гидродинамического, так и иного происхождения (например, иметь электрическую или химическую природу), взвешенные частицы будут концентрироваться преимущественно в этих областях. Таким образом, стоячая поверхностная волна может быть управляющим фактором для формирования упорядоченных структур взвешенных в жидкости наночастиц.
КАЧЕСТВЕННАЯ КАРТИНА ФОРМИРОВАНИЯ УПОРЯДОЧЕННОЙ СТРУКТУРЫ ВЗВЕШЕННЫХ В ЖИДКОСТИ НАНОЧАСТИЦ В ПОЛЕ ПЕРИОДИЧЕСКИХ СИЛ РАДИАЦИОННОГО ДАВЛЕНИЯ
Рассчитаем характер движения наночастиц с учетом радиационного давления со стороны периодической стоячей поверхностной волны. Будем исходить из уравнений (28), записанных для горизонтальной и вертикальной компонент скорости частиц. Согласно приведенным выше рассуждениям, влияние сил радиационного давления сводится к формированию акустических течений, в поле которых движется частица. Механизм радиационного воздействия, связанный с рассеянием поля акустической волны на частице и явно присутствующий в уравнении (28), учитывать не будем. Учтем также, что отношение инерционных членов к вязким имеет порядок малого времени ${{t}_{0}}$ затухания собственного движения относительно потока. Если рассматривать движение частиц на временах ${{t}_{1}} \gg {{t}_{0}},$ то их отношение будет порядка ${{{{t}_{0}}} \mathord{\left/ {\vphantom {{{{t}_{0}}} {{{t}_{1}}}}} \right. \kern-0em} {{{t}_{1}}}}.$ Это означает, что на этих временах можно пренебречь инерционными членами по сравнению с вязкими. Таким образом, в уравнениях движения частицы под скоростью жидкости будем понимать скорость акустического течения ${\mathbf{u}} = {{{\mathbf{U}}}_{{\text{т }}}}.$ Необходимо отметить, что в самом простом случае из уравнения (28) следует, что скорость частицы равна скорости потока, ${\mathbf{v}} = {{{\mathbf{U}}}_{{\text{т }}}},$ однако в нашем случае ${{{\mathbf{U}}}_{{\text{т }}}} = {{{\mathbf{U}}}_{{\text{т }}}}\left( {x,z} \right).$ В итоге для анализа движения частицы необходимо исследовать задачу ${{d{{{\mathbf{X}}}_{S}}} \mathord{\left/ {\vphantom {{d{{{\mathbf{X}}}_{S}}} {dt}}} \right. \kern-0em} {dt}} = {\mathbf{U}}({{x}_{p}},{{z}_{p}})$ движения частицы в потенциальном поле. Здесь ${{{\mathbf{X}}}_{S}}\left( t \right) = \left\{ {{{X}_{S}}\left( t \right),{{Z}_{S}}\left( t \right)} \right\}$ – радиус-вектор частицы. Используем выражения для потоков, в которых удобно ввести безразмерные переменные $X = 2k{{x}_{p}},$ $Z = 2k{{z}_{p}},$ $\theta = {t \mathord{\left/ {\vphantom {t \tau }} \right. \kern-0em} \tau },$ $\tau = {{8\eta sh2kh} \mathord{\left/ {\vphantom {{8\eta sh2kh} {{{\rho }_{0}}U_{0}^{2}kh}}} \right. \kern-0em} {{{\rho }_{0}}U_{0}^{2}kh}}$ – характерная постоянная времени движения частицы. В итоге получаем систему уравнений (точка означает производную по θ):
Рассмотрим характер движения в случае тонкого жидкого слоя $kh \ll 1.$ Тогда, ограничиваясь основными членами разложения по Z, получим:
Первое уравнение показывает, что вдоль горизонтальной оси существуют точки равновесия $X = \pi n.$ При этом учет нелинейных членов является принципиальным, поскольку показывает, что условия равновесия на границе раздела сред и на свободной поверхности различаются. Это означает, что если частица находится в области устойчивого равновесия вблизи свободной поверхности и при этом участвует в вертикальном движении вниз к границе раздела, то на определенной высоте устойчивость нарушается и частица начинает двигаться к соседнему равновесному положению.
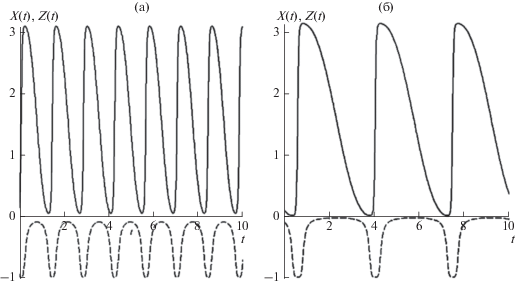
На рис. 7 представлено изменение координат взвешенных частиц со временем. Видно, что происходит периодический процесс перехода между соседними положениями равновесия. Таким образом, без наличия дополнительных сил взаимодействия между частицами формирование стабильных упорядоченных структур невозможно. Однако сравнительно большое время нахождения вблизи одной из точек равновесия создает условия для проявления взаимодействия со стороны других сил как гидродинамического, так и электромагнитного, химического и т.д. типа.
ЗАКЛЮЧЕНИЕ
Построена теория, дающая качественное объяснение экспериментам по формированию упорядоченных структур частиц при высыхании пленки коллоидного раствора на твердой подложке. Показана возможность управления процессом за счет возбуждения волны, распространяющейся вдоль границы раздела твердой и жидкой сред. Рассчитано волновое поле, радиационные силы и акустические течения в жидком слое. Учтены основные факторы, влияющие на процессы формирования акустического поля, вихревого течения и структур наночастиц. Подтверждены следующие данные наблюдений. Основным фактором упорядочения являются радиационные силы в жидком слое. Период формирующейся структуры равен половине длины волны. Радиационное давление на частицы, увлекаемые жидкостью, связанное с рассеянием акустических волн на них, можно, по-видимому, не учитывать. Важную роль должны играть силы неакустического происхождения, приводящие к агрегации частиц, сближающихся под действием течений.
В заключение следует обратить внимание на тот факт, что микропотоки, вызываемые радиационными силами при акустическом облучении или под действием вибрации, уже используются в нанотехнологиях [14] и довольно давно – в медицинских приложениях ультразвука [22]. В Акустическом журнале, например, опубликованы результаты исследования акустических течений, формирующихся при распространении поверхностной капиллярной волны вдоль свободной поверхности в плоском слое жидкости [24], в цилиндрическом объеме жидкой капли [25] и в капле сферической формы [26]. Обсуждалось воздействие радиационных и гидродинамических сил на частицы малого размера и возможности формирования упорядоченных структур из этих частиц [14]. В работах [25, 26] введен термин “акусто-микро-флюидика” для того, чтобы выделить эти работы в потоке бурно развивающегося направления, которое получило устоявшееся название “микро-флюидика”.
В дальнейшем представляет интерес исследовать акустические течения в жидкой капле, которая имеет форму шарового сегмента, помещена на вибрирующую подложку и содержит наночастицы. При этом, помимо акустических сил, следует учесть взаимодействие частиц, их адгезию и трение о подложку [27, 28]. Важно также оценить влияние нагревания капли высокочастотным акустическим полем, как дополнительный фактор конвективной неустойчивости раствора.
Работа поддержана грантом № 19-02-00937 Российского фонда фундаментальных исследований.
Список литературы
Shiokawa S., Matsui Y., Moriizumi T. Experimental Study on Liquid Streaming by SAW // Jpn. J. Appl. Phys. 1989. V. 28. Suppl. 28-1. P. 126–128.
Shiokawa S., Matsui Y., Ueda T. Study on SAW Streaming and its Application to Fluid Devices // Jpn. J. Appl. Phys. 1990. V. 29. Suppl. 2-1. P. 137–139.
Uchida T., Suzuki T., Shiokawa S. Investigation of acoustic streaming excited by surface acoustic waves // Proc. IEEE Ultrasonics Symposium. 1995. V. 2. P. 1081–1083.
Strobl C.J., Rathgeber A., Wixforth A., Gauer C., Scriba J. Planar microfluidic processor // Proc. IEEE Ultrasonics Symposium. 2002. V. 1. P. 255–258.
Wixforth A., Scriba J., Gauer C. Flatland fluidics // MST News. Nov. 2002. V. 5. P. 42–43.
Wixforth A. Acoustically driven planar microfluidics // Superlattices and Microstructures. 2003. V. 33. P. 389–396.
Strobl C.J., Guttenberg Z.V., Wixforth A. Nano- and pico -dispensing of fluids on planar substrates using SAW // IEEE Transaction on Ultrasonics. Ferroel. Freq. Contr. 2004. V. 51. P. 1432–1436.
Renaudin A., Tabourier P., Zhang V., Camart J.C., Druon C. SAW nanopump for handling droplets in view of biological applications // Sensors and Actuators B. 2006. V. 113. P. 389–397.
Tan M.K., Friend J.R., Yeo L.Y. Surface Acoustic Wave Driven Microchannel Flow // Proc. of 16th Australasian Fluid Mechanics Conference. Australia. 2007. P. 790–793.
Tan M.K., Friend J.R., Yeo L.Y. SAW Driven Microchannel Flow // Proc. of 5th Australian Congress on Applied Mechanics. ACAM 2007. P. 348–353.
White R.M., Voltmer F.W. Direct piezoelectric coupling to surface elastic waves // Applied Physics Letters. 1965. V. 7. P. 314–316.
Гуляев Ю.В., Хикернелл Ф.С. Акустоэлектроника: история, современное состояние и новые идеи для новой эры // Акуст. журн. 2005. Т. 51. № 1. С. 101–110.
Викторов И.А. Звуковые поверхностные волны в твердых телах. М.: Наука, 1981.
Rudenko O.V., Lebedev-Stepanov P.V., Gusev V.A., Korobov A.I., Korshak B.A., Odina N.I., Izosimova M.Yu, Molchanov S.P., Alfimov M.V. Control of self-assembly processes in droplet of colloidal solution by the acoustic field // Acoustical Physics. 2010. V. 56. № 6. P. 935–941.
Волькенштейн М.М., Левин В.М. Структура волны Стоунли на границе вязкой жидкости и твердого тела // Акуст. журнал. 1988. № 4. С. 34.
Guz A.N., Bagno A.M. Effect of Prestresses on the Dispersion of Lamb Waves in a System Consisting of a Viscous Liquid Layer and a Compressible Elastic Layer // International applied mechanics. 2018. V. 54 (3). P. 249–258.
Gusev V.A., Simonova P.A. Effect of Shear Components of the Acoustic Field in the Viscous Liquid on the Structure of the Stoneley Wave at the Interface between the Liquid and Elastic Half-Spaces // Physics of Wave Phenomena. 2015. V. 23. № 4. P. 268–272.
Гольдберг З.А. Давление звука. В книге: Мощные ультразвуковые поля / Под ред. Розенберга Л.Д. М.: Наука, 1968.
Горьков Л.П. О силах, действующих на малую частицу в акустическом поле в идеальной жидкости // ДАН СССР. 1961. Т. 140. В. 1. С. 88.
Акустика в задачах / Под ред. Гурбатова С.Н. и Руденко О.В. М.: Физматлит, 2009.
Лебедев-Степанов П.В., Руденко О.В. О затухании звука в жидкости, содержащей взвешенные частицы микро- и нанометровых размеров // Акуст. журн. 2009. Т. 55. № 6. С. 706–711.
Sarvazyan A.P., Rudenko O.V., Nyborg W.L. Biomedical applications of radiation force of ultrasound, Historical roots and physical basis (Review) // Ultrasound in Medicine and Biology. 2010. V. 36. № 9. P. 1379–1394.
Руденко О.В., Солуян С.И. Теоретические основы нелинейной акустики. М.: Наука, 1975.
Лебедев-Степанов П.В., Руденко О.В. Акустические течения в слое жидкости на вибрирующей подложке // Акуст. журн. 2013. Т. 59. № 6. С. 693–697.
Лебедев-Степанов П.В., Руденко О.В. Акусто-микро-флюидика: капиллярные волны и вихревые течения в цилиндрическом объеме жидкой капли // Акуст. журн. 2015. Т. 61. № 2. С. 191–195.
Лебедев-Степанов П.В., Руденко О.В. Акусто-микро-флюидика: капиллярные волны и вихревые течения в сферической жидкой капле // Акуст. журн. 2016. Т. 62. № 4. С. 408–411.
Lebedev-Stepanov P.V., Vlasov K.O. Simulation of self-assembly in an evaporating droplet of colloidal solution by dissipative particle dynamics // Colloids and Surfaces A: Physicochem. Eng. Aspects. 2013. V. 432. P. 132–138.
Лебедев-Степанов П.В. Введение в самоорганизацию и самосборку ансамблей наночастиц. М.: Изд. НИЯУ МИФИ, 2015. 304 с.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал