1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 65, № 2, 2019

Акустический журнал, 2019, T. 65, № 2, стр. 182-189

Локальные соотношения Крамерса–Кронига для коэффициента затухания и фазовой скорости продольных ультразвуковых волн в полимерных композитах

А. А. Карабутов a, b, Н. Б. Подымова c, Ю. Г. Соколовская c, *

a Московский государственный университет им. М.В. Ломоносова, Международный учебно-научный лазерный центр
119991 Москва, ГСП-1, Ленинские горы 1, стр. 62, Россия

b Национальный исследовательский технологический университет “МИСиС”
119991 Москва, Ленинский просп. 4, Россия

c Московский государственный университет им. М.В. Ломоносова, физический факультет
119991 Москва, ГСП-1, Ленинские горы 1, стр. 2, Россия

* E-mail: yu.sokolovskaya@mail.ru

Поступила в редакцию 03.09.2018
После доработки 30.10.2018
Принята к публикации 03.09.2018

Полный текст (PDF)

Аннотация

Проанализирована связь между экспериментально полученными коэффициентом затухания и дисперсией фазовой скорости продольных ультразвуковых волн в полимерных композиционных материалах. Для измерения затухания и скорости ультразвуковых волн в широком частотном диапазоне использовался лазерный оптико-акустический метод. Проведена проверка выполнения соотношений Крамерса–Кронига для рассеивающих и поглощающих ультразвук углепластиковых композиционных материалов на основе анализа связи частотных зависимостей коэффициента затухания и фазовой скорости продольных акустических волн в образцах. Показано, что в спектральном диапазоне 1–10 МГц соотношения Крамерса–Кронига между затуханием и фазовой скоростью продольных ультразвуковых волн выполняются независимо от конкретного механизма уменьшения энергии исходной акустической волны при ее распространении в композите.

Ключевые слова: полимерные композиционные материалы, широкополосная лазерно-ультразвуковая спектроскопия, продольные акустические волны, фазовая скорость

ВВЕДЕНИЕ

Хорошо известно, что частотные зависимости коэффициента затухания и фазовой скорости акустических волн связаны между собой соотношениями Крамерса–Кронига, которые являются следствием фундаментального физического принципа причинности [1–4]. Эти общие дисперсионные соотношения могут быть записаны в виде интегралов по бесконечному диапазону частот. Поэтому в общем случае для вычисления дисперсии скорости ультразвуковых волн на определенной частоте необходимо знать величину затухания на всех частотах. Соответственно, общие соотношения Крамерса–Кронига оказываются неприменимы в тех случаях, когда вклад в интегралы с бесконечными пределами не является локализованным в определенной области частот. Таким образом, поскольку в реальном эксперименте полоса исследуемых частот всегда ограничена, с научной точки зрения представляется интересным и целесообразным проанализировать справедливость соотношений Крамерса–Кронига для ограниченного диапазона частот (см., напр. [5–7]). Приближенные соотношения для ограниченной частотной полосы, называемые локальными, могут быть получены из общих нелокальных соотношений при условии отсутствия резонансов затухания и дисперсии фазовой скорости акустических волн в исследуемой полосе частот [1, 6, 7].

Затухание акустических волн в среде может быть вызвано поглощением, рассеянием или совокупностью этих механизмов. При этом соотношения Крамерса–Кронига должны выполняться независимо от особенностей конкретного физического механизма, приводящего к затуханию и дисперсии акустических волн в среде [6, 7]. Из-за известных технических трудностей, связанных с измерением затухания и скорости звука в широком спектральном диапазоне [8], проверка выполнения этих соотношений была проведена только для ограниченного числа сред, при этом затухание звука в исследованных средах было обусловлено в основном его поглощением, а рассеяние практически отсутствовало. Так, в работах [9–11] была проведена проверка локальных соотношений Крамерса–Кронига для биологических сред (белковых растворов и молока) и для химических растворов (кобальтового и марганцевого купороса). Авторами [6, 12] были проанализированы частотные зависимости поглощения и дисперсии акустических волн в ряде полимеров (полиметилметакрилат, полиэтилен и др.). Проводились также экспериментальные исследования дисперсионных соотношений для масел на касторовой и углеродной основе, а также модельных жидкостей на основе желатина и графита [13, 14]. Аналогичные исследования были проведены и для газов [15].

Целью настоящей работы является экспериментальная проверка выполнения соотношений Крамерса–Кронига в материале, в котором реализуется сразу два механизма потерь энергии акустической волны – рассеяние и поглощение. В качестве такого материала были выбраны композиты на основе полимерной матрицы и углеродных волокон – так называемые углепластики. Для изучения частотных зависимостей коэффициента затухания и дисперсии фазовой скорости ультразвука в таких материалах необходимо использовать короткие и мощные широкополосные зондирующие акустические импульсы, поскольку углепластики достаточно сильно поглощают и рассеивают ультразвук в мегагерцовом диапазоне. Для получения таких импульсов в настоящей работе предлагается использовать лазерный термооптический механизм возбуждения ультразвука (оптико-акустический эффект) [16–18]. Он позволяет получать ультразвуковые импульсы с амплитудой до сотен мегапаскалей в спектральном диапазоне от долей до десятков мегагерц [16, 17, 19]. Для проверки выполнения локальных соотношений Крамерса–Кронига для продольных акустических волн в углепластиках используется метод широкополосной акустической спектроскопии с лазерным источником ультразвука, подробно изложенный в [16].

ПОСТАНОВКА ЗАДАЧИ

Для акустических волн в изотропной среде, описываемой общей формой закона Гука, соотношения Крамерса–Кронига для реальной и мнимой частей динамической сжимаемости записываются в виде

(1)
$\begin{gathered} {{K}_{1}}(\omega ) - {{K}_{1}}(\infty ) = \frac{2}{\pi }\int\limits_0^\infty {\frac{{\omega {\text{'}}{{K}_{2}}(\omega {\text{'}})}}{{{{\omega }^{{{\text{'}}2}}} - {{\omega }^{2}}}}} d\omega {\text{'}}, \hfill \\ {{K}_{2}}(\omega ) = - \frac{{2\omega }}{\pi }\int\limits_0^\infty {\frac{{{{K}_{1}}(\omega {\text{'}}) - {{K}_{1}}(\infty )}}{{{{\omega }^{{{\text{'}}2}}} - {{\omega }^{2}}}}} d\omega {\text{'}}, \hfill \\ \end{gathered} $
где $K = {{K}_{1}} + i{{K}_{2}}$ – величина, обратная объемному модулю упругости [1, 20], $\omega = 2\pi f$ – циклическая частота, f – частота акустической волны.

С использованием дисперсионного соотношения для акустических волн

(2)
${{k}^{2}} = {{\omega }^{2}}{{\rho }_{0}}K(\omega ),$
где k – волновое число, и учитывая, что
(3)
$\,k = \frac{{\omega }}{{C({\omega })}} + i{\alpha }({\omega }),$
соотношения между сжимаемостью, коэффициентом затухания $\alpha (\omega )$ и фазовой скоростью C(ω) можно записать в виде [6, 7]

(4)
$\begin{gathered} \frac{{{{\omega }^{2}}}}{{{{C}^{2}}(\omega )}} - {{\alpha }^{2}}(\omega ) = {{\omega }^{2}}{{\rho }_{0}}{{K}_{1}}(\omega ), \\ \frac{{2\alpha (\omega )}}{{C(\omega )}} = \omega {{\rho }_{0}}{{K}_{2}}(\omega ). \\ \end{gathered} $

В случае $\frac{{\alpha (\omega )C(\omega )}}{\omega } \ll 1$ (так называемом звуковом приближении), справедливом для мегагерцового диапазона частот,

(5)
$\begin{gathered} C(\omega ) = \frac{1}{{\sqrt {{{\rho }_{0}}{{K}_{1}}(\omega )} }}, \\ \alpha (\omega ) = \frac{1}{2}{{\rho }_{0}}C(\omega )\omega {{K}_{2}}(\omega ). \\ \end{gathered} $

Выражения (5) с учетом (1) описывают соотношение между дисперсией фазовой скорости и затуханием акустических волн в неограниченной полосе частот. Они могут быть использованы для практического анализа только в том случае, когда преобладающий вклад в интегралы с бесконечными пределами сильно локализован по частоте [6, 7]. Вообще говоря, в формулах (1) бесконечные пределы интегрирования являются “условными”, так как звуковое приближение справедливо только для длин волн, значительно превышающих межатомные расстояния, и для случая твердых тел вычисление по формуле (5) проводится только до частот порядка 1014 Гц [2].

Для того чтобы проводить сравнение с экспериментальными данными, полученными в ограниченном частотном диапазоне, необходимо перейти от общих соотношений Крамерса–Кронига к локальным. Приближенные локальные соотношения в некотором диапазоне частот $\left[ {{{\omega }_{0}},\omega } \right]$ можно получить в том случае, если в этом диапазоне частотные зависимости коэффициента затухания и скорости ультразвуковых волн являются монотонными функциями (т.е. не имеют локальных экстремумов и резонансов) [7]. В этом случае выражение для мнимой части динамической сжимаемости ${{K}_{2}}(\omega )$ (1) можно разложить в ряд по частоте в окрестности ${{\omega }_{0}}$ и пренебречь слагаемыми, которые соответствуют высшим производным в данном разложении [7].

В этом случае связь мнимой части сжимаемости с локальной скоростью изменения реальной части сжимаемости на той же частоте записывается в виде

(6)
${{K}_{2}}(\omega ) = - \frac{\pi }{2}\omega \frac{{d{{K}_{1}}(\omega )}}{{d\omega }}.$

Воспользовавшись формулами (4) и (6), получаем локальные соотношения Крамерса–Кронига в диапазоне частот $\,\left[ {{{\omega }_{0}},\omega } \right]{\text{:}}$

(7)
$\alpha (\omega ) = \frac{{\pi {{\omega }^{2}}}}{{2C_{0}^{2}}}\frac{{dC(\omega )}}{{d\omega }},$
(8)
$\,C({\omega }) = {{\left( {\frac{1}{{{{C}_{0}}}} - \frac{2}{{\pi }}\int\limits_{{{{\omega }}_{{\text{0}}}}}^{\omega } {\frac{{\alpha ({\omega '})}}{{{\omega }{{{\text{'}}}^{2}}}}d{\omega '}} } \right)}^{{ - 1}}}.$

Таким образом, выражения (7) и (8) описывают связь между дисперсией фазовой скорости и коэффициентом затухания продольных акустических волн в заданном ограниченном спектральном диапазоне $\left[ {{{\omega }_{0}},\omega } \right].$ При проведении экспериментальных исследований он будет соответствовать тому диапазону, в котором измеряются частотные зависимости $\alpha (\omega )$ и $C({\omega }).$

ИССЛЕДУЕМЫЕ ОБРАЗЦЫ

В настоящей работе исследуется композиционный материал, состоящий из чередующихся слоев ткани из углеродных волокон и полимерной матрицы на основе эпоксидной смолы. Данный материал – углепластик – является так называемым однонаправленным композитом, в котором все ленты углеродных волокон, образующих армирующую ткань, сонаправлены. Объемная концентрация углеродного волокна в четырех исследованных образцах составляла 62.6% (образцы № 1 и № 3), 65.1% (образец № 2) и 55.8% (образец № 4).

Затухание ультразвуковых волн в углепластиках обусловлено поглощением в полимерной матрице и рассеянием на углеродных волокнах. Матрица представляет собой аморфный полимер, в котором поглощение происходит из-за перехода энергии ультразвуковых волн в колебательную и вращательную энергию полимерных молекулярных цепочек. Частотные зависимости коэффициента затухания и фазовой скорости продольных акустических волн в полимерах определяются энергиями внутримолекулярного и межмолекулярного взаимодействия, свойствами релаксационных процессов в данном полимере, типом и интенсивностью молекулярного движения [21]. Особенности межмолекулярного взаимодействия и наличие длинных молекулярных цепей приводят к появлению спектра времен релаксации, что, в свою очередь, приводит к появлению дисперсии фазовой скорости и частотной зависимости коэффициента затухания ультразвука.

Помимо рассеяния акустических волн на углеродных волокнах, в исследуемых композитах может возникать дополнительное рассеяние, связанное с наличием мелких пор в материале. Типичные размеры таких пор лежат в диапазоне 10–50 мкм. Пористость P (объемная концентрация пор) в углепластиках образуется из-за наличия воздушных включений, летучих продуктов и излишков влаги в процессе производства [22]. Образцы № 1 и № 2 были практически беспористыми (P < 0.1%), в образцах № 3 и № 4 средняя пористость составляла 0.7 и 1.4%. Таким образом, наличие пористости будет дополнительным фактором, влияющим на затухание ультразвуковой волны в композите. Пористость P, усредненная по всему объему образца, рассчитывается по формуле

(9)
$P = \left( {1 - \frac{\rho }{{{{\rho }_{0}}}}} \right)\; \times \;100\% ,$
где фактическая плотность образца ρ определяется по результатам его гидростатического взвешивания, плотность ρ0 твердой фазы образца (без пор) рассчитывается по известным плотностям полимерной матрицы ρm и углеродной ткани ρf и их объемным концентрациям nm и nf в данном образце (nm + nf = 1):

(10)
${{\rho }_{0}} = {{n}_{m}}{{\rho }_{m}} + {{n}_{f}}{{\rho }_{f}}.$

МЕТОДИКА ЭКСПЕРИМЕНТА

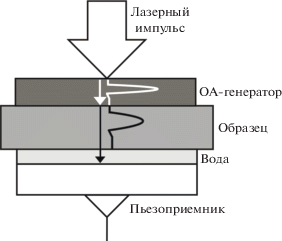
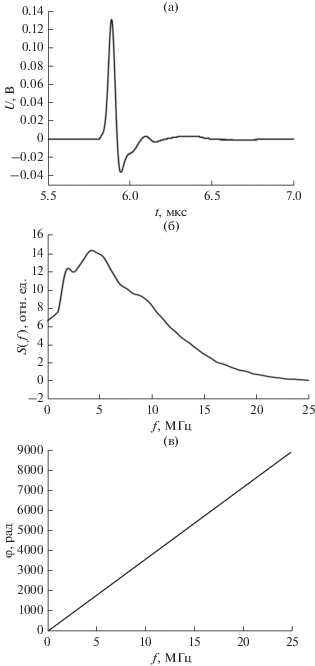
Широкополосный оптико-акустический (ОА) спектрометр, используемый в данной работе, состоит из Nd:YAG-лазера с модуляцией добротности на длине волны 1064 нм, ОА-ячейки, цифрового осциллографа и персонального компьютера. Схема ОА-ячейки показана на рис. 1. При поглощении лазерного импульса в специальном источнике звука (ОА-источнике) происходит неоднородный нестационарный нагрев его приповерхностного слоя, приводящий к возникновению в нем механических напряжений, которые, в свою очередь, являются источниками продольных акустических волн. Возбуждаемый в источнике ОА-сигнал является зондирующим (опорным) в данном спектрометре. Характерная длительность лазерного импульса составляла 10–12 нс, частота повторения импульсов 10 Гц, энергия в импульсе 10−15 мДж. В качестве ОА-источника ультразвука использовался водный раствор черной туши. Временной профиль, амплитудный и фазовый спектры зондирующего ультразвукового импульса показаны на рис. 2. Регистрация ультразвуковых импульсов, прошедших через исследуемый образец, осуществлялась с помощью широкополосного пьезоприемника с рабочей полосой частот 0.1–30 МГц, изготовленного на основе ПВДФ-пленки толщиной 30 мкм. Акустический контакт между образцом и пьезоприемником в ОА-ячейке обеспечивался слоем дистиллированной воды толщиной 3 мм. Электрические сигналы с пьезоприемника передавались на цифровой осциллограф с аналоговой полосой частот 200 МГц и затем обрабатывались на персональном компьютере. Запуск осциллографа был синхронизирован с моментом излучения лазерного импульса. Максимальное соотношение сигнал–шум регистрируемых электрических сигналов составляло порядка 2000.

Рис. 1.

Оптико-акустическая ячейка.

Рис. 2.

(а) Временной профиль, (б) амплитудный и (в) фазовый спектры зондирующего ультразвукового импульса.

Амплитудный спектр S(f) ультразвукового импульса, прошедшего исследуемый образец известной толщины H, описывается выражением [23]

(11)
$\begin{gathered} S(f) = {{S}_{0}}(f){{T}_{1}}{{T}_{2}}\exp \left[ { - \alpha (f)H} \right] = \\ = {{S}_{0}}(f){{T}_{{{\text{trans}}}}}\exp \left[ { - \alpha (f)H} \right], \\ \end{gathered} $
где f – частота продольной акустической волны, ${{T}_{1}} = {{2{{Z}_{{\text{s}}}}} \mathord{\left/ {\vphantom {{2{{Z}_{{\text{s}}}}} {\left( {{{Z}_{{\text{s}}}} + {{Z}_{{{\text{ink}}}}}} \right)}}} \right. \kern-0em} {\left( {{{Z}_{{\text{s}}}} + {{Z}_{{{\text{ink}}}}}} \right)}}$ – амплитудный коэффициент прохождения волны из источника в образец, ${{T}_{2}} = {{2{{Z}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \mathord{\left/ {\vphantom {{2{{Z}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} {\left( {{{Z}_{{\text{s}}}} + {{Z}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \right)}}} \right. \kern-0em} {\left( {{{Z}_{{\text{s}}}} + {{Z}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \right)}}$ – амплитудный коэффициент прохождения волны из образца в воду, Zs, Zink и ${{Z}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ – значения акустического импеданса образца композита, раствора туши и воды соответственно, α(f) – частотно-зависимый коэффициент затухания продольных акустических волн в образце. Зависимость α(f) может быть выражена из (11) как

(12)
$\alpha (f) = \frac{1}{H}\ln \frac{{{{S}_{0}}(f)}}{{S(f)}} + \frac{1}{H}\ln {{T}_{{{\text{trans}}}}}.$

Акустический импеданс воды считался известным: ${{Z}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}$ = 1.49 × 106 кг/(м2 с), акустический импеданс образца композита рассчитывался по определенным экспериментально значениям его плотности ρ и фазовой скорости продольных акустических волн C. В общем случае для композита может наблюдаться дисперсия фазовой скорости – частотная зависимость C(f). В этом случае акустический импеданс исследуемого образца также будет зависеть от частоты: Zs (f) = ρC(f).

Дисперсия фазовой скорости продольных акустических волн в образце C(f) рассчитывается с использованием фазовых спектров зондирующего ультразвукового импульса φ0(f) и импульса, прошедшего через образец, φ(f) [23]:

(13)
$C(f) = \frac{H}{{{{\Delta T + \left[ {\varphi (f) - {{\varphi }_{0}}(f)} \right]} \mathord{\left/ {\vphantom {{\Delta T + \left[ {\varphi (f) - {{\varphi }_{0}}(f)} \right]} {2\pi f}}} \right. \kern-0em} {2\pi f}}}},$
где $\Delta t = {{t}_{2}} - {{t}_{1}}$ – разность моментов начала записи в осциллографе ультразвукового импульса, прошедшего исследуемый образец, и опорного ультразвукового импульса. Оба значения t1 и t2 отсчитываются от момента излучения лазерного импульса [24]. “Дополнительная” разность фаз $\delta \varphi (f) = \varphi {\kern 1pt} {\kern 1pt} (f) - {{\varphi }_{0}}(f)$ не связана с набегом фазы импульса при его распространении в образце, а определяется искажением временной формы этого импульса за счет затухания и дисперсии фазовой скорости акустических волн в образце. Величины φ0(f) и φ(f) рассчитываются с использованием стандартной процедуры “развертывания фазы” для получения непрерывных фазовых спектров [24].

Спектры ультразвуковых импульсов рассчитывались с использованием стандартного программного пакета быстрого преобразования Фурье с учетом амплитудных коэффициентов отражения акустической волны на каждой границе раздела в ОА-ячейке (см. выражение (11)). Также для спектров всех импульсов применялась процедура компенсации частотно-зависимого дифракционного искажения широкополосных ультразвуковых импульсов, детально изложенная в [25].

ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

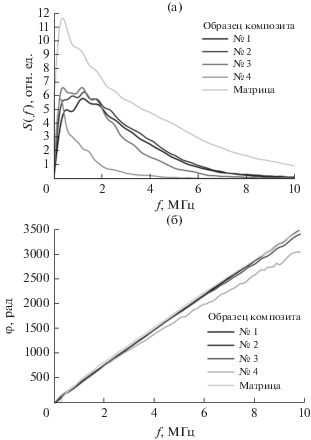
Для анализа влияния различных механизмов потерь на соотношения между коэффициентом затухания и дисперсией фазовой скорости продольных акустических волн были рассмотрены отдельно образцы полимерной матрицы без наполнителя и образцы композитов. Расчет коэффициента затухания и фазовой скорости проводился по измеренным амплитудным и фазовым спектрам с помощью формул (11) и (12). На рис. 3 показаны спектры ультразвукового импульса, прошедшего через матрицу и образцы композитов.

Рис. 3.

(а) Амплитудные и (б) фазовые спектры для исследованных образцов полимерной матрицы и композитов.

Частотные зависимости коэффициента затухания и фазовой скорости продольных ультразвуковых волн в исследованных образцах получены в частотном диапазоне от 1 до 10 МГц. Для частот f < 1 МГц коэффициент затухания не определялся из-за его малости и достаточно большой погрешности, возникающей из-за дифракции низкочастотных составляющих сигнала в образцах. Из-за сильного затухания высоких частот в композитных образцах для частот f > 10 МГц амплитуда прошедшего импульса достаточно мала и сравнима с уровнем шума, поэтому на частотах выше 10 МГц коэффициент затухания также не определялся. Точность измерения фазовой скорости и коэффициента затухания акустических волн определяется погрешностью измерения толщины исследуемого образца, а также соотношением сигнал–шум для спектральной амплитуды каждой гармоники сигнала. В данных экспериментах относительная погрешность измерения скорости ультразвука составляла около 0.5%, а для коэффициента затухания – около 10%.

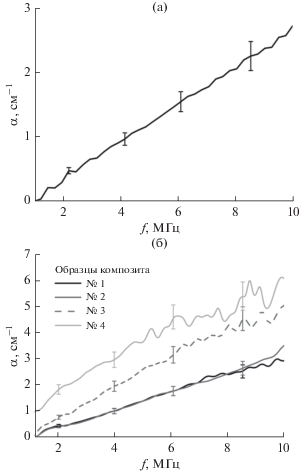
Частотные зависимости коэффициента затухания в полимерной матрице и образцах композитов представлены на рис. 4. В беспористых образцах № 1 и № 2 затухание определяется поглощением в матрице и рассеянием на углеродных волокнах. В композитах № 3 и № 4 абсолютное затухание ультразвуковых волн увеличивается (по сравнению с № 1 и № 2) из-за наличия пористости. Отсутствие резонансов затухания в исследуемых композитных образцах связано с технологией производства материала, обеспечивающей близкие значение акустических импедансов слоев волокон и матрицы и высокой адгезией волокон к матрице.

Рис. 4.

Частотная зависимость коэффициента затухания продольных акустических волн для образцов (а) полимерной матрицы и (б) композитов.

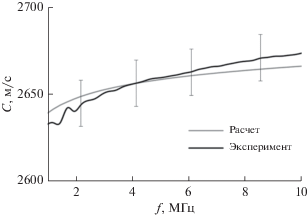
Для проверки справедливости соотношений Крамерса–Кронига были рассчитаны зависимости дисперсии фазовой скорости с использованием локального соотношения (8), в котором в качестве α(f) брался экспериментально измеренный коэффициент затухания. На рис. 5 представлен результат соответствующих расчетов, а также экспериментально полученная зависимость C(f) для матрицы. Видно, что в исследуемом спектральном диапазоне 1–10 МГц в пределах погрешности измерений экспериментальные зависимости совпадают с расчетными. Таким образом, для полимерной матрицы локальные соотношения Крамерса–Кронига выполняются. В этих образцах дисперсия фазовой скорости продольных акустических волн $\Delta C = {{C}_{{\max }}} - {{C}_{{\min }}} \approx $ 50 м/с (где Cmax и Cmin – максимальное и минимальное значения скорости в диапазоне 1–10 МГц) обусловлена особенностями молекулярного строения полимера. Существование такой дисперсии можно объяснить наличием релаксационных процессов, происходящих в результате различных типов молекулярного движения. Если частота звуковой волны мала и, соответственно, период велик по сравнению со временем релаксации самых больших элементов макромолекул, то энергия ультразвуковой волны, получаемая за период элементом объема исследуемого материала, будет быстро перераспределяться по объему среды из-за наличия сегментальной подвижности макромолекул [21]. При возрастании частоты ультразвуковой волны время, за которое происходит поглощение, будет составлять уже большую часть периода. В таком случае могут существовать сегменты, которые не успевают за один период колебаний принять участие в передаче энергии волны соседним сегментам. По отношению к внешнему воздействию они ведут себя как жесткие элементы молекулярных цепочек. Это ведет к возрастанию скорости ультразвука с увеличением частоты.

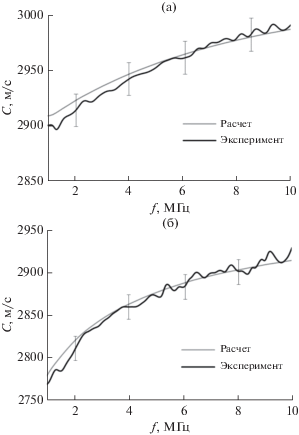
Рис. 5.

Частотная зависимость фазовой скорости продольных акустических волн для образца полимерной матрицы.

На рис. 6, 7 представлены аналогичные экспериментальные и расчетные зависимости C(f) для образцов углепластиков. В спектральном диапазоне 1–10 МГц эти зависимости совпадают в пределах погрешностей измерений. Поэтому для углепластиков соотношения Крамерса–Кронига также выполняются независимо от физического механизма, приводящего к затуханию ультразвуковых волн. В беспористых образцах № 1 и № 2 как дисперсия скорости, так и абсолютное затухание ультразвука определяются поглощением в полимерной матрице и рассеянием на углеродных волокнах. Из-за наличия пористости в композитах № 3 и № 4 относительная дисперсия фазовой скорости ультразвуковых волн увеличивается. Для образца № 3 ΔC ≈ 90 м/с при Р = 0.7%, а для № 4 ΔC ≈ 125 м/с при Р = 1.4%, в то время как для беспористых композитов ΔC ≈ 60 м/с в том же спектральном диапазоне. Следует отметить, что во всем исследуемом спектральном диапазоне абсолютное значение фазовой скорости тем выше, чем больше объемная концентрация углеродного волокна в образце (поскольку скорость ультразвука в волокне выше, чем в матрице). Увеличение относительной дисперсии фазовой скорости для пористого материала происходит из-за преобразования исходной продольной акустической волны в объемную волну, которая будет огибать поры по их границам (см., напр., [26]). Это приводит к уменьшению скорости ультразвуковых волн на низких частотах по сравнению со скоростью в беспористом материале.

Рис. 6.

Частотная зависимость фазовой скорости продольных акустических волн для образцов беспористых композитов: (а) № 1, (б) № 2.

Рис. 7.

Частотная зависимость фазовой скорости продольных акустических волн для образцов малопористых композитов: (а) № 3, (б) № 4.

ЗАКЛЮЧЕНИЕ

Метод широкополосной акустической спектроскопии с лазерным источником ультразвука позволяет получать частотные зависимости коэффициента затухания и фазовой скорости продольных ультразвуковых волн в диапазоне от единиц до десятков мегагерц для сильно поглощающих и рассеивающих ультразвук гетерогенных материалов. В настоящей работе данный метод использовался для измерения коэффициента затухания и фазовой скорости в образцах полимерной матрицы и полимерных композиционных материалов на основе углеродного волокна в частотном диапазоне 1–10 МГц. Для матрицы затухание и дисперсия фазовой скорости ультразвуковых волн обусловлены особенностями молекулярного строения и релаксационными процессами, происходящими в полимерном материале. В однонаправленных углепластиках происходит также рассеяние ультразвуковых волн на углеродных волокнах и порах размером в десятки микрон. Экспериментально показано, что для всех образцов в исследуемом диапазоне частот справедливы локальные соотношения Крамерса–Кронига, и их выполнение не зависит от особенностей конкретного механизма уменьшения энергии исходной ультразвуковой волны при распространении в материале.

Список литературы

  1. Красильников В.А., Крылов В.В. Введение в физическую акустику. М.: Наука, 1984. 403 с.

  2. Гинзбург В.Л. Об общей связи между поглощением и дисперсией звуковых волн // Акуст. журн. 1955. Т. 1. № 1. С. 31–39.

  3. Крылов В.В. О дисперсионных соотношениях для коэффициентов преломления нормальных волн // Вестник Мос. Ун-та. Физ. Астрон. 1982. Т. 23. № 2. С. 42–46.

  4. Зайцев В.Ю., Назаров В.Е., Шульга А.Е. О диссипативных и дисперсионных свойствах микронеоднородных сред // Акуст. журн. 2000. Т. 46. № 3. С. 348–355.

  5. Mobley J., Waters K.R., Miller J.G. Finite-bandwith effects on the causal prediction of ultrasonic attenuation of the power-law form // J. Acoust. Soc. Am. 2003. V. 114. № 5. P. 2782–2790.

  6. O’Donnell M., Jaynes E.T., Miller J.G. General relationships between ultrasonic attenuation and dispersion // J. Acoust. Soc. Am. 1978. V. 63. № 6. P. 1935–1937.

  7. O’Donnell M., Jaynes E.T., Miller J.G. Kramers–Kronig relationship between ultrasonic attenuation and phase velocity // J. Acoust. Soc. Am. 1981. V. 69. № 3. P. 696–701.

  8. Труэлл Р., Эльбаум Ч., Чик Б. Ультразвуковые методы в физике твердого тела. М.: Мир, 1972. 302 с.

  9. Carstensen E.L., Li K., Schwan H.P. Determination of the acoustic properties of blood and its components // J. Acoust. Soc. Am. 1953. V. 25. № 2. P. 286–289.

  10. Carstensen E.L. Relaxation processes in aqueous solutions of MnSO4 and CoSO4 // J. Acoust. Soc. Am. 1954. V. 26. № 5. P. 862–864.

  11. Carstensen E.L. Measurement of dispersion of velocity of sound in liquids // J. Acoust. Soc. Am. 1954. V. 26. № 5. P. 858–861.

  12. Zellouf D., Jayet Y., SaintPierre N., Tatibouët J., Baboux J.C. Ultrasonic spectroscopy in polymeric materials. Application of the Kramers–Kronig relations // J. Appl. Phys. 1996. V. 80. № 5. P. 2728–2732.

  13. Trousil R.L., Waters K.R., Miller J.G. Experimental validation of the use of Kramers–Kronig relations to eliminate the phase sheet ambiguity in broadband phase spectroscopy // J. Acoust. Soc. Am. 2001. V. 109. № 5. Pt. 1. P. 2236–2244.

  14. Waters K.R., Hughes M.S., Mobley J., Brandenburger G.H., Miller J.G. On the applicability of Kramers–Kronig relations for ultrasonic attenuation obeying a frequency power law // J. Acoust. Soc. Am. 2000. V. 108. № 2. P. 556–563.

  15. Alvarez F.J., Kuc R. Dispersion relation for air via Kramers–Kronig analysis // J. Acoust. Soc. Am. 2008. V. 124. № 2. P. 57–61.

  16. Карабутов А.А., Подымова Н.Б. Влияние пористости на дисперсию фазовой скорости продольных акустических волн в изотропных металломатричных композитах // Акуст. журн. 2017. Т. 63. № 3. С. 265–274.

  17. Кожушко В.В., Палтауф Г., Кренн Х. Регистрация наносекундных оптико-акустических импульсов в стали // Акуст. журн. 2013. Т. 59. № 2. С. 279–282.

  18. Юсупов В.И., Коновалов А.Н., Ульянов В.А., Баграташвили В.Н. Генерация акустических волн непрерывным лазерным излучением на торце оптического волокна в воде // Акуст. журн. 2016. Т. 62. № 5. С. 531–539.

  19. Соколовская Ю.Г., Карабутов А.А. Лазерно-ультразвуковая дефектоскопия конструкций из мультиаксиальных полимерных композиционных материалов // Конструкции из композиционных материалов. 2018. № 1. С. 56–60.

  20. Исакович М.А. Общая акустика. М.: Наука, 1973. 496 с.

  21. Перепечко И.И. Акустические методы исследования полимеров. М.: Химия, 1973. 296 с.

  22. Душин М.И., Донецкий К.И., Караваев Р.Ю. Установление причин образования пористости при изготовлении ПКМ // Электронный научный журнал “Труды ВИАМ”. 2016. № 6. С. 68–78.

  23. Fitting D.W., Adler L. Ultrasonic spectral analysis for nondestructive evaluation. New York: Plenum Press, 1981. 354 p.

  24. Podymova N.B., Karabutov A.A. Broadband laser-ultrasonic spectroscopy for quantitative characterization of porosity effect on acoustic attenuation and phase velocity in CFRP laminates // J. Nondestruct. Eval. 2014. V. 33. № 1. P. 141–151.

  25. Karabutov A.A., Savateeva E.V., Podymova N.B., Oraevsky A.A. Backward mode detection of laser-induced wide-band ultrasonic transients with optoacoustic transducer // J. Appl. Phys. 2000. V. 87. № 4. P. 2003–2014.

  26. Wright T.W. Elastic wave propagation through a material with voids // J. Mech. Phys. Solids. 1998. V. 46. № 10. P. 2033–2047.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал