Акустический журнал, 2019, T. 65, № 4, стр. 448-459
Два подхода к решению задачи дифракции плоской волны на двоякопериодической неровной поверхности
А. Г. Кюркчан a, b, c, С. А. Маненков a, *
a Московский технический университет связи и информатики
111024 Москва, ул. Авиамоторная 8а, Россия
b Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московская обл., пл. Введенского 1, Россия
c ФГУП Центральный научно-исследовательский институт связи
111141 Москва, 1-й проезд Перова поля 8, Россия
* E-mail: mail44471@mail.ru
Поступила в редакцию 25.01.2019
После доработки 17.03.2019
Принята к публикации 20.03.2019
Аннотация
На основе модифицированного метода дискретных источников и метода диаграммных уравнений разработаны два алгоритма решения трехмерной задачи рассеяния на акустически мягкой или акустически жесткой двоякопериодической неровной поверхности. В работе использован эффективный алгоритм нахождения периодической функции Грина, разработанный ранее для решения задачи дифракции на решетке из тел вращения. Получены условия применимости алгоритма на основе метода диаграммных уравнений. Проведено сравнение обоих методов на примере синусоидальной двоякопериодической поверхности. Произведена проверка выполнения закона сохранения энергии и проверка выполнения граничного условия на поверхности центрального элемента поверхности. Построены зависимости амплитуд отраженных гармоник от волнового параметра и угла падения плоской волны.
ВВЕДЕНИЕ
Дифракция волн на периодических структурах представляет большой практический интерес [1–5]. В литературе имеется также много работ, посвященных дифракции на неровных поверхностях (в том числе периодических) [6–13]. В указанных работах рассматриваются асимптотические и численные методы решения задачи дифракции на неровных поверхностях, например, метод касательной плоскости, метод малых наклонов, метод поверхностных интегральных уравнений и другие. В большинстве работ рассматриваются двумерные задачи дифракции. Однако более адекватной моделью является трехмерная двоякопериодическая поверхность. В настоящей работе рассматривается задача дифракции плоской волны на акустически мягкой или жесткой двоякопериодической волнистой поверхности. Задача решается двумя методами: модифицированным методом дискретных источников (ММДИ) и методом диаграммных уравнений (МДУ). По-существу, данная работа является обобщением работ [11] и [13], посвященных двумерной задаче дифракции на периодической поверхности. Отметим, что МДУ применим к так называемым слабоневыпуклым поверхностям, в то время как ММДИ может быть применен к существенно менее “пологим” поверхностям. Также отметим, что одним из преимуществ МДУ является, во-первых, простота алгебраизации задачи. Во-вторых, в некоторых частных случаях матричные элементы соответствующей алгебраической системы выражаются в явном виде, то есть не требуют большого объема вычислений.
Как известно (см., например, [13]), в случае применения ММДИ задача дифракции сводится к решению интегрального уравнения относительно некоторой неизвестной функции, распределенной на центральном периоде вспомогательной поверхности, расположенной под исходной (волна падает сверху). При этом ядро интегрального уравнения выражается через периодическую функцию Грина (ФГ). Известно, что двойной ряд периодической ФГ сходится чрезвычайно медленно при условии, что точка наблюдения и точка источника близки друг к другу. С использованием формулы суммирования Пуассона ряд ФГ преобразуется в ряд по гармоникам Флоке. Однако сходимость этого ряда не лучше, чем у исходного, при указанном выше условии [5]. С целью преодоления этой трудности в работе применялся алгоритм вычисления периодической ФГ, предложенный в работе [5], в которой рассмотрена задача дифракции на двоякопериодической решетке, состоящей из тел вращения.
Необходимо также заметить, что при использовании ММДИ возникает трудность, обусловленная зависимостью уравнения поверхности от двух координат. В этом случае непосредственное применение ММДИ невозможно. Для решения данной проблемы в работе использовалась “аналитическая” деформация исходной поверхности при помощи алгебры кватернионов. При таком подходе удается добиться удовлетворительной точности при относительно небольшом размере соответствующей алгебраической системы.
1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим математическую постановку задачи дифракции на двоякопериодической поверхности. Введем декартову систему координат, в которой уравнение поверхности есть $z = f(x,y),$ причем $f(x + {{d}_{x}},y)$ = $f(x,y + {{d}_{y}}) = f(x,y).$ Начало координат выберем в середине какого-либо периода поверхности (назовем его центральным периодом поверхности и обозначим через ${{S}_{{00}}}$). Считаем, что структура облучается плоской волной вида:
(1)
$\begin{gathered} {{U}^{0}} = \exp ( - ikr(\sin {{{\theta }}_{0}}\sin {\theta }\cos ({\varphi } - {{{\varphi }}_{0}}) - \\ - \,\,\cos {{{\theta }}_{0}}\cos {\theta })), \\ \end{gathered} $На поверхности выполнено условие Дирихле:
либо Неймана где ${\partial \mathord{\left/ {\vphantom {\partial {\partial n}}} \right. \kern-0em} {\partial n}}$ – производная по нормали, составляющей острый угол с осью z, $U = {{U}^{0}} + {{U}^{1}}$ – полное поле над поверхностью.Вторичное поле в области над поверхностью удовлетворяет условиям периодичности Флоке:
где ${{h}_{x}} = k{{d}_{x}}\sin {{{\theta }}_{0}}\cos {{{\varphi }}_{0}},$ ${{h}_{y}} = k{{d}_{y}}\sin {{{\theta }}_{0}}\sin {{{\varphi }}_{0}}$ – параметры Флоке. На бесконечности полное поле удовлетворяет условию излучения:(7)
$\begin{gathered} U(x,y,z) = {{U}^{0}}(x,y,z) + \sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {{{A}_{{pq}}}\exp ( - i{{\kappa }_{{pq}}}r)} } , \\ z > {{z}_{{\max }}}, \\ \end{gathered} $2. РЕШЕНИЕ ЗАДАЧИ ПРИ ПОМОЩИ ММДИ
В соответствии с ММДИ представим волновое поле над периодической поверхностью в виде [13–15]:
В этой формуле $\Sigma $ – центральный период вспомогательной поверхности, расположенной под исходной поверхностью (выбор вспомогательной поверхности описан ниже), а $J$ – неизвестная функция, заданная на поверхности $\Sigma $. Функция $G$ представляет собой периодическую ФГ, которая имеет вид [5]:
(9)
$G(r,r{\text{'}}) = \sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {{{G}_{0}}({{R}_{{pq}}})\exp ( - ip{{h}_{x}} - iq{{h}_{y}})} } ,$(10)
$\begin{gathered} {{G}_{0}}({{R}_{{pq}}}) = \frac{{\exp ( - ik{{R}_{{pq}}})}}{{4{\pi }{{R}_{{pq}}}}}, \\ {{R}_{{pq}}} = \sqrt {{{{(x - x{\text{'}} - p{{d}_{x}})}}^{2}} + {{{(y - y{\text{'}} - q{{d}_{y}})}}^{2}} + {{{(z - z{\text{'}})}}^{2}}} . \\ \end{gathered} $Таким образом, рассеянное поле, записанное в виде (8), удовлетворяет условиям периодичности Флоке. Далее подставим формулу (8) в краевое условие (3) или (4). В результате задача сводится к решению интегрального уравнения
либо(12)
$\int\limits_\Sigma {\frac{{\partial G(r,r{\text{'}})}}{{\partial n}}J(r{\text{'}})ds{\text{'}}} = - \frac{{\partial {{U}^{0}}(r)}}{{\partial n}},\,\,\,\,r \in {{S}_{{00}}},$(13)
$\begin{gathered} G(r,r{\text{'}}) = \sum\limits_{\left| p \right| \leqslant Q} {\sum\limits_{|q| \leqslant Q} {{{G}_{0}}({{R}_{{pq}}})\exp ( - ip{{h}_{x}} - iq{{h}_{y}})} } + \\ + \,\,\frac{k}{{4\pi i}}\sum\limits_{s = 0}^\infty {\sum\limits_{l = - s}^s {(2s + 1)\frac{{(s - l)!}}{{(s + l)!}}{{W}_{{sl}}}{{\Psi }_{{sl}}}(r,r{\text{'}}),} } \\ \end{gathered} $Сделаем замечание по поводу разрешимости интегрального уравнения (11) или (12). Как показано в работе [16] (см. также [15, 17]), имеет место следующая теорема существования (рассмотрим ее на примере решения задачи дифракции на компактном теле с граничным условием Дирихле на поверхности тела).
Пусть простая замкнутая поверхность S такова, что $k$ не является собственным значением внутренней однородной задачи Дирихле для области внутри S. Тогда интегральное уравнение вида (11) $\left( {{\text{г д е }}\,\,G \equiv {{G}_{0}}(R),\,\,R = \left| {{\mathbf{\vec {r}}} - {\mathbf{\vec {r}}}'} \right|} \right)$ разрешимо в том и только том случае, если $\Sigma $ охватывает все особенности решения ${{U}^{1}}(\vec {r})$ краевой задачи с граничным условием Дирихле на поверхности рассеивателя. В этом случае уравнение (11) имеет единственное решение.
Аналогичная теорема будет справедлива и для задачи дифракции на периодической поверхности. В последнем случае вспомогательная поверхность $\Sigma $ должна располагаться выше особенностей продолжения волнового поля под поверхность (плоская волна падает сверху). Отметим, что в приведенной теореме не указывается способ построения вспомогательной поверхности, нужно лишь, чтобы эта поверхность охватывала все особенности продолжения волнового поля внутрь границы тела или под периодическую поверхность. В работах [13–15] было показано, что для получения наиболее эффективных и устойчивых численных алгоритмов необходимо выбирать вспомогательную поверхность при помощи аналитической деформации границы рассеивателя.
Рассмотрим выбор вспомогательной поверхности на примере решения двумерной задачи дифракции плоской волны на неровной периодической поверхности, заданной уравнением $z = f(x).$ В соответствии с техникой ММДИ вводим комплексную переменную [13–15]:
где $\delta > 0.$ В случае если величина $\delta $ равна нулю, то переменная $\zeta \in C,$ где $C$ контур на комплексной плоскости $\zeta $, соответствующий контуру периодической поверхности (назовем его $S$) и конгруэнтный ему. Если начать увеличивать δ, то $C$ будет деформироваться и лежать в области, расположенной под контуром волнистой поверхности $S$. При этом мы получим новый контур $\Sigma $, который можно выбрать в качестве вспомогательного контура. Заметим, что такого рода деформация контура $S$ возможна до тех пор, пока отображение $\zeta (x) = x + if(x)$ остается взаимно однозначным. Если рассматривать параметры $x$ и δ в формуле (15) как некоторые криволинейные координаты, то соответствующие координатные линии будут ортогональны. Это означает, что при увеличении параметра δ вспомогательные источники движутся по траекториям, ортогональным к контуру $S$. Данный факт обеспечивает устойчивость методики, основанной на ММДИ (то есть возможность решать уравнение первого рода с гладким ядром).Очевидно, что в трехмерном случае не удается столь же просто применить ММДИ к решению задачи дифракции на неровной периодической поверхности, так как невозможно ввести соответствующую комплексную переменную. Поэтому, как указано выше, приходится использовать алгебру кватернионов. Будем считать, что периодическая поверхность задается в виде:
(16)
$f(x,y) = \sum\limits_{l = 1}^{{{L}_{1}}} {\sum\limits_{t = 1}^{{{L}_{2}}} {{{f}_{l}}(x){{g}_{t}}(y)} } ,$(19)
$\begin{gathered} {{x}_{\Sigma }} = {{q}_{1}}(x,y,\delta ),\,\,\,\,{{y}_{\Sigma }} = {{q}_{2}}(x,y,\delta ), \\ {{z}_{\Sigma }} = {{q}_{3}}(x,y,\delta ). \\ \end{gathered} $Например, для поверхности f(x, y) = = $A\sin {{\tau }_{1}}x\sin {{\tau }_{2}}y,$ где ${{\tau }_{1}} = \frac{{2\pi }}{{{{d}_{x}}}},$ ${{\tau }_{2}} = \frac{{2\pi }}{{{{d}_{y}}}},$ используя формулы
(20)
$\begin{gathered} \sin (x - iy) = \sin x\operatorname{ch} y - i\cos x\operatorname{sh} y, \\ \sin (x + jy) = \sin x\operatorname{ch} y + j\cos x\operatorname{sh} y, \\ \end{gathered} $(21)
$\left\{ \begin{gathered} {{x}_{\Sigma }} = x + A\cos {{\tau }_{1}}x\sin {{\tau }_{2}}y\operatorname{sh} {{\tau }_{1}}\delta \operatorname{ch} {{\tau }_{2}}\delta , \hfill \\ {{y}_{\Sigma }} = y + A\sin {{\tau }_{1}}x\cos {{\tau }_{2}}y\operatorname{ch} {{\tau }_{1}}\delta \operatorname{sh} {{\tau }_{2}}\delta , \hfill \\ {{z}_{\Sigma }} = - \delta + A\sin {{\tau }_{1}}x\sin {{\tau }_{2}}y\operatorname{ch} {{\tau }_{1}}\delta \operatorname{ch} {{\tau }_{2}}\delta . \hfill \\ \end{gathered} \right.$Заметим, что при дифференцировании уравнений вспомогательной поверхности по переменной δ мы получим, что в первом приближении по δ точки вспомогательной поверхности будут двигаться по ортогональным к поверхности $\Sigma $ траекториям. Этот факт обеспечивает устойчивость алгоритма, как и в случае применения стандартного ММДИ.
Необходимо также заметить, что предлагаемый подход переходит в двумерный вариант ММДИ при условии
Действительно, в этом случае
Если обозначить $f(x + j\delta )$ = $u(x,\delta ) + jv(x,\delta ),$ то в соответствии с (19) получим
(24)
$\begin{gathered} {{x}_{\Sigma }} = x + v(x,\delta ),\,\,\,\,{{y}_{\Sigma }} = y, \\ {{z}_{\Sigma }} = - \delta + u(x,\delta ). \\ \end{gathered} $Этот же результат получается из формулы (15), так как действительная и мнимая части комплексной переменной $\zeta (x)$ совпадают с выражениями для ${{x}_{\Sigma }}$ и ${{z}_{\Sigma }}$ в формуле (24) (при этом, очевидно, $f(x - i\delta ) = u(x,\delta ) - iv(x,\delta )$).
Для численного решения интегрального уравнения (11) или (12) применим метод коллокации. С этой целью поверхностные интегралы в (11) и (12) заменяем на двойные интегралы по прямоугольнику $[{{ - {{d}_{x}}} \mathord{\left/ {\vphantom {{ - {{d}_{x}}} 2}} \right. \kern-0em} 2},{{{{d}_{x}}} \mathord{\left/ {\vphantom {{{{d}_{x}}} 2}} \right. \kern-0em} 2}] \times [{{ - {{d}_{y}}} \mathord{\left/ {\vphantom {{ - {{d}_{y}}} 2}} \right. \kern-0em} 2},{{{{d}_{y}}} \mathord{\left/ {\vphantom {{{{d}_{y}}} 2}} \right. \kern-0em} 2}].$ При этом сделаем замену неизвестной функции $J$ по формуле [5]:
В формуле (25) $r{\text{'}}$ – радиус-вектор точки на вспомогательной поверхности, точка означает дифференцирование по параметру x или y. Далее выберем в области интегрирования прямоугольную сетку:
(26)
$\begin{gathered} {{x}_{n}} = - \frac{{{{d}_{x}}}}{2} + \frac{{{{d}_{x}}}}{N}\left( {n - \frac{1}{2}} \right),\,\,\,\,n = \overline {1,N} , \\ {{y}_{m}} = - \frac{{{{d}_{y}}}}{2} + \frac{{{{d}_{y}}}}{M}\left( {m - \frac{1}{2}} \right),\,\,\,\,m = \overline {1,M} . \\ \end{gathered} $Заменим двойные интегралы суммами Римана и приравняем полученные выражения в точках коллокации, которые выберем следующим образом:
(27)
$\begin{gathered} x_{{\nu \mu }}^{ * } = {{x}_{\nu }},\,\,\,\,y_{{\nu \mu }}^{ * } = {{y}_{\mu }},\,\,\,\,z_{{\nu \mu }}^{ * } = f({{x}_{\nu }},{{y}_{\mu }}), \\ \nu = \overline {1,N} ,\,\,\,\,\mu = \overline {1,M} . \\ \end{gathered} $В результате перейдем от интегрального уравнения к следующей алгебраической системе относительно неизвестных значений функции $I$ в точках $r_{{nm}}^{{}}$ на вспомогательной поверхности центрального элемента поверхности:
(28)
$\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {A_{{nm}}^{{\nu \mu }}{{c}_{{nm}}}} } = {{b}^{{\nu \mu }}}.$Здесь
(29)
$A_{{nm}}^{{\nu \mu }} = G(r_{{\nu \mu }}^{ * },{{r}_{{nm}}}),\,\,\,\,{{b}^{{\nu \mu }}} = - {{U}^{0}}(r_{{\nu \mu }}^{ * })$(30)
$A_{{nm}}^{{\nu \mu }} = \frac{{\partial G(r_{{\nu \mu }}^{ * },{{r}_{{nm}}})}}{{\partial n}},\,\,\,\,{{b}^{{\nu \mu }}} = - \frac{{\partial {{U}^{0}}(r_{{\nu \mu }}^{ * })}}{{\partial n}}$В качестве выходных характеристик задачи рассмотрим амплитуды пространственных гармоник, обусловленных дифракцией на неровной поверхности. Как описано в работе [5], амплитуды плоских волн, распространяющихся в верхнем полупространстве, будут иметь вид:
3. РЕШЕНИЕ ЗАДАЧИ ПРИ ПОМОЩИ МДУ
Рассмотрим решение задачи дифракции плоской волны на периодически неровной поверхности при помощи МДУ [11, 15, 20]. Основная идея МДУ состоит в том, что исходная задача дифракции сводится к алгебраической системе не относительно значений поля или его нормальной производной на неровной поверхности (или на вспомогательной поверхности), а относительно амплитуд отраженных плоских волн. С целью решения задачи дифракции при помощи МДУ используем интегральное представление рассеяного поля:
(32)
${{U}^{1}}(r) = \frac{1}{{4\pi }}\int\limits_{{{S}_{{00}}}} {\frac{{\partial U(r{\text{'}})}}{{\partial n{\text{'}}}}G(r,r{\text{'}})ds{\text{'}}} $(33)
${{U}^{1}}(r) = - \frac{1}{{4\pi }}\int\limits_{{{S}_{{00}}}} {U(r{\text{'}})\frac{{\partial G(r,r{\text{'}})}}{{\partial n{\text{'}}}}ds{\text{'}}} $(34)
$\begin{gathered} G = \frac{{2\pi i}}{{{{d}_{x}}{{d}_{y}}}}\sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {\frac{1}{{{{\Gamma }_{{pq}}}}}} } \exp ( - i{{u}_{p}}(x - x{\text{'}}) - \\ - \,\,i{{v}_{q}}(y - y{\text{'}}) - i{{\Gamma }_{{pq}}}\left| {z - z{\text{'}}} \right|). \\ \end{gathered} $Считая вначале, что поверхность рэлеевская (полагаем $\left| {z - z{\text{'}}} \right| = z - z{\text{'}},$ то есть $z > z{\text{'}}$), подставим выражение (34) в формулу (32) или (33). В результате перемены местами порядка интегрирования и суммирования, получим следующее представление рассеянного поля [11, 15]:
(35)
$\begin{gathered} {{U}^{1}} = \frac{{2\pi i}}{{{{d}_{x}}{{d}_{y}}}}\sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {\frac{1}{{{{\Gamma }_{{pq}}}}}} } {{g}_{{pq}}} \times \\ \times \,\,\exp ( - i{{u}_{p}}x - i{{v}_{q}}y - i{{\Gamma }_{{pq}}}z), \\ \end{gathered} $(36)
$\begin{gathered} g(u,v) = \frac{1}{{4\pi }} \times \\ \times \,\,\int\limits_{{{ - {{d}_{x}}} \mathord{\left/ {\vphantom {{ - {{d}_{x}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{x}}} \mathord{\left/ {\vphantom {{{{d}_{x}}} 2}} \right. \kern-0em} 2}} {\int\limits_{{{ - {{d}_{y}}} \mathord{\left/ {\vphantom {{ - {{d}_{y}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{y}}} \mathord{\left/ {\vphantom {{{{d}_{y}}} 2}} \right. \kern-0em} 2}} {(\hat {D}U)\exp (iux + ivy + i\Gamma f(x,y))dxdy} } , \\ \end{gathered} $(37)
$\hat {D}U = {{\left( {\frac{{\partial U}}{{\partial z}} - f_{x}^{'}\frac{{\partial U}}{{\partial x}} - f_{y}^{'}\frac{{\partial U}}{{\partial y}}} \right)}_{{z = f(x,y)}}}$(38)
$\begin{gathered} g(u,v) = - \frac{i}{{4\pi }} \times \\ \times \,\,\int\limits_{{{ - {{d}_{x}}} \mathord{\left/ {\vphantom {{ - {{d}_{x}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{x}}} \mathord{\left/ {\vphantom {{{{d}_{x}}} 2}} \right. \kern-0em} 2}} {\int\limits_{{{ - {{d}_{y}}} \mathord{\left/ {\vphantom {{ - {{d}_{y}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{y}}} \mathord{\left/ {\vphantom {{{{d}_{y}}} 2}} \right. \kern-0em} 2}} {U(x,y,f(x,y))\left( {\Gamma - uf_{x}^{'} - vf_{y}^{'}} \right) \times } } \\ \times \,\,\exp (iux + ivy + i\Gamma f(x,y))dxdy \\ \end{gathered} $(39)
$g(u,v) = {{g}^{0}}(u,v) + \sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {{{g}_{{pq}}}{{F}_{{pq}}}(u,v)} } ,$(40)
$\begin{gathered} {{F}_{{pq}}}(u,v) = \frac{1}{{2{{d}_{x}}{{d}_{y}}{{\Gamma }_{{pq}}}}}\int\limits_{{{ - {{d}_{x}}} \mathord{\left/ {\vphantom {{ - {{d}_{x}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{x}}} \mathord{\left/ {\vphantom {{{{d}_{x}}} 2}} \right. \kern-0em} 2}} {\int\limits_{{{ - {{d}_{y}}} \mathord{\left/ {\vphantom {{ - {{d}_{y}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{y}}} \mathord{\left/ {\vphantom {{{{d}_{y}}} 2}} \right. \kern-0em} 2}} {\left( {{{\Gamma }_{{pq}}} - {{u}_{p}}f_{x}^{'} - {{v}_{q}}f_{y}^{'}} \right)} } \times \\ \times \,\,\exp (i(u - {{u}_{p}})x + i(v - {{v}_{q}})y) \times \\ \times \,\,\exp (i(\Gamma - {{\Gamma }_{{pq}}})f(x,y))dxdy, \\ \end{gathered} $(41)
$\begin{gathered} {{g}^{0}}(u,v) = \frac{i}{{4\pi }}\int\limits_{{{ - {{d}_{x}}} \mathord{\left/ {\vphantom {{ - {{d}_{x}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{x}}} \mathord{\left/ {\vphantom {{{{d}_{x}}} 2}} \right. \kern-0em} 2}} {\int\limits_{{{ - {{d}_{y}}} \mathord{\left/ {\vphantom {{ - {{d}_{y}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{y}}} \mathord{\left/ {\vphantom {{{{d}_{y}}} 2}} \right. \kern-0em} 2}} {\left( {{{\Gamma }_{{00}}} + {{u}_{0}}f_{x}^{'} + {{v}_{0}}f_{y}^{'}} \right)} } \times \\ \times \,\,\exp (i(u - {{u}_{0}})x + i(v - {{v}_{0}})y) \times \\ \times \,\,\exp (i(\Gamma + {{\Gamma }_{{00}}})f(x,y))dxdy \\ \end{gathered} $(42)
$\begin{gathered} {{F}_{{pq}}}(u,v) = \frac{1}{{2{{d}_{x}}{{d}_{y}}{{\Gamma }_{{pq}}}}}\int\limits_{{{ - {{d}_{x}}} \mathord{\left/ {\vphantom {{ - {{d}_{x}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{x}}} \mathord{\left/ {\vphantom {{{{d}_{x}}} 2}} \right. \kern-0em} 2}} {\int\limits_{{{ - {{d}_{y}}} \mathord{\left/ {\vphantom {{ - {{d}_{y}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{y}}} \mathord{\left/ {\vphantom {{{{d}_{y}}} 2}} \right. \kern-0em} 2}} {\left( {\Gamma - uf_{x}^{'} - vf_{y}^{'}} \right)} } \times \\ \times \,\,\exp (i(u - {{u}_{p}})x + i(v - {{v}_{q}})y) \times \\ \times \,\,\exp (i(\Gamma - {{\Gamma }_{{pq}}})f(x,y))dxdy, \\ \end{gathered} $(43)
$\begin{gathered} {{g}^{0}}(u,v) = - \frac{i}{{4\pi }}\int\limits_{{{ - {{d}_{x}}} \mathord{\left/ {\vphantom {{ - {{d}_{x}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{x}}} \mathord{\left/ {\vphantom {{{{d}_{x}}} 2}} \right. \kern-0em} 2}} {\int\limits_{{{ - {{d}_{y}}} \mathord{\left/ {\vphantom {{ - {{d}_{y}}} 2}} \right. \kern-0em} 2}}^{{{{{d}_{y}}} \mathord{\left/ {\vphantom {{{{d}_{y}}} 2}} \right. \kern-0em} 2}} {\left( {\Gamma - uf_{x}^{'} - vf_{y}^{'}} \right)} } \times \\ \times \,\,\exp (i(u - {{u}_{0}})x + i(v - {{v}_{0}})y) \times \\ \times \,\,\exp (i(\Gamma + {{\Gamma }_{{00}}})f(x,y))dxdy, \\ \end{gathered} $(44)
${{g}_{{mn}}} = g_{{mn}}^{0} + \sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {A_{{mn}}^{{pq}}{{g}_{{pq}}}} } ,$Сделаем замечание относительно применимости МДУ к исследуемой задаче дифракции. Рассмотрим случай абсолютно мягкой поверхности. Можно показать, что имеют место следующие оценки матричных элементов $A_{{mn}}^{{pq}},$ получаемые применением метода перевала к соответствующим интегралам (см., например, [11, 15]):
(45)
$\left| {A_{{mn}}^{{pq}}} \right| \leqslant \frac{{{\text{const}}}}{{\left| m \right|}}\exp \left( {\frac{{2\lambda {{\sigma }_{{11}}}}}{{{{d}_{x}}}}\left| m \right|} \right),\,\,\,\,m \to \infty ,$(46)
$\left| {A_{{mn}}^{{pq}}} \right| \leqslant \frac{{{\text{const}}}}{{\left| n \right|}}\exp \left( {\frac{{2\lambda {{\sigma }_{{12}}}}}{{{{d}_{y}}}}\left| n \right|} \right),\,\,\,\,n \to \infty ,$(47)
$\left| {A_{{mn}}^{{pq}}} \right| \leqslant \frac{{{\text{const}}}}{{{{p}^{2}}}}\exp \left( { - \frac{{2\lambda {{\sigma }_{{21}}}}}{{{{d}_{x}}}}\left| p \right|} \right),\,\,\,\,p \to \infty ,$(48)
$\left| {A_{{mn}}^{{pq}}} \right| \leqslant \frac{{{\text{const}}}}{{{{q}^{2}}}}\exp \left( { - \frac{{2\lambda {{\sigma }_{{22}}}}}{{{{d}_{y}}}}\left| q \right|} \right),\,\,\,\,q \to \infty ,$(49)
$\begin{gathered} {{\sigma }_{{11}}} = \frac{1}{2}\mathop {\max }\limits_{({{x}_{{01}}},{{y}_{{01}}})} \operatorname{Re} \left( {kf({{x}_{{01}}},{{y}_{{01}}}) \pm ik{{x}_{{01}}}} \right), \\ {{\sigma }_{{12}}} = \frac{1}{2}\mathop {\max }\limits_{({{x}_{{02}}},{{y}_{{02}}})} \operatorname{Re} \left( {kf({{x}_{{02}}},{{y}_{{02}}}) \pm ik{{y}_{{02}}}} \right), \\ \end{gathered} $(50)
$\begin{gathered} {{\sigma }_{{21}}} = \frac{1}{2}\mathop {\min }\limits_{({{x}_{{01}}},{{y}_{{01}}})} \operatorname{Re} \left( {kf({{x}_{{01}}},{{y}_{{01}}}) \pm ik{{x}_{{01}}}} \right), \\ {{\sigma }_{{22}}} = \frac{1}{2}\mathop {\min }\limits_{({{x}_{{02}}},{{y}_{{02}}})} \operatorname{Re} \left( {kf({{x}_{{02}}},{{y}_{{02}}}) \pm ik{{y}_{{02}}}} \right), \\ \end{gathered} $(51)
$\left\{ \begin{gathered} f_{x}^{'}({{x}_{{01}}},{{y}_{{01}}}) \pm i = 0, \hfill \\ f_{y}^{'}({{x}_{{01}}},{{y}_{{01}}}) = 0, \hfill \\ \end{gathered} \right.\,\,\,\,\left\{ \begin{gathered} f_{y}^{'}({{x}_{{02}}},{{y}_{{02}}}) \pm i = 0, \hfill \\ f_{x}^{'}({{x}_{{02}}},{{y}_{{02}}}) = 0. \hfill \\ \end{gathered} \right.$В формулах (49) и (50) максимумы и минимумы берутся по всем корням систем уравнений (51), соответствующих как верхним, так и нижним знакам.
Сделаем замену неизвестных в системе (44) по формуле
(52)
${{g}_{{mn}}} = {{\tilde {g}}_{{mn}}}\exp \left( {\frac{{2\lambda {{\sigma }_{{11}}}}}{{{{d}_{x}}}}\left| m \right| + \frac{{2\lambda {{\sigma }_{{12}}}}}{{{{d}_{y}}}}\left| n \right|} \right){{\kappa }_{{mn}}},$(53)
${{\kappa }_{{mn}}} = \left\{ \begin{gathered} {{\left| {mn} \right|}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,mn \ne 0, \hfill \\ {{\left| m \right|}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,n = 0,\,\,\,\,m \ne 0, \hfill \\ {{\left| n \right|}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,m = 0,\,\,\,\,n \ne 0, \hfill \\ 1,\,\,\,\,m = 0,\,\,\,\,n = 0. \hfill \\ \end{gathered} \right.$Подставим формулу (52) в алгебраическую систему (44). В результате получим
(54)
${{\tilde {g}}_{{mn}}} = \tilde {g}_{{mn}}^{0} + \sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {\tilde {A}_{{mn}}^{{pq}}{{{\tilde {g}}}_{{pq}}}} } ,$(55)
$\begin{gathered} \tilde {A}_{{mn}}^{{pq}} = \\ = A_{{mn}}^{{pq}}\exp \left( {\frac{{2\lambda {{\sigma }_{{11}}}}}{{{{d}_{x}}}}(\left| p \right| - \left| m \right|) + \frac{{2\lambda {{\sigma }_{{12}}}}}{{{{d}_{y}}}}(\left| q \right| - \left| n \right|)} \right)\frac{{{{\kappa }_{{pq}}}}}{{{{\kappa }_{{mn}}}}}. \\ \end{gathered} $Из последней формулы и из оценок (45)–(48) видно, что с ростом индексов новые матричные элементы экспоненциально убывают при $p \to \infty $ или $q \to \infty $ при условии
В случае $m \to \infty $ или $n \to \infty $ убывание имеет степенной характер. В случае знака равенства в формуле (56) матричные элементы системы (54) имеют порядок $O\left( {{1 \mathord{\left/ {\vphantom {1 {{{{\left| p \right|}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{\left| p \right|}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right)$ или $O\left( {{1 \mathord{\left/ {\vphantom {1 {{{{\left| q \right|}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{\left| q \right|}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right)$ при $p \to \infty $ или $q \to \infty $ соответственно. Таким образом, система (44) будет разрешима методом редукции при ограничениях (56). Заметим, что область применимости МДУ, определяемая условием (56), шире, чем, например, область применимости методики, основанной на предположении о справедливости гипотезы Рэлея для неровной поверхности [11, 15].
Для численной оценки матричных элементов $A_{{mn}}^{{pq}}$ и правых частей $g_{{mn}}^{0},$ определяемых по формулам (40)–(43), необходимо использовать метод интегрирования по частям и замену $\xi = \frac{{2\pi }}{{{{d}_{x}}}}x,$ $\eta = \frac{{2\pi }}{{{{d}_{y}}}}y.$ В результате соответствующие интегралы сводятся к следующим:
(57)
$\begin{gathered} A_{{mn}}^{{pq}} = \frac{{D_{{mn}}^{{pq}}}}{{8{{\pi }^{2}}}}\int\limits_{ - \pi }^\pi {\int\limits_{ - \pi }^\pi {\exp \left( {i(m - p)\xi + i(n - q)\eta + \frac{{^{{}}}}{{}}} \right.} } \\ \left. { + \,\,i({{\Gamma }_{{mn}}} - {{\Gamma }_{{pq}}})f\left( {\frac{{{{d}_{x}}\xi }}{{2\pi }},\frac{{{{d}_{y}}\eta }}{{2\pi }}} \right)} \right)d\xi d\eta \\ \end{gathered} $(58)
$\begin{gathered} A_{{mn}}^{{pq}} = \frac{1}{2}{{\delta }_{{mp}}}{{\delta }_{{nq}}} + \frac{{i\tilde {D}_{{mn}}^{{pq}}}}{{8{{\pi }^{2}}}} \times \\ \times \,\,\int\limits_{ - \pi }^\pi {\int\limits_{ - \pi }^\pi {f\left( {\frac{{{{d}_{x}}\xi }}{{2\pi }},\frac{{{{d}_{y}}\eta }}{{2\pi }}} \right)\exp \left( {i(m - p)\xi + i(n - q)\eta } \right)d\xi d\eta } } \\ \end{gathered} $(59)
$\begin{gathered} g_{{mn}}^{0} = \frac{{i{{d}_{x}}{{d}_{y}}{{B}_{{mn}}}}}{{16{{\pi }^{3}}}}\int\limits_{ - \pi }^\pi {\int\limits_{ - \pi }^\pi {\exp \left( {im\xi + in\eta + \frac{{^{{}}}}{{}}} \right.} } \\ \left. { + \,\,i({{\Gamma }_{{mn}}} + {{\Gamma }_{{00}}})f\left( {\frac{{{{d}_{x}}\xi }}{{2\pi }},\frac{{{{d}_{y}}\eta }}{{2\pi }}} \right)} \right)d\xi d\eta . \\ \end{gathered} $В формулах (57)–(59) обозначено
(60)
$\begin{gathered} D_{{mn}}^{{pq}} = 1 + \frac{{{{u}_{p}}({{u}_{m}} - {{u}_{p}}) + {{v}_{q}}({{v}_{n}} - {{v}_{q}})}}{{{{\Gamma }_{{pq}}}({{\Gamma }_{{mn}}} - {{\Gamma }_{{pq}}})}}, \\ \tilde {D}_{{mn}}^{{pq}} = \frac{{{{u}_{p}}({{u}_{m}} - {{u}_{p}}) + {{v}_{q}}({{v}_{n}} - {{v}_{q}})}}{{{{\Gamma }_{{mn}}}}}, \\ {{B}_{{mn}}} = {{\Gamma }_{{00}}} - \frac{{{{u}_{0}}({{u}_{m}} - {{u}_{0}}) + {{v}_{0}}({{v}_{n}} - {{v}_{0}})}}{{{{\Gamma }_{{mn}}} + {{\Gamma }_{{00}}}}} \\ \end{gathered} $в случае абсолютно мягкой поверхности и
(61)
$\begin{gathered} D_{{mn}}^{{pq}} = \frac{1}{{{{\Gamma }_{{pq}}}}}\left( {{{\Gamma }_{{mn}}} + \frac{{{{u}_{m}}({{u}_{m}} - {{u}_{p}}) + {{v}_{n}}({{v}_{n}} - {{v}_{q}})}}{{{{\Gamma }_{{mn}}} - {{\Gamma }_{{pq}}}}}} \right), \\ \tilde {D}_{{mn}}^{{pq}} = \frac{{{{u}_{m}}({{u}_{m}} - {{u}_{p}}) + {{v}_{n}}({{v}_{n}} - {{v}_{q}})}}{{{{\Gamma }_{{mn}}}}}, \\ {{B}_{{mn}}} = - \left( {{{\Gamma }_{{mn}}} + \frac{{{{u}_{m}}({{u}_{m}} - {{u}_{0}}) + {{v}_{n}}({{v}_{n}} - {{v}_{0}})}}{{{{\Gamma }_{{mn}}} + {{\Gamma }_{{00}}}}}} \right) \\ \end{gathered} $Как указано во Введении, в некоторых частных случаях интегралы (57) и (59) могут быть вычислены аналитически. Например, если поверхность задана уравнением:
(62)
$f(x,y) = a\sin \left( {{{2\pi x} \mathord{\left/ {\vphantom {{2\pi x} {{{d}_{x}}}}} \right. \kern-0em} {{{d}_{x}}}}} \right)\sin \left( {{{2\pi y} \mathord{\left/ {\vphantom {{2\pi y} {{{d}_{y}}}}} \right. \kern-0em} {{{d}_{y}}}}} \right),$(63)
$\begin{gathered} \frac{1}{{4{{\pi }^{2}}}}\int\limits_{ - \pi }^\pi {\int\limits_{ - \pi }^\pi {\exp \left( {im\xi + in\eta + i\Omega f\left( {\frac{{{{d}_{x}}\xi }}{{2\pi }},\frac{{{{d}_{y}}\eta }}{{2\pi }}} \right)} \right)d\xi d\eta } } = \hfill \\ = \left\{ \begin{gathered} \cos \left( {\frac{{m\pi }}{2}} \right){{J}_{{\frac{{m + n}}{2}}}}\left( {\frac{{a\Omega }}{2}} \right){{J}_{{\frac{{m - n}}{2}}}}\left( {\frac{{a\Omega }}{2}} \right), \\ m,n\; - \;{\text{ч е т н ы е ,}} \\ i\sin \left( {\frac{{m\pi }}{2}} \right){{J}_{{\frac{{m + n}}{2}}}}\left( {\frac{{a\Omega }}{2}} \right){{J}_{{\frac{{m - n}}{2}}}}\left( {\frac{{a\Omega }}{2}} \right), \\ m,n\; - \;{\text{н е ч е т н ы е ,}} \\ {\text{0,}}\,\,m + n\; - \;{\text{н е ч е т н о е ,}} \\ \end{gathered} \right. \hfill \\ \end{gathered} $4. РЕЗУЛЬТАТЫ РАСЧЕТОВ
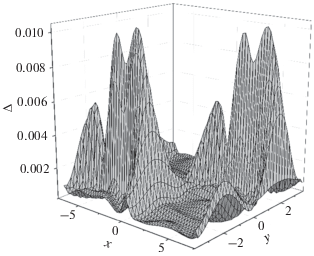
В качестве примера неровной двоякопериодической поверхности была рассмотрена синусоидальная поверхность вида (62). Ниже всюду исследуется случай абсолютно мягкой поверхности. Рассмотрим вначале результаты, касающиеся проверки корректности предлагаемых методов. На рис. 1 представлено распределение невязки краевого условия (3) на центральном периоде поверхности (62), полученной при помощи ММДИ. Невязка определяется по формуле
(64)
$\begin{gathered} \Delta (r_{{\nu \mu }}^{{{\text{**}}}}) = \left| {\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {G(r_{{\nu \mu }}^{{{\text{**}}}},{{r}_{{nm}}}){{c}_{{nm}}}} } + {{U}^{0}}(r_{{\nu \mu }}^{{{\text{**}}}})} \right|, \\ \nu = \overline {1,N} ,\,\,\,\,\mu = \overline {1,M} . \\ \end{gathered} $Здесь $r_{{\nu \mu }}^{{{\text{**}}}}$ – радиус-векторы точек на поверхности центрального периода, расположенные посередине между точками коллокации. Параметры поверхности были следующими: ${{d}_{x}} = 2{{d}_{y}},$ ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.5,$ ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda } = 1.2,$ ${{\theta }_{0}} = 45^\circ ,$ ${{\varphi }_{0}} = 0,$ где $d = \min ({{d}_{x}},{{d}_{y}}).$ Число дискретных источников (точек коллокации) было выбрано равным $N = 55,$ $M = 35.$ Параметр δ выбирался так, чтобы вспомогательная поверхность не имела точек самопересечения, и был равен $\delta = 0.2.$ Как видно из рисунка, максимальный уровень невязки не превосходит 0.01, то есть достаточно мал. В качестве еще одной проверки результатов, получаемых при помощи ММДИ, была найдена точность выполнения закона сохранения энергии, который в рассматриваемом случае имеет вид:
где ${{P}_{0}} = k\cos {{\theta }_{0}}$ – мощность падающей плоской волны (предполагается, что амплитуда падающей волны равна 1 Па). В формуле (65) суммирование проводится по всем распространяющимся гармоникам Флоке. Результаты показывают, что точность выполнения закона сохранения при выбранных параметрах модели составила $1.39 \times {{10}^{{ - 4}}}.$ Таким образом, имеет место высокая точность расчета амплитуд отраженных гармоник при наличии достаточно больших значений отношения ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d}$ неровной поверхности.В таблице 1 представлены результаты расчета амплитуд трех первых отраженных гармоник в зависимости от угла падения ${{\theta }_{0}}$ плоской волны, полученные при помощи МДУ и ММДИ. Параметры задачи имели значения ${{d}_{x}} = {{d}_{y}},$ ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09,$ ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda } = 1.2,$ ${{\varphi }_{0}} = 0.$ Как было указано выше, МДУ применим для достаточно “пологих” поверхностей, поэтому в данном случае отношение ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d}$ невелико. Отметим, что для достижения данной точности при использовании МДУ требуется относительно небольшое число базисных функций: ${{M}_{1}} = {{N}_{1}} = 15.$ Из таблицы видно, что результаты, полученные обоими методами, отличаются не более чем на $1.4 \times {{10}^{{ - 4}}}.$ Данный факт подтверждает корректность обоих методов. В таблице 2 приведены значения точности выполнения закона сохранения энергии, полученные при помощи ММДИ и МДУ для двух значений отношения ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d}$. Остальные параметры задачи были такие же, как и для табл. 1. Как видно из таблицы, в случае ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09$ относительная разность левой и правой частей в формуле (65) не превосходит 5 × 10–5 при использовании обоих методов. В то же время при увеличении отношения ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d}$ до 0.11 эта величина имеет максимальное значение, равное примерно 0.1 при использовании МДУ, а в случае применения ММДИ точность выполнения закона сохранения энергии остается примерно такой же, как и для отношения ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09$. Расчеты показывают, что предельное значение отношения ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d}$, при котором МДУ дает приемлемую точность в широком диапазоне длин волн, составляет примерно 0.1. Этот факт согласуется с условиями применимости МДУ (56).
Таблица 1.
Сравнение значений амплитуд отраженных гармоник, полученных двумя методами
| ${{\theta }_{0}}$, град. | ММДИ | МДУ | ||||
|---|---|---|---|---|---|---|
| $\left| {{{A}_{{ - 2,0}}}} \right|$ | $\left| {{{A}_{{ - 1, - 1}}}} \right|$ | $\left| {{{A}_{{00}}}} \right|$ | $\left| {{{A}_{{ - 2,0}}}} \right|$ | $\left| {{{A}_{{ - 1, - 1}}}} \right|$ | $\left| {{{A}_{{00}}}} \right|$ | |
| 0 | 0 | 0 | 1.00002 | 0 | 0 | 1.00000 |
| 9 | 0 | 0 | 1.00002 | 0 | 0 | 1.00000 |
| 18 | 0 | 0.308097 | 0.982390 | 0 | 0.308104 | 0.982375 |
| 27 | 0 | 0.288142 | 0.961820 | 0 | 0.288145 | 0.961808 |
| 36 | 0 | 0.262413 | 0.956930 | 0 | 0.262413 | 0.956920 |
| 45 | 4.08497 × 10–2 | 0.228362 | 0.959151 | 4.08552 × 10–2 | 0.228362 | 0.959142 |
| 54 | 3.47647 × 10–2 | 0.189204 | 0.965239 | 3.47682 × 10–2 | 0.189204 | 0.965228 |
| 63 | 2.67392 × 10–2 | 0.146199 | 0.973266 | 2.67413 × 10–2 | 0.146199 | 0.973251 |
| 72 | 1.79085 × 10–2 | 9.97284 × 10–2 | 0.982095 | 1.79094 × 10–2 | 9.97300 × 10–2 | 0.982076 |
| 81 | 8.93327 × 10–3 | 5.06497 × 10–2 | 0.991069 | 8.93334 × 10–3 | 5.06529 × 10–2 | 0.991048 |
Таблица 2.
Проверка точности выполнения закона сохранения энергии, полученной двумя методами
| ${{\theta }_{0}}$, град. | ММДИ | МДУ | ||
|---|---|---|---|---|
| ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09$ | ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.11$ | ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09$ | ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.11$ | |
| 0 | 4.14 × 10–5 | 3.71 × 10–5 | 5.70 × 10–6 | 1.93 × 10–2 |
| 9 | 3.99 × 10–5 | 3.56 × 10–5 | 5.74 × 10–6 | 1.85 × 10–2 |
| 18 | 3.54 × 10–5 | 3.14 × 10–5 | 8.55 × 10–6 | 2.74 × 10–2 |
| 27 | 2.80 × 10–5 | 2.39 × 10–5 | 5.32 × 10–6 | 1.57 × 10–2 |
| 36 | 2.09 × 10–5 | 1.69 × 10–5 | 7.08 × 10–7 | 6.69 × 10–4 |
| 45 | 1.44 × 10–5 | 1.10 × 10–5 | 2.48 × 10–6 | 1.03 × 10–2 |
| 54 | 9.00 × 10–6 | 6.46 × 10–6 | 1.14 × 10–5 | 3.95 × 10–2 |
| 63 | 4.90 × 10–6 | 3.27 × 10–6 | 2.31 × 10–5 | 7.43 × 10–2 |
| 72 | 2.09 × 10–6 | 1.27 × 10–6 | 3.43 × 10–5 | 0.103 |
| 81 | 4.79 × 10–7 | 2.33 × 10–7 | 3.76 × 10–5 | 0.104 |
В табл. 3 и 4 приведены результаты, касающиеся внутренней сходимости методов на основе ММДИ и МДУ соответственно. Входные данные были следующие: ${{d}_{x}} = 2{{d}_{y}},$ ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda } = 1.2,$ ${{\theta }_{0}} = 45^\circ ,$ ${{\varphi }_{0}} = 0.$ Отношение ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.5$ для таблицы 3 и ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09$ для табл. 4. Как видно из приведенных данных, результаты расчетов стабилизируются в 4-м десятичном знаке (см. результаты расчета величины $\left| {{{A}_{{ - 2,0}}}} \right|$). Из таблицы также следует, что с увеличением числа базисных функций увеличивается точность выполнения закона сохранения энергии.
Таблица 3.
Внутренняя сходимость расчета на основе ММДИ
| Число источников | $\left| {{{A}_{{00}}}} \right|$ | $\left| {{{A}_{{ - 1, - 1}}}} \right|$ | $\left| {{{A}_{{ - 2,0}}}} \right|$ | Точность выполнения закона сохранения |
|---|---|---|---|---|
| $N = 35,\,\,M = 23$ | 0.4243151 | 0.6699591 | 0.3572635 | $1.49 \times {{10}^{{ - 3}}}$ |
| $N = 40,\,\,M = 26$ | 0.4250912 | 0.6694505 | 0.3569592 | $8.07 \times {{10}^{{ - 4}}}$ |
| $N = 45,\,\,M = 29$ | 0.4255275 | 0.6691677 | 0.3568003 | $4.45 \times {{10}^{{ - 4}}}$ |
| $N = 50,\,\,M = 32$ | 0.4257779 | 0.6690058 | 0.3567170 | $2.48 \times {{10}^{{ - 4}}}$ |
| $N = 55,\,\,M = 35$ | 0.4259234 | 0.6689114 | 0.3566736 | $1.39 \times {{10}^{{ - 4}}}$ |
Таблица 4.
Внутренняя сходимость расчета на основе МДУ
| Число гармоник | $\left| {{{A}_{{00}}}} \right|$ | $\left| {{{A}_{{ - 1, - 1}}}} \right|$ | $\left| {{{A}_{{ - 2,0}}}} \right|$ | Точность выполнения закона сохранения |
|---|---|---|---|---|
| ${{M}_{1}} = 8,\,\,{{N}_{1}} = 4$ | 0.9633640 | 0.2299089 | 0.3584110 × 10–1 | $2.05 \times {{10}^{{ - 4}}}$ |
| ${{M}_{1}} = 10,\,\,{{N}_{1}} = 6$ | 0.9633924 | 0.2296109 | 0.3567328 × 10–1 | $5.78 \times {{10}^{{ - 5}}}$ |
| ${{M}_{1}} = 12,\,\,{{N}_{1}} = 8$ | 0.9633940 | 0.2295468 | 0.3563360 × 10–1 | $1.70 \times {{10}^{{ - 5}}}$ |
| ${{M}_{1}} = 14,\,\,{{N}_{1}} = 10$ | 0.9633939 | 0.2295303 | 0.3562281 × 10–1 | $5.33 \times {{10}^{{ - 6}}}$ |
| ${{M}_{1}} = 16,\,\,{{N}_{1}} = 12$ | 0.9633937 | 0.2295256 | 0.3561958 × 10–1 | $1.76 \times {{10}^{{ - 6}}}$ |
На рис. 2 и 3 изображены зависимости модулей амплитуд трех первых гармоник Флоке от параметра ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda }.$ Параметры задачи были следующие: ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09,$ углы падения волны ${{\theta }_{0}} = 45^\circ ,$ ${{\varphi }_{0}} = 0.$ Кривые 1–3 соответствуют амплитудам ${{A}_{{00}}},{{A}_{{ - 1,1}}},{{A}_{{ - 2,0}}}.$ Кривые на рисунках получены при помощи МДУ, который позволяет рассматривать случай достаточно высоких частот. Как видно из приведенных рисунков, имеются изломы кривых, соответствующие критическим значениям волнового параметра ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda },$ на которых возникают новые распространяющиеся (незатухающие) пространственные гармоники. Из рисунков следует, что модуль коэффициента отражения плоской волны, то есть величина $\left| {{{A}_{{00}}}} \right|,$ монотонно убывает, а величина $\left| {{{A}_{{ - 2,0}}}} \right|$ монотонно возрастает с увеличением параметра ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda },$ то есть происходит перераспределение энергии в высшие гармоники Флоке.
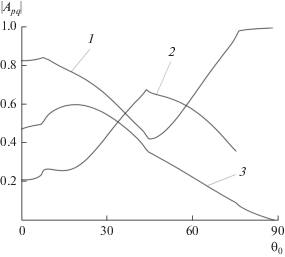
Рис. 4–7 иллюстрируют зависимости модулей отраженных гармоник указанных выше номеров от угла падения плоской волны ${{\theta }_{0}}$. Рисунки 4 и 5 соответствуют случаю “пологой” поверхности (при ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09$), а рисунки 6 и 7 – случаю, когда отношение ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.5.$ Параметры задачи были следующие: ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda } = 1.2,$ ${{\varphi }_{0}} = 0.$ Кривые 1–3 на рисунках вновь соответствуют амплитудам ${{A}_{{00}}},{{A}_{{ - 1,1}}},{{A}_{{ - 2,0}}}.$ Как следует из рисунков, в случае “пологой” поверхности зависимости модулей амплитуд ${{A}_{{ - 1,1}}},{{A}_{{ - 2,0}}}$ монотонны, при этом $\left| {{{A}_{{00}}}} \right|$ меняется незначительно. В случае, когда ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.5,$ имеется “провал” зависимости величины $\left| {{{A}_{{00}}}} \right|,$ то есть модуля коэффициента отражения плоской волны, соответствующий углу падения, примерно равному 42° (при ${{d}_{x}} = {{d}_{y}}$) и 45° (при ${{d}_{x}} = 2{{d}_{y}}$). При этом величина $\left| {{{A}_{{ - 1,1}}}} \right|$ имеет максимальное значение для этого угла падения волны.
Рис. 4.
Зависимость амплитуд трех первых гармоник от угла падения; ${{d}_{x}} = {{d}_{y}},$ ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09.$
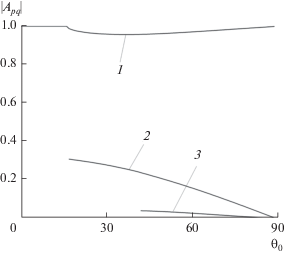
Рис. 5.
Зависимость амплитуд трех первых гармоник от угла падения; ${{d}_{x}} = 2{{d}_{y}},$ ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09.$

ЗАКЛЮЧЕНИЕ
На основе ММДИ и МДУ разработаны два подхода для решения трехмерной задачи дифракции плоской волны на неровной двоякопериодической поверхности. Выведены соотношения, позволяющие рассчитывать амплитуды гармоник Флоке для абсолютно мягкой и абсолютно жесткой поверхности двумя методами. Численные результаты приведены для абсолютно мягкой синусоидальной поверхности. Для тестирования метода на основе ММДИ построено распределение невязки краевого условия на центральном периоде поверхности. Показано, что максимальный уровень невязки не превосходит ${{10}^{{ - 2}}}$ для значения относительной высоты поверхности, равной ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.5.$ Проведена оценка точности выполнения закона сохранения энергии при помощи обеих методик. Показано, что для значения параметра ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda } = 1.2$ точность выполнения закона сохранения составляет 4 × 10–5 (при ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09$) либо 1.4 × 10–4 (при ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.5$) при использовании ММДИ и 4 × 10–5 при использовании МДУ (при ${a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d} = 0.09,$ то есть в том случае, когда этот метод применим). Проведено сравнение результатов, полученных двумя методами, для случая “пологой” поверхности. Показано, что относительная разность результатов, полученных с использованием ММДИ и МДУ, не превосходит 1.4 × 10–4. Приведены результаты, касающиеся внутренней сходимости обоих методов.
В работе построены зависимости модуля амплитуд трех первых распространяющихся гармоник Флоке от волнового параметра ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda }$ и угла падения плоской волны для синусоидальной поверхности. Показано, что в случае “пологой” поверхности модуль коэффициента отражения плоской волны монотонно убывает с ростом волнового параметра, таким образом происходит перераспределение энергии в высшие гармоники. Показано также, что в случае достаточно большого значения амплитуды неровной поверхности имеется “провал” зависимости модуля коэффициента отражения плоской волны от угла падения.
Работа выполнена при поддержке Российского фонда фундаментальных исследований, проекты № 18-02-00961 и № 19-02-00654.
Список литературы
Кюpкчан А.Г. Возбуждение нитью тока периодической ребристой структуры, обладающей свойствами искусственно жесткой поверхности // Радиотехника и электроника. 1999. Т. 44. № 7. С. 787–793.
Лапин А.Д. Поглощение звука плоской решеткой монопольно-дипольных рассеивателей // Акуст. журн. 2006. Т. 52. № 4. С. 497–501.
Кобелев Ю.А. Рассеяние плоской звуковой волны сферическими частицами с монопольным типом колебаний, расположенными в узлах плоской безграничной сетки с одинаковыми ячейками // Акуст. журн. 2014. Т. 60. № 1. С. 3–12.
Кобелев Ю.А. Многократное рассеяние звуковых волн сферическими частицами с монопольным типом колебаний, расположенными в узлах трехмерной решетки с одинаковыми ячейками // Акуст. журн. 2015. Т. 61. № 4. С. 432–441.
Маненков С.А. Решение трехмерной задачи дифракции плоской волны на плоской двупериодической решетке // Акуст. журн. 2016. Т. 62. № 2. С. 143–152.
Бреховских Л.М. Дифракция звуковых волн на неровной поверхности // Докл. Акад. наук СССР. 1951. Т. 79. Вып. 4. С. 585–588.
Лапин А.Д. Отражение поверхностной волны от периодических неровностей на границе жидкость–твердое тело // Акуст. журн. 1978. Т. 24. № 3. С. 376–382.
Вайнштейн Л.А., Суков А.И. Дифракция на волнистой поверхности: сравнение численных методов // Радиотехника и электроника. 1984. Т. 29. № 8. С. 1472–1478.
Воронович А.Г. Приближение малых наклонов в теории рассеяния волн на неровных поверхностях // Журн. эксп. теор. физ. 1985. Т. 89. С. 116–125.
Машашвили Е.С. Дифракция звуковых волн на неровной поверхности // Акуст. журн. 1987. Т. 33. № 2. С. 298–306.
Кюркчан А.Г. О новом классе уравнений в теории дифракции // Радиотехника и электроника. 1993. Т. 38. № 1. С. 48–58.
Воронович А.Г. Приближение касательной плоскости и некоторые обобщения этого приближения // Акуст. журн. 2007. Т. 53. № 3. С. 346–352.
Маненков С.А. Решение задачи дифракции на периодически неровной границе кирального полупространства // Радиотехника и электроника. 2011. Т. 56. № 8. С. 923–931.
Kюркчан А.Г., Минаев С.А., Соловейчик А.Л. Модификация метода дискретных источников на основе априорной информации об особенностях дифракционного поля // Радиотехника и электроника. 2001. Т. 46. № 6. С. 666–672.
Кюркчан А.Г., Смирнова Н.И. Математическое моделирование в теории дифракции с использованием априорной информации об аналитических свойствах решения. М.: Медиа Паблишер, 2014.
Кюркчан А.Г. О методе вспомогательных токов и источников в задачах дифракции волн // Радиотехника и электроника. 1984. Т. 29. № 11. С. 2129–2139.
Кюркчан А.Г., Стернин Б.Ю., Шаталов В.Е. Особенности продолжения волновых полей // Успехи физ. наук. 1996. Т. 166. № 12. С. 1285–1308.
Кантор И.Л., Солодовников А.С. Гиперкомплексные числа. М.: Наука, 1973. 144 с.
Kravchenko V.V. Applied quaternionic analysis. Lemgo: Heldermann Verlag, 2003. 127 p.
Кюркчан А.Г. Об одном новом интегральном уравнении в теории дифракции // Докл. Акад. наук СССР. 1992. Т. 325. № 2. С. 273–279.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971. 1108 с.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал