1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 65, № 4, 2019

Акустический журнал, 2019, T. 65, № 4, стр. 440-447

Дифракция на вытянутом теле вращения с импедансными границами. Метод граничного интегрального параболического уравнения

А. И. Корольков a, *, А. В. Шанин a, А. А. Белоус a

a Московский государственный университет им. М.В. Ломоносова, физический факультет
119991 Москва, Ленинские горы, Россия

* E-mail: korolkov@physics.msu.ru

Поступила в редакцию 20.11.2018
После доработки 02.03.2019
Принята к публикации 20.03.2019

Полный текст (PDF)

Аннотация

Изучается задача дифракции на вытянутом теле вращения с импедансными граничными условиями. Рассматривается случай приосевого падения высокочастотной волны. Дифракционный процесс описывается с помощью метода параболического уравнения. С помощью теоремы Грина выводится граничное интегральное уравнения типа Вольтерра. Для задачи дифракции на тонком импедансном конусе строится итерационное численное решение.

Ключевые слова: вытянутые тела вращения, дифракция на конусе, импедансный конус, параболическое уравнение

1. ВВЕДЕНИЕ

В настоящей работе рассматривается задача дифракции на вытянутом теле вращения. Иными словами, предполагается, что продольные размеры тела значительно превышают его поперечные размеры. Поле на поверхности удовлетворяет импедансным граничным условиям. Рассматривается случай приосевого падения. Также предполагается, что длины волн значительно меньше продольных размеров препятствия. При таких предположениях дифракционная задача значительно упрощается и может быть решена в рамках метода параболического уравнения.

Задачи дифракции на вытянутых телах привлекают значительное внимание исследователей. В частности, хорошо изучен случай идеальных граничных условий [1–8]. Этот случай также рассматривался авторами [9, 10]. Подробный обзор существующих методов может быть найден в [10]. К сожалению, задачи дифракции на телах вращения с импедансными граничными условиями практически не изучены. Исключением можно считать работы [11, 12], в которых данная задача исследована численно в рамках гибридного подхода. Известны также работы, посвященные импедансному конусу [13–15]. В данных работах с помощью интегрального представления Конторовича-Лебедева задачу удается свести к интегральному уравнению типа Фредгольма. Для случая тонкого конуса строится диаграмма направленности. В [16] исследовано дальнее поле вблизи поверхности конуса (дальнее поле понимается в том смысле, что расстояние от вершины конуса существенно превосходит длину волны).

Настоящая работа является обобщением результатов, полученных в [10], на случай импедансных граничных условий. А именно, выводится граничное интегральное уравнение в параболической постановке. Полученное уравнение относится к классу Вольтерра, что позволяет его решить с помощью метода итераций.

В работе выводятся интегральные уравнения двух типов. Уравнение первого типа, более общее, является двумерным и имеет ядро, зависящее от четырех переменных: двух координат источника и двух координат приемника на поверхности препятствия. Путем учета угловой симметрии выводится ряд одномерных уравнений для угловых мод. При осевом падении остается только уравнение для нулевой моды, которое решается методом итераций для задачи дифракции на конусе.

2. ПОСТАНОВКА ЗАДАЧИ

2.1. Постановка задачи для уравнения Гельмгольца

Рассмотрим трехмерное пространство, описываемое цилиндрическими координатами $(z,r,{\varphi }).$ Будем считать, что $z$ – продольная координата в том смысле, что все волновые процессы происходят под малым углом к оси z. Пусть везде вне тела для рассеянного поля выполняется однородное уравнение Гельмгольца:

(1)
$\begin{gathered} \left( {\frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}} + {{\Delta }_{ \bot }} + {{k}^{2}}} \right){{{\tilde {u}}}^{{{\text{sc}}}}}(z,r,{\varphi }) = 0, \\ {{\Delta }_{ \bot }} \equiv \frac{1}{r}\frac{\partial }{{\partial r}}r\frac{\partial }{{\partial r}} + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{{\varphi }}^{2}}}}. \\ \end{gathered} $

Временная зависимость имеет форму $\exp \{ - i{\omega }t\} $ и далее не выписывается. Тело вращения занимает симметричную относительно оси $z$ область $r < f(z).$ Будем обозначать поверхность тела символом Γ. Тело может быть как компактным $\left( {{{Z}_{1}} \leqslant z \leqslant {{Z}_{2}}} \right),$ так и полубесконечным $\left( {z \geqslant {{Z}_{1}}} \right).$ Важным примером тела вращения является конус:

(2)
$r = f(z) = {\alpha }z,\,\,\,\,z \geqslant 0.$

Падающая волна имеет вид:

(3)
${{\tilde {u}}^{{{\text{in}}}}} = \exp \left\{ {ik(z\cos {\theta } + r\cos {\varphi }\sin {\theta })} \right\},$
где угол падения ${\theta }$ предполагается малым.

Полное поле $\tilde {u}$ представляется в следующем виде:

(4)
$\tilde {u} = {{\tilde {u}}^{{{\text{in}}}}} + {{\tilde {u}}^{{{\text{sc}}}}}.$

Рассеянное поле понимается в смысле принципа предельного поглощения. А именно, предполагается, что волновое число k имеет малую положительную мнимую часть. Следовательно, рассеянное поле затухает при $\left| z \right| \to \infty $ или $\left| r \right| \to \infty .$

На поверхности тела должны выполняться импедансные граничные условия:

(5)
$\frac{{\partial{ \tilde {u}}}}{{\partial {\mathbf{n}}}} = {\eta }\tilde {u},$
где ${\eta }$ – импеданс, ${\mathbf{n}}$ – внешняя нормаль к поверхности тела. На импеданс накладывается условие неизлучения энергии

(6)
$\operatorname{Im} [{\eta }] \leqslant 0.$

Если на поверхности тела имеются конические точки (такие, как вершина конуса), то в них должны удовлетворяться условия Мейкснера, заключающиеся в интегрируемости “энергии” ${{\left| {\nabla \tilde {u}} \right|}^{2}} + {{\left| {\tilde {u}} \right|}^{2}}$ вблизи конической точки.

2.2. Постановка задачи для параболического уравнения

Предполагается, что тело вращения вытянуто в том смысле, в котором это понятие было введено в [10]. А именно, предполагается, что дифракционный процесс носит приосевой характер, т.е. выполнены следующие условия:

1. Угол падения мал: ${\theta } \ll 1.$

2. Наклон поверхности меняется плавно: $\dot {f} \ll 1.$ Здесь $\dot {f}$ – производная ${{df} \mathord{\left/ {\vphantom {{df} {dz}}} \right. \kern-0em} {dz}}.$

3. Угол дифракции мал: ${{\left( {{{\ddot {f}} \mathord{\left/ {\vphantom {{\ddot {f}} k}} \right. \kern-0em} k}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \ll 1.$ Здесь $\ddot {f}$ – производная ${{{{d}^{2}}f} \mathord{\left/ {\vphantom {{{{d}^{2}}f} {d{{z}^{2}}}}} \right. \kern-0em} {d{{z}^{2}}}}.$

Поясним последнее условие. Продольный размер зоны Френеля определяется выражением [17]:

(7)
$\Delta z = {{\left( {\ddot {f}} \right)}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0em} 3}}}}{{k}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}}.$

Угол дифракции может быть оценен как изменение наклона поверхности на $\Delta z,$ т.е. как $\Delta z\ddot {f} = {{\left( {{{\ddot {f}} \mathord{\left/ {\vphantom {{\ddot {f}} k}} \right. \kern-0em} k}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$

В соответствии с методом параболического уравнения представим рассеянное поле в виде

(8)
${{\tilde {u}}^{{{\text{sc}}}}}(z,r,{\varphi }) = \exp \left\{ {ikz} \right\}{{u}^{{{\text{sc}}}}}\left( {z,r,{\varphi }} \right),$
где ${{u}^{{{\text{sc}}}}}\left( {z,r,{\varphi }} \right)$ является медленной функцией $z$ по сравнению с экспоненциальным множителем. Подставляя (8) в (1) и пренебрегая членом со второй производной по z, получаем параболическое уравнение теории дифракции (ПУТД):

(9)
$\left( {\frac{\partial }{{\partial z}} + \frac{1}{{2ik}}{{\Delta }_{ \bot }}} \right){{u}^{{{\text{sc}}}}} = 0.$

Падающая волна (3) в параболическом приближении принимает вид

(10)
${{u}^{{{\text{in}}}}}\left( {z,r,{\varphi }} \right) = \exp \left\{ {ik\left( {{\theta }r\cos {\varphi } - {{z{{{\theta }}^{2}}} \mathord{\left/ {\vphantom {{z{{{\theta }}^{2}}} 2}} \right. \kern-0em} 2}} \right)} \right\},$
где учтено, что $\cos {\theta } \approx 1 - {{{{{\theta }}^{2}}} \mathord{\left/ {\vphantom {{{{{\theta }}^{2}}} 2}} \right. \kern-0em} 2},$ $\sin {\theta } \approx {\theta }$. Легко проверить, что (10) удовлетворяет (9). В случае осевого падения ${\theta } = 0$ имеем

(11)
${{u}^{{{\text{in}}}}} = 1.$

Импедансные граничные условия (5) переходят в

(12)
$N\left[ u \right]\left( {z,f\left( z \right),{\varphi }} \right) = {\eta }u,\,\,\,\,N \equiv \frac{\partial }{{\partial r}} - ik\dot {f},$
где $u = {{u}^{{{\text{in}}}}} + {{u}^{{{\text{sc}}}}}.$ Переход от ${\partial \mathord{\left/ {\vphantom {\partial {\partial {\mathbf{n}}}}} \right. \kern-0em} {\partial {\mathbf{n}}}}$ к N подробно обсуждается в [10]. А именно, непосредственно вычисляя производную от (8) и пренебрегая членами порядка ${{\left( {\dot {f}} \right)}^{2}},$ получим (12).

Как известно, наличие импедансных граничных условий может приводить к появлению поверхностных волн. Если их скорость существенно меньше скорости волн в среде, параболическое приближение не будет справедливым. Потребуем выполнения следующего условия

(13)
${{\left| {\eta } \right|} \mathord{\left/ {\vphantom {{\left| {\eta } \right|} k}} \right. \kern-0em} k} \ll 1.$

Тогда скорость распространения поверхностных волн будет близка к скорости звука [18], и, следовательно, они будут хорошо описываться параболическим приближением. Также предполагается выполнение условия неизлучения энергии (6).

Постановка задачи для ПУТД должна быть дополнена начальным условием

(14)
${{u}^{{{\text{sc}}}}} = 0,\,\,\,\,п р и \,\,\,\,{\kern 1pt} z < {{Z}_{1}},$
отражающим тот факт, что ПУТД описывает только волны, распространяющиеся в положительном направлении.

Кроме того, рассеянное поле понимается в смысле принципа предельного поглощения.

Наконец, требуется выполнение условий Мейкснера. А именно, вблизи конической точки требуется локальная интегрируемость следующего выражения [10]:

(15)
${{\left| {{{\Delta }_{ \bot }}u} \right|}^{2}} + {{\left| u \right|}^{2}}.$

3. ВЫВОД ГРАНИЧНОГО ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ДЛЯ ПРОИЗВОЛЬНОГО ТЕЛА ВРАЩЕНИЯ

3.1. Теорема Грина для параболического уравнения

Введем векторные обозначения для точек пространства ${\mathbf{r}}{\text{ = }}\left( {z,r,{\varphi }} \right).$ Определим функцию Грина как решение неоднородного параболического уравнения с источником в точке ${{{\mathbf{r}}}_{s}} = \left( {{{z}_{s}},{{r}_{s}},{{{\varphi }}_{s}}} \right)\,:$

(16)
$\left( {\frac{\partial }{{\partial z}} + \frac{1}{{2ik}}{{\Delta }_{ \bot }}} \right)g({\mathbf{r}},{{{\mathbf{r}}}_{{\mathbf{s}}}}) = {\delta }({\mathbf{r}} - {{{\mathbf{r}}}_{{\mathbf{s}}}}),$
где оператор в левой части действует на компоненты вектора r, а ${\delta }$ – дельта-функция Дирака. Решение уравнения должно удовлетворять начальному условию, то есть должно обращаться в ноль при $z < {{z}_{s}}.$ При помощи непосредственной подстановки в (16) можно убедиться, что функция Грина при $z > {{z}_{s}}$ имеет следующий вид:
(17)
$g\left( {{\mathbf{r}},{{{\mathbf{r}}}_{{\mathbf{s}}}}} \right) = \frac{k}{{2\pi i(z - {{z}_{s}})}}\exp \left\{ {\frac{{ik}}{2}\frac{{{{{(\Delta r)}}^{2}}}}{{z - {{z}_{s}}}}} \right\},$
где $\Delta r$ – расстояние между проекциями векторов в поперечной плоскости:

${{\left( {\Delta r} \right)}^{2}} = {{r}^{2}} + r_{s}^{2} - 2r{{r}_{s}}\cos \left( {{\varphi } - {{{\varphi }}_{s}}} \right).$

Сформулируем теорему Грина для параболического уравнения. Пусть $\Omega $ – конечная связная область с гладкой границей $\partial \Omega $ и внешней нормалью n. Рассмотрим пару неоднородных параболических уравнений

(18)
$\left( {\frac{\partial }{{\partial z}} + \frac{1}{{2ik}}{{\Delta }_{ \bot }}} \right)v\left( {z,r,{\varphi }} \right) = q\left( {z,r,{\varphi }} \right),$
(19)
$\left( { - \frac{\partial }{{\partial z}} + \frac{1}{{2ik}}{{\Delta }_{ \bot }}} \right)w\left( {z,r,{\varphi }} \right) = h\left( {z,r,{\varphi }} \right)$
для некоторых $v,q,w,h.$ Отметим, что второе уравнение является комплексно сопряженным к первому, то есть описывает распространение волн в отрицательном направлении.

Введем векторные функции:

(20)
$\begin{gathered} {\mathbf{v}}\left( {z,r,{\varphi }} \right) = \left( {ikv,\frac{{\partial v}}{{\partial r}},\frac{1}{r}\frac{{\partial v}}{{\partial {\varphi }}}} \right), \\ {\mathbf{w}}\left( {z,r,{\varphi }} \right) = \left( { - ikw,\frac{{\partial w}}{{\partial r}},\frac{1}{r}\frac{{\partial w}}{{\partial {\varphi }}}} \right). \\ \end{gathered} $

Наконец, сформулируем теорему Грина [10]:

(21)
$\int\limits_{\partial \Omega } {\left[ {\left( {{\mathbf{v}} \cdot {\mathbf{n}}} \right)w - \left( {{\mathbf{w}} \cdot {\mathbf{n}}} \right)v} \right]} dS = 2ik\int\limits_\Omega {\left[ {qw - hv} \right]dV.} $

3.2. Граничное интегральное уравнение для полного поля

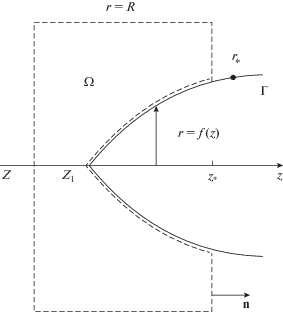
Применим теорему Грина к области $\Omega $, сечение которой изображено на рис. 1. Область ограничена плоскостью $z = Z,$ где $Z < {{Z}_{1}},$ плоскостью $z = z{\text{*}}$ для некоторого $z* > {{Z}_{1}},$ цилиндром $r = R,$ где $R \to \infty ,$ и поверхностью тела вращения Γ. Область Ω обладает осевой симметрией относительно оси z. В качестве $v$ подставим в (18) рассеянное поле ${{u}^{{{\text{sc}}}}},$ а в качестве $w$ подставим $g({\mathbf{r}}*,{\mathbf{r}}),$ где

$r* = \left( {z{\text{*}} + {\varepsilon },f\left( {z{\text{*}} + \varepsilon } \right),{\varphi *}} \right).$
Рис. 1.

Сечение области для теоремы Грина.

Здесь ${\varphi *}$ предполагается произвольным, ε – малым (ниже рассматривается предел ${\varepsilon } \to 0$). Проводя выкладки, аналогичные проведенным в [10], получим следующее интегральное уравнение:

(22)
$\begin{gathered} {{U}^{{{\text{sc}}}}}\left( {z*,{\varphi *}} \right) = \frac{i}{k}\int\limits_0^{2\pi } {\int\limits_{{{Z}_{1}}}^{z{\text{*}}} {{{U}^{{{\text{sc}}}}}\left( {z,{\varphi }} \right)} } \times \\ \times \,\,\left\{ {\bar {N}\left[ W \right]\left( {z,{\varphi }} \right) - {\eta }W(z,{\varphi })} \right\}f\left( z \right)dzd{\varphi } + \\ + \,\,\frac{i}{k}\int\limits_0^{2\pi } {\int\limits_{{{Z}_{1}}}^{z{\text{*}}} {W\left( {z,{\varphi }} \right)} } \left\{ {N\left[ {{{U}^{{{\text{in}}}}}} \right]\left( {z,{\varphi }} \right) - {\eta }{{U}^{{{\text{in}}}}}(z,{\varphi })} \right\} \times \\ \times \,\,f\left( z \right)dzd{\varphi }, \\ \end{gathered} $
где были введены обозначения:

(23)
$\begin{gathered} \bar {N} \equiv \frac{\partial }{{\partial r}} - ik\frac{{df}}{{dz}},\,\,\,\,{{U}^{{{\text{sc}}}}}(z,{\varphi }) \equiv {{u}^{{{\text{sc}}}}}(z,f(z),{\varphi }), \\ {{U}^{{{\text{in}}}}}(z,{\varphi }) \equiv {{u}^{{{\text{in}}}}}(z,f(z),{\varphi }),\,\,\,W(z,{\varphi }) \equiv w(z,f(z),{\varphi }). \\ \end{gathered} $

Введем обозначение для ядра уравнения (22):

(24)
$K\left( {z*,{\varphi }*,z,{\varphi }} \right) \equiv \frac{{if(z)}}{k}\left( {\bar {N}\left[ W \right]\left( {z,{\varphi }} \right) - {\eta }W\left( {z,{\varphi }} \right)} \right).$

Уравнение (22) может быть упрощено. Применяя теорему Грина к области $\Omega $ с функциями

$v\left( z \right) = {{u}^{{{\text{in}}}}}(z),\,\,\,\,w(z) = g({\mathbf{r}}*,{\mathbf{r}}),$
получим интегральное соотношение:

(25)
$\begin{gathered} {{U}^{{{\text{in}}}}}\left( {z*,{\varphi *}} \right) = \frac{i}{k}\int\limits_0^{2\pi } {\int\limits_{{{Z}_{1}}}^{z{\text{*}}} {{{U}^{{{\text{in}}}}}\left( {z,{\varphi }} \right)} } \times \\ \times \,\,\left\{ {\bar {N}\left[ W \right]\left( {z,{\varphi }} \right) - {\eta }W(z,{\varphi })} \right\}f\left( z \right)dzd{\varphi } - \\ - \,\,\frac{i}{k}\int\limits_0^{2\pi } {\int\limits_{{{Z}_{1}}}^{z{\text{*}}} {W\left( {z,{\varphi }} \right)} } \left\{ {N\left[ {{{U}^{{{\text{in}}}}}} \right]\left( {z,{\varphi }} \right) - {\eta }{{U}^{{{\text{in}}}}}(z,f)} \right\} \times \\ \times \,\,f\left( z \right)dzd{\varphi } + 2{{U}^{{{\text{in}}}}}\left( {z*,{\varphi *}} \right). \\ \end{gathered} $

Складывая (22) и (25), получим уравнение для полного поля $U = {{U}^{{{\text{sc}}}}} + {{U}^{{{\text{in}}}}}$ на поверхности тела:

(26)
$\begin{gathered} U\left( {z{\text{*}},{\varphi *}} \right) = \\ = \int\limits_0^{2\pi } {\int\limits_{{{Z}_{1}}}^{{{z}_{*}}} {K\left( {z{\text{*}},{\varphi *},z,{\varphi }} \right)U\left( {z,{\varphi }} \right)dzd{\varphi } + 2{{U}^{{{\text{in}}}}}\left( {z{\text{*}},{\varphi *}} \right).} } \\ \end{gathered} $

Ядро уравнения дается следующим выражением:

(27)
$\begin{gathered} K\left( {z{\text{*}},{\varphi *},z,{\varphi }} \right) = \frac{{ikf(z)}}{{2\pi }}\left( {\frac{1}{{ik}}\frac{{ik\dot {f}\left( z \right) - {\eta }}}{{z{\text{*}} - z}} + \frac{{f\left( z \right) - f\left( {z{\text{*}}} \right)\cos ({\varphi } - {\varphi *})}}{{{{{\left( {z{\text{*}} - z} \right)}}^{2}}}}} \right) \times \\ \times \,\,\exp \left\{ {\frac{{ik}}{2}\frac{{{{{\left( {f\left( z \right)} \right)}}^{2}} + {{{\left( {f\left( {z{\text{*}}} \right)} \right)}}^{2}} - 2f\left( z \right)f\left( {z{\text{*}}} \right)\cos ({\varphi } - {\varphi *})}}{{z{\text{*}} - z}}} \right\}. \\ \end{gathered} $

Уравнение (26) является уравнением Вольтерра по переменной z и уравнением с разностным ядром по переменной φ.

Стоит отметить, что ядро $K$ сингулярно при $z$, стремящемся к $z{\text{*}}.$ Данная сингулярность является интегрируемой и носит осциллирующий характер. Таким образом, интегралы по z в (22) и (26) следует понимать как несобственные интегралы второго рода.

3.3. Граничное интегральное уравнение для угловых мод

Воспользуемся осевой симметрией задачи. Представим падающее и полное поля на поверхности тела в виде рядов Фурье:

(28)
$\begin{gathered} {{U}^{{{\text{in}}}}}\left( {z,{\varphi }} \right) = \sum\limits_{n = - \infty }^\infty {U_{n}^{{{\text{in}}}}(z){{e}^{{in{\varphi }}}},} \\ U\left( {z,{\varphi }} \right) = \sum\limits_{n = - \infty }^\infty {{{U}_{n}}(z){{e}^{{in{\varphi }}}}.} \\ \end{gathered} $

Функции ${{U}_{n}}$ удовлетворяют следующим интегральным уравнениям:

(29)
${{U}_{n}}(z{\text{*}}) = \int\limits_{{{Z}_{1}}}^{z*} {{{K}_{n}}(z{\text{*}},z){{U}_{n}}(z)dz} + 2U_{n}^{{{\text{in}}}}(z{\text{*}}),$
где

(30)
${{K}_{n}}(z{\text{*}},z) = \int\limits_0^{2\pi } {K\left( {z{\text{*}},{\varphi },z,0} \right){{e}^{{ - in\varphi }}}d{\varphi }.} $

Используя (27), можно получить явное выражение для ${{K}_{n}}\left( {z{\text{*}},z} \right)\,:$

(31)
$\begin{gathered} {{K}_{n}}\left( z \right) = \frac{{ - {{{( - i)}}^{{n + 1}}}kr}}{{{{{(z{\text{*}} - z)}}^{2}}}}\exp \left\{ {\frac{{ik}}{2}\frac{{r_{*}^{2} + {{r}^{2}}}}{{z{\text{*}} - z}}} \right\} \times \\ \times \,\,\left[ {\left( {r + \left( {z{\text{*}} - z} \right)\left( {\frac{{df}}{{dz}} - \frac{{\eta }}{{ik}}} \right)} \right){{J}_{n}}\left( {\frac{{kr{\text{*}}r}}{{z{\text{*}} - z}}} \right)} \right. - \\ - \,\,\left. {\frac{{ir{\text{*}}}}{2}\left( {{{J}_{{n - 1}}}\left( {\frac{{kr{\text{*}}r}}{{z{\text{*}} - z}}} \right) - {{J}_{{n + 1}}}\left( {\frac{{k{\text{*}}r}}{{z{\text{*}} - z}}} \right)} \right)} \right], \\ \end{gathered} $
где $r = f\left( z \right),$ $r{\text{*}} = f(z{\text{*}}),{{J}_{n}}$ – функция Бесселя первого рода.

Стоит отметить, что по аналогии с [10] для конечного тела вращения может быть получено выражение для диаграммы направленности и доказана оптическая теорема.

4. ДИФРАКЦИЯ НА ИМПЕДАНСНОМ КОНУСЕ ПРИ ОСЕВОМ ПАДЕНИИ

4.1. Граничное интегральное уравнение для конической задачи при осевом падении

Рассмотрим конус, для которого ${{Z}_{1}} = 0,$ т.е. вершина конуса находится в начале координат, как показано на рис. 2. Профиль конуса представляет собой прямую линию (2), где α является тангенсом угла между осью конуса и его образующей. Предполагается, что ${\alpha } \ll 1.$

Рис. 2.

Геометрия задачи дифракции на конусе.

Пусть падающая волна распространяется вдоль оси z, то есть имеет вид (11). В этом случае полное поле обладает осевой симметрией и описывается нулевой компонентой ряда (28):

$U\left( {z,{\varphi }} \right) = {{U}_{0}}(z) = U(z).$

Задача сводится к одномерному интегральному уравнению:

(32)
$U\left( {z{\text{*}}} \right) = \int\limits_0^{z{\text{*}}} {{{K}_{0}}} \left( {z{\text{*}},z} \right)U\left( z \right)dz + 2$
с ядром

(33)
$\begin{gathered} {{K}_{0}} = \frac{{ik{{{\alpha }}^{2}}z{\text{*}}z}}{{{{{\left( {z{\text{*}} - z} \right)}}^{2}}}}\exp \left\{ {\frac{{ik{{{\alpha }}^{2}}}}{2}\frac{{z_{*}^{2} + {{z}^{2}}}}{{z{\text{*}} - z}}} \right\} \times \\ \times \,\,\left[ {{{J}_{0}}\left( {k{{{\alpha }}^{2}}\frac{{z{\text{*}}z}}{{z{\text{*}} - z}}} \right) + i{{J}_{1}}\left( {k{{{\alpha }}^{2}}\frac{{z{\text{*}}z}}{{z{\text{*}} - z}}} \right)} \right. - \\ - \,\,\left. {\frac{{{\eta }\left( {z{\text{*}} - z} \right)}}{{ikz{*\alpha }}}{{J}_{0}}\left( {k{{{\alpha }}^{2}}\frac{{z{\text{*}}z}}{{z{\text{*}} - z}}} \right)} \right]. \\ \end{gathered} $

4.2. Случай разделяющихся переменных

Пусть импеданс меняется обратно пропорционально z:

(34)
${\eta } = \frac{{{\tilde {\eta }}}}{z}.$

Тогда задача для параболического уравнения может быть решена с помощью метода разделения переменных. Перейдем в систему координат $\left( {z,{\rho },{\varphi }} \right)$ с

(35)
${\rho } = {r \mathord{\left/ {\vphantom {r z}} \right. \kern-0em} z}$
и введем новую полевую переменную $\hat {u}$:

(36)
$\begin{gathered} u\left( {z,{\rho }z,{\varphi }} \right) = {{\Xi }^{{ - 1}}}\left( {z,{\rho }} \right)\hat {u}\left( {z,{\rho },{\varphi }} \right), \\ \Xi \left( {z,{\rho }} \right) \equiv kz\exp \left\{ {{{ - ikz{{{\rho }}^{2}}} \mathord{\left/ {\vphantom {{ - ikz{{{\rho }}^{2}}} 2}} \right. \kern-0em} 2}} \right\}. \\ \end{gathered} $

Уравнение (9) переходит в

(37)
$\left( {\frac{\partial }{{\partial z}} + \frac{1}{{2ik{{z}^{2}}}}\left( {\frac{1}{{\rho }}\frac{\partial }{{\partial {\rho }}}\left( {{\rho }\frac{\partial }{{\partial {\rho }}}} \right) + \frac{1}{{{{{\rho }}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{{\varphi }}^{2}}}}} \right)} \right)\hat {u} = 0,$
а граничное условие (12) переходит в

(38)
$\frac{1}{z}\frac{{\partial{ \hat {u}}}}{{\partial {\rho }}}\left( {z,{\alpha },{\varphi }} \right) = {\eta }\hat {u}.$

При выполнении (34) условие (38) переходит в

(39)
$\frac{{\partial{ \hat {u}}}}{{\partial {\rho }}}\left( {z,{\alpha },{\varphi }} \right) = {\tilde {\eta }}\hat {u}$
и, следовательно, переменные разделяются.

Представим полное поле в виде

$\hat {u} = {{\hat {u}}^{{{\text{sc}}}}} + {{\hat {u}}^{{{\text{in}}}}},\,\,\,\,{\kern 1pt} {{\hat {u}}^{{{\text{in}}}}} = \Xi \left( {z,{\rho }} \right).$

Разделяя переменные в (37), получим следующее представление для рассеянного поля:

(40)
${{\hat {u}}^{{{\text{sc}}}}}(z,{\rho }) = \int {C\left( {\lambda } \right)H_{0}^{{(1)}}\left( {\sqrt {\lambda } {\rho }} \right)\exp \left( {i\frac{{\lambda }}{{2kz}}} \right)d{\lambda }} ,$
где $H_{0}^{{(1)}}$ – функция Ханкеля 1-го рода, а $C\left( {\lambda } \right)$ и контур интегрирования подлежат определению. Для определения $C\left( {\lambda } \right)$ подставим (40) в (39) и воспользуемся известным соотношением из теории Бесселевых функций [19]:

(41)
$kz\exp \left\{ {\frac{{ - ikz{{{\rho }}^{2}}}}{2}} \right\} = - \frac{i}{2}\int\limits_0^\infty {\exp \left\{ {\frac{{i{\lambda }}}{{2kz}}} \right\}{{J}_{0}}\left( {\sqrt {\lambda } {\rho }} \right)d{\lambda }} .$

В итоге имеем

(42)
$C\left( {\lambda } \right) = \frac{i}{2}\frac{{{\tilde {\eta }}{{J}_{0}}\left( {\sqrt {\lambda } {\alpha }} \right) - {{{\dot {J}}}_{0}}(\sqrt {\lambda } {\alpha })\sqrt {\lambda } }}{{{\tilde {\eta }}H_{0}^{{(1)}}(\sqrt {\lambda } {\alpha }) - \dot {H}_{0}^{{(1)}}(\sqrt {\lambda } {\alpha })\sqrt {\lambda } }},$
где были введены следующие обозначения:

(43)
$\begin{gathered} \frac{{d{{J}_{0}}\left( {\sqrt {\lambda } {\rho }} \right)}}{{d\left( {\sqrt {\lambda } {\rho }} \right)}} \equiv {{{\dot {J}}}_{0}}\left( {\sqrt {\lambda } {\rho }} \right), \\ \frac{{dH_{0}^{{(1)}}\left( {\sqrt {\lambda } {\rho }} \right)}}{{d\left( {\sqrt {\lambda } {\rho }} \right)}} \equiv \dot {H}_{0}^{{(1)}}\left( {\sqrt {\lambda } {\rho }} \right). \\ \end{gathered} $

Таким образом, полное поле $u\left( {z,r} \right)$ дается следующим выражением:

(44)
$\begin{gathered} u(z,r) = 1 + \frac{i}{{2kz}}\exp \left( {\frac{{ik{{r}^{2}}}}{{2z}}} \right) \times \\ \times \,\,\int\limits_0^\infty {\frac{{{\tilde {\eta }}{{J}_{0}}\left( {\sqrt {\lambda } {\alpha }} \right) - {{{\dot {J}}}_{0}}(\sqrt {\lambda } {\alpha })}}{{{\tilde {\eta }}H_{0}^{{(1)}}(\sqrt {\lambda } {\alpha }) - \dot {H}_{0}^{{(1)}}(\sqrt {\lambda } {\alpha })}}} \times \\ \times \,\,H_{0}^{{(1)}}\left( {\sqrt {\lambda } \frac{r}{z}} \right)\exp \left( {i\frac{{\lambda }}{{2kz}}} \right)d{\lambda }{\text{.}} \\ \end{gathered} $

Данный ответ можно получить и непосредственно из (32). Действительно, интегральное уравнение в данном случае сводится к уравнению с разностным ядром при помощи замены $z \to {1 \mathord{\left/ {\vphantom {1 {\tau }}} \right. \kern-0em} {\tau }}{\text{.}}$ Решение, соответственно, строится с помощью интегрального преобразования Фурье. Аналогичные выкладки были проделаны авторами в [10].

Стоит заметить, что импеданс в данном случае достигает больших значений при малых z и, следовательно, условие (13) нарушается вблизи носика. Таким образом, формула (44) является только модельным решением для параболического уравнения. Ниже формула (44) будет использована для верификации метода численного интегрирования уравнения (32).

Отметим, что аналогичный случай разделяющихся переменных для уравнения Гельмгольца рассмотрен в [20].

4.3. Численное решение уравнения (32)

Случай переменного импеданса (34). В случае переменного импеданса (34) граничные условия (12) при малых z близки к идеальным условиям Дирихле. Можно показать, что граничное интегральное уравнение для задачи Дирихле является уравнением Вольтерра 1-го рода, а такое уравнение, как известно, является некорректно поставленной задачей. Следует также отметить, что в случае условий Дирихле поле U на поверхности тождественно равно нулю, и вывод интегрального уравнения следует проводить для нормальной производной поля на поверхности $N\left[ U \right].$

Для построения численного решения будем использовать итерационный алгоритм, предложенный в [21] для некорректно поставленных задач. А именно, будем решать следующую итерационную задачу:

(45)
$U(z) = \sum\limits_{n = 0}^\infty {{{U}^{{(n)}}}} (z),$
(46)
${{U}^{{(0)}}}(z) = 2{\beta }{{U}^{{{\text{in}}}}}(z) = 2{\beta ,}$
(47)
$\begin{gathered} {{U}^{{(n + 1)}}}(z*) = (1 - {\beta }){{U}^{{(n)}}}(z*) + {\beta }\int\limits_0^{z*} {{{K}_{0}}} (z*,z){{U}^{{(n)}}}(z)dz, \\ n > 0, \\ \end{gathered} $
где β – некоторое малое положительное число, играющее роль параметра регуляризации.

Заменим интеграл в правой части (47) его дискретным аналогом. А именно, аппроксимируем $U$ кусочно-линейными функциями [22]:

(48)
${{N}_{i}}(z) = \left\{ {\begin{array}{*{20}{l}} {0,}&{{{z}_{{i - 1}}} > z,} \\ {{{(z - {{z}_{{i - 1}}})} \mathord{\left/ {\vphantom {{(z - {{z}_{{i - 1}}})} {({{z}_{i}} - {{z}_{{i - 1}}})}}} \right. \kern-0em} {({{z}_{i}} - {{z}_{{i - 1}}})}},}&{{{z}_{i}} > z > {{z}_{{i - 1}}},} \\ {{{({{z}_{{i + 1}}} - z)} \mathord{\left/ {\vphantom {{({{z}_{{i + 1}}} - z)} {({{z}_{{i + 1}}} - {{z}_{i}})}}} \right. \kern-0em} {({{z}_{{i + 1}}} - {{z}_{i}})}},}&{{{z}_{{i + 1}}} > z > {{z}_{i}},} \\ {0,}&{z > {{z}_{{i + 1}}}.} \end{array}} \right.$

Индекс $i$ пробегает значения от 1 до M, где $M$ – число базисных функций. Поле $U$ ищется в виде:

(49)
$U\left( z \right) \approx \sum\limits_{i = 1}^M {{{U}_{i}}{{N}_{i}}(z)} ,$
где ${{U}_{i}}$ – неизвестные числа, подлежащие определению. Подставляя (49) в (47), получим:

(50)
$\begin{gathered} U_{i}^{{(n + 1)}} = (1 - {\beta })U_{i}^{{(n)}} + {\beta }\sum\limits_{i = 1}^M {{{K}_{{ij}}}U_{j}^{{(n)}}} , \\ {\text{г д е }}\,\,\,\,{{K}_{{ij}}} = \int\limits_0^{{{z}_{i}}} {{{K}_{0}}({{z}_{i}},z){{N}_{j}}(z)dz} . \\ \end{gathered} $

Для корректного вычисления матричных элементов ${{K}_{{ij}}}$ необходимо учитывать поведение ядра ${{K}_{0}}(z{\text{*}},z)$ вблизи особой точки $z* = z.$ Используя асимптотические формулы для функций Бесселя большого аргумента, можно показать, что ядро имеет особенности двух типов. Первая особенность имеет осциллирующий характер:

(51)
$\begin{gathered} K_{0}^{a}(z*,z)\sim \sqrt {\frac{{zz*}}{{{{{(z* - z)}}^{3}}}}} \left( {1 + \frac{{i(z - z*)}}{{8k{{{\alpha }}^{2}}zz{\text{*}}}}} \right) \times \\ \times \,\,\exp \left\{ {\frac{{ik{{{\alpha }}^{2}}}}{2}\frac{{{{{(z{\text{*}} + z)}}^{2}}}}{{z{\text{*}} - z}}} \right\}. \\ \end{gathered} $

Вторая особенность является интегрируемой:

(52)
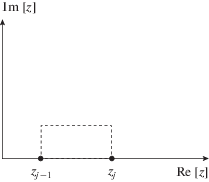
$K_{0}^{b}(z*,z)\sim \sqrt {\frac{1}{{zz{\text{*}}(z{\text{*}} - z)}}} \exp \left\{ {\frac{{ik{{{\alpha }}^{2}}}}{2}(z{\text{*}} - z)} \right\}.$

Для вычисления интеграла от $K_{0}^{a}(z*,z)$ контур интегрирования деформировался в верхнюю полуплоскость. А именно, контур интегрирования деформировался при вычислении диагональных матричных элементов

(53)
${{K}_{{jj}}} = \int\limits_{{{z}_{{j - 1}}}}^{{{z}_{j}}} {{{K}_{0}}({{z}_{j}},z)} \frac{{z - {{z}_{{j - 1}}}}}{{{{z}_{j}} - {{z}_{{j - 1}}}}}dz.$

Пример деформации изображен на рис. 3 пунктирной линией. Такая деформация законна, так как на данном участке интегрирования подынтегральные функции являются аналитическими.

Рис. 3.

Пример деформации контура интегрирования при вычислении ${{K}_{{jj}}}.$

Для вычисления интеграла, содержащего $K_{0}^{b}(z*,z),$ применялся метод вычитания сингулярности [23]. После регуляризации матричные элементы ${{K}_{{ij}}}$ вычислялись с помощью метода трапеций. На рис. 4 представлен результат итерационного решения (50) и приведено точное решение (44). Параметр регуляризации ${\beta }$ выбирался равным 0.001. Как видно из графиков, итерационное решение сходится медленно (для сходимости потребовалось 10 000 итераций). Это объясняется тем фактом, что с уменьшением номера j существенно снижается точность вычисления диагональных матричных элементов ${{K}_{{jj}}}$ и, соответственно, возникает необходимость в выборе маленького β, обеспечивающего сходимость итерационной процедуры.

Рис. 4.

Итерационное решение для случая переменного импеданса.

Случай постоянного импеданса. При постоянном импедансе уравнение (32) может быть решено с помощью стандартной итерационной процедуры. А именно, будем решать следующую итерационную задачу:

(54)
$U(z) = \sum\limits_{n = 0}^\infty {{{U}^{{(n)}}}} (z),$
(55)
${{U}^{{(0)}}}(z) = 2{{U}^{{{\text{in}}}}}(z) = 2,$
(56)
${{U}^{{(n + 1)}}}(z*) = \int\limits_0^{z{\text{*}}} {{{K}_{0}}} (z*,z){{U}^{{(n)}}}(z)dz,\,\,\,\,n > 0.$

Решение, как и раньше, ищется путем аппроксимации кусочно-линейными функциями (48). Аналогичным образом интегрируются особенности ядра ${{K}_{0}}(z*,z).$

Результат итерационного решения приведен на рис. 5. Как можно видеть из графиков, для достижения приемлемой точности достаточно совершить 10–15 итераций. Следует отметить, что аналогичное число итераций требуется и в случае идеальных граничных условий, который подробно исследовался авторами в [10]. Более того, для случая идеальных граничных условий было показано, что итерационное решение согласуется с решениями, полученными в работах [2] и [9] другими методами.

Рис. 5.

Итерационное решение для случая постоянного импеданса.

5. ЗАКЛЮЧЕНИЕ

В данной работе с помощью метода параболического уравнения была рассмотрена задача дифракции на вытянутом теле вращения с импедансными граничными условиями в случае приосевого падения. С помощью теоремы Грина выведено граничное интегральное уравнение типа Вольтерра. Для случая осевого падения на конус с переменным импедансом (34) строится как точное, так и численное итерационное решение данного уравнения. Для случая постоянного импеданса интегральное уравнение решается численно с помощью метода итераций.

Работа поддержана грантом РНФ 14-22-00042.

Список литературы

  1. Андронов И.В. Дифракция на сильно вытянутом теле вращения // Акуст. журн. 2011. Т. 57. № 2. С. 147–152.

  2. Andronov I.V., Bouche D. Diffraction by a narrow circular cone as by a strongly elongated body // J. Math. Sciences. 2012. V. 185(4). P. 517–522.

  3. Andronov I.V., Bouche D., Duruflé M. High-frequency diffraction of a plane electromagnetic wave by an elongated spheroid // IEEE Trans. on Antennas and Propagation. 2012. V. 60(11). P. 5286–5295.

  4. Kirpichnikova N.Y., Popov M.M. Leontovich-Fock parabolic equation method in the problems of short-wave diffraction by prolate bodies // J. Math. Sci. (N.Y.) 2013. V. 194. № 1. P. 30–43.

  5. Попов М.М., Кирпичникова Н.Я. О проблемах применения параболического уравнения к дифракции на вытянутых телах // Акуст. журн. 2014. Т. 60. № 4. С. 339–346.

  6. Engineer J.C., King J.R., Tew R.H. Diffraction by slender bodies // European J. Applied Mathematics. 1998. V. 9. P. 129–158.

  7. Smyshlyaev V.P. Diffraction by Conical Surfaces at High Frequencies // Wave Motion. 1990. V. 12(4). P. 329–339.

  8. Felsen L.B. Plane wave scattering by small angle cones // IRE Trans. Antennas Propagat. 1957. V. 50. P. 121–129.

  9. Шанин А.В. Асимптотики волнового поля при дифракции на конусе и дифракционный ряд на сфере // Записки научных семинаров ПОМИ. 2011. Т. 393. С. 234–258.

  10. Shanin A.V., Korolkov A.I. Diffraction by an elongated body of revolution. A boundary integral equation based on the parabolic equation // Wave motion. 2019. V. 85. P. 176–190.

  11. Medgyesi-Mitschang L.N., Dau-Sing Wang. Hybrid solutions for large-impedance coated bodies of revolution // IEEE Trans. on Ant. and Prop. 1986. V. AP-34(11). P. 1319–1329.

  12. Кюркчан А.Г., Смирнова Н.И. Математическое моделирование в теории дифракции с использованием априорной информации об аналитических свойствах решения // М.: Медиа Паблишер, 2014.

  13. Лялинов М.А. О дифракции плоской волны на импедансном конусе // Зап. научн. сем. ПОМИ. 2003. Т. 297. С. 191–215.

  14. Bernard J.-M.L., Lyalinov M.A. Electromagnetic scattering by a Smooth Convex Impedance Cone // IMA J. Appl. Math. 2004. V. 69. P. 285–333.

  15. Antipov Y.A. Diffraction of a plane wave by a circular cone with an impedance boundary condition // SIAM J. Appl. Math. 2003. V. 62. № 4. P. 1122–1152.

  16. Лялинов М.А., Полянская С.В. Волновое поле вблизи узкого выпуклого импедансного конуса полностью освещенного плоской падающей волной // Зап. научн. сем. ПОМИ. 2017. Т. 461. С. 195–211.

  17. Фок В.А. Проблемы дифракции и распространения электромагнитных волн. М.: Советское радио, 1970.

  18. Корольков А.И., Шанин А.В. Дифракция высокочастотной волны на импедансном отрезке при скользящем падении // Акуст. журн. 2016. Т. 62. № 3. С. 648–656.

  19. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз, 1963.

  20. Felsen L.B., Electromagnetic properties of wedge and cone surfaces with linearly varying surface impedance // IEEE Trans. Antennas Propag. V. 7(2). P. 231–243.

  21. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979.

  22. Зенкевич О.С. Метод конечных элементов в технике. М.: Мир, 1975.

  23. Kantorovich L.V., Krylov V.I. Approximate methods of higher analysis. Interscience publishers, Inc. New York, 1958.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал