Акустический журнал, 2019, T. 65, № 4, стр. 484-489

ВВЕДЕНИЕ

Для управления характеристиками оптического излучения используются разнообразные физические эффекты. В частности, акустооптические (АО) методы основаны на изменении оптических параметров среды в поле бегущей или стоячей акустической волны. Монографии [1–4] освещают как фундаментальные основы АО-взаимодействия, так и накопленный опыт конструирования разнообразных АО-устройств.

Известно, что использование в акустооптике анизотропных сред существенно расширяет разнообразие возможных геометрий АО-взаимодействия и диапазон их функциональных параметров. При этом необходимо учитывать специфические явления, характерные для волновых процессов в анизотропной среде. Например, оптические и акустические моды могут испытывать снос – отклонение направления переноса энергии от направления волнового вектора. Ярким примером является наиболее распространенный АО-материал – парателлурит (TeO₂), обладающий чрезвычайно большой акустической анизотропией, что вызывает интересные акустические и АО явления [5–13].

Акустический снос для используемой в АО-устройствах на основе парателлурита медленной квазипоперечной моды может составлять десятки градусов. Это создает определенные сложности при теоретическом анализе АО взаимодействия, и влияние акустического сноса остается предметом научного исследования [14–18]. Данная работа предлагает в плосковолновом приближении существенное упрощение рассматриваемой проблемы.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

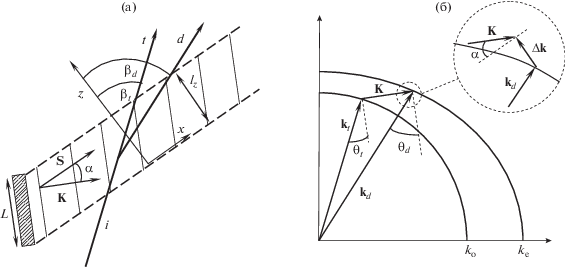
На рис. 1 представлены геометрия и векторная диаграмма возможного варианта АО-взаимодействия в анизотропной среде. Обычно ультразвук возбуждается плоским пъезопреобразователем, нормаль к которому задает направление волнового вектора K. Его модуль равен $K = \frac{\Omega }{{{{v}_{s}}}},$ где Ω – циклическая частота колебаний, ${{v}_{s}}$ – фазовая скорость звука. Вследствие сноса групповая скорость звука S отклонена от волнового вектора K на угол α. Если пренебречь дифракцией, то возмущенная звуком область среды представляет собой плоскопараллельный слой, толщина которого равна l_z = Lcos α, где L – длина преобразователя.

Анализ будем вести в такой системе координат, где ось x направлена вдоль вектора S, ось z – по нормали к слою, ось y – перпендикулярно рисунку. Пусть в плоскости АО дифракции xz на слой падает плоская монохроматическая световая волна (индекс “i”) определенной поляризационной моды. При брэгговском взаимодействии внутри слоя оптическое поле образовано совокупностью двух плоских волн: проходящей (индекс “t”, той же поляризационной моды) и дифрагированной (“d”) волны иной поляризационной моды. При использовании метода связанных волн полагают, что амплитуды оптических волн в пределах возмущенного слоя меняются вдоль оси z.

Пусть k_t и ω_t – волновой вектор и циклическая частота падающей волны, причем ${{k}_{t}} = \frac{{2\pi {{n}_{t}}}}{\lambda },$ где n_t – показатель преломления, λ – длина световой волны в вакууме. Из граничных условий при z = 0 следует, что при брэгговской дифракции в +1 порядок на параметры дифрагированной волны наложены условия: ω_d = ω_t + Ω, k_dx = k_tx + K_x. Так как Ω $ \ll $ ω_t, то длина волны света при дифракции почти не изменится. Зная угловые зависимости показателя преломления n_d и модуля волнового вектора ${{k}_{d}} = \frac{{2\pi {{n}_{d}}}}{\lambda },$ можно рассчитать проекцию волнового вектора k_dz. Эффективность АО дифракции существенно зависит от расстройки АО синхронизма Δk_z = k_tz + K_z – k_dz. Расстройку также можно считать вектором, направленным нормально к слою, т.е. Δk = k_t + K – k_d = Δk_ze_z, где e_z – единичный вектор вдоль оси z. Таким образом, вектор k_d задается такой точкой на поверхности волновых векторов (дифракционной моды), в которую можно попасть, двигаясь из конца вектора k_t + K вдоль вектора e_z. На рис. 1б показано, как определить параметры дифрагированной волны, относящейся к необыкновенной моде. Обычно такую связь выражают через углы падения θ_t и дифракции θ_d, которые составляют волновые векторы световых волн с волновым фронтом звуковой волны.

Характер взаимодействия также зависит от величины АО-связи, которая пропорциональна амплитуде звука. Величину связи характеризует индекс фазовой модуляции ${\nu }$. Наиболее компактно анализ АО взаимодействия выглядит при использовании следующих обозначений [19, 20]: Z = z/l_z, δ = ½Δk_zl_z, $V = \frac{{\nu }}{2}{\text{exp}}\left( {j{{\varphi }_{s}}} \right),$ E_t,d(z) = E_iC_t,d(z), j – мнимая единица. Таким образом, безразмерные параметры имеют следующий смысл: 0 ≤ Z ≤ 1 –длина взаимодействия, δ – расстройка синхронизма, V – комплексный коэффициент АО-связи (φ_s– фаза звуковой волны), C_t,d – амплитуды (E_i – амплитуда падающей волны). Система, описывающая эволюцию взаимодействующих волн, хорошо известна из литературы (с некоторой вариацией обозначений), и в приведенных обозначениях имеет вид:

С учетом граничных условий (C_t(0) = 1, C_d(0) = 0) легко получить аналитическое решение (здесь $W = \sqrt {{{{\left| V \right|}}^{2}} + {{\delta }^{2}}} $):

Эффективность дифракции, т.е. доля энергии, переходящей в дифрагированное излучение на выходе из области взаимодействия (при Z = 1), рассчитывается по формуле $\eta = {{\left| {{{C}_{d}}} \right|}^{2}}$ = = $\frac{{{{{\left| V \right|}}^{2}}}}{{{{{\left| V \right|}}^{2}} + {{\delta }^{2}}}}{{\sin }^{2}}\left( {\sqrt {{{{\left| V \right|}}^{2}} + {{\delta }^{2}}} } \right).$ При условии точного брэгговского синхронизма (δ = 0) это выражение примет вид $\eta = {{\sin }^{2}}\left( {\left| V \right|} \right)$. Вообще говоря, в анизотропной среде выражения (1)–(2) получают такой вид после некоторой параметризации АО-связи, обусловленной различием групповых скоростей взаимодействующих световых мод. Величина связи зависит от параметров акустической и световых волн, а также от фотоупругих свойств среды, и может быть записана в виде

Здесь h – высота преобразователя (размер вдоль оси y), P_s – акустическая мощность, γ_t,d – углы сноса оптических волн, β_t,d = θ_t,d + γ_t,d + α – углы между групповой скоростью световых волн и нормалью к возмущенному слою. Параметр M₂ = = $\frac{{n_{t}^{3}n_{d}^{3}p_{{{\text{eff}}}}^{2}}}{{\rho v_{s}^{3}}},$ где p_eff – эффективная фотоупругая константа для данной геометрии взаимодействующих волн, ρ – плотность материала, называют АО-качеством. В рассматриваемой геометрии угол падения является отрицательным, поэтому при формальном различии по форме выражение (3) фактически идентично выражениям, приведенным в [21, 22].

Пусть ${{p}_{s}} = \frac{{{{P}_{s}}}}{{Lh}}$ – звуковая мощность, излучаемая с единицы площади преобразователя, ${{l}_{t}} = \frac{{L\cos \alpha }}{{\cos {{\beta }_{t}}}}$ и ${{l}_{d}} = \frac{{L\cos \alpha }}{{\cos {{\beta }_{d}}}}$ – протяженность звукового столба, измеренная вдоль групповой скорости проходящего и дифрагированного света соответственно. Для характерных углов оптического сноса можно принять, что $\cos {{\gamma }_{t}}\cos {{\gamma }_{d}} = 1.$ Теперь АО-связь можно написать в наиболее компактном и наглядном виде (аналогичный вид предложен в [23]):

Рассмотрим мысленный эксперимент, состоящий в формальном изменении угла акустического сноса (и длины преобразователя) без изменения остальных акустических свойств. Известно, что проекция вектора S на направление волнового вектора равна фазовой скорости звука v_s, поэтому изменение ΔS будет ортогонально вектору K. Таким образом, ориентация параллельных границ звукового поля в плоскости АО-взаимодействия изменится. При этом вектор расстройки Δk повернется, его модуль изменится.

На рис. 2 показана векторная диаграмма рассматриваемого преобразования. В качестве опорной примем такую геометрию, когда вектор расстройки Δk₀ и волновой вектор дифрагированного света k_d0 параллельны (распространение дифрагированного света по нормали к звуковому слою). Штриховые прямые обозначают касательную и нормаль к поверхности волновых векторов в точке, которую задает вектор k_d0. Видно, что нормаль отклонена от волнового вектора на небольшой угол γ_d0 – явление оптического сноса. Другой вариант геометрии соответствует представленному на рис. 1. Расстройка Δk повернута в плоскости АО-дифракции (плоскость рисунка) на угол φ. Такой же угол между групповыми скоростями звука S и S₀, соответственно угол акустического сноса в опорном варианте α₀= α – φ.

При этом преобразовании вектор k_d отклонится на малый угол ψ от вектора k_d0. Вследствие оптической анизотропии может измениться модуль волнового вектора дифрагированного света. Рассмотрим это изменение в параболическом приближении: ${{k}_{d}} = {{k}_{{d0}}}\left( {1 + {{g}_{1}}\psi + {{g}_{2}}{{\psi }^{2}}} \right).$ В случае монохроматического излучения групповая скорость света направлена по нормали к поверхности волновых векторов. Отсюда следует, что ${{g}_{1}} = - \operatorname{tg} {{\gamma }_{{d0}}}.$ Так как оптическая анизотропия невелика, всегда справедливы оценки ${{g}_{{1,2}}} \ll 1.$

Рассмотрим треугольник на рис. 2, две стороны которого образованы векторами Δk и k_d. Для целей исследования необходимо определить, как зависят величина расстройки Δk и малый угол ψ от Δk₀ и угла поворота φ. Удобно использовать малые параметры ε₀ = Δk₀/k_d0 и ε = Δk/k_d0. Как известно, в случае брэгговского характера АО-взаимодействия существенную эффективность дифракции можно наблюдать при условии Δk_zl_z ≤ 2π, которое можно представить в виде ε ≤ λ/n_dl_z. При типичных значениях λ = 1 мкм, n_d = 2, l_z = 5 мм имеем оценку ε ≤ 1 × 10^–4.

Решение поставленной геометрической задачи можно представить в виде рядов:

Установим, как при рассматриваемом преобразовании меняются безразмерные параметры АО-связи |V| и расстройки δ. Для падающего света обыкновенной поляризации сноса нет, а угол между групповой скоростью и осью z изменится до некоторого угла β_t (см. рис. 1а), составив угол β_t0= β_t + φ в опорном варианте. Для дифрагированного света угол сноса изменится очень незначительно – от γ_d0 до γ_d0 – g₂ψ, соответственно второй угол изменится от β_d0 = γ_d0 до β_d = γ_d0 – g₂ψ + ψ + φ.

Если при рассматриваемом преобразовании пренебречь малым изменением эффективной фотоупругой константы p_eff, то с учетом формул (3)–(4) получим

Анализ этих выражений показывает, что при выполнении условий

указанные безразмерные параметры будут меняться слабо. В частности, в линейном по малому параметру ε₀ приближении имеем

С учетом малости оптической анизотропии (γ_d0, g₂ $ \ll $ 1) при углах φ $ \gg $ γ_d0 можно принять, что $\frac{{\left| V \right|}}{{\left| {{{V}_{0}}} \right|}} = \frac{\delta }{{{{\delta }_{0}}}}$ = $1 + \frac{{{{\varepsilon }_{0}}}}{2}{{\operatorname{tg} }^{2}}\varphi + ...,$ $\psi = {{\varepsilon }_{0}}\operatorname{tg} \varphi + ....$ Отсюда следует, что параметры |V| и δ инвариантны при условии ${{\varepsilon }_{0}}{{\operatorname{tg} }^{2}}\varphi \ll 2,$ которое выполняется в большом диапазоне углов. Например, при ε₀ ≤ 1 × 10^–4 и φ ≤ 80° имеем ${{\varepsilon }_{0}}{{\operatorname{tg} }^{2}}\varphi \leqslant 3.2 \times {{10}^{{ - 3}}}.$

Как следует из (1)–(2), при рассматриваемом преобразовании с наложенными условиями (5) результат АО-дифракции останется практически неизменным (но дифрагированный свет отклонится на малый угол ψ). Поэтому сохранятся такие важные характеристики, как ширина полосы пропускания акустических частот или оптических длин волн, доступный диапазон углов падения и др.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Рассмотрим трактовку условий (5). При формальном изменении только угла акустического сноса режим работы преобразователя не изменится (т.к. не меняется акустический импеданс), поэтому сохранится излучаемая акустическая мощность P_s = p_sLh. Поток энергии распространяется со скоростью S перпендикулярно площадке размером h × Lcosα, при этом плотность акустической энергии пропорциональна квадрату амплитуды звуковой волны. Так как Scosα = ${{v}_{s}},$ то первое условие означает, что амплитуда звуковой волны не меняется при преобразовании (при этом излучаемая мощность пропорциональна длине преобразователя: P_s ~ L). Второе условие можно трактовать как сохранение размера звукового столба вдоль групповой скорости проходящего света: l_t0 = l_t, где ${{l}_{t}} = \frac{{L\cos \alpha }}{{\cos {{\beta }_{t}}}},$ ${{l}_{{t0}}} = \frac{{{{L}_{0}}\cos \left( {\alpha - \varphi } \right)}}{{\cos \left( {{{\beta }_{t}} + \varphi } \right)}}.$ Наконец, последнее равенство имеет аналогичный смысл для дифрагированного света (l_d0 = l_d), если пренебречь малым изменением направления его распространения. Для АО-связи эти условия очевидны при анализе выражения (3a).

Полученные выражения показывают, что результат АО-дифракции не меняется при значительном отклонении от опорной геометрии, поэтому он останется инвариантным для любых геометрий в этом диапазоне. Существенное искажение возможно, только когда падающий или дифрагированный свет пересекают акустический столб почти касательно.

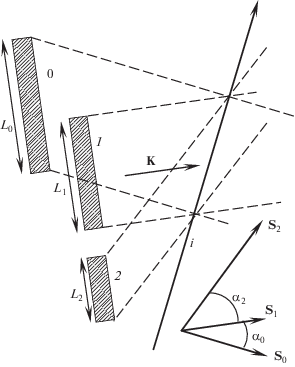
Обычно угол между падающим и дифрагированным светом мал, поэтому l_t ≈ l_d, β_t ≈ β_d. В этом случае эквивалентны такие геометрии, при которых остается неизменным расстояние вдоль групповой скорости падающего света. На рис. 3 показаны варианты такого преобразования. Вариант “0” – нормальное падение света на акустический слой, что примерно (с учетом соотношения K $ \ll $ k_t,d) соответствует обозначениям с индексом “0” на рис. 2. При варианте “1” звук распространяется без сноса (угол α₁ = 0), в случае “2” снос очень большой. Во всех случаях волновой вектор K направлен по нормали к преобразователю, в отличие от векторов групповой скорости S_0,2. При этом $\frac{{{{P}_{{s0}}}}}{{{{L}_{0}}}} = \frac{{{{P}_{{s1}}}}}{{{{L}_{1}}}} = \frac{{{{P}_{{s2}}}}}{{{{L}_{2}}}}.$

Рассмотрим качественно возможность преобразования указанного типа при переходе от плосковолнового к пучковому приближению. Учет дифракционного искажения акустического пучка, обусловленного ограниченностью размера преобразователя, приводит к сложной структуре акустического поля. В этом случае профиль звукового поля вдоль светового пучка зависит как от размера преобразователя, так и от расстояния от него до места входа пучка. Исходя из результатов работ [24, 25], можно предположить, что в пределах ближней зоны преобразователя такое преобразование допустимо. При рассмотрении пучков света мы считаем их наборами плоских волн в некотором условном угловом диапазоне. Можно предположить, что если в пределах совокупности плоских волн, несущих основной поток энергии каждого из световых пучков, выполняется условие ${{\varepsilon }_{0}}{{\operatorname{tg} }^{2}}\varphi \ll 2$ (фактически ${{\varepsilon }_{0}}{{\operatorname{tg} }^{2}}{{\beta }_{t}} \ll 2$), преобразование также допустимо.

Рассмотренная инвариантность позволяет упростить теоретический анализ АО-взаимодействия в некоторых конкретных случаях. Например, при анализе “поперечного” АО-взаимодействия можно выбрать эквивалентный столб, не имеющий сноса. В случае многочастотной АО-фильтрации удобно перейти к такой конфигурации, когда границы столба параллельны фронту звуковой волны [19, 20].

ЗАКЛЮЧЕНИЕ

1. В плосковолновом приближении получены выражения, определяющие результат брэгговского АО-взаимодействия в анизотропной среде при формальном изменении акустического сноса в плоскости АО-дифракции и длины преобразователя.

2. Сформулировано условие, при котором результат АО-дифракции практически инвариантен в широком диапазоне углов акустического сноса. Его геометрическая трактовка состоит в неизменности расстояния, проходимого падающим лучом света в звуковом поле при совместном изменении угла акустического сноса в плоскости АО-взаимодействия и ширины акустического столба. Исключением является такая геометрия, когда падающая или дифрагированная световая волна пересекает звуковой столб почти касательно.

3. Рассмотренная инвариантность позволяет в некоторых случаях упростить теоретический анализ АО-взаимодействия, выбрав в качестве области взаимодействия эквивалентный столб с иным акустическим сносом.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 16-02-00124-a).