Акустический журнал, 2019, T. 65, № 6, стр. 847-852

Настоящая статья тесно связана с работой [1] и фактически является ее продолжением. Поскольку статья [1] по техническим причинам была опубликована только на русском языке, мы вынуждены здесь повторить основные идеи и факты, объясняющие общую постановку задачи. Без такого введения англоязычную версию настоящей статьи будет трудно понять.

Как известно, метод аускультации (выслушивания) сердца используется в медицине более 200 лет и до сих пор сохраняет свою актуальность. Например, при остром инфаркте миокарда может выслушиваться шум трения перикарда. Этот звук свидетельствует о перикардите (воспалении наружной оболочки сердца). Однако, эхокардиография еще не способна выявить воспаление сердечной сорочки, поскольку патологический процесс находится на ранней стадии. Важным примером служит опасное заболевание – легочная гипертензия. Если давление в легочной артерии повышено, то врач при аускультации над легочной артерией может обнаружить усиление второго тона сердца. При этом эхокардиография также не всегда позволяет оценить давление в легочной артерии. Поэтому изучение формы и спектра акустических сигналов, выслушиваемых при аускультации, до сих пор сохраняет важное значение. Результаты физического исследования позволяют лучше понять основы весьма простого и зачастую единственного информативного метода клинической диагностики.

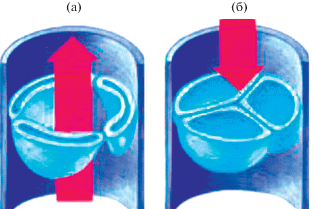
Ранее нами была предложена [1] простая модель работы полулунного клапана сердца с целью оценки спектра акустических колебаний, которые возникают при его закрытии. Был проведен теоретический анализ процесса схлопывания упругих створок легочного клапана под действием перепада давления крови в легочной артерии и правом желудочке. Показано, что при учете вязкости крови скорость движения створок ограничена, и время схлопывания имеет конечное значение. Однако оценки проводились на основе теории, которая не учитывала процесса наполнения полулунных створок клапана кровью. При учете этого процесса, иллюстрированного на рис. 1, масса клапана должна непрерывно расти вплоть до момента его схлопывания.

Чтобы включить этот эффект в предложенную ранее математическую модель, обобщим уравнение (3) работы [1] следующим образом:

Здесь $X$ – это половина ширины щели между створками клапана, $R$ – половина расстояния между створками на выходе в правый желудочек, ${{p}_{1}} - {{p}_{3}}$ – перепад давления. Далее, обозначено

Здесь $m$ – масса одной створки клапана, приходящаяся на единицу площади ее поверхности, ${{m}_{0}}$ – исходная масса (до заполнения кровью).

С учетом введенных обозначений уравнение (1) примет вид:

Видно, что при $f\left( X \right) \equiv 1$ уравнение (3) переходит в уравнение (5) работы [1].

Уравнение (3) удается один раз проинтегрировать, причем в общем виде – для произвольной функции $f\left( X \right).$ Считая $\dot {X}$ = $\dot {X}\left( X \right),$ приведем уравнение (3) к следующей форме:

Интегрируя это уравнение, найдем

Заметим, что при $f\left( X \right) \equiv 1$ из уравнения (5) следует результат (7) из статьи [1]:

В формуле (6) выполнены очевидные условия:

Время схлопывания створок, полученное из решения (6), совпадает с результатом (8) статьи [1]:

Вернемся теперь к общей форме модифицированной модели (5). Чтобы проинтегрировать модельное уравнение во второй раз, нужно разумно подобрать функцию $f\left( X \right).$ В качестве возможной формы положим

Выбор зависимости $f\left( X \right)$ в форме (9) позволяет проанализировать качественно процесс схлопывания створок клапана. Для получения более точных количественных оценок функции $f\left( X \right)$ следует провести анализ процесса заполнения створок клапана кровью с учетом их геометрических размеров. В начальный момент времени, когда $X\left( {t = 0} \right)$ = ${{X}_{0}},$ функция $f$ равна единице. В момент схлопывания, когда $X\left( {t = {{t}_{0}}} \right)$ = 0, имеем $f = F > 1.$ Подставляя (9) в уравнение (5), получим:

Вычислим интеграл в правой части (10). Обозначая $Z$ = ${X \mathord{\left/ {\vphantom {X {{{X}_{0}}}}} \right. \kern-0em} {{{X}_{0}}}},$ запишем

Интегрируем это уравнение:

Время схлопывания отсюда равно:

Интегралы (12), (13) довольно сложные и выражаются через эллиптические интегралы первого и второго рода. При необходимости можно сосчитать их численно. Это будет удобнее, чем пользоваться табулированными значениями специальных функций. Интеграл (12) вычисляется довольно просто при большом росте массы, т.е. при $F \gg 1,$ $\gamma \approx 1.$ В этом случае формула (12) примет вид:

Отсюда находим время схлопывания, полагая $X\left( {t = {{t}_{0}}} \right) = 0{\text{:}}$

Сравнивая (15) со временем схлопывания при отсутствии увеличения массы клапана ($F = 1$)

найдем простую связь между старым и новым результатами:

Видно, что время увеличивается примерно в 0.7$\sqrt F $ раз. Например, при стократном росте массы время затягивается в 7 раз. Этот факт нужно учесть при уточнении численных оценок, приведенных в работе [1]. Напомним, что там время схлопывания оценивалось величиной от единиц миллисекунд до сотых долей секунды.

Перейдем теперь ко второй части настоящей статьи, в которой будут рассмотрены упругие колебания уже закрывшегося клапана. Обсудим содержание предлагаемой модели.

Звуки, прослушиваемые при закрытии сердечного клапана, связаны с колебаниями как его створок, так и стенок легочной артерии и окружающей жидкости (крови). Простейшей моделью этой сложной колебательной системы может служить упругая пластинка, погруженная в жидкость и возбуждаемая импульсным силовым воздействием со стороны смыкающихся створок клапана [1]. Как известно [2], изгибные вынужденные колебания тонкой плоскопараллельной пластинки (мембраны), лежащей в “горизонтальной” плоскости $(y,\,\,z)$ декартовой системы координат, описываются следующим уравнением:

Здесь $\varsigma $ – смещение поверхности пластинки вдоль “вертикальной” оси x, которая ортогональна плоскости пластинки. Считаем $\varsigma = \varsigma (у,t),$ т.е. зависимостью от координаты $\,z$ пренебрегаем. Зависимости силового воздействия от времени и координаты описываются функциями $Q\left( t \right)$ и $Y\left( y \right).$ В уравнении (18) присутствует член со второй производной (по координате $y$), коэффициент $T$ при котором есть сила натяжения на единицу длины края пластинки. Коэффициент при четвертой производной D = ${{E{{h}^{3}}} \mathord{\left/ {\vphantom {{E{{h}^{3}}} {12\left( {1 - {{\sigma }^{2}}} \right)}}} \right. \kern-0em} {12\left( {1 - {{\sigma }^{2}}} \right)}}$ выражается через модуль Юнга $E$ и коэффициент Пуассона σ. Плотность пластинки и ее толщина обозначены как $\rho $ и h. Для пластинки, окруженной жидкостью, математическую модель (18) следует модифицировать. Известно, что колебания тела в жидкости сопровождаются появлением присоединенной (“соколеблющейся”) массы и силы сопротивления (реакции со стороны жидкости), действующей на тело [2]. Поэтому уравнение (18) примет вид

Здесь $m* = \rho h + m{\text{'}},$ где m' – присоединенная масса, приходящаяся на единицу площади поверхности пластинки, ${{F}_{r}}$ – сила сопротивления. Вычисление величин m' и ${{F}_{r}}$ – сложная задача, которую удается решить для немногих тел канонической формы. Например, для шара, совершающего малые колебания на низких частотах в несжимаемой жидкости, присоединенная масса равна половине массы вытесненной шаром жидкости (см. [2], параграф 11). Для силы сопротивления при тех же ограничениях получается формула Стокса: ${{F}_{r}} = 6\pi \eta ru$ (см. [2], параграф 24). Здесь $\eta $ – вязкость жидкости, $u$ – скорость движения тела, $r$ – радиус шара. Основываясь на этих фактах, положим в уравнении (19)

Здесь ${{\rho }_{b}}$ – плотность крови, $k$ – волновое число рассматриваемой моды колебаний пластины. Для основной моды, изображенной на рис. 2, распределение смещений дается функцией

где $A(t)$ – амплитуда колебаний, $l$ – ширина пластинки. Коэффициенты $\alpha ,\,\,\beta $ – это числа порядка единицы; для колеблющихся тел сложной формы их вычислить не удается. Таким образом, уравнение (19) примет вид:

Правая часть (22) конкретизирована так, чтобы происходило возбуждение колебаний на основной моде (21). Для рассматриваемой основной моды выполняются следующие граничные условия: один край пластинки закреплен, т.е. $\varsigma \left( {y = 0} \right) = 0,$ а второй – свободен, для него производная на другом конце $\frac{{\partial \varsigma }}{{\partial y}}\left( {y = l} \right) = 0.$

Подставляя (21) в (22), для изменения амплитуды во времени найдем

Рассмотрим вначале простейший случай ‑ свободные колебания пластинки. Решение уравнения (23) имеет вид:

При условии

реализуется процесс в виде затухающих колебаний. Их частота определяется выражением

Если возбуждение происходит не на основной, а на высшей моде, в формулах (21)–(26) следует заменить

Очевидно, что ${{k}_{n}} > {{k}_{0}}.$ Поэтому, как следует из формул (26) и (24), частота колебаний и затухание увеличиваются с ростом номера моды. Если возбуждается срaзу несколько мод, “долгоживущими” оказываются моды с более низким частотами (меньшими значениями числа $n$), и характерная частота колебаний с ростом времени уменьшается.

Проведем численные оценки. Начнем с частоты (26). Нетрудно видеть, что влияние вязкости оказывается пренебрежимо малым. Учтем, что

При этом формула (26) примет вид

Приравнивая силу, действующую на поверхность мембраны, $p{{l}^{2}},$ силе, действующей по ее периметру, $T4l,$ выразим растягивающую силу через давление: $T = {{pl} \mathord{\left/ {\vphantom {{pl} 4}} \right. \kern-0em} 4}.$ В момент закрытия клапана перепад давления обычно мал и составляет порядка 1 мм.рт.ст. или примерно 3 × 10² дин/см². Оценим теперь член $D{{k}^{2}}.$ Полагая модуль Юнга $E$ = 10–20 кПа, $\sigma = 0.5,$ $l$ = 1 см, $h$ = 0.1 см, найдем Dk² ≈ 0.55 × 10² дин/см². Это величина того же порядка, что и натяжение T. Таким образом, натяжение, связанное с перепадом давления в несколько мм.рт.ст., имеет определяющее значение. Поскольку плотности ткани и крови примерно равны 1 г/см³, толщина створки клапана $h$ = 0.1 см, а коэффициент α ∼ 1, то частота колебаний должна находиться в диапазоне ν ∼ 10–100 Гц. Коэффициент затухания δ, рассчитанный по формуле (24) с учетом только вязкого трения, оказывается слишком малым по сравнению с измеряемыми значениями. Поэтому сила реакции вызвана, по-видимому, гидравлическим сопротивлением. При этом уравнение (19) следует модифицировать следующим образом:

Уравнение (30) является нелинейным и решается гораздо сложнее предыдущей линейной задачи. Оно содержит квадратично-кубичную нелинейность, изучение которой систематически проводилось в последние годы [3]. В этом уравнении $\chi $ – коэффициент гидравлического сопротивления, зависящий от формы обтекаемого тела и определяемый из таблиц [4], построенных на основании многочисленных экспериментальных данных.

Ищем решение (30) в форме, обобщающей представление (21):

Здесь $A\left( t \right)$ – комплексная амплитуда, звездочка – знак комплексного сопряжения. Подставляя (31) в (30), приведем уравнение к виду:

При анализе свободных колебаний правую часть (32) положим равной нулю. Найдем вначале нелинейный закон дисперсии, для чего ищем решение (32) в виде

Искомый закон дисперсии получается таким:

Для небольших амплитуд колебаний найдем

Отсюда видим, что частота колебаний и коэффициент затухания равны:

Таким образом, обе важнейшие характеристики – частота колебаний створки клапана и коэффициент затухания этих колебаний – увеличиваются с ростом натяжения как $\sqrt T .$ Увеличение частоты есть важный признак, свидетельствующий о повышении давления в легочной артерии. Затухание колебаний растет с увеличением амплитуды, то есть представляет собой нелинейный процесс.

Функция $Q\left( t \right)$ в правой части уравнения (32) связана со схлопыванием створок клапана и описывает импульсный, то есть широкополосный сигнал, содержащий множество частот. Поэтому колебания мембраны происходят сразу на нескольких модах, то есть являются многомодовыми. При одновременном возбуждении нескольких мод “долгоживущими” оказываются те из них, частота которых мала (то есть с меньшими значениями числа $n$ (27)). Поэтому характерная частота колебаний с ростом времени уменьшается.

Этот процесс проиллюстрирован на рис. 3. При малых значениях времени отдельные моды (штриховые кривые на рис. 3) затухают слабо, а их сумма (сплошная кривая) содержит все частоты этих мод. При больших значениях времени амплитуды высших мод затухают, поэтому колебания мембраны происходят на основной моде с амплитудой ${{A}_{1}}$. Коэффициент затухания, оцененный по формуле (36), по порядку величины равен δ ∼ (10¹–10²)|A|, т.е. колебания мембраны должны затухать за времена порядка десятых-сотых долей секунды, что соответствует результатам измерений.

Перейдем теперь к отысканию точного решения нелинейного уравнения (32) для собственных колебаний. Удобно записать его в упрощенных обозначениях:

Еще проще это уравнение будет в переменных

Уравнение (37) примет вид:

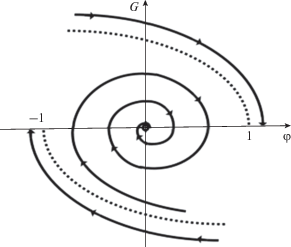
Заметим, что качественное поведение решений этого уравнения хорошо исследовано (см., например, [5], Гл. 8, параграф 9). Считаем первую производную по времени функцией от φ. Обозначим эту производную буквой $G\left( \varphi \right)$ и сведем (39) к уравнению первого порядка:

Решение уравнения (40) имеет вид

Здесь ${{D}_{1}},\,\,{{D}_{2}}$ – константы интегрирования. При значениях ${{D}_{1}} = {{D}_{2}} = - 2$ получаем изолированную особую точку $G = 0,$ $\varphi = 0$ на фазовой плоскости. При значениях ${{D}_{1}} = {{D}_{2}}$ = 0 получаем уравнения кривых

В совокупности две ветви (42) образуют сепаратрису, внутри которой лежат кривые, “скручивающиеся” по спирали к особой точке в начале координат. Сепаратриса изображена на рис. 4 штриховой линией. Сплошные кривые – это фазовые траектории. Та “спиральная” траектория, которая лежит внутри сепаратрисы, соответствует затухающему колебанию. Траектории, которые лежат вне сепаратрисы, берут начало при $\varphi \to - \infty ,$ $G > 0$ или при $\varphi \to \infty ,$ $G < 0.$ Стрелками отмечено направление движения изображающей точки. В работе [6] дана оценка интервала начальных значений скорости $G,$ при которых осцилляции, прежде чем затухнуть, совершают заданное число “переколебаний” (см. Гл. 3, параграф 11). Иными словами, указан интервал значений $G,$ для которых фазовая траектория совершит заданное число оборотов вокруг начала координат на фазовой плоскости (см. рис. 4).

В заключение укажем, что предложенная в работе простая модель содержит три основных следствия.

1. Прослушиваемый при аускультации тон представляет собой цуг, состоящий из нескольких “осцилляторных” квазипериодов. Конечная длительность цуга обусловлена, скорее всего, гидравлическим сопротивлением колеблющихся створок сердечного клапана, а не вязкостью крови, как можно было предполагать заранее.

2. Оба диагностически значимых параметра – частота осцилляций и время их затухания – увеличиваются с ростом перепада давления, что, возможно, свидетельствует о гипертензии.

3. Оба рассмотренных процесса – захлопывание створок клапана и возбуждаемые им колебания – являются нелинейными. Это означает, что частотный спектр колебаний содержит множество частот, а коэффициент затухания и средняя частота зависят от амплитуды колебаний. С увеличением времени (от начала к концу цуга) средняя частота уменьшается.

Работа выполнена при финансовой поддержке гранта РФФИ 18-02-00736.