Акустический журнал, 2020, T. 66, № 2, стр. 170-180

Пеленгование векторно-скалярным приемником в поле анизотропной помехи

С. Г. Михайлов^a, b, *

^a Институт общей физики им. А.М. Прохорова РАН
119991 Москва, ул. Вавилова 38, Россия

^b Московский государственный университет им. М.В. Ломоносова, физический факультет
Москва, Россия

^* E-mail: s.mikhailov@mail.ru

Поступила в редакцию 27.02.2019
После доработки 04.09.2019
Принята к публикации 29.10.2019

DOI: 10.31857/S0320791920020057

Полный текст (PDF)

Аннотация

На основе многомерного пуассоновского процесса построена математическая модель анизотропного акустического поля. Установлена связь вероятностных характеристик процесса и угловой плотности акустического поля. Показано, что дисперсии и функции взаимной корреляции пульсаций давления и компонент колебательной скорости зависят только от постоянной составляющей и коэффициентов первой и второй гармоник разложения угловой плотности в ряд Фурье. Найдена связь между значимыми для пеленгования параметрами анизотропии поля помехи и экспериментально измеряемыми величинами. Показана связь результатов пеленгования с параметрами анизотропии поля помехи для нескольких алгоритмов.

Ключевые слова: векторно-фазовые методы, векторно-скалярный приемник, шумы океана, анизотропия, пеленгование, угловая плотность акустического поля

ВВЕДЕНИЕ

Рассмотрим возможность определения горизонтального направления на источник акустического излучения с помощью комбинированного векторно-скалярного приемника (ВСП). Такой приемник включает в себя ненаправленный приемник давления (скалярная часть) и два или три приемных канала, имеющих взаимно перпендикулярные дипольные характеристики направленности (векторная часть). Для определенности будем считать, что выходные сигналы каналов векторной части пропорциональны компонентам колебательной скорости. Фазовые центры всех приемных каналов считаются совпадающими. ВСП обладает следующей особенностью: характеристики направленности не только канала давления, но и каналов его векторной части близки к теоретическим и практически неизменны в широком диапазоне частот, достигающем двух-трех декад [1]. Это свойство позволяет анализировать широкополосные сигналы, принятые приемником, считая характеристики направленности всех его каналов не зависящими от частоты.

Положим, что волна распространяется в горизонтальной плоскости xОy, а среда однородна и изотропна. Если монопольный точечный источник звуковой волны находится в направлении ${{\varphi }_{S}}$ ($0 \leqslant {{\varphi }_{S}} < 2\pi $), а других источников нет, в точке начала координат компоненты колебательной скорости частиц среды $V(t)$ будут равны ${{V}_{x}}(t) = V(t)\cos {{\varphi }_{S}}$ и ${{V}_{y}}(t) = V(t)\sin {{\varphi }_{S}}.$ Решая обратную задачу по измеренным значениям компонент колебательной скорости, практически в любой момент времени (за исключением моментов, когда $V(t) = 0$) можно установить, что источник лежит на прямой, проходящей через начало координат под углом ${{\varphi }_{d}},$ который вычисляется по формуле:

(1)

$\begin{gathered} {{\varphi }_{d}} = {\text{arcctg}}\frac{{{{V}_{x}}(t)}}{{{{V}_{y}}(t)}},\,\,\,\,0 \leqslant {{\varphi }_{d}} < \pi , \\ {\text{и}}\,\,\,\,{{\varphi }_{S}} = \left\{ \begin{gathered} {{\varphi }_{d}},\,\,\,\,\,\,\,\,\,\,\,0 \leqslant {{\varphi }_{S}} < \pi , \hfill \\ {{\varphi }_{d}} + \pi ,\,\,\,\,\pi \leqslant {{\varphi }_{S}} < 2\pi . \hfill \\ \end{gathered} \right. \\ \end{gathered} $

Если одновременно с компонентами колебательной скорости измеряются пульсации давления $P(t),$ можно рассчитать мгновенные значения компонент вектора Умова ${{J}_{x}}(t) = P(t){\kern 1pt} {\kern 1pt} {{V}_{x}}(t)$ и ${{J}_{y}}(t) = P(t){\kern 1pt} {{V}_{y}}(t),$ а затем однозначно определить направление на источник:

(2)

${{\varphi }_{J}} = \left\{ \begin{gathered} \operatorname{arcctg} \left[ {{{{{J}_{x}}(t)} \mathord{\left/ {\vphantom {{{{J}_{x}}(t)} {{{J}_{y}}(t)}}} \right. \kern-0em} {{{J}_{y}}(t)}}} \right],\,\,\,\,{{J}_{y}}(t) > 0, \hfill \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{J}_{y}}(t) = 0,\,\,\,\,{{J}_{x}}(t) \ne 0, \hfill \\ \operatorname{arcctg} \left[ {{{{{J}_{x}}(t)} \mathord{\left/ {\vphantom {{{{J}_{x}}(t)} {{{J}_{y}}(t)}}} \right. \kern-0em} {{{J}_{y}}(t)}}} \right] + \pi ,\,\,\,\,{{J}_{y}}(t) < 0, \hfill \\ \end{gathered} \right.$

$0 \leqslant {{\varphi }_{J}} < 2\pi $ и ${{\varphi }_{S}} = {{\varphi }_{J}}.$ В присутствии помехи ситуация усложняется. В качестве помехи будем рассматривать морской шум. Для пеленгования наиболее важной является анизотропия в горизонтальной плоскости. В прибрежных районах она проявляется благодаря шуму прибоя. Натурные измерения в открытом океане [2] показали, что при формировании регулярного волнения в поле поверхностного шума существует горизонтальный поток акустической энергии, имеющий направление, близкое к направлению распространения поверхностных волн. Более поздние теоретические исследования [3, 4] привели авторов к выводу, что направленность шумового поля, формирующегося при распространении звука под взволнованной поверхностью, может оказаться существенной в результате его избирательного рассеяния. При этом направленность остаточного поля симметрична и имеет два максимума в направлениях, ортогональных к ветру. Кроме того, причинами горизонтально анизотропного шума могут быть различные явления, источники которых расположены несимметрично относительно точки приема: полосовой дождь, шквал, судоходство, технические и биологические шумы и т.п.

В традиционных моделях [5–10] шумовое поле рассматривается как результат сложения гармонических волн, излучаемых точечными монопольными или дипольными источниками с равными среднеквадратическими интенсивностями, но со случайными фазами. Источники равномерно располагаются в объеме, на поверхности сферы, в конусе, на плоскости или прямой. Существуют примеры теоретического анализа, показывающие, что в рамках некоторых из этих моделей помехоустойчивость измерений [8] и результат пеленгования [10] при применении ВСП зависят от характера анизотропии помехи и тем самым указывают на необходимость ее учета при пеленговании слабого источника.

В работе [11] акустическое поле помехи задано произвольной функцией угловых координат Ω и случайной функцией времени ξ(Ω,t). Показано, что помехоподавление приемника потока акустической мощности зависит от отношения p/q, где (упрощено до плоского случая) $p = \int_{ - {\pi }/2}^{{\pi }/2} {\overline {{{{\xi }}^{{\text{2}}}}(\varphi ,t)} } \cos \varphi {\kern 1pt} d\varphi $ и $q = \int_{ - {\pi }/2}^{{\pi }/2} {\overline {{{{\xi }}^{{\text{2}}}}( - {\kern 1pt} \varphi ,t)} } \cos \varphi d\varphi $ – коэффициенты, характеризующие потоки акустической мощности в противоположных направлениях, черта сверху обозначает усреднение по времени, cosφ – характеристика направленности приемного канала колебательной скорости. В работе [12] для задания анизотропии в горизонтальной плоскости использована однопараметрическая функция. Варьирование параметра а позволяет значительно изменять ее вид, но только по отношению к ширине и положению единственного максимума, что с учетом результатов работ [3, 4] представляется недостаточным. Кроме того, результаты расчетов, выполненных в работах [11, 12], не показывают способа экспериментального определения значимых параметров анизотропии (которыми являются отношение p/q в [11] и параметр a в [12]) с помощью одиночного ВСП. Последнее представляется важным, так как применение совместно с ВСП антенны с высоким угловым разрешением только для оценки условий работы приемника маловероятно.

Многообразие источников морских шумов, различие присущих каждому из них пространственных свойств, возможность их появления в различных сочетаниях может приводить к многочисленным вариантам направленности суммарного шумового поля. Поэтому для анализа потенциальной возможности пеленгования источника на фоне анизотропной помехи представляется более подходящим применение модели, в которой подобно [11, 12] пространственные свойства шумового поля задаются с помощью достаточно произвольной функции угловых координат, а затем выясняются ее параметры, в наибольшей степени влияющие на результат пеленгования. Если таких параметров окажется немного, появится удобный способ описания анизотропии. Представляется также нужным указать способ измерения этих параметров, который может быть реализован в условиях эксперимента с одиночным ВСП.

МОДЕЛЬ АНИЗОТРОПНОГО АКУСТИЧЕСКОГО ПОЛЯ

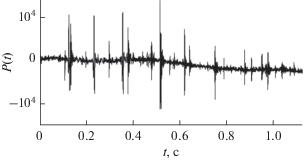
В основе ряда моделей морских шумов лежит представление, что события, заключающиеся в излучении шумов, происходят независимо друг от друга в различных точках водной толщи или на ее поверхности. Будем считать, что некоторые из этих событий порождаются сходными процессами и, возможно, при этом излучаются близкие по форме волны. Такими процессами могут быть: падение капель дождя, разрушение гребней волн, торошение льда, звуки, издаваемые животными одного вида и т.п. Общей особенностью перечисленных процессов является также то, что они создают звуки ограниченной продолжительности. В качестве примера, демонстрирующего возможность существования морского шума, удовлетворяющего перечисленным условиям, на рис. 1 приведен фрагмент записи подводного звукового давления в мелководном районе тропической части Индийского океана.

Рис. 1.

Фрагмент записи подводного шума в мелководном районе тропической части Индийского океана. Масштаб по вертикали – в отсчетах АЦП.

Для построения математической модели воспользуемся результатами исследований случайных процессов, основы которых были заложены при изучении закономерностей броуновского движения [13], а затем развивались применительно к дробовому шуму и другим случайным процессам [14–16].

Рассмотрим некоторые свойства акустического поля, создаваемого в безграничном однородном и изотропном пространстве источниками, находящимися на окружности достаточно большого радиуса R, лежащей в плоскости xОy. Такое приближение допустимо, поскольку мы будем интересоваться только направлением на источник, а не расстоянием до него. Пусть поле формируется в результате последовательности событий, заключающихся в том, что в случайные моменты времени ${{t}_{i}}$ в точках, лежащих на этой окружности под углом ${{\varphi }_{i}}$, происходит кратковременное изменение давления в среде ${{p}_{i}}(t) = {{e}_{i}}g({{\varphi }_{i}})s(t - {{t}_{i}}).$ Здесь e и φ – независимые случайные величины, $g(\varphi )$ – неслучайная функция величины $\varphi $, $s(t)$ – ограниченный во времени импульс, $s(t - {{t}_{i}}) = 0,$ если $t - {{t}_{i}} < {{ - {\theta }} \mathord{\left/ {\vphantom {{ - {\theta }} 2}} \right. \kern-0em} 2}$ и ${{\theta } \mathord{\left/ {\vphantom {{\theta } 2}} \right. \kern-0em} 2} < t - {{t}_{i}},$ ${\theta }$ – длительность импульса. Соответствующее такому случайному процессу давление в центре окружности равно:

${{P}_{\Sigma }}(t) = \frac{1}{R}\sum\limits_{i = - \infty }^\infty {{{p}_{i}}\left( {t{\kern 1pt} '\,\, - {{t}_{i}}} \right)} ,$

где $t{\kern 1pt} ' = t - {R \mathord{\left/ {\vphantom {R c}} \right. \kern-0em} c},$ с – скорость звука в среде, а компоненты колебательной скорости

(3)

$\begin{gathered} {{V}_{x}}(t) = \frac{1}{{{\rho }{\kern 1pt} cR}}\sum\limits_{i = - \infty }^\infty {{{p}_{i}}\left( {t{\kern 1pt} '\,\, - {{t}_{i}}} \right)\cos {{\varphi }_{i}}} , \\ {{V}_{y}}(t) = \frac{1}{{{\rho }{\kern 1pt} cR}}\sum\limits_{i = - \infty }^\infty {{{p}_{i}}\left( {t{\kern 1pt} '\,\, - {{t}_{i}}} \right)\sin {{\varphi }_{i}}} , \\ \end{gathered} $

ρ – плотность среды. В качестве допустимого упрощения принято, что связь между скоростью и давлением во всем рассматриваемом частотном диапазоне соответствует плоской волне. Далее будем рассматривать случайный процесс, имеющий нормированные составляющие:

(4)

$\begin{gathered} P(t) = R{{P}_{\Sigma }}(t),\,\,\,\,X(t) = \rho cR{{V}_{x}}(t), \\ Y(t) = \rho cR{{V}_{y}}(t). \\ \end{gathered} $

Таким образом, имеется трехмерный случайный процесс, у которого случайными являются: момент появления импульса ${{t}_{i}}$, его амплитуда e_i и угол ${{\varphi }_{i}}$. Зависимость от случайного угла ${{\varphi }_{i}}$ выражается неслучайными функциями $g({{\varphi }_{i}}),$ $g({{\varphi }_{i}})\cos {{\varphi }_{i}}$ и $g({{\varphi }_{i}})\sin {{\varphi }_{i}}.$ Вторые центральные моменты этого случайного процесса, в том числе смешанные (т.е. дисперсии и функции взаимной корреляции), можно найти, считая процесс пуассоновским [14] (с. 249) и повторяя процедуру, изложенную в [15] (с. 58–60) для одномерного процесса. Совместная трехмерная характеристическая функция процесса (4) будет иметь следующий вид:

(5)

$\begin{gathered} \psi ({{u}_{1}},{{u}_{2}},{{u}_{3}}) = \exp \left( {q\int\limits_{ - \infty }^\infty {{{f}_{e}}(e)de} \int\limits_0^{2\pi } {{{f}_{\varphi }}(\varphi )d\varphi } } \right. \times \\ \times \,\,\left. {\int\limits_{ - \infty }^\infty {\left\{ {\exp \left[ {i{\kern 1pt} e\sum\limits_{j = 1}^3 {{{g}_{j}}(\varphi )s(t){{u}_{j}}} } \right] - 1} \right\}dt} } \right). \\ \end{gathered} $

Здесь f_e и f_φ – плотности распределения случайных величин e_i и φ_i, а q – средняя частота появления импульсов, ${{g}_{1}}(\varphi ) = g(\varphi ),$ ${{g}_{2}}(\varphi ) = g(\varphi )\cos \varphi $ и ${{g}_{3}}(\varphi ) = g(\varphi )\sin \varphi .$ В показателе внешней экспоненты в выражении (5) стоит трехмерная кумулянтная функция, в результате дифференцирования которой получаются трехмерные кумулянты ([17], с. 87):

${{\kappa }_{{nkl}}} = {{( - i)}^{{n + k + l}}}{{\left. {\frac{{{{\partial }^{{n + k + l}}}}}{{\partial u_{1}^{n}\partial u_{2}^{k}\partial u_{3}^{l}}}\ln \psi ({{u}_{1}},{{u}_{2}},{{u}_{3}})} \right|}_{{{{u}_{1}} = {{u}_{2}} = {{u}_{3}} = 0}}}$

или

(6)

$\begin{gathered} {{\kappa }_{{nkl}}} = q\int\limits_{ - \infty }^\infty {{{e}^{{n + k + l}}}{{f}_{e}}(e)de} \times \\ \times \,\,\int\limits_0^{2\pi } {{{g}^{{n + k + l}}}(\varphi ){{{\cos }}^{k}}\varphi {{{\sin }}^{l}}\varphi {\kern 1pt} {{f}_{\varphi }}(\varphi )d\varphi } \int\limits_{ - \infty }^\infty {{{s}^{{n + k + l}}}(t)dt} . \\ \end{gathered} $

Величина $n + k + l$ – порядок кумулянта. Кумулянты первого порядка – средние значения, второго – центральные моменты второго порядка, т.е. искомые дисперсии и функции взаимной корреляции процессов P, X, Y. Таким образом, дисперсия пульсаций давления равна:

(7)

$\sigma _{P}^{2} = {{\kappa }_{{200}}} = q\sigma _{e}^{2}\sigma _{s}^{2}\int\limits_0^{2\pi } {{{g}^{2}}(\varphi ){{f}_{\varphi }}(\varphi )d\varphi } .$

Здесь $\sigma _{e}^{2} = \int_{ - \infty }^\infty {{{e}^{2}}{{f}_{e}}(e)de} ,$ $\sigma _{s}^{2} = \int_{ - \infty }^\infty {{{s}^{2}}(t)dt} .$ Так же вычисляются дисперсии компонент колебательной скорости:

$\begin{gathered} \sigma _{X}^{2} = {{\kappa }_{{020}}} = q\sigma _{e}^{2}\sigma _{s}^{2}\int\limits_0^{2\pi } {{{g}^{2}}(\varphi ){{{\cos }}^{2}}\varphi {\kern 1pt} {{f}_{\varphi }}(\varphi )d\varphi } , \\ \sigma _{Y}^{2} = {{\kappa }_{{002}}} = q\sigma _{e}^{2}\sigma _{s}^{2}\int\limits_0^{2\pi } {{{g}^{2}}(\varphi ){{{\sin }}^{2}}\varphi {\kern 1pt} {{f}_{\varphi }}(\varphi )d\varphi } . \\ \end{gathered} $

Из приведенных соотношений вытекает очевидное равенство:

(8)

$\sigma _{X}^{2} + \sigma _{Y}^{2} = \sigma _{P}^{2}.$

Взаимная корреляционная функция компонент колебательной скорости дается формулой:

${{R}_{{XY}}} = {{\kappa }_{{011}}} = q\sigma _{e}^{2}\sigma _{s}^{2}\int\limits_0^{2\pi } {{{g}^{2}}(\varphi )\cos \varphi \sin \varphi {\kern 1pt} {{f}_{\varphi }}(\varphi ){\kern 1pt} d\varphi } ,$

а взаимные корреляционные функции давления и компонент колебательной скорости равны:

$\begin{gathered} {{R}_{{PX}}} = q\sigma _{e}^{2}\sigma _{s}^{2}\int\limits_0^{2\pi } {{{g}^{2}}(\varphi )\cos \varphi {\kern 1pt} {{f}_{\varphi }}(\varphi ){\kern 1pt} d\varphi } , \\ {{R}_{{PY}}} = q\sigma _{e}^{2}\sigma _{s}^{2}\int\limits_0^{2\pi } {{{g}^{2}}(\varphi )\sin \varphi {\kern 1pt} {{f}_{\varphi }}(\varphi ){\kern 1pt} d\varphi } . \\ \end{gathered} $

Будем также пользоваться коэффициентами взаимной корреляции:

${{r}_{{XY}}} = \frac{{{{R}_{{XY}}}}}{{\sqrt {\sigma _{X}^{2}\sigma _{Y}^{2}} }},\,\,\,\,{{r}_{{PX}}} = \frac{{{{R}_{{PX}}}}}{{\sqrt {\sigma _{P}^{2}\sigma _{X}^{2}} }},\,\,\,\,{{r}_{{PY}}} = \frac{{{{R}_{{PY}}}}}{{\sqrt {\sigma _{P}^{2}\sigma _{Y}^{2}} }}.$

Если плотности распределения f_e, и f_φ, а также частота q не зависят от времени (т.е. являются стационарными), то процессы P, X, Y и связи между ними также будут стационарными. Еще одним важным свойством случайных процессов является их принадлежность к классу гауссовых (нормальных) процессов. Для пуассоновских процессов это определяется количеством импульсов, возникающих за время существования одного импульса. Для того чтобы процесс был нормальным, число налагающихся импульсов должно быть велико: $q\theta \gg 1$ ([15], с. 63). Если это условие не выполняется, распределение будет зависеть от формы импульса. Перейти к нормальному распределению можно (при заданной частоте q), увеличивая длительность импульса, что реализуется, например, при применении узкополосной фильтрации.

УГЛОВЫЕ ПЛОТНОСТИ ПОЛЕЙ ПОМЕХИ И СИГНАЛА

Из полученных формул видно, что дисперсии и взаимные корреляционные функции зависят от функции $G(\varphi ) = q\sigma _{e}^{2}\sigma _{s}^{2}{{g}^{2}}(\varphi ){{f}_{\varphi }}(\varphi ),$ которая тем самым полностью определяет свойства нормального процесса (4). Вслед за автором [7] (с. 265) назовем ее угловой плотностью поля. Под анизотропией будем понимать всякое отклонение функции G(φ) от ее среднего значения, равного ${{\int_0^{2\pi } {G(\varphi )d\varphi } } \mathord{\left/ {\vphantom {{\int_0^{2\pi } {G(\varphi )d\varphi } } {2\pi }}} \right. \kern-0em} {2\pi }}.$ На зависимость функции G(φ) от угла влияет как относительная частота попадания импульсов в различные секторы углов (плотность вероятности f_φ(φ)), так и локальная амплитуда импульсов (функция g²(φ)). По конечному результату эти факторы эквивалентны. Из определения функции G(φ) следует, что она является неотрицательной периодической функцией угла φ, а также будем считать, что она обладает всеми необходимыми свойствами, позволяющими применить к ней разложение в ряд Фурье. Коэффициенты ряда вычисляются по формулам:

$\begin{gathered} {{a}_{k}} = \frac{1}{{\pi }}\int\limits_0^{2\pi } {G(\varphi )\cos (k\varphi )d\varphi } ,\,\,\,\,{{b}_{k}} = \frac{1}{{\pi }}\int\limits_0^{2\pi } {G(\varphi )\sin (k\varphi )d\varphi } , \\ k = {\text{ }}0,{\text{ }}1,{\text{ }}2 \ldots \\ \end{gathered} $

Функция $G(\varphi )$ может быть представлена в виде бесконечной суммы:

$\begin{gathered} G(\varphi ) = \frac{{{{a}_{0}}}}{2} + \sum\limits_{k = 1}^\infty {({{a}_{k}}\cos k\varphi + {{b}_{k}}\sin k\varphi } ) = \\ = {{a}_{0}}\left( {\frac{1}{2} + \sum\limits_{k = 1}^\infty {({{{\alpha }}_{k}}\cos k\varphi + {{{\beta }}_{k}}\sin k\varphi } )} \right), \\ \end{gathered} $

где α_k = a_k/a₀ и β_k = b_k/a₀ при k = 1, 2… – нормированные коэффициенты разложения.

Для дальнейшего представляет интерес ситуация, когда поле включает в себя две независимые составляющие – сигнал и помеху:

$\begin{gathered} P(t) = {{P}_{S}}(t) + {{P}_{N}}(t),\,\,\,\,X(t) = {{X}_{S}}(t) + {{X}_{N}}(t), \\ Y(t) = {{Y}_{S}}(t) + {{Y}_{N}}(t). \\ \end{gathered} $

Здесь и далее индекс S указывает на принадлежность переменной полю сигнала, а N – полю помехи. В этом случае угловая плотность поля также будет равна сумме двух составляющих:

$G(\varphi ) = {{G}_{S}}(\varphi ) + {{G}_{N}}(\varphi ).$

Подставив угловую плотность поля помехи ${{G}_{N}}(\varphi )$ в форме разложения в ряд Фурье в формулы для дисперсий давления и компонент колебательной скорости и используя ортогональность синусов и косинусов кратных аргументов на интервале (0, 2π), найдем соответствующие дисперсии:

$\sigma _{{NP}}^{2} = \int\limits_0^{2\pi } {{{G}_{N}}(\varphi )d\varphi } = \pi {{a}_{0}},$

$\begin{gathered} \sigma _{{NX}}^{2} = \int\limits_0^{2\pi } {{{G}_{N}}(\varphi ){{{\cos }}^{2}}\varphi d\varphi } = \frac{\pi }{2}({{a}_{0}} + {{a}_{2}}), \\ \sigma _{{NY}}^{2} = \int\limits_0^{2\pi } {{{G}_{N}}(\varphi ){{{\sin }}^{2}}\varphi d\varphi } = \frac{\pi }{2}({{a}_{0}} - {{a}_{2}}), \\ \end{gathered} $

и взаимные корреляционные функции:

${{R}_{{NXY}}} = \frac{1}{2}\int\limits_0^{2\pi } {{{G}_{N}}(\varphi )\sin 2\varphi d\varphi } = \frac{{\pi {\kern 1pt} {{b}_{2}}}}{2},$

$\begin{gathered} {{R}_{{NPX}}} = \int\limits_0^{2\pi } {{{G}_{N}}(\varphi )\cos \varphi d\varphi } = \pi {{a}_{1}}, \\ {{R}_{{NPY}}} = \int\limits_0^{2\pi } {{{G}_{N}}(\varphi )\sin \varphi {\kern 1pt} d\varphi } = \pi {{b}_{1}}. \\ \end{gathered} $

Соответствующие коэффициенты корреляции можно представить в виде:

${{r}_{{NXY}}} = \frac{{{{b}_{2}}}}{{\sqrt {a_{0}^{2} - a_{2}^{2}} }} = \frac{{{{\beta }_{2}}}}{{\sqrt {1 - \alpha _{2}^{2}} }},$

$\begin{gathered} {{r}_{{NPX}}} = \frac{{{{a}_{1}}}}{{\sqrt {{{a}_{0}}({{a}_{0}} + {{{{a}_{2}})} \mathord{\left/ {\vphantom {{{{a}_{2}})} 2}} \right. \kern-0em} 2}} }} = \frac{{{{\alpha }_{1}}}}{{\sqrt {(1 + {{{{\alpha }_{2}})} \mathord{\left/ {\vphantom {{{{\alpha }_{2}})} 2}} \right. \kern-0em} 2}} }}, \\ {{r}_{{NPY}}} = \frac{{{{b}_{1}}}}{{\sqrt {{{a}_{0}}({{a}_{0}} - {{{{a}_{2}})} \mathord{\left/ {\vphantom {{{{a}_{2}})} 2}} \right. \kern-0em} 2}} }} = \frac{{{{\beta }_{1}}}}{{\sqrt {(1 - {{{{\alpha }_{2}})} \mathord{\left/ {\vphantom {{{{\alpha }_{2}})} 2}} \right. \kern-0em} 2}} }}. \\ \end{gathered} $

Таким образом, дисперсии, взаимные корреляционные функции и коэффициенты корреляции помехи зависят только от пяти коэффициентов разложения в ряд Фурье ее угловой плотности: постоянного (a₀), а также первой (a₁, b₁) и второй гармоники (a₂, b₂). Все высшие гармоники угловой плотности в формировании вторых центральных статистических моментов давления и компонент колебательной скорости не участвуют. Перечисленные коэффициенты можно найти из приведенных выше формул и вычислить на основании экспериментально измеряемых величин:

$\begin{gathered} {{a}_{0}} = {{\sigma _{{NP}}^{2}} \mathord{\left/ {\vphantom {{\sigma _{{NP}}^{2}} \pi }} \right. \kern-0em} \pi },\,\,\,\,{{a}_{1}} = {{{{R}_{{NPX}}}} \mathord{\left/ {\vphantom {{{{R}_{{NPX}}}} \pi }} \right. \kern-0em} \pi },\,\,\,\,{{b}_{1}} = {{{{R}_{{NPY}}}} \mathord{\left/ {\vphantom {{{{R}_{{NPY}}}} \pi }} \right. \kern-0em} \pi }, \\ {{a}_{2}} = (\sigma _{{NX}}^{2} - {{\sigma _{{NY}}^{2})} \mathord{\left/ {\vphantom {{\sigma _{{NY}}^{2})} \pi }} \right. \kern-0em} \pi },\,\,\,\,{{b}_{2}} = {{2{{R}_{{NXY}}}} \mathord{\left/ {\vphantom {{2{{R}_{{NXY}}}} \pi }} \right. \kern-0em} \pi }. \\ \end{gathered} $

Если все a_k = b_k = 0 при k > 0, то G(φ) = const и поле помехи изотропно.

Поле сигнала также можно представить как случайный процесс, который конструируется на основе плотностей распределения амплитуды и угла, а также функций ${{g}_{S}}(\varphi )$ и ${{s}_{S}}(t),$ отличающихся от определяющих поле помехи. Различие перечисленных функций приводит к различию угловых плотностей (и спектров) помехи и сигнала.

Угловую плотность поля точечного источника сигнала в однородной среде зададим в виде δ-функции Дирака:

${{G}_{S}}(\varphi ) = \sigma _{{SP}}^{2}\delta (\varphi - {{\varphi }_{S}}),$

где φ_S – направление на источник. Разложение этой функции в ряд Фурье:

$\begin{gathered} {{G}_{S}}(\varphi ) = \frac{{\sigma _{{SP}}^{2}}}{\pi } \times \\ \times \,\,\left( {\frac{1}{2} + \sum\limits_{k = 1}^\infty {(\cos {{\varphi }_{S}}\cos k\varphi + \sin {{\varphi }_{S}}\sin k\varphi } )} \right) = \\ = \frac{{\sigma _{{SP}}^{2}}}{\pi }\left( {\frac{1}{2} + \sum\limits_{k = 1}^\infty {\cos (k\varphi - {{\varphi }_{S}})} } \right). \\ \end{gathered} $

Таким образом, точечный источник дает бесконечный угловой спектр с постоянным уровнем угловых гармоник. Дисперсия давления, создаваемого точечным источником, равна $\int_0^{2\pi } {\sigma _{{SP}}^{2}\delta ({{\varphi }_{S}} - \varphi )d\varphi } = $ = $\sigma _{{SP}}^{2}.$ Дисперсии компонент колебательной скорости равны $\sigma _{{SX}}^{2} = \sigma _{{SP}}^{2}{{\cos }^{2}}{{\varphi }_{S}}$ и $\sigma _{{SY}}^{2} = \sigma _{{SP}}^{2}{{\sin }^{2}}{{\varphi }_{S}}.$ Взаимные корреляционные функции компонент поля сигнала:

$\begin{gathered} {{R}_{{SXY}}} = {{(\sigma _{{SP}}^{2}\sin 2{{\varphi }_{S}})} \mathord{\left/ {\vphantom {{(\sigma _{{SP}}^{2}\sin 2{{\varphi }_{S}})} 2}} \right. \kern-0em} 2},\,\,\,\,{{R}_{{SPX}}} = \sigma _{{SP}}^{2}\cos {{\varphi }_{S}}, \\ {{R}_{{SPY}}} = \sigma _{{SP}}^{2}\sin {{\varphi }_{S}}. \\ \end{gathered} $

А коэффициенты взаимной корреляции в отсутствие помехи

${{r}_{{SXY}}} = \frac{{\sin 2{{\varphi }_{S}}}}{{\left| {\sin 2{{\varphi }_{S}}} \right|}},\,\,\,\,{{r}_{{SPX}}} = \frac{{\cos {{\varphi }_{S}}}}{{\left| {\cos {{\varphi }_{S}}} \right|}},\,\,\,{{r}_{{SPY}}} = \frac{{\sin {{\varphi }_{S}}}}{{\left| {\sin {{\varphi }_{S}}} \right|}}$

представляют собой меандры с периодами π и 2π и различаются начальной фазой. Таким образом, угловая плотность поля точечного источника в однородной среде содержит все члены разложения в ряд по углу, а вторые моменты полей давления и колебательной скорости сигнала полностью описываются членами разложения в ряд Фурье угловой плотности не выше второго порядка так же, как и поля помехи.

Угловая плотность поля сигнала в реальной среде представляет собой максимум, сосредоточенный вокруг угла ${{\varphi }_{S}}$. На ширину максимума влияют: размер источника, отражение от неровных границ и преломление при распространении через неоднородную среду. Если максимум угловой плотности сигнала имеет конечный угловой размер, разложение в ряд Фурье будет обрываться, начиная с некоторого значения k = K. Как показывает расчет, угловая плотность сигнала, имеющего ширину от долей градуса до единиц градусов, содержит десятки – сотни равновеликих угловых гармоник. Таким образом, расширение максимума в пределах от 0 до ~10° заметного влияния на амплитуду первой и второй гармоник не оказывает, что позволяет во всех практически важных случаях влиянием ширины максимума угловой плотности сигнала пренебречь, а источник считать точечным.

ОЦЕНКА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ НАПРАВЛЕНИЯ НА ИСТОЧНИК СИГНАЛА ПО ОТНОШЕНИЮ МГНОВЕННЫХ ЗНАЧЕНИЙ КОМПОНЕНТ КОЛЕБАТЕЛЬНОЙ СКОРОСТИ

Найдем плотность распределения оценки направления на источник сигнала φ_d при наличии помехи, исходя из формулы (1). В этом случае φ_d является функцией двух случайных частично коррелированных процессов X и Y:

${{\varphi }_{d}} = \operatorname{arcctg} \frac{X}{Y}.$

Плотность распределения частного d = X/Y двух нормальных центрированных случайных процессов с дисперсиями $\sigma _{X}^{2}$ и $\sigma _{Y}^{2}$ и коэффициентом корреляции r равна [17]:

${{f}_{d}}(d) = \frac{{{{\sigma }_{X}}{{\sigma }_{Y}}\sqrt {1 - {{r}^{2}}} }}{{\pi (\sigma _{X}^{2} - 2r{{\sigma }_{X}}{{\sigma }_{Y}}d + \sigma _{Y}^{2}{{d}^{2}})}}.$

Найдем плотность распределения случайной величины φ = arcctg(d). Обратная функция d = = ctg(φ) на интервале (0, π) монотонна. В этом случае плотность распределения f_XY случайной величины φ связана с f_d соотношением:

${{f}_{{XY}}}(\varphi ) = {{f}_{d}}(\operatorname{ctg} \varphi )\left| {\frac{{d{\kern 1pt} (\operatorname{ctg} \varphi )}}{{d\varphi }}} \right| = \frac{{{{f}_{d}}(\operatorname{ctg} \varphi )}}{{{{{\sin }}^{2}}\varphi }}.$

Следовательно, искомая плотность распределения равна:

$\begin{gathered} {{f}_{{XY}}}(\varphi ) = \\ = \frac{{2\sqrt {1 - {{r}^{2}}} }}{{\pi \left( {\frac{{{{\sigma }_{X}}}}{{{{\sigma }_{Y}}}}(1 - \cos 2\varphi ) - 2r\sin 2\varphi + \frac{{{{\sigma }_{Y}}}}{{{{\sigma }_{X}}}}(1 + \cos 2\varphi )} \right)}}, \\ 0 \leqslant \varphi < \pi . \\ \end{gathered} $

Учитывая статистическую независимость полей сигнала и помехи, найдем входящие в эту формулу дисперсии:

$\sigma _{X}^{2} = \sigma _{{SX}}^{2} + \sigma _{{NX}}^{2} = \frac{{\sigma _{{NP}}^{2}}}{2}\left( {SN(1 + \cos 2{{\varphi }_{S}}) + \left( {1 + {{\alpha }_{2}}} \right)} \right),$

$\sigma _{Y}^{2} = \sigma _{{SY}}^{2} + \sigma _{{NY}}^{2} = \frac{{\sigma _{{NP}}^{2}}}{2}\left( {SN(1 - \cos 2{{\varphi }_{S}}) + \left( {1 - {{\alpha }_{2}}} \right)} \right)$

и коэффициент корреляции:

$r = \frac{{SN\sin 2{{\varphi }_{S}} + {{\beta }_{2}}}}{{\sqrt {\left( {SN(1 + \cos 2{{\varphi }_{S}}) + \left( {1 + {\kern 1pt} {{\alpha }_{2}}} \right)} \right)\left( {SN(1 - \cos 2{{\varphi }_{S}}) + \left( {1 - {{\alpha }_{2}}} \right)} \right)} }}.$

Таким образом, плотность распределения оценки направления на источник, рассчитанная по отношению мгновенных значений компонент колебательной скорости, дисперсии $\sigma _{X}^{2}$ и $\sigma _{Y}^{2}$, а также коэффициент корреляции $r$ зависят только от отношения сигнал/помеха SN и нормированных коэффициентов второй гармоники разложения в ряд Фурье угловой плотности поля помехи. Кроме того, все перечисленные функции содержат только аргументы двойного угла, что указывает на их периодичность с периодом π. Примеры расчетов функции f_XY(φ) при изотропной и анизотропной помехе приведены на рис. 2 и 3 .

Рис. 2.

Плотность распределения оценки направления на источник сигнала при отношении сигнал/помеха: 2, 1, 0.5 и 0 (штриховая линия), φ_S = 45°. Помеха изотропна.

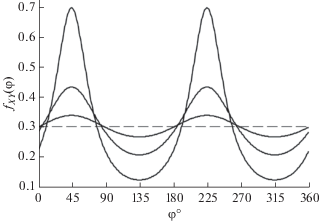
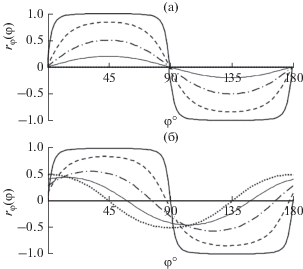
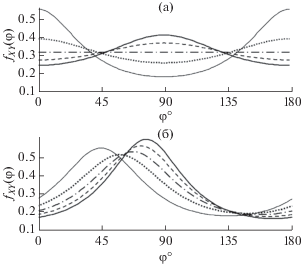
Рис. 3.

Плотность распределения оценки направления на источник сигнала (φ_S = 90°) при отношении сигнал/помеха: 1 (сплошная линия), 0.75 (штриховая), 0.5 (штрих-пунктир), 0.25 (пунктир), 0 (тонкая сплошная). Коэффициенты разложения угловой плотности помехи (а) – α₂ = 0.5, β₂ = 0 и (б) – α₂ = 0, β₂ = 0.5.

ОЦЕНКА НАПРАВЛЕНИЯ НА ИСТОЧНИК СИГНАЛА ПО КОЭФФИЦИЕНТУ КОРРЕЛЯЦИИ КОМПОНЕНТ КОЛЕБАТЕЛЬНОЙ СКОРОСТИ

По двум ортогональным компонентам колебательной скорости можно найти ортогональные компоненты скорости в системе координат, повернутой относительно исходной на угол φ в плоскости xOy ([8], с. 168):

${{X}_{\varphi }} = X\cos \varphi + Y\sin \varphi ,\,\,\,{{Y}_{\varphi }} = - X\sin \varphi + Y\cos \varphi .$

Эти формулы справедливы и для рассматриваемого вида поля скорости, в чем можно убедиться подстановкой в них компонент колебательной скорости в виде (3). Коэффициент корреляции компонент скорости в повернутой системе координат равен:

$\begin{gathered} {{r}_{\varphi }}(\varphi ) = \frac{{\overline {{{X}_{\varphi }}{{Y}_{\varphi }}} }}{{\sqrt {\overline {X_{\varphi }^{2}} \,\overline {Y_{\varphi }^{2}} } }} = \\ = \frac{{\left( {\frac{{{{\sigma }_{Y}}}}{{{{\sigma }_{X}}}} - \frac{{{{\sigma }_{X}}}}{{{{\sigma }_{Y}}}}} \right)\sin 2\varphi + 2r\cos 2\varphi }}{{{{{\left( {\frac{{{{\sigma }_{X}}}}{{{{\sigma }_{Y}}}}(1 + \cos 2\varphi ) + 2r\sin 2\varphi + \frac{{{{\sigma }_{Y}}}}{{{{\sigma }_{X}}}}(1 - \cos 2\varphi )} \right)}}^{{\frac{1}{2}}}}{{{\left( {\frac{{{{\sigma }_{X}}}}{{{{\sigma }_{Y}}}}(1 - \cos 2\varphi ) - 2r\sin 2\varphi + \frac{{{{\sigma }_{Y}}}}{{{{\sigma }_{X}}}}(1 + \cos 2\varphi )} \right)}}^{{\frac{1}{2}}}}}}, \\ \end{gathered} $

где $\sigma _{X}^{2},$ $\sigma _{Y}^{2}$ и $r$ – дисперсии и коэффициент корреляции компонент колебательной скорости суммы сигнала и помехи в исходной системе координат, найденные выше, а черта сверху означает усреднение.

В этом случае процессы X и Y могут быть не гауссовыми. Формула показывает, что, также как и в предыдущем случае, коэффициент корреляции ${{r}_{\varphi }}$ зависит только от коэффициентов второй гармоники разложения в ряд Фурье угловой плотности помехи. Кроме того, он также является функцией двойного угла, и, следовательно, периодичен с периодом π. Примеры расчетов коэффициента корреляции ${{r}_{\varphi }}(\varphi )$ приведены на рис. 4. Направлению на источник соответствует пересечение зависимостью ${{r}_{\varphi }}(\varphi )$ оси абсцисс при переходе коэффициента корреляции из области положительных значений в область отрицательных (при α₂ = 0, β₂ = 0). Если последнее условие не выполняется, появляется ошибка, зависящая от отношения сигнал/помеха и коэффициентов α₂ и β₂. На графике это выглядит как смещение точки пересечения зависимости ${{r}_{\varphi }}(\varphi )$ и оси абсцисс.

Рис. 4.

Коэффициент корреляции компонент колебательной скорости при отношении сигнал/помеха: 100 (сплошная), 5 (штриховая), 1 (штрих-пунктир), 0.25 (сплошная тонкая), 0 (пунктир), φ_S = 90°. (а) – α₂ = 0, β₂ = 0, (б) – α₂ = 0, β₂ = 0.5.

ОЦЕНКА НАПРАВЛЕНИЯ НА ИСТОЧНИК СИГНАЛА ПО ОТНОШЕНИЮ КОМПОНЕНТ ПОТОКА МОЩНОСТИ

Рассмотрим алгоритм определения пеленга источника сигнала, в ходе выполнения которого сначала вычисляются компоненты потока мощности:

$\begin{gathered} {{W}_{X}} = \overline {PX} = \overline {({{P}_{S}} + {{P}_{N}})({{X}_{S}} + {{X}_{N}})} = \\ = \overline {{{P}_{S}}{{X}_{S}}} + \overline {{{P}_{N}}{{X}_{N}}} = {{R}_{{SPX}}} + {{R}_{{NPX}}}, \\ \end{gathered} $

$\begin{gathered} {{W}_{Y}} = \overline {PY} = \overline {({{P}_{S}} + {{P}_{N}})({{Y}_{S}} + {{Y}_{N}})} = \\ = \overline {{{P}_{S}}{{Y}_{S}}} + \overline {{{P}_{N}}{{Y}_{N}}} = {{R}_{{SPY}}} + {{R}_{{NPY}}}, \\ \end{gathered} $

а затем рассчитывается оценка направления на источник подобно формуле (2) (для сокращения записи – для диапазона углов 0…π):

${{\varphi }_{W}} = \operatorname{arcctg} \frac{{{{W}_{X}}}}{{{{W}_{Y}}}} = \operatorname{arcctg} \left( {\frac{{{{R}_{{SPX}}} + {{R}_{{NPX}}}}}{{{{R}_{{SPY}}} + {{R}_{{NPY}}}}}} \right).$

Подставив сюда формулы взаимных корреляционных функций, найдем:

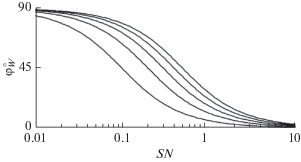
$\begin{gathered} {{\varphi }_{W}} = {\text{arcctg}}\left( {\frac{{\sigma _{{SP}}^{2}\cos {{\varphi }_{S}} + \pi {\kern 1pt} {{a}_{1}}}}{{\sigma _{{SP}}^{2}\sin {{\varphi }_{S}} + \pi {\kern 1pt} {{b}_{1}}}}} \right) = \\ = {\text{arcctg}}\left( {\frac{{SN\cos {{\varphi }_{S}} + {{\alpha }_{1}}}}{{SN\sin {{\varphi }_{S}} + {{\beta }_{1}}}}} \right). \\ \end{gathered} $

Таким образом, оценка направления полностью определяется отношением сигнал/помеха и коэффициентами первой гармоники разложения угловой плотности поля помехи в ряд Фурье. И в этом случае процессы P, X и Y могут быть не гауссовыми. При $SN \to \infty $ оценка угла приближается к его истинному значению: ${{\varphi }_{W}} \to {{\varphi }_{S}}.$ При $SN \to 0$ напротив, ${{\varphi }_{W}} \to \operatorname{arcctg} ({{{{\alpha }_{1}}} \mathord{\left/ {\vphantom {{{{\alpha }_{1}}} {{{\beta }_{1}}}}} \right. \kern-0em} {{{\beta }_{1}}}})$ и результат полностью определяется помехой. Примеры расчетов зависимости φ_W от отношения сигнал/помеха SN при различных значениях коэффициента β₁ для φ_S = 0° представлены на рис. 5.

Рис. 5.

Зависимость оценки направления на источник сигнала от отношения сигнал/помеха при различных значениях коэффициента β₁ первой гармоники угловой плотности помехи. α₁ = 0, β₁ = 0.5, 0.4, 0.3, 0.2, 0.1 (сверху вниз).

ВЫЧИСЛЕНИЕ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ОЦЕНКИ НАПРАВЛЕНИЯ НА ИСТОЧНИК СИГНАЛА ПО ЗНАЧЕНИЯМ КОМПОНЕНТ ВЕКТОРА УМОВА

Оценку плотности распределения вероятности пеленга источника по значениям компонент вектора Умова в соответствии с формулой (2) можно получить, вычисляя плотность распределения пеленга на основе измеренных или рассчитанных статистических моментов пульсаций давления и компонент градиента давления. Это возможно для случайных процессов, являющихся стационарными, нормальными и центрированными. Наиболее полно и последовательно вывод соотношений, связывающих моменты и плотность распределения оценки пеленга в этом случае, выполнен в работе [18]. Придерживаясь изложенной в этой работе процедуры, найдем плотность распределения оценки пеленга по значениям нормированных компонент вектора Умова, вычисляемых с использованием случайного процесса (4), элементами которого являются нормированные пульсации давления и компоненты колебательной скорости. Полагая компоненты процесса (4) центрированными, запишем его корреляционную матрицу в виде:

${\mathbf{C}} = \overline {{{{(P,X,Y)}}^{T}}(P,X,Y)} = \left[ {\begin{array}{*{20}{c}} {{{c}_{0}}}&{{{c}_{3}}}&{{{c}_{4}}} \\ {{{c}_{3}}}&{{{c}_{1}}}&{{{c}_{5}}} \\ {{{c}_{4}}}&{{{c}_{5}}}&{{{c}_{2}}} \end{array}} \right].$

Входящие в нее коэффициенты равны: ${{c}_{0}} = \overline {PP{\kern 1pt} } ,$ ${{c}_{1}} = \overline {XX{\kern 1pt} } ,$ ${{c}_{2}} = \overline {YY{\kern 1pt} } ,$ ${{c}_{3}} = \overline {PX{\kern 1pt} } ,$ ${{c}_{4}} = \overline {PY{\kern 1pt} } ,$ ${{c}_{5}} = \overline {XY{\kern 1pt} } ,$ а ее детерминант: $C = det({\mathbf{C}})$ = ${{c}_{0}}{{c}_{1}}{{c}_{2}} + 2{{c}_{3}}{{c}_{4}}{{c}_{5}}$ – $ - \,\,{{c}_{0}}c_{5}^{2} - {{c}_{1}}c_{4}^{2} - {{c}_{2}}c_{3}^{2}.$ Соответствующая этой матрице плотность распределения стационарного нормального случайного вектора (P, X, Y) дается выражением:

$\begin{gathered} {{f}_{{PV}}}(P,X,Y) = \frac{1}{{\sqrt {8{{\pi }^{3}}C} }} \times \\ \times \,\,\exp \left\{ { - \frac{1}{2}(P,X,Y)\left( {{{{\mathbf{C}}}^{{ - 1}}}} \right){{{(P,X,Y)}}^{T}}} \right\} = \\ = \frac{1}{{\sqrt {8{{\pi }^{3}}{\kern 1pt} C} }}\exp \left\{ { - \frac{1}{{2C}}\left[ {({{c}_{1}}{{c}_{2}} - c_{5}^{2}){{P}^{2}}} \right.} \right. + \\ \left. {\left. {\frac{{}}{{}} + \,\,({{c}_{0}}{{c}_{2}} - c_{4}^{2}){{X}^{2}} + ({{c}_{0}}{{c}_{1}} - c_{3}^{2}){{Y}^{2}}} \right]} \right\} \times \\ \times \,\,\exp \left\{ { - \frac{1}{C}\left[ {({{c}_{4}}{{c}_{5}} - {{c}_{2}}{{c}_{3}})PX} \right.} \right. + \\ \left. {\left. {\frac{{}}{{}} + \,\,({{c}_{3}}{{c}_{5}} - {{c}_{1}}{{c}_{4}})PY + ({{c}_{3}}{{c}_{4}} - {{c}_{0}}{{c}_{5}})XY} \right]} \right\}. \\ \end{gathered} $

Здесь C^–1 – матрица, обратная к С, а символ ^Т обозначает транспонирование. Сделаем замену переменных: $P = P,$ ${{I}_{x}} = PX,$ ${{I}_{y}} = PY.$ Якобиан этого преобразования равен 1/P². Новые переменные I_x и I_y отличаются от компонент вектора Умова J_x и J_y, введенных ранее (2), только постоянным множителем, что позволяет считать их компонентами нормированного вектора Умова. Плотность распределения в новых переменных будет иметь вид:

$\begin{gathered} {{f}_{{PV}}}(P,{{I}_{x}},{{I}_{y}}) = \frac{1}{{{{P}^{2}}\sqrt {{{{(2\pi )}}^{3}}C} }} \times \\ \times \,\,\exp \left\{ { - \frac{1}{C}\left[ {({{c}_{4}}{{c}_{5}} - {{c}_{2}}{{c}_{3}}){{I}_{x}} + ({{c}_{3}}{{c}_{5}} - {{c}_{1}}{{c}_{4}}){{I}_{y}}} \right]} \right\} \times \\ \times \exp \left\{ { - \frac{1}{{2C}}\left[ {{{P}^{2}}({{c}_{1}}{{c}_{2}} - c_{5}^{2}) + \frac{1}{{{{P}^{2}}}}\left( {({{c}_{0}}{{c}_{2}} - c_{4}^{2})I_{x}^{2} + } \right.} \right.} \right. \\ \left. {\left. {\frac{{}}{{}} + \,\,2({{c}_{3}}{{c}_{4}} - {{c}_{0}}{{c}_{5}}){{I}_{x}}{{I}_{y}} + ({{c}_{0}}{{c}_{1}} - c_{3}^{2})I_{y}^{2}} \right]} \right\}. \\ \end{gathered} $

Интегрирование по P от –∞ до +∞ c помощью формулы ([19], 3.478-4) приводит к следующему результату:

$\begin{gathered} {{f}_{{PV}}}({{I}_{x}},{{I}_{y}}) = \frac{1}{{\sqrt {2{{\pi }^{3}}C} }}\exp \left\{ { - \frac{1}{C}\left[ {({{c}_{4}}{{c}_{5}} - {{c}_{2}}{{c}_{3}}){{I}_{x}} + ({{c}_{3}}{{c}_{5}} - {{c}_{1}}{{c}_{4}}){{I}_{y}}} \right]} \right\} \times \\ \times \,\,\sqrt[4]{{\frac{{{{c}_{1}}{{c}_{2}} - c_{5}^{2}}}{{({{c}_{0}}{{c}_{2}} - c_{4}^{2})I_{X}^{2} + 2({{c}_{3}}{{c}_{4}} - {{c}_{0}}{{c}_{5}}){{I}_{x}}{{I}_{y}} + ({{c}_{0}}{{c}_{1}} - c_{3}^{2})I_{y}^{2}}}}} \times \\ \times \,\,{{K}_{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}}}}\left( {\frac{1}{C}\sqrt {({{c}_{1}}{{c}_{2}} - c_{5}^{2})[({{c}_{0}}{{c}_{2}} - c_{4}^{2})I_{x}^{2} + 2({{c}_{3}}{{c}_{4}} - {{c}_{0}}{{c}_{5}}){{I}_{x}}{{I}_{y}} + ({{c}_{0}}{{c}_{1}} - c_{3}^{2})I_{y}^{2}]} } \right). \\ \end{gathered} $

Здесь K_½ – функция Макдональда порядка ½. Перейдем в полярную систему координат: ${{I}_{x}} = I\cos {{\varphi }_{I}},$ ${{I}_{y}} = I\sin {{\varphi }_{I}}.$ Якобиан этого преобразования равен I. Введем обозначения: ${\gamma } = {{c}_{1}}{{c}_{2}} - c_{5}^{2}$ и $\delta = ({{c}_{0}}{{c}_{2}} - c_{4}^{2}){{\cos }^{2}}{{\varphi }_{I}}$ + $({{c}_{0}}{{c}_{1}} - c_{3}^{2}){{\sin }^{2}}{{\varphi }_{I}}$ + $ + \,\,2({{c}_{3}}{{c}_{4}} - {{c}_{0}}{{c}_{5}})\cos {{\varphi }_{I}}\sin {{\varphi }_{I}}$, и после преобразований получим

$\begin{gathered} {{f}_{{PV}}}(I,{{\phi }_{I}}) = \sqrt {\frac{I}{{2{{\pi }^{3}}C}}\sqrt {\frac{\gamma }{\delta }} } \times \\ \times \,\,\exp \left\{ { - \frac{I}{C}\left[ {({{c}_{4}}{{c}_{5}} - {{c}_{2}}{{c}_{3}})\cos {{\varphi }_{I}} + ({{c}_{3}}{{c}_{5}} - {{c}_{1}}{{c}_{4}})\sin {{\varphi }_{I}}} \right]} \right\} \times \\ \times \,\,{{K}_{{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}}}\left( {\frac{I}{C}\sqrt {{\kern 1pt} \gamma \delta } } \right) \\ \end{gathered} $

– совместную плотность распределения модуля нормированного вектора Умова I и пеленга φ_I. Интегрирование по I от 0 до ∞ с применением формулы ([19], 6.624-2) дает:

(9)

$\begin{gathered} {{f}_{{PV}}}({{\varphi }_{I}}) = \frac{1}{{2{\pi }\sqrt {\delta } }} \times \\ \times \,\,\frac{C}{{[({{c}_{4}}{{c}_{5}} - {{c}_{2}}{{c}_{3}})\cos {{\varphi }_{I}} + ({{c}_{3}}{{c}_{5}} - {{c}_{1}}{{c}_{4}})\sin {{\varphi }_{I}}] + \sqrt {{\gamma \delta }} }}. \\ \end{gathered} $

Это выражение связывает плотность распределения вероятности оценки пеленга и коэффициенты корреляционной матрицы, которые являются вторыми центральными статистическими моментами процесса (4), представляющего собой сумму полей сигнала и помехи. Формулы, позволяющие вычислить составляющие коэффициентов с_i, обусловленные помехой и сигналом по отдельности, приведены в табл. 1. Суммарные коэффициенты вычисляются следующим образом:

${{c}_{i}} = {\sigma }_{{NP}}^{{\text{2}}}\left( {\frac{{{{c}_{{Ni}}}}}{{{\sigma }_{{NP}}^{{\text{2}}}}} + SN\frac{{{{c}_{{Si}}}}}{{{\sigma }_{{SP}}^{{\text{2}}}}}} \right).$

Таблица 1

Коэффициент с_i	Функция	Помеха ${{{{c}_{{Ni}}}} \mathord{\left/ {\vphantom {{{{c}_{{Ni}}}} {\sigma _{{NP}}^{2}}}} \right. \kern-0em} {\sigma _{{NP}}^{2}}}$	Сигнал ${{{{c}_{{Si}}}} \mathord{\left/ {\vphantom {{{{c}_{{Si}}}} {\sigma _{{SP}}^{2}}}} \right. \kern-0em} {\sigma _{{SP}}^{2}}}$
с₀	$\sigma _{P}^{2}$	1	1
с₁	$\sigma _{X}^{2}$	$(1 + {{{{\alpha }_{2}})} \mathord{\left/ {\vphantom {{{{\alpha }_{2}})} 2}} \right. \kern-0em} 2}$	${{\cos }^{2}}{{\varphi }_{S}}$
с₂	$\sigma _{Y}^{2}$	$(1 - {{{{\alpha }_{2}})} \mathord{\left/ {\vphantom {{{{\alpha }_{2}})} 2}} \right. \kern-0em} 2}$	${{\sin }^{2}}{{\varphi }_{S}}$
с₃	${{R}_{{PX}}}$	${{\alpha }_{1}}$	$\cos {{\varphi }_{S}}$
с₄	${{R}_{{PY}}}$	${\kern 1pt} {{\beta }_{1}}$	$\sin {{\varphi }_{S}}$
с₅	${{R}_{{XY}}}$	${{{{\beta }_{2}}} \mathord{\left/ {\vphantom {{{{\beta }_{2}}} 2}} \right. \kern-0em} 2}$	${{(\sin 2{{\varphi }_{S}})} \mathord{\left/ {\vphantom {{(\sin 2{{\varphi }_{S}})} 2}} \right. \kern-0em} 2}$

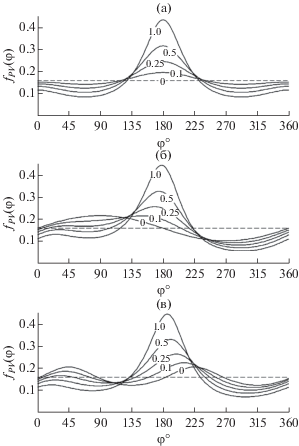
Примеры расчетов по формуле (9) при различных значениях отношения сигнал/помеха представлены на рис. 6. При SN ≈ 0.5 и более зависимость имеет острый максимум, позволяющий четко определить направление на источник сигнала. Если поле помехи обладает выраженными анизотропными свойствами, определение направления непосредственно по зависимости плотности вероятности от угла при малых отношениях сигнал/помеха будет затруднительным. Надо отметить, что в рассматриваемом случае плотность распределения вероятности пеленга источника сигнала также зависит только от коэффициентов первой и второй гармоник разложения угловой плотности помехи в ряд Фурье. Также следует подчеркнуть, что полученное выражение может применяться к широкополосным процессам, что отличает его от формулы (89) [18], верной только для узкополосных процессов.

Рис. 6.

Плотность распределения оценки направления на источник сигнала при отношении сигнал/помеха 0, 0.1, 0.25, 0.5, 1 (обозначено цифрами), φ_S = 180°: (а) – изотропная помеха; (б) – α₁ = 0, β₁ = 0.25, α₂ = 0, β₂ = 0; (в) – α₁ = 0, β₁ = 0, α₂ = 0, β₂ = 0.25. Штриховая линия соответствует изотропной помехе и SN = 0.

Интересно сравнить величины максимумов плотности распределения оценок пеленга, рассчитанных при равных значениях дисперсий и взаимных корреляционных функций компонент сигнала и помехи, для ВСП с векторной частью на основе приемника колебательной скорости и приемника градиента давления. Результаты расчетов представлены на рис. 7 как функции отношения сигнал/помеха. Графики показывают, что значения плотности распределения оценки пеленга, полученные для ВСП градиента давления, при значениях отношения сигнал/помеха более 0.2 заметно превышают рассчитанные на основе формулы (9) для ВСП колебательной скорости.

Рис. 7.

Плотности распределения оценки направления на источник сигнала, рассчитанные для комбинированного приемника на основе приемника колебательной скорости (PV) и приемника градиента давления (GP) как функции отношения сигнал/помеха при φ_I = φ_S. Помеха изотропная.

ЗАКЛЮЧЕНИЕ

Модель анизотропного акустического поля на основе многомерного пуассоновского процесса показывает связь между статистическими свойствами процесса и важной характеристикой анизотропного акустического шумового поля – его угловой плотностью. Установлена связь дисперсий и взаимных корреляционных функций пульсаций давления и компонент колебательной скорости с коэффициентами разложения угловой плотности в ряд Фурье. Найденные соотношения позволяют рассчитать амплитуды гармоник угловой плотности на основе измерений дисперсий и взаимных корреляционных функций компонент поля помехи, что дает возможность количественно оценить анизотропию поля в натурных условиях при использовании одиночного ВСП.

Анализ некоторых алгоритмов пеленгования сигнала на фоне анизотропной помехи с помощью ВСП показал, что на результат пеленгования влияют только коэффициенты первой и второй гармоник разложения в ряд Фурье угловой плотности поля помехи. Рассмотренные алгоритмы имеют различную чувствительность к величинам этих гармоник, что может быть использовано при выборе алгоритма, дающего наивысшую помехоустойчивость в сложившихся условиях.

Работа выполнена при частичной поддержке государственного задания по теме “Акустика мелкого моря, нелинейная акустическая диагностика, нелинейная динамика волн” (номер гос. регистрации АААА-А18-118021390174-1).

Список литературы

Скребнев Г.К. Комбинированные гидроакустические приемники. СПб.: Элмор, 1997. 200 с.
Щуров В.А. Векторная акустика океана. Владивосток: Дальнаука, 2003. 305 с.
Раевский М.А., Хилько А.И. О горизонтальной анизотропии динамических шумов в океанических волноводах // Акуст. журн. 2014. Т. 60. № 6. С. 633–637.
Завольский Н.А., Раевский М.А. Горизонтальная анизотропия динамических шумов в глубоком и мелком море // Акуст. журн. 2019. Т. 65. № 2. С. 197–202.
Cron B., Sherman Ch. Spatial correlation functions for various noise models // J. Acoust. Soc. Am. 1962. T. 34(II). № 11. P. 1732–1736.
Захаров Л.Н., Киршов В.А., Рожин Ф.В. Пространственно-корреляционные функции компонент колебательной скорости для двух моделей звукового поля // Акуст. журн. 1972. Т. 18. № 1. С. 49–52.
Бурдик В.С. Анализ гидроакустических систем. Л.: Судостроение, 1988. 392 с.
Гордиенко В.А. Векторно-фазовые методы в акустике. М.: Физматлит, 2007. 480 с.
Глебова Г.М., Кузнецов Г.Н., Шимко О.Е. Векторно-скалярные шумовые поля, образованные взволнованной морской поверхностью // Акуст. журн. 2013. Т. 59. № 4. С. 508–519.
Гордиенко В.А., Илюшин Я.А. О флуктуациях угла пеленга сосредоточенного источника, определяемого векторным приемником в поле шумов океана // Акуст. журн. 1996. Т. 42. № 3. С. 365–370.
Калью В.А., Самылин Л.П. Оценка помехоустойчивости некоторых векторно-фазовых алгоритмов обработки информации при измерениях с помощью комбинированного приемника // Техническая акустика. 1999. Т. 5. № 3–4. С. 29–32.
Горелов А.А., Смарышев М.Д. Моделирование алгоритмов обработки процессов на выходе каналов комбинированного приемника и комбинированной антенны // Акуст. журн. 2018. Т. 64. № 2. С. 250–256.
Мак-Доналд Д. Введение в физику шумов и флуктуаций. М.: Мир, 1964. 159 с.
Тихонов В.И. Статистическая радиотехника. М.: Радио и связь, 1982. 624 с.
Рытов С.М. Введение в статистическую радиофизику. Ч. 1. Случайные процессы. М.: Наука, 1976. 495 с.
Шиховцев И.В., Якубов В.П. Статистическая радиофизика. Новосибирск: Изд-во Новосиб. ун-та, 2011. 157 с.
Левин Б.Р. Теоретические основы статистической радиотехники. М.: Радио и связь, 1989. 656 с.
Ebeling K.J. Statistical properties of random wave fields // Mason W.P., Thurston R.N. Physical Acoustics. Principles and Methods. V. XVII. Acad. Press, 1984. P. 233–310.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматлит, 1963. 1108 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал