Акустический журнал, 2020, T. 66, № 2, стр. 181-197

ВВЕДЕНИЕ

Как известно [1–14], в стратифицированных по глубине океанических волноводах возможно формирование каустических [1, 3, 13, 14] и слаборасходящихся [2–12] акустических пучков. Каустический пучок формируется около луча, горизонтально выходящего из источника, модами, горизонты поворота которых ближе всего расположены к глубине погружения источника [1, 13, 14]. Этому опорному для каустического пучка лучу соответствует гладкий экстремум зависимости длины цикла лучей от угла выхода из источника при нулевом значении этого угла [1, 6, 13, 14]. Естественно, что в ВКБ приближении опорной для каустического пучка будет являться бриллюэновская волна, горизонт поворота которой ближе всего расположен к глубине погружения источника [1, 13], а сам пучок формируется около соответствующих частей каустических линий, сближающихся между собой с ростом горизонтального расстояния [3]. При этом его ширина заметно уменьшается с ростом частоты излучения [4, 13].

Слаборасходящийся пучок формируется около опорного луча, угол выхода которого из источника совпадает со значением положения гладкого экстремума зависимости длины цикла лучей от лучевого параметра, обратно пропорционального фазовой скорости распространения акустических волн вдоль этих лучей [2, 3, 14]. В отличие от экстремума, соответствующего обычному каустическому пучку [1, 3, 6, 13, 14], такому экстремуму отвечает уже нулевое значение производной от длины цикла лучей по лучевому параметру [2, 3, 6, 14], соответственно, даже не при нулевом значении отвечающего этому экстремуму угла выхода лучей [3, 7, 14]. При этом, слаборасходящийся пучок лучей проявляется в пространственном (по горизонтальному расстоянию и глубине) распределении интенсивности акустического поля в океаническом волноводе исключительно лишь в виде формируемой им системы каустик, которые в свою очередь уже формируют определенными своими частями каустический пучок около соответствующего слаборасходящемуся пучку опорного луча [3]. Вполне естественно, что проявление обычных каустических пучков и отвечающих слаборасходящимся пучкам каустических пучков в пространственном распределении интенсивности акустического поля возможно лишь при относительно высоких частотах излучения, то есть при достаточно многомодовом режиме распространения не только во всем допустимом диапазоне углов скольжения мод океанического волновода, но и в тех диапазонах, где расположены гладкие экстремумы угловой зависимости длины цикла соответствующих этим модам бриллюэновских волн [2, 4, 13]. Кроме того, преобладание по интенсивности акустического поля каустических и слаборасходящихся пучков становится все более существенным также и при увеличении до определенного оптимального размера апертуры соответствующим образом сфазированной вертикальной антенны [1, 6].

Отметим, что при расположении источника на определенной — критической глубине, совпадающей с горизонтом поворота луча, которому отвечает гладкий экстремум в угловой зависимости длины цикла лучей, около горизонтально выходящего из источника опорного луча формируется каустический пучок, являющийся одновременно и самым слаборасходящимся [6].

Очевидно, что на распространение каустических и слаборасходящихся пучков будут оказывать заметное влияние не только дифракционные эффекты [2, 4, 13], но и изменения акустических характеристик океанических волноводов в горизонтальном направлении [9, 10, 12]. При этом влияние горизонтальной неоднородности океанического волновода в существенно большей степени скажется на формировании и распространении каустических слаборасходящихся пучков, поскольку даже при достаточно малом изменении значения лучевого параметра, отвечающего положению гладкого экстремума у соответствующей зависимости длины цикла лучей, горизонт поворота соответствующего ему луча, а, следовательно, и критическая глубина, может существенно отличаться от глубины погружения источника. Вследствие этого формирующийся каустический пучок уже не будет являться одновременно и самым слаборасходящимся по трассе распространения. Кроме того, в горизонтально неоднородных океанических волноводах возможно существенное переформирование каустических и слаборасходящихся пучков по трассе распространения [10].

Поэтому необходимо, во-первых, дополнить сформулированные в [10, 12] качественные условия сохранения характерных свойств каустических и слаборасходящихся пучков в плавно неоднородных по трассе океанических волноводах соответствующими им приближенными аналитическими зависимостями интенсивности акустического поля, аналогичными полученным в [6] для горизонтально однородных океанических волноводов. Во-вторых, с использованием адиабатического приближения для модового представления поля [8], лучевой теории [15] и метода параболического уравнения [16] следует рассмотреть процессы переформирования каустических и слаборасходящихся пучков на конкретном, но достаточно общем примере плавно неоднородного по трассе океанического волновода. Причем, здесь представляется логичным воспользоваться с целями преемственности и обобщения полученных в [6] результатов также моделью относительно мелководного океанического волновода с неизменной по трассе стратификацией скорости звука, характеризующей вблизи расположения источника открытый ко дну подводный звуковой канал, но с увеличивающейся, в отличие от [6], глубиной водного слоя. Следует отметить, что аналогичная модель горизонтально неоднородного океанического волновода достаточно широко используется для описания наблюдаемых в реальных условиях закономерностей распространения акустических сигналов из шельфовой зоны в открытый океан [17–22].

КАУСТИЧЕСКИЕ И СЛАБОРАСХОДЯЩИЕСЯ ПУЧКИ ЛУЧЕЙ

Для получения необходимой в дальнейшем зависимости интенсивности акустического поля вдоль лучей в океаническом волноводе с плавно изменяющимися в горизонтальном направлении акустическими характеристиками воспользуемся ВКБ и адиабатическим приближениями для модового представления поля точечного источника тонального излучения с частотой ω [8]. Предположим, что в водном слое с изменяющейся глубиной ${H\left( r \right)}$ квадрат показателя преломления акустических волн ${{{n}^{{\text{2}}}}\left( {z,r} \right)}$ достаточно плавно изменяется с глубиной z и горизонтальным расстоянием r как выше ${n_{{\text{1}}}^{{\text{2}}}\left( {z,r} \right)}$, так и ниже ${n_{{\text{2}}}^{{\text{2}}}\left( {z,r} \right)}$ оси канала, расположенной на глубине $z = {{z}_{0}}\left( r \right)$:

при этом зависимости ${{{n}^{{\text{2}}}}\left( {z,r} \right)}$ и ${H\left( r \right)}$ удовлетворяют условиям применимости соответствующих приближений [8], а дно является акустически мягким [8].

Если теперь в рамках ВКБ и адиабатического приближений и при условии многомодового режима распространения волн выполнить полностью аналогичные [23–25] преобразования суммарного поля мод [8], но, как и в [25], при переходе от суммирования к интегрированию по номеру моды l ввести прежде под знак суммы тождественно равный единице множитель

то после интегрирования методом стационарной фазы получим, с учетом соответствующего этим приближениям дисперсионного уравнения следующее выражение для интенсивности акустического поля вдоль луча:

В равенствах (2)–(4) введены следующие обозначения: l_st – значение номера моды, отвечающее точке стационарной фазы соответствующего подынтегрального выражения; ${{{k}_{{\text{0}}}}\left( r \right) = {\omega \mathord{\left/ {\vphantom {\omega {{{c}_{{\text{0}}}}}}} \right. \kern-0em} {{{c}_{{\text{0}}}}}}\left( r \right)},$ ${{{c}_{{\text{0}}}}\left( r \right)}$ – скорость звука на оси канала; ${{{\chi }_{l}}\left( r \right)}$ – угол скольжения бриллюэновских волн на оси канала; ${{{{\bar {z}}}_{{\text{1}}}}\left( r \right)}$ и ${{{{\bar {z}}}_{{\text{2}}}}\left( r \right)}$ – соответственно минимальные и максимальные глубины, достигаемые бриллюэновскими волнами, для которых ${\nu \left( {{{z}_{1}},{{z}_{2}}} \right) = {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}$ либо ${\nu \left( {{{z}_{1}},{{z}_{2}}} \right) = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}},$ ${{{\beta }_{{\text{0}}}} = \beta \left( {r = {\text{0}}} \right)},$ ${\beta = {\text{cos}}{{\chi }_{{\text{0}}}}\left( r \right)},$ где ${{{\chi }_{0}}\left( r \right) = \chi \left( {z = {{z}_{0}},r} \right)}\,\, - $ угол скольжения луча на оси канала,

Проходимое лучом горизонтальное расстояние определяется при фиксированном значении β из следующего уравнения

где m₁ – целое число циклов соответствующего луча, выходящего из источника вниз ${{{\chi }_{s}} = \chi \left( {{{z}_{s}},r = 0} \right) < 0,}$ ${{{\mu }_{{\text{1}}}} = - {\text{1}}}$ или вверх ${{{\chi }_{s}} > {\text{0,}}}$ ${{{\mu }_{{\text{1}}}} = + {\text{1}}}$ и приходящего в точку приема сверху ${\chi \left( {z,r} \right) < 0,}$ ${{{\mu }_{{\text{2}}}} = + {\text{1}}}$ или снизу ${\chi \left( {z,r} \right) > 0,}$ ${{{\mu }_{{\text{2}}}} = - {\text{1}}},$ ${{{z}_{{\text{1}}}}\left( r \right)}$ и ${{{z}_{{\text{2}}}}\left( r \right)}$ – аналогичные ${{{{\bar {z}}}_{{\text{1}}}}\left( r \right)}$ и ${{{{\bar {z}}}_{{\text{2}}}}\left( r \right)}$ минимальные и максимальные глубины для лучей. Характеризующая фокусировку или дефокусировку величина Φ в (4) определяется следующим выражением:

Для дальнейшего анализа удобно с использованием (6) представить выражение (7) в виде суммы двух выражений

Выражение G_i принимает нулевое значение в однородном по трассе океаническом волноводе. В (7), (8) с целью сокращения записи введены следующие обозначения:

при этом m₂ характеризует целое число пространственных масштабов ${{{R}_{p}} = {\text{2}}\left| {R_{d}^{{\left( {\text{2}} \right)}}} \right|}$ дифракционной фокусировки групп мод, формирующих поля вдоль соответствующих геометроакустических лучей (6).

Таким образом, здесь важно отметить, что по аналогии с дифракционной фокусировкой поля многомодового пучка, т.е. фиксированной группы мод, формируемых вертикальной антенной около соответствующего опорного луча (см. [25]), модифицированное геометроакустическое приближение (4)–(9) описывает не только рефракционную, но и дифракционную фокусировку поля вдоль геометроакустических лучей в определенных пространственных областях, зависящих от характерного пространственного масштаба ${\left| {R_{d}^{{\left( {\text{2}} \right)}}} \right|}$ проявления аберрационных эффектов второго порядка ( n = 2 в (2)).

Как и в [6], рассмотрим изменения величины F  = 1/J, характеризующей пространственную расходимость интенсивности акустического поля (4), сначала для обычного каустического пучка, формирующегося лучами в достаточно узком диапазоне изменения лучевого параметра около горизонтально выходящего из источника луча:

Естественно, что с ростом горизонтального расстояния у формирующих такой пучок лучей будут изменяться значения лучевого параметра (10):

которые при r > 0 описываются соответствующим адиабатическому приближению (3) уравнением:

Тогда, с учетом (10) при разложении ${{{\gamma }_{0}}\left( {{{z}_{s}}} \right)}$ в ряд с использованием (4)–(9), получим для величины F следующее приближенное выражение:

При этом, как показано в [6] на примере однородного в горизонтальном направлении волновода, здесь (см. (13)–(15)) также выполняется неравенство ${{{\Phi }_{{{\text{1}}s}}} \ne {\text{0}}}.$ С использованием разложения в ряд с точностью до первого порядка малости по ${\Delta {{\beta }_{s}} = {{\beta }_{s}} - {{\beta }_{{{\text{0}}s}}}}$ слагаемые в выражении для Φ_2s (15), в основном влияющие на пространственную (рефракционную) расходимость обычного каустического пучка лучей, можно представить в следующем виде:

В (16) величина Δr_s характеризует фактически накапливающиеся с расстоянием различия в проявлении аберрационных эффектов первого порядка (рефракционной фокусировки и дефокусировки) при распространении обычных каустических пучков в горизонтально неоднородных волноводах от распространения таких пучков в горизонтально однородных волноводах.

Естественно предположить, что каустический пучок сохранит присущие ему свойства (13)–(15) в той области горизонтальных расстояний, где его характерная ширина Λ будет оставаться заметно меньше диапазона глубин $\Delta z = {{z}_{2}}\left( {{{\beta }_{s}}} \right) - {{z}_{1}}\left( {{{\beta }_{s}}} \right)$ между нижним и верхним горизонтами, достигаемыми соответствующим этому пучку опорным лучом. Как следует из [12], типичное для пучка соотношение Λ/Δz $ \ll $ 1 имеет место лишь при выполнении необходимого условия

в котором величина определяет интегральный пространственный масштаб переформирования интерференционной структуры поля пучка. Если в подынтегральном выражении (19) воспользоваться разложением величины D(β) в ряд с точностью до первого порядка малости по Δβ (11), а также следующими из (3), (12) приближенными равенствами то условие (18) можно переписать в более удобном для физического анализа виде интегрального неравенства выполнение которого зависит от числа эффективно формирующих каустический пучок мод Δl и изменяющейся с горизонтальным расстоянием величины $R_{d}^{{\left( 2 \right)}}$ (9), характеризующей пространственный масштаб проявления аберрационных эффектов второго порядка $\left| {R_{d}^{{\left( 2 \right)}}\left( {{{\beta }_{s}}} \right)} \right|$ [25]. По аналогии с преобразованием выражения (16), используя разложение в ряд $R_{d}^{{\left( 2 \right)}}\left( {{{\beta }_{s}}} \right)$ с точностью до первого порядка малости по Δβ_s, из (22) находим неравенство в котором функция учитывает влияние плавной горизонтальной неоднородности океанического волновода на пространственный масштаб проявления аберрационных эффектов второго порядка, то есть дифракционной расходимости каустического пучка.

Рассмотрим теперь поведение величины F для слаборасходящегося пучка лучей с определенными начальными значениями лучевого параметра

изменения которого с расстоянием описываются также решениями уравнения (12):

Изменение же значения лучевого параметра β_ca, отвечающего положению гладкого экстремума

зависимости D(β) будет определяться исключительно лишь ее трансформацией с расстоянием. С учетом сказанного (см. (24)–(26)), используя разложение величины ${{\partial D} \mathord{\left/ {\vphantom {{\partial D} {\partial \beta }}} \right. \kern-0em} {\partial \beta }}$ сначала по Δβ, а затем – ${{\left. {\left( {{{\partial D} \mathord{\left/ {\vphantom {{\partial D} {\partial \beta }}} \right. \kern-0em} {\partial \beta }}} \right)} \right|}_{{\beta = {{\beta }_{c}}}}}$ по $\Delta {{\beta }_{c}} = {{\beta }_{c}} - {{\beta }_{{ca}}}$ с точностью до первого порядка малости, получим из (4)–(9) следующее выражение

Из сравнительного анализа выражений для F_s (13)–(15) и F_c (27)–(29) следует, что аберрационные эффекты первого порядка (рефракционные эффекты) будут оказывать меньшее влияние на пространственную расходимость слаборасходящегося пучка, чем на расходимость обычного пучка при выполнении очевидного условия

Поскольку диапазон изменения лучевого параметра Δβ в соответствующих пучках (11), (25) можно сделать сколь угодно малым за счет выбора отвечающих этим пучкам достаточно малых диапазонов Δβ_0s (10), Δβ_0c (24), то неравенство (30) будет оставаться справедливым всегда при выполнении дополнительного условия

Из выражения для F_c (27)–(29) следует, что выполнение дополнительного условия (31) необходимо также и для того, чтобы пучок оставался слаборасходящимся вдоль всей трассы распространения, т.е. изменяющееся с расстоянием значение лучевого параметра $\beta = {{\beta }_{{ca}}},$ отвечающее положению гладкого экстремума у зависимости D(β), не превышало допустимых значений лучевого параметра β (25) лучей, формирующих соответствующий пучок.

Однако, для того чтобы слаборасходящийся пучок сохранял присущие пучку свойства, необходимо потребовать также выполнение аналогичного (18) условия, которое с учетом (19), (25), (26) можно приближенно представить в следующем виде

С использованием в подынтегральном выражении (32) аналогичных (20), (21) приближенных равенств, а также условия (31) и соотношения $D\left( {{{\beta }_{c}}} \right) \approx D\left( {{{\beta }_{{ca}}}} \right),$ из (32) находим следующее неравенство

в котором величина характеризует пространственный масштаб $\left| {R_{d}^{{\left( 3 \right)}}} \right|$ проявления аберрационных эффектов третьего порядка в слаборасходящемся пучке [12].

Используя полученные выше результаты для F_s (13)–(15) и F_c (27)–(29), остановимся на рассмотрении поведения величины F для самого слаборасходящегося каустического пучка с определенным начальным диапазоном изменения лучевого параметра

который изменяется с ростом горизонтального расстояния

Здесь в отличие от (10), (11) и (24), (25) предполагается, что источник расположен на критической глубине [6], на которой значение лучевого параметра β_0s горизонтально выходящего из источника опорного луча для каустического пучка совпадает со значением лучевого параметра ${{\beta }_{{сa}}}\left( {r = 0} \right)$, отвечающего положению гладкого экстремума у зависимости D(β) при r = 0 (см. (35), (36)). В этом случае, выполнив полностью аналогичные использованным при нахождении зависимостей F_s (13)–(15) и F_c (27)–(29) приближенные вычисления, получим для величины F следующее выражение

в котором ${{\Phi }_{{1g}}} \ne 0.$

Из сравнения зависимостей для F_c (27)–(29) и F_sc (37)–(39) следует, что при выполнении условия (31), как и в горизонтально однородном океаническом волноводе [6], пространственная (рефракционная) расходимость слаборасходящегося каустического пучка будет заметно меньше, чем обычного слаборасходящегося пучка.

Наряду с рассмотренными тремя вариантами пространственной расходимости пучков F_s (13)–(15), F_c (27)–(29) и F_sс (37)–(39) возможен также своеобразный промежуточный вариант, когда при распространении обычного каустического пучка в определенной области горизонтальных расстояний в присущем ему диапазоне изменения лучевого параметра (11) будет находиться значение лучевого параметра ${{\beta }_{{сa}}},$ отвечающее положению гладкого экстремума у зависимости D(β); более того, на определенном расстоянии может выполняться равенство характерных значений лучевого параметра ${{\beta }_{s}} = {{\beta }_{{ca}}}.$ В этом случае могут проявиться следующие закономерности. Во-первых, в соответствующей области горизонтальных расстояний помимо одной системы каустик, присущей обычному каустическому пучку, сформируется дополнительная система каустик, присущая слаборасходящемуся пучку; при этом возможна существенная фокусировка каустического пучка на тех горизонтальных расстояниях, где имеет место слияние определенных каустик из этих двух каустических систем. Во-вторых, очевидно, что пространственная (рефракционная) расходимость такого каустического пучка в определенной области горизонтальных расстояний будет описываться величиной F, возрастающей быстрее, чем F_sс (37)–(39), но медленнее чем F_s (13)–(15) с увеличением r. Наибольший интерес представляет собой изучение именно таких закономерностей, поскольку они могут проявляться при формировании пространственной (по горизонтальному расстоянию и по глубине) интерференционной структуры акустических полей каустических и слаборасходящихся пучков только лишь в горизонтально неоднородных океанических волноводах, в отличие от описываемых зависимостями F_s (13)–(15), F_c (27)–(29) и F_sс (37)–(39) закономерностей, которые с соответствующими изменениями проявляются и в горизонтально однородных океанических волноводах [6]. Поэтому следующий раздел статьи посвящен рассмотрению процессов переформирования интерференционной структуры акустических полей каустических и слаборасходящихся пучков в горизонтально неоднородном волноводе.

МНОГОМОДОВЫЕ КАУСТИЧЕСКИЕ И СЛАБОРАСХОДЯЩИЕСЯ ПУЧКИ

С целью количественного и достаточно строгого описания закономерностей, проявляющихся при переформировании интерференционной структуры акустических полей каустических и слаборасходящихся пучков в горизонтально неоднородном океаническом волноводе воспользуемся аналогичной [6] простейшей моделью открытого ко дну подводного звукового канала в виде неизменной с горизонтальным расстоянием билинейной зависимости квадрата показателя преломления (1) от глубины

но с увеличивающейся толщиной водного слоя при R = 3 × 10⁴ м и следующих значениях параметров (см. рис. 1, а также [6]):

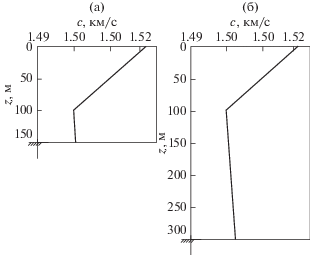
Здесь ρ – плотность среды водного слоя, ρ_g – плотность среды жидкого дна со скоростью звука c_g.

Предположим теперь, что акустическое поле в волноводе возбуждается вертикальной антенной, состоящей из N = 2n + 1 (n ≥ 0) дискретно расположенных по ее апертуре h = nλ₀ точечных источников, излучающих тональный сигнал с частотой f. Тогда пространственное распределение интенсивности акустического поля J(r, z) будет описываться в адиабатическом приближении выражением следующего вида [6, 8]:

Здесь ${{\lambda }_{0}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}}$ – минимальная длина волны излучения, ${{\psi }_{l}}\left( {z,r} \right)$ – ортонормированные собственные функции волновода сравнения и соответствующие ему горизонтальные волновые числа мод k_l с номерами $l = [1,L]$, ${{z}_{s}}$ – глубина центра антенны (j = 0), ${{\chi }_{s}}$ – угол компенсации антенны, совпадающий с углом выхода луча из источника, расположенного в ее центре (j = 0).

Как следует из (43), формирование наиболее устойчивой крупномасштабной интерференционной структуры акустического поля определяется зависимостью от номера моды интегрального пространственного масштаба интерференции соседних мод

обратно пропорционального усредненной величине, в свою очередь обратно пропорциональной текущему пространственному масштабу интерференции

Очевидно, что при многомодовом режиме распространения акустических сигналов наличие у ${{\bar {R}}_{{l,l + 1}}}$ (45) при $l = {{\bar {l}}_{{ca}}}$ достаточно гладкого экстремума в определенном диапазоне изменения l, расположение которого слабо зависит от расстояния, приведет к выделенности соответствующего масштаба интерференции в J(r, z) (43), а именно, проявлению фокусировки акустического поля в океаническом волноводе приблизительно с пространственным периодом ${{\bar {R}}_{{ca}}} = {{\left. {{{{\bar {R}}}_{{l,l + 1}}}} \right|}_{{l = {{{\bar {l}}}_{{ca}}}}}}.$ Кроме того, в J(r, z) могут заметно проявляться пространственные масштабы интерференции ${{\bar {R}}_{{l,l + 1}}}$ (45), соответствующие расположенным при определенных значениях $l = {{l}_{s}}$ достаточно узким максимумам зависимости коэффициента возбуждения мод V_l (44) от их номера.

В дальнейшем, анализ именно зависимостей величин V_l (44), ${{\bar {R}}_{{l,l + 1}}}$ (45) и ${{R}_{{l,l + 1}}}$ (46) позволит однозначно интерпретировать результаты численного моделирования для J(r, z) (43). Однако, прежде чем перейти к целенаправленному численному моделированию соответствующих процессов, выполним приближенный анализ поведения с расстоянием r зависимостей k_l, ${{\bar {R}}_{{l,l + 1}}}$ (45) и ${{R}_{{l,l + 1}}}$ (46) от l. С этой целью сделаем дополнительное упрощение модели (40)–(42) океанического волновода, предположив, что его дно является акустически мягким. Такое допущение вполне оправдано, поскольку для представляющих основной интерес достаточно малых углов скольжения мод $\left| {{{\chi }_{l}}} \right| < {{\left[ {{{c}_{g}} - c\left( H \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {{{c}_{g}} - c\left( H \right)} \right]} {{{c}_{g}}}}} \right. \kern-0em} {{{c}_{g}}}}$ коэффициент отражения акустических волн от дна весьма близок к –1.

В рамках такой упрощенной модели волновода с использованием ВКБ и адиабатического приближений (см. (3)) получим простое дисперсионное уравнение, которое для удобства анализа запишем для величины ${{\alpha }_{l}} = \sqrt {1 - \beta _{l}^{2}} = \left| {\sin {{\chi }_{l}}} \right|,$ $\left( {{{\beta }_{l}} = {{{{k}_{l}}} \mathord{\left/ {\vphantom {{{{k}_{l}}} {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}}} \right){\kern 1pt} :$

Здесь

В рамках используемых здесь приближений можно, по аналогии с горизонтально однородными волноводами [2], получить для характерных пространственных масштабов интерференции (45), (46) следующие выражения

в которых ${{D}_{l}} = - \left( {{{\partial {{J}_{l}}} \mathord{\left/ {\vphantom {{\partial {{J}_{l}}} {\partial {{\beta }_{l}}}}} \right. \kern-0em} {\partial {{\beta }_{l}}}}} \right)$ – текущая длина цикла модифицированной бриллюэновской волны, определяемая аналогичной (5) при β ⇒ β_l зависимостью, имеющей для рассматриваемой модели волновода достаточно простой вид:

Проанализируем сначала поведение $1$ решений уравнений (47)–(49). Как и следовало ожидать (см. (47)), углы скольжения чисто рефрагированных мод $0 < {{\alpha }_{l}} \leqslant {{\alpha }_{H}}$ (захваченных подводным звуковым каналом) не зависят от горизонтального расстояния (${{\partial {{\alpha }_{l}}} \mathord{\left/ {\vphantom {{\partial {{\alpha }_{l}}} {\partial r = 0}}} \right. \kern-0em} {\partial r = 0}}$). Естественно, что у представляющих здесь основной интерес рефрагированных в верхнем термоклине $0 < z < {{z}_{0}}$ и взаимодействующих с наклонным дном мод ${{\alpha }_{H}} \leqslant {{\alpha }_{l}} \leqslant {{\alpha }_{0}}$ углы скольжения уже зависят от горизонтального расстояния (${{\partial {{\alpha }_{l}}} \mathord{\left/ {\vphantom {{\partial {{\alpha }_{l}}} {\partial r \ne 0}}} \right. \kern-0em} {\partial r \ne 0}}$), поскольку в уравнении (48) присутствует величина ${{\alpha }_{H}}\left( r \right)$. В рассматриваемой ситуации a₂/a₁$ \ll $ 1 (см. (42)) в предположении малости отношения ${{\left( {{{{{\alpha }_{H}}} \mathord{\left/ {\vphantom {{{{\alpha }_{H}}} {{{\alpha }_{l}}}}} \right. \kern-0em} {{{\alpha }_{l}}}}} \right)}^{2}} \ll 1$ можно получить приближенные решения уравнения (48), соответствующие модам с относительно малыми ${{\alpha _{l}^{2}} \mathord{\left/ {\vphantom {{\alpha _{l}^{2}} {3b \ll 1}}} \right. \kern-0em} {3b \ll 1}}$ и большими ${{\alpha _{l}^{2}} \mathord{\left/ {\vphantom {{\alpha _{l}^{2}} {3b \gg 1}}} \right. \kern-0em} {3b \gg 1}}$ углами скольжения:

где $b = \frac{{{{a}_{1}}}}{2}\left( {H - {{z}_{0}}} \right).$ Как следует из (52), углы скольжения рефрагированных в термоклине и взаимодействующих с наклонным дном мод уменьшаются с ростом горизонтального расстояния, причем заметно быстрее у мод с относительно малыми углами скольжения; в результате чего возрастают глубины горизонтов поворота соответствующих мод, а формируемое ими акустическое поле в термоклине $0 < z \leqslant {{z}_{0}}$ все более локализуется вблизи оси канала. По мере уменьшения ${{\alpha }_{l}}\left( r \right)$ (52) и увеличения ${{\alpha }_{H}}\left( r \right)$ мода с изначально фиксированным при r = 0 номером ${{l}_{s}} = {{S}_{t}}\left( {{{\alpha }_{{0s}}},r = 0} \right),$ где ${{\alpha }_{{0s}}} = {{\alpha }_{{{{l}_{s}}}}}\left( {r = 0} \right),$ при r = r_H перестает взаимодействовать с дном волновода и становится чисто рефрагированной. Поскольку на этом расстоянии r_H увеличивающееся число чисто рефрагированных мод ${{l}_{H}}\left( r \right) = {{S}_{H}}\left( {{{\alpha }_{H}}} \right)$ сравнивается с фиксированным при r = 0 номером моды ${{l}_{s}}$, то из соответствующего равенства ${{l}_{H}} = {{l}_{s}}$ находим

При расположении источника в термоклине на глубинах $0 < {{z}_{s}} < z{\text{*}}$, не превышающих сопряженную глубину

которая определяется из равенства $n_{1}^{2}\left( {z{\text{*}}} \right) = n_{2}^{2}\left( {{{H}_{0}}} \right)$, акустическое поле каустического пучка при r < D_l формируется в основном рефрагированными в термоклине и взаимодействующими с дном модами, глубины горизонтов поворота которых расположены вблизи глубины погружения источника [1, 6]. Поэтому из (53) при ${{z}_{b}} = {{z}_{s}}$ можно определить величину $\alpha _{{0s}}^{2} = {{a}_{1}}\left( {{{z}_{0}} - {{z}_{s}}} \right),$ а следовательно, соответствующий ей номер моды ${{l}_{s}} = {{S}_{t}}\left( {{{\alpha }_{{0s}}},r = 0} \right)$ (48), отвечающий положению основного максимума зависимости коэффициента возбуждения мод V_l (44), и расстояние r_H (54), начиная с которого сформированный около опорной при r = 0 бриллюэновской волны с ${{\alpha }_{l}}\left( {r = 0} \right) = {{\alpha }_{{0s}}}$ каустический пучок перестанет взаимодействовать с наклонным дном океанического волновода.

Для реализации такого эффективно-согласованного перехода рефрагированных в термоклине и взаимодействующих с наклонным дном мод в чисто рефрагированные моды подводного звукового канала [17–22] на определенном участке океанического волновода $0 < r < R$ (см. (40), (41)) при $c\left( {{{z}_{s}}} \right) > c\left( H \right)$ необходимо, чтобы расстояние r_H (54) не превышало характерного масштаба неоднородности R (41), но превышало интегральный пространственный масштаб интерференции соседних мод ${{\bar {D}}_{{{{l}_{s}}}}}\left( {{{r}_{H}}} \right)$ (50):

при этом предполагается также выполнение условий применимости ВКБ и адиабатического приближений [8]. Неравенства (56) позволяют с использованием (51), (54) определить соотношения между параметрами z₀, H₀, a₁, a₂, R и z_s, при которых возможен эффективно-согласованный переход прежде взаимодействующего с наклонным дном каустического пучка в подводный звуковой канал океанического волновода (40), (41), удовлетворительно моделирующего также и соответствующие условия аналогичного распространения акустических сигналов в реальных шельфовых зонах океана [17–22].

Относительно взаимодействующих с поверхностью и дном мод (${{\alpha }_{0}} \leqslant {{\alpha }_{l}} \leqslant {{\alpha }_{g}}$) отметим лишь, что их углы скольжения также уменьшаются с ростом горизонтального расстояния; это с очевидностью следует из приближенного решения уравнения (49):

Расстояние r_t, на котором мода с фиксированным при r = 0 номером l = l_t и ${{\alpha }_{l}}\left( {r = 0} \right) = {{\alpha }_{t}}$ перестанет взаимодействовать со свободной поверхностью волновода, определится из равенства l_t = l₀(r_t):

Как уже отмечалось выше, при расположении источника в термоклине на глубинах $0 < {{z}_{s}} < z{\text{*}}$ основной интерес представляют рефрагированные в термоклине и взаимодействующие с наклонным дном моды, поэтому ниже остановимся на анализе поведения зависимости ${{D}_{l}}$ (51) в соответствующем диапазоне ${{\alpha }_{H}} \leqslant {{\alpha }_{l}} \leqslant {{\alpha }_{0}},$ где при выполнении определенных условий возможно существование у ${{D}_{l}}$ гладкого минимума [6]. При выполнении аналогичных (26) условий с использованием (51) находим для величины $\alpha _{l}^{2} = \alpha _{{ca}}^{2},$ определяющей положение гладкого минимума у зависимости ${{D}_{l}}$ (51), следующее уравнение:

Учитывая малость величины $\alpha _{{ca}}^{2} \ll 1,$ из (59) в первом приближении найдем для нее достаточно точное решение [6]

с использованием которого определим критическую глубину

Как следует из (60), (61), с ростом глубины водного слоя H(r) величина $\alpha _{{ca}}^{2}$ (60) возрастает $\alpha _{{ca}}^{2} \to \alpha _{0}^{2},$ а z_ca (61) уменьшается, ${{z}_{{ca}}} \to 0;$ при этом минимум зависимости ${{D}_{l}}$ (51), существующий лишь при выполнении условия $\alpha _{{ca}}^{2} < \alpha _{0}^{2},$ т.е. при ${{z}_{0}} < H\left( r \right) < 3{{z}_{0}}$ для a₂/a₁ $ \ll $ 1, становится все более гладким, поскольку уменьшается по абсолютной величине соответствующее значение второй производной:

Поскольку же величина ${{\alpha }_{{{{l}_{s}}}}}\left( r \right) = {{\alpha }_{s}}\left( r \right),$ соответствующая опорной бриллюэновской волне каустического пучка, с ростом расстояния наоборот уменьшается (см. (48), (52)), в отличие от возрастающей величины $\alpha _{{ca}}^{2}\left( r \right)$ (60), то при глубинах погружения источника, для которых выполняется условие $\alpha _{{0s}}^{2} > \alpha _{{ca}}^{2}\left( {r = 0} \right)$, возможно пересечение кривых, отвечающих зависимостям ${{\alpha }_{s}}\left( r \right)$ и ${{\alpha }_{{ca}}}\left( r \right)$ на определенном расстоянии r_ca, где ${{\alpha }_{s}}\left( {{{r}_{{ca}}}} \right) = {{\alpha }_{{ca}}}\left( {{{r}_{{ca}}}} \right).$

Как следует из предыдущего раздела, при r = r_ca начнет формироваться дополнительная система каустик. Однако очевидно, что она заметнее всего сможет проявиться начиная с расстояния $r\tilde { - }{{\bar {r}}_{{ca}}} > {{r}_{{ca}}},$ уменьшающегося с увеличением отношения ${{{{\alpha }_{{ca}}}\left( {r = 0} \right)} \mathord{\left/ {\vphantom {{{{\alpha }_{{ca}}}\left( {r = 0} \right)} {{{\alpha }_{{0s}}}}}} \right. \kern-0em} {{{\alpha }_{{0s}}}}} < 1$ и определяемого из уравнения

в котором номер моды $l = {{\bar {l}}_{{ca}}}\left( r \right)$ соответствует положению гладкого минимума зависимости ${{\bar {D}}_{l}}\left( r \right)$ (см. (45), (50)). Поскольку минимум ${{\bar {D}}_{l}}$ при $l = {{\bar {l}}_{{ca}}}$ будет, по аналогии с минимумом ${{D}_{l}}$ при $l = {{l}_{{ca}}},$ так же становиться все более гладким с ростом r (см. (64)), то формирование дополнительных каустических структур в J(r,z) заметнее всего проявится при определенном значении отношения ${{{{\alpha }_{{ca}}}\left( {r = 0} \right)} \mathord{\left/ {\vphantom {{{{\alpha }_{{ca}}}\left( {r = 0} \right)} {{{\alpha }_{{0s}}}}}} \right. \kern-0em} {{{\alpha }_{{0s}}}}} < 1$ в соответствующей пространственной области $r > {{\bar {r}}_{{ca}}}$, которая ограничивается не только выполнением условия ${{\bar {l}}_{{ca}}} < {{l}_{0}}\left( {{{{\bar {r}}}_{{ca}}}} \right)$, но и постепенным уменьшением эффективной ширины $\Delta {{l}_{{ca}}}$ минимума ${{\bar {D}}_{l}}$, приводящим к ослаблению влияния преобладающих по амплитуде мод на формирование отвечающих ему каустических структур.

Полученные выше результаты аналитических расчетов позволяют приступить теперь к целенаправленному численному моделированию процессов формирования пространственной интерференционной структуры акустического поля в рассматриваемом горизонтально неоднородном океаническом волноводе (40)–(42). При этом, как и в [6], выберем в соответствии с выводами аналитических исследований достаточно высокую частоту излучения f = 3 кГц и характерные для данного волновода значения глубин погружения точечного источника или центра антенны ${{z}_{s}} = {{{{z}_{0}}} \mathord{\left/ {\vphantom {{{{z}_{0}}} 2}} \right. \kern-0em} 2}$ = $50\,\,{\text{м}}\,\, < {{z}_{{ca}}}\left( {r = 0} \right)$ и ${{z}_{s}} = {{z}_{{ca}}}\left( {r = 0} \right)$ = = 72.73 м.

Из приведенных на рис. 2 зависимостей нормированного коэффициента возбуждения мод

от их номера видно, что основной (абсолютный) максимум П_l расположен при l = l_s = 40 для z_s = 50 м и при l = l_s = 25 для z_s = z_ca(r = 0). Поэтому, как показано в [1, 6], именно модами с близкими к соответствующему значению l = l_s номерами формируется каустический пучок. С учетом такого расположения абсолютных максимумов П_l (рис. 2), из представленных на рис. 3 зависимостей ${{\bar {R}}_{{l,l + 1}}}$ (45), ${{R}_{{l,l + 1}}}$ (46) следует, что равенство (62) выполняется на расстоянии ${{\bar {r}}_{{ca}}} \simeq 10$ км для l_s = 40 и ${{\bar {r}}_{{ca}}} \simeq 5$ км для l_s = 25. Это означает, что формирование дополнительных каустических структур начнет проявляться при $r > 10$ км для z_s = 50 м и $r > 5$ км для z_s = z_ca(r = 0). Последнее утверждение полностью подтверждается полученными с использованием адиабатического приближения (43) результатами численных расчетов пространственного распределения нормированной интенсивности J₀(r,z) = rJ(r,z) акустического поля точечного источника (рис. 4). При этом дополнительные каустические структуры в J₀(r,z) заметнее всего проявляются на расстояниях 15 < r < 20 км при z_s = = 50 м (рис. 4а) и на расстояниях 7.5 < r < 12.5 км при z_s = z_ca(r = 0) (рис. 4б). Таким образом, в полном соответствии с результатами аналитических расчетов с увеличением отношения ${{{{{\bar {l}}}_{{ca}}}\left( {r = 0} \right)} \mathord{\left/ {\vphantom {{{{{\bar {l}}}_{{ca}}}\left( {r = 0} \right)} {{{l}_{s}}}}} \right. \kern-0em} {{{l}_{s}}}} < 1$ (то есть ${{{{\alpha }_{{ca}}}\left( {r = 0} \right)} \mathord{\left/ {\vphantom {{{{\alpha }_{{ca}}}\left( {r = 0} \right)} {{{\alpha }_{{0s}}}}}} \right. \kern-0em} {{{\alpha }_{{0s}}}}} < 1,$ так как ${{\bar {l}}_{{ca}}}\left( {r = 0} \right)$ = ${{l}_{{ca}}}\left( {r = 0} \right)$) уменьшается горизонтальное расстояние ${{\bar {r}}_{{ca}}}$, с которого начинает заметно проявляться формирование дополнительных каустических структур в J₀(r,z), отвечающих переформированию каустического пучка в слаборасходящийся пучок в относительно узкой пространственной области.

Тот факт, что в отвечающих переформированию каустического пучка в слаборасходящийся пучок пространственных областях формируются именно каустические структуры, отвечающие за появление соответствующих им зон повышенной акустической освещенности (рис. 4), доказывают приведенные на рис. 5 результаты численного моделирования, полученные с использованием лучевой теории [15], позволяющей достаточно точно описывать и, тем самым, идентифицировать каустические структуры в пространственном распределении интенсивности акустического поля.

Применимость же адиабатического приближения (43) для достаточно корректного описания эффекта формирования дополнительных каустических структур в пространственном распределении нормированной интенсивности акустического поля точечного источника в рассматриваемой модели горизонтально неоднородного океанического волновода (40)–(42) подтверждается аналогичными результатами численного моделирования для J₀(r,z), полученными с использованием параболического уравнения (рис. 6). Поэтому далее также воспользуется именно адиабатическим приближением (43) для описания в рассматриваемом волноводе (40)–(42) формирования вертикальной антенной при ${{\chi }_{s}} = 0$ многомодового каустического пучка, при этом уделяя основное внимание его распространению в пространственной области $r > {{\bar {r}}_{{ca}}},$ где формируется дополнительная каустическая структура, соответствующая одному точечному источнику излучения, расположенному на глубине центра антенны.

Как следует из приведенных на рис. 7, 8 результатов численных расчетов, при оптимальном размере апертуры антенны h = h₀= n₀λ₀ (n₀ = 15), при котором у зависимости П_l (63) присутствует всего лишь один максимум [1, 6], расположенный при том же значении l = l_s = 40, что и у зависимости П_l для точечного источника излучения (рис. 2а, 7а), дополнительная каустическая структура в поле многомодового каустического пучка заметнее всего проявляется в том же диапазоне горизонтальных расстояний 15 < r < 20 км (рис. 8а), что и для точечного источника излучения (рис. 4а). Однако, как уже отмечалось в [1, 6], при дальнейшем увеличении размера апертуры антенны h > h₀ у зависимости П_l (63) наряду с основным (абсолютным) максимумом появляются следующие за ним относительные максимумы в диапазоне более высоких номеров мод; при этом основной максимум смещается в диапазон меньших значений l = l_s < 40 (рис. 7). В результате такого поведения зависимости П_l (рис. 7) наиболее заметная при 15 < r < 20 км каустическая структура в J₀(r,z) переформировывается и сдвигается в область меньших горизонтальных расстояний сначала в пределах одного соответствующего цикла отражения каустического пучка от дна 15 < r < 20 км (рис. 8б), а затем при N > 81 формируется уже в области расстояний 10 < r < 15 км, соответствующей предыдущему циклу отражения каустического пучка от дна (рис. 8в, г).

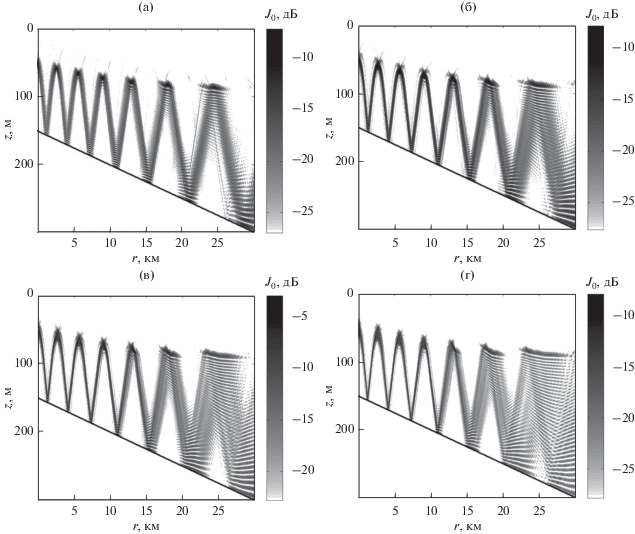
Описанный процесс переформирования дополнительной каустической структуры в поле многомодового каустического пучка на уменьшающихся с ростом апертуры h > h₀ горизонтальных расстояниях (рис. 8), обусловленный смещением основного максимума у зависимости П_l в диапазон низких номеров мод (рис. 7), полностью аналогичен рассмотренному выше процессу уменьшения горизонтального расстояния до формируемой дополнительной каустической структуры в J₀(r,z) точечным источником излучения с увеличением глубины его погружения (рис. 4– 6), при котором основной максимум при l = l_s у П_l также смещается в диапазон низких номеров мод (рис. 2).

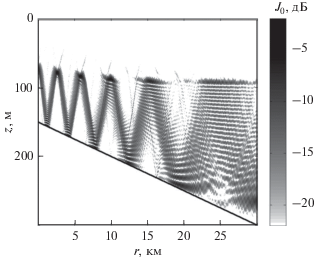
Естественно, что при расположении центра антенны на критической при r = 0 глубине ${{z}_{{ca}}}\left( {r = 0} \right) = {{z}_{s}}$ формируемый каустический пучок уже не будет являться одновременно и самым слаборасходящимся, поскольку характерная для данного волновода (40)–(42) критическая глубина z_ca уменьшается с ростом r (см. (63)) и пространственная расходимость каустического пучка при ${{z}_{s}} = {{z}_{{ca}}}\left( {r = 0} \right)$ (рис. 9) заметно превышает пространственную расходимость каустического пучка при ${{z}_{s}} = 50 < {{z}_{{ca}}}\left( {r = 0} \right)$ (рис. 8а). Кроме того, поскольку углы скольжения мод относительно низких номеров уменьшаются с ростом r заметно быстрее, чем углы скольжения мод относительно высоких номеров (см. (52)), то сформированный антенной при ${{z}_{s}} = {{z}_{{ca}}}\left( {r = 0} \right)$ и h = h₀ каустический пучок уже на расстояниях r > 22 км перестает взаимодействовать с наклонным дном волновода и полностью захватывается звуковым каналом (рис. 9).

ЗАКЛЮЧЕНИЕ

С использованием ВКБ и адиабатического приближений для модового представления поля получены аналитические зависимости, описывающие в рамках модифицированной лучевой теории изменение интенсивности акустического поля в каустических (13)–(15) и слаборасходящихся (27)–(29), (37)–(39) пучках, распространяющихся в горизонтально неоднородных рефракционных океанических волноводах при точечном источнике тонального излучения. С учетом характерных пространственных масштабов проявления аберрационных эффектов второго и третьего порядков определены пространственные области (22), (33), в которых при выполнении сформулированных необходимых условий реализуются присущие таким пучкам зависимости интенсивности акустического поля от горизонтального расстояния.

В рамках численного моделирования, основанного на теории адиабатических мод, геометроакустическом приближении и методе параболического уравнения, исследованы процессы переформирования каустических и слаборасходящихся пучков при точечном источнике тонального излучения, распространяющихся в плавно неоднородном по трассе океаническом волноводе, в качестве модели которого использовался водный слой с увеличивающейся глубиной и неизменной в горизонтальном направлении стратификацией скорости звука, характеризующей вблизи источника открытый ко дну подводный звуковой канал. При этом были установлены следующие закономерности.

Во-первых, при обычном для реальных ситуаций расположении источника выше оси канала может иметь место переформирование каустического пучка, приводящее к формированию им в определенной пространственной области $r > {{\bar {r}}_{{ca}}}$ (62) характерных для слаборасходящегося пучка дополнительных каустических структур (рис. 4).

Во-вторых, формирование таких дополнительных каустических структур, горизонтальные расстояния до которых возрастают с уменьшением глубины источника (рис. 4а, 4б), обусловлено изменением с расстоянием характерной для данного волновода зависимости пространственного масштаба интерференции соседних мод от их номера (45), приводящим к смещению отвечающего слаборасходящемуся пучку гладкого минимума этой зависимости в диапазон относительно высоких номеров мод (рис. 3), в котором расположен соответствующий каустическому пучку основной (абсолютный) максимум зависимости коэффициента возбуждения мод от их номера (рис. 2).

В-третьих, максимумы интенсивности акустического поля в такой дополнительной каустической структуре достигаются в определенной пространственной области (рис. 4), в которой значение номера моды, отвечающее положению абсолютного максимума зависимости коэффициента возбуждения мод от их номера, совпадает с изменяющимся с расстоянием значением номера моды, отвечающим положению гладкого минимума соответствующей зависимости интегрального пространственного масштаба интерференции соседних мод (см. (62)).

В рамках принятой модели рефракционного океанического волновода с плавно увеличивающейся глубиной водного слоя и с использованием численного моделирования, основанного на адиабатическом приближении для модового представления акустического поля излучающей тональный сигнал вертикальной антенны, исследованы процессы формирования и распространения каустических и слаборасходящихся пучков. При этом были установлены следующие закономерности.

Во-первых, при фиксированном по глубине расположении центра антенны с увеличением ее апертуры до определенного размера, лишь незначительно превышающего ее оптимальный размер, при котором у зависимости соответствующего коэффициента возбуждения мод от их номера присутствует всего лишь один, существенно преобладающий по величине максимум (рис. 7а), в океаническом волноводе формирующийся около горизонтально выходящего из центра антенны опорного луча многомодовый каустический пучок фокусируется и становится одновременно слаборасходящимся в той же определенной пространственной области (рис. 8а), где формируется дополнительная каустическая структура при точечном источнике излучения, расположенном на глубине центра антенны (рис. 4а).

Во-вторых, при дальнейшем увеличении размера апертуры антенны и заметном его превышении над оптимальным размером в формирующейся в океаническом волноводе многопучковой структуре поля каустического пучка уменьшается горизонтальное расстояние до пространственной области фокусировки основного (преобладающего по интенсивности) каустического пучка в этой системе каустических пучков (рис. 8б, 8в, 8г). Последнее объясняется тем, что по мере появления дополнительных (относительных) максимумов зависимости коэффициента возбуждения мод от их номера, отвечающее положению абсолютного максимума значение номера моды смещается с ростом апертуры антенны в диапазон относительно низких номеров мод (рис. 7), в котором находится гладкий минимум зависимости интегрального пространственного масштаба интерференции соседних мод от их номера, смещающийся с ростом горизонтального расстояния наоборот в диапазон относительно высоких номеров мод (рис. 3). Такое поведение пространственных областей фокусировки основного каустического пучка полностью аналогично имеющему место уменьшению горизонтального расстояния до пространственных областей формирования дополнительных каустических структур при увеличении глубины погружения точечного источника (рис. 4), когда абсолютный максимум коэффициента возбуждения мод также смещается в диапазон относительно низких номеров мод (рис. 2).

Кроме того, выполненные в настоящей работе исследования позволили также с использованием отмеченных выше приближенных методов достаточно просто аналитически описать (см. (52)), а результатами численного моделирования наглядно проиллюстрировать (рис. 9) явление эффективно-согласованного перехода рефрагированных в термоклине и взаимодействующих с наклонным дном мод относительно мелководного участка океанического волновода в рефрагированные моды подводного звукового канала относительно глубоководного океанического волновода. При этом было установлено, что эффективно-согласованный переход акустического излучения из шельфовой зоны океана в подводный звуковой канал открытого океана возможен, если расстояние, на котором ранее взаимодействующая с наклонным дном мода становится чисто рефрагированной, заметно меньше соответствующего пространственного масштаба изменения глубины водного слоя, но больше характерного интегрального пространственного масштаба интерференции (см. (56)). Здесь следует отметить, что, по-видимому, существенное влияние наклона дна мелководного участка океанического волновода на эффективно-согласованный переход прежде взаимодействующего с его дном акустического излучения в подводный звуковой канал глубоководного океанического волновода впервые экспериментально было обнаружено в [26], а в [20] подробно обосновано результатами численного моделирования. Аналогичные [20, 26] результаты экспериментальных и теоретических исследований были чуть позже получены в [21, 22] и для другого района Мирового океана; хотя на возможность проявления соответствующих закономерностей [20, 26] указывалось еще гораздо раньше в [17–19, 27, 28].

Описанные в данной работе закономерности могут проявляться также и при распространении достаточно высокочастотных, широкополосных импульсных сигналов, поэтому формирование дополнительных каустических структур в аналогичных [21, 22, 29] океанических волноводах необходимо учитывать, например, при проектировании подводных навигационных систем (см. [29]).

Данное исследование выполнено в рамках госзадания ИПФ РАН по теме № 0035-2019-0009.