Акустический журнал, 2020, T. 66, № 3, стр. 235-241
Асимптотический подход к расчету волновых полей в слое с дефектом малого характерного размера
А. О. Ватульян a, b, *, О. А. Беляк c, **
a Южный федеральный университет
344006 Ростов-на-Дону, ул. Большая Садовая 105/42, Россия
b Южный математический институт ВНЦ РАН
362027 Владикавказ, ул. Маркуса 22, Россия
c Ростовский государственный университет путей сообщения
344038 Ростов-на-Дону, пл. Народного Ополчения 2, Россия
* E-mail: vatulyan@math.rsu.ru
** E-mail: o_bels@mail.ru
Поступила в редакцию 21.04.2019
После доработки 16.10.2019
Принята к публикации 29.10.2019
Аннотация
Рассмотрены задачи о колебаниях ортотропного слоя с цилиндрической полостью произвольного поперечного сечения под действием нагрузки, приложенной на его поверхности. В случае полостей малого относительного размера предложен асимптотический подход к расчету полей. Дана оценка области применимости асимптотического подхода по сравнению с методом граничных интегральных уравнений, а также сравнение с решением, полученным на основе приближения Борна.
ВВЕДЕНИЕ
Задачи о колебаниях упругих полуограниченных тел [1–11] достаточно давно привлекают внимание многих исследователей, поскольку анализ динамических процессов весьма важен, например, при оценке динамической прочности элементов тяжелонагруженных транспортных средств, машин и механизмов, в геофизике и горной механике. Отметим, что для изотропных однородных сред динамические процессы в таких структурах хорошо изучены [1, 2], а исследование волновых процессов для сред с более сложной структурой, например, для слоистых [3, 4], функционально-градиентных [5, 6], пористых [7–9] является весьма актуальным и в настоящее время. Одним из важных классов динамических задач теории упругости являются задачи о колебаниях упругих тел с локальными неоднородностями [10–13], такими как полости, включения, трещины. Изучение рассеяния упругих волн на неоднородностях разных типов и форм позволяет устанавливать факт наличия дефекта [14–16], что дает возможность определять тип и положение повреждения в исследуемой структуре. Чаще всего решение таких задач базируется на сведении их к системам граничных интегральных уравнений [1, 2, 11, 12] при помощи фундаментальных решений или матриц-функций Грина, что позволяет снизить размерность исходной задачи на единицу. Такой подход к решению реализован в настоящей работе. При решении динамических задач теории упругости также применяется метод блочных элементов [3] и гибридные численно-аналитические схемы [10, 13]. На основе решения задач о колебаниях сред с дефектами может быть осуществлен расчет амплитудных значений волновых полей, используемых для идентификации дефекта. В настоящей работе реализован подход, основанный на расчете волнового поля в волноводе с полостью на основе метода граничных элементов [17, 18], асимптотического подхода и приближения Борна, часто используемого в акустике [19, 20], и проведено сравнение результатов.
ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ
Рассмотрим установившийся режим колебаний с частотой $\omega $ ортотропного упругого слоя толщины $h$ с цилиндрической полостью, не выходящей на его границы, направляющая которой есть гладкая замкнутая кривая ${{l}_{0}}$ с образующей, параллельной оси $O{{x}_{2}}$. Нижняя грань слоя жестко защемлена и совпадает с осью $О{{х}_{1}}$, ось $О{{х}_{3}}$ направлена перпендикулярно вверх. Оси упругой симметрии материала совпадают с осями системы координат. Колебания в слое вызваны нагрузкой ${\mathbf{p}}({{x}_{1}},t) = \operatorname{Re} ({\mathbf{p}}({{x}_{1}}){{e}^{{ - i\omega t}}}),$ приложенной к верхней части границы слоя.
Краевая задача после отделения временного множителя имеет вид:
(1)
$\begin{gathered} {{\sigma }_{{ij,j}}} + \rho {{\omega }^{2}}{{u}_{i}} = 0, \\ {{\sigma }_{{ij}}} = {{C}_{{ijkl}}}{{u}_{{k,l}}},\,\,\,\,i,j = 1,2,3, \\ \end{gathered} $(2)
${{\left. {{{u}_{i}}} \right|}_{{{{x}_{3}} = 0}}} = 0,\,\,\,\,{{\left. {{{\sigma }_{{i3}}}} \right|}_{{{{x}_{3}} = h}}} = {{p}_{i}},\,\,\,\,{{\sigma }_{{ij}}}{{\left. {{{n}_{j}}} \right|}_{{{{l}_{0}}}}} = 0,$Исходная задача (1)–(2) в зависимости от типа нагрузки распадается на две: задача об антиплоских колебаниях ортотропного слоя с цилиндрической полостью (задача 1) и плоская задача о колебаниях слоя с полостью (задача 2). В задаче 1 ненулевой является компонента ${{u}_{2}}({{x}_{1}},{{x}_{3}})$ и в краевой задаче (1)–(2) полагаем $i = 2,$ $j = 1,3$. Для задачи 2 отличными от нуля являются компоненты ${{u}_{i}}({{x}_{1}},{{x}_{3}}),$ $i = 1,3$ и в краевой задаче (1)–(2) полагаем $i,j = 1,3.$
Основным способом исследования задач 1, 2 является предварительное сведение их к интегральным уравнениям с нерегулярными ядрами на основе идей теории потенциала. Решения краевых задач 1, 2 построены на основе матриц-функций Грина для слоя $U_{i}^{{(m)}}(x,\xi ),\,\,\,\,i = 1,2,3$, удовлетворяющих однородным граничным условиям на границах, и обобщенной теоремы взаимности [2], где индекс $m$ указывает, что сосредоточенная сила приложена в направлении оси $O{{x}_{m}},\,\,m = 1,2,3$. Функция Грина для ортотропного слоя в случае задачи 1 приведена в работе [21], а для задачи 2 имеет вид:
(3)
$\begin{gathered} U_{i}^{{(m)}}({\mathbf{x}},\xi ) = \frac{1}{{4{{\pi }^{2}}{{C}_{{33}}}}} \times \\ \times \,\,\iint\limits_\Gamma {\frac{{\Delta _{i}^{{(m)}}}}{\Delta }{{e}^{{i(\alpha ,{\mathbf{x}} - \xi )}}}}d{{\alpha }_{1}}d{{\alpha }_{3}} + S_{i}^{{(m)}}({\mathbf{x}},\xi ), \\ i = 1,3, \\ (\alpha ,{\mathbf{x}} - \xi ) = {{\alpha }_{1}}({{x}_{1}} - {{\xi }_{1}}) + {{\alpha }_{3}}({{x}_{3}} - {{\xi }_{3}}), \\ \end{gathered} $(4)
$\begin{gathered} \Delta = \left| {\begin{array}{*{20}{c}} {{{\gamma }_{1}}\alpha _{1}^{2} + {{\gamma }_{5}}\alpha _{3}^{2} - {{k}^{2}}}&{({{\gamma }_{5}} + {{\gamma }_{7}}){{\alpha }_{1}}{{\alpha }_{3}}} \\ {({{\gamma }_{5}} + {{\gamma }_{7}}){{\alpha }_{1}}{{\alpha }_{3}}}&{{{\gamma }_{5}}\alpha _{1}^{2} + \alpha _{3}^{2} - {{k}^{2}}} \end{array}} \right|, \\ {{\gamma }_{1}} = {{{{C}_{{11}}}} \mathord{\left/ {\vphantom {{{{C}_{{11}}}} {{{C}_{{33}}}}}} \right. \kern-0em} {{{C}_{{33}}}}},\,\,\,\,{{\gamma }_{5}} = {{{{C}_{{55}}}} \mathord{\left/ {\vphantom {{{{C}_{{55}}}} {{{C}_{{33}}}}}} \right. \kern-0em} {{{C}_{{33}}}}}, \\ {{\gamma }_{7}} = {{{{C}_{{13}}}} \mathord{\left/ {\vphantom {{{{C}_{{13}}}} {{{C}_{{33}}}}}} \right. \kern-0em} {{{C}_{{33}}}}}. \\ \end{gathered} $Здесь $\Delta _{i}^{{(m)}},\,\,i,\,\,m = 1,3$ – определители, получающиеся путем замены $\,\,k$-го столбца ($k = 1,2$) в (4) столбцом ${{g}^{{(m)}}} = {{\left( {{{\delta }_{{1m}}}{{\delta }_{{3m}}}} \right)}^{T}},$ ${{\alpha }_{i}},\,\,i = 1,3$ – параметры преобразования Фурье, $\Gamma $ – поверхность, всюду совпадающая с плоскостью ${{R}^{2}}$, за исключением множества нулей $\Delta $, которые она огибает в соответствии с принципом предельного поглощения. Второе слагаемое в выражении (3) представляет собой некоторую регулярную при $ - h + {{\delta }_{1}} < {{x}_{3}},$ ${{\xi }_{3}} < h - {{\delta }_{1}},$ ${{\delta }_{1}} > 0$ добавку, обеспечивающую выполнение однородных граничных условий. Надо отметить, что представление функций Грина для ортотропного слоя в виде однократного интеграла по контуру $\sigma $ в комплексной плоскости [21, 22] удобно использовать при построении решения задачи (1)–(2) путем сведения ее к интегральным уравнениям с нерегулярными ядрами (6), тогда как при решении задачи в рамках асимптотического подхода использовался вид (3).
Поле перемещений в слое под действием поверхностной нагрузки с носителем на отрезке $[a,b]$ для задач 1, 2 имеет вид:
(5)
$\begin{gathered} {{u}_{m}}(\xi ) = u_{m}^{*}(\xi ) - \int\limits_{{{l}_{0}}} {\sigma _{{ij}}^{{(m)}}({\mathbf{x}},\xi ){{n}_{j}}({\mathbf{x}}){{u}_{i}}({\mathbf{x}})d{{l}_{x}}} , \\ i,j,m = 1,2,3, \\ u_{m}^{*}(\xi ) = \int\limits_a^b {{{p}_{i}}({{x}_{1}})U_{i}^{{(m)}}({{x}_{1}},h,\xi )d{{x}_{1}}} , \\ \end{gathered} $Поля перемещений в слое (5) представимы в виде суммы двух слагаемых, первое из которых $u_{m}^{*}(\xi )$ – поле смещений в среде без дефекта под действием заданной нагрузки (эталонное поле смещений), второе слагаемое обусловлено наличием полости в слое. Таким образом, на основании соотношения (5) может быть рассчитано поле смещений всюду в слое, если найдено поле смещений на границе полости. В настоящей работе поля смещений на контуре полости рассчитаны на основании двух подходов: метод интегральных уравнений и основанный на нем метод граничных элементов (МГЭ), который может быть использован для полостей любой конфигурации, и асимптотический метод для круговых полостей малого относительного радиуса.
Далее сформулированы системы граничных интегральных уравнений (ГИУ), которые за счет специального выбора матриц-функций Грина содержат операторы лишь по границе полости. Системы ГИУ для задачи 1 $(j = 1,3;\,\,i{\text{,}}m = 2)$ и задачи 2 ($i,j,m = 1,3$) имеют вид:
(6)
$\begin{gathered} \frac{1}{2}{{u}_{m}}({\mathbf{y}}) = u_{m}^{*}({\mathbf{y}}) - {\text{v}}{\text{.p}}{\text{.}}\int\limits_{{{l}_{0}}} {\sigma _{{ij}}^{{(m)}}({\mathbf{x}},{\mathbf{y}}){{n}_{j}}} ({\mathbf{x}}){{u}_{i}}({\mathbf{x}})d{{l}_{x}}, \\ {\mathbf{y}} = ({{y}_{1}},{{y}_{3}}) \in {{l}_{0}}, \\ \end{gathered} $В настоящей работе численная реализация систем ГИУ (6) с нерегулярным ядром на основе МГЭ [17, 18] выполнена следующим образом. Гладкая граница аппроксимировалась N-угольником $l = \bigcup\nolimits_{q = 1}^N {{{l}_{q}}} $, где функция ${{u}_{m}}({{x}_{1}},{{x}_{3}})$ постоянна в пределах каждого из элементов ${{l}_{q}}$, а в качестве узлов выбраны середины соответствующих отрезков. Число ГЭ $N$ выбиралось таким образом, чтобы было не менее 5–6 элементов на длину волны. Таким образом, системы ГИУ (6) сводились к линейным алгебраическим системам относительно ${{u}_{{mq}}} = {{u}_{m}}({{y}_{{1q}}},{{y}_{{3q}}}).$ Полученные алгебраические системы относительно узловых смещений на контуре хорошо обусловлены, имеют явное диагональное преобладание. Отметим, что МГЭ позволяет рассчитывать поле перемещений на поверхности слоя в случае произвольной формы и размера дефекта. Процедура решения ГИУ (6) достаточно сложна и требует значительной вычислительной работы, однако, если сечение полости представляет собой окружность малого характерного размера, то схему расчета волновых полей можно значительно упростить на основе асимптотического анализа.
Асимптотический подход к решению многопараметрической задачи (1)–(2) о колебаниях ортотропного слоя с цилиндрической полостью, поперечное сечение которой представляет собой окружность радиуса $r$ с центром в точке ${{{\mathbf{x}}}_{0}} = ({{x}_{{10}}},{{x}_{{30}}}),$ был реализован в области изменения безразмерных параметров:
где ${{\varepsilon }_{1}} = {r \mathord{\left/ {\vphantom {r h}} \right. \kern-0em} h},$ ${{\varepsilon }_{2}} = \omega r\sqrt {{\rho \mathord{\left/ {\vphantom {\rho C}} \right. \kern-0em} C}} ,$ где $C = {{C}_{{44}}}$ для задачи 1, $C = {{C}_{{33}}}$ для задачи 2, а $\varepsilon *$ соответствует частоте запирания, когда в слое нет бегущих волн.Поля перемещений, всюду в области, занятой упругой средой, отличные от соотношений (5) и полученные на основании обобщенной теоремы взаимности, имеют вид:
(8)
$\begin{gathered} {{u}_{m}}(\xi ) = u_{m}^{*}(\xi ) - \int\limits_{{{l}_{0}}} {{{K}_{{im}}}({\mathbf{x}},\xi )\left( {{{u}_{i}}({\mathbf{x}}) - {{u}_{i}}(\xi )} \right)d{{l}_{x}}} - \\ - \,\,\rho {{\omega }^{2}}\int\limits_{{{S}_{0}}} {U_{i}^{{(m)}}({\mathbf{x}},\xi )d{{S}_{x}}{{u}_{i}}(\xi )} ,\,\,\,\,i,j,m = 1,2,3, \\ {{K}_{{im}}}({\mathbf{x}},\xi ) = \sigma _{{ij}}^{{(m)}}({\mathbf{x}},\xi ){{n}_{j}}({\mathbf{x}}), \\ \end{gathered} $(9)
$\begin{gathered} {{u}_{m}}(y) = u_{m}^{*}(y) - \int\limits_{{{l}_{0}}} {{{K}_{{im}}}({\mathbf{x}},{\mathbf{y}})\left( {{{u}_{i}}({\mathbf{x}}) - {{u}_{i}}({\mathbf{y}})} \right)d{{l}_{x}}} - \\ - \,\,\rho {{\omega }^{2}}\int\limits_{{{S}_{0}}} {U_{i}^{{(m)}}({\mathbf{x}},{\mathbf{y}})d{{S}_{x}}{{u}_{i}}({\mathbf{y}})} ,\,\,\,\,{\mathbf{y}} \in {{l}_{0}},i,j,m = 1,2,3. \\ \end{gathered} $Надо отметить, что система ГИУ (9) имеет регулярные подынтегральные функции в отличие от уравнений (6), а криволинейный интеграл по контуру ${{l}_{0}}$ существует как несобственный, что позволяет при дискретизации избежать вычисления сингулярных интегралов. Функцию ${{K}_{{im}}}({\mathbf{x}},{\mathbf{y}})$ можно представить в виде суммы двух слагаемых, первое из которых соответствует статическому случаю (${{\varepsilon }_{2}} = 0$), а второе – некоторая добавка:
При этом имеют место следующие оценки:
Выше введены следующие обозначения для задачи 1:
Поля смещений на контуре полости ${{l}_{0}}\,$ представимы в виде разложения по малому параметру $\,{{\varepsilon }_{1}}$:
(10)
$\begin{gathered} {{u}_{m}}({\mathbf{x}}) = u_{m}^{0}({{{\mathbf{x}}}_{0}}) + {{\varepsilon }_{1}}({{u}_{{m,1}}}({{{\mathbf{x}}}_{0}})\cos \theta + \\ + \,\,{{u}_{{m,3}}}({{{\mathbf{x}}}_{0}})\sin \theta ) + O(\varepsilon _{1}^{2}),\,\,\,\,m = 1,2,3. \\ \end{gathered} $Коэффициенты в разложении (10) вычислены аналитически и для задачи 1 приведены в работах [11, 12], а для задачи 2 имеют вид:
(11)
$\begin{gathered} {{u}_{m}}({{{\mathbf{x}}}_{0}}) = u_{m}^{*}({{{\mathbf{x}}}_{0}}), \\ {{u}_{{1,1}}}({{{\mathbf{x}}}_{0}}) = {{\left( {{{I}_{3}}u_{{3,3}}^{*}({{{\mathbf{x}}}_{0}}) - (1 - {{I}_{6}})u_{{1,1}}^{*}({{{\mathbf{x}}}_{0}})} \right)} \mathord{\left/ {\vphantom {{\left( {{{I}_{3}}u_{{3,3}}^{*}({{{\mathbf{x}}}_{0}}) - (1 - {{I}_{6}})u_{{1,1}}^{*}({{{\mathbf{x}}}_{0}})} \right)} {{{\Delta }_{1}}}}} \right. \kern-0em} {{{\Delta }_{1}}}}, \\ {{u}_{{3,3}}}({{{\mathbf{x}}}_{0}}) = {{\left( {(1 - {{I}_{1}})u_{{3,3}}^{*}({{{\mathbf{x}}}_{0}}) + {{I}_{4}}u_{{1,1}}^{*}({{{\mathbf{x}}}_{0}})} \right)} \mathord{\left/ {\vphantom {{\left( {(1 - {{I}_{1}})u_{{3,3}}^{*}({{{\mathbf{x}}}_{0}}) + {{I}_{4}}u_{{1,1}}^{*}({{{\mathbf{x}}}_{0}})} \right)} {{{\Delta }_{1}}}}} \right. \kern-0em} {{{\Delta }_{1}}}}, \\ {{u}_{{1,3}}}({{{\mathbf{x}}}_{0}}) = {{\left( { - {{I}_{2}}u_{{3,1}}^{*}({{{\mathbf{x}}}_{0}}) + (1 - {{I}_{5}})u_{{1,3}}^{*}({{{\mathbf{x}}}_{0}})} \right)} \mathord{\left/ {\vphantom {{\left( { - {{I}_{2}}u_{{3,1}}^{*}({{{\mathbf{x}}}_{0}}) + (1 - {{I}_{5}})u_{{1,3}}^{*}({{{\mathbf{x}}}_{0}})} \right)} {{{\Delta }_{2}}}}} \right. \kern-0em} {{{\Delta }_{2}}}}, \\ {{u}_{{3,1}}}({{{\mathbf{x}}}_{0}}) = {{\left( { - (1 - {{I}_{2}})u_{{3,1}}^{*}({{{\mathbf{x}}}_{0}}) - (1 - {{I}_{5}})u_{{1,3}}^{*}({{{\mathbf{x}}}_{0}})} \right)} \mathord{\left/ {\vphantom {{\left( { - (1 - {{I}_{2}})u_{{3,1}}^{*}({{{\mathbf{x}}}_{0}}) - (1 - {{I}_{5}})u_{{1,3}}^{*}({{{\mathbf{x}}}_{0}})} \right)} {{{\Delta }_{2}}}}} \right. \kern-0em} {{{\Delta }_{2}}}}J, \\ {{\Delta }_{1}} = {{I}_{1}}{{I}_{6}} - {{I}_{3}}{{I}_{4}} - {{I}_{1}} - {{I}_{6}} + 1,\,\,\,\,{{\Delta }_{2}} = {{I}_{2}} + {{I}_{5}} - 1, \\ {{I}_{1}} = I({{\gamma }_{1}}{{\gamma }_{5}} - G,G,0), \\ {{I}_{2}} = I({{\gamma }_{5}}{{\gamma }_{7}} + {{\gamma }_{5}}, - {{\gamma }_{5}}{{\gamma }_{7}} - 2{{\gamma }_{5}},{{\gamma }_{5}}), \\ {{I}_{3}} = I({{\gamma }_{5}}{{\gamma }_{7}} + {{\gamma }_{5}}, - {{\gamma }_{5}},0), \\ {{I}_{4}} = I({{\gamma }_{1}}{{\gamma }_{5}} + {{\gamma }_{1}}{{\gamma }_{7}}, - {{\gamma }_{1}}{{\gamma }_{5}} - {{\gamma }_{1}}{{\gamma }_{7}},0), \\ {{I}_{5}} = I({{\gamma }_{1}}{{\gamma }_{5}} + {{\gamma }_{5}}{{\gamma }_{7}}, - {{\gamma }_{5}}{{\gamma }_{7}},0), \\ {{I}_{6}} = I({{\gamma }_{5}} - G + ,G - 2{{\gamma }_{5}},{{\gamma }_{5}}). \\ \end{gathered} $Интеграл $I({{C}_{1}},{{C}_{2}},{{C}_{3}}) = \frac{{{{C}_{1}}{{\Psi }_{1}} + {{C}_{2}}{{\Psi }_{2}} + {{C}_{3}}{{\Psi }_{3}}}}{\Lambda }$ вычислен аналитически по теории вычетов, где
Таким образом, для задач 1, 2 получено явное асимптотическое представление полей смещений на контуре полости, минуя процедуру дискретизации ГИУ (6) на основе МГЭ. Поля перемещений на поверхности ${{u}_{m}}({{\xi }_{1}},h),$ $m = 1,2,3$, построенные в рамках асимптотического подхода, в дальней от дефекта зоне (${{x}_{1}} < {{\xi }_{1}}$), имеют вид:
(12)
$\begin{gathered} {{u}_{m}}({{\xi }_{1}},h) = u_{m}^{*}({{\xi }_{1}},h) - \sum\limits_{p = 1}^M {A_{p}^{{(m)}}({{u}_{m}}(x)){{e}^{{i\alpha _{{1p}}^{*}{{\xi }_{1}}}}}} + \\ + \,\,O({{e}^{{ - \gamma {{\xi }_{1}}}}}),\,\,\,\,\gamma > 0,\,\,\,\,{{\xi }_{1}} > {{x}_{1}} > 0, \\ \end{gathered} $(13)
$\begin{gathered} A_{p}^{{(m)}} = \frac{{\varepsilon _{1}^{2}\pi i\exp ( - i\alpha _{{1p}}^{*}{{x}_{{10}}})}}{{2\psi (\alpha _{{1p}}^{*})}} \times \\ \times \,\,\left[ {\Phi _{1}^{{(m)}}({{x}_{{30}}})u_{1}^{*}({{{\mathbf{x}}}_{0}}) + \Phi _{3}^{{(m)}}({{x}_{{30}}})u_{3}^{*}({{{\mathbf{x}}}_{0}})} \right. + \\ \left. { + \,\,\sum\limits_{k = 1,3} {\Omega _{k}^{{(m)}}({{x}_{{30}}}){{u}_{{1,k}}}({{{\mathbf{x}}}_{0}}) + \Lambda _{k}^{{(m)}}({{x}_{{30}}}){{u}_{{3,k}}}({{{\mathbf{x}}}_{0}})} } \right], \\ m = 1,3. \\ \end{gathered} $Выражения $\psi (\alpha _{{1p}}^{*}),$ $\Phi _{k}^{{(m)}}({{x}_{{30}}}),$ $\Omega _{k}^{{(m)}}({{x}_{{30}}}),$ $\Lambda _{k}^{{(m)}}({{x}_{{30}}})$ не приводятся в виду их громоздкости, а ${{u}_{{s,k}}}({{{\mathbf{x}}}_{0}}),$ $s,k = 1,3$ заданы формулами (11).
Надо отметить, что в рамках приближения Борна, широко используемого в акустике [19, 20], перемещения на контуре заменяются эталонными полями смещений в точке ${{{\mathbf{x}}}_{0}}$, поэтому амплитуды полей перемещений на поверхности слоя в этом приближении не учитывают изменяемость полей смещений на контуре. В рамках такого приближения однократного рассеяния поля смещений на контуре полости определяются соотношением (10) при удержании лишь первого члена в разложении полей. В свою очередь, в соотношении (13) для амплитуд отсутствуют слагаемые, содержащие производные от эталонных полей $u_{m}^{*}({{{\mathbf{x}}}_{0}}),\,\,m = 1,3,$ а их выражение имеет вид:
(14)
$\begin{gathered} A_{p}^{{(m)}} = \frac{{\varepsilon _{1}^{2}\pi i\exp ( - i\alpha _{{1p}}^{*}{{x}_{{10}}})}}{{2\psi (\alpha _{{1p}}^{*})}} \times \\ \times \,\,\left[ {\Phi _{1}^{{(m)}}({{x}_{{30}}})u_{1}^{*}({{{\mathbf{x}}}_{0}}) + \Phi _{3}^{{(m)}}({{x}_{{30}}})u_{3}^{*}({{{\mathbf{x}}}_{0}})} \right],\,\,\,\,m = 1,3. \\ \end{gathered} $ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ
На основании соотношений (5), (12)–(14) построены поля перемещений ${{\upsilon }_{m}}({{\xi }_{1}},h)$ = ${{u}_{m}}({{\xi }_{1}},h) - u_{m}^{*}({{\xi }_{1}},h),$ $m = 1,2,3$ на поверхности слоя ${{x}_{3}} = h,$ обусловленные лишь наличием полости. Проведен ряд численных экспериментов по расчету волновых полей на поверхности слоя для случая цилиндрической полости кругового сечения малого относительного размера на основании трех походов: МГЭ, асимптотического подхода и приближения Борна.
В расчетах приняты следующие значения упругих постоянных для диоксида гафния HfО2 ${{С}_{{11}}} = 502,$ ${{С}_{{13}}} = 159,$ ${{С}_{{33}}} = 597,$ ${{C}_{{44}}} = 78,$ ${{С}_{{55}}} = 90,$ ${{C}_{{66}}} = 111$ (ГПа), $\rho = 13\,310$ кг/м3 [22]. Колебания в слое вызваны сосредоточенной нагрузкой ${\mathbf{p}} = \{ 0,{{ - {{p}_{0}}} \mathord{\left/ {\vphantom {{ - {{p}_{0}}} {{{C}_{{44}}},}}} \right. \kern-0em} {{{C}_{{44}}},}}0\} $ и ${\mathbf{p}} = \{ 0,0,{{ - {{p}_{0}}} \mathord{\left/ {\vphantom {{ - {{p}_{0}}} {{{C}_{{33}}}}}} \right. \kern-0em} {{{C}_{{33}}}}}\} $ для задач 1 и 2 соответственно, которая приложена в точке $(0,h)$. Направляющая цилиндрической полости ${{l}_{0}}$ – окружность с центром в точке $(0,\,\,{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}).$ Число граничных элементов $N = 12$. На рис. 1–4 приведены графики полей перемещений на поверхности слоя ${{\upsilon }_{m}}({{\xi }_{1}},h),$ $m = 1,2,3$, рассчитанных тремя способами для задач 1 и 2, при этом сплошная линия соответствует расчетам по МГЭ, графики полей, полученных на основе асимптотического подхода, изображены сплошной линией с маркером “*” и штриховой линией отмечены поля, полученные в рамках приближения Борна. На рис. 1–2 представлены графики, соответствующие случаю одной распространяющейся моды в слое для значений параметров ${{\varepsilon }_{1}} = 0.24,$ ${{\varepsilon }_{2}} = 0.98$ (задача 1) и ${{\varepsilon }_{1}} = 0.15,$ ${{\varepsilon }_{2}} = 0.3$ (задача 2).
Рис. 1.
Действительная и мнимая части поля перемещений ${{\upsilon }_{2}}({{\xi }_{1}},h)$, рассчитанные на основе МГЭ (1), асимптотического подхода (2), приближения Борна (3) для значений параметров ${{\varepsilon }_{1}} = 0.24,$ ${{\varepsilon }_{2}} = 0.98.$
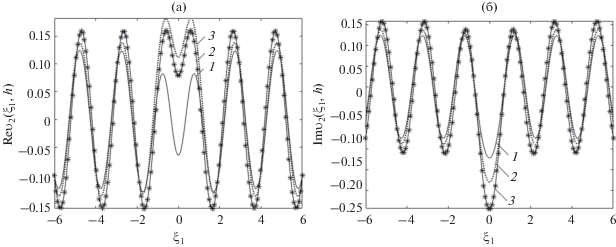
Рис. 2.
(а) – Действительная и мнимая части поля перемещений ${{\upsilon }_{1}}({{\xi }_{1}},h)$, рассчитанные на основе МГЭ (1), асимптотического подхода (2), приближения Борна (3) для значений параметров ${{\varepsilon }_{1}} = 0.15,$ ${{\varepsilon }_{2}} = 0.3$. (б) – Действительная и мнимая части поля перемещений ${{\upsilon }_{3}}({{\xi }_{1}},h)$, рассчитанные на основе МГЭ (1), асимптотического подхода (2), приближения Борна (3) для значений параметров ${{\varepsilon }_{1}} = 0.15,$ ${{\varepsilon }_{2}} = 0.3$.
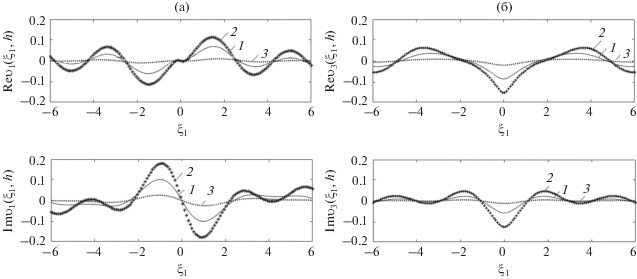
Рис. 3.
Действительная и мнимая части поля перемещений ${{\upsilon }_{2}}({{\xi }_{1}},h)$, рассчитанные на основе МГЭ (1), асимптотического подхода (2), приближения Борна (3) для значений параметров ${{\varepsilon }_{1}} = 0.15$, ${{\varepsilon }_{2}} = 0.98$.

Рис. 4.
(а) – Действительная и мнимая части поля перемещений ${{\upsilon }_{1}}({{\xi }_{1}},h)$, рассчитанные на основе МГЭ (1), асимптотического подхода (2), приближения Борна (3) для значений параметров ${{\varepsilon }_{1}} = 0.1$, ${{\varepsilon }_{2}} = 0.4$. (б) – Действительная и мнимая части поля перемещений ${{\upsilon }_{3}}({{\xi }_{1}},h)$, рассчитанные на основе МГЭ (1), асимптотического подхода (2), приближения Борна (3) для значений параметров ${{\varepsilon }_{1}} = 0.1$, ${{\varepsilon }_{2}} = 0.4$.

На рис. 3–4 представлены графики полей перемещений на поверхности слоя ${{\upsilon }_{m}}({{\xi }_{1}},h),$ $m = 1,2,3$ для двух распространяющихся мод при следующих значениях параметров ${{\varepsilon }_{1}} = 0.15,$ ${{\varepsilon }_{2}} = 0.98$ (задача 1) и ${{\varepsilon }_{1}} = 0.1,$ ${{\varepsilon }_{2}} = 0.4$ (задача 2).
ВЫВОДЫ
На основе численных экспериментов определена область корректной работы асимптотического подхода для задач 1 и 2 для среднезаглубленных полостей малого поперечного размера и приближения Борна при расчете волновых полей в дальней зоне. Эта область описывается следующими неравенствами: $\left\{ \begin{gathered} {{\varepsilon }_{1}} < 0.24 \hfill \\ {{\varepsilon }_{2}} < 1 \hfill \\ \end{gathered} \right.$ для задачи 1 и $\left\{ \begin{gathered} {{\varepsilon }_{1}} < 0.15 \hfill \\ {{\varepsilon }_{2}} < 1 \hfill \\ \end{gathered} \right.$ для задачи 2 (относительное расхождение результатов не превышало 10%). Как видно из графиков на рис. 1, на частотах, соответствующих одной распространяющейся моде в слое, волновое поле в дальней от дефекта зоне, рассчитанное на основе приближения Борна, практически совпадает с полем, рассчитанным на основе МГЭ. На тех частотах, для которых имеются две распространяющиеся моды, приближение Борна значительно отличается от расчетов по МГЭ. В то же время поле на поверхности, рассчитанное на основе асимптотического подхода, отличается от поля, полученного на основе МГЭ, не более, чем на 4%. Отметим, что для задачи 2 для любых частот, соответствующих распространяющим модам в слое, наблюдается качественное и количественное отличие полей перемещений, построенных на основании приближения Борна от полей, рассчитанных на основе МГЭ и асимптотического подхода.
Работа выполнена в рамках федеральной целевой программы “Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014–2020 годы” при финансовой поддержке государства в лице Министерства науки и высшего образования России (идентификатор проекта RFMEFI60718X0203).
Список литературы
Гринченко В.Т., Мелешко В.В. Гармонические колебания и волны в упругих телах. М.: Наука, 1981. 282 с.
Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории упругости для неклассических областей. М.: Наука, 1979.
Бабешко В.А., Бабешко О.М., Евдокимова В.О. О колебаниях слоистых упругих сред с рельефной границей // ПММ. 2010. Т. 74. № 6. С. 890–894.
Lei Huang, Jianwen Liang, Chengqing Wu. A three-dimensional indirect boundary integral equation method for modeling elastic wave scattering in a layered half-space // Int. J. Solids Structures. 2019. V. 169. P. 81–94.
Глушков Е.В., Глушкова Н.В., Фоменко С.И., Жанг Ч. Поверхностные волны в материалах с функционально-градиентными покрытиями // Акуст. журн. 2012. Т. 58. № 3. С. 370–385.
Калинчук В.В., Белянкова Т.И. О динамике среды с непрерывно изменяющимися по глубине свойствами // Изв. вузов. Сев.-Кав. регион. Естест. науки. 2004. Спецвыпуск. С. 46–49.
Gusakov D., Vatul’yan A. Dispersion properties of ingomogeneousporoelastic layer // ZAMM Zeitschrift fur AngewandteMathematik und Mechanik. 2018. V. 98. № 4. P. 532–541.
Суворова Т.В., Беляк О.А., Усошин С.А. Волновое поле, генерируемое в слоистом полупространстве движущейся осциллирующей нагрузкой // Экологический вестник научных центров Черноморского экономического сотрудничества. 2008. № 1. С. 53–61.
Глушков Е.В., Глушкова Н.В., Фоменко С.И. Влияние пористости на характеристики волн релеевского типа в многослойном полупространстве // Акуст. журн. 2011. Т. 57. № 2. С. 234–245.
Глушков Е.В., Глушкова Н.В., Евдокимов А.А. Гибридная численно-аналитическая схема для расчета дифракции упругих волн в локально неоднородных волноводах // Акуст. журн. 2018. Т. 64. № 1. С. 3–12.
Ватульян А.О., Беляк О.А. К реконструкции малых полостей в упругом слое // Дефектоскопия. Уральское отделение РАН. 2006. № 10. С. 33–39.
Ватульян А.О., Беляк О.А. О различных способах реконструкции полости в ортотропном слое // ПМТФ. 2009. Т. 50. № 3(295). С. 181–189.
Falleta S., Monegato G., Scuderi L. On the discretization and application of two space–time boundary integral equations for 3D wave propagation problems in unbounded domains // Applied Numerical Mathematics. 2018. V. 124. P. 22–43.
Гурбатов С.Н., Грязнова И.Ю., Иващенко Е.Н. Исследование обратного рассеивания акустических волн дискретными неоднородностями разных размеров // Акуст. журн. 2016. Т. 62. № 2. С. 203–207.
Буров В.А., Шуруп А.С., Румянцева О.Д., Зотов Д.И. Функционально-аналитическое решение задачи об акустической томографии по данным от точечных преобразователей // Изв. РАН. Серия физическая. 2012. Т. 76. № 12. С. 1524–1529.
Ватульян А.О. Коэффициентные обратные задачи механики. М.: Физматлит, 2019. 272 с.
Бребия К., Теллес Ж., Вроубел Л. Методы граничных элементов. М.: Мир, 1987. 524 с.
Бенерджи П., Баттерфилд Р. Методы граничных элементов в прикладных науках. М.: Мир, 1984. 494 с.
Хенл Х., Мауэ А., Вестпфаль К. Теория дифракции. М.: Мир, 1964. 428 с.
Горюнов А.А., Сасковец А.В. Обратные задачи рассеяния в акустике. М.: Изд-во МГУ, 1989. 149 с.
Ватульян А.О., Суворова О.А. Об обратной задаче для упругого слоя с полостью // Экологический вестник научных центров черноморского сотрудничества (ЧЭС). 2005. № 1. С. 10–16.
Ватульян А.О., Гусева И.А., Сюнякова И.М. О фундаментальных решениях для ортотропной среды и их применении // Изв. СКНЦ. Сер. естеств. науки. 1989. № 2. С. 81– 85.
Caravaca M.A., Mino J.C., Perez V.J., Casali R.A., Ponce C.A. Ab initio study of the elastic properties of single and polycrystal TiO2, ZrO2 and HfO2 in the cotunnite structure // J. Phys. Condens. Matter. 2009. V. 21(1). P. 1–11.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал


