Акустический журнал, 2020, T. 66, № 3, стр. 319-326

ВВЕДЕНИЕ

Задача локализации источника повышенной вибрационной активности часто возникает при диагностике и обслуживании конструкций и механизмов. С успешным решением данной задачи напрямую связано решение важных проблем снижения шумности и устранения неисправностей механизмов. Как правило, локализация вибрационного источника, находящегося в механоакуcтической конструкции, производится на основе данных измерения вибрационного или акустического поля в ряде контрольных точек (в общем случае, не совпадающих с месторасположением источника). Таким образом, задача локализации представляет собой вариант обратной задачи, целью которой является поиск пространственного положения виброисточника.

С задачей поиска вибрационного источника связана задача поиска дефекта в конструкции, поскольку часто дефект можно рассматривать как источник вторичного вибрационного поля, возникающего в результате рассеяния первичного поля на возникшей неоднородности. Таким образом, методы локализации источника можно применить и к задаче локализации дефекта.

Методам оценки параметров виброисточника, расположенного на некоторой конструкции, посвящено значительное число публикаций. Общепринятым является подход, основанный на сравнении модельных и измеренных экспериментально динамических характеристик (ускорение, перемещение) вибрационного поля конструкции. Параметры источника (положение, мощность, ориентация и т.д.), обеспечивающие наименьшее различие между модельными и экспериментальными данными, считаются истинными. Например, в работе [1] авторы используют для локализации виброисточника методы согласованной с полем обработки MFP (Matched-field processing), применяемые в акустике для определения положения источника звука в сложной среде подводного волновода. Рассматривалась ситуация, когда на закрепленном с двух концов стержне в ряде точек установлены датчики перемещения, в неизвестной точке расположен источник, воздействие которого можно представить ориентированной определенным образом гармонической силой. Далее различными методами (оцениватель Бартлетта и др.) производилось сравнение модельных данных вибрации, создаваемых установленным в определенной точке источником, и данных вибродатчиков. Точка наиболее вероятного расположения источника определялась исходя из минимума рассогласования между модельными и реальными данными.

В упомянутой работе модельные данные получены аналитически. В случае более сложных конструкций аналитическое решение невозможно. В этом случае динамические характеристики конструкции рассчитываются численно, например, с помощью конечно-элементного моделирования [2]. В исследовании [3] путем модального анализа конечно-элементной модели, состоящей из ограниченного числа узлов и расположенных между ними элементов, рассчитываются коэффициенты передачи (функции Грина) между степенями свободы приложенной в определенном узле силы и степенями свободы узлов, где установлены акселерометры. Методом наименьших квадратов с регуляризацией Тихонова авторы производят сравнение модельного и экспериментального откликов в контрольных точках, таким образом определяя положение источника. В работе [4] успешно применяется похожий подход для локализации источника и дефекта в сложной механоакустической конструкции.

Стоит отметить и другие разнообразные техники локализации виброисточника [5–8]. К примеру, в исследовании [5] для поиска виброисточника применяется машинное обучение. Обучение многослойной нейронной сети (многослойный перцептрон) происходило по методу обратного распространения ошибки, обучающими данными являлись результаты экспериментов с заранее известным положением источника. Далее обученная нейронная сеть использовалась для локализации источника с неизвестным положением. В работе [6] используется вейвлет-преобразование сигналов, получаемых на пьезоэлектрических датчиках, для определения времен прихода упругих волн, которые используются в дальнейшем для локализации источника.

Таким образом, тематика локализации источника виброактивности является весьма актуальной. Отметим, однако, что в имеющихся публикациях практически не рассматривается ситуация, когда в конструкции одновременно расположены несколько виброисточников. В работе [9] изучается вопрос о локализации двух источников, однако исследуемая конструкция предельно проста и состоит из 17 узлов. Принципиальным ограничением большинства используемых в работах алгоритмов является требование единственности источника.

В рамках настоящей работы, помимо исследования задачи локализации одного источника, разработан и экспериментально апробирован метод локализации двух (или более) одновременно работающих виброисточников в сложной механоакустической конструкции (с большим числом степеней свободы). Предложенный алгоритм основан на модификации известного метода спектрального разрешения MUSIC [10], успешно используемого в задачах оценки DOA (Direction of arrival estimation) [11], локализации акустических источников [12].

ПОСТАНОВКА ЗАДАЧИ

Будем считать, что имеется некоторая сложная механоакустическая система (конструкция), для которой построена конечно-элементная модель (КЭМ), состоящая из определенного числа узлов. Считаем также, что в некотором узле расположен виброисточник. Этот виброисточник ориентирован определенным образом в пространстве, а сигнал, возбуждающий виброисточник, является широкополосным белым гауссовским шумом. В данном исследовании в качестве виброисточника использовался пьезоэлектрический возбудитель. Будем считать, что в каждой узкой частотной полосе амплитудно-частотная характеристика виброисточника близка к константе, а сигнал, соответственно, является белым шумом. В K точках конструкции находятся вибродатчики (акселерометры), а принимаемый сигнал подвергается узкополосной фильтрации на частоте ${{f}_{0}}$. Модель принимаемого сигнала на частоте ${{f}_{0}}$ в момент времени с номером j можно записать как следующий K × 1 вектор:

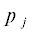где – временная форма узкополосного сигнала (комплексный белый гауссовский шум с нулевым средним и дисперсией $\sigma _{s}^{2}$, определяющей интенсивность вибрационного источника), F – вектор 3 × 1 нормированных комплексных составляющих силы (${{{\mathbf{F}}}^{H}}{\mathbf{F}} = 1$), ${{\xi }_{j}}$ – временные отсчеты аддитивного белого гауссова шума с нулевым средним и дисперсией $\sigma _{0}^{2}$, ${\mathbf{A}}({{x}_{i}},{{y}_{i}},{{z}_{i}})$ – K × 3 матрица комплексных коэффициентов передачи из узла с координатами ${{x}_{i}},{{y}_{i}},{{z}_{i}}$ (координаты виброисточника) в узлы, соответствующие контрольным точкам (в которых находятся вибродатчики). Относительно размерности A следует сделать небольшое пояснение. Считается, что каждый из K датчиков виброускорения ориентирован по одной из осей x, y, z. В таком случае, каждая из строчек матрицы A содержит три комплексных коэффициента передачи (например, $({{a}_{{xx}}},{{a}_{{xy}}},{{a}_{{xz}}})$) от степеней свободы источника в единственную степень свободы (x, y или z), соответствующую каждому из K датчиков ускорения.

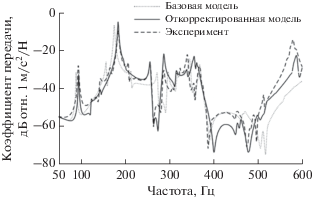
Матрица A получается путем численного моделирования с использованием КЭМ конструкции. Для уменьшения разницы между модельной и реальной матрицами A предварительно проводится процедура доводки ряда характеристик модели (см., например, [13]). Доводка производится в три этапа и в определенном частотном диапазоне. На первом этапе производится расчет собственных частот и собственных форм колебаний модели. На втором этапе проводится эксперимент с реальной конструкцией с целью определения собственных частот и форм колебаний конструкции. На последнем этапе производится корректировка КЭМ (в том числе изменение модулей Юнга элементов). Корректировка проводится до тех пор, пока собственные частоты и формы колебаний КЭМ и конструкции не совпадут. При высоком отношении сигнал/шум именно от качества доводки зависит качество результата локализации. Понятно, что большое рассогласование (разница между модельной и реальной матрицами A) может привести к высокой ошибке при поиске местонахождения источника. В качестве примера на рис. 1 приведен результат доводки. Показаны экспериментальные и расчетные (до доводки и после) коэффициенты передачи из точки возбуждения конструкции в одну из контрольных точек в зависимости от частоты. Видно, что после доводки расчетная зависимость заметно приблизилась к экспериментальной. Стоит отметить, что при этом все-таки сохраняется некоторое рассогласование между модельными и реальными данными.

МЕТОДЫ ЛОКАЛИЗАЦИИ ЕДИНСТВЕННОГО ВИБРОИСТОЧНИКА

Для модели (1) в случае отсутствия рассогласования оптимальным является метод максимального правдоподобия (МП). Метод максимального правдоподобия [14] заключается в максимизации функции правдоподобия (ФП) $w$, логарифм которой для модели (1) записывается следующим образом:

где ${\mathbf{\hat {K}}} = \frac{1}{J}\sum\nolimits_{j = 1}^J {{{{\mathbf{v}}}_{j}}} {\mathbf{v}}_{j}^{H}$ – выборочная корреляционная матрица принятого сигнала. Неизвестными параметрами здесь являются $(x,y,z)$, $\sigma _{0}^{2}$, $\sigma _{s}^{2}$, ${\mathbf{F}}$. Для дальнейших преобразований удобно сделать замену переменных ${\mathbf{F}} \to {\mathbf{g}} = {{{{\sigma }_{s}}{\mathbf{F}}} \mathord{\left/ {\vphantom {{{{\sigma }_{s}}{\mathbf{F}}} {{{\sigma }_{0}}}}} \right. \kern-0em} {{{\sigma }_{0}}}}$, $\sigma _{0}^{2} \to \sigma _{0}^{2}$. После этого логарифм ФП можно записать как

Далее легко найти частный максимум (3) по параметру $\sigma _{0}^{2}$ путем решения уравнения $\frac{{\partial \ln w}}{{\partial \sigma _{0}^{2}}} = 0$. Решение этого уравнения записывается следующим образом

Подставим (4) в ФП (3) и получим ФП ${{w}_{1}} = w(\hat {\sigma }_{0}^{2})$, не зависящую от $\sigma _{0}^{2}$:

Далее будем искать экстремум (5) по ${\mathbf{g}}$ путем решения уравнения $\frac{{\partial \ln {{w}_{1}}}}{{\partial {{{\mathbf{g}}}^{H}}}} = 0$. После некоторых преобразований это уравнение можно записать следующим образом:

где

Уравнение (6) представляет собой уравнение на собственный вектор матрицы ${{({{{\mathbf{A}}}^{H}}{\mathbf{A}})}^{{ - 1}}}{{{\mathbf{A}}}^{H}}{\mathbf{\hat {K}A}}$. Решение уравнения (6) определено с точностью до произвольного множителя. Поэтому будем искать его в виде ${\mathbf{\hat {g}}} = \gamma {\mathbf{\omega }}$, где ${\mathbf{\omega }}$ – нормированный собственный вектор матрицы ${{({{{\mathbf{A}}}^{H}}{\mathbf{A}})}^{{ - 1}}}{{{\mathbf{A}}}^{H}}{\mathbf{\hat {K}A}}$, $\gamma $ – неопределенный множитель. После подстановки этого решения в (6) получится выражение для $\gamma $:

где $\lambda $ – максимальное собственное число матрицы ${{({{{\mathbf{A}}}^{H}}{\mathbf{A}})}^{{ - 1}}}{{{\mathbf{A}}}^{H}}{\mathbf{\hat {K}A}}$. В результате получится полное решение ${\mathbf{\hat {g}}} = \hat {\gamma }{\mathbf{\omega }}$. Подстановка этого решения в (5) приведет к ФП, зависящей только от координат вибрационного источника $(x,y,z)$. В результате процедура поиска координат источника приобретает следующий вид:

Оценка положения источника производится в данном случае в одной частотной полосе. В случае широкополосного сигнала целесообразно суммировать значения целевой функции (8), полученные для разных частот.

При этом МП-метод обладает достаточно высокой вычислительной сложностью. Вместо него можно использовать другой подход. Он заключается в том, что вначале находится собственный вектор ${\mathbf{V}}$ выборочной корреляционной матрицы принятого сигнала, соответствующий максимальному собственному числу. Этот вектор является максимально правдоподобной оценкой сигнального вектора (первого слагаемого в (1)) в предположении его полной неизвестности. Далее для определения неизвестных параметров источника используется метод наименьших квадратов. В нем в качестве модели используется вектор ${\mathbf{\bar {F}}} = \psi {\mathbf{F}}$, где $\psi $ – масштабный коэффициент_. Этот коэффициент вводится из-за того, что в обработке используется нормированный собственный вектор, т.е. ${{{\mathbf{V}}}^{H}}{\mathbf{V}} = 1$. Такой подход обладает чуть меньшей эффективностью по сравнению со строгой МП-оценкой. Эта разница, однако, практически нивелируется при наличии рассогласования между реальной и модельной матрицами A, которое и определяет, в конечном счете, точность локализации. При этом упрощенный метод обладает значительной меньшей вычислительной сложностью. Целевая функция метода наименьших квадратов в рассматриваемой ситуации записывается следующим образом:

Для нахождения минимума (9) приравниваем к нулю ее частные производные по ${\mathbf{\bar {F}}}$. В результате решения уравнения $\frac{{\partial S}}{{\partial {\mathbf{\bar {F}}}}} = 0$ находим оценку неизвестных компонент действующей силы: ${\mathbf{\hat {\bar {F}}}} = {{({{{\mathbf{A}}}^{H}}{\mathbf{A}})}^{{ - 1}}}{{{\mathbf{A}}}^{H}}{\mathbf{V}}$. Далее это выражение подставляется в (9), в результате чего получается целевая функция, не зависящая от ${\mathbf{\bar {F}}}$:

Учитывая, что ${{{\mathbf{V}}}^{H}}{\mathbf{V}} = 1$, перейдем к следующему выражению целевой функции, которая, по сути, является коэффициентом корреляции между модельными данными и экспериментом:

Таким образом, в соответствии с (11) узел с наибольшим коэффициентом корреляции является местом наиболее вероятного расположения источника. Как и в случае с функцией (8), целесообразно суммировать значения функции (11), полученные для разных частотных полос.

Характерным свойством функции (11) является то, что ее значения лежат в диапазоне от 0 до 1. Вообще говоря, можно и не применять данную нормировку (${{{\mathbf{V}}}^{H}}{\mathbf{V}}$ в знаменателе). Однако, наибольшее рассогласование конечно-элементной модели и реальной конструкции наиболее велико в частотных полосах, близких к собственным частотам (модам) конструкции. Нормировка целевой функции позволяет избежать при суммировании по частотам сильного негативного влияния “плохих” (с большим рассогласованием) частотных полос. По сути дела, такая нормировка позволяет совершать выбор частот для оценки произвольно, не заботясь о возможной близости выбранной частоты к одной из мод. Вопрос же о том, как выбрать частотные полосы для оценки наилучшим образом, отбросив все “плохие” частоты, является предметом будущих исследований¹¹.

Выражения (8) и (11) получены в предположении единственного источника. Известно, что в некоторых случаях²² с их помощью можно локализовать и несколько источников. Однако такая ситуация является скорее исключением, а поиск строгого решения задачи с несколькими источниками представляет собой весьма непростую проблему. Дело в том, что для строгого решения задачи с M источниками по методу наименьших квадратов нужен полный перебор, по меньшей мере, в 3M-мерном пространстве, что неприемлемо с вычислительной точки зрения и поэтому необходимо принципиально другое решение.

МОДИФИКАЦИЯ МЕТОДА MUSIC ДЛЯ ПОИСКА НЕСКОЛЬКИХ ВИБРОИСТОЧНИКОВ

Метод сверхразрешения MUSIC (Multiple Signal Classification), возникший при решении задач спектрального оценивания, часто используется в задачах пеленгации (direction-of-arrival estimation) для разрешения близких друг к другу источников. Такая ситуация может возникнуть, когда, к примеру, источники волнового поля расположены в дальней зоне линейной антенной решетки в пределах главного лепестка диаграммы направленности. Общепринятое выражение для целевой функции метода MUSIC в таких задачах выглядит так [10]:

где ${{{\mathbf{A}}}_{{{\text{st}}}}}({\mathbf{\theta }})$ – вектор направлений (steering vector), функция Грина для данной задачи, ${\mathbf{U}}{{{\mathbf{U}}}^{H}}$ = $ = \sum\nolimits_{l = L + 1}^K {{{{\mathbf{u}}}_{l}}{\mathbf{u}}_{l}^{H}} $, ${{{\mathbf{u}}}_{l}}$ – собственные вектора выборочной корреляционной матрицы процесса ${\mathbf{\hat {K}}}$, L – параметр метода MUSIC (должен быть больше общего числа источников).

Можно считать, что в условиях нашей задачи аналогом вектора направлений ${{{\mathbf{A}}}_{{{\text{st}}}}}({\mathbf{\theta }})$ является вектор ${\mathbf{A}}(x,y,z)$F, который является функцией Грина для задачи локализации виброисточника. Учитывая это, запишем выражение для модификации целевой функции метода MUSIC для данной задачи:

Следуя общей логике метода MUSIC, для поиска неизвестных параметров необходимо максимизировать выражение (13) по этим параметрам. Для параметра F это легко сделать путем решения уравнения $\frac{{\partial {{F}_{{{\text{music + }}}}}}}{{\partial {\mathbf{F}}}} = 0$. После подстановки найденного решения в (13) получим новую целевую функцию:

где ${{\lambda }_{{{\text{MUS}}}}}$ – минимальное собственное число матрицы ${{({{{\mathbf{A}}}^{H}}{\mathbf{A}})}^{{ - 1}}}{{{\mathbf{A}}}^{H}}{\mathbf{U}}{{{\mathbf{U}}}^{H}}{\mathbf{A}}$. Параметр метода L должен быть больше числа источников M.

Алгоритм (14) обладает гораздо меньшей вычислительной сложностью, чем алгоритм полного перебора по методу наименьших квадратов для нескольких источников. Размерность матрицы ${{({{{\mathbf{A}}}^{H}}{\mathbf{A}})}^{{ - 1}}}{{{\mathbf{A}}}^{H}}{\mathbf{U}}{{{\mathbf{U}}}^{H}}{\mathbf{A}}$ – 3×3, и время решения обратной задачи для M источников сопоставимо со временем решения обратной задачи по методу наименьших квадратов для одного источника. Кроме того, целевые функции (14) для разных частот, также как и функции метода наименьших квадратов можно суммировать для улучшения качества итогового результата³³.

Остановимся теперь на вопросе определения числа источников M. Известно, что спектр собственных чисел корреляционной матрицы случайного процесса для рассматриваемой модели можно условно разделить на так называемые “сигнальные” и “шумовые”. Количество «сигнальных» собственных чисел равно количеству полезных источников, а их абсолютные значения выше абсолютных значений шумовых чисел (при достаточно большом отношении сигнал/шум). При этом не составляет труда найти сильно выделяющиеся по абсолютным значениям собственные числа корреляционной матрицы; их количество равно количеству источников M. Таким образом, в данном случае задача определения параметра метода MUSIC легко решается (для этого можно использовать, например, пороговую технику).

ЭКСПЕРИМЕНТАЛЬНАЯ АПРОБАЦИЯ АЛГОРИТМОВ

Для исследования эффективности предложенных алгоритмов был проведен эксперимент с реальной конструкцией. Характерный размер конструкции составлял 1 м, число узлов составляло более 10⁵, число элементов КЭМ было более 30 000. Предварительно была произведена доводка КЭМ данной конструкции [13], а потом выполнен численный расчет матрицы A. Эксперимент проводился как с одним (для подтверждения эффективности использования метода наименьших квадратов), так и с двумя широкополосными источниками (для сравнения эффективности метода максимума правдоподобия в предположении единственности источника и модифицированного метода MUSIC).

ЭКСПЕРИМЕНТ С ОДНИМ ИСТОЧНИКОМ

Широкополосный источник (пьезовозбудитель) устанавливался в различных точках конструкции. Возбуждение источника производилось широкополосным белым гауссовским шумом в диапазоне частот 0–2400 Гц. В контрольных точках экспериментального стенда устанавливались пьезоакселерометры, регистрирующие виброускорение в узлах, каждый из которых был ориентирован по одной из осей x, y или z. Для каждой частотной полосы строилась функция (11) метода наименьших квадратов, далее целевые функции каждой из частотных полос суммировались. Узел с наибольшим итоговым значением суммарной функции считался местом наиболее вероятного расположения источника. Ширина полосы обработки составляла 0.9 Гц. На рис. 2 для одного из местоположений источника представлен график зависимости средней ошибки локализации от числа частотных полос. Каждая точка графика – это средняя ошибка локализации (отклонение оцененного положения источника от реального) при заданном количестве полос ${{n}_{{{\text{fr}}}}}$. Для расчета значения средней ошибки локализации бралось 150 наборов по ${{n}_{{{\text{fr}}}}}$ произвольно выбранных полос в диапазоне от 100 до 600 Гц, для каждого набора ${{n}_{{{\text{fr}}}}}$ значений целевой функции суммировались, после чего производился расчет средней по всем наборам ошибки локализации.

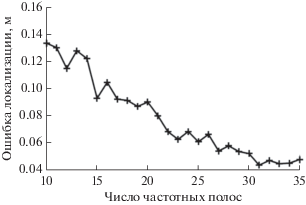
Учитывая характерные масштабы конструкции в сравнении со средней ошибкой локализации, можно считать, что алгоритм поиска единственного виброисточника по методу наименьших квадратов является достаточно точным.

ЭКСПЕРИМЕНТ С ДВУМЯ ИСТОЧНИКАМИ

В данном эксперименте виброисточники устанавливались в двух точках конструкции. Возбуждение также производилось широкополосным белым гауссовским шумом в диапазоне частот 0–2400 Гц. Акселерометры были установлены в 61 контрольной точке. Сравнивалась эффективность предложенной модификации метода MUSIC (14) и метода максимума правдоподобия (8). На рис. 3 приведен характерный случай распределения функций обоих методов на фрагменте КЭМ для одного из вариантов расположения двух источников. Слева показан результат для метода максимума правдоподобия (8), справа для MUSIC (14). Распределения приведены для частотной полосы 348 Гц, ширина полосы – 0.9 Гц.

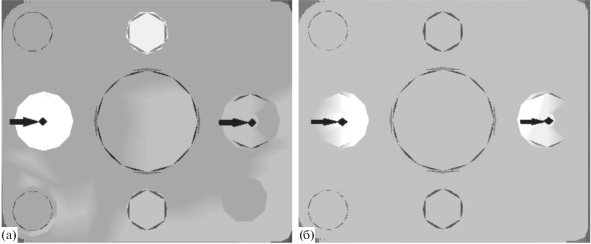
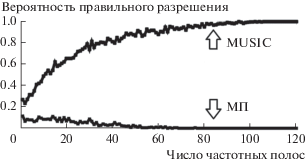
Для того же самого расположения источников на рис. 4 приведен график зависимости вероятности правильного разрешения ${{P}_{t}}$ источников в зависимости от числа частотных полос ${{n}_{{{\text{fr}}}}}$, по которым суммировались функции (14) и (8). Для каждого значения числа полос ${{n}_{{{\text{fr}}}}}$ при расчете значения ${{P}_{t}}$ бралось 1000 наборов по ${{n}_{{{\text{fr}}}}}$ произвольно выбранных полос в диапазоне от 100 до 600 Гц. Отметим, что значения целевой функции метода MUSIC (14) для каждой частотной полосы перед суммированием были нормированы на максимальное значение (14) в данной полосе. Для дальнейшей обработки около узлов, соответствующих положениям источников, выделялась область близколежащих узлов (находящихся в радиусе 5 см от источника). Если глобальный максимум суммарной целевой функции набора расположен в области одного из источников, а при исключении данной области глобальный максимум располагается в области другого источника, то считалось, что источники разрешены правильно. Таким образом, для каждого ${{n}_{{{\text{fr}}}}}$ возможно оценить вероятность правильного разрешения ${{P}_{t}}$.

Число источников M (следовательно, и параметр метода MUSIC) оценивалось по спектру выборочной корреляционной матрицы. В данном эксперименте в спектрах собственных чисел корреляционных матриц разных частот сразу можно было выделить два главных собственных числа, примерно в 1000 раз больших остальных (“шумовых”) собственных чисел. Таким образом, оценка числа источников выполнялась в каждом случае абсолютно надежно.

Из рис. 4 видно, что суммирование целевых функций метода MUSIC (14) приводит к правильному разрешению источников (при суммировании целевых функций в более чем 100 частотных полосах источники разрешаются всегда), между тем, аналогичная процедура для функций метода максимума правдоподобия (8) не позволяет правильно разрешить источники.

Следует сказать и об эффективности алгоритмов при оценке в одной частотной полосе. Как и ожидалось, алгоритм MUSIC (14) показал здесь лучшие результаты по сравнению с методом (8). При численном моделировании алгоритм (14) правильно разрешал источники во всех частотных полосах, в отличие от метода наименьших квадратов. Этот результат подтвержден экспериментально. Так, для варианта расположения, отображенного на рис. 3, алгоритм (14) сумел правильно разрешить источники во всех 120 частотных полосах при моделировании, а в эксперименте в 28 из 120 полос. При этом метод максимума правдоподобия разрешил правильно источники в 41 из 120 полос (при моделировании) и в 16 из 120 (в эксперименте).

ЗАКЛЮЧЕНИЕ

В данной работе рассмотрена задача локализации одного и двух виброисточников в механоакустической системе с большим числом степеней. В случае с одним широкополосным виброисточником показана эффективность использования обработки по методу наименьших квадратов. Для случая с двумя виброисточниками на основе метода MUSIC разработан алгоритм, позволяющий с высокой вероятностью разрешить два источника и определить их положение. Данный алгоритм обладает приемлемой для практического применения вычислительной сложностью и доказал свою эффективность на экспериментальных данных. Продемонстрирована также эффективность определения числа источников по спектру выборочной корреляционной матрицы.

Стоит отметить, что предложенный алгоритм для поиска M > 1 источников может применяться в задачах, связанных со снижением шумности, поиском неисправностей и дефектов в сложных конструкциях.

Работа выполнена в рамках госзадания по теме 0035-2014-0010 “Разработка физических основ акустических систем нового поколения”.