Акустический журнал, 2020, T. 66, № 3, стр. 327-331
Максимальное поглощение звука монополем в помещении на низких частотах
a Акустический институт им. акад. Н.Н. Андреева
117036 Москва, ул. Шверника 4, Россия
b Московский государственный технический университет им. Н.Э. Баумана
105005 Москва, Россия
* E-mail: nikolay.kanev@mail.ru
Поступила в редакцию 14.08.2019
После доработки 02.10.2019
Принята к публикации 29.10.2019
Аннотация
Рассмотрена задача о поглощении звука монополем в прямоугольном помещении с абсолютно жесткими стенками. Найден импеданс излучения монополя, реализованного в виде поршня, встроенного в одну из стенок помещения. Вычислен импеданс монополя, при котором обеспечивается максимальный коэффициент затухания первого собственного колебания помещения. Показано, что в общем случае монополь с подобранным определенным образом импедансом поглощает звук эффективнее резонатора Гельмгольца. Предложенный подход может использоваться для проектирования активных систем поглощения звука для малых помещений.
Малые рассеиватели при определенных условиях являются эффективными поглотителями звука. В свободном пространстве газовый пузырек в жидкости или резонатор Гельмгольца при оптимальном трении имеют максимально возможное поглощение, которое может быть достигнуто рассеивателем монопольного типа [1]. Параметры резонатора Гельмгольца, при которых поглощение звука, характеризуемое коэффициентами затухания собственных колебаний помещения, максимально, найдены в работе [2]. Коэффициенты затухания первых мод помещения с резонатором зависят от его массы: чем она меньше, тем больше коэффициенты затухания. Но даже при нулевой длине горла резонатора его масса ненулевая и определяется присоединенной массой отверстия. Поэтому резонатор Гельмгольца в помещении не обеспечивает максимальное поглощение, достижимое монопольным рассеивателем.
Вместе с тем, задача о максимальном поглощении звука на первых резонансах помещения актуальна для акустики малых помещений: для выравнивания частотной характеристики помещений часто используются активные методы гашения звука [3, 4]. Активные методы [5–8] позволяют реализовать любой импеданс локального рассеивателя, а следовательно, достичь максимального демпфирования собственных мод помещения. В связи с этим в настоящей работе решена задача о максимальном поглощении звука монополем в помещении с абсолютно жесткими стенками. В качестве характеристики поглощения выбран коэффициент затухания свободных колебаний системы “помещение–монополь”. Монополь представляет собой встроенный в стенку поршень, малый по сравнению с размерами помещения. В первую очередь вычисляется его импеданс излучения [9, 10], а затем определяются собственные частоты системы “помещение–монополь” [2].
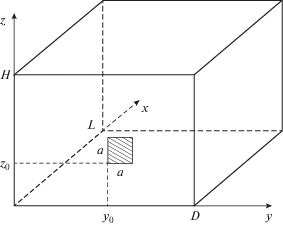
Рассмотрим прямоугольное помещение с размерами L, D, H с абсолютно жесткими стенками (рис. 1). Среда в помещении характеризуется плотностью $\rho $ и скоростью звука с. В стенке, находящейся в плоскости $x = 0,$ установлен квадратный поршень со стороной a, положение поршня задается координатами одной из его вершин $({{y}_{0}},{{z}_{0}})$. Пусть поршень колеблется по гармоническому закону с частотой $\omega $ и амплитудой скорости V.
Звуковое поле в помещении может быть найдено стандартным методом Фурье. Звуковое давление записывается в виде суммы
(1)
$p = i\omega \rho \sum\limits_{n,m} {{{V}_{{nm}}}} \frac{{\cos \left[ {{{\xi }_{{nm}}}(x - L)} \right]}}{{{{\xi }_{{nm}}}\sin {{\xi }_{{nm}}}L}}\cos {{\eta }_{n}}y\cos {{\zeta }_{m}}z,$(2)
${{V}_{{nm}}} = \frac{{4V}}{{DH{{\varepsilon }_{n}}{{\varepsilon }_{m}}}}{{\alpha }_{n}}{{\beta }_{m}},$(3)
$\begin{gathered} {{\alpha }_{{n \geqslant 1}}} = \frac{{\sin {{\eta }_{n}}({{y}_{0}} + a) - \sin {{\eta }_{n}}{{y}_{0}}}}{{{{\eta }_{n}}}}, \\ {{\beta }_{{m \geqslant 1}}} = \frac{{\sin {{\zeta }_{m}}({{z}_{0}} + a) - \sin {{\zeta }_{m}}{{z}_{0}}}}{{{{\zeta }_{m}}}}. \\ \end{gathered} $Сила, действующая на поршень со стороны среды, определяется выражением
где S – площадь поверхности поршня. Из (1) и (4) находим импеданс поршня(5)
${{Z}_{r}} = \frac{F}{V} = i\frac{{4\omega \rho }}{{DH}}\sum\limits_{n,m} {\frac{{{\text{ctg}}{{\xi }_{{nm}}}L}}{{{{\varepsilon }_{n}}{{\varepsilon }_{m}}{{\xi }_{{nm}}}}}} \alpha _{n}^{2}\beta _{m}^{2}.$Коэффициенты ${{\alpha }_{n}}$ и ${{\beta }_{m}}$ описывают влияние положения поршня на стенке на его импеданс. Если поршень расположен в углу, т.е. если ${{y}_{0}} = {{z}_{0}} = 0,$ то его колебания возбуждают все моды помещения. Если поршень расположен в центре стенки, т.е. если ${{y}_{0}} = {{(D - a)} \mathord{\left/ {\vphantom {{(D - a)} 2}} \right. \kern-0em} 2}$ и ${{z}_{0}} = {{(H - a)} \mathord{\left/ {\vphantom {{(H - a)} 2}} \right. \kern-0em} 2},$ то его колебания возбуждают только нулевую и четные по n и m моды.
Для расчетов рассмотрим два вида помещений: кубическое ($L:D:H = 1:1:1$) и вытянутое ($L:D:H = 1:0.2:0.2$). Введем безразмерные импеданс и частоту
где ${{\omega }_{1}} = {{\pi c} \mathord{\left/ {\vphantom {{\pi c} L}} \right. \kern-0em} L}$ – первая резонансная частота помещения без монополя. Далее штрихи у величин $Z_{r}^{'}$ и $\omega {\kern 1pt} '$ будем опускать.На рис. 2 приведен расчет импеданса поршня ${{Z}_{r}}$ в углу помещения и в центре стенки для двух помещений в зависимости от частоты. На собственных частотах возбуждаемых мод импеданс обращается в бесконечность. В вытянутом помещении импеданс слабо зависит от положения поршня на стенке, что также имеет место в одномодовых волноводах [11].
Рис. 2.
Импеданс излучения поршня в углу помещения (сплошные линии) и в центре помещения (пунктирные линии): (а) – кубическое помещение, (б) – вытянутое помещение.

Пусть импеданс монополя имеет произвольное комплексное значение Z, которое, как и импеданс излучения (6), приведем к безразмерному виду $Z{\kern 1pt} ' = \frac{Z}{{\rho c{{a}^{2}}}},$ опуская при этом штрих у величины $Z{\kern 1pt} '.$ Тогда собственные частоты системы “помещение–монополь” определяются уравнением [6]
В первую очередь рассмотрим влияние вещественной части импеданса на значение корней (7) для кубического помещения с монополем в углу. На рис. 3 приведены первые три корня уравнения (7), найденные численно, для двух значений мнимой части импеданса $Z$. Если рассматриваемая система бездиссипативна, т.е. $\operatorname{Re} Z = 0,$ то корни вещественны, обозначим их ${{\Omega }_{n}}$ и отметим на комплексной плоскости на рис. 3 проколотыми точками. Частоты ${{\omega }_{n}}$ – собственные частоты помещения без поршня. Наименьшая собственная частота помещения согласно (7) равна ${{\omega }_{1}} = 1,$ вторая – ${{\omega }_{2}} = \sqrt 2 .$
Рис. 3.
Собственные частоты системы “помещение–поршень” при изменении $\operatorname{Re} Z$от 0 до $\infty $. Стрелки указывают направление движения корней по кривой при увеличении $\operatorname{Re} Z$.
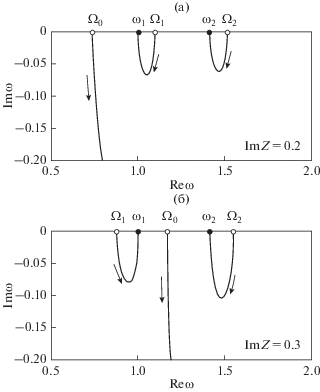
Нумерация ${{\Omega }_{n}}$ начинается с $n = 0,$ поскольку помещение с поршнем имеет дополнительную степень свободы и собственную частоту. На этой частоте звуковое давление во всем объеме помещения постоянно, что становится возможным в помещении с источником или стоком объемной скорости.
При $\operatorname{Im} Z = 0.2$ все частоты ${{\Omega }_{n}}$ оказываются выше ${{\omega }_{n}}$, при этом ${{\Omega }_{0}}$ оказываeтся ниже ${{\omega }_{1}}$. При $\operatorname{Im} Z = 0.3$ частота ${{\Omega }_{0}}$ оказывается между ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$, т.е. частота собственного колебания, связанного с дополнительной степенью свободы, обусловленной движением поршня, увеличивается с увеличением значения $\operatorname{Im} Z$.
Далее будем увеличивать значение действительной части импеданса поршня от нулевого значения до бесконечности и отслеживать, как изменяются собственные частоты. При ненулевом значении $\operatorname{Re} Z$ собственные частоты становятся комплексными, а соответствующие им моды затухающими. С увеличением $\operatorname{Re} Z$ мнимые части собственных частот уменьшаются, достигают минимального значения (за исключением нулевой моды), а затем стремятся к нулю. Мнимая часть нулевой собственной частоты не имеет экстремума, поэтому соответствующее собственное колебание системы становится все более затухающим. Таким образом, в пределе $\operatorname{Re} Z \to \infty $ собственные частоты стремятся к собственным частотам помещения без поршня ${{\omega }_{1}}$ и ${{\omega }_{2}}$, т.е. сильно задемпфированный поршень не оказывает влияния на звуковое поле в помещении.
Между значениями $\operatorname{Im} Z = 0.2$ и $\operatorname{Im} Z = 0.3$ существует значение $\operatorname{Im} Z$, при котором поведение корней (7) принципиально отличается. На рис. 4 приведены собственные частоты системы “помещение–поршень” для $\operatorname{Im} Z = 0.26$ при изменении $\operatorname{Re} Z$от 0 до $\infty $. Ветви корней, соответствующие нулевой и первой моде, имеют общую точку ${{\tilde {\omega }}_{{01}}}$. Как показано в работе [2] на примере резонатора Гельмгольца, максимальное поглощение звука на двух первых модах происходит на кратной собственной частоте. Можно также подобрать такое значение импеданса поршня, при котором одинаковую собственную частоту будут иметь нулевая и вторая моды, т.е. максимальное поглощение будет достигнуто в окрестности второй моды.
Далее вычислим коэффициент затухания первого собственного колебания системы. В окрестности первой резонансной частоты помещения ${{\omega }_{1}}$ будет два собственных колебания, имеющих в случае бездиссипативного поршня собственные частоты ${{\Omega }_{0}}$ и ${{\Omega }_{1}}$. Обозначим два первых корня уравнения (7) ${{\tilde {\omega }}_{1}}$ и ${{\tilde {\omega }}_{2}}$. Скорости затухания этих мод определяются величинами $\operatorname{Im} {{\tilde {\omega }}_{1}}$ и $\operatorname{Im} {{\tilde {\omega }}_{2}}$. Длительность затухания колебаний системы “помещение–поршень” в окрестности частоты ${{\omega }_{1}}$ будет, очевидно, определяться меньшим из двух коэффициентов затухания. Введем коэффициент затухания колебания системы следующим образом
(8)
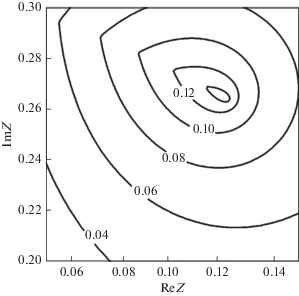
$\delta = \min ( - \operatorname{Im} {{\tilde {\omega }}_{1}}, - \operatorname{Im} {{\tilde {\omega }}_{2}}).$Коэффициент затухания $\delta $ является функцией импеданса Z. На рис. 5 приведена зависимость коэффициента затухания от комплексного импеданса Z в виде линий равных значений $\delta $, рассчитанных согласно (8). Функция $\delta (Z)$ имеет максимальное значение ${{\delta }_{m}} = 0.15$ при ${{Z}_{m}} = 0.12 + 0.26i.$
Рис. 5.
Коэффициент затухания системы “помещение–поршень” $\delta $ в окрестности первой резонансной частоты помещения в зависимости от импеданса поршня Z.
Аналогичным образом можно найти оптимальный импеданс поршня ${{Z}_{m}}$ и максимальный коэффициент затухания первого собственного колебания помещения ${{\delta }_{m}}$ для вытянутого помещения и для поршня, расположенного в центре стенки. Результаты расчетов приведены в таблице. Импедансы излучения поршня ${{Z}_{r}}$ для этих случаев приведены на рис. 2.
Таблица 1.
Оптимальный импеданс поршня для максимального поглощения звука
| Расположение поршня | Кубическое помещение $L:D:H = 1:1:1$ |
Вытянутое помещение $L:D:H = 1:0.2:0.2$ |
||
|---|---|---|---|---|
| ${{Z}_{m}}$ | ${{\delta }_{m}}$ | ${{Z}_{m}}$ | ${{\delta }_{m}}$ | |
| В углу помещения ${{y}_{0}} = {{z}_{0}} = 0$ |
0.12 + 0.26i | 0.15 | 0.33 + 0.11i | 0.53 |
| По центру стенки ${{y}_{0}} = {{(D - a)} \mathord{\left/ {\vphantom {{(D - a)} 2}} \right. \kern-0em} 2}$, ${{z}_{0}} = {{(H - a)} \mathord{\left/ {\vphantom {{(H - a)} 2}} \right. \kern-0em} 2}$ |
0.03 + 0.07i | 0.19 | 0.29 + 0.06i | 0.64 |
Как следует из расчетов, в вытянутом помещении коэффициент затухания значительно выше, чем в кубическом, из-за меньшего влияния резонансов помещения с ненулевыми номерами n и m на движение поршня. Большее поглощение обеспечивается также при расположении поршня в центре стенки, поскольку нечетные по n и m моды помещения не возбуждаются.
Найденные коэффициенты затухания также значительно выше, чем характерные коэффициенты затухания, обеспечиваемые резонатором Гельмгольца. В соразмерном помещении с поглощающим резонатором Гельмгольца [2] коэффициент затухания первого собственного колебания помещения составляет около 0.05, в то время как в кубическом помещении с монополем с оптимальным импедансом он в 3–4 раза выше.
Таким образом, найден импеданс монополя, при котором обеспечивается максимальное поглощение звука в помещении с жесткими стенками на его первой резонансной частоте. Такой монополь может быть реализован в виде поршня, встроенного в одну из стенок помещения, а требуемый импеданс может быть обеспечен с помощью активных методов управления импедансом локальных излучателей [6–8]. Рассмотренный в статье подход может быть использован для практических расчетов активных систем и подбора оптимального импеданса для демпфирования нескольких первых собственных колебаний помещения.
Список литературы
Исакович М.А. Общая акустика. М.: Наука, 1973.
Канев Н.Г. О максимальном поглощении звука резонатором Гельмгольца в помещении на низких частотах // Акуст. журн. 2018. Т. 64. № 6. С. 752–755.
Heuchel F.M., Fernandez-Grande E., Agerkvist F.T., Shabalina E. Active room compensation for sound reinforcement using sound field separation techniques // J. Acoust. Soc. Am. 2018. 143(3). P. 1346–1354.
Celestinos A., Nielsen S.B. Controlled acoustic bass system (CABS) a method to achieve uniform sound field distribution at low frequencies in rectangular rooms // J. Audio Eng. Soc. 2008. 56(11). P. 915–931.
Lissek H., Boulandet R., Fleury R. Electroacoustic absorbers: Bridging the gap between shunt loudspeakers and active sound absorption // J. Acoust. Soc. Am. 2011. 129(5). P. 2968–2978.
Boulandet R., Rivet E., Lissek H. Sensorless electroacoustic absorbers through synthesized impedance control for damping low-frequency modes in cavities // Acta Acustica united with Acustica. 2016. V. 102. № 4. C. 696–704.
Канев Н.Г., Миронов М.А. Активные резонаторы для гашения звука в узких трубах // Акуст. журн. 2008. Т. 54. № 3. С. 505–512.
Бобровницкий Ю.И., Морозов К.Д., Томилина Т.М. Импедансный подход к проектированию эффективных поглотителей колебательной энергии // Акуст. журн. 2017. Т. 63. № 2. С. 137–144.
Лапин А.Д. Импеданс излучения поршня в волноводе // Акуст. журн. 2000. Т. 46. № 3. С. 427–429.
Комкин А.И., Миронов М.А. Импеданс излучения поршня на стенке прямоугольного канала // Акуст. журн. 2013. Т. 59. № 3. С. 296–300.
Канев Н.Г. Присоединенная масса монополя и диполя в узкой трубе // Акуст. журн. 2007. Т. 53. № 5. С. 632–636.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал