Акустический журнал, 2020, T. 66, № 3, стр. 294-307
Пространственная векторно-скалярная структура низкочастотных полей мультипольных источников в зонах интерференционных максимумов
Г. Н. Кузнецов a, *, А. Н. Степанов a, b
a Институт общей физики им. А.М. Прохорова РАН
119991 Москва, ул. Вавилова 38, Россия
b Самарский национальный исследовательский университет имени академика С.П. Королева
443086 Самара, Московское шоссе 34, Россия
* E-mail: skbmortex@mail.ru
Поступила в редакцию 20.02.2019
После доработки 09.12.2019
Принята к публикации 24.12.2019
Аннотация
Для низкочастотных мультипольных источников различного порядка, находящихся в волноводе Пекериса, получены и исследуются зависимости, определяющие изменение структуры и величины интерференционных максимумов векторно-скалярных составляющих сигналов при вариации частоты, глубин волновода, приемников и источников, а также расстояния между ними. Найдены аппроксимирующие выражения, которые для разных глубин волновода и расположения источников и приемников согласуются с точными законами спадания указанных составляющих поля в этих зонах. Показано, что зависимости полей всех мультиполей по характеристикам амплитудно-фазовой структуры разделяются на две большие группы.
1. ВВЕДЕНИЕ
Основы анализа пространственной структуры и методов приближенной аппроксимации законов спадания усредненной – регулярной составляющей поля звукового давления (ЗД), создаваемого монопольным излучателем в волноводе, заложены Л.М. Бреховских в [1]. Позднее в развитие [1] для низкочастотных сигналов эта задача применительно к волноводу Пекериса рассматривалась в целом ряде работ, обзор и анализ которых, а также обобщение законов спадания на векторно-скалярную структуру звуковых полей, но для мультипольных источников выполнены в [2]. Вместе с тем из простого физического анализа следует, что кроме затухания усредненного поля представляют интерес пространственная структура и законы спадания звуковой энергии в зонах интерференционных максимумов (ИМА) – особенно для дискретных составляющих, на которых интерференция проявляется наиболее ярко. В этих зонах имеется наибольшее отношение сигнал/помеха [3], а при расположении приемной или излучающей антенны в зонах ИМА наблюдаются сравнительно гладкие и предсказуемые градиенты фазы [4, 5], что позволяет накапливать звуковую энергию на апертуре антенны и повысить помехоустойчивость обнаружения [6]. Одновременно из-за “гладкости” и предсказуемости градиентов фазы в зонах ИМА в результате фазирования сигналов на апертуре антенны имеется возможность достаточно точного пеленгования источников звуковых сигналов [6, 7].
Большой интерес к зонам ИМА связан также с особыми свойствами интерференционной пространственной структуры звукового поля [8]. В частности, с возможностью построения и анализа динамических инвариантов [9, 10]. С использованием этих “особых” характеристик интерференционной структуры связывают возможность исследования влияния динамики внутренних волн и других неоднородностей [11, 12], возможность устойчивого пеленгования широкополосных сигналов [6, 7], а также ставится и решается задача эффективного обнаружения слабых сигналов на фоне помех [13–15]. Не меньший интерес представляет возможность обнаружения и одновременно оценки расстояния до источника и радиальной скорости его движения [15, 16].
Задача оценки скорости спадания сигналов в зонах ИМА монополя поставлена и частично решена в [17]. В частности, в этой работе показано, что в волноводе Пекериса для источника и приемника, которые находятся в средней части волновода (точнее на середине его эквивалентной толщины H) квадрат потенциала поля звукового давления ${{\left| {\bar {\psi }(r,{{z}_{0}},z)} \right|}^{2}}$ ограничен сверху функцией ${{G}_{1}}(r,{{z}_{0}},z)$, для которой справедлива оценка
(1)
${{G}_{1}}(r,{{z}_{0}},z) = \frac{{k{{H}^{3}}}}{{2{{h}^{2}}\gamma }}\frac{1}{{{{r}^{2}}}}\left( {1 + O(\sqrt {\delta r} )} \right),$(2)
${{G}_{2}}(r,{{z}_{0}},z) = \frac{{k{{H}^{4}}}}{{2\pi {{h}^{2}}{{\gamma }^{2}}}}\frac{{{{{(k{{z}_{0}})}}^{2}}}}{{{{r}^{3}}}}\left( {1 + O(\sqrt {\delta r} } \right).$И, наконец, когда и источник, и приемник находятся в приповерхностной или придонной зонах волновода, ограничивающая квадрат потенциала оценка приобретает вид:
(3)
${{G}_{3}}(r,{{z}_{0}},z) = \frac{{k{{H}^{5}}}}{{2{{h}^{2}}{{\gamma }^{3}}}}\frac{{{{{(k{{z}_{0}})}}^{2}}{{{(kz)}}^{2}}}}{{{{r}^{4}}}}\left( {1 + O(\sqrt {\delta r} )} \right).$Однако в [17] анализ выполнен только для звукового давления (ЗД), в ограниченном интервале расстояний и только в предельных случаях – для приемников или источников, расположенных непосредственно в середине волновода или вблизи поверхностей раздела – у свободной поверхности или у дна. Несмотря на указанные ограничения, в [17] для этих трех зон ИМА выявлено существенное различие законов ослабления интенсивности звука (что представляется интересным и практически важным результатом). При этом обнаружена и общая закономерность – во всех случаях уменьшение или увеличение интенсивности в зонах ИМА происходит при изменении расстояния приблизительно в $\sqrt r $ быстрее, чем изменение величины регулярной составляющей в сопоставимых условиях.
В [18] выполнено обобщение результатов, изложенных в [17], на произвольные глубины и расстояния, а также выведены аналитические соотношения и проведено численное исследование характеристик полей не только для ЗД, но и для горизонтальной и вертикальной проекций колебательной скорости (ГПКС и ВПКС). Эти аппроксимирующие зависимости упрощают расчеты векторно-скалярной структуры полей, но авторам [18], несмотря на простую аппроксимацию, не удалось получить в явном – “прозрачном” виде аналитические зависимости ЗД, ГПКС и ВПКС от частоты звука, глубин волновода, глубин и расстояний между источником и приемником. Эта задача потребовала дополнительного исследования, результаты которого приведены ниже. Представленные далее результаты позволяют без выполнения численного моделирования получить количественные зависимости ЗД, ГПКС и ВПКС от целого ряда параметров, характеризующих волновод и геометрию эксперимента. Отметим, что эти зависимости можно считать справедливыми для низких частот и умеренных удалений от источника.
Следует также отметить, что в [1, 3–18] анализ выполнен только для монопольного источника, в то время как реальные объемные движущиеся низкочастотные источники характеризуются излучением, направленным в горизонтальной и вертикальной плоскости [3, 19, 20]. Известно, что для надводных и подводных источников различных типов характерно направленное звукоизлучение, поле которого может быть аппроксимировано полем эквивалентного источника – эквивалентным в том смысле, что поля реального источника и искусственного мультипольного источника в дальней зоне должны иметь близкую амплитудно-фазовую структуру. Как следует из литературы, на частотах оборотов вала и лопастных частотах, т.е. на низких частотах, корпус заменяется однородной оболочкой с “размазанными” ребрами или консолью и источниками преимущественно мультипольного характера. Гребной винт образует распределенные вдоль лопастей силовые источники, излучение которых представляет суперпозицию вращающихся диполей [21]. Турбулентная зона, примыкающая к гребному винту, согласно теории Лайтхилла, формирует квадрупольные источники. Суперпозиция этих источников образует группу мультиполей, которые на низких частотах с известными ограничениями могут быть представлены точечным мультипольным источником. Можно отметить, что дифракция звуковой волны на корпусе источника также формирует неоднородное – не осесимметричное излучение, которое на низких частотах может быть представлено полем эквивалентного сосредоточенного мультипольного источника [19, 20].
Одновременно при работе на низких частотах уменьшается влияние вертикального профиля скорости звука, что позволяет на умеренных расстояниях (на расстояниях до 10–20 км) и низких частотах (ниже 30–50 Гц) использовать модель Пекериса [1–3]. Отметим также, что численное исследование векторно-скалярной структуры акустических полей мультиполей в зонах ИМА, сформированных в плоско-слоистом волноводе, выполнено в [22]. Но аналитические аппроксимирующие зависимости поля мультиполей от глубин и расстояния не получены. Ниже в зонах ИМА исследуются аппроксимирующие зависимости, из которых для мультиполей различного типа в явном виде следуют зависимости ЗД, ГПКС и ВПКС от r, H, ω, z и z0. Очевидно, что на более высоких частотах протяженный (объемный) источник лучше заменять разнесенной вдоль корпуса системой источников и при моделировании или обработке экспериментальных данных учитывать реальные профили скорости звука [23].
Представляет интерес обобщить полученные в [17, 18, 22] результаты и получить аппроксимирующие зависимости при произвольных частотах, глубинах волновода H, источника ${{z}_{0}}$ и приемника $z$ и горизонтальных расстояниях $r$ между источником и приемником – и не только для ЗД, но и для горизонтальных и вертикальных проекций вектора колебательной скорости. Численное и аналитическое исследование необходимо выполнить для различных мультиполей при расположении приемников в зонах ИМА. Полученные аппроксимирующие зависимости необходимо сравнить с результатами точных расчетов для оценки возможности их использования при анализе указанных выше зависимостей для ЗД, ГПКС и ВПКС, а при необходимости – и проекций вектора потока мощности.
2. ПОВЕРХНОСТИ ИНТЕРФЕРЕНЦИОННЫХ МАКСИМУМОВ МУЛЬТИПОЛЬНЫХ ИЗЛУЧАТЕЛЕЙ В ВОЛНОВОДЕ ПЕКЕРИСА
Соотношения, необходимые для анализа поля мультиполей в зонах ИМА, получены в развитие предложенного Л.М. Бреховских способа [1] приближенного аналитического решения дисперсионного уравнения для волновода Пекериса ${\text{ctg}}x = \frac{i}{{\tilde {m}x}}\sqrt {{{x}^{2}} - {{{(kh\nu )}}^{2}}} $. Приближенные значения корней этого уравнения ${{x}_{l}} \approx {{l\pi h} \mathord{\left/ {\vphantom {{l\pi h} H}} \right. \kern-0em} H},$ $l = 1,2,...,N$ далее используются для записи модового представления потенциала звукового поля в волноводе Пекериса [19, 20, 22]:
(4)
$\psi (r,{{z}_{0}},z) = \frac{{2\pi }}{{kh}}\sum\limits_{n = 0}^L {\sum\limits_{m = - n}^n {\sum\limits_{l = 1}^N {{{A}_{{nml}}}H_{m}^{{(1)}}({{\xi }_{l}}r){{e}^{{im\varphi }}}} } } ,$Пренебрегая в знаменателе выражения для коэффициентов ${{A}_{{nml}}}$ всеми слагаемыми по сравнению со значением корней ${{x}_{l}}$, получим ${{A}_{{nml}}} \approx - {{\mu }_{{nm}}}{{D}_{{nm}}}{{p}_{{nml}}}$, где ${{p}_{{nml}}} = \sin \alpha _{{l0}}^{'}\sin {{\alpha }_{l}}P({{{{x}_{l}}} \mathord{\left/ {\vphantom {{{{x}_{l}}} {kh}}} \right. \kern-0em} {kh}})$. Тогда представление (4) может быть записано в более удобном для дальнейшего анализа виде
Здесь ${{\gamma }_{{nm}}} = m\varphi + \pi $ + $\pi (1 - {{{{\chi }_{{nm}}})} \mathord{\left/ {\vphantom {{{{\chi }_{{nm}}})} 4}} \right. \kern-0em} 4} + \pi (n - {{m)} \mathord{\left/ {\vphantom {{m)} 2}} \right. \kern-0em} 2}$. Корни дисперсионного уравнения ${{x}_{l}}$ входят в рассматриваемые выражения в основном в виде комбинации параметров ${{{{x}_{l}}} \mathord{\left/ {\vphantom {{{{x}_{l}}} {kh}}} \right. \kern-0em} {kh}}$. С учетом того, что эти корни приближенно равны ${{x}_{l}} \approx {{l\pi h} \mathord{\left/ {\vphantom {{l\pi h} H}} \right. \kern-0em} H}$, можно записать равенства: ${{{{x}_{l}}} \mathord{\left/ {\vphantom {{{{x}_{l}}} {kh}}} \right. \kern-0em} {kh}} = ld,$ ${{\alpha }_{{l0}}} = {{{{x}_{l}}{{z}_{0}}} \mathord{\left/ {\vphantom {{{{x}_{l}}{{z}_{0}}} h}} \right. \kern-0em} h}$ ≈ ${{ \approx l\pi {{z}_{0}}} \mathord{\left/ {\vphantom {{ \approx l\pi {{z}_{0}}} H}} \right. \kern-0em} H} = ldk{{z}_{0}}$ и ${{\alpha }_{l}} = {{{{x}_{l}}z} \mathord{\left/ {\vphantom {{{{x}_{l}}z} h}} \right. \kern-0em} h}$ ≈ ${{l\pi z} \mathord{\left/ {\vphantom {{l\pi z} H}} \right. \kern-0em} H} = ldkz$, в которых $d = {\pi \mathord{\left/ {\vphantom {\pi {kH}}} \right. \kern-0em} {kH}}$ = ${\lambda \mathord{\left/ {\vphantom {\lambda {2H}}} \right. \kern-0em} {2H}}$ – безразмерный параметр, равный отношению длины волны к удвоенной эффективной толщине волновода, и имеющий смысл величины, обратной количеству полуволн в эффективной толщине волновода.
Используя далее асимптотическое представление функции Ханкеля
(5)
$\begin{gathered} {{\left| {{{P}_{{nm}}}(r,{{z}_{0}},z)} \right|}^{2}} = \frac{{{{A}^{p}}}}{r}\left[ {\sum\limits_{l = 1}^N {p_{{nml}}^{2}} {{e}^{{ - 2\delta r{{l}^{2}}}}}} \right. + \\ \left. { + \,\,\sum\limits_{l = 1}^N {\sum\limits_{l' \ne l}^N {{{p}_{{nml}}}{{p}_{{nml'}}}{\kern 1pt} {{e}^{{ - \delta r({{l}^{2}} + {{{l'}}^{2}})}}}\cos (\Delta {{k}_{{ll'}}}r} } )} \right], \\ \end{gathered} $Анализируя (5), несложно увидеть, что второе слагаемое, представляющее собой интерференционную часть сигнала, спадает – уменьшается с увеличением расстояния – быстрее, чем первое слагаемое – его регулярная составляющая. Однако представляет интерес не только качественная, но и количественная оценка скорости спадания интерференционной части выражения (5). Такую оценку можно получить, полагая, как и в [17, 18], функции $\cos (\Delta {{k}_{{ll'}}}r)$ для всех $l$ и $l{\kern 1pt} {\kern 1pt} '$ равными единице и используя вместо коэффициентов ${{p}_{{nml}}}$ их модули. В результате для звукового давления получим функции:
(6)
$G_{{nm}}^{p}(r,{{z}_{0}},z) = \frac{{{{A}^{p}}}}{r}{{\left( {\sum\limits_{l = 1}^N {\left| {\sin \alpha _{{l0}}^{'}\sin {{\alpha }_{l}}P_{n}^{{|m|}}(ld)} \right|{{e}^{{ - \delta r{{l}^{2}}}}}} } \right)}^{2}},$В [24] получены выражения для полей ГПКС и ВПКС мультипольного источника в волноводе Пекериса в виде сумм, аналогичных сумме нормальных волн поля давления отдельных мультиполей
Применяя описанный выше подход, получим выражения
(7)
$\begin{gathered} G_{{nm}}^{{Vr}}(r,{{z}_{0}},z) = \frac{{{{A}^{V}}{{g}_{m}}}}{r} \times \\ \times \,\,{{\left( {\sum\limits_{l = 1}^N {\sqrt {1 - {{l}^{2}}{{d}^{2}}} } \left| {\sin \alpha _{{l0}}^{'}\sin {{\alpha }_{l}}P_{n}^{{|m|}}(ld)} \right|{{e}^{{ - \delta r{{l}^{2}}}}}} \right)}^{2}}, \\ \end{gathered} $(8)
$\begin{gathered} G_{{nm}}^{{Vz}}(r,{{z}_{0}},z) = {{d}^{2}}\frac{{{{A}^{V}}}}{r} \times \\ \times \,\,{{\left( {\sum\limits_{l = 1}^N {l\left| {\sin \alpha _{{l0}}^{'}\cos {{\alpha }_{l}}P_{n}^{{|m|}}(ld)} \right|} \,{{e}^{{ - \delta r{{l}^{2}}}}}} \right)}^{2}}, \\ \end{gathered} $Вычислительный эксперимент показал, что для всех мультиполей форма ПИМ ГПКС полностью совпадает с формой ПИМ ЗД, в то время как форма ПИМ ВПКС имеет существенные отличия от формы ПИМ давления. Кроме того, расчеты показали, что все мультиполи можно разделить на две группы с одинаковой общей структурой сечений поверхностей интерференционных максимумов сигналов в вертикальной плоскости, которые проведены параллельно оси глубин системы координат. Это разделение базируется на тех же самых характеристиках элементарных мультипольных источников, с которыми связано описанное в [24] уточнение принципа взаимности. В первую группу входят мультиполи, для которых сумма индексов $n + \left| m \right|$ четна и, следовательно, коэффициенты ${{p}_{{nml}}}$ в выражениях для полей ЗД и ГПКС пропорциональны $\sin ldk{{z}_{0}}\sin ldkz,$ а для полей ВПКС они пропорциональны $\sin ldk{{z}_{0}}\cos ldkz.$ Эта группа включает монополь, горизонтальный диполь, квадруполи с двумя горизонтальными или двумя вертикальными осями и т.д. Во вторую группу входят мультиполи, у которых сумма индексов $n + \left| m \right|$ нечетна, поэтому коэффициенты ${{p}_{{nml}}}$ в выражениях для полей ЗД пропорциональны $\cos ldk{{z}_{0}}\sin ldkz$, а для полей ВПКС они пропорциональны $\cos ldk{{z}_{0}}\cos ldkz$. Это вертикальный диполь, квадруполи с одной горизонтальной и одной вертикальной осью и т.д. [22, 24].
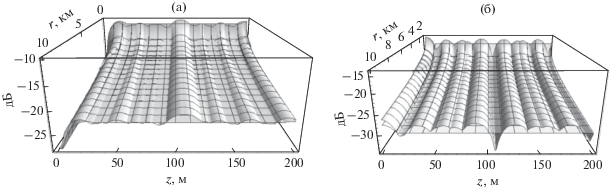
Указанные тригонометрические зависимости коэффициентов ${{p}_{{nml}}}$ от глубин источника ${{z}_{0}}$ и приемника $z$ определяют отмеченные выше общие особенности ПИМ, а также различие форм вертикальных сечений ПИМ для мультиполей первой и второй групп. Слева на рис. 1а показана форма разреза ПИМ для ЗД и ГПКС, а справа на рис. 1б – форма разреза ПИМ ВПКС. Характерным для первой группы является наличие зоны максимума у ЗД и ГПКС и зоны минимума у ВПКС на середине эквивалентной глубины волновода. Типичные формы ПИМ для мультиполей второй группы представлены на рис. 2. Характерным для этой группы сигналов является наличие на середине эквивалентной толщины волновода зоны локального минимума у ЗД и ГПКС и подъема у ВПКС. Для обеих групп наблюдается также принципиальное различие зависимостей вблизи поверхностей раздела. При уменьшении или увеличении глубины источника или приемника размах колебаний поверхностей сглаживается, но общие особенности их форм сохраняются.
Расчеты ПИМ, изображенных на рис. 1 и 2, произведены для волновода толщиной $h$ = 200 м, скорости звука в воде 1500 м/с, параметров дна $\tilde {m} = 2.7,$ $\tilde {n} = 0.83$ и коэффициента поглощения 0.01. Частота источника 50 Гц, а его глубина выбрана равной 111 м, что примерно соответствует середине эффективной толщины волновода. Горизонтальное расстояние между источником и приемником изменяется от 100 м до 10 км.
3. АППРОКСИМИРУЮЩИЕ СООТНОШЕНИЯ ДЛЯ ОПИСАНИЯ ПОВЕРХНОСТЕЙ ИНТЕРФЕРЕНЦИОННЫХ МАКСИМУМОВ
Для практических целей целесообразно иметь удобные приближенные аналитические соотношения, которыми по аналогии с оценками для спадания регулярных составляющих [2, 18] можно аппроксимировать выражения (6)–(8) для функций, определяющих ПИМ давления и проекций колебательной скорости различных мультиполей. Отметим, что в [2] при аппроксимации соотношений, описывающих регулярные составляющие квадратов модулей амплитуд давления, суммы приближенно заменялись интегралами. Однако напрямую использовать этот способ для аппроксимации функций, описывающих структуру ПИМ нельзя, так как наличие модуля произведения тригонометрических функций под знаком интеграла приводит к невозможности вычислить его аналитически. Кроме того, форма поверхностей ИМА на малых глубинах изменяется очень резко. Поэтому авторам не удалось найти общую аппроксимацию для всех глубин источника и приемника.
В связи с указанными обстоятельствами область изменения глубин $0 \leqslant z,{{z}_{0}} \leqslant h$ разбивается на три подобласти, в каждой из которых можно индивидуальными способами освободиться от знака модуля и/или подобрать подходящую аппроксимацию. Такими подобластями могут быть интервалы приповерхностных, придонных и средних глубин. В дальнейшем для краткости будем называть “приграничными” приповерхностные глубины источника и излучателя, которые удовлетворяют условиям $0 \leqslant z,{{z}_{0}} \leqslant {{H}_{1}}$, ${{H}_{1}} = {H \mathord{\left/ {\vphantom {H N}} \right. \kern-0em} N}$, а также – с учетом симметрии относительно середины эффективной толщины ${H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0em} 2}$ аргументов у функции, описывающей ПИМ, – и придонные глубины ${{H}_{2}} \leqslant z,$ ${{z}_{0}} \leqslant h,$ ${{H}_{2}} = H - {H \mathord{\left/ {\vphantom {H N}} \right. \kern-0em} N}.$ Глубины, не удовлетворяющие этим условиям, т.е. относящиеся к средней части волновода ${{H}_{1}} \leqslant z,$ ${{z}_{0}} \leqslant {{H}_{2}}$, условно назовем “средними”. Исследование выполним для низких частот на расстояниях r, когда в (6)–(8) следует учитывать экспоненциальный сомножитель $\exp ( - \delta r{{l}^{2}})$, т.е. учитывать затухание нормальных волн.
3.1. Монопольный источник
В качестве базового примера построения аппроксимирующих соотношений рассмотрим монопольный излучатель, которому в выражениях (6)–(8) соответствуют индексы $n = 0$ и $m = 0$. Следовательно, для этого излучателя коэффициент ${{g}_{0}} = 1$, аргумент $\alpha _{{l0}}^{'} = {{\alpha }_{{l0}}},$ а полином Лежандра равен единице $P_{0}^{0}(ld) = 1$.
Подставляя в (6) эти параметры, для функции ПИМ ЗД монополя получим:
(9)
$G_{{00}}^{p} = \frac{{{{A}^{P}}}}{r}{{\left( {\sum\limits_{l = 1}^N {\left| {\sin {{\alpha }_{{l0}}}\sin {{\alpha }_{l}}} \right|{{e}^{{ - \delta r{{l}^{2}}}}}} } \right)}^{2}}.$Для краткости здесь и далее список аргументов ($r,{{z}_{0}},z)$ у функций ПИМ и их аппроксимаций опускается. Для приграничных глубин аргументы ${{\alpha }_{{l0}}} = {{l\pi {{z}_{0}}} \mathord{\left/ {\vphantom {{l\pi {{z}_{0}}} H}} \right. \kern-0em} H}$ и ${{\alpha }_{l}} = {{l\pi z} \mathord{\left/ {\vphantom {{l\pi z} H}} \right. \kern-0em} H}$ входящих в (9) тригонометрических функций для любых нормальных волн не превосходят $\pi $: ${{\alpha }_{{l0}}} \leqslant \pi $ и ${{\alpha }_{l}} \leqslant \pi $, $\forall l \leqslant N,$ следовательно, $\sin {{\alpha }_{{l0}}} \geqslant 0$ и $\sin {{\alpha }_{l}} \geqslant 0$ и знак модуля в (9) можно опустить. Для получения искомой аппроксимации сумму в этом выражении предлагается считать приближенно равной аналитически вычисляемому интегралу [25]. Тогда для приграничных глубин аппроксимирующую зависимость запишем в виде:
(10)
$\begin{gathered} G_{{00}}^{p} \approx \frac{{{{A}^{p}}\pi }}{{16\delta {{r}^{2}}}} \times \\ \times \,\,{{\left( {\exp \left( { - \frac{{{{\pi }^{2}}{{{({{z}_{0}} - z)}}^{2}}}}{{4{{H}^{2}}\delta r}}} \right) - \exp \left( { - \frac{{{{\pi }^{2}}{{{({{z}_{0}} + z)}}^{2}}}}{{4{{H}^{2}}\delta r}}} \right)} \right)}^{2}}. \\ \end{gathered} $Раскладывая экспоненты выражения (10) в ряд в окрестности бесконечно удаленной точки $r$ и удерживая только члены первого порядка, получим оценку $G_{{00}}^{P}\sim \frac{{{{H}^{5}}}}{{2k{{h}^{2}}{{\gamma }^{3}}}}\frac{{{{{(k{{z}_{0}})}}^{2}}{{{(kz)}}^{2}}}}{{{{r}^{4}}}}$, которая с точностью до константы ${1 \mathord{\left/ {\vphantom {1 {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}$ совпадает с (3).
В случае, когда приграничным является источник $0 \leqslant {{z}_{0}} \leqslant H{}_{1}$ или ${{H}_{2}} \leqslant {{z}_{0}} \leqslant h$, а глубина приемника находится в диапазоне ${{H}_{1}} < z < {{H}_{2}},$ в соотношении (9) из под знака модуля можно вынести только первый положительный сомножитель $\sin {{\alpha }_{{l0}}}$. А знакопеременный сомножитель $\sin {{\alpha }_{l}}$ в сумме (9) заменяется средним по полупериоду значением: $\left| {\sin {{\alpha }_{l}}} \right| \approx {2 \mathord{\left/ {\vphantom {2 \pi }} \right. \kern-0em} \pi }$. Тогда можно считать, что $G_{{00}}^{p} \approx \frac{{4{{A}^{p}}}}{{{{\pi }^{2}}r}}{{\left( {\sum\nolimits_{l = 1}^N {\sin {{\alpha }_{l}}_{0}{{e}^{{ - \delta r{{l}^{2}}}}}} } \right)}^{2}}$и далее приближенно
(11)
$G_{{00}}^{p} \approx \frac{{4{{A}^{p}}}}{{{{\pi }^{2}}\delta {{r}^{2}}}}{\text{Daso}}{{{\text{n}}}^{2}}\left( {\frac{{\pi {{z}_{0}}}}{{2H\sqrt {\delta r} }}} \right),$Аналогичные результаты можно получить и в случае, когда условию “приграничности” удовлетворяет глубина приемника $0 \leqslant z \leqslant {{H}_{1}}$ или ${{H}_{2}} \leqslant z \leqslant h$, а источник находится на средних глубинах ${{H}_{1}} < {{z}_{0}} < {{H}_{2}}$. В этом случае в соотношении (6) из под знака модуля можно вынести положительный сомножитель $\sin {{\alpha }_{l}}$, а знакопеременным является сомножитель $\sin {{\alpha }_{{l0}}}$, который заменяется средним по полупериоду гармонической функции значением ${2 \mathord{\left/ {\vphantom {2 \pi }} \right. \kern-0em} \pi }$. Таким образом, аппроксимирующая зависимость имеет такой же как (11) вид
(12)
$G_{{00}}^{p} \approx \frac{{4{{A}^{p}}}}{{{{\pi }^{2}}\delta {{r}^{2}}}}{\text{Daso}}{{{\text{n}}}^{2}}\left( {\frac{{\pi z}}{{2H\sqrt {\delta r} }}} \right)$Подобласть средних глубин характеризуется тем, что обе глубины ${{z}_{0}}$ и $z$ не удовлетворяют условиям приграничности: ${{H}_{1}} < z,$ ${{z}_{0}} < {{H}_{2}}.$ Поэтому в сумме (9) оба тригонометрических сомножителя являются знакопеременными, и для получения приближенных зависимостей предлагается заменить их средними по полупериоду гармонической функции значениями: $\left| {\sin {{\alpha }_{{l0}}}} \right| \approx {2 \mathord{\left/ {\vphantom {2 \pi }} \right. \kern-0em} \pi }$ и $\left| {\sin {{\alpha }_{l}}} \right| \approx {2 \mathord{\left/ {\vphantom {2 \pi }} \right. \kern-0em} \pi }.$ После чего сумма в (9) приобретает вид $\sum\nolimits_{l = 1}^N {\left| {\sin {{\alpha }_{{l0}}}\sin {{\alpha }_{l}}} \right|{{e}^{{ - \delta r{{l}^{2}}}}}} $ ≈ $\frac{4}{{{{\pi }^{2}}}}\sum\nolimits_{l = 1}^N {{{e}^{{ - \delta r{{l}^{2}}}}}} $, которую предлагается считать приближенно равной интегралу $\sum\nolimits_{l = 1}^N {{{e}^{{ - \delta r{{l}^{2}}}}}} $ ≈ $({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})\sqrt {{\pi \mathord{\left/ {\vphantom {\pi {\delta r}}} \right. \kern-0em} {\delta r}}} \,{\text{erf}}(N\sqrt {\delta r} )$ [25]. В этом случае получим выражение
(13)
$G_{{00}}^{p} \approx \frac{{4{{A}^{P}}}}{{{{\pi }^{3}}\delta {{r}^{2}}}}{\text{er}}{{{\text{f}}}^{2}}\left( {N\sqrt {\delta r} } \right),$Таблица 1.
Аппроксимирующие соотношения функции ПИМ ЗД монополя
| Ограничения на ${{z}_{0}}$ | Ограничения на $z$ | Аппроксимирующее соотношение | Оценка |
|---|---|---|---|
| $0 \leqslant {{z}_{0}} \leqslant {{H}_{1}}$ или ${{H}_{2}} \leqslant {{z}_{0}} \leqslant h$ |
$0 \leqslant z \leqslant {{H}_{1}}$ или ${{H}_{2}} \leqslant z \leqslant h$ |
$G_{{00}}^{p} \approx \frac{{{{A}^{p}}\pi }}{{16\delta {{r}^{2}}}}{{\left( {\exp \left( { - \frac{{b_{1}^{2}}}{{4\delta r}}} \right) - \exp \left( { - \frac{{b_{2}^{2}}}{{4\delta r}}} \right)} \right)}^{2}}$ | $G_{{00}}^{P}\sim \frac{{{{H}^{5}}}}{{2k{{h}^{2}}{{\gamma }^{3}}}}\frac{{{{{(k{{z}_{0}})}}^{2}}{{{(kz)}}^{2}}}}{{{{r}^{4}}}}$ |
| $0 \leqslant {{z}_{0}} \leqslant {{H}_{1}}$ или ${{H}_{2}} \leqslant {{z}_{0}} \leqslant h$ |
${{H}_{1}} < z < {{H}_{2}}$ | $G_{{00}}^{p} \approx \frac{{4{{A}^{p}}}}{{{{\pi }^{2}}\delta {{r}^{2}}}}{\text{Daso}}{{{\text{n}}}^{2}}\left( {\frac{{\pi {{z}_{0}}}}{{2H\sqrt {\delta r} }}} \right)$ | $G_{{00}}^{p}\sim \frac{{8{{H}^{4}}}}{{{{\pi }^{3}}k{{h}^{2}}{{\gamma }^{2}}}}\frac{{{{{(k{{z}_{0}})}}^{2}}}}{{{{r}^{3}}}}$ |
| ${{H}_{1}} < {{z}_{0}} < {{H}_{2}}$ | $0 \leqslant z \leqslant {{H}_{1}}$ или ${{H}_{2}} \leqslant z \leqslant h$ |
$G_{{00}}^{p} \approx \frac{{4{{A}^{p}}}}{{{{\pi }^{2}}\delta {{r}^{2}}}}{\text{Daso}}{{{\text{n}}}^{2}}\left( {\frac{{\pi z}}{{2H\sqrt {\delta r} }}} \right)$ | $G_{{00}}^{p}\sim \frac{{8{{H}^{4}}}}{{{{\pi }^{3}}k{{h}^{2}}{{\gamma }^{2}}}}\frac{{{{{(kz)}}^{2}}}}{{{{r}^{3}}}}$ |
| ${{H}_{1}} < {{z}_{0}} < {{H}_{2}}$ | ${{H}_{1}} < z < {{H}_{2}}$ | $G_{{00}}^{p} \approx \frac{{4{{A}^{P}}}}{{{{\pi }^{3}}\delta {{r}^{2}}}}{\text{er}}{{{\text{f}}}^{2}}\left( {N\sqrt {\delta r} } \right)$ | $G_{{00}}^{p}\sim \frac{{32{{H}^{3}}}}{{{{\pi }^{4}}k{{h}^{2}}\gamma }}\frac{1}{{{{r}^{2}}}}$ |
| Примечание: b1 = π(z0 – z)/H, b2 = π(z0 + z)/H. | |||
Подставляя в (7) значения параметров, которыми характеризуется монопольный излучатель, получим выражение для функции ПИМ ГПКС этого излучателя в виде:
(14)
$G_{{00}}^{{Vr}} = \frac{{{{A}^{V}}}}{r}{{\left( {\sum\limits_{l = 1}^N {\sqrt {1 - {{l}^{2}}{{d}^{2}}} } \left| {\sin {{\alpha }_{{l0}}}\sin {{\alpha }_{l}}} \right|{{e}^{{ - \delta r{{l}^{2}}}}}} \right)}^{2}}.$Видно, что выражение (14) для функции $G_{{00}}^{{Vr}}$, которая ограничивает интерференционную поверхность ГПКС, отличается от выражения (9) для функции $G_{{00}}^{p}$, ограничивающей интерференционную поверхность ЗД, только наличием у каждого слагаемого сомножителя $\sqrt {1 - {{l}^{2}}{{d}^{2}}} $. Учитывая, что для любых номеров нормальных волн справедливо неравенство $ld < 1$, можно утверждать, что для любого $l$ $\sqrt {1 - {{l}^{2}}{{d}^{2}}} \leqslant \sqrt {1 - {{d}^{2}}} $ и вынести корень из под знака суммы. Следовательно, например, для приграничных глубин функции $G_{{00}}^{{Vr}}$ можно аппроксимировать выражением
Аналогично умножением соотношений (10)–(13) на двучлен $1 - {{d}^{2}}$ определяются аппроксимации функции ПИМ ГПКС (14) для всех остальных глубин.
Если значения характеризующих монополь параметров подставить в (8), то получим выражение для функции ПИМ ВПКС этого излучателя
(15)
$G_{{00}}^{{Vz}} = {{d}^{2}}\frac{{{{A}^{V}}}}{r}{{\left( {\sum\limits_{l = 1}^N {l\left| {\sin {{\alpha }_{{l0}}}\cos {{\alpha }_{l}}} \right|{{e}^{{ - \delta r{{l}^{2}}}}}} } \right)}^{2}}.$В этом выражении функция $\cos {{\alpha }_{l}} = \cos l({{\pi z} \mathord{\left/ {\vphantom {{\pi z} H}} \right. \kern-0em} H})$ остается положительной для любых номеров l, если удовлетворяется неравенство $\pi z({N \mathord{\left/ {\vphantom {N H}} \right. \kern-0em} H}) \leqslant {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Это значит, что для ВПКС “приграничными” следует считать приповерхностные $0 \leqslant z \leqslant H_{1}^{'},$ $H_{1}^{'} = {{0.5H} \mathord{\left/ {\vphantom {{0.5H} N}} \right. \kern-0em} N}$ и придонные $H_{2}^{'} \leqslant z \leqslant h,$ $H_{2}^{'} = H - H_{1}^{'}$ глубины. Соответственно изменится и понятие “средней” глубины приемника: $H_{1}^{'} \leqslant z \leqslant H_{2}^{'}$. Аппроксимирующие соотношения для функции ПИМ ВПКС монополя (15) и их асимптотические оценки приведены в табл. 2.
Таблица 2.
Аппроксимирующие соотношения функции ПИМ ВПКС монополя
| Ограничения на ${{z}_{0}}$ | Ограничения на $z$ | Аппроксимирующее соотношение | Оценка |
|---|---|---|---|
| $0 \leqslant {{z}_{0}} \leqslant {{H}_{1}}$ или ${{H}_{2}} \leqslant {{z}_{0}} \leqslant h$ |
$0 \leqslant z \leqslant H_{1}^{'}$ или $H_{2}^{'} \leqslant z \leqslant h$ |
$\begin{gathered} G_{{00}}^{{Vz}} \approx {{d}^{2}}\frac{{{{A}^{V}}\pi }}{{64{{\delta }^{3}}{{r}^{4}}}} \times \\ \times \,\,{{\left( {{{b}_{1}}\exp \left( { - \frac{{b_{1}^{2}}}{{4\delta r}}} \right) + {{b}_{2}}\exp \left( { - \frac{{b_{2}^{2}}}{{4\delta r}}} \right)} \right)}^{2}} \\ \end{gathered} $ | $G_{{00}}^{{Vz}}\sim {{d}^{2}}\frac{{{{k}^{3}}{{H}^{7}}}}{{2{{\pi }^{2}}{{h}^{2}}{{\gamma }^{3}}}}\frac{{{{{(k{{z}_{0}})}}^{2}}}}{{{{r}^{4}}}}$ |
| $0 \leqslant {{z}_{0}} \leqslant {{H}_{1}}$ или ${{H}_{2}} \leqslant {{z}_{0}} \leqslant h$ |
$H_{1}^{'} \leqslant z \leqslant H_{2}^{'}$ | $G_{{00}}^{{Vz}} \approx {{d}^{2}}\frac{{{{A}^{V}}\pi }}{{4{{H}^{2}}{{\delta }^{3}}}}\frac{{z_{0}^{2}}}{{{{r}^{4}}}}\exp \left( { - \frac{{{{\pi }^{2}}z_{0}^{2}}}{{2{{H}^{2}}\delta r}}} \right)$ | $G_{{00}}^{{Vz}}\sim {{d}^{2}}\frac{{2{{k}^{3}}{{H}^{7}}}}{{{{\pi }^{4}}{{h}^{2}}{{\gamma }^{3}}}}\frac{{{{{(k{{z}_{0}})}}^{2}}}}{{{{r}^{4}}}}$ |
| ${{H}_{1}} < {{z}_{0}} < {{H}_{2}}$ | $0 \leqslant z \leqslant H_{1}^{'}$ или $H_{2}^{'} \leqslant z \leqslant h$ |
$G_{{00}}^{{Vz}} \approx {{d}^{2}}\frac{{{{A}^{V}}}}{{{{\pi }^{2}}{{\delta }^{2}}}}\frac{1}{{{{r}^{3}}}}{{\left( {1 - \frac{{\pi z}}{{H\sqrt {\delta r} }}{\text{Dason}}\left( {\frac{{\pi z}}{{2H\sqrt {\delta r} }}} \right)} \right)}^{2}}$ | $G_{{00}}^{{Vz}}\sim {{d}^{2}}\frac{{8{{k}^{3}}{{H}^{6}}}}{{{{\pi }^{5}}{{h}^{2}}{{\gamma }^{2}}}}\frac{1}{{{{r}^{3}}}}$ |
| ${{H}_{1}} < {{z}_{0}} < {{H}_{2}}$ | $H_{1}^{'} \leqslant z \leqslant H_{2}^{'}$ | $G_{{00}}^{{Vz}} \approx {{d}^{2}}\frac{{4{{A}^{V}}}}{{{{\pi }^{4}}{{\delta }^{2}}{{r}^{3}}}}{{\left( {1 - {{e}^{{ - \delta r{{N}^{2}}}}}} \right)}^{2}}$ | $G_{{00}}^{{Vz}}\sim {{d}^{2}}\frac{{32{{k}^{3}}{{H}^{6}}}}{{{{\pi }^{7}}{{h}^{2}}{{\gamma }^{2}}}}\frac{1}{{{{r}^{3}}}}$ |
| Примечание: b1 = π(z0 – z)/H, b2 = π(z0 + z)/H. | |||
3.2. Горизонтальные диполи
В выражениях (6)–(8) горизонтальным диполям с различной ориентацией осей соответствуют индексы $n = 1$ и $m = \pm 1$. Все характеристики этих диполей одинаковы, так как зависят от $\left| m \right|$, поэтому здесь и далее для квадруполей для краткости рассматриваются только мультиполи, соответствующие положительным значениям $m$. Для указанных индексов коэффициент ${{g}_{1}} = 1 + {1 \mathord{\left/ {\vphantom {1 {{{k}^{2}}}}} \right. \kern-0em} {{{k}^{2}}}}{{r}^{2}},$ $\alpha _{{l0}}^{'} = {{\alpha }_{{l0}}} = ld{{z}_{0}},$ а присоединенные полиномы Лежандра равны $P_{1}^{1}(ld) = \sqrt {1 - {{l}^{2}}{{d}^{2}}} .$ Запишем функции ПИМ для горизонтального диполя:
(16)
$\begin{gathered} G_{{11}}^{p} = \frac{{{{A}^{p}}}}{r}{{\left( {\sum\limits_{l = 1}^N {\sqrt {1 - {{l}^{2}}{{d}^{2}}} \left| {\sin {{\alpha }_{{l0}}}\sin {{\alpha }_{l}}} \right|{{e}^{{ - \delta r{{l}^{2}}}}}} } \right)}^{2}}, \\ G_{{11}}^{{Vr}} = \frac{{{{A}^{V}}{{g}_{1}}}}{r}{{\left( {\sum\limits_{l = 1}^N {(1 - {{l}^{2}}{{d}^{2}})\left| {\sin {{\alpha }_{{l0}}}\sin {{\alpha }_{l}}} \right|{{e}^{{ - \delta r{{l}^{2}}}}}} } \right)}^{2}}, \\ G_{{11}}^{{Vz}} = {{d}^{2}}\frac{{{{A}^{V}}}}{r}{{\left( {\sum\limits_{l = 1}^N {l\sqrt {1 - {{l}^{2}}{{d}^{2}}} \left| {\sin {{\alpha }_{{l0}}}\cos {{\alpha }_{l}}} \right|{{e}^{{ - \delta r{{l}^{2}}}}}} } \right)}^{2}}. \\ \end{gathered} $Сравнивая выражения (16) для функций ПИМ горизонтального диполя с выражениями (9), (14), (15) для функций ПИМ монополя, несложно заметить, что они отличаются только наличием у слагаемых дополнительного множителя $\sqrt {1 - {{l}^{2}}{{d}^{2}}} $. Поэтому рассуждая, как и в п. 3.1 при определении верхних оценок для ПИМ горизонтальных компонент колебательной скорости, получим, что для горизонтального диполя можно использовать умноженные на двучлен $1 - {{d}^{2}}$ аппроксимации из табл. 1 и 2 функций ПИМ монополя.
3.3. Вертикальный диполь
В выражениях (6)–(8) вертикальной диполь представлен индексами $n = 1$ и $m = 0$. По определению присоединенных полиномов Лежандра $P_{1}^{0}(ld) = ld$. Для этого диполя ${{g}_{0}} = 1$, ${{\chi }_{{10}}} = - 1$ и $\sin \alpha _{{l0}}^{'} = \cos {{\alpha }_{{l0}}}$. Поэтому функция ПИМ ЗД этого диполя записывается в виде:
(17)
$G_{{10}}^{p} = {{d}^{2}}\frac{{{{A}^{P}}}}{r}{{\left( {\sum\limits_{l = 1}^N {l\left| {\cos {{\alpha }_{{l0}}}\sin {{\alpha }_{l}})} \right|{{e}^{{ - \delta r{{l}^{2}}}}}} } \right)}^{2}}.$Зона приграничных глубин для ЗД этого источника определяется по-другому — это приповерхностные $0 \leqslant {{z}_{0}} \leqslant H_{1}^{'}$ и придонные $H_{2}^{'} \leqslant {{z}_{0}} \leqslant h$ глубины источника, и приповерхностные $0 \leqslant z \leqslant {{H}_{1}}$ и придонные ${{H}_{2}} \leqslant z \leqslant h$ глубины приемника. Полученные с учетом указанной особенности аппроксимирующие соотношения для функции ПИМ ЗД вертикального диполя (17) и их асимптотические оценки приведены в табл. 3. Функция ПИМ ГПКС вертикального диполя
(18)
$G_{{10}}^{{Vr}} = {{d}^{2}}\frac{{{{A}^{V}}}}{r}{{\left( {\sum\limits_{l = 1}^N {l\sqrt {1 - {{l}^{2}}{{d}^{2}}} } \left| {\cos {{\alpha }_{{l0}}}\sin {{\alpha }_{l}}} \right|{{e}^{{ - \delta r{{l}^{2}}}}}} \right)}^{2}}$(19)
$G_{{10}}^{{Vz}} = {{d}^{4}}\frac{{{{A}^{V}}}}{r}{{\left( {\sum\limits_{l = 1}^N {{{l}^{2}}\left| {\cos {{\alpha }_{{l0}}}\cos {{\alpha }_{l}}} \right|} {{e}^{{ - \delta r{{l}^{2}}}}}} \right)}^{2}}.$Таблица 3.
Аппроксимирующие соотношения функции ПИМ ЗД вертикального диполя
| Ограничения на ${{z}_{0}}$ | Ограничения на $z$ | Аппроксимирующее соотношение | Оценка |
|---|---|---|---|
| $0 \leqslant {{z}_{0}} \leqslant H_{1}^{'}$, или $H_{2}^{'} \leqslant {{z}_{0}} \leqslant h$ |
$0 \leqslant z \leqslant {{H}_{1}}$, или ${{H}_{2}} \leqslant z \leqslant h$ |
$\begin{gathered} G_{{10}}^{p} \approx {{d}^{2}}\frac{{{{A}^{P}}\pi }}{{64{{\delta }^{3}}{{r}^{4}}}} \times \\ \times \,\,{{\left( {{{b}_{2}}\exp \left( { - \frac{{b_{2}^{2}}}{{4\delta r}}} \right) - {{b}_{1}}\exp \left( { - \frac{{b_{1}^{2}}}{{4\delta r}}} \right)} \right)}^{2}} \\ \end{gathered} $ | $G_{{10}}^{p}\sim {{d}^{2}}\frac{{k{{H}^{7}}}}{{2{{\pi }^{2}}{{h}^{2}}{{\gamma }^{3}}}}\frac{{{{{(kz)}}^{2}}}}{{{{r}^{4}}}}$ |
| $0 \leqslant {{z}_{0}} \leqslant H_{1}^{'}$, или $H_{2}^{'} \leqslant {{z}_{0}} \leqslant h$ |
${{H}_{1}} \leqslant z \leqslant {{H}_{2}}$ | $G_{{10}}^{p} \approx {{d}^{2}}\frac{{{{A}^{P}}}}{{{{\pi }^{2}}{{\delta }^{2}}}}\frac{1}{{{{r}^{3}}}}{{\left( {1 - \frac{{\pi {{z}_{0}}}}{{H\sqrt {\delta r} }}{\text{Dason}}\left( {\frac{{\pi {{z}_{0}}}}{{2H\sqrt {\delta r} }}} \right)} \right)}^{2}}$ | $G_{{10}}^{p}\sim {{d}^{2}}\frac{{8k{{H}^{6}}}}{{{{\pi }^{5}}{{h}^{2}}{{\gamma }^{2}}}}\frac{1}{{{{r}^{3}}}}$ |
| $H_{1}^{'} \leqslant {{z}_{0}} \leqslant H_{2}^{'}$ | $0 \leqslant z \leqslant {{H}_{1}}$, или ${{H}_{2}} \leqslant z \leqslant h$ |
$G_{{10}}^{p} \approx {{d}^{2}}\frac{{{{A}^{P}}\pi }}{{4{{H}^{2}}{{\delta }^{3}}}}\frac{{z_{{}}^{2}}}{{{{r}^{4}}}}\exp \left( { - \frac{{{{\pi }^{2}}z_{{}}^{2}}}{{2{{H}^{2}}\delta r}}} \right)$ | $G_{{10}}^{p}\sim {{d}^{2}}\frac{{2k{{H}^{7}}}}{{{{\pi }^{4}}{{h}^{2}}{{\gamma }^{3}}}}\frac{{{{{(kz)}}^{2}}}}{{{{r}^{4}}}}$ |
| $H_{1}^{'} \leqslant {{z}_{0}} \leqslant H_{2}^{'}$ | ${{H}_{1}} \leqslant z \leqslant {{H}_{2}}$ | $G_{{10}}^{p} \approx {{d}^{2}}\frac{{4{{A}^{P}}}}{{{{\pi }^{4}}{{\delta }^{2}}{{r}^{3}}}}{{\left( {1 - {{e}^{{ - \delta r{{N}^{2}}}}}} \right)}^{2}}$ | $G_{{10}}^{p}\sim {{d}^{2}}\frac{{32k{{H}^{6}}}}{{{{\pi }^{7}}{{h}^{2}}{{\gamma }^{2}}}}\frac{1}{{{{r}^{3}}}}$ |
| Примечание: b1 = π(z0 – z)/H, b2 = π(z0 + z)/H. | |||
Отметим, что для построения аппроксимации функции ПИМ ВПКС вертикального диполя следует считать “приграничными” приповерхностные глубины $0 \leqslant {{z}_{0}},$ $z \leqslant H_{1}^{'}$ и придонные глубины $H_{2}^{'} \leqslant {{z}_{0}},\,\,z \leqslant h$. Кроме того, под знаком суммы находится ${{l}^{2}}$, а не $l$, что приводит к существенным изменениям. Полученные аппроксимирующие соотношения для функции ПИМ ВПКС вертикального диполя (19) и их асимптотические оценки приведены в табл. 4.
Таблица 4.
Аппроксимирующие соотношения функции ПИМ ВПКС вертикального диполя
| Ограничения на ${{z}_{0}}$ | Ограничения на $z$ | Аппроксимирующее соотношение | Оценка |
|---|---|---|---|
| $0 \leqslant {{z}_{0}} \leqslant H_{1}^{'}$ или $H_{2}^{'} \leqslant {{z}_{0}} \leqslant h$ |
$0 \leqslant {{z}_{0}} \leqslant H_{1}^{'}$ или $H_{2}^{'} \leqslant z \leqslant h$ |
$\begin{gathered} G_{{10}}^{{Vz}} \approx {{d}^{4}}\frac{{{{A}^{V}}\pi }}{{256{{\delta }^{5}}{{r}^{6}}}} \times \\ \times \,\,{{\left( {c_{1}^{{}}\exp \left( { - \frac{{b_{1}^{2}}}{{4\delta r}}} \right) + {{c}_{2}}\exp \left( { - \frac{{b_{2}^{2}}}{{4\delta r}}} \right)} \right)}^{2}} \\ \end{gathered} $${{c}_{1}} = 2\delta r - b_{1}^{2}$, ${{c}_{2}} = 2\delta r - b_{2}^{2}$ | $G_{{10}}^{{Vz}}\sim {{d}^{4}}\frac{{{{k}^{5}}{{H}^{9}}}}{{2{{\pi }^{4}}{{h}^{2}}{{\gamma }^{3}}}}\frac{1}{{{{r}^{4}}}}$ |
| $0 \leqslant {{z}_{0}} \leqslant H_{1}^{'}$ или $H_{2}^{'} \leqslant {{z}_{0}} \leqslant h$ | $H_{1}^{'} \leqslant z \leqslant H_{2}^{'}$ | $\begin{gathered} G_{{10}}^{{Vz}} \approx {{d}^{4}}\frac{{{{A}^{V}}}}{{4\pi {{\delta }^{3}}{{r}^{4}}}} \times \\ \times \,\,{{\left( {1 - \frac{{{{\pi }^{2}}z_{0}^{2}}}{{2{{H}^{2}}\delta r}}} \right)}^{2}}\exp \left( { - \frac{{{{\pi }^{2}}z_{0}^{2}}}{{2{{H}^{2}}\delta r}}} \right) \\ \end{gathered} $ | $G_{{10}}^{{Vz}}\sim {{d}^{4}}\frac{{2{{k}^{5}}{{H}^{9}}}}{{{{\pi }^{6}}{{h}^{2}}{{\gamma }^{3}}}}\frac{1}{{{{r}^{4}}}}$ |
| $H_{1}^{'} \leqslant {{z}_{0}} \leqslant H_{2}^{'}$ | $0 \leqslant z \leqslant H_{1}^{'}$ или $H_{2}^{'} \leqslant z \leqslant h$ |
$G_{{10}}^{{Vz}} \approx {{d}^{4}}\frac{{{{A}^{V}}}}{{4\pi {{\delta }^{3}}{{r}^{4}}}}{{\left( {1 - \frac{{{{\pi }^{2}}z_{{}}^{2}}}{{2{{H}^{2}}\delta r}}} \right)}^{2}}\exp \left( { - \frac{{{{\pi }^{2}}z_{{}}^{2}}}{{2{{H}^{2}}\delta r}}} \right)$ | $G_{{10}}^{{Vz}}\sim {{d}^{4}}\frac{{2{{k}^{5}}{{H}^{9}}}}{{{{\pi }^{6}}{{h}^{2}}{{\gamma }^{3}}}}\frac{1}{{{{r}^{4}}}}$ |
| $H_{1}^{'} \leqslant {{z}_{0}} \leqslant H_{2}^{'}$ | $H_{1}^{'} < z < {{H'}_{2}}$ | $G_{{10}}^{{Vz}} \approx {{d}^{4}}\frac{{{{A}^{V}}}}{{{{\pi }^{3}}{{\delta }^{3}}{{r}^{4}}}}{{\left( {{\text{erf}}(N\sqrt {\delta r} ) - 2N\sqrt {\frac{{\delta r}}{\pi }} {{e}^{{ - \delta r{{N}^{2}}}}}} \right)}^{2}}$ | $G_{{10}}^{{Vz}}\sim {{d}^{4}}\frac{{8{{k}^{5}}{{H}^{9}}}}{{{{\pi }^{8}}{{h}^{2}}{{\gamma }^{3}}}}\frac{1}{{{{r}^{4}}}}$ |
| Примечание: b1 = π(z0 – z)/H, b2 = π(z0 + z)/H. | |||
3.4. Квадруполи
Для квадруполей с двумя горизонтальными осями ${{g}_{2}} = 1 + {4 \mathord{\left/ {\vphantom {4 {{{k}^{2}}{{r}^{2}}}}} \right. \kern-0em} {{{k}^{2}}{{r}^{2}}}},$ ${{\chi }_{{22}}} = 1$, $\alpha _{{l0}}^{'} = {{\alpha }_{{l0}}}$, а полиномы Лежандра равны $P_{2}^{2}(ld) = 3(1 - {{l}^{2}}{{d}^{2}})$. Поэтому для функций ПИМ ЗД и ГПКС этих квадруполей могут быть использованы аппроксимации из табл. 1, а для функций ПИМ ВПКС – аппроксимации функций ПИМ монополя, приведенные в табл. 2 после их умножения на коэффициент $9{{(1 - {{d}^{2}})}^{2}}$. Для функций ПИМ ГПКС необходимо дополнительное умножение на коэффициент ${{g}_{2}}$.
Для квадруполей с горизонтальной и вертикальной осями ${{g}_{1}} = 1 + {1 \mathord{\left/ {\vphantom {1 {{{k}^{2}}{{r}^{2}}}}} \right. \kern-0em} {{{k}^{2}}{{r}^{2}}}},$ ${{\chi }_{{21}}} = - 1$, а полиномы Лежандра равны $P_{2}^{1}(ld) = 3ld\sqrt {1 - {{l}^{2}}{{d}^{2}}} $. Следовательно, для функций ПИМ ЗД и ГПКС этих квадруполей могут быть использованы аппроксимации вертикального диполя из табл. 3, а для функций ПИМ ВПКС – приведенные в табл. 4 аппроксимации функций ПИМ ВПКС вертикального диполя, после их умножения на коэффициент $9(1 - {{d}^{2}})$. Для функций ПИМ ГПКС необходимо дополнительное умножение на коэффициент ${{g}_{1}}$.
У квадруполя с двумя вертикальными осями ${{g}_{0}} = 1$, ${{\chi }_{{20}}} = 1$, а полиномы Лежандра равны $P_{2}^{0}(ld) = (3{{l}^{2}}{{d}^{2}} - {{1)} \mathord{\left/ {\vphantom {{1)} 2}} \right. \kern-0em} 2}.$ Поэтому вновь можно использовать аппроксимации функций ПИМ монополя из табл. 1 и 2 после их умножения на коэффициент $(3{{d}^{2}} - {{1{{)}^{2}}} \mathord{\left/ {\vphantom {{1{{)}^{2}}} 4}} \right. \kern-0em} 4}.$
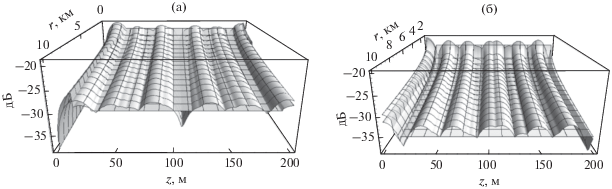
На рис. 3 показаны ПИМ и полученные с помощью соотношений из табл. 1 и 2 аппроксимирующие поверхности для ЗД и ВПКС монополя – характерного представителя мультиполей первой группы. Расчеты также выполнены для источника с частотой 50 Гц, находящегося на глубине 110 м в волноводе с указанными выше параметрами.
На рис. 4 показаны полученные для тех же условий и соотношений из табл. 3 и 4 ПИМ и аппроксимирующие поверхности для ЗД и ВПКС вертикального диполя – характерного представителя мультиполей второй группы. Максимальные неточности аппроксимации наблюдаются только у поверхностей раздела и в середине эквивалентного волновода – 1.7 дБ для ЗД и 5.5 дБ для ВПКС (рис. 3), 3.9 дБ для ЗД и 5.1 дБ для ВПКС (рис. 4). Это является результатом “сглаживания” огибающих интерференционных максимумов.
3.5. Обобщенный анализ функций ПИМ для двух групп мультиполей
В табл. 5 приведены асимптотические оценки функций ПИМ для ЗД (соответственно, и ГПКС) и ВПКС для двух групп мультиполей и различных зон размещения приемников и излучателей. Видно, что для различных типов мультиполей наблюдается существенное различие зависимостей этих характеристик от расстояния, частоты звука (волнового числа), глубины волновода и глубин расположения приемников и излучателей. В частности, при расположении корреспондирующих точек в приграничных зонах величины ЗД или ГПКС быстро уменьшаются при приближении к поверхностям раздела, а ВПКС в этих же условиях стремится к постоянным, зависящим от частоты и глубины волновода, значениям.
Таблица 5.
Сводная таблица оценок функций ПИМ для двух групп мультиполей

Примечание: $A = {{{{H}^{5}}} \mathord{\left/ {\vphantom {{{{H}^{5}}} {2k{{h}^{2}}{{\gamma }^{3}}}}} \right. \kern-0em} {2k{{h}^{2}}{{\gamma }^{3}}}}$, $B = {{{{k}^{3}}{{H}^{7}}} \mathord{\left/ {\vphantom {{{{k}^{3}}{{H}^{7}}} {2{{\pi }^{2}}{{h}^{2}}{{\gamma }^{3}}}}} \right. \kern-0em} {2{{\pi }^{2}}{{h}^{2}}{{\gamma }^{3}}}}$, $D = {{{{k}^{5}}{{H}^{9}}} \mathord{\left/ {\vphantom {{{{k}^{5}}{{H}^{9}}} {2{{\pi }^{4}}{{h}^{2}}{{\gamma }^{3}}}}} \right. \kern-0em} {2{{\pi }^{4}}{{h}^{2}}{{\gamma }^{3}}}}$.
При расположении излучателей и приемников в зоне середины волновода зависимость всех характеристик гидроакустического поля от глубины практически отсутствует, а зависимости ЗД и ВПКС при размещении приемников или излучателей в середине волновода для первой и второй группы изменяют свои характеристики зеркально – с точностью до критерия подобия (показано стрелками в табл. 5). Следует также отметить ускоренное ослабление ВПКС по сравнению с ЗД при увеличении расстояния как для первой, так и второй групп мультиполей (последняя строка в табл. 5), а также практически независимость значений ВПКС от глубин и зон размещения приемников и излучателей для второй группы мультиполей.
Перечисленные аналитические зависимости хорошо согласуются с результатами точных расчетов вертикальной структуры ПИМ для всех мультиполей.
В табл. 5 предпринимается попытка дополнительно обобщить зависимости от расстояния всех типов составляющих поля, объединенных для двух групп мультиполей. Обобщение выполняется с учетом влияющих факторов: глубин источников, приемников и волновода, частоты звука и типа (группы) мультиполей. Очевидно, что такое обобщение может иметь право на существование только для асимптотических характеристик поля.
Из формул, приведенных в табл. 1–4, в явном виде следуют аппроксимирующие зависимости от расстояния ЗД, ГПКС и ВПКС для мультиполей различного типа. Из табл. 5 можно получить асимптотические зависимости. Полученные формулы позволяют прогнозировать ослабление различных составляющих поля при изменении расстояния с учетом влияющих факторов: глубин волновода, источника и приемника, частоты звука и т.д.
На рис. 5–7 сравниваются закономерности ослабления различных компонент поля для разных мультиполей, полученные путем компьютерного моделирования поля в волноводе с указанными выше параметрами для глубины приемника $z$ = 200 м и источника с частотой 30 Гц, который находится на глубинах ${{z}_{0}}$ = 3 и 100 м. На рисунках приведены сечения поверхностей ИМА сигналов (точные значения), аппроксимирующие соотношения и асимптотические оценки. Видно, что точные и аппроксимирующие зависимости хорошо согласуются на всех расстояниях даже для низкой частоты 30 Гц (при малом числе нормальных волн), а асимптотической зависимостью можно пользоваться только на больших расстояниях. Можно показать, что при увеличении частоты из-за увеличения числа нормальных волн сходимость всех зависимостей улучшается.
Рис. 5.
Сечения ПИМ ЗД монополя: 1 – точные значения ЗД в сечении ПИМ; 2 — аппроксимирующие сечения; 3 — асимптотические оценки функций ПИМ. Глубины источника (а) – z0 = 3 м, (б) – z0 = 100 м.

Рис. 6.
Сечения ПИМ ВПКС: 1 – монополя; 2 – квадруполя с двумя горизонтальными осями; 3 – вертикального диполя; 4 – квадруполя с двумя ортогональными осями.
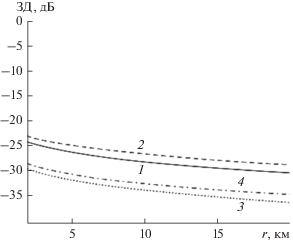
Рис. 7.
Асимптотические оценки (см. табл. 5): ПИМ ЗД первой (кривая 1) и второй (кривая 2) групп мультиполей; ПИМ ВПКС первой (кривая 3) и второй (кривая 4) групп мультиполей.
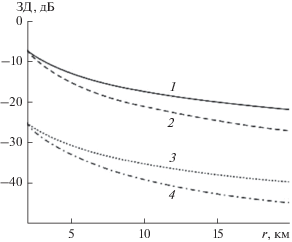
Из рис. 6 следует, что ВПКС всех групп мультиполей ослабевают быстрее, чем остальные зависимости. Особенно интенсивное ослабление наблюдается для компонент поля, образованных вертикальным диполем или квадруполем с ортогональными осями. Из рис. 7 можно увидеть, что независимо от типа (группы) мультиполей асимптотические значения ВПКС уменьшаются значительно быстрее, чем для ЗД.
Из табл. 1–5 и рис. 1–7 следует, что для всех типов мультиполей наблюдается существенное различие зависимостей ЗД, ГПКС или ВПКС от различных влияющих факторов. Видно также значимое влияние частоты звука и глубины волновода, особенно на характеристики ВПКС, которые спадают при увеличении расстояния заметно быстрее и имеют отличительные особенности вблизи границ волновода.
ЗАКЛЮЧЕНИЕ
Введение функций ПИМ позволяет дать укрупненное описание пространственно-частотной структуры поля в зонах ИМА при изменении глубин, расстояния и частоты звука. Согласие зависимостей от глубин, расстояния или частоты характеристик ПИМ для ЗД и ГПКС свидетельствует о высокой корреляции огибающих этих характеристик. Корреляция между ВПКС и ЗД или ГПКС существенно меньше. Ослабление ВПКС во всех зонах и для всех расстояний происходит существенно быстрее, чем ЗД или ГПКС.
Характеристики всех составляющих звукового поля — ЗД, ГПКС и ВПКС существенно различаются в зависимости от типа мультиполей, особенно при анализе структуры вертикального сечения поля. Наибольшие отличия наблюдаются при расположении источников или приемников вблизи поверхностей раздела или в зоне середины эквивалентного волновода. При их расположении у поверхностей раздела все составляющие звукового поля убывают при увеличении расстояния значительно быстрее, чем при расположении приемников и излучателей в середине волновода – это хорошо видно из анализа полученных аппроксимирующих зависимостей. Зависимости ЗД и КС в зонах ИМА от расстояния для малых и больших расстояний также различаются. При размещении корреспондирующих точек в зонах ИМА ослабление всех составляющих поля для всех типов мультиполей происходит приблизительно в $\sqrt r $ раз быстрее, чем для регулярных составляющих или при их расположении в произвольных точках. Иными словами, ускоренный спад в зонах ИМА распространяется на все глубины и расстояния и характерен не только для ЗД, но и для проекций КС.
По вертикальным структурам поля всех мультиполей могут быть разбиты на две укрупненные группы, соответствующие двум типам мультиполей: 1) монополи, горизонтальные диполи, квадруполи с двумя горизонтальными или двумя вертикальными осями и т.д. и 2) вертикальные диполи и квадруполи с одной вертикальной осью (группы I и II).
Аппроксимирующие зависимости для низкочастотных сигналов и выбранных расстояний и глубин дают наглядный и достаточно точный прогноз вырождения интерференционной структуры поля в зонах ИМА, как для ЗД, так и для проекций КС. Это позволяет выполнять численные оценки законов спадания характеристик всех составляющих поля, не прибегая к сложным расчетам полей. Полученные зависимости позволяют просто и в явном виде прогнозировать зависимости от расстояния, частоты звука, глубины волновода, координат источника и приемника и характеристик грунта.
Аппроксимирующие соотношения для вертикальных диполей и квадруполей для функций ПИМ давления и колебательной скорости существенно отличаются от зависимостей, полученных для монополя и горизонтальных проекций диполей и квадруполей, из чего следует необходимость при решении практических задач учитывать реальную пространственную структуру излучаемого поля. Особенно это важно для малых расстояний при решении измерительных или контрольных задач. На больших расстояниях влияние вертикальных проекций существенно уменьшается. Полученные простые соотношения позволяют для малых и больших расстояний наглядно и достаточно точно проследить зависимости ЗД и КС от параметров среды и условий эксперимента, а также характеристик сигнала. Результаты могут использоваться при прогнозе характеристик излучаемого поля, выборе и обосновании алгоритмов обнаружения и оценки параметров, например, измерения в ближней зоне шумности источников, учитывающих интерференцию звукового поля.
Авторы выражают благодарность В.Г. Петникову за полезный совет.
Работа выполнена при финансовой поддержке программы “Акустика мелкого моря, нелинейная акустическая диагностика, нелинейная динамика волн” (номер гос. регистрации AAAA-A18-118021390174-1) и программы РФФИ (проект № 19-08-00941).
Список литературы
Бреховских Л.М. Волны в слоистых средах. М.: Изд-во АН СССР, 1957. 502 с.
Кузнецов Г.Н., Степанов А.Н. Аппроксимирующие модели регулярной составляющей инфразвукового поля мультипольных источников в плоском волноводе // Акуст. журн. 2013. Т. 59. № 3. С. 378–390.
Урик Р.Дж. Основы гидроакустики. Л.: Судостроение, 1978.
Грачев Г.А., Кузнецов Г.Н. О средней скорости изменения фазы акустического поля вдоль плоского волновода // Акуст. журн. 1985. Т. 31. № 2. С. 266–268.
Kuznetsov G.N., Stepanov A.N. Interference and phase structure of the low-frequency vector-scalar field in shallow water for variable reception or transmission depths // Phys. Wave Phenom. 2015. V. 23. № 4. P. 279–291.
Kuznetsov G.N., Lebedev O.V. The use of effective phase velocity to decrease the direction finding error for a low-frequency signal in a waveguide // Phys. Wave Phenom. 2012. V. 20. № 1. P. 58–66.
Кузнецов Г.Н., Степанов А.Н. Амплитудно-фазовая структура векторно-скалярного низкочастотного поля в мелком море // Гидроакустика. 2016. Вып. 27. № 3. С. 23–37.
Орлов Е.Ф., Шаронов Г.А. Интерференция звуковых волн в океане. Владивосток: Дальнаука, 1998. 196 с.
Чупров С.Д. Интерференционная структура звукового поля в слоистом океане // Акустика океана. Современное состояние. М.: Наука, 1982. С. 71–82.
Касаткин Б.А. Инвариантные характеристики звукового поля в слоистом океане // Докл. АН СССР. 1986. Т. 291. № 6. С. 1483–1487.
Кузькин В.М., Лин Й.-Т., Луньков А.А., Линч Дж.Ф., Петников В.Г. Частотные смещения интерференционной структуры звукового поля в летний период времени на океанском шельфе // Акуст. журн. 2011. Т. 57. № 3. С. 387–397.
Kuz’kin V.M., Lyakhov G.A., Pereselkov S.A. Method for measuring the frequency shifts of interference maxima in monitoring of dispersion media: theory, implementation, and prospects // Phys. Wave Phenom. 2010. V. 18. № 3. P. 196−222.
Каришнев Н.С., Кузнецов Г.Н., Луньков А.А. Анализ надводной обстановки с использованием векторно-скалярной цилиндрической антенны // Гидроакустика. 2015. Т. 23. № 3. С. 27–40.
Казначеев И.В., Кузнецов Г.Н., Кузькин В.М., Переселков С.А. Интерферометрический метод обнаружения движущегося источника звука векторно-скалярным приемником // Акуст. журн. 2018. Т. 64. № 1. С. 33−45.
Кузнецов Г.Н., Кузькин В.М., Переселков С.А. Обнаружение и оценка скорости быстро движущейся цели с использованием интерференционной структуры звукового поля // Гидроакустика. 2017. Т. 29. № 1. С. 18–32.
Кузнецов Г.Н., Кузькин В.М., Переселков С.А., Просовецкий Д.Ю. Помехоустойчивость интерферометрического метода оценки скорости источника звука в мелком море // Акуст. журн. 2016. Т. 62. № 5. С. 556−572.
Грачев Г.А., Кузнецов Г.Н. Ослабление интерференционных максимумов акустического поля в мелком море // Акуст. журн. 1985. Т. 31. № 5. С. 675–678.
Кузнецов Г.Н., Степанов А.Н. Закономерности ослабления векторно-скалярных звуковых полей в зонах интерференционных максимумов // Акуст. журн. 2019. Т. 65. № 2. С. 203–213.
Быковцев Г.И., Кузнецов Г.Н., Степанов А.Н. Акустическое поле направленного источника в океанических волноводах // ДАН СССР. 1985. Т. 280. № 1. С. 57–59.
Кузнецов Г.Н., Степанов А.Н. Поле эквивалентного мультипольного составного излучателя в волноводе // Акуст. журн. 2007. Т. 53. № 3. С. 377–385.
Миниович И.Я., Перник А.Д., Петровский В.С. Гидродинамические источники звука. Л.: Судостроение, 1972. 482 с.
Kuznetsov G.N., Stepanov A.N. Attenuation of vector-scalar fields of multipole sources in interference maxima regions // Phys. Wave Phenom. 2018. V. 26. № 4. P. 334–341.
Сазонтов А.Г., Малеханов А.И. Согласованная пространственная обработка сигналов в подводных звуковых каналах (обзор) // Акуст. журн. 2015. Т. 61. № 2. С. 233–253.
Кузнецов Г.Н., Степанов А.Н. О возможности применения принципа взаимности в векторно-скалярных полях мультипольных источников в волноводе Пекериса // Акуст. журн. 2017. Т. 67. № 3. С. 296–305.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. 4-е изд. М.: Физматгиз, 1963. 1100 с.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал