Акустический журнал, 2020, T. 66, № 3, стр. 258-264
Модульные “солитоны”: взаимное поглощение и аннигиляция в диссипативных средах
О. А. Васильева a, b, *, О. В. Руденко c, d, e, **
a Московский государственный строительный университет
129337 Москва, Ярославское ш. 26, Россия
b Российский химико-технологический университет им. Д.И. Менделеева
125047 Москва, Миусская пл. 9, Россия
c Физический факультет Московского государственного университета им. М.В. Ломоносова
119991 Москва, Ленинские горы 1, стр. 2, Россия
d Институт общей физики им. А.М. Прохорова РАН
119991 Москва, ул. Вавилова 38, Россия
e Институт физики Земли им. О.Ю. Шмидта РАН
123995 Москва, ул. Б. Грузинская 10, стр. 1, Россия
* E-mail: vasilievaoa@mgsu.ru
** E-mail: rudenko@acs366.phys.msu.ru
Поступила в редакцию 03.12.2019
После доработки 03.12.2019
Принята к публикации 24.12.2019
Аннотация
Исследованы столкновения двух импульсных сигналов в среде с модульной (М) нелинейностью и со специальным законом релаксации. Процессы описываются интегро-дифференциальным уравнением, ядро которого отлично от нуля на конечном интервале времени. Считается, что внутри этого интервала “память среды” постоянна, а вне его обращается в ноль. Для этой модели анализ сводится к решению простого дифференциально-разностного уравнения; при этом объем вычислений заметно сокращается. Описаны явления, сопровождающие столкновения импульсов – нелинейное взаимное затухание, аннигиляция, уширение сигналов во времени. Выяснено влияние параметров сигналов и свойств среды на протекание указанных процессов. Рассмотрено столкновение двух модульных солитонов, описываемых М-уравнением типа Кортевега–де Вриза. Показано, что в рамках этой модели взаимодействие может отличаться от обычного поведения солитонов, обнаруживающих аналогию с упругим взаимодействием частиц.
ВВЕДЕНИЕ
Солитонами обычно называют уединенные волны, форма которых не изменяется благодаря двум конкурирующим процессам. Конкурентами являются нелинейное “обострение” волнового профиля и его дисперсионное “сглаживание”. Солитонные решения, допускаемые некоторыми хорошо известными нелинейными уравнениями, безусловно, важны как точные результаты математической физики. Однако наибольший интерес, наблюдавшийся в течение последних 50 лет, по-видимому, связан с “корпускулярным” поведением солитонов. Сталкиваясь друг с другом, солитоны ведут себя как упругие частицы [1]. Они могут притягиваться или отталкиваться между собой, образуя связанные состояния. Именно с перспективами физических приложений солитоники была связана необычайная популярность и высокая цитируемость соответствующих работ.
Однако корпускулярные свойства обнаруживают не только консервативные солитоны, но и волны в диссипативных системах. Например, слабые ударные волны сталкиваются между собой и слипаются при этом как абсолютно неупругие частицы [2]. Ансамбль треугольных импульсов, образующих пилообразную волну, ведет себя как совокупность неупругих частиц, “испаряющихся” в промежутках между соударениями в результате нелинейного затухания [3]. Такие явления хорошо известны для интенсивных акустических волн и наблюдаются в средах, где нет дисперсии, т.е. скорость распространения волны не зависит от частоты.
Недавно появились работы по взаимодействию уединенных импульсов в средах с модульной нелинейностью, которые для краткости назовем М-средами. Такие взаимодействия имеют интересные физические особенности, изучение которых представляет несомненный интерес. Эволюцию возмущений в М-среде, обладающей высокочастотной дисперсией и диссипацией, можно описать следующей математической моделью:
(1)
$\frac{{\partial V}}{{\partial z}} - \frac{\partial }{{\partial \theta }}\left| V \right| = \Gamma \frac{{{{\partial }^{2}}V}}{{\partial {{\theta }^{2}}}} + D\frac{{{{\partial }^{3}}V}}{{\partial {{\theta }^{3}}}}.$При $\Gamma = D = 0$ из (1) получается М-уравнение Хопфа, при $\Gamma \ne 0,\,\,D = 0$ – М-уравнение Бюргерса, при $\Gamma = 0,\,\,D \ne 0$ – М-уравнение Кортевега–де Вриза.
Модель (1) есть частный случай более общего интегро-дифференциального уравнения
(2)
$\frac{{\partial V}}{{\partial z}} - \frac{\partial }{{\partial \theta }}\left| V \right| = \frac{{{{\partial }^{2}}}}{{\partial {{\theta }^{2}}}}\int\limits_0^\infty {K\left( s \right)} V\left( {\theta - s} \right)ds.$Уравнение (1) следует из (2) для ядра $K\left( s \right) = \Gamma \delta \left( s \right) + D\delta {\kern 1pt} '\left( s \right)$, выражаемого через дельта-функцию и ее производную.
Среди моделей типа (2), обладающих невырожденными ядрами $K\left( s \right)$, наиболее известны уравнения с экспоненциальным ядром
Ядро (3) предсказывается релаксационной моделью Мандельштама–Леонтовича [4]. В этом случае из общего уравнения (2) получается:
(4)
$\frac{\partial }{{\partial \theta }}\left[ {\frac{{\partial V}}{{\partial z}} - \frac{\partial }{{\partial \theta }}\left| V \right|} \right] + \frac{1}{{{{\theta }_{{{\text{rel}}}}}}}\left[ {\frac{{\partial V}}{{\partial z}} - \frac{\partial }{{\partial \theta }}\left| V \right|} \right] = D\frac{{{{\partial }^{2}}V}}{{\partial {{\theta }^{2}}}}.$Такое уравнение в дифференциальной форме (4) для квадратично нелинейной среды выведено в работе [5]; его интегральная форма представлена в работе [6].
Однако экспоненциальное ядро, характеризуемое единственной парой чисел $D,\,\,{{\theta }_{{{\text{rel}}}}}$, есть лишь простейший пример релаксационной внутренней динамики среды. Часто физически адекватными являются более сложные модели, содержащие несколько времен релаксации ${{\theta }_{{{\text{rel}},\,n}}}$ и соответствующих им чисел ${{D}_{n}}$ или даже непрерывный спектр таких времен. Сложная перестройка внутренней структуры инициируется, например, в процессе динамического деформирования полимеров, содержащих разномасштабные структурные элементы [7], а также при распространении акустических волн в неоднородных средах и искусственно создаваемых матаматериалах.
Разнообразные формы ядер, полезные для приложений, обсуждаются в статье [8]. В частности, степенные зависимости коэффициента затухания волны от частоты с дробными показателями степени, типичные для биологических тканей и геофизических структур, принципиально требуют интегро-дифференциального описания.
Кратко напомним схему нахождения ядра $K(s)$ в каждом конкретном случае. Частотные зависимости дисперсии и поглощения, которые
даются действительной и мнимой частями  волнового числа$\,\,k$, измеряются в эксперименте или определяются из физической модели типа Мандельштама–Леонтовича.
Затем решается обратная задача и ядро реконструируется стандартными методами, использующими
принцип причинности и соотношения типа Крамерса–Кронига [9].
волнового числа$\,\,k$, измеряются в эксперименте или определяются из физической модели типа Мандельштама–Леонтовича.
Затем решается обратная задача и ядро реконструируется стандартными методами, использующими
принцип причинности и соотношения типа Крамерса–Кронига [9].
Известно, например, что показатель степени в частотной зависимости затухания ультразвука
в биологических тканях является дробным и, согласно измерениям, в МГц-диапазоне изменяется
от 2.1 (кости черепа) до 0.6 (кожа) [10]. Для частот порядка нескольких МГц, используемых в медицинской практике, обычно
полагают 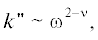 $0 < \nu < 1$. При этом ядро имеет вид $K(s)\sim {{s}^{{\nu - 1}}}\,$. Особенность функции $K(s)$ в точке $s = 0$ часто оказывается несущественной, поскольку уравнение содержит “свертку” сингулярного
ядра с осциллирующей функцией, описывающей поле ультразвуковой волны.
$0 < \nu < 1$. При этом ядро имеет вид $K(s)\sim {{s}^{{\nu - 1}}}\,$. Особенность функции $K(s)$ в точке $s = 0$ часто оказывается несущественной, поскольку уравнение содержит “свертку” сингулярного
ядра с осциллирующей функцией, описывающей поле ультразвуковой волны.
Когда представляют интерес волны не в конкретной релаксирующей среде, а общие закономерности совместного проявления нелинейных и релаксационных процессов, удобен прием, сводящий интегро-дифференциальное уравнение к дифференциально-разностной модели или даже к простому отображению. Этот переход [8] эффективен для ядер, отличных от нуля на конечном интервале. Простейший случай соответствует среде с постоянной “памятью” [11], для которой
(5)
$K\left( s \right) = D\left\{ \begin{gathered} 1,\,\,\,\,\,0 < s < {{\theta }_{{{\text{rel}}}}}, \hfill \\ 0,\,\,\,\,\,s < 0,\,\,s > {{\theta }_{{{\text{rel}}}}}. \hfill \\ \end{gathered} \right.$Ядро (5) означает, что в течение промежутка времени $0 < s < {{\theta }_{{{\text{rel}}}}}$ среда “все помнит”, а в момент времени $s = {{\theta }_{{{\text{rel}}}}}$ “все забывает”. Для такого ядра (5) уравнение (2) принимает вид дифференциально-разностного уравнения:
(6)
$\frac{{\partial V}}{{\partial z}} - \frac{\partial }{{\partial \theta }}\left| V \right| = D\frac{\partial }{{\partial \theta }}\left[ {V\left( {z,\theta } \right) - V\left( {z,\theta - {{\theta }_{{{\text{rel}}}}}} \right)} \right].$Нетрудно показать, что и для некоторых других ядер, отличных от нуля на конечном интервале, анализ сложных интегро-дифференциальных уравнений (2) удается свести к решению более простого уравнения типа (6); при этом объем вычислений заметно сокращается.
Нелинейные явления, сопровождающие распространение одиночных импульсных сигналов в релаксирующей среде с ядром (5) для трех видов нелинейности (модульной, квадратичной и квадратично-кубичной) изучены в работе [11]. Однако взаимодействие таких импульсов между собой в [11] не рассматривалось.
Итак, мы перечислили уравнения, которые будут использованы в дальнейшем изложении. Перейдем теперь к пояснению принятых обозначений и примерам сред с М-нелинейностью. Чтобы придать физический смысл обозначениям, будем для определенности иметь в виду упругие (акустические) плоские волны. Для понимания достаточно ограничиться наиболее простой исходной моделью, приводящей к уравнению Хопфа. Эта модель состоит из уравнения динамической теории упругости:
(7)
$\,\rho \frac{{{{\partial }^{2}}\varepsilon }}{{\partial {{t}^{2}}}} - \frac{{{{\partial }^{2}}\sigma }}{{\partial {{x}^{2}}}} = 0\,\,$Здесь $\sigma ,\,\,\varepsilon $ – механическое напряжение и деформация, $\rho $ – плотность среды, $E$ – модуль Юнга, $g$ – параметр М-нелинейности.
Ограничимся рассмотрением волн, бегущих в положительном направлении оси$\,x$ со скоростью, близкой к скорости звука $с = \sqrt {{E \mathord{\left/ {\vphantom {E \rho }} \right. \kern-0em} \rho }} $. Считаем искажения волны медленными, что обусловлено малостью нелинейного члена. Используя метод медленно изменяющегося профиля [9, 12], придем к эволюционному уравнению (2), в котором
(9)
$z = \frac{x}{{{{l}_{{NL}}}}},\,\,\,\,\theta = \omega \left( {t - \frac{x}{c}} \right),\,\,\,\,V = - \frac{\sigma }{{{{\sigma }_{0}}}}.$Смысл констант: $\omega $ и$\,{{\sigma }_{0}}$ – характерные частота и амплитуда исходного сигнала, а характерное нелинейное расстояние равно ${{l}_{{NL}}} = {{2c} \mathord{\left/ {\vphantom {{2c} {\left( {g\omega } \right)}}} \right. \kern-0em} {\left( {g\omega } \right)}}$. Числа $\Gamma ,\,\,D$ в уравнении (1) представляют собой отношения нелинейной длины ${{l}_{{NL}}}$ к характерным значениям диссипативной и дисперсионной длин.
Укажем, что теоретические и экспериментальные исследования волн в средах с “модульной” нелинейностью были начаты сравнительно недавно [13–17]. Например, М-среды, встречающиеся в механике, имеют различную упругость при деформациях растяжения и сжатия. Такими свойствами обладают армированные полимеры и бетоны (см. [18], гл. 1). М-уравнения (1), (2), (4), (6) линейны для функции, сохраняющей знак, т.е. для $V > 0$ или $V < 0$. Нелинейные эффекты проявляются лишь для знакопеременных решений.
Примером таких эффектов является генерация высших гармоник при подаче на вход нелинейной среды одночастотного гармонического колебания. Очевидно, что М-нелинейность приводит к линейной зависимости амплитуды второй гармоники от амплитуды первой (${{A}_{2}}\sim {{A}_{1}}$). С другой стороны, обычная квадратичная нелинейность дает иную зависимость (${{A}_{2}}\sim A_{1}^{2}$). В общем случае существенны обе нелинейности, и показатель степени в зависимости$\,{{A}_{2}} = KA_{1}^{m}\,$ лежит в области от единицы до двух [19]. Проведя несколько измерений, можно решить обратную задачу [17] и восстановить нелинейные модули среды. Важным примером М-нелинейной среды может служить метаматериал, содержащий искусственно изготовленные сосредоточенные М-нелинейные элементы [20], которые включены в однородную матрицу.
ВЗАИМНОЕ ПОГЛОЩЕНИЕ И АННИГИЛЯЦИЯ ИМПУЛЬСОВ В СРЕДЕ С РЕЛАКСАЦИЕЙ
Перейдем теперь к анализу процесса столкновения импульсных сигналов разной полярности в М-нелинейной релаксирующей среде. Взаимодействие волн описывается уравнением (2) с ядром (5), которое сводится к дифференциально-разностному уравнению (6). Результаты численного расчета иллюстрированы на рис. 1.
Рис. 1.
Столкновение двух импульсных сигналов: отрицательной полярности и положительной полярности с большей амплитудой. Значения параметров $D = 0.1,\,\,{{\theta }_{{{\text{rel}}}}} = 1$. Кривые 1–7 изображают профиль волны на расстояниях $z$ = 0, 1.5, 3.75, 5, 6, 7.5, 10.

Исходный сигнал (кривая 1) задан в виде двух импульсов разной полярности, находящихся на некотором “расстоянии” (временной задержке) друг от друга:
(10)
$\begin{gathered} V\left( {z = 0,\theta } \right) = \\ = \left\{ \begin{gathered} - 0.7\sin (\theta + \frac{3}{2}\pi ),\,\,\,\, - \frac{3}{2}\pi < \theta < - \frac{1}{2}\pi , \hfill \\ 0,\,\,\,\, - \frac{1}{2}\pi < \theta < \frac{1}{2}\pi , \hfill \\ \sin (\theta - \frac{1}{2}\pi ),\,\,\,\frac{1}{2}\pi < \theta < \frac{3}{2}\pi . \hfill \\ \end{gathered} \right. \\ \end{gathered} $В отсутствие релаксации ($D = 0$) решение уравнения (6) имеет вид
Здесь знаки ($ \pm $) соответствуют импульсам соответствующей полярности. Видно, что отрицательный импульс движется в положительном направлении оси $\theta $, а положительный импульс – в отрицательном направлении. Это означает, что импульсы начинают сближаться, не взаимодействуя друг с другом. При этом М-нелинейность не искажает их форму. Искажение на этом этапе происходит лишь вследствие релаксационных процессов, проявляющихся как линейное поглощение и образование дисперсионных фазовых сдвигов между гармониками.
В результате столкновения положительного и отрицательного импульсов образуется связанное состояние с общим ударным фронтом (кривая 2). В этот момент “включается” нелинейное затухание (сравните кривые 2 и 3), которое продолжается до тех пор, пока отрицательный импульс не исчезнет. Таким образом, происходит взаимное поглощение сигналов разной полярности. Сформировавшийся положительный импульс задержан по фазе и имеет меньшую амплитуду по сравнению с исходным. В дальнейшем он распространяется без изменения формы (сравните кривые 6 и 7).
Взаимное поглощение имеет место при различной амплитуде одинаковых по форме и длительности импульсов или, в более общем случае, при различной площади под кривыми ${{V}_{ \pm }}\left( \theta \right)$. Если площади одинаковы, в результате взаимного поглощения может наступить аннигиляция, т.е. полное взаимное уничтожение сигналов.
Процесс аннигиляции изображен на рис. 2. Исходная форма волны (кривая 1) дается двумя разнесенными полупериодами синусоиды (10), но с одинаковыми амплитудами. Как и на рис. 1, до столкновения импульсов (кривая 2) их нелинейного поглощения не происходит. С увеличением расстояния взаимное поглощение усиливается, и однополярные импульсы исчезают полностью.
Рис. 2.
Столкновение двух импульсных сигналов: отрицательной и положительной полярности с одинаковыми амплитудами. Значения параметров $D = 0.3,\,\,{{\theta }_{{{\text{rel}}}}} = 0.75$ Кривые 1–7 соответствуют расстояниям $z$ = 0, 1, 1.5, 2, 3, 4, 5

Таким образом, взаимодействие уединенных волн в М-среде обнаруживает свойства, отличные от наблюдаемых при упругих столкновениях обычных солитонов и неупругих слияниях ударных волн. Имеется аналогия с взаимодействием сгустков химически реагирующих веществ, например, горючего и окислителя. В результате реакции один (меньший) компонент исчезает, а масса второго (большего) уменьшается.
СТОЛКНОВЕНИЯ МОДУЛЬНЫХ СОЛИТОНОВ
Недавно был исследован другой тип уединенных волн, названный нами “модульные солитоны” [22]. Эти волны обнаружили новые физические свойства. В средах с высокочастотной дисперсией и модульной нелинейностью эволюция волн описывается модифицированным уравнением Кортевега–де Вриза (это уравнение (1) при значении диссипативного параметра $\Gamma = 0$):
(12)
$\frac{{\partial V}}{{\partial z}} - \frac{\partial }{{\partial \theta }}\left| V \right| = D\frac{{{{\partial }^{3}}V}}{{\partial {{\theta }^{3}}}}.$Аналитическое выражение для одного из стационарных солитонных решений
имеет вид:(14)
$\begin{gathered} {{V}_{ - }} = - \frac{C}{{2\left( {1 + \beta } \right)}}\left\{ {1 - \exp \left[ {\sqrt {\frac{{1 + \beta }}{D}} \left( { - \left| T \right| + T{\text{*}}} \right)} \right]} \right\}, \\ \left| T \right| \geqslant T{\text{*}}, \\ {{V}_{ + }} = \frac{C}{{2\left( {1 - \beta } \right)}}\left\{ {1 + \sqrt {\frac{2}{{1 + \beta }}} \cos \left( {T\sqrt {\frac{{1 - \beta }}{D}} } \right)} \right\}, \\ \left| T \right| \leqslant T{\text{*}}. \\ \end{gathered} $Здесь $C > 0,\,\,\,0 < \beta < 1$ – константы. В двух точках $ \pm T{\text{*}}$ отрицательная ${{V}_{ - }}$ и положительная ${{V}_{ + }}$ ветви решения непрерывно сшиваются, причем непрерывной оказывается и первая производная. Принято обозначение:
(15)
$T{\text{*}} = \sqrt {\frac{D}{{1 - \beta }}} \left( {\frac{\pi }{2} + \arcsin \sqrt {\frac{{1 + \beta }}{2}} } \right).$Заметим, что модульный солитон (14) не может распространяться по невозмущенной среде, т.е. иметь профиль, для которого $V\left( \theta \right) \to 0,$ $\left| \theta \right| \to \infty $. Причиной является тот факт, что солитоны формируются в результате конкуренции между нелинейным “укручением” и диперсионным “расплыванием” волны, а в М-модели один из конкурирующих факторов (нелинейность) для возмущения, сохраняющего знак, отсутствует. В этом основное отличие (14) от солитонных решений обычного уравнения КдВ; отличие связано с исчезновением одной из симметрий для М-уравнения (12).
Как следует из решения (14), солитон является возмущением относительно уровня
(16)
${{V}_{ - }}\left( {\left| \theta \right| \to \infty } \right) = - \frac{C}{{2\left( {1 + \beta } \right)}}.$Если имеются два солитона, возмущающие один и тот же уровень (16), должно выполняться условие
(17)
$\frac{{{{C}_{1}}}}{{\left( {1 + {{\beta }_{1}}} \right)}} = \frac{{{{C}_{2}}}}{{\left( {1 + {{\beta }_{2}}} \right)}}.$Амплитуды этих солитонов, как следует из (14) при $T = 0$, равны соответственно:
(18)
${{A}_{{1,2}}} = {{\left( {{{V}_{ + }}} \right)}_{{\max }}} = \frac{{{{C}_{{1,2}}}}}{{2\left( {1 - {{\beta }_{{1,2}}}} \right)}}\left( {1 + \sqrt {\frac{2}{{1 + {{\beta }_{{1,2}}}}}} } \right).$Из последних двух формул получим
(19)
$\frac{{{{A}_{2}}}}{{{{A}_{1}}}} = \frac{{\sqrt {1 + {{\beta }_{2}}} }}{{\sqrt {1 + {{\beta }_{1}}} }}\frac{{\left( {\sqrt 2 - \sqrt {1 + {{\beta }_{1}}} } \right)}}{{\left( {\sqrt 2 - \sqrt {1 + {{\beta }_{2}}} } \right)}}.$Как нетрудно видеть, при${{A}_{2}} > {{A}_{1}}$ должно быть ${{\beta }_{2}} > {{\beta }_{1}}$, т.е. импульс с большей амплитудой должен двигаться с большей скоростью. При этом столкновение импульсов возможно, если больший импульс будет находиться позади меньшего и сможет его “догнать”.
Рассмотрим в качестве примера взаимодействие двух разных солитонов. Пусть эти солитоны, находясь на значительном удалении друг от друга, бегут по одному и тому же “невозмущенному уровню” (16):
(20)
${{V}_{ - }}\left( {\left| T \right| \to \infty } \right) = - \frac{C}{{2\left( {1 + \beta } \right)}} \equiv - {{V}_{0}}.$Введем для удобства функцию $U = V + {{V}_{0}}$, которая обращается в ноль $U\left( {\left| T \right| \to \infty } \right) = 0$ на бесконечности. Это означает, что $U$-солитоны возмущают нулевое значение параметра, описывающего состояние среды. Выражения для этих солитонов, соответствующие формулам (14), имеют вид:
(21)
$\begin{gathered} {{U}_{ - }}(2) = \frac{{{{C}_{2}}}}{{2\left( {1 + {{\beta }_{2}}} \right)}}\exp \left[ {\sqrt {\frac{{1 + {{\beta }_{2}}}}{D}} \left( { - \left| T \right| + {{T}_{2}}} \right)} \right], \\ \left| T \right| \geqslant {{T}_{2}}, \\ {{U}_{ + }}(2) = \frac{{{{C}_{2}}}}{{1 - \beta _{2}^{2}}} + \frac{{{{C}_{2}}}}{{2\left( {1 - {{\beta }_{2}}} \right)}}\sqrt {\frac{2}{{1 + {{\beta }_{2}}}}} \cos \left( {T\sqrt {\frac{{1 - {{\beta }_{2}}}}{D}} } \right), \\ \left| T \right| \leqslant {{T}_{2}}, \\ {{T}_{2}} = \sqrt {\frac{D}{{1 - {{\beta }_{2}}}}} \left( {\frac{\pi }{2} + \arcsin \sqrt {\frac{{1 + {{\beta }_{2}}}}{2}} } \right). \\ \end{gathered} $(22)
$\begin{gathered} {{U}_{ - }}(1) = \frac{{{{C}_{1}}}}{{2\left( {1 + {{\beta }_{1}}} \right)}}\exp \left[ {\sqrt {\frac{{1 + {{\beta }_{1}}}}{D}} \left( { - \left| {T + {{T}_{0}}} \right| + {{T}_{1}}} \right)} \right], \\ \left| {T + {{T}_{0}}} \right| \geqslant {{T}_{1}}, \\ {{U}_{ + }}(1) = \frac{{{{C}_{1}}}}{{1 - \beta _{1}^{2}}} + \frac{{{{C}_{1}}}}{{2\left( {1 - {{\beta }_{1}}} \right)}} \times \\ \times \,\,\sqrt {\frac{2}{{1 + {{\beta }_{1}}}}} \cos \left( {\left( {T + {{T}_{0}}} \right)\sqrt {\frac{{1 - {{\beta }_{1}}}}{D}} } \right),\,\,\,\left| {T + {{T}_{0}}} \right| \leqslant {{T}_{1}}, \\ {{T}_{1}} = \sqrt {\frac{D}{{1 - {{\beta }_{1}}}}} \left( {\frac{\pi }{2} + \arcsin \sqrt {\frac{{1 + {{\beta }_{1}}}}{2}} } \right). \\ \end{gathered} $В этих обозначениях постановка задачи такова. Нужно проанализировать процесс столкновения, т.е. рассчитать $U\left( {z,\,\,T} \right)$ для различных расстояний $z$. Фактически требуется проинтегрировать уравнение (12), записав его в следующем виде:
(23)
$\frac{{\partial U}}{{\partial z}} + \beta \frac{{\partial U}}{{\partial T}} - \frac{\partial }{{\partial T}}\left| {U - \frac{C}{{2\left( {1 + \beta } \right)}}} \right| = \frac{{{{\partial }^{3}}U}}{{\partial {{T}^{3}}}}.$Область по переменной $T$ должна включать оба солитона. Для $z = 0$ начальная конфигурация есть $U\left( {z = 0,\theta = T} \right)$ $ = U(2) + U(1)$, где $U(2),\,\,\,\,\,\,U(1)$ даются формулами (21) и (22).
При численном анализе задачи положим значения констант равными ${{\beta }_{2}} = 0.8,$ ${{\beta }_{1}} = 0.2$. При этом, в соответствии с (19) и (17) ${{{{A}_{2}}} \mathord{\left/ {\vphantom {{{{A}_{2}}} {{{A}_{1}}}}} \right. \kern-0em} {{{A}_{1}}}} = 5.4$, ${{{{С}_{2}}} \mathord{\left/ {\vphantom {{{{С}_{2}}} {{{С}_{1}}}}} \right. \kern-0em} {{{С}_{1}}}} = 1.5$. Возьмем также ${{С}_{2}} = 1.5,$ ${{С}_{1}} = 1,$ $D = 1,$ ${{T}_{0}} = 15$.
На рис. 3 видно, что солитоны в исходной точке $z = 0$ разнесены и начинают сближаться. Передний (маленький) солитон “перетекает” во второй (большой), находящийся позади него. Образуется связанное состояние, процесс формирования которого иллюстрирован кривыми для $z$ = 8, 12, 16, 20. Затем это состояние распадается на два новых солитона, показанных штриховыми кривыми для $z$ = 40, 50, 60. Теперь уже большой солитон находится впереди маленького, и с увеличением пройденного волной расстояния$z$ они все сильнее удаляются друг от друга.
Однако, в отличие от обычного уравнения КдВ с квадратичной нелинейностью, здесь наблюдаются отклонения от абсолютно упругого столкновения. Как видно на рис. 3, малый солитон имеет заметно меньшую амплитуду после столкновения, чем до него.
Рис. 3.
Столкновение двух модульных солитонов. Значения параметров $D = 1,\,\,{{T}_{0}} = 15$. При каждой кривой указано соответствующее ей расстояние $z$ = 0, 8, 12, 16, 20, 40, 50, 60.
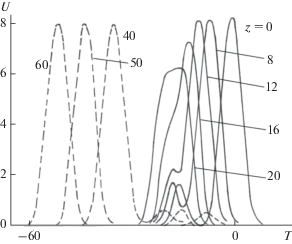
Возникает вопрос: сохраняется ли суммарная площадь под кривыми на рис. 3 (количество движения) в процессе соударения? Ответ на него не столь очевиден, как это кажется на первый взгляд.
Изучим вопрос о сохранении полной площади под кривой, описывающей одиночный импульсный сигнал (14). Перейдем в уравнении (12) к переменным ${{z}_{1}} = z,$ $T = \theta + \beta z$. Оно примет вид:
(24)
$\frac{{\partial V}}{{\partial {{z}_{1}}}} + \beta \frac{{\partial V}}{{\partial T}} - \frac{\partial }{{\partial T}}\left| V \right| = D\frac{{{{\partial }^{3}}V}}{{\partial {{T}^{3}}}}.$Проинтегрируем это уравнение по переменной $T$ в бесконечных пределах:
(25)
$\frac{\partial }{{\partial z}}\int\limits_{ - \infty }^\infty {VdT} + \beta \left. V \right|_{{ - \infty }}^{\infty } - \left| V \right|_{{ - \infty }}^{\infty } = D\left. {\frac{{{{\partial }^{2}}{{V}_{ - }}}}{{\partial {{T}^{2}}}}} \right|_{{ - \infty }}^{\infty }.$Для солитона (14) имеем (20)
(26)
$\begin{gathered} {{V}_{ - }}\left( {\left| T \right| \to \infty } \right) = - \frac{C}{{2\left( {1 + \beta } \right)}} = - {{V}_{0}}, \\ \left| {{{V}_{ - }}} \right|\left( {\left| T \right| \to \infty } \right) = {{V}_{0}},\,\,\,\,\frac{{{{\partial }^{2}}{{V}_{ - }}}}{{\partial {{T}^{2}}}}\left( {\left| T \right| \to \infty } \right) = 0. \\ \end{gathered} $С учетом (26) из интеграла (25) следует закон сохранения:
(27)
$\frac{{dS}}{{dz}} = \frac{\partial }{{\partial z}}\int\limits_{ - \infty }^\infty {VdT} = 0,\,\,\,\,S = \int\limits_{ - \infty }^\infty {VdT} = {\text{const}}.$Однако при выводе формулы (27) не учтено, что в точках $T = \pm T{\text{*}}$ могут существовать особенности второй производной. Поэтому правую часть интеграла (25) следует записать так:
(28)
$D\left[ {\left. {\frac{{{{\partial }^{2}}{{V}_{ - }}}}{{\partial {{T}^{2}}}}} \right|_{{ - \infty }}^{{ - T{\text{*}}}} + \left. {\frac{{{{\partial }^{2}}{{V}_{ + }}}}{{\partial {{T}^{2}}}}} \right|_{{ - T{\text{*}}}}^{{T{\text{*}}}} + \left. {\frac{{{{\partial }^{2}}{{V}_{ - }}}}{{\partial {{T}^{2}}}}} \right|_{{T{\text{*}}}}^{\infty }} \right].$Поскольку (см. (16))
(29)
${{\lim }_{{\left| T \right| \to \infty }}}V = - \frac{C}{{2\left( {1 + \beta } \right)}},\,\,\,\,{{\lim }_{{\left| T \right| \to \infty }}}\frac{{{{d}^{2}}V}}{{d{{T}^{2}}}} = 0,$(30)
$\frac{{dS}}{{dz}} = D\left[ {\left. {\frac{{{{\partial }^{2}}{{V}_{ - }}}}{{\partial {{T}^{2}}}}} \right|_{{ - \infty }}^{{ - T{\text{*}}}} + \left. {\frac{{{{\partial }^{2}}{{V}_{ + }}}}{{\partial {{T}^{2}}}}} \right|_{{ - T{\text{*}}}}^{{T{\text{*}}}} + \left. {\frac{{{{\partial }^{2}}{{V}_{ - }}}}{{\partial {{T}^{2}}}}} \right|_{{T{\text{*}}}}^{\infty }} \right].$Заметим еще раз, что в обеих точках “сшивания” $T = \pm T{\text{*}}$ как сама функция $V$ (14), так и ее первая производная непрерывны. Зато вторая производная при переходе через эти точки испытывает скачок. Как показывают несложные вычисления на основе решения (14), вторые производные справа и слева в точках $T = \pm T{\text{*}}$ равны:
(31)
$\begin{gathered} {{\left. {\frac{{{{\partial }^{2}}{{V}_{ - }}}}{{\partial {{T}^{2}}}}} \right|}_{{ - T{\text{*}}}}} = {{\left. {\frac{{{{\partial }^{2}}{{V}_{ - }}}}{{\partial {{T}^{2}}}}} \right|}_{{T{\text{*}}}}} = \frac{C}{{2D}}, \\ {{\left. {\frac{{{{\partial }^{2}}{{V}_{ + }}}}{{\partial {{T}^{2}}}}} \right|}_{{ - T{\text{*}}}}} = {{\left. {\frac{{{{\partial }^{2}}{{V}_{ + }}}}{{\partial {{T}^{2}}}}} \right|}_{{T{\text{*}}}}} = - \frac{C}{{2D}}. \\ \end{gathered} $Таким образом, правая часть в соотношении (29) все же равна нулю. Это означает, что “площадь” солитона $S$ (или его количество движения) при распространении не изменяется. Не изменяется и энергия, т.е. для модульного солитона система оказывается консервативной. Однако консервативность может не иметь места для более сложных сигналов.
В общем случае волны произвольной формы этот вопрос весьма сложен, и ответ на него нам пока не ясен. Для процесса столкновения двух солитонов, показанного на рис. 3, величина площади $S\left( z \right)$ рассчитывалась численно. Оказалось, что она сохраняется с точностью до третьего знака. По-видимому, затухание малого солитона в процессе столкновения сопровождается ростом “хвоста”, формирующегося позади него (см. рис. 3).
ЗАКЛЮЧЕНИЕ
Анализ процессов столкновения одиночных импульсных сигналов, результаты которого описаны выше, должен быть продолжен, поскольку многие особенности взаимодействий волн на модульной нелинейности до конца не выяснены. С точки зрения физики интересно продолжить изучение корпускулярных аналогий. Остаются, конечно, вопросы, требующие математических исследований, связанных с использованными нелинейными уравнениями.
Работа поддержана грантом Российского научного фонда (РНФ) № 19-12-00098.
Список литературы
Zabusky N.J., Kruskal M.D. Interaction of “solitons” in a collisionless plasma and the recurrence of initial states // Phys. Rev. Lett. 1965. V. 15. P. 240.
Руденко О.В., Хохлова В.А. Кинетический подход к описанию одномерной акустической турбулентности // Акуст. журн. 1988. Т. 34. № 3. С. 500–506.
Руденко О.В., Хохлова В.А. Кинетика одномерных пилообразных волн // Акуст. журн. 1991. Т. 37. № 1. С. 182–188.
Landau L.D., Lifshitz E.M. Fluid Mechanics. New York: Elsevier, 2018.
Polyakova A.L., Soluyan S.I., Khokhlov R.V. Propagation of finite disturbances in a relaxing medium // Sov. Phys. Acoustics. 1962. V. 8. № 1. P. 78–82.
Rudenko O.V., Soluyan S.I. The scattering of sound by sound // Sov. Phys. Acoustics. 1973. V.18. № 3. P. 352–355.
Перепечко И.И. Акустические методы исследования полимеров. М.: Химия, 1973.
Rudenko O.V. Nonlinear integro-differential models for intense waves in media like biological tissues and geostructures with complex internal relaxation-type dynamics // Acoust. Phys. 2014. V. 60. № 4. P. 398–404.
Vinogradova M.B., Rudenko O.V., Sukhorukov A.P. Theory of Waves (3rd Edition). Moscow: Lenand, 2015 [in Russian].
Physical Principles of Medical Ultrasound (2nd Edition, Editors Hill C.R., Bamber J.C., ter Haar G.R.). New York: John Wiley&Sons, 2004.
Vasilyeva O.A., Lapshin E.A., Rudenko O.V. Intense pulses in relaxing media with limited “memory time”, power-law and nonanalytic nonlinearities // Acoust. Phys. 2019. V. 65. № 1. P. 23–29.
Rudenko O.V., Gurbatov S.N., Hedberg C.M. Nonlinear Acoustics through Problems and Examples. Victoria, Canada: Trafford, 2011.
Назаров В.Е., Кияшко С.Б., Радостин А.В. Волновые процессы в микронеоднородных средах с разномодульной нелинейностью и релаксацией // Известия ВУЗов. Радиофизика. 2016. Т. 59. № 3. С. 275–285.
Radostin A.V., Nazarov V.E., Kiyashko S.B. Propagation of nonlinear acoustic waves in bimodular media with linear dissipation // Wave Motion. 2013. V. 50. № 2. P. 191–196.
Назаров В.Е., Кияшко С.Б., Радостин А.В. Самоподобные волны в средах с разномодульной упругой нелинейностью и релаксацией // Нелинейная динамика. 2015. Т. 11. № 2. С. 209–218.
Rudenko O.V. Equation admitting linearization and describing waves in dissipative media with modular, quadratic, and quadratically cubic nonlinearities // Doklady Mathematics. 2016. V. 94. №3. P. 703–707.
Gray A.L., Rudenko O.V. An intense wave in defective media containing both quadratic and modular nonlinearities: shock waves, harmonics and nondestructive testing // Acoust. Phys. 2018. V. 64. № 4. P. 402–407.
Амбарцумян С.А. Разномодульная теория упругости. М.: Наука, 1982. 318 с.
Korobov A.I., Kokshaiskii A.I., Prokhorov V.M., Evdokimov I.A., Perfilov S.A., Volkov A.D. Mechanical and nonlinear elastic characteristics of polycrystalline ${\text{A}}{\text{Mg}}6$ aluminum alloy and $n{\text{ - }}{{{\text{AMg}}6} \mathord{\left/ {\vphantom {{{\text{AMg}}6} {{{{\text{C}}}_{{60}}}}}} \right. \kern-0em} {{{{\text{C}}}_{{60}}}}}$ nanocomposite // Phys. of Solid State. 2016. V. 58. № 12. P. 2472–2480.
Mikhailov S.G., Rudenko O.V. A simple bimodular nonlinear element // Acoust. Phys. 2018. V. 64. № 3. P. 293–298.
Hedberg C.M., Rudenko O.V. Collisions, mutual losses and annihilation of pulses in a modular nonlinear medium // Nonlinear Dynamics. 2017. V. 90. № 3. P. 2083–2091. https://link.springer.com/article/10.1007%2Fs11071-017-3785-6
Rudenko O.V. Modular solitons // Doklady Mathematics. 2016. V. 94. № 3. P 708–711.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал


