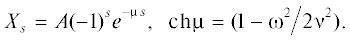Акустический журнал, 2020, T. 66, № 3, стр. 265-272
Распространение упругих волн в динамически-самоподобных структурах (динамических фракталах)
Л. Я. Банах *
Федеральное государственной бюджетное учреждение науки Институт машиноведения им. А.А. Благонравова Российской академии наук
101990 Москва, Малый Харитоньевский пер. 4, Россия
* E-mail: banl@inbox.ru
Поступила в редакцию 19.04.2018
После доработки 21.10.2019
Принята к публикации 29.10.2019
Аннотация
Введено понятие динамически-самоподобной структуры (динамического фрактала), заключающееся в подобии динамических параметров образующих ячеек. Исследуется распространение упругих волн в неразветвленных динамически-самоподобных структурах. Показано, что такие структуры эквивалентны по частотам периодической структуре с дополнительным закреплением, однако характер распространения волн в них существенно различен. В динамическом фрактале возможны как затухающие волны, так и нарастающие вдоль длины структуры, а интенсивность затухания волн сильнее, чем в периодической структуре.
ВВЕДЕНИЕ
В настоящее время повышается интерес к волновым свойствам периодических структур, состоящих из сложных ячеек. К таким структурам относятся, в частности, метаматериалы, которые обладают необычными волновыми свойствами, не встречающимися в природе, например акустической невидимостью [1, 2]. Поэтому первостепенное значение приобретает изучение распространения волн в таких средах.
Однако класс периодических структур может быть существенно расширен и дополнен классом самоподобных фрактальных структур. Согласно Б. Мандельброту [3], отличительными чертами фракталов являются “самоподобие, инвариантность относительно изменения масштаба или скейлинга, инвариантность при мультипликативных изменениях масштаба. Кратко говоря, самоподобный объект выглядит неизменным и после увеличения и после уменьшения его размеров”.
Хорошо известные геометрические фракталы Мандельброта [3, 4] описывают структуры, подобные по геометрическим параметрам. Их отличительной чертой является нецелая размерность. Фракталы вообще можно рассматривать как системную связь локального и глобального порядка. Именно такой класс структур преобладает в природе и технике. Изучению волновых и акустических свойств фрактальных структур посвящены работы Л.М. Лямшева, В.В. Зосимова, И.А Урусовского [5–7]. В этих работах исследованы упругие колебания и волны в материалах с геометрически-фрактальной структурой, найдены их дисперсионные уравнения. Исследуются также колебания фрактальных кластеров, для которых характерна зависимость упругих свойств от масштаба деформации.
Тем не менее, динамические свойства системы определяют ее упруго-инерционные параметры. Поэтому представляет интерес изучить волновые свойства структур, состоящих из ячеек, подобных по динамическим параметрам, а не по геометрическим. Для этого необходимо ввести понятие динамического фрактала, в отличие от геометрического фрактала Мандельброта. С этой целью логично потребовать масштабирования параметров системы, определяющих ее динамические свойства, т.е. упругих и инерционных параметров [8, 9].
САМОПОДОБНЫЕ МАТЕРИАЛЫ СТРУКТУРЫ В МЕХАНИКЕ. ДИНАМИЧЕСКИЙ ФРАКТАЛ
Рассмотрим вначале наиболее простую дискретную неразветвленную одномерную структуру, состоящую из масс, соединенных упругими элементами.
Определение. Динамически–самоподобными (динамическим фракталом) назовем такие структуры, в которых упругие и инерционные параметры меняются с одинаковым масштабом γ для каждой ячейки структуры (или подсистемы):
Ks – жесткость, Js – инерционный параметр s-й ячейки. Это определение динамического фрактала справедливо и для структур, в которых число степеней свободы образующих ячеек больше единицы. При этом для каждой координаты могут быть свои коэффициенты масштабирования (п.5).Необходимым следствием условий (1) является равенство парциальных частот для всех образующих ячеек:
(2)
$\begin{gathered} {\nu }_{s}^{2} = {{\left( {{{K}_{s}} + {{K}_{{s - 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{K}_{s}} + {{K}_{{s - 1}}}} \right)} {{{J}_{s}}}}} \right. \kern-0em} {{{J}_{s}}}} = {\nu }{{_{{s + 1}}^{2}}^{{}}} = {{\left( {{{K}_{{s + 1}}} + {{K}_{s}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{K}_{{s + 1}}} + {{K}_{s}}} \right)} {{{J}_{{s + 1}}}}}} \right. \kern-0em} {{{J}_{{s + 1}}}}} = \\ = {\text{const}} = {{{\nu }}^{2}}\,\,\,\,(s = 1....N). \\ \end{gathered} $Условие равенства парциальных частот (2) – это условие динамического самоподобия структуры (динамического фрактала).
Рассмотрим теперь бесконечную дискретную одномерную цепочку, в которой s-я ячейка состоит из сосредоточенной массы ms и пружинки с жесткостью ks. Пусть упругие и инерционные параметры меняются с одинаковым масштабом γ от ячейки к ячейке (рис. 1а). Тогда жесткость и масса для элемента s + 1:
Рис. 1.
(а) – Динамически-самоподобная стержневая структура с сосредоточенными массами, (б) – эквивалентная периодическая структура, имеющая такие же собственные частоты, (в) – парциальная подсистема динамически-самоподобной структуры.
Следовательно, такая структура представляет собой динамический фрактал.
Коэффициенты упругости, необходимые для определения парциальных частот образующей ячейки, находятся при закрепленных границах ячейки (рис. 1в). (Если в уравнениях используются коэффициенты податливости, то парциальные частоты определяются при свободных границах ячейки.) Для этой цепочки
Условие (2) равенства парциальных частот для каждой ячейки выполнено:
Замечание. Отметим, что условия (2) для динамического фрактала не всегда совпадают с условиями геометрического подобия (scaling), использующегося в геометрических фракталах Мандельброта. Действительно, пусть упругие элементы моделируют продольную жесткость стержня, равную EFs/ls, а инерционный элемент представлен в виде жесткого шара радиуса R (рис. 1а), т.е. ms = ${{4\rho \pi R_{s}^{3}} \mathord{\left/ {\vphantom {{4\rho \pi R_{s}^{3}} 3}} \right. \kern-0em} 3}$ (здесь Fs – площадь поперечного сечения s-й ячейки, ls – ее длина). Условия геометрического скейлинга имеют вид: Fs +1= γ2Fs, ls = γls, Rs = γRs. Очевидно, что при этом условия (2) для динамического фрактала не выполняются:
Верно и обратное: условия (1), (2) могут быть выполнены без геометрического подобия всех элементов, а лишь только некоторых из них. Пусть, например,
Несмотря на то, что радиус шара меняется с другим коэффициентом подобия, γ1/3, условия (2) выполнены:
Таким образом, выполнение условий (1), (2) для динамического фрактала требует различного масштабирования геометрических параметров, что является определенным обобщением геометрического фрактала.
ЧАСТОТНАЯ ЭКВИВАЛЕНТНОСТЬ ДИНАМИЧЕСКИ-САМОПОДОБНЫХ И ПЕРИОДИЧЕСКИХ СТРУКТУР. ДИСПЕРСИОННОЕ УРАВНЕНИЕ
Уравнение динамически-самоподобной дискретной структуры, представленной на рис. 1а, можно записать в виде уравнений в конечных разностях. Так, уравнение для s + 1-й ячейки:
(4)
$ - {{k}_{s}}{{x}_{s}} + ( - {{m}_{{s + 1}}}{{{\omega }}^{2}} + {{k}_{s}}(1 + {\gamma })){{x}_{{s + 1}}} - {\gamma }{{k}_{s}}{{x}_{{s + 2}}} = 0,$Уравнение (4) – это общий вид уравнения дискретной динамически-самоподобной цепной структуры (рис. 1). При γ < 1 получим структуру с убывающими по длине параметрами, а при γ > 1 – с возрастающими.
Сделаем теперь в (4) замену переменных:
(5)
${{x}_{s}} = {{{{{\tilde {x}}}_{s}}} \mathord{\left/ {\vphantom {{{{{\tilde {x}}}_{s}}} {{{{\left( {\sqrt {\gamma } } \right)}}^{s}}}}} \right. \kern-0em} {{{{\left( {\sqrt {\gamma } } \right)}}^{s}}}}.$В результате найдем уравнение для s + 1-й ячейки в новых переменных:
Полагая ${{k}_{s}} = {{k}_{1}}{{{\gamma }}^{s}},$ ${{m}_{s}} = {{m}_{1}}{{{\gamma }}^{s}}$, видим, что это уравнение справедливо для любого номера s, так как отношение его коэффициентов от s не зависит. Его удобно записать в виде, описывающем s-ю ячейку
(6)
$\begin{gathered} {{ - {{k}_{1}}{{{\tilde {x}}}_{{s - 1}}}} \mathord{\left/ {\vphantom {{ - {{k}_{1}}{{{\tilde {x}}}_{{s - 1}}}} {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }} + \left( { - {{m}_{1}}{{{\omega }}^{2}} + \frac{{{{k}_{1}}(1 + {\gamma })}}{{\gamma }}} \right){{{\tilde {x}}}_{s}} - \\ - \,\,{{{{k}_{1}}{{{\tilde {x}}}_{{s + 1}}}} \mathord{\left/ {\vphantom {{{{k}_{1}}{{{\tilde {x}}}_{{s + 1}}}} {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }} = 0. \\ \end{gathered} $Уравнение (6) описывает периодическую структуру на рис. 1б. Парциальные частоты каждой массы ${\nu }_{s}^{2} = {{\left( {{{k}_{{s - 1}}} + {{k}_{s}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{{s - 1}}} + {{k}_{s}}} \right)} {{{m}_{s}}}}} \right. \kern-0em} {{{m}_{s}}}}$ одинаковы в силу условия (3), жесткость между массами равна ${{{{k}_{1}}} \mathord{\left/ {\vphantom {{{{k}_{1}}} {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }},$ но при этом имеется дополнительное закрепление масс $k* = \frac{{{{k}_{1}}(1 + {\gamma })}}{{\gamma }}$ – $\frac{{2{{k}_{1}}}}{{\sqrt {\gamma } }}$ = $\frac{{{{k}_{1}}{{{(1 - \sqrt {\gamma } )}}^{2}}}}{{\gamma }}.$ Следовательно, величина упругих элементов в структуре на рис. 1б одинакова для каждой ячейки и определяется только коэффициентом подобия.11 В интервале 0.16 < γ < 6.76 жесткость дополнительного закрепления меньше жесткости, соединяющей массы: $k* < {{{{k}_{1}}} \mathord{\left/ {\vphantom {{{{k}_{1}}} {\sqrt \gamma }}} \right. \kern-0em} {\sqrt \gamma }}.$
Частное решение уравнения (6) имеет вид [10, 11]:
ω – собственная частота, μ – волновой параметр, характеризующий изменение фазы при переходе от элемента s к s + 1. Здесь μ = κl, где κ – волновое число, l – длина ячейки.Подставляя (7) в (6), находим дисперсионное уравнение для периодической структуры на рис. 1б:
– для действительных μ: $ - {{m}_{1}}{{{\omega }}^{2}} + \frac{{{{k}_{1}}(1 + {\gamma })}}{{\gamma }}$ – $ - \,\,2\frac{{{{k}_{1}}}}{{\sqrt {\gamma } }}\cos {\mu } = 0,$ ${{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{k}_{1}} = {{{{m}_{s}}} \mathord{\left/ {\vphantom {{{{m}_{s}}} {{{k}_{s}} = }}} \right. \kern-0em} {{{k}_{s}} = }}{{\nu }^{2}} = {\text{const}}}}} \right. \kern-0em} {{{k}_{1}} = {{{{m}_{s}}} \mathord{\left/ {\vphantom {{{{m}_{s}}} {{{k}_{s}} = }}} \right. \kern-0em} {{{k}_{s}} = }}{{\nu }^{2}} = {\text{const}}}};$
– для чисто мнимых ${\mu } = i{\mu }{\kern 1pt} {\text{'}}$: $ - {{m}_{1}}{{{\omega }}^{2}} + \frac{{{{k}_{1}}(1 + {\gamma })}}{{\gamma }}$ – 
Дисперсионная кривая для γ = 0.5 (ω0 = 0.41ν, ω*= 2.41ν) изображена на рис. 2а, дисперсионная поверхность в зависимости от параметра γ представлена на рис. 2б.
Рис. 2.
(а) – Дисперсионная кривая для γ = 0.5: ω0 = 0.41ν, ω* = 2.41ν, (б) – дисперсионная поверхность в зависимости от коэффициента подобия.

Линейное преобразование координат (5) не меняет частотных свойств, поэтому динамический фрактал на рис. 1а и периодическая структура на рис. 1б имеют одинаковые частоты. Периодическая структура представляет собой механический полосовой частотный фильтр с полосой пропускания гармонического сигнала: ω0 < ω < ω* (рис. 2а), где:
(8)
${\omega }_{0}^{2} = {{\nu }^{2}}\frac{{{{{\left( {1 - \sqrt {\gamma } } \right)}}^{2}}}}{{\gamma }},\,\,\,\,{{{\omega }}^{{*2}}} = {{\nu }^{2}}\frac{{{{{\left( {1 + \sqrt {\gamma } } \right)}}^{2}}}}{{\gamma }}.$Полоса пропускания $\Delta {\omega = \omega *} - {{{\omega }}_{0}}.$ При этом:
– для уменьшающейся по длине цепочки, как следует из (8), $\Delta {\omega = 2\nu ,}$ т.е. ширина полосы пропускания не зависит от параметра γ и совпадает с шириной полосы пропускания периодической структуры без дополнительного закрепления. Тем не менее, сами граничные частоты, а, следовательно, и расположение полосы пропускания зависят от γ;
– для увеличивающейся по длине цепочки $\Delta {\omega = \omega *} - \left| {{{{\omega }}_{0}}} \right|$ = ${{2{\nu }} \mathord{\left/ {\vphantom {{2{\nu }} {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }},$ т.е. ширина полосы пропускания обратно пропорциональна $\sqrt {\gamma } $, при этом ${\omega *} + {{{\omega }}_{0}} = 2{\nu }{\text{.}}$ При достаточно большом ${\gamma }$ полоса пропускания в пределе становится очень узкой, расположенной вблизи парциальной частоты ν, т.е. тогда система настроена только на одну определенную частоту.
Эти результаты подтверждает и табл. 1, в которой представлены граничные частоты полосы пропускания в зависимости от коэффициента γ. Из таблицы следует, что в уменьшающейся по длине цепочке (γ < 1) нижняя граница полосы пропускания снижается с увеличением γ и стремится к 0, как в периодической цепочке без закрепления. В увеличивающейся цепочке (γ > 1), напротив, при увеличении γ нижняя граница полосы пропускания повышается.
Таблица 1.
Граничные частоты полос пропускания при различных коэффициентах γ
| γ > 1 | γ < 1 | γ =1 (периодическая цепочка) | ||||||
|---|---|---|---|---|---|---|---|---|
| γ | 1.2 | 1.5 | 2.0 | 4.0 | 0.2 | 0.5 | 0.8 | 1 |
| ${{{{{\omega }}_{0}}} \mathord{\left/ {\vphantom {{{{{\omega }}_{0}}} {\nu }}} \right. \kern-0em} {\nu }}$ | 0.1 | 0.17 | 0.3 | 0.5 | 1.24 | 0.41 | 0.1 | 0 |
| ${{{\omega }_{0}^{*}} \mathord{\left/ {\vphantom {{{\omega }_{0}^{*}} {\nu }}} \right. \kern-0em} {\nu }}$ | 1.91 | 1.82 | 1.70 | 1.5 | 3.24 | 2.41 | 2.11 | 2 |
Однако разность квадратов граничных частот не зависит от вида цепочки
Преобразование координат (5) – это преобразование квадратичных форм, описывающих потенциальную и кинетическую энергию: ${{{\mathbf{x}}}^{T}}{\mathbf{Kx}} = {{{\mathbf{\tilde {x}}}}^{T}}{\mathbf{\tilde {K}\tilde {x}}},$ ${{{\mathbf{\dot {x}}}}^{T}}{\mathbf{M\dot {x}}} = {{{\mathbf{\tilde {\dot {x}}}}}^{T}}{\mathbf{\tilde {M}\tilde {\dot {x}}}}.$ Следовательно, динамический фрактал и соответствующая периодическая структура эквивалентны по энергии.
РАСПРОСТРАНЕНИЕ ВОЛН В ДИНАМИЧЕСКИ-САМОПОДОБНЫХ СТРУКТУРАХ
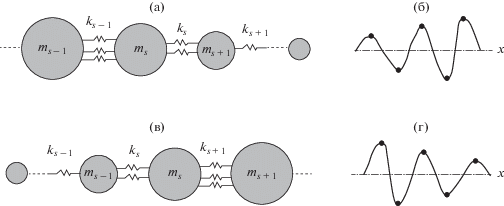
Характер распространения волн в периодической и динамически-самоподобной структурах (динамическом фрактале) существенно различен. Поэтому представляет интерес изучить волновое поведение динамического фрактала в полосе пропускания, а также и вне ее. Волна в такой структуре, как видно из преобразования координат (5), получается из соответствующей волны в периодической структуре на рис. 1б путем пропорционального изменения амплитуды колебаний каждого участка в ${1 \mathord{\left/ {\vphantom {1 {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }}$ раз. На рис. 3 представлены высшие формы колебаний динамического фрактала при закрепленных концах. Для периодической структуры на рис. 1б это, как известно, синусоида, в которой соседние массы находятся в противофазе. В динамическом фрактале (рис. 1а) амплитуда колебаний получается путем увеличения (при γ < 1) соответствующей амплитуды периодической структуры в ${1 \mathord{\left/ {\vphantom {1 {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }}$ раз (или уменьшения амплитуды при γ > 1). Поэтому получаем волну с постоянно увеличивающимися (уменьшающимися) амплитудами (рис. 3а, 3б). Огибающая этой волны – экспонента. Таким образом, в динамическом фрактале с увеличивающимися по длине параметрами в полосе пропускания происходит снижение уровня колебаний, а во фрактале с уменьшающимися параметрами, наоборот, можно добиться существенного усиления входного сигнала.
Рис. 3.
Формы колебаний динамически-самоподобной структуры при ω0 < ω < ω*: (а), (б) – цепочка с уменьшающимися по длине параметрами, γ < 1; (в), (г) – цепочка с увеличивающимися по длине параметрами, γ > 1.
Неожиданные волновые свойства приобретают динамические фракталы в полосе непропускания. Для периодической структуры (γ = 1) в этих полосах, как известно, происходит экспоненциальное затухание гармонического сигнала вдоль цепочки [11]:
Однако, в динамических фракталах возможно не только затухание, но и усиление гармонического сигнала и даже превращение полосы непропускания в полосу прозрачности. Действительно, решение для динамического фрактала, учитывая преобразование координат (5), имеет вид:
Следовательно, волновое число – комплексное и волна неоднородная. Рис. 2б можно рассматривать как дисперсионную поверхность в комплексной плоскости, полагая ${\gamma = exp(2\alpha )}{\text{.}}$ В этом случае фазовая скорость становится комплексной величиной сф = ω/κ = ω/l(μ + iα).
Для динамического фрактала с увеличивающимися параметрами (γ > 1) (рис. 3б), как в полосе пропускания периодической структуры, так и вне ее, возможно только увеличение скорости затухания, равной μ + iα: $X_{s}^{*} = A{{( - 1)}^{s}}\exp ( - \left( {{\mu + }i{\alpha }} \right)s)$.
Однако, динамический фрактал с уменьшающимися параметрами обладает следующими особенностями, а именно: в такой системе γ < 1, поэтому ${\alpha }$ < 0, что означает, по существу, отрицательное демпфирование. При этом возникают три различные ситуации:
– если |α| > μ, то полоса непропускания исчезает и в ней возникают волны, амплитуда которых нарастает вдоль цепочки со скоростью exp((|α| – μ)s),
– если |α| < μ, то возникают затухающие волны, скорость затухания: $X_{s}^{*} = A{{( - 1)}^{s}}\exp ( - \left( {{\mu } - \left| {\alpha } \right|} \right)s),$
– если |α| = μ > 1, то возникает частота Ω прозрачности гармонического сигнала.
В табл. 2 приведены значения Ω для цепочки с убывающими параметрами в полосах непропускания при различных коэффициентах масштаба γ = 0.2, 0.5, 0.8.
Таблица 2.
Значения частоты прозрачности гармонического сигнала Ω во 2-й полосе непропускания ($\omega > {\omega *}$)
| γ | 0.2 | 0.5 | 0.8 |
|---|---|---|---|
| |α| | 0.8 | 0.35 | 0.1 |
| ${{{{{\omega }}^{{{\text{*2}}}}}} \mathord{\left/ {\vphantom {{{{{\omega }}^{{{\text{*2}}}}}} {{{{\nu }}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\nu }}^{{\text{2}}}}}}$ | 10.47 | 5.83 | 4.49 |
| ${{\left( {{{{{\Omega }^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{\Omega }^{{\text{2}}}}} {{{{\nu }}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\nu }}^{{\text{2}}}}}}} \right)}_{{{\alpha = \mu }}}}$ | 12.0 | 6.3 | 4.9 |
Как показывают расчеты, в первой полосе непропускания 0 < ω < ω0 при всех значениях γ выполнено неравенство |α| > μ. Следовательно, эта полоса непропускания для динамического фрактала исчезает и в ней происходит увеличение амплитуды колебаний пропорционально exp(|α| – μ), при этом μ уменьшается при приближении к граничной частоте интервала ω0.
Во второй полосе непропускания ($\omega > \omega {\text{*}}$) существует частота возбуждения Ω, своя для каждого значения γ, при которой |α| = μ >1. Это частота прохождения гармонического сигнала. Тогда при ω* < ω < Ω коэффициент |α| > μ. В этой области полоса непропускания также исчезает и возникают волны, нарастающие по длине структуры с интенсивностью exp(|α| – μ). Но, как следует из табл. 2, эта область очень мала, частоты Ω расположены достаточно близко к границе областей непропускания, и эта область уменьшается с увеличением γ < 1. При ω > Ω остается полоса непропускания, но интенсивность затухания в ней равна exp (μ – |α|), что меньше, чем в периодической системе γ = 1.
Уравнение Вебстера. Отметим определенную аналогию с распространением акустических волн в волноводах переменного сечения, которые описываются уравнением Вебстера [12]
(9)
$\frac{1}{{S(x)}}\frac{\partial }{{\partial x}}\left( {S(x)\frac{{\partial p}}{{\partial x}}} \right) = \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}p}}{{\partial {{t}^{2}}}}.$Пусть площадь сечения меняется по экспоненциальному закону $S(x) = {{S}_{0}}\exp ({\beta }x).$ В зависимости от знака β получим уменьшающуюся или увеличивающуюся по длине структуру. Из (9) найдем
Таким образом, получили диссипативное уравнение. Дисперсионное уравнение
Фазовая скорость при этом зависит от частоты и, кроме того, оказывается комплексной [13]. В зависимости от знака β будут либо затухающие, либо нарастающие колебания:
Распространение акустических волн в более сложных системах с переменной акустической проводимостью стенки исследованы в [14, 15]. Доказано, что скорость волны может замедляться и даже обращаться в нуль, не доходя до края трубы. Волновое уравнение в этом случае – это обобщенное уравнение Вебстера.
ДИНАМИЧЕСКИЕ ФРАКТАЛЫ С МНОГОМЕРНЫМИ ЯЧЕЙКАМИ
В предыдущих разделах рассматривались одномерные цепные структуры, ячейки которых имеют только одну степень свободы. Но совершенно аналогично можно исследовать неразветвленные структуры с многомерными ячейками. В качестве примера рассмотрим распространение изгибных волн в динамически-самоподобной балке ступенчатого сечения с насаженными дисками (рис. 4). Будем исследовать волны в вертикальной плоскости с учетом инерции поворота поперечного сечения. Полагаем участки балок невесомыми, инерционные элементы дисков: масса ms, момент инерции Js. Перемещение s-го узла описывается двумерным вектором ${{{\mathbf{X}}}_{s}}$ с координатами [$y,{\theta }$], где y – перемещение узла, ${\theta }$ – угол поворота. Примем конечно-элементную модель балки; при этом каждый элемент балочной системы будем представлять в виде одного конечного элемента. Такая идеализация допустима для низкочастотного диапазона, если длина участка не превосходит ¼ длины волны [8].
Матрица жесткости плоского балочного конечного элемента имеет вид [8, 16]:
(10)
$\begin{gathered} {\mathbf{K}} = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{K}}}_{{11}}}}&{{{{\mathbf{K}}}_{{12}}}} \\ {{{{\mathbf{K}}}_{{21}}}}&{{{{\mathbf{K}}}_{{22}}}} \end{array}} \right];\,\,\,\,{{{\mathbf{K}}}_{{11}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{12EI}}{{{{l}^{3}}}}}&{\frac{{6EI}}{{{{l}^{2}}}}} \\ {\frac{{6EI}}{{{{l}^{2}}}}}&{\frac{{4EI}}{l}} \end{array}} \right], \\ {{{\mathbf{K}}}_{{12}}} = {{{\mathbf{K}}}^{T}}_{{21}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{12EI}}{{{{l}^{3}}}}}&{ - \frac{{6EI}}{{{{l}^{2}}}}} \\ {\frac{{6EI}}{{{{l}^{2}}}}}&{\frac{{2EI}}{l}} \end{array}} \right], \\ \\ {{{\mathbf{K}}}_{{22}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{12EI}}{{{{l}^{3}}}}}&{ - \frac{{6EI}}{{{{l}^{2}}}}} \\ { - \frac{{6EI}}{{{{l}^{2}}}}}&{\frac{{4EI}}{l}} \end{array}} \right] = {\mathbf{T}}{{{\mathbf{K}}}_{{11}}}{\mathbf{T}},\,\,\,\,{\mathbf{T}} = \left[ {\begin{array}{*{20}{c}} 1&{} \\ {}&{ - 1} \end{array}} \right]. \\ \end{gathered} $(11)
${{{\mathbf{K}}}_{{12}}}{{{\mathbf{x}}}_{{s - 1}}} + \left( {{{{\mathbf{K}}}_{{11}}} + {{{\mathbf{K}}}_{{22}}}} \right){{{\mathbf{x}}}_{s}} + {{{\mathbf{K}}}_{{21}}}{{{\mathbf{x}}}_{{s + 1}}} = {\mathbf{P}}.$Пусть для каждого участка изгибная жесткость ${{12E{{I}_{s}}} \mathord{\left/ {\vphantom {{12E{{I}_{s}}} {{{l}_{s}}^{3}}}} \right. \kern-0em} {{{l}_{s}}^{3}}}$ меняется с коэффициентом подобия γ. Этому условию удовлетворяет фрактальная балка с геометрическим самоподобием, если радиус участка и его длина меняются в одинаковом отношении γ. Действительно, тогда ${{12E{{I}_{s}}} \mathord{\left/ {\vphantom {{12E{{I}_{s}}} {{{l}_{s}}^{3}}}} \right. \kern-0em} {{{l}_{s}}^{3}}}$ = ${{12E{{I}_{{s - 1}}}{{{\gamma }}^{4}}} \mathord{\left/ {\vphantom {{12E{{I}_{{s - 1}}}{{{\gamma }}^{4}}} {{{{\gamma }}^{3}}l_{{s - 1}}^{3}}}} \right. \kern-0em} {{{{\gamma }}^{3}}l_{{s - 1}}^{3}}} = $ = ${{{\gamma }12E{{I}_{{s - 1}}}} \mathord{\left/ {\vphantom {{{\gamma }12E{{I}_{{s - 1}}}} {l_{{s - 1}}^{3}}}} \right. \kern-0em} {l_{{s - 1}}^{3}}},$ ${{4E{{I}_{s}}} \mathord{\left/ {\vphantom {{4E{{I}_{s}}} {{{l}_{s}}}}} \right. \kern-0em} {{{l}_{s}}}} = {{{\gamma }}^{3}}{{4E{{I}_{{s - 1}}}} \mathord{\left/ {\vphantom {{4E{{I}_{{s - 1}}}} {{{l}_{{s - 1}}}}}} \right. \kern-0em} {{{l}_{{s - 1}}}}}.$
Каждый блок матрицы жесткости ${{{\mathbf{K}}}_{s}}$ для участка s можно записать в виде:
Для удовлетворения условиям динамического фрактала необходимо потребовать, чтобы инерционные элементы диска – масса ms и момент инерции Js – менялись с таким же масштабом, т.е. ${{m}_{s}} = {\gamma }{{m}_{{s - 1}}},$ ${{J}_{s}} = {{{\gamma }}^{3}}{{J}_{{s - 1}}}.$
Таким образом, в отличие от одномерной ячейки здесь каждая степень свободы может иметь свой коэффициент подобия, и поэтому теперь необходимо вводить в рассмотрение матрицу подобия Г. Тогда уравнение (11) для фрактальной балки в матричном виде:
Это уравнение в конечных разностях с переменными, зависящими от s коэффициентами. Применяем, как и выше, преобразование координат ${{{\mathbf{x}}}_{s}} = {\mathbf{x}}_{s}^{*}{{\Gamma }^{{ - s/2}}}.$ Тогда в новых координатах найдем для s-го узла балки:
(12)
$\begin{gathered} {{{\mathbf{\Gamma }}}^{{ - 1/2}}}{{{\mathbf{K}}}_{{21}}}{\mathbf{x}}_{{s - 1}}^{*} + ( - {{{\mathbf{M}}}_{s}}{{\omega }^{2}} + {{{\mathbf{\Gamma }}}^{{ - 1/2}}}{{{\mathbf{K}}}_{{22}}}{{{\mathbf{\Gamma }}}^{{ - 1/2}}} + \\ + \,\,{{{\mathbf{K}}}_{{11}}}){\mathbf{x}}_{s}^{*} + {{{\mathbf{K}}}_{{12}}}{{{\mathbf{\Gamma }}}^{{ - 1/2}}}{\mathbf{x}}_{{s + 1}}^{*} = 0. \\ \end{gathered} $Таким образом, получили уравнение в конечных разностях с коэффициентами, не зависящими от номера ячейки, т.е. уравнение периодической структуры. Для физической интерпретации упругой части уравнения (12) представим выражение, стоящее в скобках, в виде:
Тогда замечаем, что уравнение (12) описывает регулярную структуру, состоящую из одинаковых балочных элементов вида (10), но имеющих в каждом узле дополнительное закрепление $\Delta {\mathbf{K}}$. Это дополнительное закрепление представляет собой балку, жесткость которой пропорциональна разности между жесткостями балок первого и второго участков.
В заключение отметим, что рассмотренные выше динамические фракталы можно рассматривать как элементы метаматериала. Их применение может оказаться успешным в силу их компактности, а также увеличения интенсивности затухания (или усиления) входного сигнала.
ВЫВОДЫ
1. Введено понятие динамически-самоподобной структуры (динамического фрактала), заключающееся в подобии динамических параметров образующих ячеек.
2. Доказана частотная эквивалентность динамического фрактала и периодической структуры с дополнительным закреплением масс.
3. В динамических фракталах с увеличивающимися по длине параметрами происходит более интенсивное снижение уровня колебаний по сравнению с периодическими структурами, что важно для систем виброизоляции.
4. В динамических фракталах с уменьшающимися по длине параметрами:
– возникают неоднородные волны с усилением входного сигнала, что отличает динамический фрактал от периодической структуры, в которой не происходит усиления сигнала;
– частота пропускания гармонического сигнала динамического фрактала находится в области непропускания периодической структуры, но достаточно близко к ее границе.
5. В многомерных неразветвленных цепочках каждая степень свободы может иметь свой коэффициент подобия, поэтому необходимо рассматривать матрицу подобия.
Автор благодарит проф. Ю.И. Бобровницкого за обсуждение работы.
Список литературы
Acoustic metamaterials and phononic crystals / Ed. Deymier P.A. Berlin: Springer-Verlag. 2013. 378 p.
Бобровницкий Ю.И., Томилина Т.М. Поглощение звука и метаматериалы (Обзор) // Акуст. журн. 2018. Т. 64. № 5. С. 517–525.
Мандельброт Б. Фрактальная геометрия природы. М.: Институт компьютерных исследований, 2002. 656 с.
Федер Е. Фракталы. М.: Мир, 1991. 254 с.
Зосимов В.В., Лямшев Л.М. Фракталы и скейлинг в акустике (обзор) // Акуст. журн. 1994. Т. 40. № 5. С. 709–737.
Копыл Е.А., Лысанов Ю.П., Лямшев Л.М. Рассеяние звука случайными фрактальными неоднородностями в океане // Акуст. журн. 2012. Т. 48. С. 517–522.
Лямшев Л.М., Урусовский И.А. Дифракция звука на ковре Серпинского // Акуст. журн. 2003. Т. 49. С. 820–823.
Banakh L.Ya., Kempner M.L. Vibrations of mechanical systems with regular structure. Springer, 2010. 262 p.
Банах Л.Я., Бармина О.В. Колебания самоподобных структур в механике // Проблемы машиностроения и надежность машин. 2013. № 2. С. 3–9.
Карман Т., Био М. Математические методы в инженерном деле. М.: Гостехиздат, 1948. 424 с.
Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. М.: Наука, 1984. 432 с.
Исакович М.А. Общая акустика. М.: Наука, 1973. 502 с.
Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. М.: Физматлит, 2008. 496 с.
Миронов М.А. Распространение изгибной волны в пластине, толщина которой плавно уменьшается до нуля на конечном интервале // Акуст. журн. 1988. № 3. С. 546–547.
Миронов М.А., Писляков В.В. Одномерные волны в замедляющих структурах со скоростью распространения, стремящейся к нулю // Акуст. журн. 2002. № 3. С. 400–405
Постнов В.А., Хархурим И.А. Метод конечных элементов в расчетах судовых конструкций. Л.: Судостроение, 1974. 341 с.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал