Акустический журнал, 2020, T. 66, № 4, стр. 351-356

Условия фокусировки волны давления в пузырьковом клине

И. К. Гималтдинов^a, *, Е. Ю. Кочанова^a

^a ФГБОУ ВО “Уфимский государственный нефтяной технический университет”
450062 Уфа, ул. Космонавтов 1, Россия

Поступила в редакцию 25.06.2019
После доработки 06.02.2020
Принята к публикации 25.02.2020

DOI: 10.31857/S0320791920040024

Аннотация

Исследована динамика волн давления в плоском канале с расположенной под углом границей пузырьковой и “чистой” жидкостей. Показано, что при переходе границы водовоздушная смесь–вода отражение для волн, падающих на эту границу со стороны водовоздушной смеси, аналогично отражению от жесткой стенки, что влечет за собой интерференцию волн. Установлено, что c увеличением объемного содержания и с уменьшением радиуса пузырьков максимальное значение амплитуды давления результирующей волны на стенке увеличивается.

Ключевые слова: пузырьковая жидкость, волны давления, двумерность, граница водовоздушная смесь–вода, наклонная граница

ВВЕДЕНИЕ

Пузырьковая жидкость по своим акустическим свойствам является уникальной средой [1, 2]. В частности, завесу из смеси жидкости с газовыми пузырьками можно использовать в качестве защитного слоя для подводных объектов от воздействия ударных волн, для “маскировки” при гидролокации, а также в качестве подводного звукового канала [3]. Особенности акустических свойств пузырьковой жидкости позволяют определять размеры и структуру пузырьковых “облаков”, образовавшихся при выбросах газа со дна водоема [4].

Особенности отражения и преломления акустических волн при прямом падении на границу “чистой” жидкости и жидкости с пузырьками газа изучались в [5, 6], при косом падении – в работах [7, 8]. В работе [7] на основе анализа полученных аналитических решений установлено, что в случае падения акустической волны на границу раздела со стороны пузырьковой жидкости существует критический угол падения, зависящий от частоты и параметров дисперсной системы, после превышения которого волна полностью отражается от границы. Математическая модель, описывающая наклонное падение акустической волны на границу двухфазной среды, а также на слой газокапельной смеси или пузырьковой жидкости конечной толщины, представлена в работе [8]. Для случая падения низкочастотной акустической волны на границу раздела “чистого” газа и газовзвеси, а также на границу “чистой” и пузырьковой жидкости, установлены основные закономерности отражения и прохождения волны.

В данной работе исследуется динамика волн давления в двумерной области при прохождении через границу пузырьковой и чистой жидкости в случае, когда эта граница расположена под углом к направлению распространения волн. Отметим, что изучению динамики двумерных волн в области, содержащей пузырьковые зоны, посвящены работы [9, 10].

ОСНОВНЫЕ УРАВНЕНИЯ

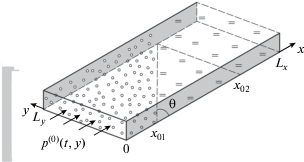
Рассмотрим плоский канал, заполненный пузырьковой (газонасыщенной) и чистой жидкостью с границей раздела этих сред, расположенной под углом по длине канала (рис. 1).

Рис. 1.

Плоский канал с расположенной под углом θ границей пузырьковой и чистой жидкости.

Для описания волнового движения запишем систему макроскопических уравнений для масс, числа пузырьков, импульсов и давления в пузырьках, принимая общие допущения для пузырьковых жидкостей [9, 10]:

(1)

$\begin{gathered} \frac{{d{{\rho }_{i}}}}{{dt}} + {{\rho }_{i}}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right) = 0\,\,\,\,(i = l,g), \\ \frac{{dn}}{{dt}} + n\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right) = 0,\,\,\,\,\rho \frac{{du}}{{dt}} + \frac{{\partial {{p}_{l}}}}{{\partial x}} = 0, \\ \rho \frac{{dv}}{{dt}} + \frac{{\partial {{p}_{l}}}}{{\partial y}} = 0,\,\,\,\,\rho = {{\rho }_{g}} + {{\rho }_{l}}, \\ \left( {\frac{d}{{dt}} = \frac{\partial }{{\partial t}} + u\frac{\partial }{{\partial x}} + v\frac{\partial }{{\partial y}}} \right),\,\,\,\,{{\alpha }_{l}} + {{\alpha }_{g}} = 1, \\ {{\rho }_{i}} = \rho _{i}^{0}{{\alpha }_{i}},\,\,\,\,{{\alpha }_{g}} = \frac{4}{3}\pi n{{a}^{3}}, \\ \end{gathered} $

где $\rho _{i}^{0}$, α_i, p_l, n, a – соответственно плотность, объемное содержание i-й фазы, давление несущей жидкости, число и радиус пузырьков, u и $v$ – проекции скорости на оси координат x и y соответственно. Нижними индексами i = l, g отмечены параметры жидкой и газовой фаз.

При описании радиального движения будем полагать, что скорость радиального движения w состоит из двух слагаемых:

(2)

$w = {{w}_{R}} + {{w}_{A}},$

где w_R описывается уравнением Рэлея–Ламба:

(3)

$a\frac{{d{{w}_{R}}}}{{dt}} + \frac{3}{2}w_{R}^{2} + 4{{\nu }_{l}}\frac{{{{w}_{R}}}}{a} = \frac{{{{p}_{g}} - {{p}_{l}}}}{{\rho _{l}^{0}}}.$

Добавка w_A определяется из решения задачи о сферической разгрузке на сфере радиуса a в несущей жидкости в акустическом приближении:

(4)

${{w}_{A}} = \frac{{{{p}_{g}} - {{p}_{l}}}}{{\rho _{l}^{0}{{C}_{l}}\alpha _{g}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}.$

Уравнение для давления внутри пузырьков с учетом однородности давления записывается в виде [1]:

(5)

$\frac{{d{{p}_{g}}}}{{dt}} = - \frac{{3\gamma {{p}_{g}}}}{a}w - \frac{{3\left( {\gamma - 1} \right)}}{a}q,$

где γ – показатель адиабаты для газа, q – интенсивность теплообмена или тепловой поток от жидкости к газу, отнесенный к единице площади межфазной поверхности. Интенсивность межфазного теплообмена примем в виде [1]:

(6)

$q = \frac{{{{\lambda }_{g}}{\text{Nu}}\left( {{{T}_{g}} - {{T}_{0}}} \right)}}{{2a}},$

где T₀= const – температура жидкости, Nu – число Нуссельта. При описании число Нуссельта задается в виде:

(7)

${\text{Nu}} = \left\{ \begin{gathered} \sqrt {{\text{Pe}}} ,\,\,{\text{Pe}} \geqslant 100, \hfill \\ \,\,\,\,\,10,\,\,{\text{Pe}} < 100. \hfill \\ \end{gathered} \right.$

Для числа Пекле примем выражение:

(8)

${\text{Pe}} = 12(\gamma - 1)\frac{{{{T}_{0}}}}{{\left| {{{T}_{g}} - {{T}_{0}}} \right|}}\frac{{a\left| w \right|}}{{{{\kappa }_{g}}}},$

где $\kappa $_g = λ_g/c_gρ_g0, λ_g, c_g – коэффициенты температуропроводности и теплопроводности, теплоемкость газа соответственно.

Уравнение состояния для несущей фазы примем в акустическом приближении:

(9)

${{p}_{l}} = {{p}_{0}} + C_{l}^{2}(\rho _{l}^{0} - \rho _{{l0}}^{0}),$

где нижний индекс 0 относится к исходному, невозмущенному состоянию, С_l – скорость звука в чистой жидкости.

Считая газ калорически совершенным, запишем уравнение Клайперона–Менделеева:

(10)

${{p}_{g}} = \rho _{g}^{0}R{{T}_{g}},$

где R – газовая постоянная.

Для численного анализа задачи о распространении волн давления в двумерной области, содержащей пузырьковую зону, удобнее пользоваться системой уравнений (1)–(10), записанной в лагранжевых координатах [11]. Это, в частности, связано с тем, что в лагранжевых координатах первоначальные границы неоднородностей остаются неподвижными.

Приведем систему уравнений в лагранжевых координатах:

(11)

$\begin{gathered} \frac{{\partial {{p}_{l}}}}{{\partial t}} = \frac{{C_{l}^{2}\rho _{l}^{0}}}{{(1 - {{\alpha }_{g}})}}\left[ {\frac{{3{{\alpha }_{g}}}}{a}w - \left( {\frac{{{{\alpha }_{g}}}}{J} + \frac{{{{\rho }_{{l0}}}}}{{{{J}^{2}}\rho _{l}^{0}}}} \right)\frac{{\partial J}}{{\partial t}}} \right], \\ \frac{{\partial {{\alpha }_{g}}}}{{\partial t}} = \frac{{3{{\alpha }_{g}}}}{a}w - \frac{{{{\alpha }_{g}}}}{J}\frac{{\partial J}}{{\partial t}}, \\ \frac{{\partial u}}{{\partial t}} = - \frac{1}{{J\rho }}\left( {\frac{{\partial {{p}_{l}}}}{{\partial {{x}_{0}}}}\frac{{\partial y}}{{\partial {{y}_{0}}}} - \frac{{\partial {{p}_{l}}}}{{\partial {{y}_{0}}}}\frac{{\partial y}}{{\partial {{x}_{0}}}}} \right),\,\,\,\,\frac{{\partial x}}{{\partial t}} = u, \\ \frac{{\partial v}}{{\partial t}} = - \frac{1}{{J\rho }}\left( {\frac{{\partial {{p}_{l}}}}{{\partial {{y}_{0}}}}\frac{{\partial x}}{{\partial {{x}_{0}}}} - \frac{{\partial {{p}_{l}}}}{{\partial {{x}_{0}}}}\frac{{\partial x}}{{\partial {{y}_{0}}}}} \right),\,\,\,\,\frac{{\partial y}}{{\partial t}} = v, \\ \frac{{\partial {{p}_{g}}}}{{\partial t}} = - \frac{{3\gamma {{p}_{g}}}}{a}w - \frac{{3(\gamma - 1)}}{{{{a}_{0}}}}q,\,\,\,\,\frac{{\partial a}}{{\partial t}} = w = {{w}_{R}} + {{w}_{A}}, \\ \frac{{\partial {{w}_{R}}}}{{\partial t}} = \left[ {\frac{{{{p}_{g}} - {{p}_{l}}}}{{\rho _{l}^{0}}} - \frac{3}{2}w_{R}^{2} - 4{{\nu }_{l}}\frac{{{{w}_{R}}}}{a}} \right]\frac{1}{a},\,\,\,\,{{w}_{A}} = \frac{{{{p}_{g}} - {{p}_{l}}}}{{\rho _{l}^{0}{{C}_{l}}\alpha _{g}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}, \\ q = \frac{{{{\lambda }_{g}}{\text{Nu}}\left( {{{T}_{g}} - {{T}_{0}}} \right)}}{{2a}},\,\,\,\,{\text{Nu}} = \left\{ \begin{gathered} \sqrt {{\text{Pe}}} ,\,\,\,\,{\text{Pe}} \geqslant 100, \hfill \\ 10,\,\,\,\,\,\,\,\,{\text{Pe}} < 100, \hfill \\ \end{gathered} \right. \\ {\text{Pe}} = 12(\gamma - 1)\frac{{{{T}_{0}}}}{{\left| {{{T}_{g}} - {{T}_{0}}} \right|}}\frac{{a\left| w \right|}}{{{{\kappa }_{g}}}},\,\,\,\,J = \frac{{\partial x}}{{\partial {{x}_{0}}}}\frac{{\partial y}}{{\partial {{y}_{0}}}} - \frac{{\partial x}}{{\partial {{y}_{0}}}}\frac{{\partial y}}{{\partial {{x}_{0}}}}, \\ \frac{{\partial J}}{{\partial t}} = \frac{{\partial u}}{{\partial {{x}_{0}}}}\frac{{\partial y}}{{\partial {{y}_{0}}}} - \frac{{\partial u}}{{\partial {{y}_{0}}}}\frac{{\partial y}}{{\partial {{x}_{0}}}} + \frac{{\partial x}}{{\partial {{x}_{0}}}}\frac{{\partial \upsilon }}{{\partial {{y}_{0}}}} - \frac{{\partial x}}{{\partial {{y}_{0}}}}\frac{{\partial v}}{{\partial {{x}_{0}}}}. \\ \end{gathered} $

Cистема уравнений (11) решается численно по явной схеме [11].

НАЧАЛЬНЫЕ И ГРАНИЧНЫЕ УСЛОВИЯ

Запишем условия при t = 0 для исходного состояния системы, состоящей из областей однородной водовоздушной смеси и воды в канале, разделенных границей с наклоном:

$\begin{gathered} u = v = 0,\,\,\,\,\,{{p}_{l}} = {{p}_{0}},\,\,\,\,\,{{p}_{g}} = {{p}_{0}},\,\,\,\,\,a = {{a}_{0}}, \\ w = 0,\,\,\,\,{{T}_{g}} = {{T}_{0}},\,\,\,\,\rho = \rho _{{l0}}^{0}\left( {1 - {{\alpha }_{{g0}}}} \right), \\ \end{gathered} $

$\begin{gathered} {{\alpha }_{g}} = \left\{ \begin{gathered} {{\alpha }_{{g0}}},\,\,\,\,\left( {{{x}_{0}},{{y}_{0}}} \right) \in {{\Omega }_{1}}, \\ 0,\,\,\,\,\left( {{{x}_{0}},{{y}_{0}}} \right) \notin {{\Omega }_{1}}, \\ \end{gathered} \right. \hfill \\ {{\Omega }_{1}} = \left\{ \begin{gathered} 0 \leqslant {{y}_{0}} \leqslant {{L}_{y}}, \hfill \\ 0 \leqslant {{x}_{0}} \leqslant {{x}_{{01}}} + \frac{{{{y}_{0}}}}{{{{L}_{y}}}}\left( {{{x}_{{02}}} - {{x}_{{01}}}} \right). \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $

Инициирующее возмущение давления на границе пузырьковой жидкости (x₀ = 0) зададим в виде “ступеньки”. Соответствующее граничное условие запишется в виде:

$p\left( {t,{{y}_{0}}} \right) = {{p}_{0}} + \Delta {{p}_{0}}\,\,\,\,{\text{при}}\,\,\,\,{{x}_{0}} = 0.$

На границах y₀ = 0 и y₀ = L_y расчетной области приняты условия как на жесткой стенке, т.е. равенство нулю нормальной компоненты скорости. На границе x₀ = L_x задается неотражающее граничное условие на основе импедансного соотношения [12]. Схематическая постановка задачи представлена на рис. 1.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

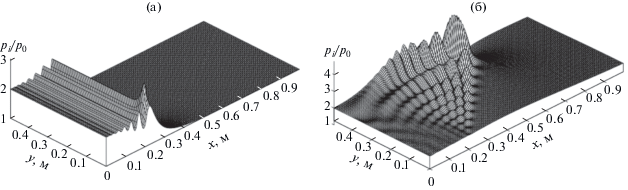
На рис. 2 представлено распределение давления в разные моменты времени. Картинки 2а и 2б соответствуют моментам времени 1.5 и 3.5 мс. Известно [3], что при определенных параметрах пузырьковой смеси акустическое сопротивление пузырьковой жидкости может быть намного меньше этого же физического параметра для чистой жидкости. Например, для представленного на рис. 2 случая отношение соответствующих удельных сопротивлений составляет около 7.5. Таким образом, отражение от границы водовоздушная смесь‑вода для волн, падающих на эту границу со стороны водовоздушной смеси, аналогично отражению от жесткой стенки. Поэтому при отражении волны от такой границы происходит увеличение амплитуды. Видно, что в момент времени 1.5 мс волна, распространяющаяся в зоне, заполненной водовоздушной смесью, имеет осцилляционную структуру. Видно также, что происходит преломление волны в область чистой жидкости, и при этом происходит увеличение амплитуды волны. Отметим, что в дальнейшем волна, отраженная от границы водовоздушная смесь–вода, распространяется в области водовоздушной смеси. Таким образом, после отражения волны от границы, разделяющей области водовоздушной смеси и воды, в области смеси распространяются две волны: отраженная и первоначальная, которая инициирована повышением давления на границе x₀ = 0. Тогда в каждой точке результирующее колебание представляет собой сумму колебаний, соответствующих каждой из складывающихся волн, т.е. происходит интерференция волн. Именно такая интерференционная картина представлена на рис. 2б. Видно, что из-за наложения падающей и отраженной волн вдоль границы, разделяющей области водовоздушной смеси и воды, происходит формирование пульсационного профиля давления с амплитудой лидирующего всплеска, намного превышающей амплитуду первоначального сигнала. Так как граница расположена под углом, то амплитуда результирующей волны при распространении вдоль границы будет увеличиваться, т.е. будет происходить фокусировка волны.

Рис. 2.

Эпюры давления (а) – в момент времени 1.5 мс, (б) – 3.5 мс. Параметры несущей фазы (воды): $\rho _{l}^{0}$ = 1000 кг/м³, v_l = 10^–6 м²/с, c_l = 4.2 кДж/(кг К), λ_l = 0.59 Вт/(м К), С_l = 1500 м/с, Т₀ = 293 К; газовой фазы (воздух): α_g0 = 0.001, а = 1.0 мм, $\rho _{g}^{0}$ = 1.2 кг/м³, λ_g = 2.59 × 10^–2 Вт/(м К), γ = 1.4, c_g = 1.005 кДж/(кг К). Остальные параметры расчета: L_x = = 1.0 м, L_y = 0.5 м, x₀₁ = 0.2 м, x₀₂ = 0.7 м, p₀ = 0.1 МПа, Δp₀ = 0.1 МПа.

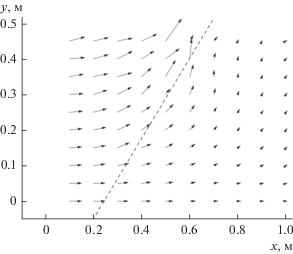
На рис. 3 представлено поле скоростей движения среды в момент времени 3.5 мс для случая, представленного на рис. 2. Анализ поля течения показывает, что формируется движение среды, направленное вдоль границы, разделяющей области однофазной и многофазной сред.

Рис. 3.

Поле скоростей в момент времени 3.5 мс.

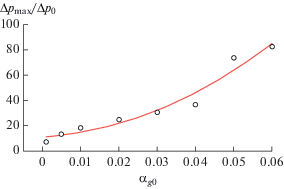
После того как результирующая волна, распространяющаяся вдоль прямой раздела, доходит до границы y₀ = L_y, где ставятся условия как на жесткой стенке, т.е. нормальная компонента скорости равна нулю, происходит отражение волны. Исследуем зависимость максимального значения амплитуды давления на границе y₀ = L_y от различных параметров задачи. Очевидно, максимальное значение давления будет локализовано около точки (x₀₂, L_y). На рис. 4 представлена зависимость максимального значения амплитуды давления на стенке y₀ = L_y от объемного содержания пузырьков. Анализ влияния удельной доли газовой фазы в области газожидкостной среды на амплитуду давления показал, что с увеличением α_g0 амплитуда результирующей волны на стенке растет (рис. 4) и может быть аппроксимирована зависимостью:

$\frac{{\Delta {{p}_{{\max }}}}}{{\Delta {{p}_{0}}}} = 10.79 + 201.7{{{\alpha }}_{{g0}}} + 17\,301.8{\alpha }_{{g0}}^{2},$

которая получена при сохранении остальных параметров, использованных в расчетах, представленных на рис. 2, 3 .

Рис. 4.

Зависимость максимальной амплитуды воздействия на стенку результирующей волны от объемного содержания газа. Все остальные параметры такие же, как на рис. 2.

На рис. 5 представлена зависимость максимальной амплитуды давления на стенке y₀ = L_y, отнесенной к начальной амплитуде инициирующего давления, от угла θ между границей области водовоздушной смеси и воды и нижней границей расчетной области y₀ = 0. Видно, что эта зависимость носит немонотонный характер и может быть аппроксимирована следующим выражением:

$\frac{{\Delta {{p}_{{\max }}}}}{{\Delta {{p}_{0}}}} = 8.37 + 0.51{\theta } - 0.0066{{{\theta }}^{2}}.$

Рис. 5.

Влияние угла наклона границы между водовоздушной средой и водой на максимальную амплитуду воздействия на стенку результирующей волны давления. Параметры расчета такие же, как на рис. 2.

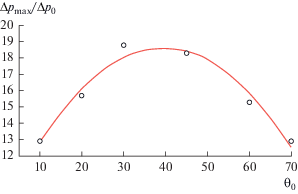
Из рис. 5 следует, что максимальная амплитуда соответствует значению угла приблизительно 40 градусов. Отметим, что при θ = 0° вся область будет заполнена пузырьковой смесью и очевидно, что фокусировки волны в данном случае не будет. При θ = 90° преломление волны давления на границе, разделяющей области водовоздушной смеси и воды, будет сопровождаться увеличением амплитуды, связанным только с переходом волны из акустический более мягкой среды в акустический более жесткую, но при этом не происходит наложения волн, описанного выше. Таким образом, в интервале 0° < θ < 90° существует значение угла, при котором происходит максимальное увеличение амплитуды давления на стенке.

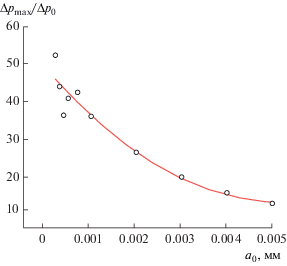
Зависимость максимальной амплитуды давления на стенке от начального радиуса пузырьков представлена на рис. 6. Из рис. 6 видно, что с увеличением радиуса пузырьков максимальная амплитуда воздействия на стенку уменьшается. Эта зависимость может быть аппроксимирована следующим соотношением:

$\frac{{\Delta {{p}_{{\max }}}}}{{\Delta {{p}_{0}}}} = 48.65 - 14\,117.9{{a}_{0}} + 1.36a_{0}^{2}.$

Рис. 6.

Зависимость максимальной амплитуды воздействия на стенку результирующей волны от радиуса пузырьков. Все остальные параметры такие же, как на рис. 2.

ЗАКЛЮЧЕНИЕ

Исследована динамика волн давления в двумерной области при переходе границы между пузырьковой и “чистой” жидкостью в случае, когда эта граница расположена под углом к направлению распространения волн. Показано, что наличие наклонной границы, разделяющей области водовоздушной смеси и воды, приводит к интерференции волн в области, занятой смесью. Установлено, что при увеличении объемного содержания и уменьшении радиуса пузырьков максимальное значение амплитуды давления результирующей волны на стенке увеличивается. Обнаружено, что зависимость максимальной амплитуды давления на стенке результирующей волны при фокусировке на пузырьковом клине зависит немонотонно от угла наклона границы разделяющей области водовоздушной смеси и воды.

Работа выполнена в рамках государственного задания в сфере научной деятельности № FEUR-2020-0004 “Решение актуальных задач и исследование процессов в нефтехимических производствах, сопровождающихся течениями многофазных сред”.

Список литературы

Нигматулин Р.И. Динамика многофазных сред. Ч. 1. М.: Наука, 1987. 464 с.
Накоряков В.Е., Покусаев Б.Г., Шрейбер И.Р. Волновая динамика газо– и парожидкостных сред. М.: Энергоатомиздат, 1990. 248 с.
Shagapov V.Sh., Gimaltdinov I.K., Khabeev N.S., Bailey S.S. Acoustic waves in a liquid with a bubble screen // Shock Waves. 2003. T. 13. № 1. C. 49–56.
Диденкулов И.Н., Кустов А.М., Мартьянов А.И., Прончатов-Рубцов Н.В. Акустическая диагностика пузырьковых объектов в жидкости // Акуст. журн. 2011. Т. 57. № 2. С. 246–251.
Karpov S., Prosperetti A., Ostrovsky L. Nonlinear wave interactions in bubble layers // J. Acoust. Soc. Am. 2003. V. 113(3). P. 1304–1316.
Baranowska A. Theoretical studies of nonlinear generation efficiency in a bubble layer // Archives of Acoustics. 2012. V. 37. P. 287–294.
Шагапов В.Ш., Сарапулова В.В. Особенности преломления и отражения звука на границе пузырьковой жидкости // Акуст. журн. 2015. Т. 61. № 1. С. 40–48.
Губайдуллин Д.А., Федоров Ю.В. Особенности отражения акустических волн от границы или слоя двухфазной среды // Акуст. журн. 2018. Т. 64. № 2. С. 162–173.
Галимзянов М.Н., Гималтдинов И.К., Шагапов В.Ш. Двумерные волны давления в жидкости, содержащей пузырьки // Известия РАН. Механика жидкости и газа. 2002. № 2. С. 139–147.
Нигматулин Р.И., Шагапов В.Ш., Гималтдинов И.К., Галимзянов М.Н. Двумерные волны давления в жидкости, содержащей пузырьковые зоны // Докл. Акад. наук. 2001. Т. 378. № 6. С. 763–766.
Самарский А.А., Попов Ю.П. Разностные задачи газовой динамики М.: Наука, 1980. 352 с.
Ильгамов М.А., Гильманов А.Н. Неотражающие условия на границах расчетной области. М.: ФИЗМАТЛИТ, 2003. 240 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал