Акустический журнал, 2020, T. 66, № 4, стр. 357-365

ВВЕДЕНИЕ

Резино-жидкостный резонатор (РЖР), показанный в разрезе на рис. 1, включает в себя: полость 1 в резине 2; узкое горло 3; жидкость 4, заполняющую полость и горло; воздушную камеру 5 за горлом. Конструктивные элементы резонатора могут иметь произвольные формы. Необходима лишь малость всех его размеров в сравнении с длиной звуковой волны сжатия в резине, чтобы резонатор можно было считать сосредоточенным. Для удобства расчетов примем полость 1 сферической радиуса R, горло 3 – цилиндрическим радиуса a и заполненным жидкостью 4 на высоту h. Воздушная камера 5 произвольной формы имеет объем V₀.

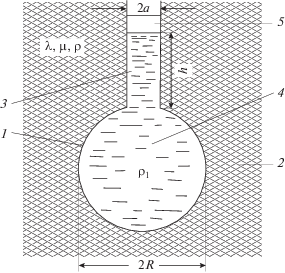
По принципу действия РЖР похож на воздушный резонатор Гельмгольца [1, с. 370], а также на водно-воздушный резонатор, предложенный В.С. Григорьевым и исследованный В.И. Сорокиным [2]. Общее у всех этих резонаторов – использование инерционных свойств жидкости в узком горле. Отличием РЖР является его выполнение в вязкоупругой “водоподобной” [1, с. 482] среде (резина, мягкие пластмассы, смолы, битумы и т.п.), в которой сосредоточены его упругость и основные потери. Таким образом, прототипами РЖР служат полость в резине и резонатор Гельмгольца.

ВЫВОД УРАВНЕНИЯ ДВИЖЕНИЯ РЕЗОНАТОРА

Теория сферической полости в резине была разработана М.А. Исаковичем, а затем Д.В. Сивухиным [3]. Здесь принят (по совету Ю.М. Сухаревского) иной подход, основанный на применении принципа наименьшего действия Гамильтона–Остроградского [4, с. 10].

Из него следует уравнение движения системы в виде уравнения Лагранжа, которое в случае единственной обобщенной координаты x(t) имеет вид

где $L = T - E$ – функция Лагранжа; T и E – кинетическая и потенциальная энергии системы соответственно; F(t) – внешняя обобщенная сила, действующая на систему.

Будем считать резину 2 однородной, изотропной, упругой средой, имеющей первый коэффициент Ламе λ, модуль сдвига μ и плотность ρ, а жидкость 4 в резонаторе – несжимаемой, вязкой, с плотностью ρ₁ и кинематической вязкостью ν₁. Стенки горла 3 и камеры 5 полагаем жесткими.

Когда длина волны падающего звука много больше размеров резонатора, он испытывает в основном переменное давление всестороннего сжатия, его полость совершает сферически-симметричные пульсационные колебания и излучает сферическую волну. Мы примем, что узкое горло и малая воздушная камера практически не нарушают сферической симметрии деформаций полости (к тому же, в ней они могут быть и размещены). Ниже учтены только объемные пульсации полости.

Вектор смещения в сферической волне чисто радиальный:

Он определяется волновым уравнением [5, с. 126]

решение которого для расходящейся волны при гармонических колебаниях $U(r,t) = U(r){{e}^{{ - i\omega t}}}$ имеет вид: где $U(R)$ – комплексная амплитуда смещения стенки полости 1; ${{k}_{l}} = \frac{\omega }{{{{c}_{l}}}}$ – волновое число; ${{c}_{l}} = \sqrt {\frac{{{\lambda } + 2{\mu }}}{{\rho }}} $ – скорость распространения в резине продольной звуковой волны.

Формула (2) при ${{k}_{l}}r \ll 1$ дает для произвольных радиальных смещений зависимость

т.е. резина с любым модулем сдвига здесь подобна несжимаемой жидкости.

Полная кинетическая энергия системы складывается из кинетических энергий резины и жидкости, заполняющей полость резонатора объемом V и его горло:

Здесь U₁ – смещение в жидкости; $V{\kern 1pt} '$ – малый объем жидкости, примыкающий к устью горла, где формируется присоединенная масса с кинетической энергией $T{\kern 1pt} '$, учет которой эквивалентен увеличению высоты h столбика жидкости в горле на некоторую величину Δh. Последнее слагаемое в (4) – это кинетическая энергия столбика жидкости, где, в силу несжимаемости жидкости,

– смещение столбика. Используя (3), (5) и пренебрегая вторым слагаемым в (4) (если считать 12hR $ \gg $ a²), найдем: где введено обозначение:

Эффективное значение высоты жидкости в горле можно оценить:

где функция Фока [6, с. 155].

Потенциальная энергия E системы складывается из упругой сдвиговой энергии E_μ резины 2 вблизи полости 1 и упругой энергии E_g воздуха, заключенного в камере 5 (см. рис. 1). Упругая энергия сдвига единицы объема резины равна [5, § 4]

где при радиальной деформации резины в сферических координатах [5, с. 12]

Учитывая (3), (9), (10), найдем:

Потенциальная энергия воздуха, заключенного в объеме V₀, равна

где ${{P}_{g}}(t)$ – звуковое давления в газе, ξ(t) – смещение (5) жидкости в горле (положительное значение соответствует смещению внутрь воздушного объема).

Колебания газа в воздушной камере 5 представляют собой политропический процесс, близкий к адиабатическому, а состояние газа приближенно описывается уравнением $P{{V}^{q}} = {\text{const}},$ где q ≤ γ, γ = c_p/c_v – отношение теплоемкостей газа. Поэтому

где ${{P}_{0}}$ – статическое давление в газе. Подставив давление ${{P}_{g}}(t)$ в (12), получим: где $V = \frac{4}{3}{\pi }{{R}^{3}}$ – объем полости 1. Объединяя (11) и (13), найдем полную потенциальную энергию системы: где введено обозначение

Используя найденные значения кинетической T(t) (6) и потенциальной E(t) (14) энергий, составим функцию Лагранжа системы:

где α и β представлены формулами (7) и (15). Обобщенной координатой в (16) служит смещение U(R,t) стенки полости 1 резонатора. Подставим функцию L в уравнение Лагранжа (1), где обобщенной силой следует считать $ - 4\pi {{R}^{2}}P(t),$ $P(t)$ – звуковое давление на резонатор. В результате получим уравнение движения системы:

ДИССИПАЦИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ В РЕЗОНАТОРЕ

Потери в резине 2 и в вязкой жидкости 4 обусловлены поглощением энергии в этих материалах за счет внутреннего трения. Поглощение энергии в воздушной камере 5 происходит из-за неполной адиабатичности процесса колебаний газа. Имеются еще потери на излучение сферической волны, рассеянной пульсирующей полостью 1 резонатора. Так как окружающую резонатор резину и заполняющую его жидкость можно считать несжимаемыми, то пренебрежем поглощением энергии в этих средах за счет их теплопроводностей и вторых вязкостей.

Для описания потерь используем обобщенную диссипативную функцию Рэлея [4, с. 102]. В нашем случае она имеет вид:

где величина X = const обусловлена характером преобладающих механических потерь. Функция $\Psi (t)$ определяет интенсивность диссипации энергии в системе:

Обобщенная диссипативная сила по определению равна

Ее следует добавить в правую часть уравнения (1). Тогда уравнениe движения (17) примет вид:

Будем интересоваться гармоническими вынужденными пульсациями резонатора, когда смещение стенки полости 1 можно представить в виде $U(R,t) = U(R){{e}^{{ - i\omega t}}},$ а звуковое давление на резонатор как $P(t) = P{{e}^{{ - i\omega t}}},$ где $U(R) = U$ и P – комплексные амплитуды величин. Для этого случая из уравнения (20), учитывая (7) и (15), найдем:

где – собственная круговая частота резонатора; – затухание резонатора – величина, обратная его добротности Q = $\frac{1}{\delta }$. Значение $\delta $ будет найдено при рассмотрении механизмов диссипации звуковой энергии в резонаторе.

Для вычисления параметра, определяющего поглощение X, далее используются известные выражения для комплексных упругих параметров резины, плотности жидкости в горле, показателя политропы газа [1, с. 405]. В формуле (21) следует заменить материальные параметры μ, ρ₁, q их комплексными значениями, мнимые части которых содержат информацию о соответствующих механизмах поглощения звуковой энергии. Результат такой замены будет тот же, что и при использовании диссипативной функции (18).

Основные потери в резонаторе – это вязкое поглощение энергии в резине, окружающей полость 1. Модули упругости резины при гармонических колебаниях являются принципиально комплексными и частотно-зависимыми величинами. Более того, их вещественные и мнимые части взаимозависимы, поскольку связаны дисперсионными соотношениями, отражающими принцип причинности [7, §123, 8, §77]. Важнейшим для резины является комплексный динамический модуль сдвига

где $\mu (\omega )$ – модуль сдвига, $\eta (\omega )$ – коэффициент сдвиговых потерь, причем где K – модуль всестороннего сжатия. Модули сдвига разных резин отличаются друг от друга в десятки и сотни раз и лежат в пределах ${\mu }({\omega }) = {{10}^{5}}{{...10}^{8}}$ Па. Коэффициенты сдвиговых потерь резин обычно порядка ${\eta }({\omega }) = 0.1...1.0.$ Модули всестороннего сжатия резин примерно такие же, как у воды, и в диапазоне звуковых и ультразвуковых частот практически от частоты не зависят, т.е. они вещественны. Соотношения (24) и (25), по существу, служат определением вязкоупругих “практически несжимаемых”, “водоподобных” веществ [1, с. 446].

Усредненный по сечению удельный импеданс вязкой жидкости в трубе радиуса a и длины h был найден Крендаллом [9, с. 155], [6. с. 166]:

где – волновое число вязкой волны в жидкости; ν₁ – кинематическая вязкость жидкости; J₀, J₂ – бесселевы функции. В случае идеальной жидкости ${{Z}_{h}} = - i\omega {{\rho }_{1}}h.$ Сравнивая это с (26), найдем комплексную плотность вязкой жидкости в горле 3:

В частных случаях малых и больших длин вязких волн по сравнению с шириной горла выражение (28) упрощается. Так, при $\left| {\kappa a} \right| > 10$

Видим, что значение комплексной плотности вязкой жидкости здесь мало отличается от ее значения для идеальной жидкости. Поглощение энергии в этом случае происходит в тонком слое у стенок горла. При $\left| {\kappa a} \right| < 2$ из выражения (28) следует:

Теперь энергия поглощается по всему сечению горла (как в течении Пуазейля), а величина эффективной плотности за счет вязкости на 1/3 больше, чем в случае идеальной жидкости.

Тепловые потери в газе возможны лишь в случае, когда соседние участки газа имеют разную температуру и могут обмениваться теплом. Уравнение переноса тепла в идеальном (подчиняющемся уравнению Менделеева–Клапейрона) невязком газе отличается от случая несжимаемой жидкости [10, с. 277, (50,1)] дополнительным слагаемым:

где параметры газа – плотность ρ_g, удельную теплоемкость c_p, коэффициент теплопроводности κ_g – можно считать постоянными; T – температура в газе.

Наиболее интересен случай, когда длина тепловой волны много меньше линейных размеров камеры. Тогда каждый элемент dS поверхности камеры S можно считать плоским и рассматривать независимо от других, что позволяет рассчитать потери в камере произвольной формы. Положим T = T₀ + dT = T₀ +T(x)e^–iωt, P = P₀ + dP = P₀ + P_ge^–iωt, где x – расстояние от dS вглубь камеры. Из (30) найдем:

где ${{\chi }_{g}} = \frac{{{{\kappa }_{g}}}}{{{{\rho }_{g}}{{c}_{p}}}}$ – коэффициент температуропроводности газа. Считая стенки камеры абсолютно теплопроводящими, когда T(0) = 0, получим решение уравнения (31):

Выделим малый объем v газа у стенки на расстоянии x от нее. Пусть dv(x,t) – изменение этого объема при изменении давления на dP и температуры на dT. Дифференцируя уравнение состояния, получим: dPv + P₀dv = m_g(c_p – с_v)dT, где m_g – масса газа. Подставив сюда dT, найдем:

Интегрируя по всему объему V₀ камеры, получим дифференциальное уравнение состояния газа при наличии тепловых потерь:

Обозначим:

Тогда (32) примет вид:

Из уравнения (34) следует, что для учета тепловых потерь в камере 5 резонатора надо в формуле (21) заменить показатель политропы q его комплексным значением

Потери на излучение найдем, положив в (21), (23) δ = δ_rad, X = X_rad, где

Согласно [1, с. 480] и (18), (19) мощность сферической волны, излучаемая резонатором в окружающую среду, равна:

Найденное отсюда значение ${{X}_{{{\text{rad}}}}}$ подставим в (36) и получим:

Из формул (21), (22) с учетом (37) следует:

Заменим в (38) μ, q, ρ₁ их комплексными выражениями (24), (35), (28), в формуле (22) используем только вещественные части этих выражений. В результате получим:

где – затухание резонатора, включающее четыре вида потерь механической энергии. Собственная частота резонатора

Здесь учтена инерция вязкой жидкости в горле, несколько изменяющая ее эффективную плотность [10, с. 127]. Поскольку $\delta (\omega )$ играет роль лишь вблизи резонанса, в (41) можно считать ω = ω_p.

Жидкость в горле резонатора можно заменить твердым, например, металлическим поршеньком с плотностью ρ_m, как предложено в книге [14, с. 326, рис. 81 ]. В этом случае в формулах (39)–(42) следует сделать замены:_{$\rho _{1}^{'}(\omega ) \to {{\rho }_{m}},$}

где ${{\eta }_{1}} = {{\rho }_{1}}{{\nu }_{1}}$ – динамическая вязкость жидкости, d – ширина узкой щели между поршнем и стенками горла. Поршень может быть продолжен вглубь полости 1 для увеличения эффективного значения ${{\rho }_{m}}$ и дополнительного снижения частоты ${{{\omega }}_{{\text{p}}}}$.

Для РЖР можно пренебречь тепловыми потерями в камере и потерями на излучение по сравнению с вязкими потерями в резине и в жидкости горла. Поэтому формула (41) упростится. Так, при $\left| {\kappa a} \right| > 10$ согласно (29), (27), (7)

Задачу можно расширить, приняв, что полость 1 резонатора окружена слоем резины 2 конечной толщины s и помещена в другую вязкоупругую водоподобную среду с плотностью ρ₀ и модулем сдвига μ₀. Изменения энергий системы T(t) (6) и E(t) (14) сведутся к заменам в формулах (6) и (14):

Это приведет к таким же заменам в формуле (38), где, однако, в последнем слагаемом знаменателя (поскольку теперь излучение происходит во внешнюю среду с плотностью ρ₀ и волновым числом k_l0) нужны другие замены: ρ → ρ₀, k_l → k_l0. Все указанные замены следует выполнить в итоговых формулах (39)–(42), при этом (41) примет вид:

где

ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА

Как следует из формулы (42), собственная частота РЖР может быть в десятки и сотни раз меньше, чем у пустой полости в резине. Это подтверждает демонстрационный опыт, схема которого показана на рис. 2.

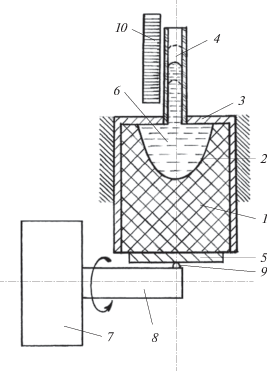
Резиновый цилиндр 1 с полостью 2 плотно вдавлен до упора в стакан 3, в центре которого над полостью 2 имеется отверстие, куда плотно вставлена стеклянная трубка 4, выполняющая роль горла резонатора. Снизу к резине приклеена эбонитовая шайба 5. Полость 2 и частично горло 4 заполнены ртутью 6 (при 20°C ρ₁ = 13.6 × 10³ кг/м³, ν₁ = 1.15 × 10^–7 м²/с). Ртуть выбрана исключительно из-за стремления получить при заданных размерах возможно большее снижение частоты ω_p. К тому же, малая кинематическая вязкость ртути позволяет пренебречь вязкими потерями в горле 4.

В патроне 7 токарного станка зажат стержень 8 с небольшим (~2 мм) боковым выступом 9 на конце. Стакан–держатель 3 жестко закреплен в резцедержателе суппорта станка так, что оси стакана и стержня пересекаются. При вращении патрона 7 выступ 9 периодически бьет по центру шайбы 5 и возбуждает резонатор. При этом полость 2 РЖР пульсирует с частотой оборотов, на что указывают колебания столбика ртути в горле 4. Размах этих колебаний измерялся визуально по миллиметровой шкале 10 с точностью ~ ±0.5 мм. Обороты патрона устанавливались либо дискретно, либо плавно путем торможения патрона куском пенопласта. Контролировались обороты стробоскопом.

На рис. 3 приведены измеренные амплитудно-частотные характеристики РЖР при следующих значениях высоты столбика ртути в горле: h = 58.5, 43, 28, 19 мм. По формуле (8) найдем: Δh = 1.3 мм. При заданных параметрах формула (42) принимает вид:

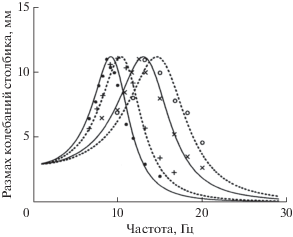
Модуль сдвига резины неизвестен, но может быть оценен с помощью формулы (46) по измерениям. Результаты вполне правдоподобны: (0.820, 0.809, 0.838, 0.804) × 10⁶ Па, разброс небольшой. Среднее значение μ_ср = 0.818 × 10⁶ Па. Значение собственной частоты пустой полости при таком модуле сдвига и ρ = 1200 кг/м³ составляет ${{f}_{{\text{p}}}} = \frac{1}{{{\pi }R}}\sqrt {\frac{{{{{\mu }}_{{{\text{ср}}}}}}}{{\rho }}} $ = 692 Гц. Таким образом, частота резонатора снижена от 47 до 80 раз. Фактически это снижение еще большее, поскольку с частотой зависимость μ(ω) возрастает. Так как согласно (46) ${{f}_{{\text{p}}}}$ ~ a, то уменьшением диаметра горла можно получить дальнейшее снижение собственной частоты РЖР.

ЗАКЛЮЧЕНИЕ

В РЖР объединены свойства нескольких акустических резонаторов: полости в резине, газового пузыря в вязкоупругой среде и в оболочке, пузырька в жидкости, резонаторов Гельмгольца и водно-воздушного. Поэтому известные основные соотношения для этих резонаторов можно получить из общих выражений (39)–(45) для РЖР путем предельных переходов. Так, положив ρ₁ → 0, ν₁ → 0, P₀ → 0, получим для пустой полости в безграничной резине:

Потерями на излучение здесь можно пренебречь, поскольку

Если полость в вязкоупругой среде заполнена газом (например, плавательный пузырь рыбы), то, считая в общих формулах ρ₁ = 0, V₀ = V, найдем:

где $\tilde {\mu }(\omega ) = \mu (\omega )\left[ {1 + \beta (\omega )} \right],$

Эти формулы впервые получены в работе [15]. При малых значениях μ, на глубинах более 200 м 3P₀q $ \gg $ 4μ. Выражение (47) для резонансной частоты радиальных адиабатических (q → γ) колебаний газового пузырька в упругой среде получено также в работе [16].

Значение резонансной частоты объемных колебаний газового пузыря в вязкоупругой оболочке, помещенного в другую вязкоупругую среду, легко найдем из формулы (47) с помощью замен (43):

Для рассматриваемого случая эта формула (дополненная учетом поверхностных натяжений на границах сред) впервые получена в работе [17, (14)].

Собственную частоту резинового “мячика” в воде найдем из (48), положив μ₀ = 0:

откуда при P₀ = 0, s = ∞ следует резонансная частота пустой полости в резине, а при s = 0 – известная формула Минаэрта для газового пузырька в воде. Газовый пузырек в воде соответствует случаю: μ → 0, ρ₁ → 0, V₀ = V, ρ → ρ₀, c_l → c₀. Для него имеем: – формула Минаэрта, где k₀ = ω/c₀; c₀ – скорость звука в воде; ρ₀ – плотность воды. В общем случае для q и δ_T здесь следует использовать формулы Девина [11], [12], [13, с. 146].

Для резонаторов Гельмгольца и водно-воздушного, положив в формулах (39)–(42) μ → 0, ρ₁ = ρ = ρ₀, c_l = c₀, α $ \gg $ 1, где ρ₀ – плотность воздуха (воды), c₀ – скорость звука в воздухе (в воде), и учитывая (5), найдем:

– комплексная амплитуда среднего по сечению горла смещения жидкости;

Согласно Л.Я. Гутину для открытого в среду́ конца горла без фланца (поршень без экрана) можно считать $\tilde {h} = h + \frac{{2a}}{\pi }$ [6, с. 154].

Резино-жидкостные акустические резонаторы могут найти применение в низкочастотных звукогасящих устройствах. Например, с их помощью можно изготовить широкополосное звукопоглощающее покрытие для измерительных гидроакустических бассейнов со звуконепроницаемыми либо имеющими инерционный импеданс стенками. Оно может состоять из совокупности одиночных, настроенных на разные частоты резонаторов в оболочках, точечно размещенных на защищаемой поверхности и разделенных водными промежутками. Последние устраняют упругое взаимодействие резонаторов, что дает возможность увеличить их объемное содержание в поглотителе. Такая конструкция позволит полнее использовать резину или экономить ее расход.

Для резонаторов покрытия оптимальное значение затухания δ(ω_p) ≈ 1. Регулировать величину δ(ω_p) можно подбором вязкости жидкости. Наиболее предпочтительны для РЖР полиметилсилоксановые жидкости (ПМС) с огромным диапазоном вязкостей. Они обладают для данного применения спектром уникальных свойств: не воздействуют на резины; практически не испаряются; имеют аномально низкую (сравнительно с другими маслами) температурную зависимость вязкости; допускают получение жидкости с необходимой вязкостью путем простого смешивания ПМС разных сортов. Возможно также использование РЖР в одиночных избирательных поглотителях звука и вибраций. Малые волновые размеры РЖР этому способствуют.