1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 66, № 4, 2020

Акустический журнал, 2020, T. 66, № 4, стр. 420-436

Оценка влияния внутреннего и вязкого трения на дисперсию и затухание звука в неконсолидированных морских осадках

В. А. Лисютин a, *, О. Р. Ластовенко a

a Севастопольский государственный университет
299053 Севастополь, ул. Университетская 33, Россия

* E-mail: vlisiutin@mail.ru

Поступила в редакцию 04.12.2019
После доработки 10.02.2020
Принята к публикации 24.02.2020

Полный текст (PDF)

Аннотация

Проанализировано влияние внутреннего и вязкого трения на распространение звука в неконсолидированных морских осадках. Приводятся основные положения GS (Grain Shearing) теории межгранулярного трения M. Buckingham’а. Согласно GS теории, осадки рассматриваются как однофазная среда, затухание звука объясняется только внутренним трением, а вязкой диссипацией пренебрегается. Представлена модификация GS теории, заключающаяся в преобразовании ее в двухфазную. Вместо однофазного уравнения состояния применяется уравнение состояния двухфазной среды, выведенное ранее в работе И.А. Чабан. Подстановка этого уравнения состояния в дисперсионное уравнение GS теории приводит к квадратному уравнению, корни которого дают волновые числа двух типов волн – быстрой и медленной волн в неконсолидированной среде с внутренним трением (GS + EC, Grain Shearing + Effective Compressibility). Результаты, даваемые модифицированной теорией, сравниваются с результатами экспериментальных измерений, взятых из открытых источников. Показывается, что существенная дисперсия скорости звука на средних частотах обусловлена консервативным влиянием жидкости, а затухание – совместным диссипативным влиянием внутреннего и вязкого трения. Выявляются типы сред и частотные диапазоны, в которых затухание определяется преимущественно силами внутреннего либо вязкого трения.

Ключевые слова: неконсолидированные морские осадки, дисперсия фазовой скорости, коэффициент затухания, тангенс угла потерь, межгранулярное трение, деформационное упрочнение, вязкое трение

ВВЕДЕНИЕ

Одним из важнейших объектов исследования в акустике мелкого моря являются дно и морские осадки [1–18]. Дно мелкого моря имеет сложную вертикальную структуру, в которой особо можно выделить переходный слой неконсолидированных осадков типа песка, ила, глины, смеси разнообразных обломочных материалов [1]. В переходном слое с ростом глубины и геостатического давления происходит уплотнение осадков, увеличивается физическое взаимодействие между гранулами, вследствие чего возникают значительные вертикальные градиенты акустических характеристик [1, 2].

В неконсолидированных осадках могут распространяться упругие волны двух типов: продольная (компрессионная, p-волна) и поперечная (сдвиговая, s-волна) [1, 2, 15]. Акустическими характеристиками этих волн являются фазовые скорости, коэффициенты затухания и их частотные зависимости.

В акустике мелкого моря в первом приближении сдвиговую волну считают нераспространяющейся (жидкое дно), скорость звука в дне не зависящей от частоты, а коэффициент затухания – прямо пропорциональным частоте ω = 2πf, что позволяет представлять волновое число в дне в виде [1]

(1)
${{k}_{p}} = \frac{\omega }{{{{c}_{p}}}} - i{{\alpha }_{p}} = \frac{\omega }{{{{c}_{p}}}}(1 - i{{\beta }_{p}}),$
где сp – скорость звука; αp – коэффициент затухания, Нп/м; βp – постоянный тангенс угла потерь или постоянная добротность Q, ${{\beta }_{p}} = \frac{{{{\alpha }_{p}}{{c}_{p}}}}{\omega } = \frac{1}{{2Q}}$ (временной множитель в (1) принимается в виде exp(iωt)). Предположение о постоянной добротности дает возможность экстраполировать результаты измерений, выполненных на частотах сотни килогерц, в область низких частот. Такая модель осадков и дна хорошо соответствует основной модели волновода мелкого моря – волноводу Пекериса. Модель Пекериса и в настоящее время используется наиболее часто [3–6], поскольку дно в виде поглощающего полупространства требует минимальных априорных знаний и является осреднением всех слоев вместе с внутренними градиентами [7].

Следующие по сложности модели дна – слоистые, когда с ростом глубины проявляются поперечно-упругие свойства осадков, но их акустические характеристики принимаются независящими от частоты (cp,s = const, βp,s = const) [7–9], и пористо-вязкоупругие [9–13]. В последнем случае частотные зависимости коэффициента затухания и фазовых скоростей волн вычисляются либо в рамках теории Био–Столла [9–11, 13], либо GS или VGS теории M. Buckingham’а [9, 12, 13].

При расчетах звуковых полей на тональной частоте и правильном выборе величины потерь представления дна в виде жидких слоев вполне достаточно [3–7]. Ситуация меняется, когда ставится задача инверсии акустических и физических характеристик дна и требуются расчеты в широкой полосе частот. Здесь правильное отображение частотных зависимостей скорости звука и затухания имеет важное значение [8–14].

В сухих гранулированных средах, как установлено экспериментально, коэффициент затухания (α, дБ/м = 8.69α, Нп/м) оказывается пропорциональным первой степени частоты, αp = αp0 f ε, ε = 1 – показатель затухания (${{\alpha }_{{p0}}} = \frac{{2\pi 8.69{{\beta }_{p}}}}{{{{c}_{p}}}}$ – отнесенный к единице частоты коэффициент затухания, дБ/м/Гц). Измерения в водонасыщенных средах подтверждают пропорциональность коэффициента затухания α ~ ω1 для сред с низкой проницаемостью, но обнаруживают отклонения от закона α ~ ω1 для сред с высокой проницаемостью [15]. Сложная частотная зависимость затухания предполагает как минимум два физических механизма потерь. Основной, присущий как сухим, так и насыщенным средам получил название “внутреннее трение”, второй – вязкая диссипация при движении поровой жидкости относительно гранул. Внутреннее трение дает прямо пропорциональную зависимость, вязкое трение – отклонения от прямой пропорциональности в определенном диапазоне частот [15]. Вязкое трение может проявляться в большей или меньшей степени в зависимости от возможности существования тех или иных течений в пространстве пор.

Наиболее известная теория распространения упругих волн в морских осадках – теория Био–Столла и ее современные модификации [16–18]. В теории Био–Столла осадки рассматриваются как двухфазная среда, в которой зерна минералов консолидированы упругим скелетом, а поровая жидкость подвижна. Затухание объясняется вязкостью флюида и внутренним трением. Для учета внутреннего трения к упругим константам приписывается малая комплексная часть. При этом на частоте согласования соотношение между действительными и мнимыми частями упругих модулей оказывается верным, а на высоких частотах – нарушенным, доминирует вязкое затухание, пропорциональное ω1/2, что противоречит экспериментальным данным. Модификации теории Био–Столла [16–18] сохраняют положение о упругом скелете, развивая взятую из геофизики (обзор в [19]) идею о локальных “сквирт” потоках. Итог – теории EB (Extended Biot) [16, 17] и BIMGS [18], согласно которым упругие модули скелета полагаются зависящими от частоты.

В начале нынешнего века M. Buckingham разработал GS (Grain Shearing) и VGS (Viscous Grain Shearing) теории, объясняющие распространение и затухание упругих волн в осадках межгранулярным трением [20, 21]. Трение придает среде продольную и поперечную жесткость, но и в тоже время вызывает потери энергии. В GS теории осадки рассматриваются как однофазная среда, и вязкие потери не учитываются. Частотная зависимость коэффициента затухания оказывается ~ω1, что соответствует экспериментам только на высоких частотах [20]. В VGS теории вязкое трение “симулируется” подобным жидкости реологическим элементом [21]. Симуляция вязкого трения не позволяет устанавливать связь между акустическими характеристиками деформационных волн и физическими характеристиками среды. Дисперсионные кривые VGS теории показывают хорошее совпадение с экспериментом на средних и высоких частотах в случаях, когда вязкость жидкости невелика.

В настоящей работе предлагается модификация GS теории – преобразование ее в двухфазную с подключением вязкого трения. Проводится сопоставление результатов модифицированной GS теории с некоторыми экспериментальными данными. Выявляются диапазоны частот и типы сред, в которых определяющую роль оказывает либо внутреннее, либо вязкое трение. Представляемая статья является уточнением и развитием работ [22, 23].

1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

1.1. Среда без дисперсии

В самой верхней части переходного слоя морские осадки практически представляют собой суспензию – самые верхние частицы прижаты к нижележащим только собственным весом. Скорость звука в суспензии с пористостью P определяется формулой Вуда [2]:

(2)
${{c}_{0}} = \sqrt {\frac{{{{K}_{0}}}}{{{{\rho }_{0}}}}} ,$
где K0 – объемный модуль упругости среды (суспензии),
(3)
$\frac{1}{{{{K}_{0}}}} = \frac{P}{{{{K}_{f}}}} + \frac{{1 - P}}{{{{K}_{g}}}},$
(4)
${{\rho }_{0}} = P{{\rho }_{f}} + (1--P){{\rho }_{g}}$
– равновесная плотность среды; Kf, Kg, ρf, ρg – модули упругости и плотности жидкости и твердой фазы соответственно; ${{K}_{f}} = {{\rho }_{f}}c_{f}^{2}$, cf – скорость звука в поровой жидкости.

Ф. Гассман предложил идею упругого скелета, консолидирующего упругие зерна. В модели Гассмана скорости распространения продольных cp и поперечных cs волн выражаются формулами [2]:

(5)
${{c}_{{p0}}} = \sqrt {\frac{{K + {4 \mathord{\left/ {\vphantom {4 {3\mu }}} \right. \kern-0em} {3\mu }}}}{{{{\rho }_{0}}}}} ,\,\,\,\,{{c}_{{s0}}} = \sqrt {\frac{\mu }{{{{\rho }_{0}}}}} ,$
где $K = {{K}_{0}} + \frac{{{{K}_{b}}{{{({{K}_{g}} - {{K}_{0}})}}^{2}}}}{{K_{g}^{2} - {{K}_{b}}{{K}_{0}}}}$ – объемный модуль флюидонасыщенной среды [20]; Kb, μ – вещественные объемный и сдвиговый модули упругости скелета. Формулы (5) применимы только на низких частотах, когда скелет и флюид колеблются вместе. Если при возрастании частоты жидкая фаза имеет возможность проскальзывать относительно скелета, возникает дисперсия скорости и диссипация энергии.

Э. Гамильтон [24], предполагая отсутствие дисперсии и взяв за основу уравнения (5), считает объемный и сдвиговый модули комплексными, с не зависящей от частоты добавкой, что дает α ~ ω1. Величины вещественных и мнимых частей вязкоупругих модулей определяются инверсией экспериментальных данных и, в отличие от (5), модули Гамильтона будут соответствовать высокой частоте измерений.

1.2. Основные положения и результаты GS теории

Центральная идея в GS теории – деформационное упрочнение гранул и особый процесс релаксации механического напряжения. Модель частицы – шероховатая сфера, реологическая модель межгранулярного контакта – последовательно соединенные пружина и демпфер, сопротивление которого возрастает в процессе деформации.

Явление деформационного упрочнения, отражающее нелинейные свойства микронеоднородных сред, было отмечено, экспериментально исследовано, подтверждено и качественно объяснено в работах [25–27] наличием дефектов на контактирующих поверхностях, вследствие чего они имеют повышенную мягкость по сравнению с основным минералом гранул. Смешивание мелких и крупных гранул приводит к возрастанию нелинейности среды в целом.

Согласно GS теории, комплексные фазовые скорости ${{\tilde {c}}_{{p,s}}} = \frac{\omega }{{{{k}_{{p,s}}}}}$ продольной и поперечной волн можно представить в виде:

(6)
${{\tilde {c}}_{p}} = \sqrt {\frac{{{{K}_{0}} + \gamma {{{(i\omega {{t}_{0}})}}^{n}}}}{{{{\rho }_{0}}}}} ,\,\,\,\,{{\tilde {c}}_{s}} = \sqrt {\frac{{{{\gamma }_{s}}{{{(i\omega {{t}_{0}})}}^{m}}}}{{{{\rho }_{0}}}}} ,$
где γ, γs – модули композитной и сдвиговой межгранулярной жесткости, Па; n, m – продольный и поперечный показатели деформационного упрочнения (стресс-релаксации), отражающие величину нелинейности среды, 0 < n < 1, 0 < m < 1; t0 = 1 с – константа релаксации, восстанавливающая правильную физическую размерность [20, 21]. Четыре параметра γ, γs, n, m характеризуют межгранулярное взаимодействие на микроуровне, и могут быть определены только путем инверсии экспериментальных данных.

Вещественные скорости cp,s и коэффициенты затухания αp,s могут быть получены из комплексных как ${{c}_{{p,s}}} = {{\left( {\operatorname{Re} (\tilde {c}_{{p,s}}^{{ - 1}})} \right)}^{{ - 1}}},$ ${{\alpha }_{{p,s}}} = - \omega \operatorname{Im} (\tilde {c}_{{p,s}}^{{ - 1}})$, Нп/м.

Результат GS теории – затухание αp ~ ω1 +n/2, слабая дисперсия, что не соответствует некоторым экспериментальным данным на средних частотах.

2. ПОДКЛЮЧЕНИЕ ТЕЧЕНИЙ ФЛЮИДА К GS ТЕОРИИ

2.1. Уравнение состояния двухфазной неконсолидированной среды

В дальнейшем среда предполагается макроскопически однородной, изотропной, безграничной и полностью водонасыщенной.

Как видно из первого уравнения (6), в рамках GS теории неконсолидированная среда составлена из несущей суспензии с добавкой межгранулярного трения. Обобщим первое уравнение (6), предполагая далее заменить уравнение состояния, и, нормируя упругости и жесткости на c0, представим его в виде

(7)
$\tilde {c}_{p}^{2} = c_{0}^{2}\left( {\frac{{{{K}_{u}}}}{{{{\rho }_{0}}c_{0}^{2}}} + \chi D} \right),$
где Ku – искомый ниже объемный модуль упругости среды, $\chi = \frac{\gamma }{{{{\rho }_{0}}c_{0}^{2}}}$ – безразмерный относительный коэффициент межгранулярного трения [20], D = (iωt0)n – дисперсионный член внутреннего трения. Если содержание жидкости в представительном объеме среды постоянно, то Ku = K0.

Положим теперь, что жидкость подвижна относительно гранул. При компрессии среды с межгранулярным трением возможны два типа движения жидкости. Первый тип: жидкость по сквозным порам будет перетекать из области повышенного давления в область пониженного – это “глобальное течение Био”, интенсивность которого прямо связана с проницаемостью среды. Второй тип: флюид, заключенный в щелях между гранулами, будет вытесняться в более емкую часть порового пространства, что соответствует локальным – “сквирт” потокам [16–18]. Интенсивность локальных потоков не имеет прямой связи с проницаемостью среды.

Вычислим сжимаемость двухфазной среды, пренебрегая трением между частицами. Следуя вначале работе [28], рассмотрим плоскую продольную волну p = p0exp(iωt – ikpx), распространяющуюся вдоль оси X, и колеблющиеся в акустическом поле шероховатые гранулы, едва соприкасающиеся друг с другом своими наиболее выступающими и наиболее мягкими частями. Выделим кубический объем Vu среды с размером l, малым по сравнению с длиной волны, но большим по сравнению с сечением пор. Часть жидкости (=ΔVf) будет выжиматься из выделенного объема (=Vu) и сжимаемость среды будет иметь вид:

(8)
$K_{u}^{{ - 1}} = \frac{1}{p}\frac{{\Delta {{V}_{u}}}}{{{{V}_{u}}}} = \left( {\frac{P}{{{{K}_{f}}}} + \frac{{1 - P}}{{{{K}_{g}}}}} \right) + \frac{1}{p}\frac{{\Delta {{V}_{f}}}}{{{{V}_{u}}}}.$

Вычислим объем выжатой жидкости ΔVf, предполагая пока, что поры имеют цилиндрическое сечение с постоянным радиусом и не пересекаются [28].

Решая уравнение Навье–Стокса [28], можно получить формулу для средней по сечению поры относительной скорости течения флюида:

(9)
${{u}_{{av}}} = \frac{{{{p}_{0}}{{k}_{p}}({{\rho }_{g}} - {{\rho }_{f}})}}{{\omega {{\rho }_{g}}{{\rho }_{f}}}}\left( {1 - \frac{{2{{J}_{1}}({{i}^{{3/2}}}w)}}{{{{i}^{{3/2}}}w{{J}_{0}}({{i}^{{3/2}}}w)}}} \right),$
где
(10)
$w = \sqrt {\frac{{{{a}^{2}}{{\rho }_{f}}}}{\eta }\omega {\kern 1pt} } ,$
J0,1– функции Бесселя, a – радиус пор, η – динамическая вязкость жидкости, Па с. Обозначим функцию частотной коррекции в (9)

(11)
${{F}_{C}}(w) = 1 - \frac{{2{{J}_{1}}({{i}^{{3/2}}}w)}}{{{{i}^{{3/2}}}w{{J}_{0}}({{i}^{{3/2}}}w)}}.$

Вычислим объем флюида, протекающий по одной из пор: $\Delta {{V}_{0}} = \pi {{a}^{2}}{{u}_{{av}}}T$ = $\pi {{a}^{2}}{{u}_{{av}}}\frac{l}{{{{c}_{p}}}}$ = $\frac{{\pi {{a}^{2}}{{u}_{{av}}}l{{k}_{p}}}}{\omega }.$ Тогда, считая, что в выделенном объеме заключено N пор, последнее слагаемое в (8) можно записать как $\frac{1}{p}\frac{{\Delta {{V}_{f}}}}{{{{V}_{u}}}}$ = $ - \frac{{k_{p}^{2}}}{{{{\omega }^{2}}}}\frac{{({{\rho }_{g}} - {{\rho }_{f}})}}{{{{\rho }_{g}}{{\rho }_{f}}}}$ $\frac{{\pi {{a}^{2}}lN}}{{{{V}_{u}}}}{{F}_{C}}$. Подставляя это выражение в (8), получаем сжимаемость неконсолидированной среды в виде

(12)
$K_{u}^{{ - 1}}(\omega ) = \frac{1}{{{{K}_{0}}}} - \frac{{k_{p}^{2}}}{{{{\omega }^{2}}}}AP{{F}_{C}}(w),$
где $A = \frac{{({{\rho }_{g}} - {{\rho }_{f}})}}{{{{\rho }_{g}}{{\rho }_{f}}}}$,$P = \frac{{\pi {{a}^{2}}lN}}{{{{V}_{u}}}}$ – геометрическая пористость среды. Формула (12) была получена ранее в работе И.А. Чабан [28].

Однако поровое пространство реальной среды имеет структуру сети, состоящей из последовательно-параллельно включенных отрезков с различным поперечным сечением [29, 30]. Внутри широких пор между крупными гранулами располагаются мелкие частицы, сужающие или вообще закупоривающие проходное сечение. Стенки пор не жесткие, а образованы отдельными колеблющимися гранулами. В такой среде возможны и глобальные, и локальные потоки. Долю объема среды, в которой возможно течение Био, будем называть эффективной пористостью и обозначать ϕ [19, 31].

Свяжем эффективную пористость с проницаемостью, сравнивая стационарный закон Дарси $\varphi {{u}_{{av}}} = - \frac{{{{\kappa }_{0}}}}{\eta }\frac{{\partial p}}{{\partial x}}$ с формулой Пуазейля ${{u}_{{av}}} = - \frac{{{{a}^{2}}}}{{b\eta }}\frac{{\partial p}}{{\partial x}}$ [2], что дает

(13)
$\varphi = \frac{{b{{\kappa }_{0}}}}{{{{a}^{2}}}},$
где κ0 – статическая проницаемость среды, м2; b – коэффициент, зависящий от геометрии порового пространства, для прямых труб b = 8.

При выводе (12) предполагалось, что все поры ориентированы вдоль направления распространения плоской волны. На самом деле ориентация пор равновероятна в трех направлениях. Внутри пор, перпендикулярных к направлению распространения волны, движения флюида не будет, поэтому второе слагаемое в (12) следует дополнить коэффициентом Sv, имеющим смысл обратной извилистости пор, величина которого для изотропной среды принимается здесь Sv = 1/3.

Заменяя в (12) геометрическую пористость на эффективную, получаем:

(14)
$K_{u}^{{ - 1}} = \frac{1}{{{{\rho }_{0}}c_{0}^{2}}} - {{S}_{v}}A\frac{1}{{\tilde {c}_{p}^{2}}}\phi {{F}_{C}}(w).$

Формула (14) представляет двухфазное уравнение состояния, связывающее акустическое давление и сжимаемость неконсолидированной среды.

2.2. Дисперсионное уравнение для продольной волны

Подставляя (14) в (7), после преобразований имеем квадратное уравнение:

(15)
$\begin{gathered} {{\left( {\frac{{{{{\tilde {c}}}_{p}}}}{{{{c}_{0}}}}} \right)}^{4}} - {{\left( {\frac{{{{{\tilde {c}}}_{p}}}}{{{{c}_{0}}}}} \right)}^{2}}\left( {1 + \chi D + {{S}_{v}}\phi {{\rho }_{0}}A{{F}_{C}}} \right) + \\ + \,\,{{S}_{v}}\phi {{\rho }_{0}}A\chi D{{F}_{C}} = 0. \\ \end{gathered} $

Корни (15) равны ${{\left( {\frac{{{{{\tilde {c}}}_{p}}}}{{{{c}_{0}}}}} \right)}^{2}} = \frac{{ - b \pm \sqrt {{{b}^{2}} - 4ac} }}{{2a}}$, где a = 1, b = – (1 + χD + Svϕρ0AFC), c = Svϕρ0AχDFC, и дают квадраты относительных фазовых скоростей двух типов волн – быстрой и медленной.

Следует отметить, что замена K0 на Ku не эквивалентна двум раздельным уравнениям движения для твердой и жидкой фаз, поскольку пренебрегает изменением плотности среды в результате инерционного взаимодействия между гранулами и флюидом. Уравнение (15) включает две консервативно-диссипативные компоненты дисперсии: “GS” – внутреннее трение, действующее во всем диапазоне частот, и “Compressibility” – компрессионную дисперсию – вязкое трение, проявляющееся в ограниченном диапазоне частот. Уравнение, аналогичное (15), было получено с использованием иного подхода и в работе [23]. Представленную модифицированную GS теорию будем называть далее GS + EC, Grain Shearing + Effective Compressibility.

Проанализируем полученное решение. Исключим возможность движения флюида, положив ϕ = 0. Тогда b = – (1 + χD), c = 0, Ku = K0, и формула (15) переходит в (6). Если плотность гранул равна плотности флюида, среда представляет взвесь, гранулы и флюид колеблются с одинаковой скоростью и амплитудой. Тогда A = 0 и (15) переходит в (6). Если же эти невесомые гранулы друг за друга никак не зацепляются, то χ = 0, и (15) переходит в формулу Вуда (2). Сомножитель A отражает отсутствие скелета и возможность превращения неконсолидированной среды в суспензию при равенстве плотностей компонент. Этот сомножитель принципиально отличает GS + EC модель от расширенных версий [16–18] теории Био.

Для подразделения всего диапазона частот на “низкие”, “средние” и “высокие” частоты определим в (10) переходную частоту

(16)
${{f}_{r}} = \frac{\eta }{{{{a}^{2}}{{\rho }_{f}}}},$
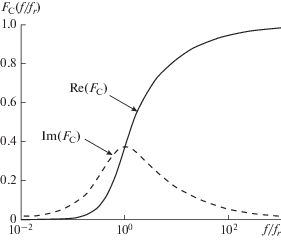
тогда (10) принимает вид $w = \sqrt {2\pi \frac{f}{{{{f}_{r}}}}} $. На рис. 1 показаны действительная и мнимая части функции коррекции FC(w) в зависимости от относительной частоты f/fr .

Рис. 1.

Частотные зависимости действительной и мнимой частей функции коррекции.

На низких (f $ \ll $ fr) частотах Re(FC) → 0, Im(FC) → 0, Ku ≈ K0, поры проницаемы для жидкости. В этом случае b = – (1 + χD), c ≈ 0, GS + EC модель снова переходит в GS теорию, проявляется только внутреннее трение, α ~ ω1. На средних (f ≈ fr) частотах величина Im(FC), характеризующая относительное межфазное ускорение и соответственно вязкие силы, максимальна. На высоких (f  $ \gg $ fr) частотах Im(FC) → 0, межфазное ускорение стремится к нулю, поры вследствие инерции жидкости непроницаемы. На очень низких, сейсмических частотах дисперсией можно пренебречь, считая D = 1, тогда

(17)
${{c}_{{p0}}} = \sqrt {\frac{{{{K}_{0}} + \gamma }}{{{{\rho }_{0}}}}} .$

Следует обратить внимание на принципиальную разницу между микропараметрами трения, устанавливаемыми в рамках GS и GS + EC теорий. Предполагая, что n = m, M. Buckingham определяет γ = γp + 4/3γs, где γp – модуль продольной жесткости [20]. Суммарная жесткость (γp + + 4/3γs) инвертируется по формулам GS теории [21] без симуляции вязкого трения. Композитная GS +EC жесткость γ вычисляется как результат решения уравнения (15) вместе с вкладом порового флюида, поэтому γGSEC и (γp + 4/3γs)GS друг с другом не сопоставляются. Кроме того, результаты инверсий показывают, что n ≠ m, взаимодействие гранул друг с другом и с жидкостью при сжатии и при сдвиге существенно различается [22].

Корень (15) со знаком минус соответствует медленной волне Био. В быстрой волне частички среды колеблются так, что фазы сжатия твердой (гранул и скелета) и жидкой компонент совпадают, в медленной волне колебания скелета и флюида противофазны. В неконсолидированной среде нет дальнодействующих упругих сил, возвращающих твердую фазу к положению равновесия, поэтому медленная “волна” – это осциллирующие потоки флюида, направленные от большего порового давления к меньшему. Наблюдать распространение медленной волны можно, наступив ногой на мелкий водонасыщенный песок.

3. СОПОСТАВЛЕНИЕ РЕЗУЛЬТАТОВ GS + EC МОДЕЛИ С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ

3.1. Входные параметры GS + EC модели

При проведении инверсий возникает проблема “уникальности” – является ли восстановленный набор параметров единственным. Для последующего анализа отобраны результаты инструментальных измерений, где наблюдается существенная дисперсия фазовой скорости – только в этом случае благодаря консервативно-диссипативной связи между скоростью звука и затуханием возможна более или менее однозначная (в пределах входных неопределенностей) инверсия параметров среды.

Входными параметрами, определяющими скорость звука и затухание, являются модуль композитной межгранулярной жесткости γ и показатель стресс-релаксации n соответственно. Эти параметры восстанавливаются инверсией экспериментальных данных. Величины γ и n зависят от важного и спорного [32–34] параметра – модуля упругости гранул Kg, определяющего суспензионную скорость звука (2), а совместно с композитной жесткостью γ – нижнюю границу фазовой скорости cp0 (17). Как следствие, от величины Kg зависит “вертикальный размах” и “крутизна” дисперсионной кривой. Приведенные ниже результаты инверсий в основном получены при общепринятых, “исторических” [32] значениях Kg. Прямые измерения Kg, описанные в работе [33], выполнены в условиях “чистой” среды. Реальное морское дно всегда содержит включения, которые могут быть более сжимаемы по сравнению с гранулами песка.

Наклон, форма дисперсионной кривой, отклонение коэффициента затухания от закона αp ~ f  1 определяется эффективной пористостью ϕ – внутренним параметром модели GS + EC, связывающим акустические и физические характеристики среды. Величина ϕ характеризует и состояние среды – чем меньше разница между статической пористостью P и эффективной ϕ, тем ближе среда к суспензии. Наоборот, ϕ = 0 соответствует плотным мелкодисперсным осадкам типа мусора с низкой гидравлической проницаемостью.

Показатель стресс-релаксации n и эффективная пористость ϕ оказывают конкурирующее влияние на показатель ε в степенном законе затухания αp ~ f ε. В рамках GS теории ε ≈ 1 + n/2, с увеличением неупругости межгранулярного взаимодействия наклон графика αp(f) растет. Наоборот, увеличение интенсивности вязких сил и эффективной пористости уменьшает ε и угол наклона графика αp(f).

Трудно подобрать точное определение для характерного размера пор. Р.Д. Столл связывает размер пор со средним размером гранул и считает a = d/7 = 0.142d. M. Kimura в работе [35] заключает, что a = (0.125…0.167)d.

Уникальные оценки можно получить, измеряя частотную зависимость проницаемости и определяя по соответствующему графику переходную частоту (16). Согласно результатам, приведенным в работе [36], для шариков диаметром d = 0.5 мм при гармонической прокачке воды релаксационная частота fr = 216 Гц. Тогда, обращая (16), получаем a = d/7.35. Результаты оптических измерений в тех же шариках дают эффективный радиус пор a = d/7, радиус горла (суженной части пор) – d/12 [36].

Поставим в соответствие реальной среде с гранулами разнообразных размеров среду из стеклянных шариков диаметром de с равной статической проницаемостью. Пористость среды из шариков не зависит от их размера и при случайной упаковке равна P0 = 0.363 [19]. Обращая формулу Козени–Кармана $\kappa = \frac{1}{{180}}\frac{{{{P}^{3}}}}{{{{{(1 - P)}}^{2}}}}{{d}^{2}}$ и измерив проницаемость среды, можно вычислить эквивалентный диаметр шариков:

(18)
${{d}_{e}} = 39\sqrt {{{\kappa }_{0}}} ,$
тогда

(19)
$a = {{{{d}_{e}}} \mathord{\left/ {\vphantom {{{{d}_{e}}} {7.35}}} \right. \kern-0em} {7.35}} = 0.136{{d}_{e}}.$

После инверсии, зная γ, n, ϕ, вклад внутреннего трения в дисперсию и затухание может быть вычислен, полагая в (15) ϕ = 0, а вклад вязкого трения – полагая n = 0.

3.2. Стеклянные шарики в различных жидкостях

Рассмотрим результаты измерений скорости и затухания в эксперименте с модельной средой – стеклянными шариками в воде и в силиконовом масле [21, 37]. Этот интересный эксперимент был специально задуман для проверки GS и Био–Столла теорий. Поскольку вязкость силиконового масла в 100 раз больше чем вязкость воды, ожидалось, что переходная частота (16), где зависимость затухания меняется с ~ f 2 на ~ f 1/2, сдвинется вверх и окажется внутри диапазона измерений.

Входные и инвертированные параметры приведены в табл. 1, графики cp(f), αp(f), βp(f) и двух дисперсионных компонент – внутреннего и вязкого трения – на рис. 2. Алгоритм инверсии был настроен на лучшее соответствие между экспериментальными точками и графиком тангенса угла потерь (1) βp(f). Для сравнения показаны так же и дисперсионные кривые теорий GS и Био–Столла (GS, B-S). На рис. 2б, 2в, 2г зависимость αp (f) теории Био–Столла совпадает с вязкой компонентой затухания.

Таблица 1.  

Входные и инвертированные характеристики среды. Стеклянные шарики в воде и в силиконовом масле

Входные параметры
  Диаметр,
d, мм 		ρg, кг/м3 Kg, Па ρf, кг/м3 Kf, Па η, Па с P κ, м2
Вода 0.4 2500 3.8 × 1010 [33] 1000 2.23 × 109 1 × 10–3 0.384 11 × 10–11
Масло 968 9.68 × 108 98 ×10–3 0.36 8.43 × 10–11
Инвертированные параметры
  K0, Па α0, дБ/м/кГц γ, Па n a, мкм ϕ
Шарики + вода 5.28 × 109 0.12 (200 кГц) 1.9 × 108 0.06 54 (d/7.35) 0.3
Шарики + масло 2.57 × 109 0.85 1.02 × 104 0.67 54 (d/7.35) 0.345
Рис. 2.

Результаты эксперимента “стеклянные шарики в воде и в силиконовом масле”. (а) – Частотные зависимости относительной скорости звука; (б) и (г) – коэффициента затухания; (в) – тангенса угла потерь и двух дисперсионно-диссипативных компонент – вязкого и внутреннего трения

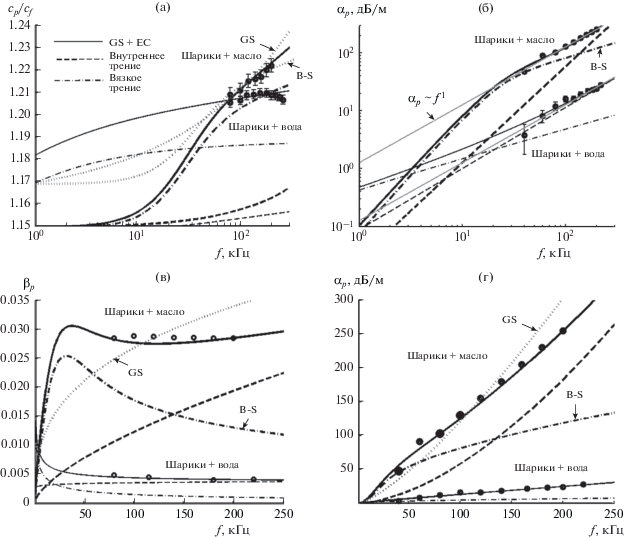
Как видно из рис. 2б, частотная зависимость затухания следует закону αp ~ f  1 во всем диапазоне, из чего в работе [37] был сделан вывод, что теория Био–Столла не подтверждается, затухание определяется не вязким, а внутренним трением. Однако, теория Био–Столла дает хорошее соответствие с измерениями скорости звука, что свидетельствует о правильном воспроизведении вязкой компоненты дисперсии.

С другой стороны, не подтверждается и GS теория – линии сp(f) и αp(f) пересекают экспериментальные тренды, т.е. только внутренним трением объяснить постоянную добротность среды вместе с существенной дисперсией скорости тоже невозможно. Соответствие не становится лучше и в рамках VGS теории [21, стр. 1497].

Рассмотрим, что показывает GS + EC модель. Сопоставление графиков компонент скорости и затухания убеждает, что только суммарным влиянием внутреннего и вязкого трения можно объяснить и постоянную добротность, и дисперсию скорости. Вязкое и внутреннее трение в данном эксперименте сложились так, что дисперсия скорости в основном обусловлена консервативным влиянием флюида, внутреннее трение проявляется только на верхней границе частотного диапазона измерений – рис. 2а. Влияние же внутренней и вязкой компонент затухания (рис. 2б, 2в, 2г) случайно разделилось пополам – до середины диапазона измерений в основном вязкое трение, выше середины – внутреннее, но в сумме получилось α ~ f 1, β ≈ const.

Инверсия возвращает низкое значение межгранулярной жесткости, высокое значение деформационного упрочнения и высокую эффективную пористость – существенно нелинейное взаимодействие между гранулами в вязкой среде. Физически это можно объяснить любрикацией поверхностей гранул маслом, вязкость которого уменьшает внутреннее трение, но в то же время препятствует вытеснению этого флюида из межгранулярной щели.

В работе [23] приведены аналогичные дисперсионные кривые, восстановленные при рекомендованном [21, 37] значении упругости гранул Kg = = 7 × 1010 Па. В этом случае межгранулярная жесткость оказывается предельно низкой, γ = 192 Па, а показатель деформационного упрочнения – предельно высоким, n = 0.98.

Рассмотрим заполнение пор водой. Скорость звука в пределах доверительного интервала практически постоянна, частотная зависимость затухания следует закону α ~ f  1, β ≈ const, с угадываемым трендом к снижению, соответствующему стремлению к постоянной добротности. Считая теперь известным размер пор, применим для вычисления эффективной пористости формулу (13). Как видно из рис. 2, дисперсия скорости звука обусловлена в основном упругостью жидкости, а затухание – внутренним трением. Отклонение теоретической зависимости от закона α ~ f  1 на самой низкой частоте не больше доверительного интервала. Высокая межгранулярная жесткость и малая величина показателя деформационного упрочнения характеризуют среду как упругую.

3.3. Слабоуплотненное и суспензионное состояние среды

Рассмотрим еще один необычный случай: очень крупный и очень мелкий коралловый песок Гавайских островов. Данные взяты из [38]. Измерения выполнены на месте, глубина погружения датчиков измерительной системы в песок – 10…20 см.

Гранулы кораллового (карбонатного) песка угловаты, пронизаны сквозными и тупиковыми отверстиями, некоторые имеют форму плоских спиральных пружинок [2]. Статическая пористость такого песка не будет согласована с его проницаемостью.

Входные и инвертированные параметры приведены в табл. 2, экспериментальные точки и графики – на рис. 3. Вязкость воды далее везде взята η = 1 × 10–3 Па с. Измерения проводились в диапазоне 20–100 кГц, что соответствует длине волны 8…1.6 см. На низких частотах длина волны сопоставима с глубиной погружения измерительной системы в песок, и, как видно из рис. 3, экспериментальные точки αp(f) имеют хаотическое расположение, не укладывающeеся ни в какой закон. С ростом частоты постепенно выстраивается зависимость, где αp ~ f ε, ε ≥ 1.

Таблица 2.  

Входные и инвертированные характеристики среды. Коралловый песок Гавайских островов

Входные параметры
  Диаметр,
d, мм 		ρg, кг/м3 Kg, Па ρf, кг/м3 Kf, Па P κ*, м2
Крупный 0.75 2750 7.4 × 1010 1023 2.38 × 109 0.45 3.5 × 10–11
Мелкий 0.069 0.56 0.34 × 10–11
* Не измерялась инструментально, а определена в [38] по наилучшему соответствию с моделью Био–Столла
Инвертированные параметры
  K0, Па α0, дБ/м/кГц γ, Па n a, мкм ϕ
Крупный 5.09 × 109 0.75 (100 кГц) 60 216 0.623 24 (d/31) 0.32
Мелкий 4.14 × 109 0.62 (100 кГц) 196 0.99 17 (d/4) 0.24
Рис. 3.

Результаты эксперимента “коралловый песок Гавайских островов”. Частотные зависимости скорости звука, коэффициента затухания и двух дисперсионно-диссипативных компонент – вязкого и внутреннего трения.

Ажурное строение гранул кораллового песка и малая глубина погружения датчиков порождают сложный закон дисперсии. Из сопоставления графиков внутренней и вязкой компонент фазовой скорости видно, что, как и в предыдущем случае, дисперсия скорости обусловлена консервативным действием жидкости. Наоборот, основная причина затухания в среде – внутреннее трение. Вязкое трение проявляется на самых низких частотах и “путает” закон αp(f), отклоняя его в сторону ~ f 1/2. Еще более интересно, что вязкие компоненты затухания для крупного и мелкого песка одинаковы, размер пор сопоставим, проницаемости же различаются на порядок. Эти факты показывают, что на высоких частотах жидкость не двигается относительно гранул, а на низких частотах вязкое трение будет обусловлено не глобальными, а локальными, “сквирт” потоками.

Инверсия возвращает очень низкие значения межгранулярной жесткости и предельно высокий показатель деформационного упрочнения (мелкий песок). Физически, такое состояние среды можно представить как мягкое, но невязкое, когда ажурное строение гранул способствует их высокой начальной контактной сжимаемости, но двойная пористость, с другой стороны, препятствует истечению флюида и увеличивает нелинейность среды в целом.

Следующий пример показывает противоположный результат. Актуальной и поныне является задача о распространении звука в концентрированных суспензиях, где кроме вязкого трения, постепенно проявляется и трение между частицами. Данные взяты из [39], где лабораторно измерялись скорость звука и затухание в средах типа “глинистый ил” и “песчаный ил”. Экспериментальные точки и дисперсионные кривые представлены на рис. 4, входные и инвертированные данные – в табл. 3.

Рис. 4.

Результаты эксперимента “глинистый ил” (clayey silt) и “песчаный ил” (sandy silt). (а) – Частотные зависимости относительной скорости звука; (б) и (г) – коэффициента затухания; (в) – тангенса угла потерь и двух дисперсионно-диссипативных компонент – вязкого и внутреннего трения.

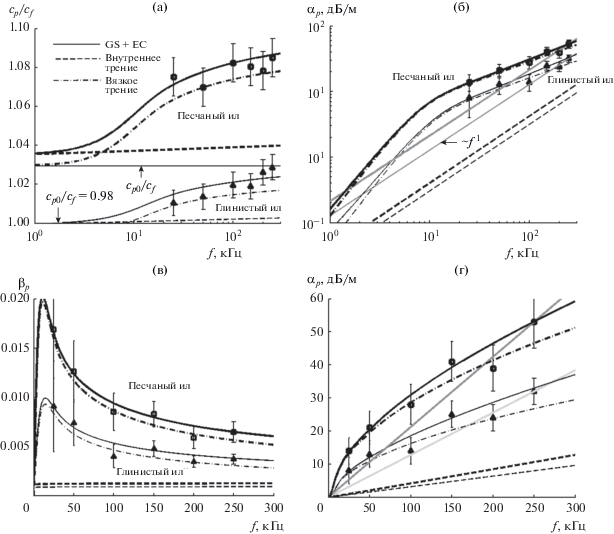
Таблица 3.

Входные и инвертированные характеристики среды. Глинистый ил и песчаный ил

Входные параметры
  Диаметр,
d, мм 		ρ0, кг/м3 ρg, кг/м3 ρf, кг/м3 Kf, Па P
Глин. ил 2.8 × 10–2 1520 2385 1023 2.395 × 109 0.635
Песч. ил 7.97 × 10–2 1790 2683 0.538
Инвертированные параметры
  K0, Па Kg, Па α0, дБ/м/кГц γ, Па n a, мкм ϕ
Глин. ил 3.31 ×109 1.0 × 1010 0.13 2.1 × 108 0.016 8.2 (d/3.4) 0.2
Песч. ил 4.17 × 109 3.0 × 1010 0.21 2.8 ×108 0.02 9.3 (d/4.1) 0.34

Как видно, зависимость αp(f) на высоких частотах не следует закону α ~ f1. Среда представляет собой не уплотненные внешним давлением осадки, а концентрированную суспензию, характерную для самой верхней, пограничной части илистого дна.

В обоих случаях во всем диапазоне частот определяющий вклад вносит вязкое трение. Результаты инверсии показывают высокую межгранулярную жесткость вместе с низкими показателями деформационного упрочнения. Такое сочетание микропараметров трения свидетельствует о практически упругом, линейном взаимодействии между гранулами. В этом единственном случае упругость гранул Kg = 3.2 × 1010 Па не подходит для моделирования, поскольку дает слишком высокую суспензионную скорость звука, при которой уравнения (15) не решаются.

3.4. Влияние неоднородностей среды

Немалую трудность для обобщения результатов экспериментальных измерений составляют гидродинамическая, пространственная изменчивость и неоднородность состава самой среды.

Сравним результаты трех измерений, выполненных “на месте” St. Andrews Bay [21] и Currituck Sound, мелководная и глубоководная точки [40, 41]. Дно в первых двух локациях состоит из хорошо сортированного среднего песка, глубина водного слоя соответственно десятки метров и 0.8 м, погружение датчика внутрь осадков до 2.5 и 0.3 м. В глубоководной (2.3 м) точке Currituck Sound песок мелкий и заиленный. Входные и инвертированные параметры – в табл. 4, экспериментальные точки и графики – на рис. 5.

Таблица 4.  

Входные и инвертированные характеристики среды. Точки St. Andrews Bay и Currituck Sound

Входные параметры
  Диаметр,
d, мм 		ρg, кг/м3 Kg, Па ρf, кг/м3 cf, м/с P
St. Andrews Bay 0.22 2653 3.2 × 1010 1023 1523.6 0.379
Currituck Sound, 0.8 м 2633 998 1490.1 0.44
Currituck Sound, 2.3 м 0.14 2562 0.67
Инвертированные параметры
  c0, м/с α0, дБ/м/кГц γ, Па n P a, мкм ϕ
St. Andrews Bay 1656 0.3 2.36 × 107 0.192 0.380 17(d/13) 0.11
Currituck Sound, 0.8 м 1571 0.3 7.1 × 107 0.06 0.44 13(d/17) 0.44
1557 0.1 × 107 0.364 24(d/9)
Currituck Sound, 2.3 м 1453 0.55 1.6 × 107 0.2 0.67 – 0
Рис. 5.

(а) и (б) – Результаты экспериментов “Точки St. Andrews Bay и Currituck Sound, мелководная”; (в) и (г) – “Currituck Sound, глубоководная”. (а) и (в) – Частотные зависимости относительной скорости звука; (б) и (г) – коэффициента затухания и двух дисперсионно-диссипативных компонент – вязкого и внутреннего трения.

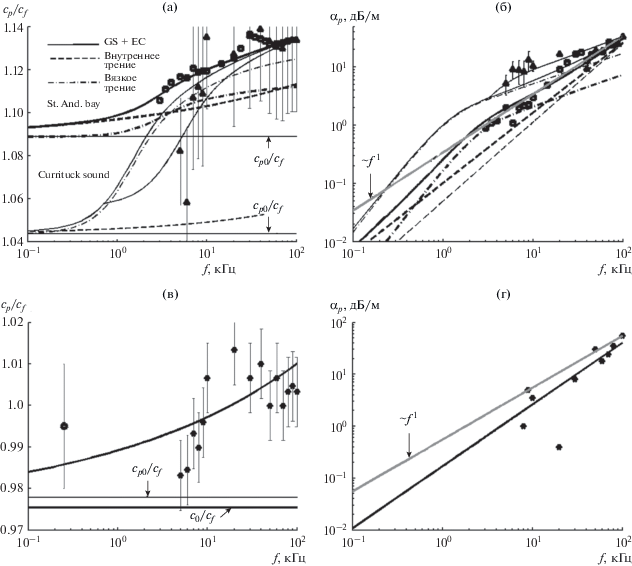
Удивительно, но измерения, выполненные в различное время, в разных местах, разными методами, показывают на высоких частотах совпадающий результат – одинаковую относительную скорость и одинаковое приведенное затухание – αp0 = = 0.3 дБ/м/кГц. Состояния среды и дисперсионные кривые, однако, разные. В мелководной точке Currituck Sound высокая пористость, песок находится в неуплотненном состоянии, с большим размером пор. Принимая результаты инверсии St. Andrews Bay за основное состояние, можно видеть, что возмущенное состояние показывает значительно меньшую межгранулярную жесткость, но большее деформационное упрочнение. На средних частотах причина затухания – вязкое трение, внутреннее трение мало. С увеличением частоты внутреннее трение быстро растет и на 80 кГц “догоняет” внутреннее трение в основном состоянии, превышая здесь вязкое трение. В итоге внутреннее трение на частоте 80 кГц в точках St. Andrews Bay и Currituck Sound оказывается одинаковым.

Неоднозначность инверсии в возмущенной точке Currituck Sound отражается в существовании альтернативного результата, показывающего суспензионное состояние среды (на рис. 5б – верхняя линия на графике коэффициента затухания и на рис. 5а –нижняя линия на графике скорости звука). Возможно, расположенные ближе или дальше от верхней границы осадков зерновые наборы обладают своими уникальными дисперсионными свойствами, воспринимаемыми как инструментальные ошибки.

Расположение экспериментальных точек глубоководной локации Currituck Sound с заиленным песком (рис. 5в, 5г) и результат инверсии показывают, что вязкие силы здесь могли проявиться только как случайные возмущения некоторой части среды, накладывающиеся на основное внутреннее трение, определяющее и дисперсию и затухание. Заметим, что скорость звука в дне оказывается меньше чем в воде.

3.5. Осредненные микропараметры трения. Неопределенность пористости

Проанализируем результаты измерений, полученные в морских экспериментах St. Andrews Bay, SAX-99, TREX-13 [21, 34, 42]. Скорость звука и затухание измерялись в разное время, в разных местах различными системами и способами. В первых двух точках песок чистый, а в точке Transition 1 [42] – замусоренный. Входные и восстановленные параметры – в табл. 5, точки и графики – на рис. 6. На самых низких частотах добавлены результаты волноводных инверсий, приведенные в работах [43–46].

Таблица 5.  

Входные и инвертированные характеристики среды. Эксперименты SAX99, St. Andrews Bay, TREX-13

Входные параметры
  Диаметр,
d, мм 		ρg, кг/м3 Kg, Па ρf, кг/м3 cf, м/с P κ, м2
SAX99 0.38 [21]
0.29…0.5 6 [29] 		2690 3.2 × 1010 1023 1530.1 0.372 ± 0.0073 [29] 2.5 × 10–11 [21]
(3.3 ± 0.6) ×10–11 [29]
TREX-13 Transition 1 0.4 1030 1528 0.4 –
Инвертированные параметры
  Экв. диаметр,
de, мм (7.35a) 		c0, м/с κ, м2 (de/39)2 γ, Па n a, мкм P, ϕ
SAX99 0.176 1662 2.02 × 10–11 2.36 × 107 0.192 23.8 0.372, 0.23
St. Andrews Bay 0.124 1656 1.01 × 10–11 17 0.380, 0.11
TREX-13 0.11 1633 0.80 × 10–11 15 0.40, 0.14
Рис. 6.

Результаты экспериментов “SAX99, St. Andrews Bay, TREX-13 (Transition 1)”. (а) – Частотные зависимости относительной скорости звука; (б) – коэффициента затухания и (в) – степенного показателя затухания, приведенного коэффициента затухания αp0 = αp/f; (г) – консервативной и диссипативной частей модуля упругости среды и модуля межгранулярного взаимодействия.

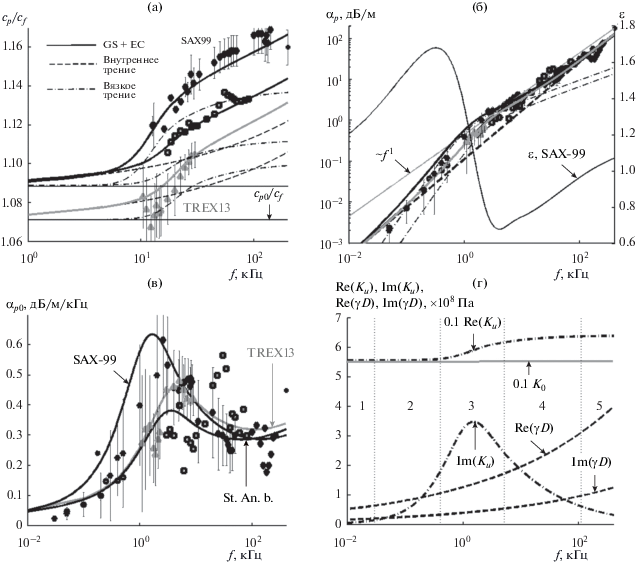
Обратим вначале внимание на экспериментальные точки на рис. 6а–6в – частотные зависимости скорости звука и коэффициента затухания. Как видно, все измерения показывают на высоких частотах одинаковое затухание – (0.3 ± 0.1) дБ/м/кГц, но существенно различающуюся скорость звука.

Из сопоставления величин K0 и γ (табл. 1–3) следует, что во всех случаях K0$ \gg $ γ, объемный модуль упругости среды является подавляющим фактором влияния на скорость звука. Основную неопределенность величины K0 дает неопределенность пористости – формулы (2)–(4). Кажущаяся изменчивость межгранулярной жесткости [21] (влияющей в основном на скорость) вместе с показателем стресс-релаксации (влияющим в основном на затухание) является компенсатором изменчивости скорости звука из-за неопределенности пористости. Этот вывод следует из равенства величин коэффициентов затухания звука на высоких частотах, где проявляется только межгранулярное трение.

Вряд ли пористость среды, даже составленной из стеклянных шариков, может быть измерена с точностью более двух цифр, что подтверждает разброс значений, приведенных в работе [35]. Измерения SAX99 показывают, что уже и вторая цифра пористости является сомнительной [47]. Увеличение пористости на 0.01, от 0.37 до 0.38 дает приращение K0 на 1.24 × 108 Па, скорости c0 на 11 м/с, изменяет γ на 2.32 × 107 Па (что сопоставимо с самой величиной – табл. 5), меняет n от 0.2046 до 0.1634.

Примем за основу результаты измерений SAX99 [21, 29, 34, 46] и будем считать здесь эту среду эталонной. Поскольку скорость звука в измерениях SAX99 наибольшая, возьмем наименьшее значение пористости – 0.372 [29]. Параметры согласования: 400 кГц, скорость звука 1785 м/с, затухание 0.3 × 400 дБ/м – рис. 6в. Восстановленные по этим входным параметрам величины γ и n будем считать осредненными для дна, показывающего на высоких частотах удельное затухание (0.3 ± 0.1) дБ/м/кГц и типичную частотную зависимость затухания (что исключает рассмотренный выше случай Currituck Sound). Приведенные на рис. 6а–6в графики построены, подбирая только три свободных параметра: объемную пористость P, размер пор a, эффективную пористость ϕ. Как видно из табл. 5, восстановленная пористость соответствует указанной во входных параметрах (TREX-13 в табл. 5 и St.An.Bay в табл. 4 и табл. 5, выделено жирным) с погрешностью в третьей цифре. Из рис. 5б видно, что вклад внутреннего трения в суммарное затухание во всех случаях одинаковый, вязкого – разный, изменяющийся пропорционально эффективной пористости.

Обратим внимание на совпадение результатов наших инверсий, основанных на разнообразных инструментальных измерениях, с результатами волноводных инверсий на самых низких частотах. Частотная зависимость затухания для эксперимента SW2006 [45] почти совпадает с зависимостью St. Andrews Bay и Transition 1. Результаты волноводных инверсий [46], ориентированные на модель Пекериса, показывают несколько большую крутизну зависимости αp(f), такую, что экспериментальные точки в диапазоне 30–50 Гц располагаются ниже линии TREX13, вдоль вязкой компоненты затухания SAX99, а в диапазоне 600–1000 Гц – между линиями TREX13 и SAX99 (рис. 6б).

В табл. 5 приведены результаты реверсного определения физических параметров осадков – эквивалентного диаметра гранул и проницаемости с помощью формул (18), (19). Сопоставление размера пор, восстановленного по дисперсионной кривой, с измеренным оптическими методами (35–40 мкм [29, 30]) и с измеренной статической проницаемостью соответствует смыслу переходной частоты (16) – в крупных порах характер течения уже существенно отличается от пуазейлевского.

На рис. 6г показаны частотные зависимости консервативной и диссипативной частей модуля упругости среды Re(Ku), Im(Ku) и модуля межгранулярного взаимодействия Re(γD), Im(γD). Консервативные части управляют дисперсией скорости звука, диссипативные – затуханием. На рис. 6б ось справа – частотная зависимость показателя затухания ε, если записать степенной закон в виде, аналогичном [46]: αp = С(f)fε, С(f) ≠ αp0. Показатель вычислен по формуле: $\varepsilon = \frac{{{{\partial {{\alpha }_{p}}} \mathord{\left/ {\vphantom {{\partial {{\alpha }_{p}}} {\partial f}}} \right. \kern-0em} {\partial f}}}}{{{{\alpha }_{{p0}}}}}$. Эти параметры восстановлены для точки SAX99.

Анализируя и сопоставляя теперь все графики на рис. 2–6, можно по соотношению между силами внутреннего и вязкого трения выделить характерные диапазоны частот и типы сред.

1) Очень низкие, сейсмические частоты. Re(Ku) ≈ K0, Re(Ku) $ \gg $ Re(γD) – добавка скорости за счет внутреннего трения мала, Im(Ku) < Im(γD) – внутреннее трение много больше вязкого. Слабая дисперсия за счет роста Re(γD). Мягкая среда вследствие легкого вытеснения флюида.

На этих частотах дисперсионные кривые GS + EC и VGS [21] теории принципиально различаются. Согласно VGS теории, при f → 0, cp(f) → c0, αp ~ f  2 – внутреннее трение “исчезает”, всякая среда обращается в суспензию. Согласно GS + EC (и теории Био–Столла), cp(f) → cp0, αp → f 1 – проявляется только внутреннее трение.

2) Частоты ниже релаксационной. Этот участок – в окрестности первой точки пересечения графиков Im(Ku) и Im(γD) – рис. 6г. Здесь упругость среды Re(Ku) возрастает, Re(Ku) $ \gg $ Re(γD), Im(Ku) ≈ Im(γD). Скорость звука увеличивается, показатель затухания ε приближается к двум. Силы вязкого и внутреннего трения сопоставимы.

3) Частота в окрестности релаксационной (максимум Im(Ku)). Величина дисперсии ∂cp/∂f максимальна, Im(Ku) > Im(γD), вязкое трение больше внутреннего, тангенс угла потерь и удельное затухание максимальны. В этой области в средах с разнообразным гранулометрическим составом вязкие силы могут проявиться как эпизодический возмущающий фактор. Показатель ε уменьшается от максимума и становится меньше единицы. Характер течения в порах меняется.

4) Частота выше релаксационной. Участок в окрестности второй точки пересечения графиков Im(Ku) и Im(γD) – рис. 6г. Упругость среды Re(Ku) уже почти постоянна, дисперсия скорости звука ∂cp/∂f резко уменьшается, показатель затухания возрастает от минимума и приближается к единице. Вязкие силы становятся меньше сил внутреннего трения.

5) Высокие частоты. Здесь Re(Ku) ≈ const, Im(Ku) $ \ll $ Im(γD). Слабая дисперсия, затухание αp ~ f  1.

6) Очень высокие частоты, граница применимости GS + EC теории. Длина волны сравнима с размером гранул, вследствие рассеяния возрастает затухание, скорость звука уменьшается.

ВЫВОДЫ

Пограничная область переходного слоя дна толщиной десятки сантиметров показывает сложные и изменчивые дисперсионные характеристики. В “очень мелком море” с глубинами 0.5–6 м приливы, волны, штормы, судоходство нарушают покой пограничного слоя, и он приобретает диссипативные свойства суспензии. На глубинах десятки метров упомянутые факторы уже не оказывают влияния, состояние пограничного слоя уплотненное, и на высоких частотах αp ~ f 1.

При восстановлении микропараметров трения по результатам инструментальных измерений наиболее надежный, воспроизводимый параметр – величина коэффициента затухания (дБ/м/кГц) на высоких (200–400 кГц) частотах. Скорость звука изменчива, поскольку сильно зависит от неопределенности пористости.

Во всех рассмотренных случаях GS + EC теория явилась эффективным и гибким инструментом для анализа механики взаимодействия между неконсолидированной средой и жидкостью. Согласно представленной модели, механизм вязкой дисперсии в неконсолидированной среде реализуется следующим образом. Компрессия приводит к истечению флюида из мелких пор и щелей между гранулами сквозь крупные сквозные поры, что увеличивает сжимаемость среды на низких частотах. С ростом частоты характер течения в сквозных порах постепенно меняется, их проницаемость уменьшается, поры “запираются”, гранулы и жидкость колеблются вместе. Флюиду, заключенному в щелях, деваться некуда, что приводит к возрастанию упругости среды и скорости звука. Так проявляется консервативное влияние жидкости. Вязкое трение дает вклад в диапазоне средних частот, когда флюид еще мобилен, но и вязкие силы уже достаточно велики. На высоких частотах вязкие силы могут проявляться как возмущения скорости и затухания за счет движения флюида в самых мелких порах, где еще сохраняется пуазейлевское течение. Такой механизм взаимодействия фаз известен как локальные “сквирт” потоки (BISQ, BIot SQuirt), и в этой части наша модель сходится с представлениями EB (Extended Biot) моделей.

Проведенный анализ соотношений между силами внутреннего и вязкого трения относился только к продольной волне. Однако, отклонения затухания от закона α ~ f 1 обнаружены, хотя и в меньшей степени, и для сдвиговой волны [2, 15–17]. Совместный анализ результатов измерений акустических характеристик продольной и сдвиговой волн является принципиально важным для углубления понимания механики взаимодействия между неконсолидированной средой и флюидом.

Работа выполнена в лаборатории теоретических основ перспективных методов исследования шельфа СевГУ при финансовой поддержке РФФИ в рамках научного проекта № 18-42-920001.

Список литературы

  1. Katsnelson B., Petnikov V., Lynch J. Fundamentals of shallow water acoustics. New York, Dordrecht, Heildelberg, London: Springer, 2012.

  2. Jackson D.R., Richardson M.D. High-Frequency Seafloor Acoustics. New York: Springer, 2007.

  3. Григорьев В.А., Луньков А.А., Петников В.Г. Затухание звука в мелководных акваториях с газонасыщенным дном // Акуст. журн. 2015. Т. 61. № 1. С. 90–100.

  4. Григорьев В.А., Кацнельсон Б.Г., Lynch J.F. Определение эффективных параметров дна мелкого моря по спектрам широкополосных сигналов в условиях гидродинамической изменчивости // Акуст. журн. 2016. Т. 62. № 3. С. 330–340.

  5. Белов А.И., Кузнецов Г.Н. Оценка акустических характеристик поверхностных слоев морского дна с использованием четырехкомпонентных векторно-скалярных приемников // Акуст. журн. 2016. Т. 62. № 2. С. 194–202.

  6. Григорьев В.А., Петников В.Г., Шатравин А.В. Звуковое поле в мелководном волноводе арктического типа с дном, содержащим газонасыщенный осадочный слой // Акуст. журн. 2017. Т. 63. № 4. С. 389–405.

  7. Григорьев В.А., Петников В.Г., Росляков А.Г., Терехина Я.Е. Распространение звука в мелком море с неоднородным газонасыщенным дном // Акуст. журн. 2018. Т. 64. № 3. С. 342–358.

  8. Гринюк А.В., Кравченко В.Н., Лазарев В.А., Малеханов А.И., Петухов Ю.В., Романова В.И., Хилько А.И. Реконструкция параметров осадочных слоев морского дна мелкого моря с использованием широкополосных сейсмоакустических источников // Акуст. журн. 2013. Т. 59. № 3. С. 354–362.

  9. Camin H.J., Isakson M.J. A comparison of sediment reflection coefficient measurements to elastic and poro-elastic models // J. Acoust. Soc. Am. 2006. V. 120. № 5. P. 2437–2449.

  10. Bonomo A.L., Chotiros N.P., Isakson M.J. On the validity of the effective density fluid model as an approximation of a poroelastic sediment layer // J. Acoust. Soc. Am. 2015. V. 138. № 2. P. 748–757.

  11. Schock S.G. A Method for estimating the physical and acoustic properties of the sea bed using chirp sonar data // IEEE J. Ocean. Eng. 2004. V. 29. № 4. P. 1200–1217.

  12. Holland C.W., Dettmer J. In situ sediment dispersion estimates in the presence of discrete layers and gradients // J. Acoust. Soc. Am. 2013. V. 133. № 1. P. 50–61.

  13. Bonomo A.L., Isakson M.J. A comparison of three geoacoustic models using Bayesian inversion and selection techniques applied to wave speed and attenuation measurements // J. Acoust. Soc. Am. 2018. V. 143. № 4. P. 2501–2513.

  14. Rakotonarivo S., Legris M., Desmare R., Sessarego J.-P., Bourillet J.-F. Forward modelling sediment characterization using chirp sonars // Geophysics. 2011. V. 76. № 4. P. T91–T99.

  15. Kibblewhite A.C. Attenuation of sound in marine sediments: a review with emphasis on new low frequency data // J. Acoust. Soc. Am. 1989. V. 86. № 2. P. 716–738.

  16. Chotiros N.P. Acoustics of the Seabed as a Poroelastic Medium. Springer Briefs in Oceanography, 2017. 99 p.

  17. Chotiros N.P., Isakson M.J. Shear wave attenuation and micro-fluidics in water-saturated sand and glass beads // J. Acoust. Soc. Am. 2014. V. 135. № 6. P. 3264–3279.

  18. Kimura M. Frame bulk modulus of porous granular marine sediments // J. Acoust. Soc. Am. 2006. V. 120. № 2. P. 699–710.

  19. Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook. Tools for Seismic Analysis of Porous Media. Cambridge university press, 2009. 511 p.

  20. Buckingham M.J. Wave propagation, stress relaxation, and grain-to-grain shearing in saturated, unconsolidated marine sediments // J. Acoust. Soc. Am. 2000. V. 108. № 6. P. 2796–2815.

  21. Buckingham M.J. On pore-fluid viscosity and the wave properties of saturated granular materials including marine sediments // J. Acoust. Soc. Am. 2007. V. 122. №. 3. P. 1486–1501.

  22. Лисютин В.А. Простая акустическая модель неконсолидированных морских осадков с внутренним и вязким трением // Экологический вестник научных центров ЧЭС. 2018. Т. 15. № 3. С. 39–51.

  23. Лисютин В.А. Обобщенная реологическая модель неконсолидированных морских осадков с внутренним трением и эффективной сжимаемостью // Морской гидрофизический журнал. 2019. Т. 35. № 1. С. 85–100. Lisyutin V.A. Generalized rheological model of the unconsolidated marine sediments with internal friction and effective compressibility // Physical Oceanography [e-journal]. 2019. V. 26(1). P. 77–91.https://doi.org/10.22449/1573-160X-2019-1-77-91https://doi.org/10.22449/0233-7584-2019-1-85-100

  24. Hamilton E.L. Compressional wave attenuation in marine sediments // Geophysics. 1972. V. 37. № 4. P. 620–646.

  25. Машинский Э.И. Процессы микропластичности в осадочных породах и физическая нелинейность в области сейсмических деформаций. Автореферат дис. докт. геол.-минералог. наук: 04.00.22. Новосибирск, 1999. 32 с.

  26. Зайцев В.Ю., Назаров В.Е. О линейной частотной зависимости коэффициента поглощения упругих волн в микронеоднородных твердых телах // Акуст. журн. 1999. Т. 45. № 5. С. 622–627.

  27. Зайцев В.Ю., Назаров В.Е., Шульга А.Е. О диссипативных и дисперсионных свойствах микронеоднородных сред // Акуст. журн. 2000. Т. 46. № 3. С. 348–355.

  28. Чабан И.А. Затухание звука в грунтах и горных породах // Акуст. журн. 1993. Т. 39. № 2. С. 362–369.

  29. Reed A.H., Briggs K.B., Lavoie D.L. Porometric properties of siliciclastic marine sand: A comparison of traditional laboratory measurements with image analisis and effective medium modeling // IEEE J. Ocean. Eng. 2002. V. 27. № 3. P. 581–592.

  30. Reed A.H., Thompson K.E., Briggs K.B., Willson C.S. Physical pore properties and grain interactions of SAX04 sands // IEEE J. Ocean. Eng. 2010. V. 35. № 3. P. 488–501.

  31. Urumović K., Urumović Sr.K. The referential grain size and effective porosity in the Kozeny‑Carman model // Hydrol. Earth Syst. Sci. 2016. 20. P. 1669–1680.

  32. Chotiros N.P. Response to: Comments on “Biot model of sound propagation in water-saturated sand” [J. Acoust. Soc. Am. 103, 2723–2725 (1998)] // Acoust. Soc. Am. 1998. V. 103. №. 5. P. 2726–2729.

  33. Richardson M.D., Williams K.L., Briggs K.B., Thorsos E.I. Dynamic measurement of sediment grain compressibility at atmospheric pressure: acoustic applications // IEEE J. Ocean. Eng. 2002. V. 27. № 3. P. 593–601.

  34. Williams K.L., Jackson D.R., Thorsos E.I., Tang D., Schock S.G. Comparison of sound speed and attenuation measured in a sandy sediment to predictions based on the Biot theory of porous media // IEEE J. Ocean. Eng. 2002. V. 27. № 3. P. 413–428.

  35. Kimura M. Prediction of tortuosity, permeability, and pore radius of water-saturated unconsolidated glass beads and sands // J. Acoust. Soc. Am. 2018. V. 143. № 5. P. 3154–3168.

  36. Glover P.W.J., Walker E., Ruel J., Tardif E. Frequency-dependent streaming potential of porous media. Pt. 2. Experimental measurement of unconsolidated materials // Int. J. Geophysics. V. 2012. Article ID 728495. P. 1–17.

  37. Hefner B.T., Williams K.L. Sound speed and attenuation measurements in unconsolidated glass-bead sediments saturated with viscous pore fluids // J. Acoust. Soc. Am. 2006. V. 120. № 5. P. 2538–2548.

  38. Nosal E.-M., Tao C., Baffi S., Wilkens R.H. Compressional wave speed dispersion and attenuation in carbonate sediments, Kaneohe Bay, Oahu, Hi // IEEE J. of Ocean. Eng. 2008. V. 33. № 4. P. 367–374.

  39. Wang J., Liu B., Kan G., Li G., Zheng J., Meng X. Frequency dependence of sound speed and attenuation in fine-grained sediments from 25 to 250 kHz based on a probe method // Ocean Engineering. 2018. V. 160. P. 45–53.

  40. Lee K.M., Ballard M.S., McNeese A.R., Muir T.G., Wilson P.S. In situ measurements of acoustic properties in Currituck Sound and comparison to models // J. Acoust. Soc. Am. 2016. V. 140. № 5. P. 3593–3606.

  41. Ballard M.S., Costley R.D., Sagers J.D., Lee K.M., McNeese A.R., Hathaway K.K., Wilson P.S., Smith E.W. A comparison between directly measured and inferred wave speeds from an acoustic propagation experiment in Currituck Sound // J. Acoust. Soc. Am. 2018. V. 143. № 1. P. 237–247.

  42. Yang J., Tang D. Direct measurement of sediment sound speed and attenuation in the frequency band of 2–8 kHz at the target and reverberation experiment site // IEEE J. Ocean. Eng. 2017. V. 42. № 4. P. 1102–1109.

  43. Белов А.И., Кузнецов Г.Н. Пространственное затухание различных составляющих звуковых полей в водном слое и в осадках мелкого моря // Акуст. журн. 2017. Т. 63. № 6. С. 614–622.

  44. Bevans D.A., Buckingham M.J. Estimating the sound speed of a shallow-water marine sediment from the head wave excited by a low-flying helicopter // J. Acoust. Soc. Am. 2017. V. 142. № 4. P. 2273–2287.

  45. Wan L., Badiey M., Knobles D.P. Geoacoustic inversion using low frequency broadband measuremetnts from L-shaped arrays in the Shallow Water 2006 Experiment // J. Acoust. Soc. Am. 2016. V. 140. № 4. P. 2358–2373.

  46. Zhou J.-X., Zhang X.-Z., Knobles P. Low-frequency geoacoustic model for the effective properties of sandy seabottoms // J. Acoust. Soc. Am. 2009. V. 125. № 5. P. 2847–2866.

  47. http://www.apl.washington.edu/programs/SAX99/ SAX99/coremeas.html (дата обращения 19.10.2019).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал