Акустический журнал, 2020, T. 66, № 4, стр. 437-445

ВВЕДЕНИЕ

Обнаружение и оценка координат источников по их шумовому полю является одной из актуальных проблем пассивной гидроакустики [1]. В настоящее время для ее решения в низкочастотном диапазоне (десятки и сотни герц), когда применимо модовое описание структуры поля, разработан и успешно апробирован интерферометрический метод локализации шумового источника [2–8]. В его основе лежат механизмы межмодовой интерференции и волноводной дисперсии, обусловливающие формирование частотно-временной (пространственной) интерференционной картины (интерферограммы) [9–11]. В отличие от традиционной согласованной со средой обработки [12, 13] интерферометрическая обработка позволяет реализовать одновременно обнаружение источника и определение его параметров (пеленг, расстояние, глубина, скорость). При этом она может быть реализована в отсутствие знаний о передаточной функции волновода [7, 8], что значительно расширяет ее область применения. В настоящее время, на примере интенсивных внутренних волн, экспериментально показана возможность применения интерферометрии для восстановления передаточной функции невозмущенного волновода и диагностики временной изменчивости океанической среды [14, 15].

В области высокочастотного (килогерцового) диапазона интерферометрическая обработка применяется впервые и нуждается в экспериментальной проверке, так как изменяется механизм формирования интерферограммы. Если в области низких частот физико-математические принципы, лежащие в основе локализации малошумных источников, ясны [2–4], то остается открытым вопрос: насколько успешно этот метод может применяться в высокочастотном диапазоне?

В настоящей работе представлены результаты обработки высокочастотного эксперимента по локализации движущегося шумового источника в окрестности траверса, когда одновременно изменяются расстояние и пеленг. Прием осуществлялся на цилиндрическую вертикальную векторно-скалярную антенну (далее антенна). Изложен алгоритм интерферометрической обработки шумового поля и на его основе получены временные оценки параметров источника. Теоретически проанализирована динамика модельной двухлучевой интерферограммы, адекватно передающей основные свойства экспериментальной интерферограммы.

РЕЗУЛЬТАТЫ НАТУРНОГО ЭКСПЕРИМЕНТА

Цель эксперимента заключалась в проверке работоспособности интерферометрического метода локализации шумового источника в высокочастотной области. Эксперимент проводился в мелководной акватории с глубиной волновода $H\sim 87$ м и скоростью звука, практически не зависящей от глубины, $c\sim 1400$ м/с. Обрабатывался сигнал с одиночного приемника антенны, расположенного на глубине ${{z}_{q}} = 30$ м. Интерферограмма источника регистрировалась в полосе $\Delta f = 1{\kern 1pt} --{\kern 1pt} 15$ кГц. Длительность принимаемой шумовой реализации $\delta t = 0.2$ с. Входное отношение сигнал/помеха (по мощности) $q\sim 8$. Априорная информация о гидрофизических характеристиках акватории отсутствовала.

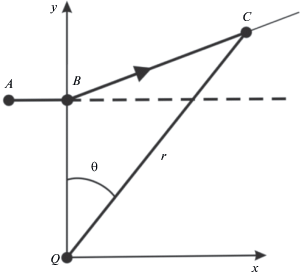
Схема движения источника относительно антенны в окрестности траверса показана на рис. 1. Оси x и y векторно-скалярного приемника (далее приемника) Q совпадают с положительными направлениями системы координат. Из начальной точки A источник приближался к приемнику, проходил точку B траверса и далее от нее удалялся по направлению к точке C. После прохождения точки C источник совершал петлеобразные траектории (на рис. 1 они не отображены). Горизонтальное расстояние от источника до антенны обозначено r, пеленг – θ.

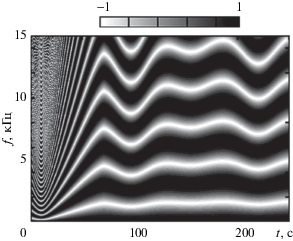
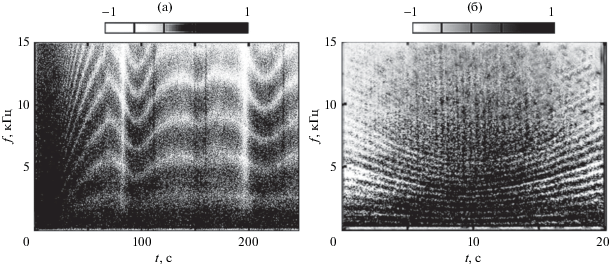
На рис. 2 приведена экспериментальная интерферограмма ${{I}_{e}}\left( {f,~t} \right) = {{\left| {P\left( {f,~t} \right)} \right|}^{2}}$ скалярной компоненты (давление P) поля источника. С целью повышения контрастности и информативности на ней вырезано среднее значение. В момент времени $~t = 10$ с, отвечающий прохождению точки траверса, частотный масштаб изменчивости интерферограммы оценивается как $\Lambda = 404$ Гц. При удалении от точки траверса частотный масштаб возрастает, что, естественно, приводит к увеличению ширины интерференционной полосы. При этом он практически от частоты не зависит. Временной масштаб D изменчивости интерферограммы с возрастанием частоты уменьшается и увеличивается с возрастанием времени наблюдения (расстояния). В точке траверса, например, на частоте $f = 3.5$ кГц он равен $D = 2.9$ c. Крутизна интерференционных полос в области траверса возрастает со временем и частотой, и по мере удаления от нее уменьшается. Данные закономерности характерны до момента времени $t{\kern 1pt} '\sim 70$ c, т.е. по истечении 60 с после удаления от точки траверса. Для значений $t > t{\kern 1pt} '$ интерферограмма носит осциллирующий характер, вызванный многократным изменением направления движения источника (см. рис. 8).

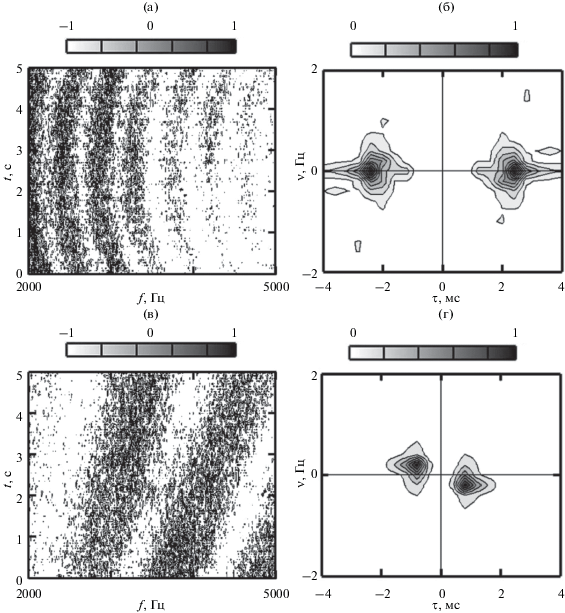
Спектральные плотности, получаемые двукратным преобразованием Фурье интерферограммы $I\left( {\omega ,~t} \right)$ скалярной компоненты поля,

которые условно назовем голограммой, для двух моментов времени ${{t}_{i}} = 10~$ и 50 с представлены на рис. 3. Здесь $\tilde {\nu } = 2{\pi }$, $\omega = 2\pi f$, ${\tau }$ и t – циклическая частота, время голограммы и интерферограммы соответственно; $\Delta t$ и $\Delta {\omega }$ – время наблюдения и ширина спектра, ${{{\omega }}_{0}}$ – средняя частота спектра. Интерферограммы и голограммы различных компонент векторно-скалярного поля и их комбинаций когерентны и различаются помехоустойчивостью [3]. Изображение источника на голограмме локализовано в форме двух фокальных пятен, зеркально перевернутых относительно начала координат. Одно из них, лежащее во втором и третьем квадрантах, можно рассматривать как мнимое изображение источника, второе, лежащее в первом и четвертом квадрантах, − как действительное изображение. Число фокальных пятен определяет число лучей, формирующих интерферограмму: каждое фокальное пятно обусловлено интерференцией двух лучей. В эксперименте на голограммах в различные моменты времени наблюдался один ярко выраженный максимум. Следовательно, интерферограмма на всей траектории источника в основном формировалась двумя энергонесущими лучами, в качестве которых можно принять прямой луч и отраженный от верхней границы, $z = 0$. Координаты положений максимумов фокальных пятен: $\tau = 2.4$ мс, $\nu = 0$ Гц – момент времени ${{t}_{i}} = 10$ с; ${\tau } = 0.9$ мс, $\nu = --0.2$ Гц – ${{t}_{i}} = 50$ с. Этим моментам времени соответствуют частотные масштабы $\Lambda = 404$ Гц; $\Lambda = 2.5$ кГц (см. рис. 2).

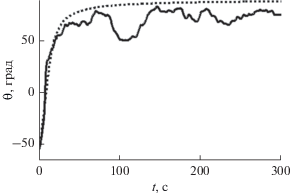
Для оценки направления на источник применялся интерферометрический метод пеленгования, основанный на отношении очищенных от помех интерферограмм

в фиксированные моменты времени ${{t}_{i}}$, где $R = {{V}_{r}}V_{r}^{*}$, $G = {{V}_{x}}V_{r}^{*}$ [7]. Верхний индекс звездочка “*” означает комплексное сопряжение. Здесь ${{V}_{{x,~y}}}$ – горизонтальные проекции вектора колебательной скорости, ${{V}_{r}} = \sqrt {V_{x}^{2} + V_{y}^{2}} $. При обработке очищение интерферограмм от помехи не требовалось, так как входное отношение сигнал/помеха было достаточно большим для отчетливого наблюдения локализованных полос. На рис. 4 экспериментальная зависимость пеленга от времени $\theta \left( t \right)$ изображена сплошной линией, пунктиром – модельная зависимость в предположении движения источника вдоль прямой, параллельной оси x (см. рис. 1, пунктир). Мелкомасштабные осцилляции обусловлены колебаниями антенны в вертикальной плоскости, крупномасштабные осцилляции – изменением траектории движения источника.

Определение параметров источника осуществлялось с использованием согласованной обработки по отношению к интерферограмме, формируемой движущимся источником. Горизонтальное расстояние до приемника r, глубина z и скорость w оценивались как координаты основного максимума трехмерной взаимокорреляционной функции экспериментальной ${{I}_{e}}$ и модельной ${{I}_{m}}$ интерферограмм

т.е. $\max ~E\left( {r*,~z*,~w{\text{*}}} \right) = E\left( {r,~z,~w} \right)$. Варьируемые (подбираемые) величины обозначены нижним индексом звездочка (*). При обработке (3) априори считалось, что источник расположен на глубине $1~\,\, \leqslant z \leqslant 70~\,\,{\text{м}}$, удален от приемника на $50~\,\,{\text{м}} \leqslant r \leqslant 3\,\,{\text{\;}}{\kern 1pt} {\text{км}}$, скорость $2 \leqslant w \leqslant 35\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$. Перебор параметров проводился с шагом: расстояние − $\delta r = 25$ м, глубина − $\delta z = 0.5$ м, скорость − $\delta w = 1$ м/с. Шаг дискретизации по частоте $\delta f = 0.5$ Гц, по времени $\delta t = 2$ с. Обработка проводилась во временном интервале $\Delta t = 20$ с и полосе частот $\Delta f = 1{\kern 1pt} - {\kern 1pt} 15$ кГц.

Отметим, что ранее в килогерцовом диапазоне с применением двух- и многолучевой моделей поля, используя многоэлементные приемные вертикальную или горизонтальную антенны, основываясь на алгоритме традиционной согласованной обработки, экспериментально показана возможность оценки глубины и расстояния излучателя от антенны [16–18], однако, источник был неподвижным.

Для отслеживания временного восстановления параметров источника использовалось каскадное вычисление взаимокорреляционной функции. В начальный момент времени ${{t}_{0}} = 0$ осуществлялась обработка (3) во временном интервале $\Delta t = 20$ с. В момент времени ${{t}_{1}} = {{t}_{0}} + \,\,~\delta t{\kern 1pt} '$ проводилась следующая обработка в течение времени $\Delta t$, $\delta t{\kern 1pt} ' = 5$ с, и т.д. В результате за время наблюдения $T = 275$ с получено $N = \left[ {{{\left( {T - \Delta t} \right)} \mathord{\left/ {\vphantom {{\left( {T - \Delta t} \right)} {\delta t{\kern 1pt} '}}} \right. \kern-0em} {\delta t{\kern 1pt} '}}} \right] + 1 = 52$ оценок параметров источника.

Модельная интерферограмма ${{I}_{m}}\left( {f,~t} \right)$ (рис. 5), адекватно передающая основные свойства экспериментальной интерферограммы, строилась на основе интерференции полей двух лучей с использованием лучевой программы. При этом предполагалось, что в зоне траверса источник двигался по прямолинейной траектории.

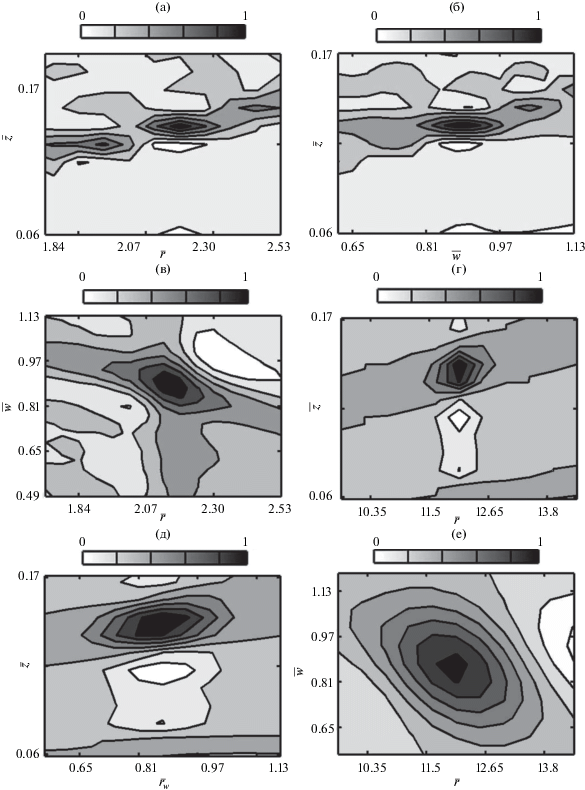
Для иллюстрации на рис. 6 изображены двумерные разрезы нормированной трехмерной взаимокорреляционной функции (3) для двух моментов времени. Нормированные восстановленные параметры источника обозначены сверху прямой линией. Скорость нормирована на значение 30 м/с; расстояние и глубина нормированы на значение 87 м. По результатам моделирования параметры источника оцениваются как $r = 189$ м, $z = 10.9$ м, $w = 27.6$ м/с для ${{t}_{i}} = 10$ с; $r = 1049$ м, $z = 12.8$ м, $w = 26.9$ м/с для ${{t}_{i}} = 50$ с. За время наблюдения $T = 0{\kern 1pt} - {\kern 1pt} 275$ c были обработаны интерферограммы для всех временных интервалов и с использованием алгоритма (3) восстановлены временные зависимости параметров источника $~z\left( t \right)$, $r\left( t \right)$, $w\left( t \right)$.

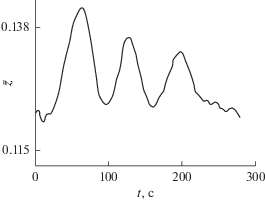
На рис. 7 показана нормированная зависимость глубины $z\left( t \right)$. Как видно, во время эксперимента глубина источника изменялась в пределах ~1.5 м (в основном, при поворотах) и в среднем оценивается как $z = 11.4$ м.

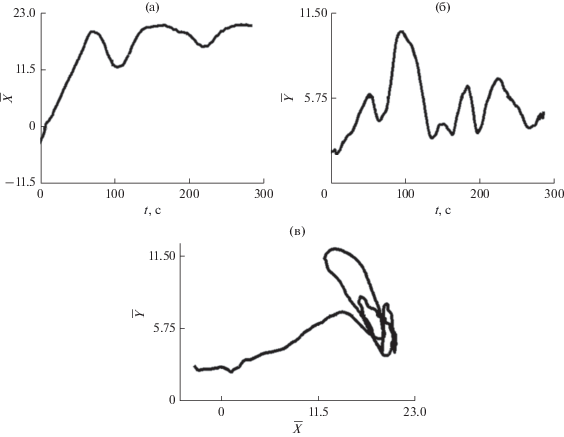
С использованием зависимостей $\theta \left( t \right)$ и $r\left( t \right)$ вычислены координаты источника

и траекторная зависимость $Y\left( X \right)$, представленные на рис. 8. Из него следует, что точка траверса была удалена от антенны на расстояние $r = 188$ м. Данная оценка близка к оценке, полученной из рис. 6. После прохождения точки траверса источник также перемещался прямолинейно, но по прямой, не параллельной оси x. В момент времени $t{\kern 1pt} '\sim 70$ с источник начинал совершать петлеобразные траектории.

Скорость источника w на временном интервале $\Delta t$ определялась как

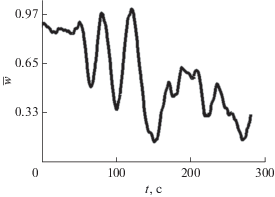
Нормированная временная зависимость $w\left( t \right)$ отображена на рис. 9. Видно, что на поворотах не только изменяется глубина, но и уменьшается скорость. Как следствие, зависимость скорости от времени имеет сложный изрезанный характер. Восстановленные координаты источника соответствуют реальным значениям, погрешность не превышает 10%.

ТЕОРЕТИЧЕСКАЯ МОДЕЛЬ ИНТЕРФЕРОГРАММЫ

Задача теоретического рассмотрения состояла в том, чтобы разобраться, как характеристики интерферограммы (или положения максимумов фокальных пятен голограммы) связаны с параметрами движущегося источника. Обсудим это на простом примере удаления источника от точки траверса B по прямолинейной траектории параллельно оси x с постоянной скоростью w и на фиксированной глубине z (рис. 1, пунктир). Допустим, что коэффициент отражения от свободной поверхности не зависит от частоты, угла падения и равен –1.

Рассмотрим для примера зону, в которой источник начинал движение из точки траверса в сторону удаления от приемника. Тогда двухлучевая интерферограмма принимает вид [19]

где

Здесь $\eta = {{2{{z}_{q}}z} \mathord{\left/ {\vphantom {{2{{z}_{q}}z} c}} \right. \kern-0em} c}$, c – скорость звука, ${{z}_{q}}$ – глубина приемника; $~r\left( t \right) = \sqrt {r_{0}^{2} + {{{\left( {wt} \right)}}^{2}}} $ – горизонтальное расстояние от приемника до источника в момент времени t, $~{{r}_{0}}$ – расстояние в начальный момент времени $t = 0$ от точки траверса до приемника; $\bar {R}\left( t \right) = \sqrt {{{r}^{2}}\left( t \right) + z_{q}^{2}} $; ${{W}^{2}}$ – коэффициент, характеризующий мощность излучения. Принимая в среднем глубину источника $z = 11$ м, имеем $\eta = 0.47$ м с.

Кривая интерференционных максимумов определяется условием

Используя (7), из (8) для производной кривой постоянной фазы получаем

Отсюда следует, что крутизна интерференционных полос в области траверса возрастает при увеличении времени, частоты, скорости источника и по мере удаления от точки траверса уменьшается. Подобный результат зарегистрирован и в эксперименте. Решая дифференциальное уравнение (9) при начальном условии $f\left( 0 \right) = {{f}_{0}}$, находим уравнение кривой интерференционных максимумов поля источника

Частотный масштаб изменчивости интерферограммы в момент времени t, как следует из (7), равен

так что он возрастает с возрастанием скорости источника и удалением от приемника, уменьшается с увеличением заглубления и не зависит от частоты. Подобные закономерности наблюдались и в эксперименте. Например, в точке траверса (${{r}_{0}} = 189$ м) получаем $\Lambda \left( 0 \right) = 402$ Гц, что согласуется с экспериментальным значением $\Lambda = 404$ Гц. Если ширину интерференционной полосы $\Delta f\left( t \right)$ определить как ширину, в пределах которой фаза (7) меняется на ${{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2}$, то $\Delta f\left( t \right) = {{\Lambda \left( t \right)} \mathord{\left/ {\vphantom {{\Lambda \left( t \right)} 4}} \right. \kern-0em} 4}$. Величина $\Delta {\tau }$, обратная частотному масштабу, $\Delta {\tau } = {1 \mathord{\left/ {\vphantom {1 \Lambda }} \right. \kern-0em} \Lambda }$, представляет собой разность времен прихода прямого и отраженного от свободной поверхности лучей.

Временной масштаб D изменчивости интерферограммы, как следует из (7), определяется условием

Аналитического решения эта задача не имеет, поэтому обратимся к тем результатам, которые можно извлечь из (12) в некоторых предельных случаях.

1. Пусть $r_{0}^{2} \gg {{\left( {wt} \right)}^{2}}$, т.е. рассматривается окрестность точки траверса, когда радиальная скорость равна нулю. Тогда, как следует из (12),

где $a = {{2r_{0}^{3}} \mathord{\left/ {\vphantom {{2r_{0}^{3}} {f{{w}^{2}}}}} \right. \kern-0em} {f{{w}^{2}}}}$. На практике можно ограничиться более слабым неравенством $r_{0}^{2} \geqslant 3{{\left( {wt} \right)}^{2}}$. Для условий эксперимента данное приближение реализуется уже при $t \leqslant 4$ с. В точке траверса $t = 0$ имеем

Для полученных оценок (${{r}_{0}} = 189$ м, $\eta = 0.47$ м с), задаваясь частотой $f = 3.5$ кГц, имеем $D\left( 0 \right) = 3.3$ с, что близко к экспериментальному значению $D = 2.9$ с.

2. Пусть $r_{0}^{2} \ll {{\left( {wt} \right)}^{2}}$, т.е. расстояние от источника до приемника больше траверсного расстояния. В этом случае, согласно (12),

где $b = {w \mathord{\left/ {\vphantom {w {\eta f}}} \right. \kern-0em} {\eta f}}$. С ростом времени слагаемое bt растет и при значении ${{t}_{{{\text{cr}}}}} = {1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0em} b}$ временной масштаб становится бесконечным, так что локализация интерференционных полос производится вдоль горизонтальных линий. Предельному значению ${{t}_{{{\text{cr}}}}}$ отвечает удаление источника от антенны ${{r}_{{{\text{cr}}}}} = f$. Задаваясь значениями $\eta = 0.47$ м с, $f = 3.5$ кГц, получаем: ${{t}_{{{\text{cr}}}}} = 60$ с, ${{r}_{{{\text{cr}}}}} = 1.64$ км. Данный эффект наблюдается на экспериментальной (см. рис. 2а) и модельной (см. рис. 5) интерферограммах и полностью согласуется с известными характеристиками поля для модели, когда справедлив эффект Ллойда [20].

Очевидным условием наблюдаемости интерферограммы является требование, чтобы ширина спектра $\Delta f$ хотя бы в несколько раз превышала частотный масштаб $\Lambda \left( t \right)$ (11). В качестве критерия наблюдаемости интерферограммы примем неравенство

которое эквивалентно условию, что наблюдается одна и более интерференционных полос. Ширина спектра ограничивает удаление источника от приемника, при этом максимальное удаление, соответствующее условию реализации одной полосы, оценивается как так что с увеличением полосы анализа и заглубления источника максимальное удаление возрастает. Для условий эксперимента ${{r}_{{{\text{max}}}}} = 3.29$ км.

Можно показать также, что координаты максимума фокального пятна на голограмме (1), отвечающие действительному изображению источника, в точке траверса равны ${\tau } = {\eta \mathord{\left/ {\vphantom {\eta {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}$, $\nu = 0$. Для оценок $\eta = 0.47$ м с, ${{r}_{0}} = 189$ м получаем ${\tau } = 2.5$ мс, что близко к экспериментальному значению ${\tau } = 2.4$ мс (см. рис. 3).

Таким образом, модельная интерферограмма адекватно передает основные свойства экспериментальной интерферограммы до момента времени, когда источник начал совершать петлеобразные траектории.

ЗАКЛЮЧЕНИЕ

Изложен высокочастотный интерферометрический метод локализации шумового источника, использующий сигнал с одного из одиночных приемников антенны. В основе метода лежит частотно-временная обработка шумовых сигналов, согласованная с интерферограммой, формируемой движущимся источником. Модельная интерферограмма строилась на основе интерференции полей двух лучей: прямого и отраженного от свободной поверхности лучей. Метод апробирован на данных натурного эксперимента. По результатам обработки восстановлены временные зависимости пеленга, расстояния до антенны, скорости и глубины источника.

Двухлучевая модельная интерферограмма не требует знаний о параметрах дна и устойчива к поверхностному волнению, поэтому предложенная согласованная обработка оказалась работоспособной, позволив получить правильные временные зависимости параметров шумового источника. Совокупная картина фокальных пятен голограммы позволяет определять число лучей, формирующих поле, в различных акваториях. С удалением источника от приемника число лучей может увеличиваться, что будет приводить к усложнению интерференционной картины волнового поля. Если фокальные пятна не перекрываются, то на голограмме можно будет вырезать отдельные фокальные пятна и по отношению к ним реализовать обратное двукратное преобразование Фурье. Это даст возможность работать с двухлучевой интерферограммой, устойчивой по отношению к вариациям параметров дна.

Работа выполнена при финансовой поддержке грантов РФФИ (№ 19-08-00941, № 19-29-06075). Научно-исследовательская работа Д.Ю. Просовецкого поддержана грантом Президента РФ (№ МК-933.2019.8).