Акустический журнал, 2020, T. 66, № 4, стр. 391-400

1. Одним из важных объектов исследования в теории волн (в том числе акустических) являются волны в различных диспергирующих средах [1–13]. В широком смысле среда называется диспергирующей (средой с дисперсией), если в такой среде отклик на воздействие зависит не только от возмущения в данный момент времени в данной точке пространства, но и от возмущения в предыдущие моменты времени (временная дисперсия) в некоторой области среды, окружающей данную точку (пространственная дисперсия). Временная дисперсия приводит к зависимости функций отклика (диэлектрической или/и магнитной проницаемости, проводимости и т.д.) от частоты, поэтому она также называется частотной дисперсией. Пространственная дисперсия при распространении линейных волн обычно проявляется на достаточно высоких частотах, поэтому ее иногда называют высокочастотной дисперсией.

Учет сильной дисперсии приводит к тому, что уравнения, описывающие распространение возмущений в среде, становятся интегро-дифференциальными [1–3, 10–23]. Вообще говоря, оба вида дисперсии могут присутствовать в каждой диспергирующей среде, однако довольно часто в рамках рассматриваемой задачи удается выделить наиболее существенную из них. Временная дисперсия существенна, когда частоты распространяющихся в среде волн близки к собственным частотам колебаний среды, а также когда в среде имеются процессы типа поглощения или релаксации. В акустике сильная временная дисперсия при распространении линейных и нелинейных волн возникает, например, в релаксирующих жидкостях и газах, полимерах, биологических тканях и других сложно устроенных средах [1–3, 6, 13–23]. Образующиеся здесь интегро-дифференциальные уравнения обладают тем свойством, что содержащиеся в них интегралы ограничены сверху текущим моментом времени (либо сводятся к таковым). Последнее непосредственно следует из принципа причинности: реакция среды в текущий момент времени определяется воздействием на нее в прошлом и настоящем. Пространственная дисперсия обусловлена пространственной нелокальностью среды (влиянием всего окружения на каждую точку среды), что приводит в уравнениях к интегралам по всему объёму, занимаемому средой.

Одна из наиболее сложных проблем в анализе интегро-дифференциальных уравнений состоит в том, что часто точный вид ядра интегрального члена не известен. Точный вид ядра можно определить из микроскопического рассмотрения проблемы, что далеко не всегда возможно и выходит за рамки феноменологического подхода. С другой стороны, уравнения не могут быть решены без формального задания ядра. Поэтому возникает необходимость привлечь к моделированию ядра дополнительные физические или математические соображения. Во многих случаях про ядра интегральных членов уравнений заранее можно сказать следующее [1–5, 10–15]. В случае временной дисперсии в ядра наиболее существенный вклад дают времена, меньшие или сравнимые с характерным временем среды (например, со временем релаксации). В случае же пространственной дисперсии основной вклад в ядро вносят пространственные масштабы, меньшие или сравнимые с характерным для рассматриваемой среды размером (постоянной кристаллической решетки, длиной свободного пробега частиц, дебаевским радиусом, толщиной слоя жидкости, характерным размером зерен, диаметром поперечного сечения упругой или электропроводящей проволоки и т.д.). Дальнейшие предположения о структуре ядра могут быть получены, например, из свойств однородности и изотропности среды, однородности времени, соображений симметрии, поведения асимптотик, условий нормировки и т.д. В случае временной дисперсии важным фактором, позволяющим судить о структуре ядра, являются соотношения Крамерса–Кронига, которые являются следствием принципа причинности [1‒6]. Соотношения Крамерса–Кронига давно и активно используются в акустике [24–27]. Другие методы, широко используемые в акустике, основаны на восстановлении ядер либо из экспериментальных данных, либо из модельных представлений о внутренней динамике молекулярных или надмолекулярных структур. Такие подходы широко практикуются, например, в медицинской акустике и эластографии [15–17]. Соответствующая математическая процедура восстановления ядра описана в работах [1, 28].

В данной работе на примере конкретного нелинейного интегро-дифференциального уравнения с пространственной дисперсией (так называемого уравнения Уизема) предложен подход к моделированию ядра, основанный на выделении из него “главной” и “поправочной” частей. “Главная” часть учитывает фундаментальные требования к ядру в пределах рассматриваемой задачи (симметрии, нормировки, особенности асимптот и т.д.). Поправки же предназначены для того, чтобы учесть некоторые более тонкие свойства распространяющихся волн (например, особенности законов дисперсии). В рамках данного подхода анализируются уединенные волны на поверхности жидкости. Показано, что для волн на поверхности мелкой воды с помощью подбора параметров можно получить правильное значение угла Стокса.

2. Одним из модельных уравнений, используемых для исследования нелинейных волн в системах гидродинамического типа с сильной пространственной дисперсией, является уравнение [10–12]

где ${{с}_{0}}$ – скорость звука. В теории распространения волн на поверхности воды и математической физике уравнение (1) получило название уравнения Уизема. Это уравнение достаточно универсально. Оно встречается в теории поверхностных и внутренних волн в жидкости, в физике бесстолкновительной плазмы, в нелинейной оптике и т.д. [10–12, 29–37]. Уравнение (1) является интересным объектом для математических исследований, не только как нелинейное интегро-дифференциальное уравнение в частых производных, но и как уравнение, из которого при соответствующем выборе ядра $\kappa (x)$ следуют многие известные нелинейные уравнения: Бенджамина–Оно, Бюргерса, Кортевега–де Фриза (КдФ) и некоторые другие [11, 30, 37–41]. Отметим, что в уравнении (1) с формально математической точки зрения (отвлекаясь от смысла переменных x и t) можно представить ядро ${\kappa }$ в виде произведения $\kappa (x) = \theta (x)K(x),$ где θ(x) – θ-функция Хэвисайда, а K(x) – произвольная функция. Тогда в интегральном члене рассматриваемого уравнения верхний предел интегрирования становится переменным, равным x. В таком виде уравнение (1) становится подобным уравнениям, используемым для описания волн в средах с временной дисперсией. Заметим, что в этом случае уравнение (1) не совпадает с полученным в работе [14] и обобщенным в работе [15] интегро-дифференциальным уравнением (упрощенным за счет одномерности и пренебрежения вязкостью): в (1) не достает дополнительной производной в интегральном слагаемом. Как уже отмечалось, наличие переменного верхнего предела (или, что эквивалентно, θ-функции в ядре) связано с действием принципа причинности, который обязан выполняться, если речь идет о времени t. В случае пространственной дисперсии наличие в ядре θ-функции, зависящей от пространственной переменной x, соответствует ситуации, когда реакция среды в данной точке пространства x определяется областью, находящейся только с одной стороны от этой точки (например, слева), что представляется достаточно специфичным. Поэтому, когда речь идет о пространственной переменной x, будем предполагать, что интеграл в (1) берется по всей области пространства, занимаемого средой, в данном случае – в бесконечных пределах.

Для удобства анализа в (1) выбрана калибровка, когда коэффициент перед нелинейным слагаемым равен единице. В результате величина $\eta $ в (1) имеет размерность скорости. Первое слагаемое в (1) ответственно за нестационарность процесса, второе – учитывает типичную для гидродинамических сред нелинейность, а последний (интегральный) член описывает пространственную дисперсию. Будем считать, что ядро $\kappa (x)$ удовлетворяет следующим условиям: 1) в силу пространственной однородности среды зависит только от разности координат: $\kappa (x - x{\kern 1pt} ')$; 2) в силу изотропии среды (эквивалентности прямого и обратного направлений распространения волны) является четной функцией: $\kappa ( - x) = \kappa (x)$; 3) спадает на бесконечности $\kappa ( \pm \infty ) = 0$; 4) нормировано на единицу:

В общем случае ядро $\kappa (x)$ может быть получено из фазовой скорости линейной волны

где $\omega (k)$ – закон дисперсии волны, с помощью обратного преобразования Фурье [10–12]

При известном законе дисперсии выражение (4) определяет ядро $\kappa (x)$.

Часто ограничиваются случаем, когда закон дисперсии линейных волн имеет полиномиальный (степенной) характер

В частности, при N = 1 в правой части выражения (5) получаем полином третьей степени. Соответствующий закон дисперсии имеют волны в средах со слабой пространственной дисперсией. Выражению (5) соответствует ядро

где $\delta (x)$ – дельта-функция Дирака. В этом случае уравнение (1) сводится к виду

Значение N = 1 соответствует уравнению Кортевега–де Фриза, которое является уравнением третьего порядка. При N > 1 возникают различные уравнения более высоких порядков [35, 42–45].

Если закон дисперсии не является полиномиальным, то в общем случае ядро $\kappa (x)$ вычислить не удается. Иногда ядро $\kappa (x)$ удается аппроксимировать более простой функцией $\gamma (x)$ и тем самым преобразовать интегро-дифференциальное уравнение (1) в дифференциальное. Однако при такой аппроксимации может потеряться часть важной информации, содержащейся в функции

Последнее может приводить к искажению характеристик исследуемых нелинейных волн, а также, например, к тому, что законы дисперсии линейных волн, соответствующие $\kappa (x)$ и $\gamma (x)$, могут существенно различаться.

Примером такой ситуации является применение уравнения (1) к исследованию слабо нелинейных волн на поверхности слоя жидкости [10–12]. В этом случае закон дисперсии линейных волн имеет вид

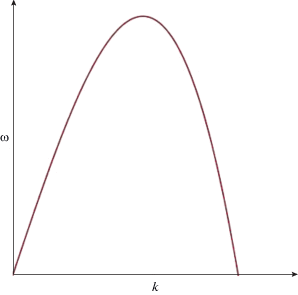
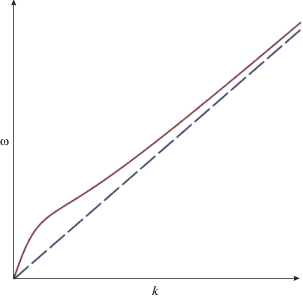
где ускорение свободного падения g, глубина слоя ${{h}_{0}}$ и скорость ${{c}_{0}} = \sqrt {g{{h}_{0}}} $ приняты равными единице: $g = {{h}_{0}} = {{c}_{0}} = 1$, а частота $\omega $ и волновое число k считаются безразмерными. График функции (9) приведен на рис. 1.

Ядро интегрального слагаемого в (1), соответствующее закону дисперсии (9), равно

Функция (10) имеет асимптоты [10–12]

Основываясь на (11) и (12), Уизем предложил аппроксимировать ядро $\kappa (x)$ функцией

которая является фундаментальным решением уравнения

Подставляя в уравнение (1) вместо ядра $\kappa (x)$ выражение (13) (т.е. считая, что $\kappa (x) = \gamma (x)$) и действуя на обе части получившегося уравнения оператором $\partial _{x}^{2} - {{\left( {\tfrac{\pi }{2}} \right)}^{2}}$, получим дифференциальное уравнение

Линеаризуя (15), получим закон дисперсии волн, соответствующих ядру (13)

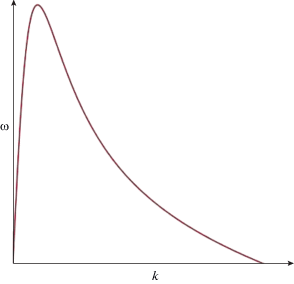
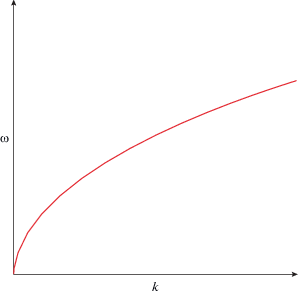
График функции (16) приведен на рис. 2.

Из рис. 1 и 2 видим, что кривые дисперсии, соответствующие исходному $\kappa (x)$ (9) и аппроксимированному $\gamma (x)$ (13) ядрам, качественно совпадают только при малых $k$, а при больших $k$ существенно различаются: первая дисперсионная кривая неограниченно возрастает, а вторая – стремится к нулю. Другим недостатком указанной аппроксимации является невозможность получить значение угла заострения на вершине уединенной волны предельной амплитуды, равное углу Стокса ${{\vartheta }_{S}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-0em} 3}$ [10–12]. Приведенный пример указывает на то, что необходима модификация подхода Уизема, лишенная указанных недостатков.

3. Подстановка $\kappa (x) = \gamma (x) + r(x)$ в интегральный член в (1) приводит к появлению двух интегральных слагаемых. Считаем функции $r(x)$ и $\gamma (x)$ четными. Тогда слагаемое, обусловленное функцией $r(x)$, можно представить в виде следующего бесконечного ряда

где

В результате уравнение (1) сводится к интегро-дифференциальному уравнению бесконечного порядка, которое эквивалентно тому же уравнению Уизема с ядром

При известном законе дисперсии из выражений (4) и (19) можно получить функцию $\gamma (x)$. В силу обращения в нуль интегралов, содержащих производные от дельта-функций, условие нормировки (2) после подстановки в него выражения (19) дает

Как видим, слагаемые с номерами $n \geqslant 1$ не дают вкладов в условие нормировки.

В выражении (17) по порядку величины

где $\Delta $ – характерный масштаб изменения функции $\eta (x)$, $\ell $ – характерный масштаб, на котором спадает на бесконечность ядро $r(x)$. Когда функция $\eta (x)$ является гладкой по сравнению с ядром $r(x)$, величина $\Delta $ значительно превышает $\ell $: соответственно, каждый последующий член ряда (17) будет по порядку величины меньше предыдущего члена в ${{\left( {{\ell \mathord{\left/ {\vphantom {\ell \Delta }} \right. \kern-0em} \Delta }} \right)}^{2}} \ll 1$ раз. В результате, отбрасывая члены, имеющие более высокий порядок малости, ряд (17) (и, соответственно, ряд в выражении (19)) с нужной степенью точности может быть оборван на каком-либо слагаемом с номером n = N. В этом случае уравнение (1) принимает вид

Уравнению (23) отвечает закон дисперсии

где $\tilde {\gamma }(k)$ – Фурье-образ функции $\gamma (x)$. Выражение (24) кроме полинома степени 2N содержит также неполиномиальный вклад, определяемый функцией $\tilde {\gamma }(k)$.

Выберем ядро $\gamma (x)$ в уравнении (23) в виде

где $\beta $ – произвольная постоянная, а функция удовлетворяет уравнению

Величина, обратная $q$, определяет характерный размер, на котором происходит спадание функции ${{\gamma }_{0}}(x)$.

Используя условие нормировки (20) и обозначая ${{\alpha }_{0}} = - \alpha $, из (25) и (26) получаем

Как видим, в рассматриваемом случае в силу условия нормировки константа $\beta $ полностью определяется значением $\alpha $.

Подставляя выражения (25) и (26) в уравнение (23), действуя на обе части получившегося уравнения оператором $\left( {\partial _{x}^{2} - {{q}^{2}}} \right)$, учитывая (27) и (28), получим дифференциальное уравнение

Данное уравнение содержит производные высших порядков и нелинейности вида $\eta {{\eta }_{x}}$,$\eta {{\eta }_{{xxx}}}$, $\eta {}_{x}{{\eta }_{{xx}}}$. Различные варианты такого типа уравнений обсуждаются в литературе [35, 42–45].

4. Остановимся более подробно на случае, когда в (29) слагаемым, содержащим сумму по $n$, можно пренебречь. В этом случае уравнение (29) сводится к виду

Отметим, что уравнение (30) зависит от единственного параметра $\alpha $, который входит в него в качестве коэффициента перед третьей производной $\partial _{x}^{3}\eta $.

Уравнение (30) соответствует выбору ядра $\kappa (x)$ в виде

Функция $\kappa (x)$ (31) содержит два независимых параметра $\alpha $ и $q$, которые, соответственно, характеризуют ее амплитуду и ширину. Частный случай ядра (31) рассматривался в работе [46] при исследовании нелинейных волн в упругих средах с сильной пространственной дисперсией. Рассмотренный Уиземом случай, когда ядро аппроксимируется функцией (13), соответствует $\alpha = 0$ и $q = \frac{\pi }{2}$.

Линеаризуя (30), получим закон дисперсии ${\omega }(k)$, который запишем в виде

Значение $\alpha = - 1$ соответствует акустическому закону дисперсии $\omega = {{c}_{0}}k$. В этом случае в ядре (31) остается единственное слагаемое, равное дельта-функции Дирака. Экстремумы функции (32) находятся в точках, где обращается в нуль групповая скорость

что достигается при значениях k, равных

Корень ${{k}_{ - }}$ будет вещественным при $ - \tfrac{1}{9} \leqslant \alpha < 0$, а ${{k}_{ + }}$– при $ - \tfrac{1}{9} \leqslant \alpha $. Таким образом, в области $ - \tfrac{1}{9} \leqslant \alpha < 0$ имеется два вещественных корня ${{k}_{ \pm }}$, отвечающих максимуму и минимуму функции $\omega (k)$, а в области $0 \leqslant \alpha $ – один вещественный корень, отвечающий максимуму $\omega (k)$.

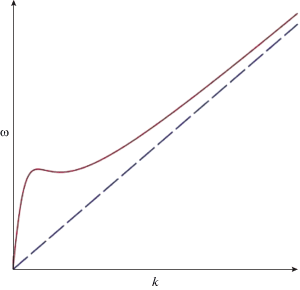
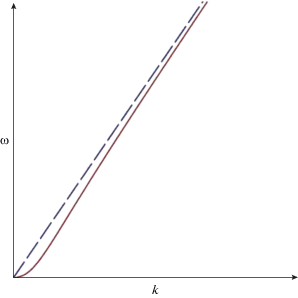
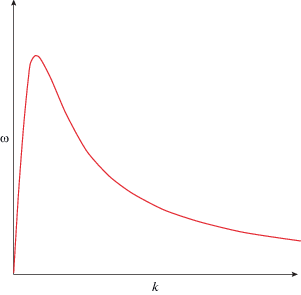
Характерные графики законов дисперсии приведены на рис. 3–7 (${{c}_{0}} = 1,\,q = 1$). Из приведенных графиков следует, что ядро (31) описывает достаточно широкий спектр законов дисперсии. График для случая $\alpha = 0$ аналогичен графику на рис. 2. Если значение $\alpha $ неотрицательно ($\alpha \geqslant 0$), то, как видно из рис. 2–4, кривые дисперсии ограничены сверху. Для отрицательных значений параметра $\alpha $ ($\alpha < 0$) при больших значениях волнового числа $k$ кривые дисперсии (32) асимптотически выходят на прямую линию

которая изображена на рис. 5–7 пунктирной линией.

Несмотря на наличие указанной асимптоты, закон дисперсии (32) при отрицательных значениях параметра $\alpha < 0$ качественно отражает свойство функции (9) неограниченно возрастать при $k \to \infty $. Последнее позволяет сделать вывод о предпочтительности выбора ядра (31) по сравнению с ядром (13) при описании с помощью уравнения Уизема гравитационных волн в слое жидкости.

Отметим, что наличие асимптот в виде прямой линии на графике дисперсионных кривых при $\alpha < 0$ является следствием выбранного приближения, согласно которому в уравнении (29) пренебрегли членами, содержащими все высшие производные, кроме третьей. Действительно, если взять уравнение (29) полностью, то после его линеаризации получим закон дисперсии

Поскольку выражение (36) является аппроксимацией точного закона дисперсии, то число N и коэффициенты ${{\alpha }_{{2n}}}$ могут быть подобраны так, что (36) будет качественно правильно отражать особенности аппроксимируемого выражения при любых значениях k. При больших значениях волнового числа ($k \gg q$) из (36) получаем

Как видим, при больших $k$ закон дисперсии является полиномиальным и асимптоты в виде прямых (35) появляются только в случае, когда в выражении (37) мы пренебрегаем слагаемыми, содержащими все степени $k$, кроме первой.

5. Рассмотрим теперь стационарные нелинейные волны, удовлетворяющие уравнению (30). Считаем $\eta = \eta (\xi )$, где$\xi = x - ct$, c – скорость возмущения. Тогда в целях удобства дальнейшего анализа уравнение (30) запишем для безразмерной функции $y(\xi )$:

где

Рассматривая спадающие на бесконечности решения $\partial _{\xi }^{n}y( \pm \infty ) = 0,$ $n = 0,\,\,1$, преобразуем уравнение (38) к виду

где штрих означает производную по $\xi $, а

Уравнение (41) имеет решение в виде волны предельной амплитуды [10–12], для которой

В этом случае уравнение (41) сводится к виду $y{\kern 1pt} ' = \pm qy$, а его решение запишется в форме

где ${{\xi }_{0}}$ – произвольная постоянная. Видим, что для волны предельной амплитуды $0 \leqslant y \leqslant \tfrac{4}{3}$, а сама волна имеет характерное заострение на гребне волны (в точке $\xi = {{\xi }_{0}}$) [10–12]. Возвращаясь к исходной функции $\eta (\xi )$, получаем

где

Из условия $\sigma = \tfrac{4}{3}$ и (40) находим, что скорость волны предельной амплитуды равна

Из (46) и (47) следует, что амплитуда ${{\eta }_{ \pm }}$ и скорость $c$ волны предельной амплитуды зависят от параметра $\alpha $. Так как $c > 0$, то волны предельной амплитуды существуют только при $\alpha > - 4$. При $ - 4 < \alpha < - 1$ имеем дозвуковую волну ($c < {{c}_{0}}$), отрицательная амплитуда которой ограничена снизу значением ${{\eta }_{{\min }}} = - 4{{c}_{0}}$: ${{\eta }_{{\min }}} < {{\eta }_{ \pm }} < 0$. Если же $\alpha > - 1$, то волна будет сверхзвуковой ($c > {{c}_{0}}$) и иметь положительную амплитуду (${{\eta }_{ \pm }} > 0$).

Угол заострения на вершине волны предельной амплитуды $\vartheta $ также определяется параметром $\alpha $:

Угол $\vartheta $ отрицателен при $ - 4 < \alpha < - 1$, т.е. для сверхзвуковых волн положительной амплитуды, и положителен при $\alpha > - 1$, т.е. для дозвуковых волн отрицательной амплитуды. Из (48) видим, что при ${{c}_{0}} = 1$ и $q = \tfrac{\pi }{2}$ для волн на поверхности воды угол Стокса ${{\vartheta }_{S}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-0em} 3}$ [10] соответствует значению $\alpha = \frac{{3\sqrt 3 }}{\pi } - 1 \approx 0.65$. Таким образом, с помощью подбора параметра $\alpha $ можно получить значение угла заострения для волн предельной амплитуды на поверхности слоя воды, равное углу Стокса.

6. Вблизи $\sigma = 1$ величина ${{y}_{ - }}$ мала

а ${{y}_{ + }} \approx \tfrac{4}{3}$. Вследствие этого при значениях $\sigma $, близких к 1, имеем $\left| y \right| \leqslant {{y}_{ - }} \ll \sigma < {{y}_{ + }}$, а уравнение (41) принимает вид

Это уравнение имеет решение c профилем, характерным для односолитонного решения уравнения Кортевега–де Фриза. В результате для исходной функции $\eta (\xi )$ получаем

где амплитуда ${{\eta }_{ - }}$ определяется выражениями (39), (49), а ширина $\Delta $ равна

Из полученных выражений следует, что чем ближе $\sigma $ к 1, тем меньше амплитуда солитона и больше его ширина. Учитывая (40), получаем, что ширина солитона

а его амплитуда в исходных переменных согласно (39) и (49) равна

Как видим из (53) и (54), амплитуда возмущения ${{\eta }_{ - }}$ не зависит от параметра $\alpha $, а определяется разностью $\Delta с$ между скоростью возмущения $c$ и скоростью звука ${{c}_{0}}$. Ширина $\Delta $, наоборот, зависит как от $\Delta с$, так и от параметра $\alpha $. В результате получаем, что при $\alpha > - 1$ мы имеем дело со сверхзвуковым солитоном ($c > {{c}_{0}}$) положительной амплитуды ${{\eta }_{ - }} > 0$, а при $\alpha < - 1$ – с дозвуковым ($c < {{c}_{0}}$) солитоном отрицательной амплитуды ${{\eta }_{ - }} < 0$.

7. Будем считать, что профиль волны медленно изменяется в пространстве, а уравнение (30) запишем в сопровождающей (сопутствующей) системе координат [1–3]. Для этого положим $\eta = \eta (\tau ,\varepsilon x)$, где $\tau = t - \frac{x}{{{{c}_{0}}}}$, а $\varepsilon $ – малый параметр. В нулевом порядке по $\varepsilon $ получаем

где $\theta = {{с}_{0}}\tau $. Для уединенных возмущений в результате чего уравнение (55) преобразуется к виду

Положим

где функция z (соответственно ${{\eta }_{1}}$) удовлетворяет условиям

После несложных преобразований уравнение (57) приводится к виду

где $s = 1 - {{z}_{0}}$, штрих означает производную по $\theta $, а

Волнам предельной амплитуды соответствует

что приводит к решению

Волна малой амплитуды возникает вблизи ${{z}_{0}} = 0$. В этом случае

Считая, что $\left| z \right| \leqslant {{z}_{ - }} \ll 1 < {{z}_{ + }}$, получаем уравнение

которое по форме совпадает с (50). Из (65) и (58) получаем где

Нетрудно видеть, что функции $\eta (\xi )$ и $\eta (\theta )$ связаны между собой преобразованием

Для волн предельной амплитуды ${{\eta }_{0}} = - {{{{c}_{\alpha }}} \mathord{\left/ {\vphantom {{{{c}_{\alpha }}} 3}} \right. \kern-0em} 3}$, а для волн малой амплитуды ${{\eta }_{0}} = - \Delta c$.

Поскольку преобразование (68) не затрагивает параметров q и α, то выводы, сделанные в координатах $\xi $ о связи этих параметров со свойствами уединенных волн, остаются справедливыми также в координатах $\theta $.