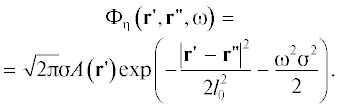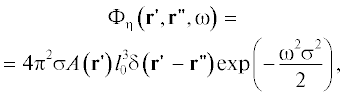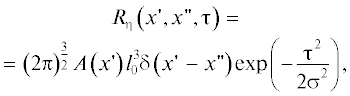Акустический журнал, 2020, T. 66, № 5, стр. 540-555

ВВЕДЕНИЕ

Шум турбулентной струи, как известно, является одной из важных составляющих шума современного самолета на местности. На протяжении уже свыше 60 лет он находится в фокусе экспериментальных, теоретических и расчетных исследований. Одним из возможных способов снижения шума струи на местности является его экранирование различными элементами планера самолета. Вместе с тем, несмотря на значительную предысторию, теоретическое описание экранирования шума струи далеко от завершения.

Задача экранирования шума струи имеет длительную историю, берущую свое начало в 70-х годах XX-го века. Первые расчетно-экспериментальные исследования экранирования шума струи были выполнены в работах [1–3], в которых также были предложены упрощенные расчетные модели для описания самого шума струи. Так, струя, как источник звука, представлялась в виде набора распределенных вдоль оси монополей, или в виде расположенного на срезе сопла точечного источника с диаграммой направленности, соответствующей излучению струи в дальнем поле. Дифракция звука, излучаемого такими источниками, рассчитывалась с помощью метода Маекавы [4] или решения Макдональда для полуплоскости [5]. Результаты данных исследований, выполненные для одноконтурных турбореактивных двигателей и двигателей с малой степенью двухконтурности, продемонстрировали чрезвычайно высокий потенциал снижения шума струи с помощью эффекта экранирования, что послужило толчком к проработке новых компоновочных схем для самолетов нового поколения, в которых эффект экранирования мог бы быть реализован в полной мере.

Однако активное совершенствование конструкции турбореактивных двигателей (переход на двигатели большой и сверхбольшой степени двухконтурности, применение звукопоглощающих конструкций и проч.) привело к тому, что интерес к исследованию эффекта экранирования шума струи существенно снизился. Тем не менее, когда в начале XXI века требования по снижению шума самолетов на местности начали опять ужесточаться, а резервы для дальнейшего снижения шума современных двухконтурных двигателей стали уменьшаться, снижение шума с помощью эффекта экранирования снова стало актуальной научно-исследовательской и конструкторской задачей.

Выполненные в последнее время экспериментальные исследования продемонстрировали существенно меньшую эффективность экранирования шума струи [6–10], чем предсказывали ранние расчеты, проведенные на основе методов, разработанных в [1–3]. Детальный анализ показал, что причиной расхождения экспериментальных и теоретически предсказанных результатов является не только использование упрощенных методов расчета дифракции звука [11, 9 ] и неучет свойства некомпактности источника звука [9, 10], но и применение грубых моделей, описывающих турбулентную струю как источник шума [12].

На данный момент нет общепринятого ответа на вопрос о том, какая часть турбулентности отвечает непосредственно за излучение звука струей, что и обуславливает большое разнообразие моделей шума струи. В работах рассматриваются модели источников шума, связанные с различными их представлениями и механизмами аэродинамической генерации: мелкомасштабной турбулентностью [13–19], волнами неустойчивости [19, 20], собственными колебаниями крупномасштабных вихрей [21–23], рождением вихревых структур [24–26] и др. Эти теории в том или ином виде использовались также и в приложении к задаче экранирования шума турбулентных струй [27–47].

Одной из первых работ по расчетной оценке эффекта экранирования шума струи стала работа [27], в которой источники шума струи описывались на основе акустической аналогии Лайтхилла [28], а для описания экранирования рассматривался экран конечных размеров. В данной работе применялся гибридный подход: предполагалось, что струя находится в бесконечном пространстве, в котором отсутствует экран, а расчет экранирования излучаемого струей шума осуществлялся с помощью метода Маекавы [4] путем разбивания струи на излучающие звук объемы малых размеров. Однако в то время для надежного использования подобного подхода было недостаточно информации о корреляционных свойствах источника.

В работах [29–34], исходя из представлений о шуме струи как шуме волн неустойчивости, был проведен расчет эффективности экранирования с помощью метода граничных элементов [35], а форма и параметры волновых пакетов определялись на основе подгонки под экспериментальные данные, полученные для шума изолированной струи в дальнем поле. Проведенное сравнение расчетных и экспериментальных данных излучаемого волновыми пакетами шума продемонстрировало хорошее качественное, а при определенных скоростях истечения струи и количественное совпадение. Однако эта расчетная модель продемонстрировала высокую чувствительность к форме и параметрам волнового пакета, что делает модель крайне зависимой от заложенных в нее параметров.

В работах [36–41] проводилось исследование шума, излучаемого при взаимодействии ближнего гидродинамического поля волн неустойчивости с кромкой экранирующей поверхности. При этом в работах [36–41] волны неустойчивости моделировались с помощью тензора напряжений Рейнольдса, параметры которого подбирались из условия совпадения с экспериментом в дальнем поле, а в [42–44] моделировались непосредственно пульсации давления в ближнем поле, свойства которых определялись на основании теории гидродинамической устойчивости для слоя смешения и данных эксперимента. Было показано, что такое взаимодействие приводит к возникновению звукового поля, интенсивность которого экспоненциально зависит от расстояния между плоскостью экрана и слоем смешения струи. Особенностью данного поля является его симметричность относительно экранирующей поверхности, т.е. оно присутствует также в зоне тени, и, при близком расположении струи и экрана, может нивелировать эффект экранирования в области низких и средних частот.

Изучению взаимодействия шума струи с экранами различного типа посвящены работы [45–47], в которых в приложении к задачам экранирования развивалась теория мелкомасштабной турбулентности. В статье [45] рассматривалось экранирование шума бесконечной полуплоскостью, а в работе [47] было рассмотрено влияние скоса задней кромки крыла на снижение шума, причем расчет в обоих случаях осуществлялся на основании точного решения Макдональда [5]. При этом с целью учета эффекта низкочастотного усиления шума, описанного в [36–44], в исходную модель [15] были добавлены волны, экспоненциально затухающие по радиальной координате, амплитуды и фазовые скорости которых определялись из численного моделирования. Сравнение экспериментальных и расчетных данных показало хорошее количественное соответствие для низкочастотного усиления, однако для эффекта экранирования в области высоких частот соответствие было скорее качественным, чем количественным.

Из числа работ, посвященных прямому расчету шума струи в присутствии экранирующих поверхностей, следует обратить внимание на работу [48], где был выполнен расчет шума круглой двухконтурной струи, расположенной вблизи крыла. Сравнение расчетных и экспериментальных спектров шума продемонстрировало приемлемое согласие, однако значительные вычислительные мощности, необходимые в данном случае, ограничивают область применения вихреразрешающих численных методов в задачах расчета эффективности экранирования.

В целом, анализ работ, посвященных исследованию экранирования шума струи, свидетельствует, что точность расчета эффективности экранирования существенно зависит как от качества моделей, описывающих шум струи, так и от точности используемых методов расчета дифракции звука. При этом к настоящему времени отсутствуют модели для расчетной оценки эффективности экранирования шума струи, которые, с одной стороны, являлись бы сравнительно простыми и универсальными, а с другой – обеспечивали приемлемую точность расчета.

В настоящей работе для описания процесса звукового излучения турбулентной струей используется корреляционная модель источников шума, разработанная в [24–26]. В этой модели генерация возмущений описывается случайным полем с некоторой эмпирической пространственно-временной корреляционной функцией. В качестве основной стохастической переменной используется интенсивность генерации турбулентных возмущений. Это дает возможность, в отличие от прямого стохастического моделирования интенсивности турбулентных пульсаций [29–31], свести звуковые источники к локальным процессам с малым пространственным масштабом, исключив конвекцию источников из корреляционной функции, и минимизировать неопределенность, связанную с эмпирическим моделированием характеристик случайного поля источников. Этот подход в совокупности с выбором квадрупольного типа источников дает возможность построить простую и эффективную модель, позволяющую предсказывать не только мощность звукового излучения струи, но и фазовые характеристики акустического поля, что необходимо для анализа взаимодействия шума струи с располагающимися вблизи нее твердыми поверхностями.

Поскольку источники авиационного шума располагаются в непосредственной близости к экранирующей поверхности и являются акустически некомпактными (как, например, реактивная струя), то для корректного описания дифракции звука необходимо, чтобы метод расчета дифракции, применяемый для определения эффективности экранирования, достаточно точно описывал как амплитудные, так и фазовые характеристики дифрагированного поля [9, 10]. Так как точные аналитические решения дифракционной задачи для рассматриваемых в приложениях геометрий экранов отсутствуют, то при расчете экранирования шума необходимо рассматривать приближенные методы теории дифракции, позволяющие описать в том числе распределение звукового поля в различных точках наблюдения при экранировании шума, излучаемого некомпактными источниками. Ниже рассмотрены основные подходы, используемые в таких задачах и их сравнительные достоинства и недостатки.

Применение приближения физической оптики, основанного на методе Кирхгофа [49], к задаче дифракции звука на бесконечной полуплоскости показывает, что при расчете функции Грина имеется значительное отклонение амплитудно-фазовых характеристик от точного решения, что, в свою очередь, приводит к существенным качественным отклонениям при расчете дифракции звука от некомпактного источника на частотах, характерных для авиационных приложений [50]. В то же время модификация этого метода применительно к конечным экранам позволяет увеличить точность вычисления фазовых характеристик в зоне глубокой тени для монопольного источника, что, однако, требует значительных вычислительных затрат. Отметим также, что для некомпактных источников звука проблема точности расчета дифракционной картины сохраняется. Поэтому часто используется либо высокочастотное приближение метода Кирхгофа–метод Маекавы [4], либо теория дифракции Рубиновича–Магги [49].

Метод Маекавы, базирующийся на приближении Френеля [49], справедлив при описании дифракции звука только в случае достаточно высоких частот и акустически компактных источников, расположенных на большом расстоянии от экрана, поскольку предполагает, что фазовые фронты падающих на экран волн близки к плоским волнам. В теории Рубиновича–Магги точность расчета амплитудно-фазовых характеристик поля в зоне полутени и в зоне глубокой тени существенно выше, чем при расчете с помощью метода Маекавы, более того, этот метод допускает обобщение на случай экранов сложной формы [51, 52], однако условие достаточно высоких частот и акустической компактности источника требуется и в этом случае.

Использование численных методов расчета экранирования, как правило, ограничивается различными вариантами метода граничных элементов [35] или разрывного метода Галеркина [53]. Применение этих методов к решению прикладных задач для натурных объектов сталкивается с необходимостью использования значительных вычислительных ресурсов, что крайне затрудняет решение оптимизационных задач. Достаточно часто в прикладных задачах расчета экранирования точечных источников или шума струи используют решение Макдональда [5], являющееся точным решением для случая дифракции звука на бесконечной полуплоскости. Несмотря на его прозрачный физический смысл и математическую простоту, главным недостатком этого метода является сложность при обобщении на случай экранов произвольной формы (например, полигональных экранов), что снижает его практическую применимость.

Метод геометрической теории дифракции (ГТД) [54–57], описывающий дифракцию волн в предположениях, что расстояние от источника и от точки наблюдения до препятствия много больше длины волны, удобен для описания экранирования шума плоскими полигональными экранами [9, 58 ]. Сравнение результатов, полученных в рамках ГТД, с точным решением для случая дифракции звука на бесконечной полуплоскости [9, 50], продемонстрировало высокую точность расчета как амплитудных, так и фазовых характеристик дифрагированного поля для частот и геометрических параметров, характерных для авиационных приложений [9]. Более того, проведенные расчеты показали, что ГТД дает удовлетворительное согласие с точным решением в случаях относительно небольших значений kR (kR > 2), где k – волновое число, R – расстояние от источника до кромки экрана, т.е. при достаточно близком расположении источника и экрана, но при условии, что точка наблюдения расположена на расстояниях много больше длины волны [9, 50]. Кроме этого, ГТД может быть относительно просто обобщена на случай дифракции волн при наличии однородного спутного потока [10]. В совокупности указанные выше особенности показывают, что ГТД может быть применена к задаче экранирования шума турбулентной струи как в случае натурных параметров, так и для описания результатов испытаний на маломасштабных моделях. Именно этот метод расчета дифракционного поля выбран в настоящей работе.

В настоящей работе рассматривается приложение корреляционной теории к задаче расчета эффективности экранирования шума турбулентной струи прямоугольным экраном с помощью ГТД. В первом разделе представлены основные положения корреляционной теории шума турбулентной струи, необходимые для проведения дальнейших расчетов эффективности экранирования. Поскольку изначально ГТД развивалась для случая дифракции звука, излучаемого точечными монопольными источниками, в то время как в рамках корреляционной теории излучение звука описывается квадрупольными источниками, во втором разделе выполнено обобщение ГТД на случай генерации шума точечными квадрупольными источниками. Заметим, что обсуждение выражений для дифракции электромагнитных волн на бесконечной полуплоскости, излучаемых точечными диполями, представлено в [59].

В третьем разделе приведено описание эксперимента, в котором исследовался эффект экранирования шума турбулентной струи, а также дано описание расчетной модели, построенной на основе корреляционной теории и ГТД. В четвертом разделе проводится сравнение экспериментальных и расчетных данных для спектров шума турбулентной струи при различных положениях экрана и заданной скорости истечения струи. В пятом разделе представлен пример расчета эффективности экранирования шума круглой струи плоским прямоугольным экраном, и в последнем разделе работы представлены выводы к полученным результатам.

В целом, настоящая работа является этапом в адаптации низкоуровневой модели источников шума струи к задачам экранирования, направленных на проведение быстрых и эффективных оценок в ходе поисковых исследований по снижению шума турбулентных струй с помощью эффекта экранирования.

1. ГЕНЕРАЦИЯ ШУМА СЛУЧАЙНЫМИ ТОЧЕЧНЫМИ КВАДРУПОЛЬНЫМИ ИСТОЧНИКАМИ В СТРУЕ НА ОСНОВЕ КОРРЕЛЯЦИОННОЙ МОДЕЛИ

Ниже рассмотрены необходимые в дальнейшем основные положения корреляционной модели источников шума в турбулентной струе. В этой работе используется вариант корреляционной модели, в котором не учитывается эффект рефракции звуковых волн на среднем поле струи [24–26]. Это дает возможность сравнительно просто обобщить модель на случай взаимодействия звукового излучения струи с отражающими поверхностями. В этом варианте модели распространение звуковых возмущений описывается с помощью простого волнового оператора на основе акустической аналогии Лайтхилла [28]:

где $p$ – возмущение давления, ${{c}_{0}}$ – скорость звука, ${{T}^{{ij}}}$ – нестационарная часть тензора напряжений Рейнольдса ${\rho }{{v}^{i}}{{v}^{j}}$. Выполнив преобразование Фурье уравнения (1) по временной переменной, получим неоднородное уравнение Гельмгольца: где $k = {{\omega } \mathord{\left/ {\vphantom {{\omega } {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$ – волновое число, ω – частота звукового поля.

Решение уравнения (2) можно представить в следующем виде:

где $G\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} ',{\omega }} \right)$ – функция Грина рассматриваемой краевой задачи, а $G_{{}}^{{ij}}\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} ',{\omega }} \right)$ – ее вторые производные, вычисленные по координатам точки наблюдения. Для случая свободного пространства выражения для функции Грина уравнения Гельмгольца $G\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} ',{\omega }} \right)$ и ее второй производной $G_{{}}^{{ij}}\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} ',{\omega }} \right)$ имеют вид:

Необходимо отметить, что в общем случае выражение для функции Грина зависит от геометрии задачи и применительно к задаче дифракции звука на бесконечной полуплоскости будет рассмотрено далее.

Нестационарная часть тензора напряжений Рейнольдса ${{T}^{{ij}}}$ описывает источники звука в уравнении (2). В рамках подхода, обычно используемого в корреляционных моделях [13–15], плотность источников представляется как стохастическое поле, которое описывается некоторой корреляционной функцией. В случае квадрупольных источников случайными полями должна описываться каждая из компонент квадруполя ${{T}^{{ij}}}\left( {{\mathbf{r}},t} \right)$. Однако более удобным является представление источников в виде разложения по базисным квадруполям:

где ${{{\xi }}_{n}}$ – стационарные случайные поля с заданными корреляционными характеристиками, базисные квадруполи $D_{n}^{{ij}}$ выбираются таким образом, что ${{{\xi }}_{n}}$ для разных n являются статистически независимыми [24–26].

Вследствие симметричности тензора ${{T}^{{ij}}}$ в сумму (6) должны входить 6 членов. В качестве базисных выбираются квадруполь вида $D_{1}^{{ij}} = {{{\delta }}^{{ij}}}$, где ${{{\delta }}^{{ij}}}$ – символ Кронекера, и 5 квадруполей с нулевым следом:

Квадруполи (7) характеризуются тем, что их свертки с функцией Грина (5) представляют собой отдельные азимутальные гармоники в цилиндрической системе координат с осью x, совпадающей с направлением истечения струи, причем квадруполи $D_{1}^{{ij}}$ и $D_{2}^{{ij}}$ соответствует нулевой азимутальной гармонике, квадруполи $D_{3}^{{ij}}$ и $D_{4}^{{ij}}$ – первой азимутальной гармонике, а $D_{5}^{{ij}}$ и $D_{6}^{{ij}}$ – второй азимутальной гармонике.

Используя уравнения (3), (6), а также условие статистической независимости для ${{{\xi }}_{n}}$, получим выражение для спектра звукового давления:

где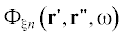 – функция взаимной спектральной плотности случайного поля ${{{\xi }}_{n}}$, верхний индекс * обозначает комплексное сопряжение, а интегрирование проводится по объему, занятому струей.

Для описания характеристик источников звука используется преобразование случайных полей ${\xi }\left( {{\mathbf{r}},t} \right)$, описывающих интенсивность турбулентных пульсаций, к переменным ${\eta }\left( {{\mathbf{r}},t} \right)$, описывающим интенсивность генерации пульсаций [16, 24–26]. Это преобразование задается уравнением Ланжевена:

где U – скорость конвекции источников, x – продольная координата, ε(x) – скорость затухания возмущений. Переход к новой переменной позволяет исключить конвекцию из корреляционных характеристик источников, что позволяет разделить пространственную и временную корреляцию.

Корреляционная функция генерации возмущений ${\eta }\left( {{\mathbf{r}},t} \right)$ выбирается в следующем виде:

Отсюда следует выражение для взаимного спектра:

Оценки корреляционной длины ${{l}_{0}}$ дают значения, существенно меньшие по сравнению с другими характерными размерами задачи. В этом случае выражение (11) может быть переписано в виде

где ${\delta }\left( {\mathbf{r}} \right)$ – дельта-функция.

В модели источников звука мы пренебрегаем распределением источников по сечению струи и сносим эти источники на ось струи. Это приближение может быть принято, поскольку рефракция звуковых волн на среднем течении струи не учитывается, а рассматриваемый диапазон частот соответствует длине звуковой волны, большей, чем диаметр сечения струи. В этом случае корреляционная функция и взаимный спектр определяются для источников, распределенных на оси струи:

При этом 2-кратный интеграл по объему (8) сводится к интегралу по продольной координате, что существенно упрощает вычисления.

В соответствии с (9) корреляционная функция турбулентных пульсаций определяется уравнением:

где $H\left( {x,{\tau }} \right)$ – функция Грина уравнения Ланжевена (9):

Пренебрегая зависимостью мощности процесса $A\left( x \right)$ от продольной координаты x, в локально-однородном приближении получим:

Функциональный вид выражения (17) соответствует эмпирической корреляционной функции источников звука в струе, обычно используемой в корреляционных моделях [13–15]. Это служит основанием для выбора корреляционной функции генерации возмущений ${\eta }\left( {{\mathbf{r}},t} \right)$ в виде (10).

Взаимный спектр турбулентных пульсаций определяется уравнением

где $\hat {H}\left( {x,{{x}_{0}},{\omega }} \right) = \int {\exp \left( { - i{\omega \tau }} \right)} H\left( {x,{{x}_{0}},{\tau }} \right)d{\tau }{\text{.}}$

В результате получим следующее выражение для спектра звукового давления:

Главным преимуществом выражения (19) является явная зависимость от функции Грина, что позволяет использовать его не только для расчета распространения излучаемого струей шума в свободном пространстве, но и при наличии различных отражающих и/или экранирующих поверхностей.

Предложенная модель была валидирована в работах [24–26] на основе экспериментальных данных, полученных с помощью метода азимутальной декомпозиции, разработанного специально для разделения различных азимутальных гармоник звукового поля. В работе [26] показано, что данная модель позволяет с высокой степенью точности вычислять характеристики шума струи под большими углами к оси струи. Однако для малых углов наблюдения, близких к оси струи, точность расчетов снижается, что связано с эффектом рефракции акустического излучения на среднем течении струи, который не учитывается в этой модели.

2. ОБОБЩЕНИЕ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ ДИФРАКЦИИ НА СЛУЧАЙ ИЗЛУЧЕНИЯ ЗВУКА ТОЧЕЧНЫМ КВАДРУПОЛЬНЫМ ИСТОЧНИКОМ

Использование выражения (19) для расчета дифракции звукового поля, генерируемого струей, требует вычисления вторых производных функции Грина $G_{{}}^{{ij}}\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} ',{\omega }} \right)$ по пространственным координатам местоположения монопольного источника звука применительно к задаче дифракции на полигональных экранах при наличии потока. В настоящей работе для расчета эффективности экранирования полигональными экранами применяется приближенный метод ГТД, и, тем самым, необходимо получить вторые производные для функции Грина, вычисляемой по этому методу, причем в качестве канонической задачи теории дифракции целесообразно использовать задачу дифракции на бесконечной полуплоскости.

Рассмотрим задачу построения функции Грина для дифракции звука, излучаемого точечным квадрупольным источником на бесконечной полуплоскости. Как известно [54–56], в рамках ГТД функция Грина $G\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} ',{\omega }} \right)$ для дифракции точечного монопольного источника на акустически абсолютно жесткой полуплоскости представляется в следующем виде:

где ${{G}_{G}}\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} ',{\omega }} \right)$ – геометроакустическое поле для точечного монопольного источника, а ${{G}_{D}}\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} ',{\omega }} \right)$ – дифрагированное поле для точечного монопольного источника.

Тогда для геометроакустического поля ${{G}_{G}}\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} ',{\omega }} \right)$ точечного монопольного источника справедливо следующее выражение:

где А – начальная амплитуда поля, $k = {{\omega } \mathord{\left/ {\vphantom {{\omega } {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$ – волновое число, ${{{\mathbf{R}}}_{{{\mathbf{obs}}}}}$ – радиус-вектор точки наблюдения, ${{{\mathbf{r}}}_{{\mathbf{s}}}}$ – радиус-вектор источника, $\Theta (z)$ – ступенчатая функция Хэвисайда, равная нулю, если точка наблюдения располагается в зоне геометрической тени, и единице в противоположном случае.

Для дифрагированного поля ${{G}_{D}}\left( {{\mathbf{r}},{\mathbf{r}}{\kern 1pt} ',{\omega }} \right)$ точечного монопольного источника справедливо следующее выражение [53–55]:

где А – начальная амплитуда поля, $k = {{\omega } \mathord{\left/ {\vphantom {{\omega } {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$ – волновое число, ${{{\mathbf{r}}}_{{{\mathbf{sc}}}}}$ – радиус-вектор точки рассеяния, ${{R}_{{{\text{sc}}}}}$ – расстояние от источника до точки рассеяния, ${{R}_{d}}$ – расстояние от точки рассеяния до точки наблюдения, D_coeff – дифракционный коэффициент, определяемый из решения канонической задачи дифракции.

При дифракции на бесконечной полуплоскости дифракционный коэффициент имеет вид [55]:

где ${{{\varphi }}_{{{\text{obs}}}}}$ – угол наблюдения относительно рассеивающей грани и ${{{\varphi }}_{{{\text{inc}}}}}$ – угол падения звуковой волны на рассеивающую грань, ${{{\beta }}_{0}}$ – угол рассеяния звуковой волны (рис. 1). Функции $F({{p}_{m}})$ выражаются через интегралы Френеля в следующем виде [54]:

С учетом (2), (3) и (20) выражение для полного звукового поля квадруполя при наличии экрана записывается в виде свертки с базисными квадруполями:

где $D_{n}^{{ij}}$ – n-ый базисный квадруполь, а дифференцирование производится по координатам точки источника (в выражении (25) учитывается, что базисный квадруполь не зависит от расположения источника).

Выражение для второй производной от геометроакустического поля по координатам источника полностью аналогично выражению (5), а выражение для второй производной от дифрагированного поля имеет вид:

причем при вычислении второй производной необходимо учитывать, что угол падения ${{{\varphi }}_{{{\text{inc}}}}}$ и расстояние от источника до точки рассеяния ${{R}_{{{\text{sc}}}}}$ явно зависят от местоположения источника, а расстояние от точки рассеяния до точки наблюдения ${{R}_{d}}$ и угол наблюдения ${{{\varphi }}_{{{\text{obs}}}}}$ нет.

Тогда, выполнив двукратное дифференцирование выражения (26) как сложной функции от ${{{\mathbf{r}}}_{{\mathbf{s}}}}$ с учетом выражений (23) и (24) для дифракционного коэффициента, получим необходимые соотношения для расчета звукового поля, излучаемого точечным квадрупольным источником при наличии бесконечной акустически жесткой полуплоскости. Выражения (5), (25) и (26) совместно с выражением (19) решают задачу вычисления спектра звукового давления для шума струи в произвольной точке наблюдения при наличии полубесконечного экрана.

С учетом сделанных выше предположений о малом влиянии вторично дифрагированных волн, а также волн, рассеянных углами экрана [59], выражения (5), (25) и (26) путем непосредственного применения к каждой стороне экрана обобщаются на случай прямоугольного бесконечно тонкого акустически жесткого экрана.

Сравнение полученных выражений со случаем дифракции звука, излучаемого четырьмя точечными монопольными источниками, показала, что для всех положений экрана в рассматриваемом диапазоне частот (см. ниже) относительная ошибка между вычисленными значениями звукового поля в различных точках наблюдения составляет не более 0.005%.

Сделаем некоторые замечания относительно возможности пренебрежения вкладами волн вторичной дифракции и волн, рассеянных вершинами экрана. Хорошо известно [51, 54, 56], что если экран целиком закрывает первую зону Френеля или рассеивающая грань экрана не содержит резких изменений геометрии формы, таких как углы или вершины, то в первом случае можно пренебречь вкладом вторичных волн, а во втором – вкладом волн, рассеянных углами и вершинами. Таким образом, для корректного использования полученных выражений продольный и поперечный размеры экрана должны быть больше, чем характерный размер первой зоны Френеля для всех частот, для которых проводится расчет.

3. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ И РАСЧЕТНОЙ МОДЕЛИ ДЛЯ ИССЛЕДОВАНИЯ ЭКРАНИРОВАНИЯ ШУМА КРУГЛОЙ ОДНОКОНТУРНОЙ СТРУИ

Экспериментальные исследования экранирования шума струи проводились в заглушенной камере с потоком АК-2 ЦАГИ, входящей в состав стенда АС-1. На рис. 2 представлена фотография, а на рис. 3 схема экспериментальной установки для исследования экранирования шума круглой одноконтурной струи. В качестве объекта исследований было выбрано круглое одноконтурное сопло диаметром D = 39.5 мм, причем внутренние обводы канала сопла выполнены в соответствии с профилем Витошинского, что обеспечивает равномерный поток на срезе сопла. Для измерения шума струи использовалась полярная решетка микрофонов радиусом R = 2 м (рис. 3), состоявшая из десяти преполяризованных ½-дюймовых микрофонов фирмы Bruel&Kjaer типа 4189 с предусилителем. Динамический диапазон микрофонов составлял 14.6–146 дБ, а частотный диапазон от 6.3 Гц до 25 кГц.

В качестве экрана использовалась устанавливавшаяся вблизи среза сопла прямоугольная стальная пластина размером 1300 × 450 × 4.2 мм, которая могла перемещаться в плоскости, перпендикулярной плоскости расположения микрофонов, что позволяло проводить измерения, изменяя область геометрической тени для различных микрофонов. Исследования экранирования шума одноконтурной струи были выполнены для трех различных скоростей истечения струи (173, 233, 273 м/с) и при двух положениях экрана относительно среза сопла: положение № 1 – x = 2D, z = 2D, и положение № 2 – x = 2D, z = 3D.

Расчет экранирования шума круглой одноконтурной струи прямоугольным экраном проводился для набора точечных квадрупольных источников, расположенных на оси струи (рис. 4). Расположение сопла относительно кромки экрана, геометрия экрана, скорость истечения струи U, а также координаты точек наблюдения соответствовали условиями проведения эксперимента. Расчет спектров шума струи проводился для дискретного набора частот: 400, 500, 630, 800, 1000, 1200, 1600, 2000, 2500, 3150, 4000 и 5000 Гц (данные частоты соответствуют центральным частотам при расчете 1/3-октавных спектров шума).

Для расчета спектров уровней шума струи использовалось выражение (19), где для второй производной от функции Грина использовались выражения (26), (27)–(33). Поскольку выражение (19) зависит от ряда свободных параметров, определяемых на основе анализа результатов экспериментальных данных или численных расчетов, то при проведении расчетов для величин ${{A}_{n}}$ и ${{{\tau }}_{n}}$ использовались значения, полученные при анализе шума струи методом азимутальной декомпозиции, полученные в работе [26].

При проведении расчетов экран рассматривался как бесконечно тонкая, акустически абсолютно жесткая прямоугольная пластина размером 1300 × 450 мм. Расчет проводился для всех рассмотренных в эксперименте скоростей истечения струи и положениях экрана.

Для рассматриваемого диапазона частот, геометрии экрана и взаимных положений сопла и точки наблюдения оценим размеры первой зоны Френеля [49]. Для этого сделаем предположение, что во всем рассматриваемом диапазоне частот источники располагаются непосредственно вблизи среза сопла. Тогда для частоты 500 Гц радиус первой зоны Френеля составит ~220 мм, а для частоты 5 кГц – 71 мм. Сравнив полученные расстояния с размерами экранирующей пластины, видим, что для диапазона частот от 500 Гц до 5 кГц характерные размеры пластины превосходят диаметр первой зоны Френеля, что оправдывает сделанные выше предположения о малости вклада волн вторичной дифракции. А поскольку сопло располагается в центре длинной стороны пластины, то также можно пренебречь вкладом волн, рассеянных углами экрана.

Сделаем замечание относительно частоты 400 Гц, для которой радиус первой зоны Френеля составляет ~250 мм. В данном случае для корректного расчета необходимо оценить вклад волн вторичной дифракции. Однако, как показывают экспериментальные данные [57, 59], по сравнению с вкладом первично рассеянных волн этот вклад мал. Тогда, учитывая, что для рассматриваемого сопла частоты ниже 1 кГц эффективно излучаются существенно ниже по потоку (на расстояниях от среза сопла порядка 10D…15D), вкладом вторично дифрагированных волн на данной частоте можно пренебречь.

Здесь необходимо отметить, что струя является акустически некомпактным источником, для которого понятия зоны Френеля, вводимое для точечного источника, является не совсем корректным. Однако в данном случае нам необходимо провести только оценку порядка величины для первой зоны Френеля, для чего вышеизложенные рассуждения представляются справедливыми.

4. СРАВНЕНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ И РАСЧЕТНЫХ ДАННЫХ

Проведем сравнение экспериментально измеренных (синяя кривая) узкополосных спектров шума и расчетных (красная кривая) 1/3-октавных спектров шума струи при наличии и отсутствии экрана для скорости истечения, равной 273 м/с (М = 0.8), и углов наблюдения 30°, 60°, 90° и 120° градусов. Выбор данных углов позволяет четко проследить основные тенденции, возникающие при экранировании шума струи, и обусловлен тем, что эти углы описывают направление максимального излучения шума струей (30°), зону частичной тени (60°–90°) и зону глубокой тени (120°) относительно среза сопла. Выбор данной скорости истечения струи обусловлен тем, что позволяет четко выявить общие тенденции при проведении сравнительного анализа расчетных и экспериментальных данных, которые справедливы и при более низких скоростях истечения струи, которые были рассмотрены в эксперименте.

Рассмотрим сначала сравнение расчетных данных с экспериментом для струи без экрана. На рис. 5 для четырех углов наблюдения (90°, 60°, 120° и 30°) представлено сравнение экспериментально измеренных спектров шума струи при скорости истечения струи 273 м/с с расчетными спектрами шума струи при отсутствии экрана.

Для углов наблюдения 90°, 60°, 120°, представленных на рис. 5а, 5б и 5в, видно, что расчетные кривые корректно передают форму огибающей экспериментально измеренного спектра, отличаясь в пределах 1.5–2 дБ. При меньших скоростях истечения струи, исследованных в эксперименте, сравнение экспериментальных и расчетных спектров уровней шума струи продемонстрировало аналогичное поведение для тех же углов наблюдения.

На рис. 5г видно, что при данной скорости истечения струи под углом наблюдения 30° имеет место значительное (до 7 дБ на частотах ниже 1500 Гц) расхождение между расчетными и экспериментальными спектрами шума струи. Это обусловлено тем, что используемая расчетная модель не рассматривает явление рефракции звуковых волн, которое наиболее значительно проявляется при углах наблюдения, близких к оси струи [60]. Кроме того, в модели не рассматривается вклад волн неустойчивости, которые при скоростях струи M ~ 0.8 могут вносить уже значительный вклад в области углов, близких к оси струи.

Рассмотрим далее сравнение расчетных и измеренных спектров шума струи в случае экранирования струи прямоугольным экраном, расположенным на расстоянии x = 2D, z = 2D (рис. 4) от среза сопла (положение экрана № 1). Как при отсутствии экрана, рассмотрим спектры уровней звукового давления струи для рассмотренных ранее углов наблюдения, представленные на рис. 6.

Для рассматриваемой скорости истечения струи и положения экрана № 1 сравнение расчетных и экспериментально измеренных кривых показывает, что для углов наблюдения до 60°–90° во всем диапазоне частот наблюдается хорошее совпадение между расчетными и экспериментальными данными (рис. 6а и 6б). Однако для угла наблюдения 120° (рис. 6в) в диапазоне частот от 400 Гц до 2.5 кГц расчетный спектр шума струи на 1.5–2 дБ превосходит экспериментально измеренный, хотя на частотах свыше 2.5 кГц расчетная кривая корректно описывает экспериментальную форму спектра. Сравнение кривых под углом наблюдения 30°, представленное на рис. 6г, как и в случае отсутствия экрана, демонстрирует расхождение между расчетными и измеренными значениями уровня шума. Для других скоростей истечения струи сравнение расчетных и экспериментальных спектров шума струи при наличии экрана в положении № 1 имело схожий характер, причем разница между расчетными и экспериментальными кривыми для угла наблюдения 120° составляла 2.5–3 дБ.

Рассмотрим, наконец, экранирование шума струи прямоугольным экраном, расположенным на расстоянии x = 2D, z = 3D (рис. 4) от среза сопла (положение экрана № 2), т.е. в случае большей удаленности струи от экрана. Результаты сравнения расчетных и экспериментальных спектров представлены на рис. 7. Как и для всех ранее представленных случаев, для углов наблюдения 60° и 90° (рис. 7а и 7б) видно хорошее согласие между расчетными и экспериментальными спектрами, причем разница не превышает 2 дБ. Для угла наблюдения 30° градусов имеет место значительное (до 7.5 дБ) расхождение между расчетными и экспериментально измеренными спектрами шума струи (рис. 7г).

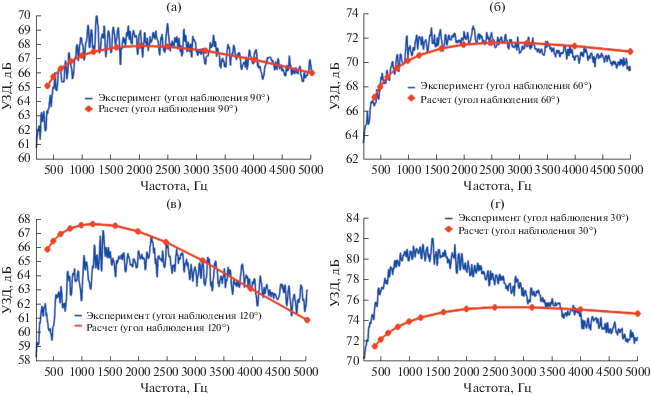
Для угла наблюдения 120° имеет место тенденция, отличная от рассмотренных ранее случаев: на частотах ниже 1.5 кГц расчетные уровни шума на 2–3 дБ превосходит измеренные, а на частотах свыше 2.5 кГц уже экспериментально измеренные уровни шума превосходят расчетные, причем при увеличении частоты разность между спектрами монотонно возрастает и достигает величины ~2.2 дБ (рис. 7в). Для других скоростей истечения струи поведение расчетных и экспериментально измеренных спектров шума при положении экрана № 2 имело аналогичный характер.

Представленное сравнение расчетных и экспериментально измеренных спектров шума струи демонстрирует, что для углов наблюдения, близких к оси струи (угол 30°), имеет место существенное расхождение между рассматриваемыми кривыми, причем оно увеличивается при увеличении скорости истечения струи и не зависит от присутствия экранирующей поверхности. Причиной этого, как уже было упомянуто, является то, что рассматриваемая здесь модель источников шума не принимает во внимание явление рефракции звука струей (более подробно см. [25, 26]) и вклад волн неустойчивости.

Для диапазона углов наблюдения 60°–90° градусов при наличии и отсутствии экрана имеет место хорошее совпадение между расчетными и экспериментальными кривыми, что свидетельствует о корректности используемых подходов как при описании излучения звука струей, так и при описании явления дифракции звука на прямоугольном экране.

При этом наблюдается некоторое отличие между расчетными и экспериментальными спектрами при размещении экрана дальше от струи в положении № 2 на частотах свыше 2.5 кГц. Одной из возможных причин этого отличия является то, что в корреляционной теории, рассматриваемой в данной работе, высокочастотные источники шума струи предполагаются расположенными только в области вблизи сопла, а незначительным наличием высокочастотных источников также и в области основного участка струи пренебрегается. Это приводит к расхождению между рассматриваемыми кривыми при увеличении расстояния между задней кромкой экрана и срезом сопла с увеличением частоты. Результаты для угла наблюдения 120°, представленные на рис. 7в, подтверждают этот вывод. Можно ожидать, что учет рефракции звука струей, а также более точный учет распределения источников в струе позволит корректно описать распространение звука во всем диапазоне углов.

5. ПРИМЕР РАСЧЕТА ЭФФЕКТИВНОСТИ ЭКРАНИРОВАНИЯ ШУМА КРУГЛОЙ ОДНОКОНТУРНОЙ СТРУИ

Для рассмотренных выше положений экрана приведем пример расчета эффективности экранирования шума круглой одноконтурной струи под углами наблюдения 60° и 90°, поскольку именно они представляют наибольший интерес с точки зрения снижения шума на местности. Расчет эффективности экранирования Δ проводился с помощью соотношения:

где ${\text{УЗ}}{{{\text{Д}}}_{S}}$ – выраженный в дБ уровень звукового давления струи при наличии экрана, ${\text{УЗ}}{{{\text{Д}}}_{F}}$ – выраженный в дБ уровень звукового давления для свободной струи. При таком определении эффективности экранирования положительным значениям Δ соответствует усиление шума, а отрицательным снижение шума струи.

На рис. 8 представлен сравнительный расчет эффективности экранирования для скорости истечения струи 173 м/с, а на рис. 9 – для скорости истечения струи 273 м/с. Синяя кривая соответствует положению экрана № 1, а красная кривая – положению экрана № 2.

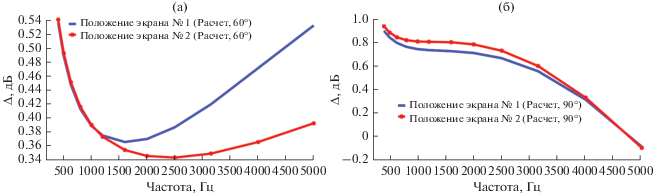
Для угла наблюдения 60° расчет эффективности экранирования при рассмотренных скоростях истечения струи продемонстрировал положительную эффективность экранирования, что свидетельствует об отсутствии снижения шума для обоих рассмотренных положений экрана (рис. 8а и 9а). Представленные на рис. 8а и 9а зависимости имеют характерный ложкообразный вид, демонстрируют наличие минимума в диапазоне частот от 1.5 до 2.5 кГц для положения экрана № 2, и в диапазоне частот от 800 Гц до 1.6 кГц для положения экрана № 1. Несмотря на то что для рассматриваемого угла наблюдения экранирование отсутствует, отметим, что усиление шума невелико и не превышает 0.7 дБ для всех рассмотренных случаев.

Сравнение расчетных зависимостей для угла наблюдения 90°, представленное на рис. 8б, демонстрирует, что при скорости истечения струи 173 м/с максимальная эффективность экранирования шума струи не зависит от положения экрана и начинает проявляться на частотах свыше 3.5 кГц, достигая 0.9 дБ на частоте 5 кГц. На частотах ниже 3.5 кГц имеет место слабое монотонное усиление шума струи, достигающее 0.9 дБ на частотах ниже 500 Гц. При скорости истечения струи 273 м/с (рис. 9б) вычисленные эффективности экранирования для шума струи имеют схожее поведение на частотах ниже 2.5 кГц, однако в данном случае экранирования на частотах выше 3.5 кГц не наблюдается, хотя зависимости и демонстрируют монотонное уменьшение Δ при увеличении частоты.

В целом, полученные расчетные зависимости согласуются с экспериментальными и расчетными данными, полученными при проведении исследований эффекта экранирования шума турбулентных струй и описанными в работах [1–3, 9, 10, 18, 27, 29–32, 45–47].

ЗАКЛЮЧЕНИЕ

В представленной работе на основе корреляционной теории шума струи и геометрической теории дифракции предложен метод для расчета экранирования шума круглой струи произвольным плоским экраном. Проведена адаптация ГТД для расчета экранирования шума турбулентной струи, для чего в рамках ГТД получено выражение для дифракции звука, излучаемого точечным квадрупольным источником на плоском полигональном экране при произвольной ориентации источника относительно декартовой системы координат, связанной с экраном.

Для валидации предложенного метода расчета экранирования выполнено сравнение экспериментальных и расчетных спектров уровней звукового давления шума струи при различных скоростях истечения струи и при различных положениях прямоугольного экрана относительно кромки сопла.

Сравнительный анализ экспериментальных спектров шума струи с расчетными спектрами, выполненными на основе корреляционной теории, продемонстрировал хорошее качественное, а при углах наблюдения 60°–90° и количественное согласие при всех рассмотренных скоростях истечения струи и положениях экрана, а также при его отсутствии в рассматриваемом диапазоне частот. Однако для углов, близких к оси струи (30°), имеется существенное расхождение между расчетными и измеренными спектрами, что связано с тем, что в использованной здесь модели источников звука в струе не учитывается явление рефракции и не учитывался вклад волн неустойчивости.

Настоящая модель в сочетании с моделью шума взаимодействия, разработанной в [41, 42], позволит проводить расчетную оценку шума струи, расположенной вблизи элементов конструкции самолета, с учетом эффекта экранирования, принимая во внимание возможность низкочастотного усиления шума струи. Предложенный метод позволяет давать оценки экранирования в ситуациях, представляющих технологический интерес. В дальнейших исследованиях предполагается расширить предложенный подход на случай более сложной версии корреляционной модели с учетом эффекта рефракции на слое смешения струи и более сложного распределения источников по струе.

Работа выполнена на базе УНУ “Заглушенная камера с потоком АК-2” ФГУП "ЦАГИ” и при финансовой поддержке Министерства науки и высшего образования Российской Федерации по соглашению № 075-11-2018-178 (уникальный идентификатор соглашения RFMEFI62818X0011).