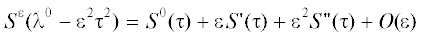Акустический журнал, 2020, T. 66, № 5, стр. 489-508
Аномалии рассеяния акустических волн вблизи точек отсечки непрерывного спектра (обзор)
С. А. Назаров *
Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская наб. 7–9, Россия
* E-mail: srgnazarov@yahoo.co.uk
Поступила в редакцию 29.03.2020
После доработки 29.03.2020
Принята к публикации 28.04.2020
Аннотация
Описаны несколько аномалий рассеяния волн в акустических волноводах с цилиндрическими или гофрированными жесткими стенками на частотах, близких к точкам отсечки (порогам) непрерывного спектра. Вводится понятие пороговых резонансов, которые порождены “почти стоячими волнами”, не переносящими энергию в бесконечность. Для гофрированных волноводов приведены примеры раскрытия спектральных лакун (зон торможения волн) и собственных чисел около их краев, обычных или вырожденных порогов. Описываются аномалии Вайнштейна и Вуда, возникающие выше и ниже порогов и заключающиеся соответственно в “почти полном” отражении или прохождении волн и в непропорционально быстрой изменяемости дифракционной картины. Обсуждаются примеры полного прохождения волны (“невидимости препятствия”) и процедуры обострения или сглаживания аномалии Вуда, в частности, построение собственных чисел внутри непрерывного спектра и соответствующих захваченных волн. Сравниваются принципы излучения Зоммерфельда, Умова–Мандельштама и предельного поглощения, а также особенности их применения на порогах.
МОТИВИРОВКА
Наряду с привычной, плавной изменяемостью дифракционной картины в волноводе при вариации частоты волны, приходящей из бесконечности, в спектре возникают особые изолированные частоты, около которых картина приобретает разнообразные “всплески” и “провалы”, т.е. ее изменения происходят в “быстром” масштабе. Настоящая статья посвящена описанию именно этих особых частот (пороги, собственные числа, точки комплексного резонанса) и сопутствующих разнообразных аномалий рассеяния волн. Такие объекты далее выделены аббревиацией и определены при первом появлении в тексте.
Точки отсечки (ТО) в спектре цилиндрических акустических волноводов, называемые также порогами (рис. 1a), характеризуются тем, что в них, во-первых, происходят скачок кратности непрерывного спектра и перестройка базиса распространяющихся волн, и во-вторых, появляются волна, не зависящая от продольной координаты, и волна, линейно растущая на бесконечности. Именно с последней обычно связываются разнообразные аномалии дифракционной картины в волноводе с резонатором (рис. 2a), однако в работах [1, 2] при помощи асимптотического анализа было обнаружено, что, наоборот, за аномалии рассеяния ответственны волны на пороговой частоте, которые ограничены и, что главное, не переносят энергию на бесконечности. Такие волны, именуемые “почти стоячими” (рис. 1в), оказывают влияние на многие результаты применения асимптотических процедур (см. [3–6] и др.), а сам феномен их возникновения был назван пороговым резонансом (ПР).
Рис. 1.
(а) – Внешний ◆ (${{\lambda }_{\dag }} = 0$) и внутренние ◇ (${{\pi }^{2}}{{k}^{2}}$, $k = 1,2,3, \ldots $) пороги (ТО). (б) – Захваченная волна $u$ – затухающая и (в) – почти стоячая волна $u$ – стабилизирующаяся на правой бесконечности.

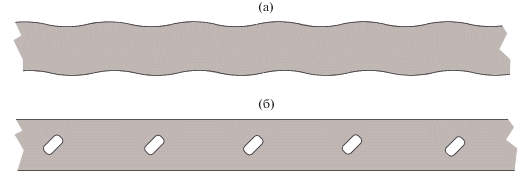
Рис. 2.
Волноводы $\Omega $ с резонаторами $\Theta $, выделенными тонированием: (а) – цилиндрический и (б) – периодический с глубоко тонированной ячейкой $\varpi $.

В акустическом волноводе с жесткими стенками на нулевой частоте всегда наблюдается ПР, так как постоянная функция – ограниченное решение однородной задачи Неймана для уравнения Лапласа, однако ПР на внутренних (положительных) ТО – явление неустойчивое: сколь угодно малое возмущение стенок резонатора способно уничтожить его. В то же время устранение порожденных ПР аномалий (ср. рис. 3в и рис. 3г) обычно требует точной настройки параметров возмущения стенок волноводов.
Рис. 3.
Аномалия Вуда: (а) – точка ⚫ комплексного резонанса и (в) – “всплеск” коэффициента рассеяния. (б) – Сглаживание аномалии Вуда: сохранение СЧ $ \circ $ и (г) – гладкая изменяемость коэффициента рассеяния. На пороге $\diamondsuit $ коэффициент рассеяния претерпевает разрыв.

Существенный cпектр ${{\sigma }_{e}}$ волноводов с гофрированными стенками (рис. 2б) зачастую устроен более сложно, нежели непрерывный спектр ${{\sigma }_{c}} = [0, + \infty )$ волноводов с цилиндрическими рукавами: между спектральными сегментами (зоны прохождения волн) могут образоваться открытые лакуны (зоны торможения волн), а также изолированные собственные частоты (СЧ) – точки дискретного спектра ${{\sigma }_{d}}$. В случае цилиндрических рукавов все СЧ располагаются на непрерывном спектре, образуют точечный спектр ${{\sigma }_{p}}$ и оказываются неустойчивыми, покидающими вещественную ось и превращающимися в точки комлексного резонанса при “почти всех” малых вариациях стенок (см. [7, 8] и др.). Однако в статьях [1, 9] было введено понятие “принудительной устойчивости” СЧ, опирающееся на процедуру “точной настройки” нескольких параметров профиля возмущения и обеспечивающее как захват волны, так и сохранение СЧ вкрапленным в непрерывный спектр (рис. 1б и рис. 3в). Нарушение настройки провоцирует аномалию Вуда (рис. 3в). Еще однo околопороговое явление – аномалия Вайнштейна схематично изображена на рис. 4.
Рис. 4.
Аномалии Вайнштейна: (а) прямая – почти полное отражение и (б) инвертированная – почти полное прохождение. Приходящая волна изображена штрих-пунктирной линией, а отраженная и проходящая – сплошными. Их интенсивность пропорциональна длине стрелки.

Интересное и малоисследованное явление – вырожденные пороги и сопутствующие ПР, характеризующиеся тем, что помимо линейных возникают полиномиально растущие волны высоких порядков. В цилиндрических акустических и квантовых11 волноводах все пороги невырожденные и, в частности, поэтому СЧ, порожденная ПР, неспособна подняться выше ТО. Однако для гофрированных стенок или волноводов иной природы, например, упругих22, вырожденные пороги существуют, и в этом случае возможно совершенно необычное явление – СЧ внутри непрерывного спектра поднимается вверх от ТО.
Еще один примечательный феномен на пороге – полное разногласие известных принципов излучения: принцип Зоммерфельда идентификации направления распространения волн не годится из-за линейного роста одной из волн, принцип предельного поглощения распознает все, даже незатухающие почти стоячие волны как захваченные, и только применение принципа излучения Умова–Мандельштама не влечет за собой видимых противоречий, т.е. этот энергетический принцип оказывается универсальным, так как вне порогов все три типа условий излучения равноценны.
Данная статья носит обзорный характер и в ней перечислены известные автору факты об упомянутых характеристиках волноводов, а также сформулированы открытые вопросы. Схематичное и упрощенное изображение обсуждаемых эффектов представлено на рис. 1, 3, 4.
ЦИЛИНДРИЧЕСКИЕ ВОЛНОВОДЫ И ИХ СПЕКТРЫ
Акустический волновод $\Omega $ с жесткими стенками $\partial \Omega $ (рис. 2a) состоит из двух цилиндрических рукавов
(1)
$\begin{array}{*{20}{c}} \begin{gathered} {{\Pi }_{ \pm }} = \{ x = (y,z) \in {{\mathbb{R}}^{{d - 1}}} \times \mathbb{R}: \\ y = ({{y}_{1}},{{y}_{{d - 1}}}) \in \omega , \pm z > \ell > 0\} ,\,\,\,\,d = 2,3, \\ \end{gathered} \end{array}$Волновые процессы в волноводе $\Omega $ описываются при помощи решений задачи Неймана
(2)
$\begin{gathered} - {{\Delta }_{x}}u(x) = \lambda u(x),\,\,\,\,x \in \Omega , \\ {{\partial }_{\nu }}u(x) = 0,\,\,\,\,\,x \in \partial \Omega , \\ \end{gathered} $Непрерывный спектр ${{\sigma }_{c}}$ задачи (2) занимает замкнутую положительную полуось $\overline {{{\mathbb{R}}_{ + }}} = [0, + \infty )$ (см., например, книги [10, 11]) и ТО (порогами)
(3)
$\begin{array}{*{20}{c}} {0 = {{\Lambda }_{1}} < {{\Lambda }_{2}}\,\,\leqslant \,\,{{\Lambda }_{3}}\,\,\leqslant \ldots \leqslant \,\,{{\Lambda }_{m}}\,\,\leqslant \ldots \to + \infty } \end{array}$(4)
$\begin{array}{*{20}{c}} {\lambda = {{\kappa }^{2}} \in ({{\Lambda }_{m}},{{\Lambda }_{{m + 1}}}) \ne } \end{array}\emptyset $(5)
$\begin{array}{*{20}{c}} {w_{j}^{ \pm }(x) = {{a}_{j}}{{e}^{{ \pm i{{\alpha }_{j}}z}}}{{U}_{j}}(y),\,\,\,\,j = 1, \ldots ,m} \end{array}$(6)
$\begin{array}{*{20}{c}} {{{\alpha }_{j}} = {{{\left| {\lambda - {{\Lambda }_{j}}} \right|}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,{{a}_{j}} = {{{(2{{\alpha }_{j}})}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}.} \end{array}$Здесь фигурируют собственные числа (СЧ) (3) модельной задачи на сечении цилиндра
(7)
$\begin{gathered} - {{\Delta }_{y}}U(y) = \Lambda U(y),\,\,\,\,y \in \omega , \\ {{\partial }_{\nu }}U(y) = 0,\,\,\,\,y \in \partial \omega , \\ \end{gathered} $(8)
$\begin{array}{*{20}{c}} {{{{({{U}_{j}},{{U}_{k}})}}_{\omega }} = {{\delta }_{{j,k}}},\,\,\,\,j,k \in \mathbb{N}: = \{ 1,2,3, \ldots \} ,} \end{array}$ВОЛНОВОДЫ С ГОФРИРОВАННЫМИ СТЕНКАМИ
В статье описаны разнообразные аномалии дифракционной картины в волноводе $\Omega $ на околопороговых частотах, как ниже, так и выше ТО. Некоторые особенности строения спектра и характеристик рассеяния (лакуны, вырожденные пороги и пр.) отсутствуют в цилиндрических акустических волноводах, но проявляются в волноводах иной природы, например, упругих, а также в случае гофрированных рукавов, имеющих периодически изменяющееся сечение. Поэтому далее обсуждается и задача (2) на множестве $\Omega $, у которого рукава
(9)
$\begin{array}{*{20}{c}} {{{\Pi }_{ \pm }} = \{ x \in \Pi : \pm z\,\, \geqslant \,\,\ell \} } \end{array}$При этом масштабированием период сведен к единице, а декартовы координаты и все геометрические параметры, в частности, полудлина $\ell $ резонатора $\Theta = \Omega {\kern 1pt} \backslash {\kern 1pt} \overline {({{\Pi }_{ - }} \cup {{\Pi }_{ + }})} $ сделаны безразмерными. Известно (см. публикации [12–16] и др.), что согласно теории Флоке–Блоха–Гельфанда существенный спектр33 ${{\sigma }_{e}} = {{\sigma }_{c}} \cup ({{\sigma }_{p}}{\kern 1pt} \backslash {\kern 1pt} {{\sigma }_{d}})$ у задачи (2) в волноводе $\Omega $ с жесткими и гладкими по предположению стенками $\partial \Omega $ и периодическими рукавами (9) имеет зонное строение
(10)
$\begin{array}{*{20}{c}} {{{\sigma }_{e}} = \bigcup\limits_{j \in N} {{{\beta }_{j}}} ,} \end{array}$(11)
$\begin{array}{*{20}{c}} {{{\beta }_{j}} = \{ \left. {{{\Lambda }_{j}}(\eta )} \right|\eta \in [ - \pi ,\pi ]\} } \end{array}$(12)
$\begin{array}{*{20}{c}} \begin{gathered} 0\,\,\leqslant \,\,{{\Lambda }_{1}}(\eta )\,\,\leqslant \,\,{{\Lambda }_{2}}(\eta )\,\,\leqslant \,\,{{\Lambda }_{3}}(\eta )\,\,\leqslant \ldots \leqslant \\ \leqslant \,\,{{\Lambda }_{m}}(\eta )\,\,\leqslant \ldots \to + \infty \\ \end{gathered} \end{array}$(13)
$\begin{gathered} - {{\Delta }_{x}}\mathcal{U}(x;\eta ) = \Lambda (\eta )\mathcal{U}(x;\eta ),\,\,\,\,x \in \varpi , \\ {{\partial }_{\nu }}\mathcal{U}(x;\eta ) = 0,\,\,\,\,x \in {{\theta }_{0}}:\, = \partial \varpi {\kern 1pt} \backslash {\kern 1pt} \bigcup\limits_ \pm {\overline {{{\theta }_{ \pm }}} } , \\ \end{gathered} $(14)
$\begin{array}{*{20}{c}} \begin{gathered} \mathcal{U}\left( {y, + \frac{1}{2};\eta } \right) = {{e}^{{i\eta }}}\mathcal{U}\left( {y, - \frac{1}{2};\eta } \right), \\ {{\partial }_{z}}\mathcal{U}\left( {y, + \frac{1}{2};\eta } \right) = {{e}^{{i\eta }}}{{\partial }_{z}}\mathcal{U}\left( {y, - \frac{1}{2};\eta } \right), \\ \left( {y, + \frac{1}{2}} \right) \in {{\theta }_{ \pm }}. \\ \end{gathered} \end{array}$СЧ (12) задачи (13), (14) оказываются вещественными и непрерывно и $2\pi $-периодически зависят от переменной $\eta $, т.е. в самом деле ${{\beta }_{j}}$ – компактные связные множества на полуоси $[0, + \infty )$. Каждая спектральная пара $\{ {{\Lambda }_{m}}(\eta ),{{\mathcal{U}}_{m}}(x;\eta )\} $ с параметром44 $\eta \in ( - \pi ,\pi ]$ порождает волну Флоке
(15)
$\begin{array}{*{20}{c}} {{{\mathcal{W}}_{m}}(x;\eta ) = {{e}^{{i\eta q}}}{{\mathcal{U}}_{m}}(y,z - q;\eta ),\,\,\,\,x \in {{\varpi }_{q}},\,\,\,\,q \in \mathbb{Z},} \end{array}$(16)
$\begin{array}{*{20}{c}} \begin{gathered} \mathcal{W}_{m}^{{(k)}}(x;\eta ) = {{e}^{{i\eta q}}}\sum\limits_{j = 0}^k {\frac{{{{z}^{q}}}}{{q!}}\mathcal{U}_{m}^{{(k - j)}}} (y,z;\eta ),\,\,\,\,x \in \Pi , \\ j = 0, \ldots ,K - 1, \\ \end{gathered} \end{array}$Цилиндрические рукава (1) можно считать $1$-периодическими, и следовательно, непрерывный спектр ${{\sigma }_{c}} = [0, + \infty )$ также представим в виде (10), но в нем соседние спектральные сегменты ${{\beta }_{j}}$ и ${{\beta }_{{j + 1}}}$ примыкают один к другому или пересекаются, а значит, ${{\sigma }_{c}}$ – связное множество. В самом деле, “обычная” волна ${{e}^{{i\zeta z}}}{{U}_{m}}(y)$, удовлетворяющая задаче (2) с параметром
превращается в волну Флоке следующим образом:(18)
$\begin{array}{*{20}{c}} \begin{gathered} {{e}^{{i\zeta z}}}{{U}_{m}}(y) = {{e}^{{inq}}}\left( {{{e}^{{i(\eta + 2\pi p)(z - q)}}}{{U}_{m}}(y)} \right) = \\ = {{e}^{{i\eta q}}}{{\mathcal{U}}_{{n(m,p)}}}(y,z - q;\eta ),\,\,\,\,x \in {{\varpi }_{q}},\,\,\,\,q \in \mathbb{Z}. \\ \end{gathered} \end{array}$При этом целое число $p \in \mathbb{Z}$ выбрано так, что $\eta = \zeta - 2\pi p \in ( - \pi ,\pi ]$, а функция $\varpi \mathrel\backepsilon (y,z) \mapsto $ $ \mapsto {{U}_{{n(m,p)}}}(y,z;\eta )$ – решение задачи (13), (14) с параметром
(19)
$\begin{array}{*{20}{c}} \begin{gathered} {{\Lambda }_{{n(m,p)}}}(\eta ) = {{\Lambda }_{m}} + {{(\eta + 2\pi p)}^{2}}, \\ \eta \in [ - \pi ,\pi ],\,\,\,\,p \in \mathbb{Z}. \\ \end{gathered} \end{array}$В итоге график (17) – парабола на рис. 5а – превращается в набор дисперсионных дуг (19), образующих связную “ферму” на рис. 5б.
Рис. 5.
Дисперсионные кривые: (а) – в цилиндрическом волноводе и (б) – при интерпретации его как периодического. (в) – После возмущения стенок возникают узкие лакуны – проекции тонированных прямоугольников на ось ординат.

В периодической ситуации между соседними расцепленными сегментами ${{\beta }_{j}}$ и ${{\beta }_{{j + 1}}}$ может быть открыта спектральная лакуна (зона торможения волн)
Один из способов образования лакун – малое периодическое возмущение прямых цилиндрических волноводов: регулярное, пологое с высотой $\varepsilon \ll 1$ (рис. 6а), или сингулярное, с отверстиями диаметром ${{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 d}} \right. \kern-0em} d}}}}$ (рис. 6б). В работах [18–21] и др. показано, что при подходящих параметрах возмущения стенок узлы, помеченные символом $ \circ $ на рис. 5б, дробятся и между сглаженными дисперсионными кривыми раскрываются лакуны шириной $O(\varepsilon )$ как внутри зоны Бриллюена, так и выше нее. Отметим, что узлы, отмеченные значками ▶ и ◀ на рис. 5б и полученные пересечением двух восходящих или нисходящих дуг, не распадаются и не формируют лакуны (пояснения см., например, в статье [21]).
Многочисленные примеры зонного строения спектров волноводов, предложенные изначально в оригинальных работах [22, 23] и [24–26] и нашедшие продолжение в публикациях [27–31] и др., опираются на асимптотический анализ дифференциальных уравнений с контрастными коэффициентами и краевых задач на сочленениях областей различных предельных размерностей (см. статьи [32, 33] и [35–42], а также многие другие) и получаются вариацией физических или геометрических параметров. В первом случае (рис. 7а и 7б) акустическая среда является кусочно-однородной и возникновение раскрытых лакун как в низко-, так и в среднечастотном диапазонах спектра обусловлено контрастными свойствами разных сред: отношение скоростей распространения волн в них – малый или большой параметр.
Рис. 7.
Периодические волноводы (а) – с мелкими неоднородностями и (б) – стратифицированный. Периодическое семейство контейнеров, соединенных тонкими каналами: (в) – длинными и (г) – короткими. (д) – Пологие дисперсионные кривые, разделенные широкими лакунами.
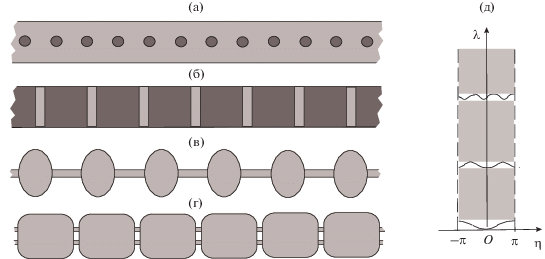
Во втором случае (рис. 7в и 7г), как и у волноводов на рис. 6, лакуны появляются при малом геометрическом параметре $\varepsilon $: волноводы образованы периодическим семейством массивных контейнеров, соединенных тонкими, диаметром $O(\varepsilon )$, каналами, соответственно короткими или длинными. В противоположность графикам на рис. 5в, где спектральные сегменты и лакуны приобрели соответственно размеры $O(1)$ и $O(\varepsilon )$ при $\varepsilon \to + 0$, спектральные сегменты у графиков на рис. 7д для волновода с короткими каналами (рис. 7г) имеют длину $O(\varepsilon )$, локализованы около точек дискретного спектра задачи Неймана в изолированном контейнере и отделены один от другого лакунами шириной $O(1)$. В случае длинных каналов (рис. 7в) предельный спектр прирастает СЧ задачи Дирихле на оси канала. Для таких периодических квазицилиндров можно образовать любое наперед заданное количество непустых лакун. Проведенный анализ для волноводов на рис. 7г и 7б приспособлен [43, 44] к задачам теории упругости, однако для волноводов на рис. 6а, 6б и рис. 7в, 7а аналогичные результаты неизвестны до сих пор, так как в большинстве ситуаций векторные задачи оказываются значительно более сложными, чем скалярные, и нуждаются в новых методах исследования.
Упомянем гипотезу Бете–Зоммерфельда о том, что в спектрах многомерных ($d > 1$) волноводов количество раскрытых лакун всегда конечно, – она подтверждена лишь для некоторых краевых задач, и задача Неймана в этот список не входит. В работе [45] рассмотрен волновод на рис. 7г, однако при условии, что поперечные размеры соединительных каналов между контейнерами с номерами $N$ и $N \pm 1$ стремятся к нулю при $N \to \pm \infty $. В этом случае существенным спектром служит счетное множество на полуоси $[0, + \infty )$ без конечных точек сгущения55, и в нем обнаруживается бесконечное количество лакун. Вместе с тем нарушена периодичность волновода и в упомянутой работе не получена полная информация о дискретном спектре ${{\sigma }_{d}}$ (изолированные СЧ) и точечном спектре ${{\sigma }_{p}}$ (бесконечнократные СЧ).
Еще одна специфическая черта периодических волноводов – возможность “схлопывания” какого-то сегмента (11) в точку, когда СЧ ${{\Lambda }_{j}}(\eta )$ задачи (13), (14) не зависит от парaметра Флоке $\eta $, а значит, становится бесконечнократным в задачe Неймана в самом квазицилиндре $\Pi $. Соответствующие примеры известны для волноводов различной физической природы (см. [46–48] и др.), а невозможность коллапса любого из сегментов установлена при существенных геометрических ограничениях (см. [49–51] и др.). Вместе с тем в цилиндрах $\Pi = \omega \times \mathbb{R}$ бесконечнократных собственных чисел нет (ср. [52], [16; замечание 3.1.5]), т.е. ${{\sigma }_{{{\text{ess}}}}} = {{\sigma }_{c}}$ в случае рукавов (1).
ПОРОГОВЫЕ РЕЗОНАНСЫ
В работах [3, 4] при изучении сочленений полубесконечных квантовых волноводов (спектральная задача Дирихле для оператора Лапласа) было введено понятие порогового резонанса (ПР) – он возникает при условии, что у задачи со спектральным параметром, лежащим на нижней грани непрерывного спектра (нижней точки отсечки), есть нетривиальное ограниченное решение (ОР), которое не обязательно затухает на бесконечности, но может быть и захваченной волной, исчезающей на бесконечности с экспоненциальной скоростью. Наличие или отсутствие ПР в узлах решетки тонких квантовых волноводов предопределяют структуру асимптотической одномерной модели решетки, на которую (модель) влияют и указанные качества ОР (подробности см. в статье [4]). В работе [53] было сформулировано достаточное условие отсутствия ПР, а в работе [54] – два разных по существу критерия, названные критериями отсутствия и существования ПР, причем второй из них позволяет узнать качества ОР. Кроме того, в публикациях [55–58, 53, 5 ] и др. разобраны многие конкретные сочленения квантовых волноводов и проверено отсутствие ПР или окольным путем доказано их появление при изолированных значениях варьируемого геометрического параметра. В периодической ситуации аналогичные результаты неизвестны.
Если какое-либо нетривиальное ОР на пороге исчезает на бесконечности и тем самым оказывается истинной собственной функцией, то порог – СЧ оператора задачи, но в том случае, когда все ОР не затухают, говорим, что ПР подлинный (ППР).
Замечание 1. Привести пример СЧ на пороге непрерывного спектра квантового волновода $\Omega $ нетрудно. Пусть у области $\Omega \subset {{\mathbb{R}}^{3}}$ есть плоскость зеркальной симметрии $\{ x:{{x}_{2}} = 0\} $, а $0 < {{\Lambda }_{1}} < {{\Lambda }_{2}}$ – первые два СЧ задачи Дирихле на сечении $\omega $. Используя прием из статьи [59], рассмотрим задачу Дирихле на половине волновода ${{\Omega }_{ + }} = \{ x \in \Omega :{{x}_{1}} > 0\} $, у которой (задачи) по предположению ТО непрерывного спектра – число ${{\Lambda }_{2}}$. Согласно классическому результату [60] раздутие $\Theta (\gamma ) = \{ x:{{\gamma }^{{ - 1}}}x \in \Theta \} $ резонатора $\Theta $ обеспечивает при больших $\gamma > 1$ возникновение изолированного СЧ $\lambda (\gamma )$ в спектре квантового волновода ${{\Omega }_{ + }}(\gamma ) = {{\Pi }_{ + }} \cup \Theta (\gamma ) \cup {{\Pi }_{ - }}$, причем $\lambda (\gamma ) \to + 0$ при $\gamma \to + \infty $. Поскольку $[1, + \infty ) \mathrel\backepsilon \gamma \mapsto (0,{{\Lambda }_{2}}]$ – непрерывная монотонно убывающая функция, то СЧ $\lambda (\gamma *)$ попадает при каком-то $\gamma * > 1$ на истинную ТО ${{\Lambda }_{1}}$ целого волновода $\Omega $. Более богатая геометрическая симметрия волновода дает возможность по намеченной схеме образовать СЧ на любом внутреннем пороге непрерывного спектра. Так, двойная зеркальная симметрия позволяет построить пример акустического волновода $\Omega \subset {{\mathbb{R}}^{3}}$ с СЧ ${{\Lambda }_{2}} > 0$. Впрочем, открытым остается вопрос, можно ли обеспечить одновременное включение нескольких членов последовательности (3) в точечный спектр ${{\sigma }_{p}}$.
В акустическом волноводе нижняя ТО ${{\Lambda }_{1}}$ нулевая и в ней всегда реализуется ППР: постоянная функция – ОР задачи (2) с $\lambda = 0$. Поскольку других ОР нет, такой резонанс имеет кратность один. Помимо нижнего порога $\lambda = {{\Lambda }_{1}}$ ПР можно приписать и внутренним (положительным) порогам $\lambda = {{\Lambda }_{m}}$ при $m > 1$, однако прежнее определение [3] не годится, так как ограниченной оказывается любая распространяющаяся волна.
Пусть ${{\Lambda }_{m}}$ – СЧ задачи (7) с кратностью ${{\varkappa }_{m}}$, т.е.
(20)
$\begin{array}{*{20}{c}} {{{\Lambda }_{{m{\kern 1pt} - {\kern 1pt} {{\varkappa }_{m}}}}} < {{\Lambda }_{{m{\kern 1pt} - {\kern 1pt} {{\varkappa }_{m}} + 1}}} = \ldots = {{\Lambda }_{m}} < {{\Lambda }_{{m + 1}}}} \end{array}$(21)
$\begin{array}{*{20}{c}} {w_{j}^{ \pm }(x) = {{a}_{j}}{{e}^{{ \pm i{{\alpha }_{j}}z}}}{{U}_{j}}(y),\,\,\,\,j = 1, \ldots ,m - {{\varkappa }_{m}},} \end{array}$(22)
$\begin{array}{*{20}{c}} \begin{gathered} w_{k}^{0}(y,z) = {{U}_{m}}(y),\,\,\,\,w_{k}^{1}(y,z) = z{{U}_{m}}(y), \\ k = m - {{\varkappa }_{m}} + 1, \ldots ,m. \\ \end{gathered} \end{array}$Решение $u$ задачи (2) назовем почти стоячей волной (ПСВ), если для него справедливо разложение
(23)
$\begin{array}{*{20}{c}} {u(x) = \tilde {u}(x) + \sum\limits_ \pm {{{\chi }^{ \pm }}(z)} \sum\limits_{k = m - {{\varkappa }_{m}} + 1}^m {a_{k}^{ \pm }{{U}_{k}}(y)} ,} \end{array}$ПСВ характеризуются важным свойством: они не переносят энергию на бесконечность (ср. форму переноса энергии (28)). Такое определение ПСВ годится и для периодических волноводов (см. работу [61]).
ПР возникает при $\lambda = {{\Lambda }_{m}}$ в том случае, если имеется хотя бы одна нетривиальная ПСВ. Линейную оболочку таких решений обозначим через ${{\mathcal{L}}^{{st}}}$, а пространство захваченных волн (собственных функций, отвечающих СЧ $\lambda = {{\Lambda }_{m}}$) – через ${{\mathcal{L}}^{{tr}}}$. В обоих пространствах можно ввести вещественные базисы. Если ${{\mathcal{L}}^{{tr}}} = \{ 0\} $, т.е. нет нетривиальных решений (23) со столбцами ${{a}^{ \pm }} = 0$, то возникает ППР и размерность $dim{{\mathcal{L}}^{{st}}}$ – его кратность.
Для периодических рукавов ПР могут быть устроены более сложно. Сами пороги – точки экстремума или перегиба дисперсионных кривых (ср. рис. 5б и рис. 7д). Края лакун и точка $\Lambda = 0$ – внешние пороги, но остальные пороги – внутренние точки существенного спектра (последние отсутствуют на рис. 7д, но их можно обнаружить на рис. 5в). Пусть $\Lambda = {{\Lambda }_{m}}({{\eta }^{0}})$ – порог, т.е. ${{\partial }_{\eta }}{{\Lambda }_{m}}({{\eta }^{0}}) = 0$ при некотором ${{\eta }^{0}} \in ( - \pi ,\pi ]$ и
(24)
$\begin{array}{*{20}{c}} {\partial _{\eta }^{k}{{\Lambda }_{m}}({{\eta }^{0}}) = 0,\,\,\,\,k = 1, \ldots ,K,\,\,\,\,\partial _{\eta }^{{K + 1}}{{\Lambda }_{m}}({{\eta }^{0}}) \ne 0.} \end{array}$В случае $K = 1$ порог называется невырожденным, но он имеет порядок вырождения $K$ при $K > 1$. Вырожденные пороги обладают многими необычными свойствами, в частности, для них приходится изменить определение ПСВ, а порожденные ими волны Флоке (16) – полиномы переменной $z$ порядка не выше $K - 1$ c $1$-периодическими коэффициентами в квазицилиндре $\Pi $ (см. [16; гл. 3, §4]). Для цилиндрических акустических и квантовых волноводов все пороги невырожденные, а полиномиальная зависимость от $z$ становится линейной (см. формулы (22)).
Замечание 2. Если для периодических акустических волноводов вырожденные пороги – явление неординарное и редкое, то для цилиндрических и периодических упругих волноводов, в частности, для бесконечных пластин Кирхгофа (см. [62; §30]) нижняя точка отсечки $\Lambda = 0$ непрерывного спектра – вырожденный порог порядка четыре всегда (см. [63, 64] и др.). Это обстоятельство предопределяет существенное отличие дифракционных задач для систем и дифференциальных уравнений высших порядков от обсуждаемых скалярных задач для оператора Лапласа.
УСЛОВИЯ ИЗЛУЧЕНИЯ
Для цилиндрических волноводов во внепороговой ситуации простейшим в применении является принцип излучения Зоммерфельда (см. [10, 11] и др.), и в соответствии с ним знак $ \pm $ волнового числа $ \pm {{\alpha }_{j}}$ определяет направление “от $ \mp \infty $ к $ \pm \infty $” распространения волны (5). Такая же классификация порождена энергетическим принципом излучения Умова–Мандельштама [65, 66] или принципом предельного поглощения (см., например, [16, 1 ] и [68, 69]).
Как обычно (ср. монографии [10, 11] и др.), решению неоднородной задачи Неймана
(25)
$\begin{array}{*{20}{c}} \begin{gathered} - {{\Delta }_{x}}u(x) - \lambda u(x) = f(x),\,\,\,\,x \in \Omega , \\ {{\partial }_{\nu }}u(x) = 0,\,\,\,\,x \in \partial \Omega , \\ \end{gathered} \end{array}$(26)
$\begin{array}{*{20}{c}} {u(x) = \tilde {u}(x) + \sum\limits_ \pm {{{\chi }^{ \pm }}(z)} \sum\limits_{j = 1}^m {c_{j}^{ \pm }w_{j}^{ \pm }(x)} .} \end{array}$Здесь $\tilde {u}(x)$ – остаток, затухающий на бесконечности со скоростью $O({{e}^{{ - |z|\sqrt {{{\Lambda }_{{m + 1}}} - \lambda } }}})$, коэффициенты при волнах (5) определяются при решении задачи и потому зависят от внешнего воздействия $f$, а в остальном использованы те же обозначения, что и в разложении (23). Понятно, что однородной ($f = 0$) задаче (25), (26) удовлетворяет любая захваченная волна $u \in {{\mathcal{L}}^{{tr}}}$, у которой, конечно же, $a_{j}^{ \pm } = 0$. Кроме того, условиями разрешимости задачи (25), (26) служат равенства
(27)
$\begin{array}{*{20}{c}} {{{{(f,u)}}_{\Omega }} = 0\,\,\,\forall u \in {{\mathcal{L}}^{{tr}}}.} \end{array}$Таким образом, оператор задачи с условиями излучения обладает нулевым индексом, т.е. размерности его ядра ${{\mathcal{L}}^{{tr}}}$ и коядра (количество линейно независимых условий ортогональности (27)) совпадают. Корректную постановку задачи (25), (26) на специальных весовых пространствах с отделенной асимптотикой можно найти в книге [16; гл. 5], статьях [1, 69] и др. публикациях.
Перезапись волн (5) в форме Флоке (18) демонстрирует проблему применения принципа излучения Зоммерфельда в периодических волноводах: положительному волновому числу $\zeta \in (\pi ,2\pi )$ в левой части (18) отвечает отрицательный показатель $\eta \in ( - \pi ,0)$ в правой. Вместе с тем принцип предельного поглощения и энергетический принцип Умова–Мандельштама приспособлены и к гофрированным волноводам: если показатель $\eta $ в (15) располагается на восходящем (нисходящем) участке дисперсионной кривой, то волна ${{\mathcal{W}}_{m}}$ оказывается уходящей (приходящей) в рукаве ${{\Pi }_{ + }}$, но, разумеется, меняет свое существо в ${{\Pi }_{ - }}$. Итак, во внепороговой ситуации соответствующие классификации и обозначения $w_{1}^{ \pm }, \ldots ,w_{m}^{ \pm }$ для элементарных волн Флоке (15) полностью сохраняют постановку задачи (25) с условиями излучения (26) и указанные выше ее основные свойства.
На порогах принцип излучения Зоммерфельда неприменим хотя бы потому, что в списке (22) фигурируют линейно растущие волны, а принцип предельного поглощения также может привести к ошибочному результату (см. замечание 3). Единственно универсальным остается энергетический принцип излучения Умова–Мандельштама [65, 66], в котором классификация волн основана на применении симплектической (полуторалинейной и антиэрмитовой) формы переноса энергии
(28)
$\begin{array}{*{20}{c}} \begin{gathered} Q(u,v) = \\ = \int\limits_{\omega (R)} {\left( {\overline {v(y,R)} {{\partial }_{z}}u(y,R) - u(y,R)\overline {{{\partial }_{z}}v(y,R)} } \right)} dz, \\ \end{gathered} \end{array}$(29)
$\begin{array}{*{20}{c}} {Q(w_{j}^{\vartheta },w_{k}^{\tau }) = \pm i{{\delta }_{{\vartheta ,\tau }}}{{\delta }_{{j,k}}},} \end{array}$На пороге $\lambda = {{\Lambda }_{m}}$ при ограничении (20) волны (21) удовлетворяют соотношениям (29) с $j,k = 1, \ldots ,m - {{\varkappa }_{m}}$, однако $Q(w_{j}^{0},w_{j}^{0}) = 0$ и $Q(w_{j}^{1},w_{j}^{1}) = 0$ для волн (22) ввиду их вещественности. Следуя [16; гл. 5], введем линейные комбинации
(31)
$\begin{array}{*{20}{c}} {w_{k}^{ \pm }(x) = {{2}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}(z \mp i){{U}_{j}}(y),\,\,\,\,j = m - {{\varkappa }_{m}} + 1, \ldots ,m.} \end{array}$Нетрудно убедиться в том, что благодаря условиям ортогональности и нормировки (8) для набора волн (22), (31) выполнены соотношения (29) при всех индексах (30). В результате и на пороге задача (25), (26) сохраняет все перечисленные выше свойства.
Приведенные определения на основе формы переноса энергии (29) годятся и для волноводов с периодическими рукавами (9), причем ввиду $1$-периодичности в качестве области интегрирования в (28) можно взять любую ячейку ${{\varpi }_{k}}$ вместо сечения $\omega (R)$. В [16; гл. 5] доказано, что волны Флоке (16), периодически и полиномиально зависящие от $z$, всегда можно выбрать так, чтобы были выполнены условия ортогональности и нормировки (29), и тем самым указать направление распространения каждой из волн в базисе $\{ w_{1}^{ \pm }, \ldots ,\,\,w_{m}^{ \pm }\} $, а затем и сформировать условия излучения (26).
Замечание 3. Согласно принципу предельного поглощения [68, 67 ] решение задачи (25) с соответствующими условиями излучения определяется как предел при $\varepsilon \to + 0$ решения ${{u}^{\varepsilon }}$ задачи (25) с комплексным параметром
Такая задача однозначно разрешима в пространстве Соболева ${{H}^{1}}(\Omega )$, и ее решение допускает разложение
Ясно, что $\alpha _{j}^{{\varepsilon \pm }} \to \pm {{\alpha }_{j}}$ и $\alpha _{k}^{{\varepsilon \pm }} \to 0$ при $\varepsilon \to + 0$, а значит, принцип предельного поглощения устанавливает такие условия излучения:
(32)
$\begin{array}{*{20}{c}} \begin{gathered} {{u}^{0}}(x) = {{{\tilde {u}}}^{0}}(x) + \sum\limits_ \pm {{{\chi }^{ \pm }}(z)} \sum\limits_{j = 1}^{m - {{\varkappa }_{m}} - 1} {c_{j}^{{0 \pm }}w_{j}^{ \pm }(x)} + \\ + \,\,\sum\limits_ \pm {{{\chi }^{ \pm }}(z)} \sum\limits_{k = m - {{\varkappa }_{m}}}^m {c_{k}^{{0 \pm }}w_{k}^{0}(x)} . \\ \end{gathered} \end{array}$Решение (32) оказывается ограниченным в отличие от решения (26). Вместе с тем условия излучения, назначенные принципом предельного поглощения на пороге, обладают следующими видимыми недостатками: во-первых, любая, даже незатухающая ПСВ – решение однородной задачи (2), (32), во-вторых, в случае ПР условия разрешимости (27) необходимо расширить за счет равенств
КЛАССИЧЕСКАЯ, ПОРОГОВАЯ И РАСШИРЕННАЯ МАТРИЦЫ РАССЕЯНИЯ
Классический объект теории дифракции – матрица рассеяния $s(\lambda )$ (МР), составленная из коэффициентов рассеяния (КР) в разложении
(33)
$\begin{array}{*{20}{c}} \begin{gathered} \zeta _{j}^{ \pm }(x) = \tilde {\zeta }_{j}^{ \pm }(x) + {{\chi }_{ \mp }}(z)w_{j}^{ \pm }(x) + \\ + \,\,\sum\limits_{\tau = \pm } {{{\chi }_{\tau }}(z)} \sum\limits_{k = 1}^m {{{s}_{{j \pm ,k\tau }}}} (\lambda )w_{k}^{\tau }(x),\,\,\,\,j = 1, \ldots ,m, \\ \end{gathered} \end{array}$Как показано в [16; гл. 5] (см. также [1, 69]), благодаря сохранению условий (29) для волн (21), (31) на пороге $\lambda = {{\Lambda }_{m}}$ по-прежнему существуют решения $\zeta _{1}^{ \pm }, \ldots ,\zeta _{m}^{ \pm }$ задачи (2), а их КР образуют унитарную и симметричную ($2m \times 2m$)-матрицу ${\mathbf{s}}({{\Lambda }_{m}})$, называемую пороговой матрицей рассеяния (ПМР). Выделим из нее нижний правый блок ${{{\mathbf{s}}}^{{\centerdot \centerdot }}}({{\Lambda }_{m}})$ размером $2{{\varkappa }_{m}} \times 2{{\varkappa }_{m}}$. В статьях [69, 57, 54 ] установлена формула
(34)
$\begin{array}{*{20}{c}} {dimker\left( {{{{\mathbf{s}}}^{{\centerdot \centerdot }}}({{\Lambda }_{m}}) + {{\mathbb{I}}_{{_{m}}}}} \right) = dim\left( {{{\mathcal{L}}^{{{\text{st}}}}} \ominus {{\mathcal{L}}^{{{\text{tr}}}}}} \right),} \end{array}$Вернемся к рассмотрению внепороговой ситуации (4). Помимо распространяющихся волн (5) в цилиндре $\Pi $ возникают экспоненциальные волны, затухающие (плюс) или растущие (минус) при $z \to + \infty $,
(35)
$\begin{array}{*{20}{c}} {v_{j}^{ \pm }(x) = {{a}_{j}}{{e}^{{ \mp {{\alpha }_{j}}z}}}{{U}_{j}}(y),\,\,\,\,j = m + 1,\,\,m + 2, \ldots ,} \end{array}$(36)
$\begin{array}{*{20}{c}} \begin{gathered} w_{j}^{ \pm }(x) = {{2}^{{ - 1/2}}}(v_{j}^{ - }(x) \mp iv_{j}^{ + }(x)), \\ j = m - {{\varkappa }_{m}} + 1, \ldots ,m, \\ \end{gathered} \end{array}$Зафиксируем такое натуральное число $N > m$, что ${{\Lambda }_{{N + 1}}} > {{\Lambda }_{N}}$. Как показано в [16; гл. 5], вне зависимости от того, является или нет число $\lambda $ собственным, задача (2) обладает решениями
(37)
$\begin{array}{*{20}{c}} \begin{gathered} Z_{j}^{ \pm }(x) = \tilde {Z}_{j}^{ \pm }(x) + {{\chi }_{ \mp }}(z)w_{j}^{ \pm }(x) + \\ + \,\,\sum\limits_{\tau = \pm } {{{\chi }_{\tau }}(z)} \sum\limits_{k = 1}^N {{{S}_{{j \pm ,k\tau }}}} (\lambda )w_{k}^{\tau }(x),\,\,\,\,j = 1, \ldots ,N, \\ \end{gathered} \end{array}$(38)
$\begin{array}{*{20}{c}} {S(\lambda ) = \left( {\begin{array}{*{20}{c}} {{{S}_{{\sharp \sharp }}}(\lambda )}&{{{S}_{{\sharp \centerdot }}}(\lambda )} \\ {{{S}_{{\centerdot \sharp }}}(\lambda )}&{{{S}_{{\centerdot \centerdot }}}(\lambda )} \end{array}} \right),} \end{array}$(39)
$\begin{array}{*{20}{c}} {dimker\left( {{{S}_{{\centerdot \centerdot }}}(\lambda ) + {{\mathbb{I}}_{{N - m}}}} \right) = dim\mathcal{L}_{N}^{{{\text{tr}}}}(\lambda ),} \end{array}$Замечание 4. МР восстанавливается по блокам РМР (38) при помощи формулы (см. [1] и др.)
(40)
$\begin{array}{*{20}{c}} {s(\lambda ) = {{S}_{{\sharp \sharp }}}(\lambda ) - {{S}_{{\sharp \centerdot }}}(\lambda ){{{({{S}_{{\centerdot \centerdot }}}(\lambda ) + {{\mathbb{I}}_{{N - m}}})}}^{{ - 1}}}{{S}_{{\centerdot \sharp }}}(\lambda ),} \end{array}$(41)
$\begin{array}{*{20}{c}} \begin{gathered} b \in ker({{S}_{{\centerdot \centerdot }}}(\lambda ) + {{\mathbb{I}}_{{N - m}}}) \subset {{\mathbb{C}}^{{N - m}}} \Rightarrow \\ \Rightarrow {{S}_{{\sharp \centerdot }}}(\lambda )b = 0 \in {{\mathbb{C}}^{m}}. \\ \end{gathered} \end{array}$Кроме того, ${{S}_{{\centerdot \sharp }}}(\lambda )$ – транспонированный блок ${{S}_{{\sharp \centerdot }}}(\lambda )$ из-за симметричности РМР и, следовательно, равенство (40) сохраняется в сингулярном случае. Теперь возможен такой сценарий: при искажении стенок волновода блоки матрицы (38) приобретают возмущения и в правой части (40) возникает малый знаменатель в том случае, если матрица ${{S}_{{\centerdot \centerdot }}}(\lambda ) + {{\mathbb{I}}_{{N - m}}}$ становится неособенной и одновременно $\lambda $ перестает быть СЧ. Этот механизм проявляется при анализе аномалий Вуда в следующем разделе.
ВОЗНИКНОВЕНИЕ И ОБОСТРЕНИЕ АНОМАЛИЙ ВУДА
В случае порогового резонанса (например, $\Omega = \Pi $ – цилиндр или квазицилиндр) малые локальные возмущения стенок волновода, а также появление каверны или другого дефекта (рис. 8а, 8б и 8в) могут спровоцировать непропорционально быструю изменяемость дифракционной картины вблизи точек отсечки непрерывного спектра, называемую аномалией Вуда [80] (АВД) (см. также [81, 82] и др.). Опишем обнаруженные в работе [83] эффекты на примере пологого искажения волновода-полосы ${{\Pi }^{0}}$ (рис. 8а); при этом возмущение стенок волновода
(42)
$\begin{array}{*{20}{c}} \begin{gathered} {{\Pi }^{\varepsilon }} = \left\{ {x = (y,z): - \varepsilon {{H}_{ - }}(z) - \frac{1}{2}} \right. < y < \\ \left. { < \,\,\varepsilon {{H}_{ + }}(z) + \frac{1}{2},z \in ( - \infty , + \infty )} \right\} \\ \end{gathered} \end{array}$Рис. 8.
(а) – Пологое возмущение стенок волновода, (б) – возмущение уступами и (в) – возмущение малыми бугорками, кавернами или препятствиями.

Рассмотрим ТО $\kappa _{m}^{0} = \pi m$ при некотором $m \in \mathbb{N}$ и возмущенный спектральный параметр
(43)
$\begin{array}{*{20}{c}} {{{\lambda }^{\varepsilon }} = {{\lambda }^{0}} - {{\varepsilon }^{2}}{{\tau }^{2}} + {{{\tilde {\lambda }}}^{\varepsilon }},\,\,\,\,\tau > 0,\,\,\,\,\left| {{{{\tilde {\lambda }}}^{\varepsilon }}} \right|\,\,\leqslant \,\,c{{\varepsilon }^{3}},} \end{array}$Расчеты, проведенные в [83], показывают, что, во-первых, РМР гладко зависит от параметра $\tau > 0$ и, во-вторых, главные асимптотические члены элементов РМР
принимают вид(45)
$\begin{array}{*{20}{c}} \begin{gathered} S_{{\centerdot \centerdot }}^{0}(\tau ) = \frac{{\tau - i(\tau - 2{{J}_{m}}(H))}}{{\tau - 2{{J}_{m}}(H) - i\tau }}, \\ S_{{j \pm ,m + 1}}^{0}(\tau ) = \pm \frac{{2{{\alpha }_{j}}\sqrt {2\tau } (1 + i)}}{{\tau - 2{{J}_{m}}(H) - i\tau }}J_{{jm}}^{ \pm }(H), \\ \end{gathered} \end{array}$(46)
$\begin{array}{*{20}{c}} \begin{gathered} {{J}_{m}}(H) = {{\pi }^{2}}{{m}^{2}}\int\limits_{ - \ell }^\ell {({{H}_{ + }}(z) + {{H}_{ - }}(z))} dz, \\ J_{{jm}}^{ \pm }(H) = {{\pi }^{2}}{{m}^{2}}\int\limits_{ - \ell }^\ell {{{e}^{{ \pm i{{\alpha }_{j}}z}}}} ({{H}_{ + }}(z) + {{( - 1)}^{{j + m}}}{{H}_{ - }}(z))dz. \\ \end{gathered} \end{array}$Эти формулы позволяют обнаружить первичную АВД. Заметим, что
(47)
$\begin{array}{*{20}{c}} {{{\tau }_{m}} = {{J}_{m}}(H) \Rightarrow S_{{\centerdot \centerdot }}^{0}({{\tau }_{m}}) = - 1,} \end{array}$В первом случае ингредиенты $S_{{\sharp \sharp }}^{'}(\tau )$ и $S_{{\sharp \centerdot }}^{0}(\tau )$, $S_{{\centerdot \sharp }}^{0}(\tau )$ вытекающего из (40) представления
(50)
$\begin{array}{*{20}{c}} {{{s}^{\varepsilon }}({{\lambda }^{0}} - {{\varepsilon }^{2}}{{\tau }^{2}}) = S_{{\sharp \sharp }}^{0} + \varepsilon S_{{\sharp \sharp }}^{'}(\tau ) - \varepsilon \frac{{S_{{\sharp \centerdot }}^{0}(\tau )S_{{\centerdot \sharp }}^{0}(\tau )}}{{1 + S_{{\centerdot \ne }}^{0}(\tau )}} + \ldots } \end{array},$В случае (49) знаменатель $1 + S_{{\centerdot \centerdot }}^{0}(\tau )$ обращается в нуль в точке $\tau = {{\tau }_{ * }}$ и формула (50) теряет смысл при условии
(51)
$\begin{array}{*{20}{c}} {S_{{\sharp \centerdot }}^{0}({{\tau }_{m}}) \ne 0 \in {{\mathbb{C}}^{{2m}}},} \end{array}$(52)
$\begin{array}{*{20}{c}} {2{\text{Re}}S_{{\centerdot \centerdot }}^{'}({{\tau }_{m}}) = {{{\left| {S_{{\sharp \centerdot }}^{0}({{\tau }_{m}})} \right|}}^{2}} > 0.} \end{array}$Введем “быструю” переменную
и при учете (45), (47), (51) преобразуем формулу (50) к виду(54)
$\begin{array}{*{20}{c}} {{{s}^{\varepsilon }}({{\lambda }^{0}} - {{\varepsilon }^{2}}{{\tau }^{2}}) = S_{{\sharp \sharp }}^{0}({{\tau }_{m}}) - \frac{{S_{{\sharp \centerdot }}^{0}({{\tau }_{m}})S_{{\centerdot \sharp }}^{0}({{\tau }_{m}})}}{{2\tau _{m}^{{ - 1}}it + S_{{\centerdot \centerdot }}^{'}({{\tau }_{m}})}} + O(\varepsilon t).} \end{array}$Теперь в силу неравенства (52) знаменатель отличен от нуля при всех $t \in \mathbb{R}$. Таким образом, в отличие от соотношения (50), справедливого при ограничении (48) и обуславливающего гладкую зависимость МР от переменной $\tau > 0$, главный член асимптотики (54) в случае (49) характеризуется быстрой изменяемостью МР в масштабе (53), так как
Иными словами, приращение спектрального параметра ${{\lambda }^{0}} - {{\varepsilon }^{2}}\tau _{m}^{2}$ на величину $O({{\varepsilon }^{3}})$ приводит к кардинальной перестройке всей МР согласно формуле (54). Именно в этом и состоит одно из проявлений АВД.
В силу соотношений (45) и (46) выбор профильных функций ${{H}_{ \pm }}$ позволяет обеспечить равенство
(55)
$\begin{array}{*{20}{c}} {S_{{\sharp \centerdot }}^{0}({{\tau }_{m}}) = 0 \in {{\mathbb{C}}^{{2m}}}.} \end{array}$В этом случае вычитаемое в правой части (54) становится нулевым, однако это обстоятельство вовсе не означает, что АВД исчезает или сглаживается, – наоборот, аномалия может усилиться. Будем считать, что профильные функции в волноводе (42) сами зависят от малого параметра $\varepsilon $, а именно,
(56)
$\begin{array}{*{20}{c}} \begin{gathered} H_{ \pm }^{\varepsilon }(z) = {{H}_{ \pm }}(z) + \varepsilon H_{ \pm }^{'}(z), \\ H_{ \pm }^{'} \in {{C}^{\infty }}([ - \ell ,\ell ] \times [0,1]),\,\,\,\,{\text{supp}}H_{ \pm }^{'} \subset ( - \ell ,\ell ). \\ \end{gathered} \end{array}$Пусть еще для интегралов (46) выполнены требования (49) и (55). Как показано в [83], поправки $H_{ \pm }^{'}(z)$ в правой части (56) можно подобрать так, чтобы выполнялись соотношения
При этом формула (46) для МР превращается в
где используется сверхбыстрая переменная а знаменатель не обращается в нуль, так как выполнено аналогичное (52) неравенство ${\text{Re}}S_{{\centerdot \centerdot }}^{{'''}}({{\tau }_{m}}) > 0$.При малом $\varepsilon $ переменной (58) свойственен значительно более быстрый рост, чем у прежней переменной (53), а значит, соотношение (57) следует интерпретировать как обострение АВД.
Замечание 5. Одно из толкований АВД и РФ – возникновение точек комплексного резонанса (ТКР), приближенных к вещественной оси. Асимптотические формулы для этих точек и проистекающие от них наблюдения приведены в статье [83]. В частности, описанное обострение АВД обусловлено уменьшением расстояния от ТКР до вещественной оси. В принципе за счет выбора профилей $H_{ \pm }^{'}(z,\varepsilon )$ в формулах (42), (56) этому расстоянию можно придать порядок ${{\varepsilon }^{{2K - 1}}}$ с любым заданным наперед $K \in N$.
СГЛАЖИВАНИЕ АНОМАЛИЙ ВУДА – ОБРАЗОВАНИЕ СОБСТВЕННЫХ ЧИСЕЛ
Продолжим рассмотрение возмущенной полосы (42) с профильными функциями (56). Допустим, что выполнены соотношения (49) и (55), способные привести к обострению АВД, однако произведем дальнейшую настройку профилей, применив предложенную в [73, 1 ] процедуру образования СЧ (43), вкрапленного в непрерывный спектр.
Поскольку у задачи (2) в прямой полосе ${{\Pi }^{0}} = ({{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2},{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}) \times \mathbb{R}$, разумеется, нет захваченных волн, упомянутое в предыдущем разделе достаточное условие $S_{{\centerdot \centerdot }}^{\varepsilon }({{\lambda }^{\varepsilon }}) = - 1$ превращается в критерий захвата волны, который, следуя работам [1, 83], переформулируем в виде
(59)
$\begin{array}{*{20}{c}} {{\text{Im}}S_{{\centerdot \centerdot }}^{\varepsilon }({{\lambda }^{\varepsilon }}) = 0,\,\,\,\,{\text{Re}}\left( {{{e}^{{i\psi }}}S_{{\sharp \centerdot }}^{\varepsilon }({{\lambda }^{\varepsilon }})} \right) = 0 \in {{\mathbb{R}}^{{2m - 2}}},} \end{array}$Нужные профили будем искать в виде (56), где
(60)
$\begin{array}{*{20}{c}} {H_{ \pm }^{'}(z;\beta {\kern 1pt} ') = \sum\limits_{k = 1}^{m - 1} {\sum\limits_\vartheta {{{\beta }_{{k \pm }}}H_{ \pm }^{{(k\vartheta )}}(z)} } ,} \end{array}$(61)
$\begin{array}{*{20}{c}} {{{\lambda }^{\varepsilon }} = {{\pi }^{2}}{{m}^{2}} - {{{({{\tau }_{k}} + {{\beta }_{0}})}}^{2}}.} \end{array}$Образуем вектор неизвестных параметров
(62)
$\begin{array}{*{20}{c}} {\beta = ({{\beta }_{0}},\beta {\kern 1pt} ') = \left( {{{\beta }_{0}},{{\beta }_{{1 + }}},{{\beta }_{{1 - }}}, \ldots ,{{\beta }_{{m - 1 + }}},{{\beta }_{{m - 1 - }}}} \right) \in {{\mathbb{R}}^{{2m - 1}}}.} \end{array}$Наконец, назначим условия ортогональности и нормировки для компонент $H$ и $H_{\vartheta }^{{(q)}}$, согласованные с формулами (59):
(63)
$\begin{gathered} {{J}_{m}}({{H}^{{(q\vartheta )}}}) = 0,\,\,\,\,{\text{Re}}\left( {{{e}^{{i\psi }}}J_{{pm}}^{ \pm }({{H}^{{(q\vartheta )}}})} \right) = {{\delta }_{{p,q}}}{{\delta }_{{ \pm ,\vartheta }}}, \\ {{J}_{m}}(H) = 1,\,\,\,\,{\text{Re}}\left( {{{e}^{{i\psi }}}J_{{pm}}^{ \pm }(H)} \right) = 0, \\ p,q = 1, \ldots ,m - 1,\,\,\,\,\vartheta = \pm . \\ \end{gathered} $В результате при учете асимптотических формул (45) переписываем соотношения (59) как векторное трансцендентное уравнение в евклидовом пространстве ${{\mathbb{R}}^{{2m - 1}}}$ для неизвестных (62)
со сжимающим оператором ${{B}^{\varepsilon }}$ на шаре $\mathbb{B}_{\rho }^{{2m - 1}} \subset {{\mathbb{R}}^{{2m - 1}}}$ некоторого радиуса $\rho > 0$. При малом $\varepsilon $ принцип Банаха сжимающих отображений (см., например, [84; гл. 2, §4]) доставляет единственное решение $\beta \in \mathbb{B}_{\rho }^{{2m - 1}}$, которое к тому же допускает оценкуВ итоге найдены профили (56), (60) и спектральный параметр (61), при которых выполнены соотношения (59), а значит, и достаточное условие $S_{{\centerdot \centerdot }}^{\varepsilon }({{\lambda }^{\varepsilon }}) = - 1$ (критерий в данном случае) захвата волны.
Благодаря формулам (41) и (40) справедливо равенство ${{s}^{\varepsilon }}({{\tau }_{k}}) = S_{{\sharp \sharp }}^{\varepsilon }({{\tau }_{k}})$, а значит, АВД сглаживается. Напомним, что исчезновение этой аномалии также происходит при соблюдении неравенства (48) или сохранении ПР (см. пояснения в работе [83]).
Подчеркнем, что на этапе решения транcцендентного уравнения (64) формулы (62) для СЧ и (61) для профильных функций становятся неявными. В статье [85] пояснено, как следует толковать приближенное (например, численное) решение ${{\beta }_{{{\text{appr}}}}}$ уравнения (64). Условия (63), наложенные на составляющие разложения (60), можно соблюсти многими способами (один из них – вариация фазы $\psi $ в (59)), причем каждый набор функций $\{ H_{ \pm }^{{1\vartheta }}, \ldots ,H_{ \pm }^{{m - 1\vartheta }}\} $ порождает свои профили (61) для СЧ (62).
Намеченная процедура “точной настройки” успешно применялась в разных вариантах для построения околопороговых СЧ (см. [73, 86, 1, 87, 69 ] и др.), но также для сохранения ПР [83] или СЧ внутри непрерывного спектра [9]. Кроме того, она же позволяет построить примеры “невидимости” препятствий в акустическом волноводе на заданных наперед частотах (см. [88–90] и др.).
В статье [59] предложен уже обсуждавшийся в замечании 1 наиболее простой и изящный прием построения СЧ в непрерывном спектре симметричного акустического волновода – постановка искусственного условия Дирихле на средней линии (ось $z$ на рис. 2а), которые образуют искусственную ТО $\lambda _{D}^{\dag } > 0$ в спектре ополовиненного волновода. Найти СЧ смешанной краевой задачи на интервале $(0,\lambda _{D}^{\dag })$ удается при помощи простого вариационного подхода (см. [59, 91, 92, 55 ] и многие др.), и это же СЧ попадает на непрерывный спектр исходного акустического волновода.
У задачи (2) в волноводе с цилиндрическими рукавами (1) дискретный спектр заведомо пуст, так как непрерывный спектр занимает всю положительную полуось $[0, + \infty )$. При раскрытии лакун в них все-таки могут появиться изолированные СЧ. Неожиданно применить вариационный подход для их отыскания не удалось, однако работает описанный выше асимптотический метод (см., например, статью [69]), причем со значительными упрощениями (не нужно проводить настройку) и явными выражениями для членов асимптотических формул.
Результат [91] о появлении СЧ ниже ТО в спектре изогнутого квантового двумерного волновода постоянной ширины (рис. 8а) нашел многочисленные применения и обобщения (см. обзор в книге [93]). Пример двумерного акустического волновода постоянной ширины, у которого в непрерывном спектре имеется СЧ, не построен до сих пор. В трехмерном случае известны [94] примеры непустого точечного спектра ${{\sigma }_{p}}$ у волновода
с постоянным сечением $\omega \subset {{R}^{2}}$ и изогнутой осью $Y$ в плоскости $\{ x:{{y}_{2}} = 0\} $, на которой введены локальные криволинейные координаты $(n,s)$, где $s$ – длина дуги, а $n$ – ориентированное расстояние до $Y$. Именно, при двойной симметрии сеченияи любой нетривиальной кривизне $\varkappa $ оси всегда имеется СЧ на интервале $(0,{{\Lambda }_{1}})$, а в случае полной потери симметрии сечением $\omega $ удается построить СЧ ${{\lambda }^{\varepsilon }} = {{\Lambda }_{1}} - {{\varepsilon }^{2}} + O({{\varepsilon }^{3}})$ при специально подобранной малой кривизне $\varkappa (x) = O(\varepsilon )$ конечного участка оси. Наконец, в работе [95] показано, что подбором положения патрубка единичной ширины в плоском коленчатом волноводе на рис. 8б, можно добиться возникновения СЧ внутри непрерывного спектра.
Замечание 6. Поясним, почему при локальном возмущении формы волновода с цилиндрическими рукавами (1) СЧ не имеет возможности подняться вверх от порога непрерывного спектра, но в гофрированном волноводе может отцепиться в обе стороны от вырожденного порога (ср. замечание 2).
В цилиндрическом волноводе $\Pi = \omega \times \mathbb{R}$ все пороги $\lambda = {{\Lambda }_{m}}$ невырожденные, причем $K = 1$ и $\partial _{\eta }^{2}{{\Lambda }_{m}}(0) < 0$ в формуле (24) при интерпретации его как $1$-периодического множества. У задачи
(65)
$\begin{array}{*{20}{c}} {w_{{m\varepsilon }}^{{{\text{osc}} \pm }}(y,z) = {{e}^{{ \pm i\varepsilon z}}}{{U}_{m}}(y)\,\,\,\,{\text{при}}\,\,\,\,\vartheta = + ,} \end{array}$(66)
$\begin{array}{*{20}{c}} {w_{{m\varepsilon }}^{{{\text{exp}} \pm }}(y,z) = {{e}^{{ \pm \varepsilon z}}}{{U}_{m}}(y)\,\,\,\,{\text{при}}\,\,\,\,\vartheta = - .} \end{array}$В случае $\vartheta = - $, т.е. ниже ТО ${{\Lambda }_{m}}$ исчезающие при $z \to \mp \infty $ волны (65) могут породить захваченную волну в возмущенном волноводе ${{\Omega }_{\varepsilon }}$ – процедура точной настройки профиля возмущения стенок представлена в работе [1] и др. Если $\vartheta = + $ и точка ${{\Lambda }_{m}} + \vartheta {{\varepsilon }^{2}}$ расположена выше порога $\lambda = {{\Lambda }_{m}}$, в списке (66) нет затухающих волн и построение захваченной волны, происходяшей от порога, невозможно (строгое доказательство этого факта приведено в [1, 96]).
Пусть в спектре квазицилиндра $\Pi $ найден простой вырожденный порог, причем ${{\eta }^{0}} = 0$, $K = 3$ и $\partial _{\eta }^{4}{{\Lambda }_{m}}(0) < 0$ в формуле (24) (ср. замечание 2). Классические результаты [97; гл. 7], [98; гл. 9] (см. также статью [71]) о возмущении СЧ операторных пучков показывают, что у задачи (65) в квазицилиндре при $\vartheta = - $ имеются волны
(67)
$\begin{array}{*{20}{c}} \begin{gathered} w_{{m\varepsilon }}^{{{\text{dec}} \pm }}(y,z) = {{e}^{{ + \varphi _{\varepsilon }^{ \pm }z}}}\mathcal{U}_{{m\varepsilon }}^{{{\text{dec}} \pm }}(y,z), \\ w_{{m\varepsilon }}^{{{\text{gro}} \pm }}(y,z) = {{e}^{{ - \varphi _{\varepsilon }^{ \pm }z}}}\mathcal{U}_{{m\varepsilon }}^{{{\text{gro}} \pm }}(y,z), \\ \end{gathered} \end{array}$(68)
$\begin{array}{*{20}{c}} \begin{gathered} w_{{m\varepsilon }}^{{{\text{osc}} \pm }}(y,z) = {{e}^{{ \pm i\varphi _{\varepsilon }^{0}z}}}\mathcal{U}_{{m\varepsilon }}^{{{\text{osc}} \pm }}(y,z), \\ w_{{m\varepsilon }}^{{{\text{exp}} \pm }}(y,z) = {{e}^{{ \pm \varphi _{\varepsilon }^{0}z}}}\mathcal{U}_{{m\varepsilon }}^{{{\text{exp}} \pm }}(y,z). \\ \end{gathered} \end{array}$При этом показатели экспонент удовлетворяют соотношениям
К сожалению, автор не знает конкретного гофрированного акустического волновода, у которого в спектре существует вырожденный порог, однако в публикациях [99] и [64] эффект поднятия СЧ с вырожденного порога подтвержден для задач теории упругости и теории пластин Кирхгофа. Остался открытым вопрос о построении возмущения, при котором у волновода возникает максимально возможное количество СЧ – два ниже и одно выше ТО.
АНОМАЛИИ ВАЙНШТЕЙНА
В акустических и квантовых волноводах АВД и СЧ могут возникать только ниже невырожденного порога, а выше него зачастую образуются аномалии Вайнштейна (АВН), связанные с почти полным отражением (ППО) или почти полным прохождением (ППП) некоторых волн. Впервые такая необычная дифракционная картина была описана в книге [100], где на основе явных формул для акустического поля было обнаружено ППО поршневой моды в полубесконечной цилиндрической круговой трубе, открытой в пространство. Изучению АВН посвящено большое количество публикаций (см. [101, 96, 2, 102–105 ] и др.), в том числе и для упругих волноводов [106].
Приведем один из результатов статьи [2], относящихся к цилиндрическим волноводам с резонаторами (рис. 2а), и для упрощения формулировок предположим зеркальную симметрию волновода относительно плоскости $\{ x:z = 0\} $ (ср. замечание 6), перпендикулярной оси цилиндра $\Pi $. Рассмотрим какое-то простое СЧ ${{\Lambda }_{m}}$ модельной задачи (7) и отвечающую ему частоту отсечки ${{\kappa }_{\dag }} = \sqrt {{{\lambda }_{\dag }}} $. Спектральному параметру
(69)
$\begin{array}{*{20}{c}} {{{{({{\kappa }^{\varepsilon }})}}^{2}} = {{\lambda }^{\varepsilon }} = {{\Lambda }_{m}} + {{\varepsilon }^{2}} \in ({{\Lambda }_{m}},{{\Lambda }_{{m + 1}}})\,\,\,\,{\text{при}}\,\,\,\,\varepsilon > 0} \end{array}$$1^\circ .$ при $k = 0$ (нет ПСВ) происходит ППО, т.е.
$2^\circ .$ при $k = 1$ (пространство ПСВ одномерно) происходит ППП, т.е.
$3^\circ .$ при $k = 2$ (есть две линейно независимые ПСВ) происходит ППО, т.е.
Ситуации $1^\circ $ и $3^\circ $ можно смоделировать при помощи слабопроницаемой перегородки на торце $\omega ( - \ell )$ рукава ${{\Pi }_{ - }}$, причем она мягкая в случае $1^\circ $ и жесткая в случае $3^\circ $. Ясно, что ПР – неустойчивый феномен, и в статье [94] описана процедура, позволяющая сохранить его, но, как и в случае СЧ, вкрапленного в непрерывный спектр, требующая “точной настройки” формы возмущения стенок. Поэтому $1^\circ $ – ситуация общего положения. Пример ПР с кратностью $k = 1$ очевиден: прямой цилиндр или полоса. Известный автору пример88 ситуации $3^\circ $ весьма экзотичен, а именно, два полуцилиндра соединены тонкими изогнутыми трубками в количестве $N \leqslant 8$ штук при специальном подборе их длин (см. схему на рис. 9а).
Рис. 9.
Схематичные ($N = 3$) изображения (а) – волновода с двойным пороговым резонансом и (б) – сочленение нескольких полуцилиндров.

Как упоминалось, на нулевой ТО реализуется простой ПР. Рассмотрим задачу рассеяния на низких частотах $\kappa \ll 1$ в волноводе $\Omega $, состоящем из конечного ядра $\Theta $ и полуцилиндров ${{\Pi }_{1}}, \ldots ,{{\Pi }_{N}}$ (рис. 9б с $N = 3$), т.е. задачу Неймана (2) с малым параметром $\lambda = {{\kappa }^{2}}$. Пусть сечения рукавов
(70)
$\begin{array}{*{20}{c}} {{{\Pi }_{n}} = \{ ({{y}^{n}},{{z}_{n}}):{{y}^{n}} \in \omega ,{{z}_{n}} > 0\} } \end{array}$Таким образом, при $N = 1$ и $N = 2$ реализуются ППО ($S_{{11}}^{0} = 1$) и ППП ($S_{{22}}^{0} = 0$ и $S_{{21}}^{0} = 1$) соответственно, однако в случае $N\,\, \geqslant \,\,3$ никаких особенностей в картине рассеяния нет.
Замечание 6. При $N = 2$ при разных площадях сечений рукавов или при потере волноводом зеркальной симметрии ПСВ приобретают разложение
В этом случае согласно вычислениям из [2] коэффициенты отражения и прохождения на частоте ${{\kappa }^{\varepsilon }}$ из (69) принимают вид
Ясно, что в случае $\left| {{{K}_{ - }}} \right| = \left| {{{K}_{ + }}} \right|$ реализуется ППП и без симметрии волновода, но в случаях ${{K}_{ - }} = 0$ или ${{K}_{ + }} = 0$ – ППО.
Работа финансово поддержана Российским научным фондом (проект 17-11-01003).
Список литературы
Назаров С.А. Асимптотика собственных чисел на непрерывном спектре регулярно возмущенного квантового волновода // Теоретическая и математическая физика. 2011. Т. 167, 2. С. 239–262.
Korolkov A.I., Nazarov S.A., Shanin A.V. Stabilizing solutions at thresholds of the continuous spectrum and anomalous transmission of waves // ZAMM. 2016. V. 96. 10. P. 1245–1260.
Molchanov S., Vainberg B. Scattering solutions in networks of thin fibers: small diameter asymptotics // Comm. Math. Phys. 2007. V. 273. 2. P. 533–559.
Grieser D. Spectra of graph neighborhoods and scattering // Proc. London Math. Soc. 2008. V. 97. P. 718–752.
Назаров С.А. Спектр прямоугольных решеток квантовых волноводов // Известия РАН. Серия матем. 2017. Т. 81, 1. С. 31–92.
Назаров С.А. Разрушение циклов и возможность раскрытия спектральных лакун в квадратной решетке тонких акустических волноводов // Известия РАН. Серия матем. 2018. Т. 82, 6. С. 3–51.
Aslanyan A., Parnovski L., Vassiliev D. Complex resonances in acoustic waveguides // Q. J. Mech. Appl. Math. 2000. V. 53. P. 429–447.
Linton C. M., McIver P. Embedded trapped modes in water waves and acoustics // Wave Motion. 2007. V. 45. 1–2. P. 16–29.
Назаров С.А. Принудительная устойчивость простого собственного числа на непрерывном спектре волновода // Функциональный анализ и его приложения. 2013. Т. 47, 3. С. 37–53.
Wilcox C.H. Scattering Theory for Diffraction Gratings. Applied Mathematical Sciences Series Vol. 46. Singapure: Springer, 1997.
Митра P., Ли С. Аналитические методы теории волноводов. М.: Мир, 1974.
Рид М., Саймон Б. Методы современной математической физики. Т. 3. Теория рассеяния. М.: Мир, 1982.
Кучмент П.А. Теория Флоке для дифференциальных уравнений в частных производных // Успехи матем. наук. 1982. Т. 37, 4. С. 3–52.
Скриганов М.М. Геометрические и арифметические методы в спектральной теории многомерных периодических операторов // Труды матем. ин-та им. В.А. Стеклова АН СССР. Т. 171. Ленинград: Наука, 1985. 122 с.
Kuchment P. Floquet theory for partial differential equations. Basel: Birchäuser, 1993.
Nazarov S.A., Plamenevsky B.A. Elliptic problems in domains with piecewise smooth boundaries. Berlin, New York: Walter de Gruyter, 1994.
Гельфанд И.М. Разложение по собственным функциям уравнения с периодическими коэффициентами // Доклады АН СССР. 1950. Т. 73. С. 1117–1120.
Назаров С.А. Открытие лакуны в непрерывном спектре периодически возмущенного волновода // Матем. заметки. 2010. Т. 87, 5. С. 764–786.
Bakharev F.L., Nazarov S.A., Ruotsalainen K.M. A gap in the spectrum of the Neumann–Laplacian on a periodic waveguide // Applicable Analysis. 2012. V. 88. P. 1–17.
Borisov D., Pankrashkin K. Quantum waveguides with small periodic perturbations: gaps and edges of Brillouin zones // J. Physics A: Mathematical and Theoretical. 2013. V. 46, 23. 235203.
Назаров С.А. Асимптотика спектральных лакун в регулярно возмущенном периодическом волноводе // Вестник СПбГУ. Сер. 1. 2013. Вып. 2(7). С. 54–63.
Hempel R., Lienau K. Spectral properties of periodic media in the large coupling limit // Commun. Partial Differ. Equ. 2000. V. 25. P. 1445–1470.
Hempel R., Post O. Spectral gaps for periodic elliptic operators with high contrast: an overview // In: Progress in analysis, proceedings of the 3rd international ISAAC congress Berlin. 2001. P. 577–587.
Post O. Periodic manifolds with spectral gaps // J. Differential Equations. 2003. V. 187. P. 23–45.
Exner P., Post O. Convergence of spectra of graph-like thin manifolds // J. Geom. and Phys. 2005. V. 54(1). P. 77–115.
Post O. Spectral analysis on graph-like spaces. Lecture Notes in Mathematics, 2009. Heidelberg: Springer, 2012.
Жиков В.В. О лакунах в спектре некоторых дивергентных эллиптических операторов с периодическими коэффициентами // Алгебра и анализ. 2004. Т. 16, 5. С. 34–58.
Назаров С.А. Лакуна в существенном спектре задачи Неймана для эллиптической системы на периодической области // Функциональный анализ и его приложения. 2009. Т. 43, 3. С. 92–95.
Назаров С.А., Руотсалайнен К., Таскинен Я. Спектральные лакуны в задачах Дирихле и Неймана на плоскости, перфорированной двоякопериодическим семейством круговых отверстий // Проблемы матем. анализа. Вып. 62. Новосибирск, 2011. С. 51–100.
Бахарев Ф.Л., Назаров С.А. Лакуны в спектре волновода, составленного из областей с различными предельными размерностями // Сибирск. матем. журнал. 2015. Т. 56, 4. С. 732–751.
Bakharev F.L., Cardone G., Nazarov S.A., Taskinen J. Effects of Rayleigh waves on the essential spectrum in perturbed doubly periodic elliptic problems // Integral Equations and Operator Theory. 2017. V. 88, 3. P. 373–386.
Sanchez Hubert J., Sanchez-Palencia E. Vibration and coupling of continuous systems. Berlin: Springer-Verlag, 1989.
Lobo M., Perez E. High frequency vibrations in a stiff problem // Mathematical Models and Methods in Applied Sciences. 1997. V. 7, 2. P. 291–311.
Назаров С.А. Лакуна в спектре формально самосопряженной эллиптической системы дифференциальных уравнений // Дифференциальные уравнения. 2010. Т. 46, 5. С. 726–736.
Beale J.T. Scattering frequencies of resonators // Commun. Pure Appl. Math. 1973. V. 26, 4. P. 549–563.
Арсеньев А.А. О существовании резонансных полюсов и резонансов при рассеянии в случае краевых условий II и III рода // Журн. вычисл. математики и мат. физики. 1976. Т. 16, 3. С. 718–724.
Гадыльшин Р.Р. О собственных частотах тел с тонкими отростками. I // Матем. заметки. 1993. Т. 54, 6. С. 10–21. II. // ibid. 1994. Т. 55, 1. С. 20–34. III. // ibid. 1997. Т. 61, 4. С. 494–502.
Назаров С.А. Соединения сингулярно вырождающихся областей различных предельных размерностей. 1 // Труды семинара им. И.Г. Петровского. Вып. 18. М.: изд-во МГУ. 1995. С. 3–78. 2 // ibid. Вып. 20. М.: изд-во МГУ. 1997. С. 155–195.
Kozlov V.A., Maz’ya V.G., Movchan A.B. Asymptotic analysis of fields in multi-structures. Oxford: Clarendon Press, 1999.
Гадыльшин Р.Р. О собственных значениях “гантели с тонкой ручкой” // Изв. РАН. Сер. мат. 2005. Т. 69, 2. С. 45-–110.
Joly P., Tordeux S. Matching of asymptotic expansions for wave propagation in media with thin slots. I: The asymptotic expansion // SIAM J. Multiscale Model. Simul. 2006. V. 5, 1. P. 304–336.
Joly P., Tordeux S. Matching of asymptotic expansions for waves propagation in media with thin slots. II: The error estimates // Math. Model. Numer. Anal. 2008. V. 42, 2. P. 193–221.
Nazarov S.A., Ruotsalainen K., Taskinen J. Essential spectrum of a periodic elastic waveguide may contain arbitrarily many gaps // Applicable Anal. 2010. V. 89, 1. P. 109–124.
Назаров С.А. Дискретный спектр коленчатых квантовых и упругих волноводов // Журн. вычисл. матем. и матем. физ. 2016. Т. 56, 5. С. 879–895.
Назаров С.А., Таскинен Я. Строение спектра периодического семейства идентичных ячеек, соединенных через сужающиеся отверстия // Записки научн. семинаров петербург. отделения матем. института РАН. 2012. Т. 409. С. 130–150.
Sobolev A.V., Walthoe J. Absolute continuity in periodic waveguides // Proc. London Math. Soc. 2002. V. 85, 1. P. 717–741.
Суслина Т.А., Штернберг Р.Г. Абсолютная непрерывность спектра оператора Шредингера с метрикой в двумерном периодическом волноводе // Алгебра и Анализ. 2002. Т. 13, 2. С. 159–206.
Shargorodskii E., Sobolev A.V. Quasi-conformal mappings and periodic spectral problems in dimension two // J. d’Analise Math. 2003. V. 91, 1. P. 63–103.
Miller K. Nonunique continuation for uniformly parabolic and elliptic equations in self-adjoint divergence form with Höolder continuous coefficients // Arch. Rat. Mech Anal. 1974. V. 54, 2. P. 105-–117.
Филонов Н.Д. Эллиптическое уравнение второго порядка в дивергентной форме, имеющее решение с компактным носителем // Проблемы матем. анализа. Т. 22. С. 246–257.
Демченко М.Н. О неединственности продолжения решения системы Максвелла // Записки научн. семинаров петербург. отделения матем. института РАН. 2011. Т. 393. С. 803–100.
Агранович М.С., Вишик М.И. Эллиптические задачи с параметром и параболические задачи общего вида // Успехи матем. наук. 1964. Т. 19, 3. С. 53–160.
Pankrashkin K. Eigenvalue inequalities and absence of threshold resonances for waveguide junctions // J. of Math. Anal. and Appl. 2017. V. 449, 1. P. 907–925.
Bakharev F.L., Nazarov S.A. Criteria for the absence and existence of bounded solutions at the threshold frequency in a junction of quantum waveguides. https://arxiv.org/abs/1705.10481
Назаров С.А. Локализованные волны в Т-образном волноводе // Акуст. журн. 2010. Т. 56, 6. С. 747–758.
Nazarov S.A., Ruotsalainen K., Uusitalo P. The Y-junction of quantum waveguides // ZAMM. 2014. V. 94, 6. P. 477–486.
Назаров С.А. Ограниченные решения в Т-образном волноводе и спектральные свойства лестницы Дирихле // Журн. вычисл. матем. и матем. физ. 2014. Т. 54, 8. С. 1299–1318.
Бахарев Ф.Л., Матвеенко С.Г., Назаров С.А. Дискретный спектр крестообразных волноводов // Алгебра и анализ. 2016. Т. 28, 2. С. 32–45.
Evans D.V., Levitin M., Vasil’ev D. Existence theorems for trapped modes // J. Fluid Mech. 1994. V. 261. P. 21–31.
Jones D.S. The eigenvalues of ${{\nabla }^{2}}u + \lambda u = 0$ when the boundary conditions are given on semi-infinite domains // Proc. Camb. Phil. Soc. 1953. V. 49. P. 668–684.
Назаров С.А. Почти стоячие волны в периодическом волноводе с резонатором и околопороговые собственные числа // Алгебра и анализ. 2016. Т. 28, 3. С. 111–160.
Михлин С.Г. Вариационные методы в математической физике. М.: Наука, 1970.
Назаров С.А. Энергетические условия излучения Мандельштама и вектор Умова–Пойнтинга в упругих волноводах // Проблемы матем. анализа. Вып. 72. Новосибирск, 2013. С. 101–146.
Назаров С.А. Бесконечная пластина Кирхгофа на компактном упругом основании может иметь сколь угодно малое собственное число // Доклады РАН. 2019. Т. 488, 4. С. 360–364.
Умов Н.А. Уравнения движения энергии в телах. Одесса: Типогр. Ульриха и Шульце, 1874.
Мандельштам Л.И. Лекции по оптике, теории относительности и квантовой механике. Сб. трудов. Т. 2. М.: Изд-во АН СССР, 1947.
Вайнберг Б.Р. Принципы излучения, предельного поглощения и предельной амплитуды в общей теории уравнений с частными производными // Успехи матем. наук. 1966. Т. 21, 6. С. 115–194.
Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории упругости для неклассических областей. М.: Наука, 1979. 20 с.
Назаров С.А. Лакуны и собственные частоты в спектре периодического акустического волновода // Акуст. журн. 2013. Т. 59, 3. С. 312–321.
Poynting J. H. On the transfer of energy in the electromagnetic field // Phil. Trans. of the Royal Society of London. 1884. V. 175. P. 343–361.
Назаров С.А. Условия излучения Умова–Мандельштама в упругих периодических волноводах // Матем. сборник. 2014. Т. 205, 7. С. 43–72.
Камоцкий И.В., Назаров С.А. Расширенная матрица рассеяния и экспоненциально затухающие решения эллиптической задачи в цилиндрической области // Записки научн. семинаров петербург. отделения матем. института РАН. 2000. Т. 264. С. 66–82.
Камоцкий И.В., Назаров С.А. Аномалии Вуда и поверхностные волны в задачах рассеяния на периодической границе. I // Матем. сборник. 1999. Т. 190, 1. С. 109–138; II // ibid. 1999. Т. 190, 2. С. 43–70.
Назаров С.А. Критерий существования затухающих решений в задаче о резонаторе с цилиндрическим волноводом // Функциональный анализ и его приложения. 2006. Т. 40, 2. С. 20–32.
Chesnel L,. Nazarov S. A. Non reflection and perfect reflection via Fano resonance in waveguides // Commun. Math. Sci. 2018. V. 16, 7. P. 1779–1800.
Fano U. Effects of configuration interaction on intensities and phase shifts // Phys. Rev. 1961. V. 124, 6. P. 1866–1878.
Shipman S.P., Venakides S. Resonant transmission near nonrobust periodic slab modes // Phys. Rev. E. 2005. V. 71, 2. 026611.
Shipman S.P., Tu H. Total resonant transmission and reflection by periodic structures // SIAM J. Appl. Math. 2012. V. 72, 1. P. 216–239.
Shipman S.P., Welters A.T. Resonant electromagnetic scattering in anisotropic layered media // J. Math. Phys. 2013. V. 54, 10. 103511.
Wood R. On the remarkable case of uneven distribution of light in a difraction grating spectrum // Proc. Phys. Soc. London. 1902. V. 18. P. 269–275.
Seabrook W. Doctor Wood, Modern Wizard of the Laboratory. New York: Harcourt Brace, 1941.
Hessel A., Oliner A.A. A new theory of Wood’s anomalies on optical gratings // Appl. Optics. 1965. V. 4, 10. P. 1275–1297.
Назаров С.А. Обострение и сглаживание околопороговых аномалий Вуда в акустическом волноводе // Акуст. журн. 2018. Т. 64, 5. С. 534–546.
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 1976.
Nazarov S.A., Ruotsalainen K.M. A rigorous interpretation of approximate computations of embedded eigenfrequencies of water waves // Z. Anal. Anwend. 2016. V. 35, 2. P. 211–242.
Назаров С.А. Собственные числа оператора Лапласа с условиями Неймана на регулярно возмущенных стенках волновода // Проблемы матем. анализа. Вып. 53. Новосибирск, 2011. С. 104–119.
Назаров С.А. Волны, захваченные тонким искривленным экраном в волноводе с жесткими стенками // Акуст. журн. 2012. Т. 58, 6. С. 683–691.
Боннэ-Бен Диа А.-С., Назаров С.А. Препятствия в акустическом волноводе, становящиеся “невидимыми” на заданных частотах // Акуст. журн. 2013. Т. 59, 6. С. 685–692.
Chesnel L., Nazarov S.A. Team organization may help swarms of flies to become invisible in closed waveguides // Inverse Problems and Imaging. 2016. V. 10, 6. P. 977–1006.
Bonnet-Ben Dhia A.-S., Lunéville E., Mbeutcha Y., Nazarov S.A. A method to build non-scattering perturbations of two-dimensional acoustic waveguides // Math. Methods Appl. Sci. 2017. V. 40, 2. P. 335–349.
Duclos P., Exner P. Curvature-induced bound states in quantum waveguides in two and three dimensions // Review Math. Phys. 1995. V. 7, 1. P. 73–102.
Назаров С.А. Вариационный и асимптотический методы поиска собственных чисел под порогом непрерывного спектра // Сибирск. матем. журнал. 2010. Т. 51, 5. С. 1086–1101.
Exner P., Kovarîk H. Quantum waveguides. Theoretical and Mathematical Physics. Cham: Springer, 2015.
Назаров С.А. Захват волны в искривленном цилиндрическом акустическом волноводе с неизменным сечением // Алгебра и анализ. 2019. Т. 31, 5. С. 154–183.
Назаров С.А. Захваченные волны в коленчатом волноводе с жесткими стенками // Акуст. журн. 2011. Т. 57, 6. С. 746–754.
Назаров С.А. Аномалии рассеяния в резонаторе выше порогов непрерывного спектра // Матем. сборник. 2015. Т. 206, 6. С. 15–48.
Като Т. Теория возмущений линейных операторов. М.: Мир, 1972.
Вайнберг М.М., Треногин В.А. Теория ветвления решений нелинейных уравнений. М.: Наука, 1969.
Назаров С.А. Построение захваченной волны на малых частотах в упругом волноводе // Функциональный анализ и его приложения. 2020. Т. 54, 1. С. 41–57.
Вайнштейн Л.А. Теория дифракции и метод факторизации. М.: Советское радио, 1966.
Shanin A.V. Weinstein’s diffraction problem: embedding formula and spectral equation in parabolic approximation // SIAM J. Appl. Math. 2009. V. 70. P. 1201–1218.
Корольков А.И., Шанин А.В. Дифракция на решетке из поглощающих экранов разной высоты. Новые уравнения // Записки научн. семинаров петербург. отделения матем. института РАН. 2014. Т. 422. С. 62–89.
Shanin A.V., Korolkov A.I. Diffraction by a transversal screen in a planar waveguide // Proc. of Progress In Electromagnetics Research Symposium (PIERS –SPb). 2017. P. 3521–3525.
Shanin A.V., Korolkov A.I. Diffraction of a mode close to its cut-off by a transversal screen in a planar waveguide // Wave Motion. 2017. V. 68. P. 218–241.
Назаров С.А. О прохождении волн через малое отверстие в перегородке акустического волновода // Сибирск. матем. журнал. 2018. Т. 59, 1. С. 110–129.
Назаров С.А. Почти полное прохождение низкочастотных волн в локально поврежденном упругом волноводе // Проблемы матем. анализа. Вып. 100. Новосибирск, 2019. С. 83–121.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал