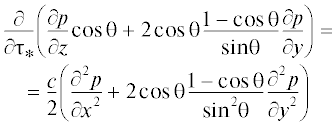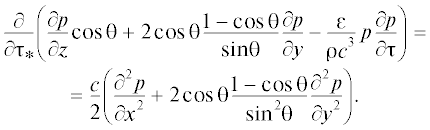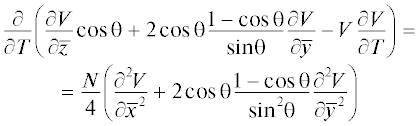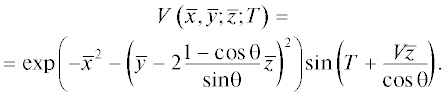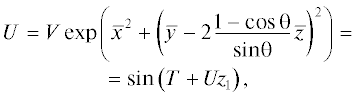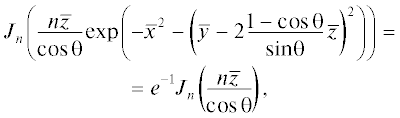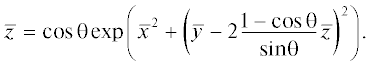Акустический журнал, 2020, T. 66, № 6, стр. 583-598
Аппроксимация пространственного спектра нелинейных пучков с осью, наклоненной к излучающей поверхности
a Физический факультет Московского государственного университета им. М.В. Ломоносова
119991 Москва, ГСП-1, Ленинские горы, Россия
b Институт физики Земли им. О.Ю. Шмидта РАН
123995 Москва, ул. Большая Грузинская 10, стр. 1, Россия
* E-mail: vgusev@bk.ru
Поступила в редакцию 08.06.2020
После доработки 08.06.2020
Принята к публикации 07.07.2020
Аннотация
Рассмотрено наклонное распространение по отношению к излучающей плоскости акустических пучков большой интенсивности. Предложена аппроксимация оператора Даламбера, позволяющая вывести эволюционное уравнение, пригодное при любых углах распространения пучка. Сформулировано уравнение типа Хохлова–Заболотской для наклонного распространения пучка.
ВВЕДЕНИЕ
В настоящее время активно развиваются методы анализа и расчета волновых полей с широким угловым спектром. Можно указать две характерные задачи, различающиеся подходами к их решению. Первая задача требует учета максимального числа компонент пространственного спектра, соответствующих приходу сигналов с различных направлений. Такая ситуация реализуется, в частности, в акустике океана [1, 2]. Вторая задача связана с излучением, возможно, и узконаправленного пучка, но с осью, наклоненной под некоторым углом к нормали к плоскости излучателя. Здесь отметим использование составных антенных решеток с переменным положением фокуса, в частности, для медицинских приложений [3, 4]. Для ускорения ультразвукового воздействия на биоткани удобно электронным образом перемещать фокус волны за счет изменения фазы и амплитуды элементарных излучателей, не изменяя геометрию и положение излучателя в целом. В этом случае излучение происходит под некоторым углом к геометрической оси излучателя. Ситуации наклонного распространения интенсивных волн встречаются и в аэроакустических и геофизических приложениях. Например, волна с ударными фронтами, генерируемая сверхзвуковым самолетом, распространяется под углом $\theta = \arcsin {c \mathord{\left/ {\vphantom {c {v}}} \right. \kern-0em} {v}}$ к направлению полета, где $с$ – скорость звука в воздухе, ${v}$ – скорость самолета. Эта волна падает на турбулентный пограничный атмосферный слой, который эффективно моделируется случайным фазовым экраном [5–7]. При скоростях самолета, несколько превышающих скорость звука, угол падения волны на этот фазовый экран оказывается большим. Аналогичная ситуация складывается и при излучении звука в атмосферу сейсмоиндуцированными волнами на поверхности Земли [8]. Отметим также задачи излучения и распространения волн в придонном газонасыщенном волноводе при различных расположениях источника [9, 10].
Во многих случаях излучаемые волны можно считать квазиплоскими, что позволяет описать их распространение упрощенными эволюционными уравнениями. Для пучков большой интенсивности обычно используются эволюционные уравнения, например уравнение Хохлова–Заболотской [11], позволяющие упростить математическую модель и построить точные и приближенные аналитические решения. Однако подобные уравнения обычно выводятся при условии распространения, близкого к нормальному к излучающей плоскости. В дальнейшем направление распространения может изменяться за счет неоднородности среды. В указанных выше ситуациях угол между нормалью к плоскости, на которой задается граничное условие, и направлением распространения нельзя считать малым. Поэтому необходимо вывести более точное эволюционное уравнение для интенсивных пучков.
Основные сложности при расчете полей широкоугольных волн вызваны двумя причинами. Первая носит вычислительный характер и состоит в расчете обратного преобразования Фурье при сложении полей отдельных компонент пространственного спектра. Вторая возникает при расчете полей большой интенсивности, когда метод спектрального разложения становится неэффективным из-за нелинейного взаимодействия. Соответственно, аналитические результаты могут быть получены только в некоторых частных случаях или при использовании различных упрощений. Поэтому обычно применяются численные методы, однако и при их использовании задача остается достаточно трудоемкой. Основным подходом является применение различных способов аппроксимации пространственного спектра, позволяющих сохранить достаточную точность и в тоже время добиться упрощения расчетов. Среди них отметим построение псевдодифференциальных уравнений [1, 12], использование аппроксимации Паде [13–15]. Причем в последнем случае эффективной оказывается аппроксимация не самого пространственного спектра, а всего пропагатора $\exp (i{{k}_{z}}z).$
Далее рассматривается вторая ситуация, когда распространяется пучок с узким пространственным спектром, но в направлении, отличном от нормали к плоскости излучателя. В этом случае будем говорить о наклонном распространении пучка. Для этой ситуации могут быть обобщены известные подходы к описанию пучков, распространяющихся вдоль нормали к плоскости излучателя. Это позволит как упростить численные расчеты, так и получить аналитические решения, выявляющие основные качественные особенности эволюции пучков. В частности, наиболее распространенным уравнением пучковой акустики является уравнение Хохлова–Заболотской (ХЗ). В ряде работ, например [16], показано, что при сравнении с более точными моделями (например, уравнением Вестервельта или нелинейным волновым уравнением) численное решение уравнений ХЗ обеспечивает хорошую точность при существенном выигрыше в скорости расчета. Кроме того, имеется достаточно большой набор точных и приближенных решений этого уравнения [11, 17, 18].
В литературе представлено несколько подходов к выводу упрощенных уравнений и их решению при наклонном распространении пучков. Во-первых, отметим работу [4], в которой рассмотрено наклонное падение на фазовый экран в рамках нелинейной геометрической акустики. Достоинством развитого подхода является возможность построения аналитического решения для произвольных начальных временного профиля и поперечной структуры пучка, что позволяет провести анализ обратной задачи оптимизации параметров излучателя [19, 20]. Однако этот подход непосредственно не может быть применен для описания поля в области фокусировок и каустик. Эволюционные уравнения для наклонного распространения, учитывающие дифракцию, в линейном и нелинейном случаях были получены в работе [21] на основе параболической аппроксимации пространственного спектра. Близкие по методике аппроксимации были предложены в работах [22, 23] для линейных задач. Проведенное в этих работах сравнение с экспериментом показало работоспособность предложенных аппроксимаций. Однако, более детальный анализ, проведенный ниже, показывает ограниченность этих моделей и существенную зависимость от характеристик излучателя.
Целью данной работы является выявление ограничений предложенных ранее моделей и конструирование новой аппроксимации пространственного спектра, позволяющей с достаточной точностью описывать наклонное распространение пучков под большими углами к нормали к плоскости излучателя. На основе данной аппроксимации получено новое нелинейное эволюционное уравнение для расчета полей интенсивных пучков.
АППРОКСИМАЦИЯ ПРОСТРАНСТВЕННОГО СПЕКТРА И ЭВОЛЮЦИОННОЕ УРАВНЕНИЕ ПРИ РАСПРОСТРАНЕНИИ ВДОЛЬ НОРМАЛИ
Одной из исходных задач “пучковой” акустики является получение упрощенных эволюционных уравнений, позволяющих рассчитать трансформацию временного профиля и поперечной формы пучка при его распространении. В ряде случаев эти уравнения позволяют получить аналитические решения, в том числе, и для нелинейных пучков.
Существует два формально независимых способа вывести эволюционное уравнение, описывающее распространение квазиплоского пучка при распространении по нормали к плоскости излучателя. Первый способ связан с переходом к пространственному спектру и его упрощению. Второй способ основан на методе медленно изменяющегося профиля (МИП) и использует условия медленности изменения характеристик пучка в различных направлениях. Первый способ более нагляден, но применим только к линейным задачам. Второй применим и к нелинейным задачам, но требует специального подбора малых параметров. Рассмотрим кратко эти способы на примере вывода параболического уравнения теории дифракции [24].
Пусть плоский излучатель расположен в плоскости $z = 0,$ на которой задано граничное условие для акустического давления ${{\left. p \right|}_{{z = 0}}}$ =${{p}_{0}}\left( {t;x,y} \right),$ где зависимость от поперечных координат $x,y$ описывает структуру волнового пучка (рис. 1). Далее эту плоскость будем называть плоскостью излучателя. Распространение волны в однородном полупространстве $z \geqslant 0$ подчиняется линейному волновому уравнению
(1)
$\frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}p}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}p}}{{\partial {{z}^{2}}}} - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}p}}{{\partial {{t}^{2}}}} = 0.$Рис. 1.
Расположение плоскости излучателя и направление оси пучка, наклоненной к этой плоскости под углом θ.
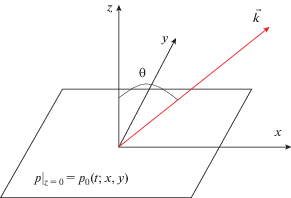
Используя прямое преобразование Фурье по времени и прямое и обратное преобразования по поперечным координатам, точное решение уравнения (1) можно записать в виде:
(2)
$\begin{gathered} p = \frac{1}{{4{{\pi }^{2}}}}\iint\limits_\infty {{{S}_{0}}\left( {\omega ;x{\kern 1pt} ',y{\kern 1pt} '} \right)dx{\kern 1pt} 'dy{\kern 1pt} '}\int\limits_{ - \infty }^\infty {\exp \left( { - i\omega t} \right)d\omega } \times \\ \times \,\,\iint\limits_\infty {\exp \left( {i{{k}_{x}}\left( {x - x{\kern 1pt} '} \right) + i{{k}_{y}}\left( {y - y{\kern 1pt} '} \right) + } \right.} \\ \left. { + \,\,iz\sqrt {{{k}^{2}} - k_{x}^{2} - k_{y}^{2}} } \right)d{{k}_{x}}d{{k}_{y}}. \\ \end{gathered} $Здесь S0(ω, x, y) – частотный спектр граничного условия при $z = 0$, kx, ky – поперечные волновые числа (поперечные компоненты волнового вектора), k = ω/c. При вычислении внутренних интегралов в выражении (2) удается продвинуться, однако это зависит от конкретной исходной поперечной формы и симметрии пучка. Кроме того, конечное интегральное выражение содержит помимо распространяющихся волн еще и неоднородные, экспоненциально затухающие. Поэтому для получения явных аналитических решений необходимо прибегать к упрощениям. Одним из часто используемых в теории волн упрощений является переход к рассмотрению квазиплоских ограниченных волновых пучков с узким пространственным спектром. В этом случае продольное волновое число
можно заменить первыми членами разложения в ряд Тейлора вблизи направления распространения волны. Акустическое поле, рассчитанное в таком приближении, подчиняется некоторому эволюционному уравнению.При распространении пучка преимущественно вдоль нормали к начальной плоскости, т.е. вдоль оси $z,$ пространственный спектр сосредоточен в области ${{k}_{z}}\sim k,$ ${{k}_{x}},{{k}_{y}} \ll k,$ и вместо точного выражения (3) можно использовать первые два ненулевых члена ряда Тейлора:
(4)
${{k}_{z}} = k - {{\left( {k_{x}^{2} + k_{y}^{2}} \right)} \mathord{\left/ {\vphantom {{\left( {k_{x}^{2} + k_{y}^{2}} \right)} {2k}}} \right. \kern-0em} {2k}}.$Выражение (4) представляет параболическую аппроксимацию продольного волнового числа. Акустическое поле, отвечающее соотношению (4), удовлетворяет линеаризованному уравнению Хохлова–Заболотской (ЛХЗ) (обобщению параболического уравнения дифракции для негармонических сигналов):
(5)
$\frac{{{{\partial }^{2}}p}}{{\partial \tau \partial z}} = \frac{c}{2}\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}p}}{{\partial {{y}^{2}}}}} \right),$Подставляя аппроксимацию (4) в решение (2), получаем общее решение уравнения (5) для граничного условия ${{\left. p \right|}_{{z = 0}}}$ = ${{p}_{0}}\left( {t;x,y} \right)$
(7)
$\begin{gathered} p = \frac{1}{{2\pi cz}}\frac{\partial }{{\partial \tau }} \times \\ \times \,\iint\limits_\infty {{{p}_{0}}\left( {\tau - \frac{{{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}}}}{{2cz}};\,\,x{\kern 1pt} ',y{\kern 1pt} '} \right)}dx{\kern 1pt} 'dy{\kern 1pt} '. \\ \end{gathered} $При решении нелинейных задач преобразование Фурье и спектральное представление становятся неэффективными. Поэтому для вывода нелинейных эволюционных уравнений принципиально важно, что уравнение (5) может быть получено другим, формально независимым способом – методом МИП. Согласно этому методу необходимо приписать определенные степени медленности изменения характеристик пучка вдоль различных направлений, которые в общем случае заранее могут быть неизвестны. В рассматриваемом случае квазиплоского пучка, распространяющего по нормали, эти степени медленности хорошо известны. Предполагается, что волна как целое переносится со скоростью звука c, медленно искажается в поперечном направлении и еще более медленно – в продольном направлении. Эти предположения о форме решения формализуются выражением $p = p\left( {\tau ,\sqrt \mu x,\sqrt \mu y,\mu z} \right),$ где μ $ \ll $ 1 – малый параметр. Собирая слагаемые, пропорциональные $\mu $, и пренебрегая более малыми слагаемыми, получаем (5). Как известно, применение метода МИП к нелинейному волновому уравнению позволяет вывести уравнение Хохлова–Заболотской для ограниченных пучков большой интенсивности.
Метод МИП определяет “быстрые” и “медленные” переменные и накладывает условия медленности изменения временного профиля и поперечной формы пучка. Спектральный метод накладывает условие малой ширины пространственного спектра. Совпадение результатов – уравнение (5) – устанавливает связь между выбором аппроксимации пространственного спектра и выводом упрощенных уравнений в квазиоптическом приближении. Поэтому в дальнейшем будем параллельно рассматривать результаты, получаемые с помощью спектрального разложения и метода МИП.
АППРОКСИМАЦИЯ РЯДОМ ТЕЙЛОРА ПРИ НАКЛОННОМ РАСПРОСТРАНЕНИИ
Для того чтобы волна распространялась под углом θ к нормали к плоскости излучателя в плоскости $yz,$ необходимо ввести линейную по координате временную задержку и задать граничное условие вида
(8)
$\begin{gathered} {{\left. p \right|}_{{z = 0}}} = {{p}_{0}}\left( {t - \frac{y}{c}\sin \theta ;x,y} \right) = \\ = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {{{S}_{0}}\left( {\omega ;x,y} \right)\exp \left( { - i\omega t + i\frac{\omega }{c}y\sin \theta } \right)} d\omega . \\ \end{gathered} $При этом граничное условие, включая поперечную форму пучка, по-прежнему задается на плоскости $z = 0.$ Решение волнового уравнения для граничного условия (8) имеет вид
(9)
$\begin{gathered} p = \frac{1}{{4{{\pi }^{2}}}}\iint\limits_\infty {{{S}_{0}}\left( {\omega ;x{\kern 1pt} ',y{\kern 1pt} '} \right)dx{\kern 1pt} 'dy{\kern 1pt} '} \times \\ \times \,\,\int\limits_{ - \infty }^\infty {\exp \left( { - i\omega t + i\frac{\omega }{c}y{\kern 1pt} '\sin \theta } \right)d\omega } \,\, \times \\ \times \,\,\iint\limits_\infty {\exp \left( {i{{k}_{x}}\left( {x - x{\kern 1pt} '} \right) + i{{k}_{y}}\left( {y - y{\kern 1pt} '} \right) + } \right.} \\ \left. { + \,\,iz\sqrt {{{k}^{2}} - k_{x}^{2} - k_{y}^{2}} } \right)d{{k}_{x}}d{{k}_{y}}. \\ \end{gathered} $Рассмотрим вначале плоскую волну ${{\left. p \right|}_{{z = 0}}}$ == ${{p}_{0}}\left( {t - \frac{y}{c}\sin {\theta }} \right)$ со спектром S0(ω). Подставляя это выражение в (9), найдем решение $p = {{p}_{0}}\left( {{\tau *}} \right),$ где фаза задается выражением
Таким образом, плоская волна распространяется в направлении, задаваемом вектором ${\mathbf{l}} = \left\{ {0,\sin {\theta },\cos {\theta }} \right\}.$ Тогда кажется, что для получения требуемого эволюционного уравнения достаточно повернуть систему координат так, чтобы новая продольная ось Z была направлена вдоль вектора l, а новая поперечная координата была ей перпендикулярна и задавалась вектором ${\mathbf{m}} = \left\{ {0,\cos {\theta }, - \sin {\theta }} \right\}.$ Итак, получаем преобразование координат
(11)
$\begin{gathered} X = x,\,\,\,\,Y = y\cos {\theta } - z\sin {\theta }, \\ Z = z\cos {\theta } + y\sin {\theta }. \\ \end{gathered} $Отыскивая решение вида $p = p\left( {{\tau }*,\sqrt {\mu } X,\sqrt {\mu } Y,{\mu }Z} \right),$ получим эволюционное уравнение
(12)
$\frac{{{{\partial }^{2}}p}}{{\partial {\tau *}\partial Z}} = \frac{c}{2}\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{X}^{2}}}} + \frac{{{{\partial }^{2}}p}}{{\partial {{Y}^{2}}}}} \right).$Уравнение (12) по форме совпадает с уравнением (5), т.е. эволюционное уравнение оказывается инвариантным относительно преобразования координат, согласованного с методом МИП. Это можно использовать для определения новых подходящих переменных в случае, когда их выбор не очевиден. Более подробно это будет рассмотрено далее.
Однако в данном случае уравнение (12) подразумевает постановку граничного условия при Z = 0, т.е. вдоль плоскости $z\cos {\theta } + y\sin {\theta } = {\text{0}}{\text{.}}$ На самом деле граничное условие ставится при $z = 0.$ Кроме того, при формальном повороте системы координат остается вопрос выбора правильного вида переменной τ. Таким образом, применение поворота системы координат – одного из инвариантных преобразований уравнения ХЗ [25] – не решает исходную задачу.
Вернемся к решению (9). Для вычисления внутреннего интеграла при наклонном распространении можно также применить аппроксимацию продольного волнового числа первыми членами ряда Тейлора. В этом случае пространственный спектр пучка сосредоточен вблизи волновых чисел ${{k}_{x}} = 0,$ ${{k}_{y}} = k\sin \theta ,$ ${{k}_{z}} = k\cos \theta .$ Разложение точного выражения (3) вблизи этих значений приводит к соотношению [19]
(13)
$\begin{gathered} {{k}_{z}} = k\cos \theta - \tan \theta \left( {{{k}_{y}} - k\sin \theta } \right) - \\ - \,\,\frac{{k_{x}^{2}}}{{2k\cos \theta }} - \frac{{{{{\left( {{{k}_{y}} - k\sin \theta } \right)}}^{2}}}}{{2k{{{\cos }}^{3}}\theta }}. \\ \end{gathered} $Очевидно, что при θ = 0 выражение (13) сводится к аппроксимации (4). Отметим, что подобная (13) методика аппроксимации продольного волнового числа в более общем формализме применена в работе [15].
Решение (9) с учетом аппроксимации (13) имеет вид:
(14)
$\begin{gathered} p = \frac{{{{{\cos }}^{2}}\theta }}{{2\pi cz}}\frac{\partial }{{\partial \tau {\text{*}}}}\iint\limits_\infty {{{p}_{0}}\left( {\tau {\text{*}} - \Phi \left( {x{\kern 1pt} ',y{\kern 1pt} '} \right);x{\kern 1pt} ',y{\kern 1pt} '} \right)}dx{\kern 1pt} 'dy{\kern 1pt} ', \\ \Phi \left( {x{\kern 1pt} ',y{\kern 1pt} '} \right) = \\ = \frac{{\cos \theta }}{{2cz}}\left[ {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} ' - ztg\theta } \right)}}^{2}}{{{\cos }}^{2}}\theta } \right] \\ \end{gathered} $(15)
$\frac{\partial }{{\partial \tau {\text{*}}}}\left( {\frac{{\partial p}}{{\partial z}}\cos \theta + \frac{{\partial p}}{{\partial y}}\sin \theta } \right) = \frac{c}{2}\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + \frac{1}{{{{{\cos }}^{2}}\theta }}\frac{{{{\partial }^{2}}p}}{{\partial {{y}^{2}}}}} \right),$Заметим, что уравнение (15) можно свести к виду уравнения (5) заменой переменных
Замена переменных (16) соответствует переходу в непрямоугольную систему координат, определяемую векторами ${\mathbf{s}} = \left\{ {0,0,\frac{1}{{\cos {\theta }}}} \right\}$ и ${\mathbf{m}} = \left\{ {0,\cos \theta , - \sin \theta } \right\}.$ Здесь $Y = {\mathbf{m}} \cdot {\mathbf{r}}$ – это поперечная координата в повернутой на угол θ системе координат, как определено в (11). При этом, в отличие от (11), продольная переменная $Z$ не подвергается преобразованию поворота. Масштабный фактор $\frac{1}{{\cos \theta }}$ приравнивает расстояния вдоль $z$ и вдоль направления распространения падающей волны. Таким образом, преобразование (16) и задаваемый им переход от уравнения (15) к уравнению (5) не являются обычным преобразованием поворота системы координат. Это подтверждается также тем, что в полученном после преобразования уравнении вида (5) сохраняется переменная $\tau {\text{*}}$ (10) вместо введенной в (5) τ. Переход в непрямоугольную систему координат связан с наличием граничного условия при $z = 0,$ из-за которого продольная координата в эволюционном уравнении не подвергается повороту.
Теперь пренебрежем формально дифракционными эффектами в уравнении (15), т.е. его правой частью. Решение получившегося квазилинейного уравнения для граничного условия (1) имеет вид $p = {{p}_{0}}\left( {\tau ;x,y - z\operatorname{tg} \theta } \right).$ Таким образом, при пренебрежении дифракцией начальная поперечная форма пучка сносится без искажений под углом θ к плоскости излучателя. Можно провести аналогию с распространением волновых пакетов в диспергирующих средах, когда разложение в ряд зависимости волнового числа от частоты определяет фазовую и групповую скорости. В случае разложения типа (13) первый член определяет направление распространения плоской волны и ее фазу, второй член – угол сноса пучка как целого, третий – дифракционные искажения.
Преобразование (16) и $\tau {\text{*}}$ (10) определяют новые характерные переменные для наклонного распространения пучка. Это позволяет определить их в качестве быстрых и медленных переменных при использовании метода МИП. Отыскивая решение волнового уравнения (2) вида $p = p\left( {\tau ,\sqrt \mu X,\sqrt \mu Y,\mu Z} \right),$ приходим к (15). Если же эту процедуру применить к нелинейному волновому уравнению [26]
(17)
$\begin{gathered} \frac{\partial }{{\partial \tau }}\left( {\frac{{\partial p}}{{\partial z}}\cos \theta + \frac{{\partial p}}{{\partial y}}\sin \theta - \frac{\varepsilon }{{{{c}^{3}}\rho }}p\frac{{\partial p}}{{\partial \tau }}} \right) = \\ = \frac{c}{2}\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + \frac{1}{{{{{\cos }}^{2}}\theta }}\frac{{{{\partial }^{2}}p}}{{\partial {{y}^{2}}}}} \right). \\ \end{gathered} $Здесь ε – нелинейный параметр среды, ρ – ее плотность.
Перейдем к анализу области применимости уравнений (15) и (17). Видно, что коэффициенты при второй производной по y в этих уравнениях при больших углах падения сильно возрастают и в пределе $\theta \to {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ обращаются в бесконечность. Это означает, что эти уравнения, а также решение (14), полученные в работе [19], применимы только при небольших углах наклона.
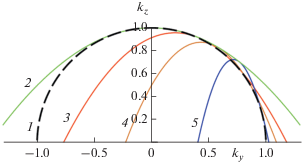
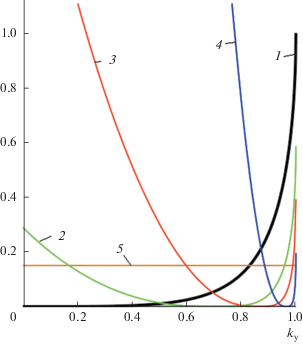
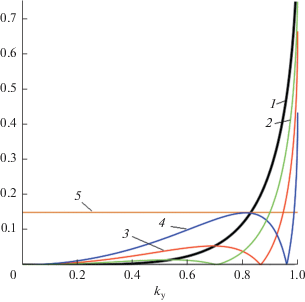
Причина расходимости заключена в аппроксимации (13). При увеличении угла θ уменьшается область пространственных частот, в которой парабола (13) адекватно описывает точную дисперсионную кривую (3). Более того, при больших углах парабола (13) даже качественно весьма далека от точной кривой, несмотря на то что при kx = 0, ky = k sin θ они совпадают друг с другом вплоть до второй производной. На рис. 2 жирной линией изображена точная дисперсионная кривая, тонкими линиями – аппроксимации первыми двумя членами ряда Тейлора при разных θ. Видно, что при больших углах аппроксимация становится неудовлетворительной и совпадает с точной кривой только в очень узком диапазоне пространственных частот. На рис. 3 приведена область применимости аппроксимации (13). В качестве критерия выбрано относительное отклонение аппроксимации (13) от точной кривой (3) по уровню 0.15 (горизонтальная линия 5). Относительное отклонение рассчитывалось по формуле:
АППРОКСИМАЦИИ СПЕКТРА И МОДЕЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ПРОИЗВОЛЬНОГО УГЛА НАКЛОНА
Таким образом, аппроксимация продольного волнового числа (13), полученная формально строгим методом, оказывается неудовлетворительной. С другой стороны, подобные аппроксимации необходимы только для аналитического вычисления интегралов и вывода упрощенного уравнения. Это означает, что для вывода уравнений, применимых при больших углах распространения, можно использовать другую аппроксимацию дисперсионной кривой.
Рассмотрим возможные варианты построения аппроксимации кривой (3). Примем в качестве исходных следующие требования к аппроксимации. Для возможности аналитического расчета необходимо ограничиться квадратичной зависимостью по поперечным волновым числам. Такая зависимость также будет соответствовать эволюционным уравнениям типа ХЗ. Желательно, чтобы допустимая ширина пространственного спектра не уменьшалась при увеличении угла наклона, а коэффициенты получаемого эволюционного уравнения были ограниченными.
Таким образом, в качестве исходного аппроксимирующего выражения выбираем квадратичную форму с неопределенными коэффициентами
(18)
${{k}_{z}} = - \frac{{Ak_{x}^{2}}}{{2k}} - \frac{{Bk_{y}^{2}}}{{2k}} + C{{k}_{x}}{{k}_{y}} + D{{k}_{x}} + E{{k}_{y}} + Gk.$(19)
$\begin{gathered} p = \frac{1}{{2\pi cz\sqrt {AB} }}\frac{\partial }{{\partial {{\tau }_{1}}}} \times \\ \times \,\,\iint\limits_\infty {{{p}_{0}}\left( {{{\tau }_{1}} - \Phi \left( {x{\kern 1pt} ',y{\kern 1pt} '} \right);x{\kern 1pt} ',y{\kern 1pt} '} \right)}dx{\kern 1pt} 'dy{\kern 1pt} ', \\ \end{gathered} $(20)
$\begin{gathered} \Phi \left( {x{\kern 1pt} ',y{\kern 1pt} '} \right) = \\ = \frac{1}{{2cz}}\left[ {\frac{{{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}}}}{A} + \frac{{{{{\left( {y - y{\kern 1pt} ' - z\left( {B\sin \theta + E} \right)} \right)}}^{2}}}}{B}} \right], \\ {{\tau }_{1}} = t - \frac{y}{c}\sin \theta - \frac{z}{c}\left( {G - \frac{{B{{{\sin }}^{2}}\theta }}{2} - E\sin \theta } \right). \\ \end{gathered} $Решение (20) удовлетворяет эволюционному уравнению
(21)
$\frac{\partial }{{\partial \tau }}\left( {\frac{1}{A}\frac{{\partial p}}{{\partial z}} + \frac{{B\sin \theta - E}}{A}\frac{{\partial p}}{{\partial y}}} \right) = \frac{c}{2}\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + \frac{B}{A}\frac{{{{\partial }^{2}}p}}{{\partial {{y}^{2}}}}} \right).$Аппроксимация (18) задается 4 коэффициентами, требующими определения. Ее частный случай – параболоид (13) – определяется первыми членами ряда Тейлора точного соотношения (3) в точке ${{k}_{x}} = 0,$ ${{k}_{y}} = k\sin \alpha .$ Поэтому его коэффициенты однозначно определяются четырьмя условиями – равенствами в этой точке соответствующих значений волновых чисел и их производных для параболоида (15) и точного выражения (3):
(22)
$1)\,{{k}_{z}},\,\,2)\,{{{{\partial }^{2}}{{k}_{z}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{k}_{z}}} {\partial {{x}^{2}}}}} \right. \kern-0em} {\partial {{x}^{2}}}},\,\,3)\,{{\partial {{k}_{z}}} \mathord{\left/ {\vphantom {{\partial {{k}_{z}}} {\partial y}}} \right. \kern-0em} {\partial y}},\,\,4)\,{{{{\partial }^{2}}{{k}_{z}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{k}_{z}}} {\partial {{y}^{2}}}}} \right. \kern-0em} {\partial {{y}^{2}}}}.$Построить новую аппроксимацию, отличную от (13), можно, только отказавшись от одного из условий в (22). Определим роль этих условий. Первое и третье условия определяют фазу плоской волны и направление сноса пучка как целого. Второе условие определяет дифракционные эффекты вдоль оси x, предполагаем, что они не должны измениться при наклоне направления распространения в плоскости xz. Постараемся эти условия сохранить. Четвертое условие отвечает за дифракционные искажения вдоль оси y и является основным источником особенности, т. к. определяет коэффициент при второй производной по y в уравнении (15). Если отказаться только от четвертого условия, получим следующие выражения для коэффициентов:
(23)
$\begin{gathered} A = {1 \mathord{\left/ {\vphantom {1 {\cos \theta }}} \right. \kern-0em} {\cos \theta }},\,\,\,\,E = B\sin \theta - {\text{tg}}\theta , \\ G = \cos \theta + \sin \theta {\text{tg}}\theta - \left( {{B \mathord{\left/ {\vphantom {B 2}} \right. \kern-0em} 2}} \right){{\sin }^{2}}\theta . \\ \end{gathered} $Отметим, что часть из этих условий можно также получить, накладывая условие совпадения быстрой переменной τ1 (20) с переменной τ* (10). Коэффициент $B$ здесь пока не определен. Уравнение (21) принимает вид
(24)
$\frac{\partial }{{\partial \tau }}\left( {\frac{{\partial p}}{{\partial z}}\cos \theta + \frac{{\partial p}}{{\partial y}}\sin \theta } \right) = \frac{c}{2}\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + B\cos \theta \frac{{{{\partial }^{2}}p}}{{\partial {{y}^{2}}}}} \right).$Можно попытаться подобрать коэффициент $B$ так, чтобы компенсировать или ограничить сингулярность коэффициентов аппроксимации при больших углах наклона. Вершина параболоида с коэффициентами (23) расположена в точке ${{k}_{x}} = 0,$ ${{k}_{y}} = k\sin {\theta } - k{{B}^{{ - 1}}}tg{\theta }$ и смещается по горизонтали при увеличении угла пропорционально $tg{\theta }{\text{.}}$ Значение в вершине парабалоида
неограниченно возрастает при увеличении угла θ пропорционально $t{{g}^{2}}\theta {\text{.}}$ Это следствие того, что при увеличении угла касательная плоскость стремится стать “вертикальной”, т.е. параллельной оси $z.$ Сравнивая законы смещения по горизонтали и вертикали, а также коэффициент в уравнении (24), получаем противоречивые требования к коэффициенту $B.$ Для устранения вертикального смещения вершины параболоида он должен расти как $\sim {\kern 1pt} \frac{1}{{{{{\cos }}^{2}}{\theta }}},$ а согласно уравнению (24) должен быть ограничен. Определенным компромиссом является вариант $B = {1 \mathord{\left/ {\vphantom {1 {\cos \theta }}} \right. \kern-0em} {\cos \theta }}.$ В этом случае получаем параболоид(26)
${{k}_{z}} = k\cos \theta \left( {1 + \frac{1}{2}{\text{t}}{{{\text{g}}}^{2}}\theta } \right) - \frac{{k_{x}^{2}}}{{2k\cos \theta }} - \frac{{k_{y}^{2}}}{{2k\cos \theta }}$(27)
$\frac{\partial }{{\partial \tau }}\left( {\frac{{\partial p}}{{\partial z}}\cos \theta + \frac{{\partial p}}{{\partial y}}\sin \theta } \right) = \frac{c}{2}\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}p}}{{\partial {{y}^{2}}}}} \right).$Достоинство аппроксимации (26) в том, что она совпадает с точной дисперсионной кривой с точностью по крайней мере до первой производной, тем самым правильно учитывая фазу плоской волны и угол сноса пучка, и приводит к уравнению с ограниченными коэффициентами. Однако качественное поведение аппроксимации при больших углах наклона также далеко от точной поверхности, как это видно на рис. 4. На рис. 5 приведена область применимости аппроксимации (26) по относительному отклонению от точного выражения (3) аналогично рис. 3. Данная модель позволяет немного продвинуться в сторону увеличения углов наклона и ширины спектра, в частности, для угла наклона 45° допустимая ширина спектра даже несколько расширяется по сравнению со случаем нормального распространения. Однако в целом, особенно при больших углах, результат пока далек от желаемого.
Рис. 4.
Сравнение точной кривой (3) (кривая 1) и аппроксимации (26) при различных углах наклона при kx = 0. Кривые 2–5 соответствуют углу наклона 0, π/4, π/3, 5π/12 рад.
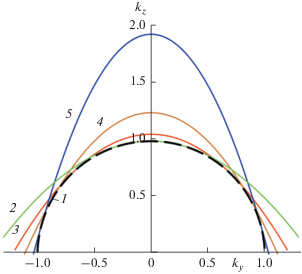
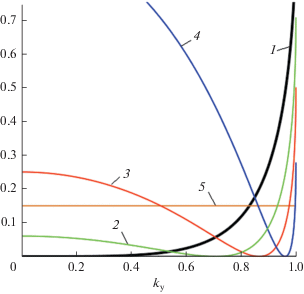
Рис. 5.
Относительное отклонение аппроксимации (26) от точной кривой (3) при kx = 0. Кривые 1–4 соответствуют углу наклона 0, π/4, π/3, 5π/12 рад. Горизонтальная линия 5 на уровне 0.15 – принятый критерий пригодности аппроксимации.
Отметим, что процедура модификации пространственного спектра пучка для упрощения расчетов проводилась, например, в работе [23]. Выражение для формы спектра также выбиралось из соображений простоты вычислений, а коэффициенты этой формы находились при численной минимизации функционала невязки. Данная работа направлена на вывод нелинейных эволюционных уравнений с дальнейшей перспективой нахождения их точных решений. Поэтому форма спектра по возможности должна быть найдена аналитически.
Теперь посмотрим, какие возможности и ограничения возникают при использовании метода МИП. Обобщая замену переменных (16), отыскиваем решение волнового уравнения вида $p = p\left( {\tau ,\sqrt \mu X,\sqrt \mu Y,\mu Z} \right),$ где
(28)
$\begin{gathered} \tau = t - {{\left( {\alpha z + \beta y} \right)} \mathord{\left/ {\vphantom {{\left( {\alpha z + \beta y} \right)} c}} \right. \kern-0em} c},\,\,\,\,X = x, \\ Y = ay - bz,\,\,\,\,Z = gz, \\ \end{gathered} $(29)
$\begin{gathered} \frac{\partial }{{\partial \tau }}\left( {\mu \alpha g\frac{{\partial p}}{{\partial Z}} + \sqrt \mu \left( {a\beta - \alpha b} \right)\frac{{\partial p}}{{\partial Y}}} \right) = \\ = \mu \frac{c}{2}\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + \left( {{{a}^{2}} + {{b}^{2}}} \right)\frac{{{{\partial }^{2}}p}}{{\partial {{Y}^{2}}}}} \right). \\ \end{gathered} $Согласно строгой методике нужно потребовать выполнение равенства $a\beta - \alpha b = 0,$ чтобы все старшие члены уравнения сократились. Далее, налагая условия ${{a}^{2}} + {{b}^{2}} = 1$ и $g = {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0em} \alpha },$ сведем уравнение (29) к виду уравнения ЛХЗ (5). Отсюда получаем:
В частности, полагая $\alpha = \cos \theta ,$ $\beta = \sin \theta ,$ чтобы время $\tau $ в (28) совпадало с ${{\tau }_{1}}$ в (10), найдем $a = \cos \theta ,$ $b = \sin \theta ,$ $g = {1 \mathord{\left/ {\vphantom {1 {\cos \alpha }}} \right. \kern-0em} {\cos \alpha }}.$ Возвращаясь к исходным переменным при данном выборе коэффициентов, получим в точности уравнение (15). Таким образом, при фиксировании фазы (10) метод МИП в строгой постановке однозначно приводит к уравнению (15) и соответствующей аппроксимации (13), применимой только для небольших углов. Это ограничение достаточно очевидно, поскольку при задании переменных $Y$ и $Z$ в (28) переменная $z$ одновременно должна иметь порядок медленности и $\sqrt \mu ,$ и $\mu ,$ что может выполняться только при небольших углах.
Можно получить уравнение более общего типа, если формально считать, что $a\beta - \alpha b\sim \sqrt \mu $ (это также соответствует не очень большим углам наклона) и ${{a}^{2}} + {{b}^{2}}\sim {{\mu }^{0}}.$ Возвращаясь к исходным переменным, получим
(30)
$\frac{\partial }{{\partial \tau }}\left( {\alpha \frac{{\partial p}}{{\partial z}} + \beta \frac{{\partial p}}{{\partial y}}} \right) = \frac{c}{2}\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + \frac{{{{a}^{2}} + {{b}^{2}}}}{{{{a}^{2}}}}\frac{{{{\partial }^{2}}p}}{{\partial {{y}^{2}}}}} \right).$Сравнивая уравнения (21) и (30), можно найти связь коэффициентов аппроксимирующей поверхности (18) и замены переменных (28): $A = {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0em} \alpha },$ $B\sin \theta - E,$ $\alpha B = 1 + {{{{b}^{2}}} \mathord{\left/ {\vphantom {{{{b}^{2}}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}.$ Второе равенство удовлетворяется при произвольном $B$ за счет выбора коэффициента $E.$ Выбор коэффициента $B$ определяется наилучшей аппроксимацией дисперсионной кривой.
Таким образом, как коэффициенты замены переменных (28), так и коэффициенты квадратичной формы (18) связаны рядом соотношений, заданных фазой волны и условиями применимости аппроксимирующих выражений, и не могут быть заданы произвольно. В частности, уравнение (27) может быть получено методом МИП при введении переменных (28) с коэффициентами $a = g = 1,$ $b = 0.$
НОВАЯ АППРОКСИМАЦИЯ НА ОСНОВЕ СОХРАНЕНИЯ КАЧЕСТВЕННОГО ПОВЕДЕНИЯ СПЕКТРА
Поскольку обе поверхности – и (13) и (26) – качественно плохо воспроизводят точную дисперсионную поверхность в целом, что является источником неравномерности аппроксимации и возникновения особенностей, то поставим следующую задачу. Найдем такую поверхность, которая отражала бы качественное поведение дисперсионной поверхности в целом, пусть даже эта аппроксимирующая поверхность будет неточно воспроизводить поведение в близкой окрестности направления распространения. При выводе (26) мы отказались от условия 4) в (22). Откажемся теперь и от условия 3). Для определения четырех коэффициентов в (18) добавим два условия, определяющие поведение кривой в целом, а именно, потребуем, чтобы вершина аппроксимирующего параболоида совпадала с вершиной точной дисперсионной поверхности $\left( {{{k}_{x}} = 0,\,\,{{k}_{y}} = 0,\,\,{{k}_{z}} = k} \right).$ Из условия совпадения положения вершин получаем, что коэффициент $E = 0,$ а совпадение значений в вершине определяет коэффициент G = 1. Тогда из условия пересечения точной и аппроксимирующей поверхностей в точке ${{k}_{x}} = 0,$ ${{k}_{y}} = k\sin \theta $ находим $B = 2\frac{{1 - \cos \theta }}{{{{{\sin }}^{2}}\theta }}.$ Далее, коэффициент $A = \frac{1}{{\cos {\theta }}},$ переменная $\tau $ определяется (10). Таким образом, получаем аппроксимацию
(31)
${{k}_{z}} = k - \frac{{k_{x}^{2}}}{{2k\cos {\theta }}} - \frac{{1 - \cos {\theta }}}{{{\text{si}}{{{\text{n}}}^{{\text{2}}}}{\theta }}}\frac{{k_{y}^{2}}}{k}.$Эта аппроксимация качественно отражает точную дисперсионную поверхность при произвольном угле распространения (см. рис. 6). На рис. 7 приведена область применимости аппроксимации по тому же критерию, что и на рис. 3 и 5.
Отметим, что в аппроксимации (31) осталась особенность, связанная с неограниченным нарастанием коэффициента A при $\theta \to {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. В диапазоне углов из области применимости (31) (будет определена далее) это нарастание не оказывает принципиального влияния. Тем не менее, поскольку аппроксимация (31) построена из условия качественного повторения точного спектра, то можно рассмотреть и аналогичную ей аппроксимацию с коэффициентом A = 1. Эта модифицированная аппроксимация является более равномерной по углу наклона пучка, однако она менее точна и обладает меньшей допустимой шириной пространственного спектра по сравнению с (31).
Рис. 6.
Сравнение точной кривой (3) (кривая 1) и аппроксимации (31) при различных углах наклона при kx = 0. Кривые 2–5 соответствуют углу наклона 0, π/4, π/3, 5π/12 рад.
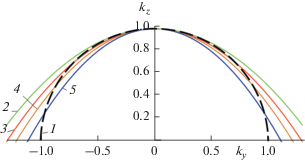
Рис. 7.
Относительное отклонение аппроксимации (31) от точной кривой (3) при kx = 0. Кривые 1–4 соответствуют углу наклона 0, π/4, π/3, 5π/12 рад. Горизонтальная линия 5 на уровне 0.15 – принятый критерий пригодности аппроксимации.
Аппроксимация (31) приводит к уравнению с ограниченными коэффициентами
и его нелинейному обобщениюУравнение (33) является обобщенным уравнением типа Хохлова–Заболотской, пригодным для описания распространения интенсивных акустических пучков вдоль оси, наклоненной к плоскости излучателя под достаточно большими углами.
Полученные аппроксимация (31) и уравнение (32) удовлетворяют предельному переходу при θ = 0, т.е. совпадают с выражениями (4) и (5) соответственно для пучка, распространяющегося вдоль нормали.
Рассмотрим области применимости аппроксимации рядом Тейлора (13) и моделей (26) и (31) на основе рис. 3, 5 и 7. На оси абсцисс отложена проекция волнового числа ${{k}_{y}},$ а по оси ординат отложено относительное отклонение аппроксимации от точной зависимости. Зададим общий критерий применимости для всех моделей: величина относительного отклонения не должна превышать 0.15, при необходимости более точной аппроксимации этот критерий можно варьировать. С учетом данного критерия аппроксимация рядом Тейлора для угла наклона 45° дает ошибку (хотя допустимая ширина спектра велика), а для угла больше 60° уже не применима (так как ширина спектра примерно от 0.7 до 1). Модель (26) применима для углов наклона ≤45° во всем диапазоне, а для угла 60° область применения такая же как и для аппроксимации рядом Тейлора. Модель (31) применима для углов наклона ≤60° практически во всем диапазоне, а для остальных углов ширина спектра области допустимого значения относительного отклонения более широкая, чем у других моделей. Предельный угол наклона, для которого модель (31) применима, можно оценить как 60°–70°.
Поскольку модель (32) получена без условия равенства производных по ky в (22), то ей присущ новый недостаток, отсутствующий у модели (26) – направление
сноса пучка не точно соответствует направлению распространения волны. Действительно,
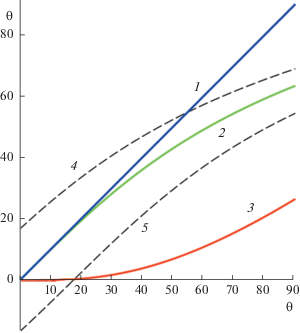
отношение коэффициента при ${{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial y}}} \right. \kern-0em} {\partial y}}$ к ${{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial z}}} \right. \kern-0em} {\partial z}}$ в левой части уравнения (32) должно быть равно $tg{\theta ,}$ а это не выполняется. На рис. 8 приведена зависимость направления сноса пучка, задаваемого уравнением (32), в сравнении с точным значением. Кривая 1 соответствует точному значению угла сноса и представляет собой прямую линию θb = θ. Кривая 2 задается соотношением 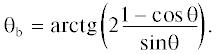 Кривая 3 – разность соответствующих значений, задаваемых кривыми 1 и 2. Видно, что начиная с угла порядка 45° появляется заметная ошибка в угле сноса пучка,
возрастающая при дальнейшем увеличении угла. Таким образом, расширение допустимого
углового спектра пучка потребовало снизить требования к точности угла сноса пучка.
В определенной степени это компенсируется тем, что пучок с широким угловым спектром
распространяется не вдоль одного угла, а в некотором конусе с углом раскрытия, определяемым
дифракционной длиной. Кривые 4 и 5 определяют характерные границы пучка в поперечном направлении. Их построение будет
описано ниже.
Кривая 3 – разность соответствующих значений, задаваемых кривыми 1 и 2. Видно, что начиная с угла порядка 45° появляется заметная ошибка в угле сноса пучка,
возрастающая при дальнейшем увеличении угла. Таким образом, расширение допустимого
углового спектра пучка потребовало снизить требования к точности угла сноса пучка.
В определенной степени это компенсируется тем, что пучок с широким угловым спектром
распространяется не вдоль одного угла, а в некотором конусе с углом раскрытия, определяемым
дифракционной длиной. Кривые 4 и 5 определяют характерные границы пучка в поперечном направлении. Их построение будет
описано ниже.
Рис. 8.
Сравнение угла сноса пучка, задаваемого точным соотношением (кривая 1) и уравнением (32) (кривая 2). Кривая 3 – разность соответствующих значений на кривых 1 и 2. Кривые 4 и 5 – углы наклона для характерных границ пучка.
В отличие от рассмотренных выше эволюционных уравнений, уравнение (32) согласуется с уравнением (30), полученным в соответствии с методом МИП из волнового уравнения, только при нормальном распространении θ = 0. Это означает, что уравнение (32) является самостоятельным уравнением, основанным на новой аппроксимации дисперсионной поверхности для волновых пучков, и представляет новую аппроксимацию дифракционного оператора в волновом уравнении. В частном случае нормального падения это уравнения сводятся к стандартному уравнению ЛХЗ. В отличие от предыдущих аппроксимаций это уравнение применимо для произвольных углов распространения и пучков с достаточно широким угловым спектром.
Отметим, что аппроксимация (32) может быть обобщена следующим образом. При выводе (32) было использовано условие равенства продольных волновых чисел в вершине параболоида при kx = ky = 0. Это условие может быть заменено на равенство продольных волновых чисел при некотором ky0 = ksinθ0. Аппроксимация (32) тогда трансформируется к виду
Такая аппроксимация может быть полезной, в частности, при расчете вторичных акустических полей, генерируемых при нелинейном взаимодействии волн накачки, например, в параметрических излучателях [26] или при рассеянии звука на звуке [27, 28]. В этих случаях помимо угла наклона излучаемой волны задается еще и угол наклона (волновой вектор) падающей волны накачки, пространственный спектр которой также нужно учесть как можно точнее.
ПОЛЕ ГАУССОВСКОГО ПУЧКА ПРИ НАКЛОННОМ РАСПРОСТРАНЕНИИ
Перейдем к рассмотрению эволюции ограниченных пучков в рамках линейной задачи на основе нового уравнения (32). Для этого исследуем трансформацию некоторых точных решений этого уравнения, имеющих важный физический смысл. Пусть при $z = 0$ пучок имеет плоский фазовый фронт и гауссово распределение амплитуды давления в поперечной плоскости (x, y):
(34)
$p(x,y,z = 0,{\tau }*) = {{P}_{0}}\exp \left( { - \frac{{{{x}^{2}} + {{y}^{2}}}}{{a_{0}^{2}}}} \right){{e}^{{ - i{\omega \tau }*}}},$(35)
$\begin{gathered} p(x,y,z,{{{\tau }}_{*}}) = \frac{{{{P}_{0}}{{e}^{{ - i{\omega }{{{\tau }}_{*}}}}}}}{{\sqrt {\left( {1 + iAd} \right)\left( {1 + iBd} \right)} }} \times \hfill \\ \times \,\,\exp \left( { - \frac{{{{x}^{2}}}}{{a_{0}^{2}\left( {1 + iAd} \right)}} - \frac{{{{{(y - zB\sin {\theta })}}^{2}}}}{{a_{0}^{2}\left( {1 + iBd} \right)}}} \right). \hfill \\ \end{gathered} $Здесь $d = \frac{{2z}}{{ka_{0}^{2}}}$ – безразмерная дифракционная длина [24], коэффициенты аппроксимации (31) $A = \frac{1}{{\cos {\theta }}},$ $B = \frac{{2(1 - \cos {\theta })}}{{{{{\sin }}^{2}}{\theta }}}$ и учтено, что E = 0. Представим (35) в виде $p = {{P}_{A}}\exp \left( {ik\Phi } \right)$ и выделим из (34) выражения для действительной амплитуды PA и фазы kФ гауссовского пучка:
(36)
$\begin{gathered} {{P}_{A}} = \frac{{{{P}_{0}}}}{{\sqrt[4]{{1 + {{A}^{2}}{{d}^{2}}}}\sqrt[4]{{1 + {{B}^{2}}{{d}^{2}}}}}} \times \\ \times \,\,\exp \left( { - \frac{{{{x}^{2}}}}{{a_{0}^{2}(1 + {{A}^{2}}{{d}^{2}})}} - \frac{{{{{(y - zB\sin {\theta })}}^{2}}}}{{a_{0}^{2}(1 + {{B}^{2}}{{d}^{2}})}}} \right), \\ \end{gathered} $(37)
$\begin{gathered} k\Phi = \frac{{Ad{{x}^{2}}}}{{a_{0}^{2}(1 + {{A}^{2}}{{d}^{2}})}} + \frac{{Bd{{{(y - zB\sin {\theta })}}^{2}}}}{{a_{0}^{2}(1 + {{B}^{2}}{{d}^{2}})}} - \\ - \,\,\frac{1}{2}arctg(Ad) - \frac{1}{2}arctg(Bd). \\ \end{gathered} $В частном случае нормального распространения θ = 0, A = B = 1 решение (35)–(37) сводится к обычному выражению для гауссовского пучка [24].
Полученные выражения для амплитуды и фазы учитывают снос пучка в поперечном направлении, описываемый зависимостью $y - zB\sin \theta .$ Введем понятие оси пучка при наклонном распространении. Осью пучка является линия, вдоль которой перемещается точка с максимальным значением амплитуды, в данном случае она имеет вид:
Из формулы (36) следует, что зависимость поперечной формы пучка по-прежнему имеет вид гауссоиды, но изначально круглый в поперечном сечении пучок становится эллиптическим. Ширина пучка вдоль осей x и y увеличивается по разным законам:
(39)
${{a}_{x}}(z) = {{a}_{0}}\sqrt {1 + {{A}^{2}}{{d}^{2}}} ,\,\,\,\,{{a}_{y}}(z) = {{a}_{0}}\sqrt {1 + {{B}^{2}}{{d}^{2}}} .$Амплитуда волны на оси уменьшается как
(40)
${{P}_{A}}\left( {x = 0,y = {{y}_{0}}} \right) = \frac{{{{P}_{0}}}}{{\sqrt[4]{{1 + {{A}^{2}}{{d}^{2}}}}\sqrt[4]{{1 + {{B}^{2}}{{d}^{2}}}}}}.$Как видно, амплитуда (40) пучка зависит от угла распространения волны, причем с увеличением угла амплитуда уменьшается. Значения коэффициентов A и B равны 1 при θ = 0 и возрастают с увеличением угла, поэтому приводят к увеличению эффективного расстояния. Это связано, в частности, с тем, что при одном и том же расстоянии z от плоскости излучателя расстояние, пройденное волной вдоль наклонной оси, возрастает с увеличением угла наклона. Зависимость максимальной амплитуды от угла наиболее сильно проявляется на небольших расстояниях порядка дифракционной длины, d ~ 1. На больших же расстояниях влияние угла наклона на максимальную амплитуду уменьшается и при d $ \gg $ 1 амплитуды волны для разных углов сближаются. На расстояниях $d \gg 1$ первоначально плоская волна превращается в сферически расходящуюся: ее амплитуда убывает как ${{P}_{A}} \approx {{P}_{0}}/\sqrt {AB} d = k{{a}^{2}}{{P}_{0}}/2z\sqrt {AB} $, а ширина пучка растет по линейному закону ${{a}_{x}}(z) \approx {{2zA} \mathord{\left/ {\vphantom {{2zA} {ka}}} \right. \kern-0em} {ka}},$ ${{a}_{y}}(z) \approx {{2zB} \mathord{\left/ {\vphantom {{2zB} {ka}}} \right. \kern-0em} {ka}}.$ Последнее означает, что волна распространяется в эллиптическом конусе с углами раскрытия, пропорциональными ${{a(z)} \mathord{\left/ {\vphantom {{a(z)} z}} \right. \kern-0em} z}\sim {2 \mathord{\left/ {\vphantom {2 {ka}}} \right. \kern-0em} {ka}} = {\lambda \mathord{\left/ {\vphantom {\lambda {\pi a}}} \right. \kern-0em} {\pi a}}.$
Если в исходном сечении $z = 0$ волна имела плоский фазовый фронт, то по мере распространения появляется дополнительный фазовый сдвиг $\frac{1}{2}(arctg(Ad) + arctg(Bd)),$ соответствующий изменению скорости распространения волны.
Используя выражения для траектории оси пучка (38) и ширины пучка (39), можно оценить, в каком интервале углов будет находиться пучок. Ясно, что границы пучка в поперечном направлении, например, в плоскости yz, можно задать выражением ${{y}_{b}} = {{y}_{0}} \pm {{a}_{y}}\left( z \right).$ Тогда тангенс угла наклона траектории к оси z равен ${{d{{y}_{b}}} \mathord{\left/ {\vphantom {{d{{y}_{b}}} {dz}}} \right. \kern-0em} {dz}}.$ Производная от ${{y}_{0}}$ равна постоянному углу сноса пучка, а производная от ширины пучка дает изменение угла сноса пучка на его периферии. Рассчитанные отсюда углы наклона для левой и правой границ пучка в плоскости yz приведены на рис. 8 как кривые 4 и 5. Видно, что конечный размер пучка в поперечном направлении несколько компенсирует уход рассчитанного угла сноса пучка от истинного. Таким образом, действительно предельный угол применимости модели (31) можно оценить примерно в 60°.
ИЗМЕНЕНИЕ ПОПЕРЕЧНОЙ ФОРМЫ ГАУССОВСКОГО ПУЧКА
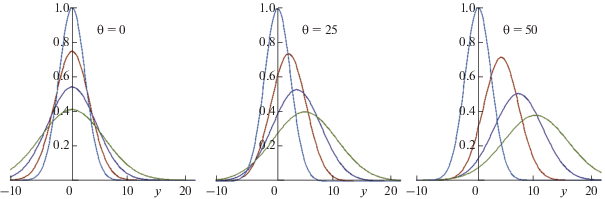
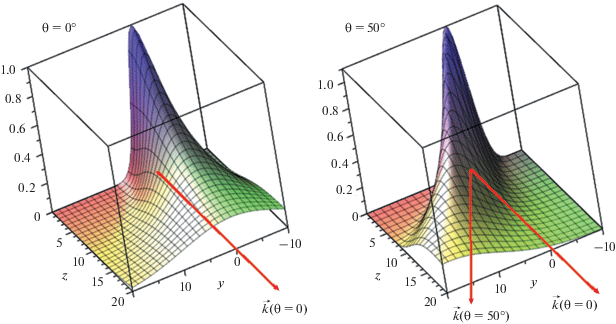
Рассматривается волна с плоским фазовым фронтом и гауссовским поперечным распределением амплитуды, начальное условие для которой задается на излучающей плоскости $(x,y).$ Рассчитаем изменение амплитуды волны при различных углах наклона к излучающей плоскости. Для этого построим зависимость амплитуды от поперечной координаты y на различных расстояниях z (безразмерная дифракционная длина $d\sim z$). На рис. 9 приведены амплитуды волны в поперечном сечении на различных расстояниях от излучающей плоскости для разных углов. Видно, что при различных углах наклона гауссового пучка направление распространения фронта волны изменяется, чем больше угол, под которым распространяется волна, тем больше смещение направления распространения волны. На рис. 10 также приведена в более наглядном виде трансформация пространственной структуры гауссовского пучка при распространении под углами ${\theta } = 0^\circ $ и ${\theta } = 50^\circ .$ При наклонном распространении видно, как пучок сносится в поперечном направлении и расплывается из-за дифракционных эффектов.
НАКЛОННОЕ РАСПРОСТРАНЕНИЕ СФОКУСИРОВАННЫХ ПУЧКОВ
Перейдем теперь к рассмотрению распространения под наклоном сфокусированных пучков. Для того чтобы пучок был сходящимся, он должен иметь искривленный волновой фронт. В рамках уравнения ЛХЗ (5) и параболического уравнения дифракции фокусировка достигается параболической модуляцией фронта. В случае нормального распространения пучок сохраняет цилиндрическую симметрию, поэтому радиусы кривизны фронта вдоль осей x и y равны. В предыдущем разделе было показано, что при наклонном распространении ширина пучка вдоль разных осей оказывается различной. Конус, в котором распространяется пучок, превращается в эллиптический и теряет цилиндрическую симметрию. Можно ожидать, что при фокусировке вдоль наклонной оси потребуется ввести различные радиусы кривизны вдоль разных осей. Поэтому условие на границе примем в следующем виде:
(41)
$\begin{gathered} p(x,y,z = 0,{{{\tau }}_{{\text{*}}}}) = \\ = {{P}_{0}}\exp \left( { - \frac{{{{x}^{2}} + {{y}^{2}}}}{{a_{0}^{2}}} - \frac{{ik{{x}^{2}}}}{{2{{R}_{x}}}} - \frac{{ik{{y}^{2}}}}{{2{{R}_{y}}}}} \right){{e}^{{ - i{\omega }{{{\tau }}_{{\text{*}}}}}}}. \\ \end{gathered} $где радиусы Rx и Ry используются в выражениях, содержащих коэффициенты A и B соответственно.
В итоге получаем выражения для действительной амплитуды и фазы cфокусированного пучка:
(42)
$\begin{gathered} {{P}_{A}} = \frac{{{{P}_{0}}}}{{\sqrt[4]{{{{{\left( {1 - \frac{{zA}}{{{{R}_{x}}}}} \right)}}^{2}} + {{d}^{2}}{{A}^{2}}}}\sqrt[4]{{{{{\left( {1 - \frac{{zB}}{{{{R}_{y}}}}} \right)}}^{2}} + {{d}^{2}}{{B}^{2}}}}}} \times \\ \times \exp \left( { - \frac{{{{x}^{2}}}}{{a_{0}^{2}\left( {{{{\left( {1 - \frac{{zA}}{{{{R}_{x}}}}} \right)}}^{2}} + {{A}^{2}}{{d}^{2}}} \right)}}} \right. - \\ - \left. {\frac{{{{{(y - zB\sin {\theta })}}^{2}}}}{{a_{0}^{2}\left( {{{{\left( {1 - \frac{{zB}}{{{{R}_{y}}}}} \right)}}^{2}} + {{B}^{2}}{{d}^{2}}} \right)}}} \right), \\ \end{gathered} $Из решения (42)–(43) видно, что при равных начальных радиусах кривизны волнового фронта Rx = Ry поле будет фокусироваться на различных расстояниях z. Для того чтобы фокусировка происходила в одну и ту же точку на расстоянии z = F от плоскости излучателя, в геометроакустическом приближении (т.е. малых дифракционных длинах) необходимо выполнение равенств
Таким образом, при фокусировке пучка при наклонном распространении необходимо вводить различные радиусы кривизны вдоль разных осей. При учете дифракционных эффектов необходимо подбирать радиусы кривизны волнового фронта в зависимости от требуемого положения максимальной амплитуды, угла наклона и параметра пучка ${{ka_{0}^{2}} \mathord{\left/ {\vphantom {{ka_{0}^{2}} 2}} \right. \kern-0em} 2}.$
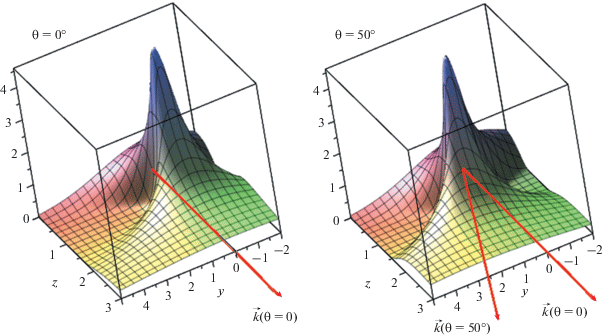
На рис. 11 приведена пространственная структура амплитуды сфокусированного гауссовского пучка в виде трехмерных графиков по аналогии с рис. 10. Условие согласования (44) выполнено. При построении фиксировалась координата x = 0 и строилась зависимость амплитуды от поперечной координаты y и продольной координаты z. Видно, что в области фокуса происходит сужение пучка и значительный рост амплитуды.
НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ В ИНТЕНСИВНОМ ПУЧКЕ
Перепишем уравнение (33) в безразмерном виде:
где $V = p/{{p}_{0}}$, $\bar {z} = z/{{z}_{{nl}}}$, ${{z}_{{nl}}} = \frac{{\rho {{c}^{3}}}}{{\varepsilon \omega {{p}_{0}}}}$ – нелинейная длина, $T = {\omega }{{{\tau }}_{*}}$, $\bar {x} = x/{{a}_{0}}$, $\bar {y} = y/{{a}_{0}}$, a0 – характерная ширина пучка. Параметр $N = \frac{{2{{z}_{{nl}}}}}{{ka_{0}^{2}}}$ (число Хохлова) отвечает за относительную роль нелинейных и дифракционных эффектов. Ограничимся рассмотрением сильно нелинейной волны при $N \to 0$. В этом случае правой частью уравнения (45) можно пренебречь и оно сводится к уравнению типа простых римановых волн. Его решение для граничного условия в виде гауссовского пучка гармонических волн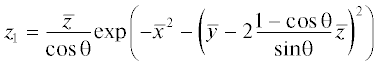 . Неявное решение (46) для функции U позволяет записать спектральное разложение на расстояниях до образования разрыва
в профиле и определить координату образования этого разрыва.
. Неявное решение (46) для функции U позволяет записать спектральное разложение на расстояниях до образования разрыва
в профиле и определить координату образования этого разрыва.
Разложение Бесселя-Фубини для решения (46) имеет вид:
или, возвращаясь к функции V,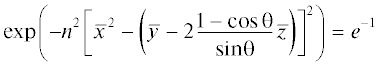 , откуда следует, что ширина пучка n-й гармоники равна ${{a}_{n}} = \frac{{{{a}_{0}}}}{{\sqrt n }}$, т.е. обратно пропорциональна корню из номера гармоники. Очевидно, что наиболее сильные
нелинейные искажения и генерация гармоник происходит вблизи оси, и ширина пучков высших
гармоник меньше ширины пучка основной частоты. От угла наклона оси распространения
ширина пучка не зависит.
, откуда следует, что ширина пучка n-й гармоники равна ${{a}_{n}} = \frac{{{{a}_{0}}}}{{\sqrt n }}$, т.е. обратно пропорциональна корню из номера гармоники. Очевидно, что наиболее сильные
нелинейные искажения и генерация гармоник происходит вблизи оси, и ширина пучков высших
гармоник меньше ширины пучка основной частоты. От угла наклона оси распространения
ширина пучка не зависит.
Длина образования разрыва в профиле (46) находится из условия z1 = 1, откуда получаем
Длина образования разрыва оказывается наименьшей на оси пучка, в области наибольшей амплитуды, и экспоненциально возрастает при переходе на периферию с меньшей амплитудой. При увеличении угла наклона оси распространения пучка длина образования разрыва уменьшается, поскольку при увеличении угла наклона расстояние, пройденное волной вдоль наклонной оси для достижения данной координаты z, быстро возрастает.
ЗАКЛЮЧЕНИЕ
Предложены модели, аппроксимирующие пространственный спектр ограниченных волновых пучков и позволяющие рассчитать поле пучка с широким угловым спектром при наклонном распространении по отношению к плоскости излучателя. Предельный угол наклона между вектором нормали к плоскости излучателя и волновым вектором пучка, при котором предложенные аппроксимации остаются достаточно точными, оценен примерно как ${\theta } = 60^\circ .$ По-видимому, для задач, связанных с электронным перемещением фокуса, такого предельного угла вполне достаточно. Возникающие неточности, вызванные ошибкой угла сноса пучка с широким угловым спектром, нивелируются большим углом его раскрытия на расстояниях, больших дифракционной длины. Для расчета полей при скользящем распространении, когда указанный угол приближается к ${\theta } = 90^\circ $, требуется разработка другого подхода.
Работа выполнена при поддержке гранта РФФИ (проект № 20-02-00493-а).
Список литературы
Авилов К.В. Псевдодифференциальные параболические уравнения распространения звука в океане, плавно неоднородном по горизонтали, и их численное решение // Акуст. журн. 1995. Т. 41. Вып. 1. С. 5–12.
Авилов К.В., Куличков С.Н., Попов О.Е. Применение сверхширокоугольной модификации волнового метода псевдодифференциального параболического уравнения для расчета звуковых полей и сигналов в различных средах // Акустика океана. Доклады XVI школы-семинара им. академика Л.М. Бреховских совмещенной с XXXI сессией Российского акустического общества. М.: ГЕОС, 2018. С. 13–16.
Гаврилов Л.Р. Эволюция мощных фокусирующих систем для применения в различных областях медицины (обзор) // Акуст. журн. 2010. Т. 56. С. 844-861.
Ильин С.А., Юлдашев П.В., Хохлова В.А., Гаврилов Л.Р., Росницкий П.Б., Сапожников О.А. Применение аналитического метода для оценки качества акустических полей при электронном перемещении фокуса многоэлементных терапевтических решеток // Акуст. журн. 2015. Т. 61. С. 57–64.
Rudenko O.V., Enflo B.O. Nonlinear N-wave propagation through a one-dimensional phase screen // Acustica. 2000. 2(XX). V. 86. P. 229–238.
Дубровский А.Н., Руденко О.В., Хохлова В.А. Флуктуационные характеристики волны звукового удара после прохождения случайно-неоднородного слоя // Акуст. журн. 1996. Т. 42. № 5. С. 623–628.
Blanc-Benon P., Lipkens B., Dallois L., Hamilton M.F., Blackstock D.T. Propagation of finite-amplitude sound through turbulence: Modeling with geometrical acoustics and the parabolic approximation // J. Acoust. Soc. Am. 2002. V. 111. № 1. Pt 2. P. 487–498.
Голицын Г.С., Кляцкин В.И. Колебания в атмосфере, вызванные движением земной поверхности // Изв. АН СССР. Физика атмосферы и океана. 1967. Т. 3. № 10. С. 1044–1052.
Гусев В.А., Руденко О.В. Нелинейный звук в слое газонасыщенных осадков // Акуст. журн. 2015. Т. 61. № 2. С. 169–181.
Гусев В.А., Окунев А.О. Наклонное распространение интенсивных акустических пучков в жидкости с газовыми пузырьками // Учен. зап. физ. фак.-та. 2015. № 4. С. 154 321.
Руденко О.В. К 40-летию уравнения Хохлова–Заболотской // Акуст. журн. 2010. Т. 56. С. 452–462.
Авилов К.В. Вычисление гармонических звуковых полей в волноводах в уточненном широкоугольном параболическом приближении // Волны и дифракция-85. IX Всес. симп. по дифракции и распространению волн. Тбилиси: ТГУ, 1985. Т. 2. С. 236–239.
Юлдашев П.В., Мездрохин И.С., Хохлова В.А. Моделирование высокоинтенсивных полей сильно фокусирующих ультразвуковых излучателей с использованием широкоугольного параболического приближения // Акуст. журн. 2018. Т. 64. С. 318–329.
Collins M.D. A split-step Pade solution for parabolic equation method // J. Acoust. Soc. Am. 1993. V. 93. P. 1736–1742.
Collins M.D., Cederberg R.J., King D.B., Chin-Bing S.A. Comparison of algorithms for solving parabolic wave equations // J. Acoust. Soc. Am. 1996. V. 100. P. 178–183.
Росницкий П.Б., Юлдашев П.В., Высоканов Б.А., Хохлова В.А. Граничное условие для расчета полей сильно фокусирующих излучателей на основе уравнения Хохлова–Заболотской // Акуст. журн. 2016. Т. 62. С. 153–162.
Маков Ю.Н. Локализованные волновые структуры, определяемые точными решениями уравнения Хохлова–Заболотской // Акуст. журн. 2019. Т. 65. С. 291–297.
Маков Ю.Н. Относительно неискажающиеся волны и профили в нелинейной акустике. Точные решения уравнений // Акуст. журн. 2009. Т. 55. С. 160–170.
Rudenko O.V. High-power focused ultrasound: nonlinear effects, shear wave excitation and medical diagnostics // Moscow Univ. Phys. Bulletin. 1996. № 6. P. 18–32.
Руденко О.В., Гурбатов С.Н. Обратная задача нелинейной акустики: синтез интенсивных сигналов для усиления теплового и радиационного воздействия ультразвука // Акуст. журн. 2016. Т. 62. С. 412–423.
Гусев В.А. Прохождение широкополосных звуковых ударов через случайный фазовый экран // Известия РАН. Серия Физическая. 2002. Т. 66. № 12. С. 1742–1746.
Голанд В.И., Кушкулей Л.М. Сильно фокусирующие многоэлементные терапевтические излучатели для неинвазивной ультразвуковой абляции жировой ткани // Акуст. журн. 2009. Т. 55. С. 481–495.
Антонов С.Н., Вайнер А.В., Проклов В.В., Резвов Ю.Г. Модификация параболического приближения теории дифракции ультразвукового пучка в сильноанизотропном кристалле // Журн. техн. физики. 2013. Т. 83. Вып. 12. С. 11–16.
Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн (2-е издание, перераб. и доп.). М.: Наука, 1990. 432 с.
Кудрявцев А.Г., Сапожников О.А. Симметрии обобщенного уравнения Хохлова–Заболотской // Акуст. журн. 1998. Т. 44. С. 628–633.
Новиков Б.К., Руденко О.В., Тимошенко В.И. Нелинейная гидроакустика. Л.: Судостроение, 1981. 264 с.
Зверев В.А., Калачев А.И. Модуляция звука звуком при пересечении акустических волн // Акуст. журн. 1970. Т. 16. С. 245–251.
Руденко О.В., Солуян С.И. К вопросу о рассеянии звука на звуке // Акуст. журн. 1972. Т. 18. С. 421–425.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал