Акустический журнал, 2020, T. 66, № 6, стр. 599-609
Движущийся объект: спектры сигналов пассивной, активной локации и переходное излучение
О. В. Руденко a, b, c, В. А. Гусев a, c, *
a Физический факультет Московского государственного университета им. М.В. Ломоносова
119991 Москва, ГСП-1, Ленинские горы, Россия
b Институт общей физики им. А.М. Прохорова РАН
119991 Москва, ГСП-1, ул. Вавилова 38, Россия
c Институт физики Земли им.О.Ю. Шмидта РАН
123995 Москва, ул. Большая Грузинская 10, стр. 1, Россия
* E-mail: vgusev@bk.ru
Поступила в редакцию 29.06.2020
После доработки 29.06.2020
Принята к публикации 07.07.2020
Аннотация
Дан анализ базовых проблем формирования сигналов движущимся объектом как задач об излучении и отражении волн при учете подвижности границ. Рассмотрена обратная задача – восстановление закона перемещения объекта по известной форме профиля зондирующей и отраженной волн. Найден спектр гармоник, рождающихся при отражении от поступательно движущегося и осциллирующего препятствия. Рассчитана корреляционная функция шума, излучаемого движущимся объектом. Приведены общие соображения о переходном излучении летящего тела в условиях плотной городской застройки.
ВВЕДЕНИЕ
Как известно, при движении источника и (или) приемника звука относительно покоящейся среды возникает сдвиг той частоты, которая регистрировалась бы в отсутствие движения. Изменение частоты называют эффектом Доплера. Это явление всесторонне изучено. Особенности отражения механических волн от подвижных границ подробно описаны в монографиях А.И. Весницкого [1] и В.А. Поздеева [2]. Аналогичные явления изучались в оптике (см. обзор [3]). Нужно указать также на весьма общее рассмотрение вопросов акустики неоднородной движущейся среды в монографиях Д.И. Блохинцева [4] и В.Е. Осташева [5].
Доплеровский сдвиг частоты давно используется в приложениях акустики (при измерении скорости движущихся объектов в атмосфере, скорости течения крови и колебаний внутренних органов при медицинском УЗИ-обследовании, скорости потоков жидкости в закрытых резервуарах и трубах) и электродинамики (радиолокация и задачи астрофизики – космологическое и гравитационное красное смещение, измерение скоростей удаленных космических тел). Однако сегодня становятся актуальными задачи, “на выходе” которых – конкретные результаты (возможно, следующие из материалов работ [1–5]). Среди них – анализ спектров сигналов, отраженных от объектов, совершающих сложные движения и сопровождающиеся собственным излучением сигналов сложного спектрального состава. Например, учет изменений частоты нужен при расчете спектров отраженных сигналов от таких объектов, как лопасти вращающегося винта [6].
Разобравшись в этой непростой картине, можно получить информацию не только о скорости движения, но и о более детальных характеристиках объекта, позволяющих провести его классификацию.
Расчет сигнала, излучаемого или отраженного от произвольным образом движущегося объекта, представляет собой трудную задачу, которая в наиболее интересных случаях не может быть решена аналитически. Поэтому целесообразно обсудить простейшие решения, чтобы добиться общего понимания и затем использовать численные методы.
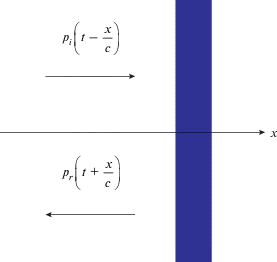
Будем рассматривать задачу в одномерной постановке, которую иллюстрирует рис. 1. Пусть наблюдатель находится в начале координат, в точке $x = 0.$ Здесь же расположены неподвижные излучатель зондирующего сигнала и приемник отраженной волны. Плоская и ортогональная к оси $x$ стенка с абсолютно жесткой поверхностью в начальный момент времени находится правее наблюдателя и удаляется от него по закону $x = X\left( t \right).$ От поверхности к наблюдателю, в отрицательном направлении оси $x,$ будет бежать отраженная волна, учитывающая вклад излучаемой движущимся объектом волны при его перемещении аналогично поршневому излучателю. Среда распространения считается однородной и стационарной, ее параметры – скорость звука c и плотность ρ – известны.
Поле слева от стенки представляет собой сумму падающей (нижний индекс i) и отраженной (нижний индекс r) волн. Для акустического давления p решение волнового уравнения имеет вид:
Для колебательной скорости
(2)
$u = \frac{1}{{\rho c}}{{p}_{i}}\left( {t - \frac{x}{c}} \right) - \frac{1}{{{\rho }c}}{{p}_{r}}\left( {t + \frac{x}{c}} \right).$Скорость (2) волны в среде должна совпадать на поверхности стенки со скоростью ее движения $V\left( t \right) = {{dX} \mathord{\left/ {\vphantom {{dX} {dt}}} \right. \kern-0em} {dt}},$ т.е. должно выполняться граничное условие
(3)
$\rho c\frac{{dX}}{{dt}} = {{p}_{i}}\left( {t - \frac{{X\left( t \right)}}{c}} \right) - {{p}_{r}}\left( {t + \frac{{X\left( t \right)}}{c}} \right).$Если формы падающей и отраженной волн известны, соотношение (3) представляет собой функциональное уравнение, из которого можно найти закон движения стенки $X\left( t \right)$ [7, 8]. Неизвестная функция $X\left( t \right)$ содержится в аргументах функций ${{p}_{i}},{{p}_{r}},$ т.е. входит в уравнение (3) нелинейным образом.
ПАССИВНЫЙ И АКТИВНЫЙ РЕЖИМЫ
Наиболее просто уравнение (3) решается, когда зондирующая волна отсутствует, т.е. ${{p}_{i}} \equiv 0.$ В этом случае мы имеем режим пассивной локации, в котором по форме принимаемого сигнала ${{p}_{r}}\left( t \right)$ требуется определить скорость движения источника $u\left( t \right){\text{:}}$
(4)
$\begin{gathered} \frac{{\frac{1}{c}\frac{{dX}}{{d{\varsigma }}}}}{{1 - \frac{1}{c}\frac{{dX}}{{d{\varsigma }}}}} = - \frac{1}{{{\rho }{{c}^{2}}}}{{p}_{r}}\left( {\varsigma } \right), \\ \frac{u}{c} = \frac{1}{c}\frac{{dX}}{{dt}} = - \frac{{\frac{1}{{{\rho }{{c}^{2}}}}{{p}_{r}}\left( t \right)}}{{1 - \frac{1}{{{\rho }{{c}^{2}}}}{{p}_{r}}\left( t \right)}}. \\ \end{gathered} $Здесь в первой формуле осуществлен переход к новой переменной ${\varsigma } = t + {X \mathord{\left/ {\vphantom {X c}} \right. \kern-0em} c}$ по аналогии с неявной функцией в решении простой римановой волны. Во второй формуле (4) изменено обозначение переменной: $\varsigma \leftrightarrow t.$
Заметим, что движение границы приводит к искажению сигнала, напоминающему нелинейную трансформацию римановой волны. Чтобы в этом убедиться, достаточно записать первое выражение (4) в параметрическом виде:
Видим, что первое уравнение описывает профиль волны, а второе – нелинейные искажения и образование неоднозначности профиля.
Другая просто решаемая задача формулируется так: найти закон движения стенки $X\left( t \right),$ при котором для заданной формы зондирующего сигнала ${{p}_{i}}\left( t \right)$ отраженная волна отсутствует (${{p}_{r}} \equiv 0$). По аналогии с формулой (4) получаем:
(5)
$\begin{gathered} \frac{u}{c} = \frac{1}{c}\frac{{dX}}{{dt}} = \frac{{\frac{1}{{{\rho }{{c}^{2}}}}{{p}_{i}}\left( t \right)}}{{1 - \frac{1}{{{\rho }{{c}^{2}}}}{{p}_{i}}\left( t \right)}}, \\ \frac{{\omega }}{c}X = - {\omega }\left( {t - {{t}_{0}}} \right) + \int {\frac{{d\left( {{\omega }t} \right)}}{{1 - \frac{1}{{{\rho }{{c}^{2}}}}{{p}_{i}}\left( {{\omega }t} \right)}}} . \\ \end{gathered} $(6)
$\begin{gathered} \frac{{\omega }}{c}X = - {\omega }\left( {t - {{t}_{0}}} \right) + \frac{2}{{\sqrt {1 - {{{\left( {\frac{{{{P}_{0}}}}{{{\rho }{{c}^{2}}}}} \right)}}^{2}}} }} \times \\ \times \,\,{\text{arctg}}\left[ {\frac{1}{{\sqrt {1 - {{{\left( {\frac{{{{P}_{0}}}}{{{\rho }{{c}^{2}}}}} \right)}}^{2}}} }}\left( {{\text{tg}}\frac{{{\omega }t}}{2} - \frac{{{{P}_{0}}}}{{{\rho }{{c}^{2}}}}} \right)} \right]. \\ \end{gathered} $Для слабого сигнала эта формула упрощается и получается очевидный результат.
(7)
$\frac{1}{c}\frac{{dX}}{{dt}} = \frac{{{{P}_{0}}}}{{{\rho }{{c}^{2}}}}\sin \left( {{\omega }t} \right).$Он также непосредственно следует из формулы (5).
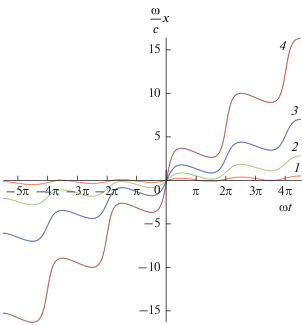
Вид решения (6) показан на рис. 2 при значениях параметра ${{{{P}_{0}}} \mathord{\left/ {\vphantom {{{{P}_{0}}} {{\rho }{{c}^{2}}}}} \right. \kern-0em} {{\rho }{{c}^{2}}}} = 1{\text{/}}4;1{\text{/}}2;{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. \kern-0em} 2};{{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-0em} 2}$ (кривые 1–4 соответственно). При построении учтено, что арктангенс задан на интервале от ${{ - {\pi }} \mathord{\left/ {\vphantom {{ - {\pi }} 2}} \right. \kern-0em} 2}$ до ${\pi /}2$ и проведено сшивание различных ветвей для получения гладкого решения. Видно, что при уменьшении параметра ${{{{P}_{0}}} \mathord{\left/ {\vphantom {{{{P}_{0}}} {{\rho }{{c}^{2}}}}} \right. \kern-0em} {{\rho }{{c}^{2}}}}$ решение (6) действительно приближается к синусоидальному сигналу, задаваемому уравнением (7).
Рис. 2.
Закон движения стенки (6), при котором отсутствует отраженная волна. Кривые 1–4 соответствуют значениям параметра ${{{{P}_{0}}} \mathord{\left/ {\vphantom {{{{P}_{0}}} {\rho {{c}^{2}}}}} \right. \kern-0em} {\rho {{c}^{2}}}}$ = $1{\text{/}}4;1{\text{/}}2;{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. \kern-0em} 2};{{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-0em} 2}.$
Рассмотрим теперь режим активной локации, считая, что известны форма падающей волны и закон $X\left( t \right),$ а также параметры среды распространения. При этом, пользуясь уравнением (3), можно рассчитать форму отраженной волны, ее спектр и другие характеристики. В частности, если стенка движется с постоянной скоростью $V = {\text{const,}}$ из (3) следует
(8)
${{p}_{r}}\left[ {t\left( {1 + \frac{V}{c}} \right)} \right] = {{p}_{i}}\left[ {t\left( {1 - \frac{V}{c}} \right)} \right] - {\rho }cV.$Второй член в правой части (8) представляет собой постоянное дополнительное разрежение, создаваемое движущейся стенкой. Для переменной составляющей имеем
(9)
${{p}_{r}}\left( {{{t}_{1}}} \right) = {{p}_{i}}\left( {\frac{{1 - \frac{V}{с}}}{{1 + \frac{V}{с}}}{{t}_{1}}} \right),\,\,\,\,{{t}_{1}} = t\left( {1 + \frac{V}{с}} \right).$Видим, что в спектре отраженного сигнала каждая из частот преобразуется так:
(10)
${{{\omega }}_{r}} = {{{\omega }}_{i}}\frac{{1 - \frac{V}{с}}}{{1 + \frac{V}{с}}} \equiv {\beta }{{\omega }_{i}}.$Преобразование (10) есть очевидное проявление эффекта Доплера: вначале частота изменяется при падении сигнала на движущийся объект, затем при отражении от этого объекта.
Рассмотрим более сложный закон движения стенки:
Здесь предполагается, что на движение с постоянной скоростью наложены вариации, в качестве которых могут выступать равномерное ускорение, регулярные либо случайные колебания. При этом формула (8) примет вид:
(12)
$\begin{gathered} {{p}_{r}}\left[ {t\left( {1 + \frac{V}{c}} \right) + \frac{{\xi \left( t \right)}}{c}} \right] = \\ = {{p}_{i}}\left[ {t\left( {1 - \frac{V}{c}} \right) - \frac{{\xi \left( t \right)}}{c}} \right] - \rho cV - \rho c\dot {\xi }\left( t \right). \\ \end{gathered} $Переходя по формуле (9) к переменной ${{t}_{1}},$ перепишем (12) в удобной форме:
(13)
$\begin{gathered} {{p}_{r}}\left[ {{{t}_{1}} + \frac{1}{с}{\xi }\left( {\frac{{{{t}_{1}}}}{{\alpha }}} \right)} \right] = \\ = {{p}_{i}}\left[ {{\beta }{{t}_{1}} - \frac{1}{с}{\xi }\left( {\frac{{{{t}_{1}}}}{{\alpha }}} \right)} \right] - {\rho }cV - {\rho }c{\alpha }\frac{d}{{d{{t}_{1}}}}{\xi }\left( {\frac{{{{t}_{1}}}}{{\alpha }}} \right). \\ \end{gathered} $Здесь для краткости введены обозначения:
Поскольку нас интересует спектр отраженного сигнала, обозначим
(15)
$\eta = {{t}_{1}} + \frac{1}{с}\xi \left( {\frac{{{{t}_{1}}}}{\alpha }} \right) = \alpha t + \frac{1}{с}\xi \left( t \right)$(16)
$\begin{gathered} {{p}_{r}}\left( \eta \right) = {{p}_{i}}\left[ {\beta \eta - \frac{{\left( {1 + \beta } \right)}}{с}\xi \left( {\frac{{{{t}_{1}}\left( \eta \right)}}{\alpha }} \right)} \right] - \\ - \,\,\rho с\alpha \frac{d}{{d{{t}_{1}}}}\xi \left( {\frac{{{{t}_{1}}\left( \eta \right)}}{\alpha }} \right). \\ \end{gathered} $Иногда может быть удобнее другая запись:
(17)
${{p}_{r}}\left( \eta \right) = {{p}_{i}}\left[ {\beta \eta - \frac{2}{{\alpha с}}\xi \left( t \right)} \right] - \rho с\frac{d}{{dt}}\xi \left( t \right).$Пример 1. Будем считать, что объект облучается гармоническим сигналом и одновременно сам совершает колебания с другой частотой. Положим в (17)
(18)
${{p}_{i}}\left( t \right) = {{P}_{0}}\sin \left( {{{\omega }_{0}}t} \right),\,\,\,\,\xi \left( t \right) = {{\xi }_{0}}\sin \left( {\Omega t} \right).$Выражение (17) примет вид:
(19)
$\begin{gathered} {{p}_{r}}\left( \eta \right) = {{P}_{0}}\sin \left[ {{{\omega }_{0}}\beta \left( {\eta - \frac{{2{{\xi }_{0}}}}{{\alpha \beta с}}\sin \left( {\Omega t} \right)} \right)} \right] - \\ - \,\,\rho с{{\xi }_{0}}\Omega \cos \left( {\Omega t} \right),\,\,\,\,\eta = \alpha t + \frac{{{{\xi }_{0}}}}{с}\sin \left( {\Omega t} \right). \\ \end{gathered} $Удобно снова, как в формуле (4), изменить обозначения переменных: $t \leftrightarrow {\eta ,}$
(20)
$\begin{gathered} {{p}_{r}}\left( t \right) = {{P}_{0}}\sin \left[ {{{\omega }_{0}}\beta \left( {t - \frac{{2{{\xi }_{0}}}}{{\alpha \beta с}}\sin \left( {\Omega \eta } \right)} \right)} \right] - \\ - \,\,\rho с{{\xi }_{0}}\Omega \cos \left( {\Omega \eta } \right),\,\,\,\,t = \alpha \eta + \frac{{{{\xi }_{0}}}}{с}\sin \left( {\Omega \eta } \right). \\ \end{gathered} $Вначале будем считать амплитуду колебаний малой, то есть ${{{{\xi }_{0}}{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\xi }_{0}}{{\omega }_{0}}} с}} \right. \kern-0em} с} \ll 1,$ и положим в формуле (20) ${\eta } = {t \mathord{\left/ {\vphantom {t {\alpha }}} \right. \kern-0em} {\alpha }}{\text{.}}$ При этом выражение (20) упрощается:
(21)
$\begin{gathered} {{p}_{r}}\left( t \right) = {{P}_{0}}\sin \left[ {{{\omega }_{0}}\beta \left( {t - \frac{{2{{\xi }_{0}}}}{{\alpha \beta с}}\sin \left( {\Omega \frac{t}{\alpha }} \right)} \right)} \right] - \\ - \,\,\rho с{{\xi }_{0}}\Omega \cos \left( {\Omega \frac{t}{\alpha }} \right) = {{P}_{0}}\sin \left( {{{\omega }_{0}}\beta t} \right) \times \\ \times \,\,\cos \left[ {{{\omega }_{0}}\beta \frac{{2{{\xi }_{0}}}}{{\alpha \beta с}}\sin \left( {\Omega \frac{t}{\alpha }} \right)} \right] - {{P}_{0}}\cos \left( {{{\omega }_{0}}\beta t} \right) \times \\ \times \,\,\sin \left[ {{{\omega }_{0}}\beta \frac{{2{{\xi }_{0}}}}{{\alpha \beta с}}\sin \left( {\Omega \frac{t}{\alpha }} \right)} \right] - \rho с{{\xi }_{0}}\Omega \cos \left( {\Omega \frac{t}{\alpha }} \right) \approx \\ \approx {{P}_{0}}\sin \left( {{{\omega }_{0}}\beta t} \right) - {{P}_{0}}\frac{{2{{\xi }_{0}}{{\omega }_{0}}}}{{\alpha с}}\cos \left( {{{\omega }_{0}}\beta t} \right) \times \\ \times \,\,\sin \left( {\Omega \frac{t}{\alpha }} \right) - \rho с{{\xi }_{0}}\Omega \cos \left( {\Omega \frac{t}{\alpha }} \right). \\ \end{gathered} $Видим, что частоты отраженных волн таковы:
(22)
$\begin{gathered} {{{\omega }}_{{\text{0}}}}{\beta } = \frac{{1 - \frac{V}{с}}}{{1 + \frac{V}{с}}}{{{\omega }}_{{\text{0}}}},\,\,\,\,\frac{\Omega }{{\alpha }} = \frac{\Omega }{{1 + \frac{V}{с}}}, \\ {{{\omega }}_{{\text{0}}}}{\beta } \pm \frac{\Omega }{{\alpha }} = \frac{{\left( {1 - \frac{V}{с}} \right){{{\omega }}_{{\text{0}}}} \pm \Omega }}{{1 + \frac{V}{с}}}. \\ \end{gathered} $Амплитуды этих волн равны соответственно
(23)
${{P}_{0}},\,\,\,\,{\rho }с{{\xi }_{0}}\Omega ,\,\,\,\,{{P}_{0}}\frac{{2{{{\xi }}_{{\text{0}}}}{{{\omega }}_{0}}}}{{с\left( {1 + \frac{V}{c}} \right)}}.$Теперь рассмотрим более сложную ситуацию, когда амплитуда колебаний не мала, то есть неравенство ${{{{\xi }_{0}}{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\xi }_{0}}{{\omega }_{0}}} с}} \right. \kern-0em} с} \ll 1$ не выполняется. В этом случае формулу (21) можно уточнить следующим образом, где введено обозначение ${\theta } = {{{\omega }}_{0}}t{\text{:}}$
(24)
$\begin{gathered} \frac{{{{p}_{r}}\left( \theta \right)}}{{{{P}_{0}}}} = \sin \left( {\beta \theta } \right)\cos \left[ {\frac{{2{{\omega }_{0}}{{\xi }_{0}}}}{{\alpha с}}\sin \left( {\frac{\Omega }{{{{\omega }_{0}}}}\frac{\theta }{\alpha }} \right)} \right] - \\ - \,\,\cos \left( {\beta \theta } \right)\sin \left[ {\frac{{2{{\omega }_{0}}{{\xi }_{0}}}}{{\alpha с}}\sin \left( {\frac{\Omega }{{{{\omega }_{0}}}}\frac{\theta }{\alpha }} \right)} \right] - \\ - \,\,\frac{{\rho {{с}^{2}}}}{{{{P}_{0}}}}\frac{{{{\omega }_{0}}{{\xi }_{0}}}}{c}\frac{\Omega }{{{{\omega }_{0}}}}\cos \left( {\frac{\Omega }{{{{\omega }_{0}}}}\frac{\theta }{\alpha }} \right). \\ \end{gathered} $По-прежнему, для получения приближенных аналитических выражений здесь принято 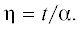 Используем теперь разложения [9]:
Используем теперь разложения [9]:
(25)
$\begin{gathered} \cos \left[ {Z\sin \left( T \right)} \right] = {{J}_{0}}\left( Z \right) + 2\sum\limits_{k = 1}^\infty {{{J}_{{2k}}}\left( Z \right)} \cos \left( {2kT} \right), \\ \sin \left[ {Z\sin \left( T \right)} \right] = 2\sum\limits_{k = 0}^\infty {{{J}_{{2k + 1}}}\left( Z \right)} \sin \left( {\left( {2k + 1} \right)T} \right). \\ \end{gathered} $Обозначая для краткости $D = {{{{\xi }_{0}}{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\xi }_{0}}{{\omega }_{0}}} с}} \right. \kern-0em} с}$ и ${{{{{\omega }}_{0}}} \mathord{\left/ {\vphantom {{{{{\omega }}_{0}}} \Omega }} \right. \kern-0em} \Omega } = N,$ приведем (23), (24) к следующему виду:
(26)
$\begin{gathered} \frac{{{{p}_{r}}\left( \theta \right)}}{{{{P}_{0}}}} = \sin \left( {{\beta \theta }} \right){{J}_{0}}\left( {\frac{{2D}}{{\alpha }}} \right) + 2\sin \left( {{\beta \theta }} \right) \times \\ \times \,\,\sum\limits_{k = 1}^\infty {{{J}_{{2k}}}\left( {\frac{{2D}}{{\alpha }}} \right)} \cos \left( {2k\frac{\theta }{{N{\alpha }}}} \right) - 2\cos \left( {{\beta \theta }} \right) \times \\ \times \,\,\sum\limits_{k = 0}^\infty {{{J}_{{2k + 1}}}\left( {\frac{{2D}}{{\alpha }}} \right)} \sin \left( {\left( {2k + 1} \right)\frac{\theta }{{N{\alpha }}}} \right) - \frac{{{\rho }{{с}^{2}}}}{{{{P}_{0}}}}\frac{D}{N}\cos \left( {\frac{{\theta }}{{N{\alpha }}}} \right). \\ \end{gathered} $Видим, что в более общем случае, когда число $D$ не мало, спектр отраженного сигнала содержит такие спектральные компоненты:
(27)
$\begin{gathered} {{\omega }_{0}}\beta = \frac{{1 - \frac{V}{с}}}{{1 + \frac{V}{с}}}{{\omega }_{0}},\,\,\,\,\frac{\Omega }{\alpha } = \frac{\Omega }{{1 + \frac{V}{с}}}, \\ {{\omega }_{0}}\beta \pm \frac{\Omega }{\alpha } = \frac{{\left( {1 - \frac{V}{с}} \right){{\omega }_{0}} \pm \Omega }}{{1 + \frac{V}{с}}}, \\ {{\omega }_{0}}\beta \pm 2k\frac{\Omega }{\alpha } = \frac{{\left( {1 - \frac{V}{с}} \right){{\omega }_{0}} \pm 2k\Omega }}{{1 + \frac{V}{с}}}, \\ {{\omega }_{0}}\beta \pm \left( {2k + 1} \right)\frac{\Omega }{\alpha } = \frac{{\left( {1 - \frac{V}{с}} \right){{{\omega }}_{0}} \pm \left( {2k + 1} \right)\Omega }}{{1 + \frac{V}{с}}}. \\ \end{gathered} $Этот результат можно записать в более компактном виде:
(28)
${{{\omega }}_{{\text{0}}}}{\beta } \pm n\frac{\Omega }{{\alpha }} = \frac{{\left( {1 - \frac{V}{с}} \right){{{\omega }}_{0}} \pm n\Omega }}{{1 + \frac{V}{с}}},\,\,\,\,\frac{\Omega }{\alpha } = \frac{\Omega }{{1 + \frac{V}{с}}}.$Итак, отраженный сигнал содержит основную частоту волны, сдвинутую в соответствии с формулой эффекта Доплера для равномерно движущегося объекта, а также комбинационные частоты. Последние представляют собой суммы и разности сдвинутой основной частоты и $(n + 1)$ гармоник частоты колебаний объекта, сдвинутой по Доплеру для удаляющегося (при $V > 0$) источника.
Для построения графиков точного решения (20) его удобно переписать в параметрическом виде:
Рис. 3.
Характерный профиль отраженного от движущейся стенки сигнала (кривая 1). Параметр D = 0.5, N = 10, безразмерная амплитуда третьего слагаемого B0 = 0.3 (именно это слагаемое обеспечивает модуляцию амплитуды), β = 0.8. Кривая 2 – синусоидальный сигнал такой частоты, что его первая осцилляция совпадает с первой осцилляцией на кривой 1.
Пример 2. Будем теперь считать, что объект облучается гармоническим сигналом и одновременно сам совершает случайные колебания, описываемые функцией $\xi \left( t \right).$ Функция $\xi \left( t \right)$ – это нормальный стационарный случайный процесс с нулевым средним значением. Положим также в (16)
Считаем случайные “дрожания” объекта слабыми, т.е. ${{\xi {{{\omega }}_{0}}} \mathord{\left/ {\vphantom {{\xi {{{\omega }}_{0}}} с}} \right. \kern-0em} с} \ll 1.$ Воспользуемся формулой, упрощенной по аналогии с (20):(30)
$\begin{gathered} \frac{{{{p}_{r}}\left( t \right)}}{{{{P}_{0}}}} = \sin \left( {{{\omega }_{0}}\beta t} \right) - \\ - \,\,\frac{{2{{\omega }_{0}}}}{{\alpha с}}\xi \left( t \right)\cos \left( {{{\omega }_{0}}\beta t} \right) - \frac{{\rho c}}{{{{P}_{0}}}}\frac{d}{{dt}}\xi \left( t \right). \\ \end{gathered} $Проведем статистическое усреднение выражения, следующего из (30):
(31)
$\begin{gathered} \frac{{\left\langle {{{p}_{r}}\left( {{{t}_{1}}} \right){{p}_{r}}\left( {{{t}_{2}}} \right)} \right\rangle }}{{P_{0}^{2}}} = \sin \left( {{{\omega }_{0}}\beta {{t}_{1}}} \right)\sin \left( {{{\omega }_{0}}\beta {{t}_{2}}} \right) + \\ + \,\,{{\left( {\frac{{2{{\omega }_{0}}}}{{\alpha с}}} \right)}^{2}}\left\langle {\xi \left( {{{t}_{1}}} \right)\xi \left( {{{t}_{2}}} \right)} \right\rangle \cos \left( {{{\omega }_{0}}\beta {{t}_{1}}} \right)\cos \left( {{{\omega }_{0}}\beta {{t}_{2}}} \right) + \\ + \,\,{{\left( {\frac{{\rho c}}{{{{P}_{0}}}}} \right)}^{2}}\frac{{{{d}^{2}}}}{{d{{t}_{1}}d{{t}_{2}}}}\left\langle {\xi \left( {{{t}_{1}}} \right)\xi \left( {{{t}_{2}}} \right)} \right\rangle . \\ \end{gathered} $Положим в силу стационарности ${{t}_{2}} - {{t}_{1}} = \tau $ и проведем усреднение по переменной ${{t}_{1}}.$ Обозначая корреляционные функции шума и отраженной волны как
(32)
$\left\langle {\xi \left( {{{t}_{1}}} \right)\xi \left( {{{t}_{2}}} \right)} \right\rangle = {{R}_{\xi }}\left( \tau \right),\,\,\,\,\left\langle {{{p}_{r}}\left( {{{t}_{1}}} \right){{p}_{r}}\left( {{{t}_{2}}} \right)} \right\rangle = {{R}_{p}}\left( \tau \right),$(33)
$\begin{gathered} \frac{{{{R}_{p}}\left( \tau \right)}}{{P_{0}^{2}}} = \frac{1}{2}\cos \left( {{{\omega }_{0}}\beta \tau } \right) \times \\ \times \,\,\left[ {1 + {{{\left( {\frac{{2{{\omega }_{0}}}}{{\alpha с}}} \right)}}^{2}}{{R}_{\xi }}\left( \tau \right)} \right] - {{\left( {\frac{{\rho c}}{{{{P}_{0}}}}} \right)}^{2}}\frac{{{{d}^{2}}}}{{d{{\tau }^{2}}}}{{R}_{\xi }}\left( \tau \right). \\ \end{gathered} $Второй член в правой части (33) связан с излучением шума удаляющегося объекта. Наибольший интерес представляет первый член, описывающий влияние шума на отраженный сигнал. Корреляционную функцию для шумовой составляющей примем в виде
(34)
${{R}_{\xi }} = {{\sigma }^{2}}\exp \left( { - \frac{{{{\tau }^{2}}}}{{\tau _{c}^{2}}}} \right).$(35)
$\begin{gathered} \frac{{{{S}_{p}}\left( {\omega } \right)}}{{P_{0}^{2}}} = \frac{1}{2}{{\left( {\frac{{{{{\omega }}_{{\text{0}}}}{\sigma }}}{{{\alpha }с}}} \right)}^{2}}\sqrt {{\pi \tau }_{c}^{2}} \times \\ \times \,\,\left[ {\exp \left( { - {\kern 1pt} \frac{{{\tau }_{c}^{2}}}{4}{{{\left( {{\omega } - {\beta }{{{\omega }}_{0}}} \right)}}^{2}}} \right)\, + \,\exp \left( { - {\kern 1pt} \frac{{{\tau }_{c}^{2}}}{4}{{{\left( {{\omega } + {\beta }{{{\omega }}_{0}}} \right)}}^{2}}} \right)} \right]\, + \\ + \,\,\frac{{\pi }}{2}\left[ {{\delta }\left( {{\omega } - {\beta }{{{\omega }}_{{\text{0}}}}} \right) + {\delta }\left( {{\omega } + {\beta }{{{\omega }}_{{\text{0}}}}} \right)} \right]. \\ \end{gathered} $Видим, что наряду с дельта-образной спектральной линией на частоте ${\omega } = {\beta }{{{\omega }}_{{\text{0}}}}$ появляется уширенная линия с той же центральной частотой и с характерной шириной $2{\text{/}}{{{\tau }}_{c}},$ обратной времени корреляции шума.
Интенсивность отраженной волны, как получается из (33) при ${\tau } = 0,$ равна
(36)
${{I}_{p}} = \frac{{P_{0}^{2}}}{2}\left[ {1 + {{{\left( {\frac{{2{{{\omega }}_{{\text{0}}}}{\sigma }}}{{{\alpha }с}}} \right)}}^{2}}} \right] + 2{{\left( {\frac{{{\rho }c{\sigma }}}{{{{{\tau }}_{с}}}}} \right)}^{2}}.$Отсюда следует, что в отсутствие шума интенсивность равна ${{P_{0}^{2}} \mathord{\left/ {\vphantom {{P_{0}^{2}} 2}} \right. \kern-0em} 2},$ т.е. совпадает с интенсивностью регулярного гармонического сигнала. При наличии шума интенсивность отраженного сигнала увеличивается.
ЧИСЛЕННЫЙ РАСЧЕТ ОТРАЖЕННЫХ СИГНАЛОВ
Пример 3. Рассмотрим теперь переход покоящегося объекта к равномерному движению, для чего положим в формулах (11), (12), (15) $V = 0,$ ${\alpha } = 1.$ Итак, в момент времени t = 0 стенка начинает двигаться с постоянным ускорением a. В этом случае закон движения стенки (11) принимает вид:
Пользуясь формулой ${\eta } = t + \frac{{a{{t}^{2}}}}{{2c}},$ найдем явное выражение
(здесь выбрана положительная ветвь решения) и подставим его в решение (14):(38)
$\begin{gathered} {{p}_{r}}\left( {\eta } \right) = {{p}_{i}}\left[ {{\eta } - \frac{{2с}}{a}\left( {1 + \frac{{a{\eta }}}{c} - \sqrt {1 + \frac{{2a{\eta }}}{c}} } \right)} \right] - \\ - \,\,{\rho }{{с}^{2}}\left( {\sqrt {1 + \frac{{2a{\eta }}}{c}} - 1} \right). \\ \end{gathered} $Пусть объект облучается гармонической волной ${{p}_{i}}\left( t \right) = {{P}_{0}}\sin \left( {{{{\omega }}_{0}}t} \right).$ Введем безразмерное время ${\theta } = {{{\omega }}_{{\text{0}}}}{\eta }$ и безразмерное ускорение ${\gamma } = \frac{a}{{c{{{\omega }}_{0}}}}.$ Тогда решение запишется так:
(39)
$\begin{gathered} \frac{{{{p}_{r}}\left( {\eta } \right)}}{{{{P}_{0}}}} = \sin \left[ { - {\theta } + \frac{2}{{\gamma }}\left( {\sqrt {1 + 2\gamma \theta } - 1} \right)} \right] - \\ - \,\,\frac{{{\rho }{{с}^{2}}}}{{{{P}_{0}}}}\left( {\sqrt {1 + 2{\gamma \theta }} - 1} \right). \\ \end{gathered} $В результате движения объекта фаза осциллирующей части отраженной волны ψ = –θ + $ + \,\frac{2}{{\gamma }}\left( {\sqrt {1 + 2{\gamma \theta }} - 1} \right)$ перестает быть линейной функцией времени. При $\gamma \theta \ll 1$ фаза ψ ≈ θ – $ - \,\frac{{{\gamma }{{{\theta }}^{2}}}}{4} = {\theta }\left( {1 - \frac{{{\gamma \theta }}}{4}} \right),$ что соответствует уменьшению мгновенной частоты на промежутке времени до порядка ${\theta } < \frac{1}{{\gamma }}.$ При ${\gamma \theta } \gg 1$ $\psi \approx - \theta \left( {1 - \sqrt {\frac{8}{{\gamma \theta }}} } \right)$ и мгновенная частота нарастает. Таким образом, фаза $\psi $ обладает экстремумом, в котором мгновенная частота равна нулю. Этот экстремум достигается при ${{\theta }_{m}} = \frac{3}{{2\gamma }}.$ Определим, какое значение скорости движения объекта соответствует этому моменту времени. Найдем последовательно ${{{\eta }}_{m}} = \frac{3}{{2{\gamma }{{{\omega }}_{0}}}} = \frac{{3c}}{{2a}},$ ${{t}_{m}} = \frac{3}{{2{\gamma }{{{\omega }}_{0}}}} = \frac{c}{a}.$ При равноускоренном движении $V\left( t \right) = at,$ соответственно ${{V}_{m}} = a{{t}_{m}} = c.$ Таким образом, экстремум соответствует переходу значения скорости движения объекта через скорость звука в среде. В соответствии с общей теорией при удалении стенки от точки наблюдения мгновенная частота уменьшается. Однако после перехода через скорость звука стенка начинает догонять сигналы, излученные в более ранние моменты времени, в результате мгновенная частота начинает возрастать.
Необходимо подчеркнуть, что одномерная задача о движении плоскости с околозвуковыми скоростями является сильной идеализацией, поскольку для преодоления сопротивления среды в этом случае требуется приложение бесконечно большой силы. Движение же ограниченных тел с околозвуковыми скоростями является существенно неодномерным.
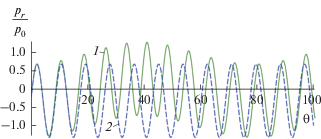
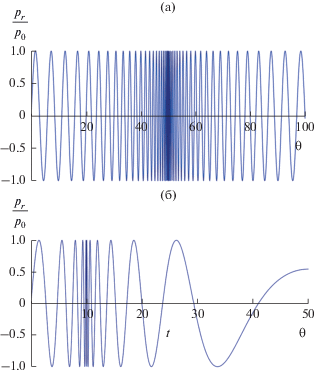
Характерный вид сигнала приведен на рис. 4 при $\gamma = 0.01,$ соответственно экстремум фазы находится при ${{{\theta }}_{m}} = 150.$ Видно, что при прохождении экстремума фазы образуется характерный “перескок” профиля сигнала. Он связан с тем, что в точке экстремума фазы мгновенная частота проходит через ноль и меняет знак, а сигнал меняет полярность. Положение экстремума ${{{\theta }}_{m}}$ и перескока зависят от параметра γ, т.е. ускорения. При малых γ (малых ускорениях) экстремум отстоит далеко во времени относительно начала движения и его легко выявить. При увеличении γ экстремум сдвигается к началу сигнала и попадает на первые осцилляции, в результате его выделение из сигнала становится практически неосуществимым. Эта ситуация соответствует большим ускорениям и быстрому набору скорости.
Рис. 4.
Характерный временной профиль сигнала при равноускоренном движении объекта при $\gamma = 0.01.$
Сигнал, изображенный на рис. 4, рождается при удалении стенки от точки наблюдения. При приближении стенки к источнику, наоборот, происходит увеличение мгновенной частоты источника вплоть до момента достижения стенкой скорости звука (рис. 5). Затем стенка догоняет излученные ранее сигналы и мгновенная частота начинает уменьшаться. На рис. 5а представлен отраженный сигнал при ${\gamma } = 0.01,$ на рис. 5б – при ${\gamma } = 0.05.$ При построении графиков на рис. 5 можно использовать формулы (37)–(39) с заменой $a \to - a.$ Однако нужно учесть, что после достижения движущейся стенкой скорости звука необходимо переключиться на другую ветвь решения
Рис. 5.
Характерные временные профили сигнала при равноускоренном движении объекта при приближении к точке наблюдения: (а) – $\gamma = 0.01,$ (б) – $\gamma = 0.05.$
Пример 4. Зададим падающую волну в виде импульсного сигнала ${{p}_{i}}\left( t \right)$ = ${{P}_{0}}{\kern 1pt} \exp {\kern 1pt} \left( {{{ - {{t}^{2}}} \mathord{\left/ {\vphantom {{ - {{t}^{2}}} {t_{0}^{2}}}} \right. \kern-0em} {t_{0}^{2}}}} \right).$ Пусть стенка движется со средней скоростью $V\, \ne \,0$ и совершает гармонические колебания, $\xi \left( t \right)\, = \,{{\xi }_{0}}{\kern 1pt} \sin {\kern 1pt} \left( {\Omega t} \right).$ Общая формула решения в безразмерных переменных имеет следующий вид:
(40)
$\frac{{{{p}_{r}}\left[ {{{{\eta }}_{1}}} \right]}}{{{{P}_{0}}}} = \exp \left[ { - {{{\left( {{\mu \theta } - D\sin \left( {\frac{{\theta }}{N}} \right)} \right)}}^{2}}} \right] - {{B}_{0}}\cos \left( {\frac{{\theta }}{N}} \right),$(41)
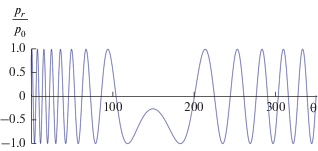
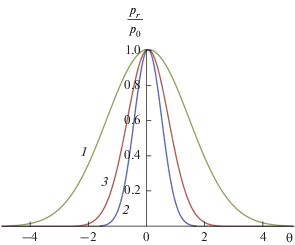
${{{\eta }}_{1}} = \frac{{{\mu \theta }}}{{\beta }} + D\sin \left( {\frac{{\theta }}{N}} \right).$На рис. 6 представлен профиль отраженной волны (кривые 1 и 2) при отсутствии колебаний стенки, B0 = 0, $D = 0.$ Кривая 1 соответствует β = 0.5 – удалению стенки от точки наблюдения, кривая 2 – β = 1.5, приближению стенки. Для сравнения приведен также профиль падающего импульса (кривая 3). Как видно, при удалении стенки от точки наблюдения импульс растягивается, а при приближении – сжимается. При многократном отражении импульса от движущейся границы возможно получение очень коротких импульсов. Этот способ используется в оптике [11].
Рис. 6.
Растяжение отраженного импульса при удалении стенки от точки наблюдения. Кривая 1 соответствует удалению стенки от точки наблюдения (β = 0.5), кривая 2 – приближению стенки (β = 1.5), кривая 3 – падающий импульс.
На рис. 7 представлены характерные профили отраженного сигнала при наличии колебательного движения стенки при ее удалении от точки наблюдения. Видно, что появляется модуляция профиля импульса периодическим сигналом. При увеличении параметра D возрастает амплитуда пиков. При уменьшении параметра N, имеющего в данном случае смысл отношения периода колебаний стенки к характерной длительности падающего импульса, частота модуляции увеличивается. На рис. 8 приведен аналогичный профиль отраженного сигнала в случае приближения стенки к точке наблюдения. Здесь наблюдается сужение длительности сигнала при его дополнительной модуляции.
Рис. 7.
Характерные профили отраженной волны при наличии колебательного движения стенки при ее удалении от точки наблюдения: (а) – B0 = 0.1, D = 0.05, N = 0.1, β = 0.5, (б) – B0 = 0.1, D = 0.1, N = 0.08, β = 0.5.
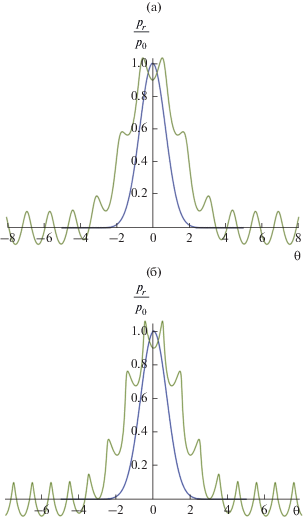
Рис. 8.
Характерный профиль отраженной волны при наличии колебательного движения стенки при ее приближении к точке наблюдения: B0 = 0.1, D = 0.05, N = 0.1, β = 1.5.
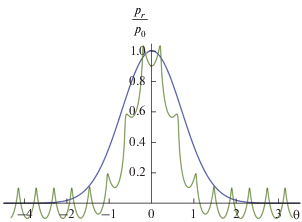
Сравнивая рис. 7а и 7б, а также рис. 8, можно отметить тенденцию к укручению и формированию острого положительного пика при изменении параметров сигналов. Это связано с неоднозначностью преобразования, обратного к (41). Действительно, с математической точки зрения преобразование похоже на запись решения для простой римановой волны (в безразмерных переменных) $p = {{p}_{0}}\left( {{\theta } + pz} \right)$ в параметрическом виде $p = {{p}_{0}}\left( \xi \right),$ $\theta = \xi - {{p}_{0}}\left( \xi \right)z,$ в профиле которого по мере распространения (увеличении z) появляются перехлесты и участки неоднозначности профиля. Подобный эффект наблюдается и на рис. 7, 8, только определяющим фактором является изменение параметров μ, β, N, D. Легко определить, при каких параметрах неоднозначность возникает. Взяв производную от (38) и приравняв ее нулю, найдем, при каком значении θ интервал между соседними точками η текущего профиля становится равным нулю:
Неоднозначность профиля отраженной волны появляется, если комбинация параметров в правой части (42) оказывается меньше или равной единицы, т.е. при увеличении “глубины модуляции” D, малых скоростях стенки при удалении от точке наблюдения (параметр β стремится к единице снизу) или при приближении стенки к точке наблюдения (параметр β возрастает), уменьшении параметра N – отношения характерных частот падающей волны и колебаний стенки. В этих ситуациях из-за движения стенки отраженные сигналы “перепутываются” и сигнал, отраженный в более поздний момент времени, может прийти в точку наблюдения раньше сигнала, отраженного в более ранний момент времени. В этом случае для построения однозначного профиля необходимо адаптировать правило равенства площадей. Это планируется сделать в дальнейшем.
Пример 5. Пусть падающей волной, как и в примере 4, является импульсный сигнал ${{p}_{i}}\left( t \right)$ = = ${{P}_{0}}\exp \left( {{{ - {{{\left( {t - {{t}_{1}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left( {t - {{t}_{1}}} \right)}}^{2}}} {T_{0}^{2}}}} \right. \kern-0em} {T_{0}^{2}}}} \right).$ Отличие от примера 4 состоит в добавлении в начальное условие временной задержки t1, указывающей время излучения максимума импульсного сигнала. В качестве закона движения стенки зададим равноускоренное движение (37) из примера 3. При этом скорость начинает возрастать в момент t = 0. Исходя из общей формулы (38), можно записать явное решение для данного примера:
(43)
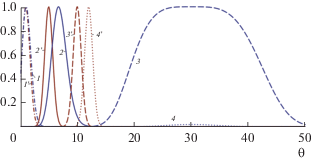
$\begin{gathered} \frac{{{{p}_{r}}\left( {\eta } \right)}}{{{{P}_{0}}}} = \exp \left( { - {{{\left[ {{\eta } - {{{\eta }}_{1}} - \frac{2}{{\gamma }}\left( {1 + {\gamma \eta } - \sqrt {1 + 2{\gamma \eta }} } \right)} \right]}}^{2}}} \right) - \\ - \,\,{{B}_{0}}\left( {\sqrt {1 + 2{\gamma \eta }} - 1} \right), \\ \end{gathered} $Профили решения (43) для различных значений временной задержки t1 приведены на рис. 9 без учета второго слагаемого в (43), описывающего смещение графика по вертикали. Кривые с номерами 1–4 соответствуют отраженным волнам с безразмерными временными задержками t1 = 1, 5, 10, 12. Кривые с номерами со штрихом 1 ', 2 ', 3 ', 4 ' изображают профили падающих волн с соответствующими временными задержками. Видно, что при увеличении времени задержки (а значит, и скорости движения стенки) отраженная волна начинает все сильнее отставать от падающего сигнала. Длительность отраженной волны также возрастает. При этом для временных задержек, меньших t1m = 1/2γ пиковое значение отраженной волны сохраняет значение, равное пиковому значению в падающей волне. При увеличении временной задержки амплитуда отраженной волны резко убывает. Это связано с тем, что при излучении волны с задержкой t1m скорость стенки как раз успевает достичь скорости звука в среде. Соответственно, в формировании отраженной волны участвуют только “хвосты” импульсного сигнала с малой амплитудой.
ЗАМЕЧАНИЯ ПО ПЕРЕХОДНОМУ ИЗЛУЧЕНИЮ
Известно, что электрически заряженные частицы могут излучать электромагнитные волны, если они движутся с ускорением. Однако и при равномерном движении в среде может возникнуть “второй” вид излучения – Вавилова–Черенкова. Для этого частица должна двигаться со сверхсветовой скоростью, большей фазовой скорости света в этой среде. “Третий” вид (переходное излучение) возникает при пересечении зарядом границы раздела двух сред с разными показателями преломления [12]. Когда частица переходит из одной среды в другую, окружающее ее поле изменяется, порождая волну. Это излучение было теоретически предсказано В.Л. Гинзбургом и И.М. Франком в 1945 г. Нобелевская премия присуждена В.Л. Гинзбургу в 2003 г. “За основополагающий вклад в теорию сверхпроводников и сверхтекучих жидкостей” [13], однако сам Виталий Лазаревич считал своим основным достижением именно открытие переходного излучения [12, 14].
Акустическим аналогом “второго” типа излучения (Вавилова–Черенкова) являются “волны Маха”, возбуждаемые телом, движущимся в атмосфере со сверхзвуковой скоростью. Эти волны предсказаны и теоретически изучены в середине 19 века К. Доплером за 40 лет до их экспериментальной визуализации Э. Махом (информация Ю.Н. Макова) и за 100 лет до наблюдения соответствующего оптического эффекта. В отличие от оптики, где эффект очень слаб и был обнаружен во многом благодаря хорошему зрению П. Черенкова, его акустический аналог весьма силен и чувствительных приборов для регистрации не требует. Достаточно сослаться на волну звукового удара, возникающую при движении самолета на сверхзвуковых скоростях. Создание современных сверхзвуковых пассажирских самолетов тормозится именно серьезными экологическими последствиями звукового удара, а полеты на малых высотах могут вообще привести к летальному воздействию на организмы.
“Третий тип” – переходное излучение – в акустике изучен в гораздо меньшей степени и обсуждается много реже, чем в оптике. Однако акустический эффект и в этом случае гораздо сильнее оптического. Его наблюдал (слышал) каждый пассажир поезда, движущегося по мосту с периодически расположенными фермами, или при поездке в автомобиле мимо череды колонн или других конструкций, создающих сильные неоднородности границ. Более слабое переходное излучение сопровождает движение судов на воздушной подушке или экранопланов над неровной поверхностью воды. Сравнительный анализ особенностей переходного излучения в акустике и электродинамике дан в обзоре [15].
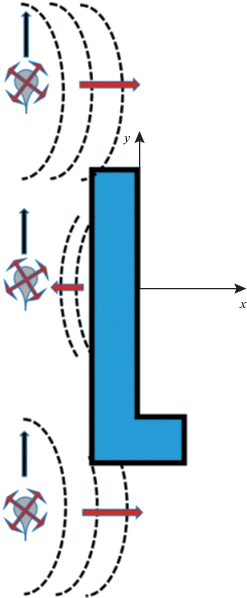
Строгий расчет характеристик направленности и спектров акустического переходного излучения довольно сложен. Для обсуждения основных закономерностей рассмотрим движение беспилотного летательного аппарата (ЛА) мимо близко расположенного здания в условиях плотной городской застройки. Эта задача допускает простейшую одномерную постановку (см. рис. 10).
Пусть ЛА движется параллельно стене с постоянной скоростью $V.$ В системе координат, связанной с ЛА, можно воспользоваться моделью (3). В уравнении (3) смещение границы $X\left( t \right)$ должно скачком измениться от бесконечности до нуля при входе ЛА в область за стеной здания, оставаться нулевым в течение движения и затем вновь скачком устремиться к бесконечности при выходе из этой области. Понятно, что в момент выхода область повышенного давления, сформировавшаяся между ЛА и стеной, быстро расширяется, излучая волну. Это излучение можно сравнить с генерацией волны в ударной трубе, содержащей неподвижный газ в камерах высокого и низкого давления, разделенных перегородкой. В момент разрыва перегородки начинается быстрое истечение газа из камеры высокого давления, то есть возбуждение акустической (ударной) волны.
Для качественного понимания процесса удобно воспользоваться даже не уравнением (3), а еще более простой моделью. Как известно, профили падающей и отраженной волн в случае идеальных границ связаны соотношением
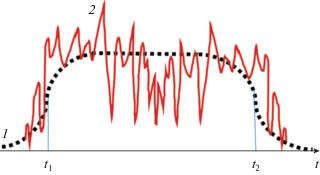
Если ЛА движется не около здания, а вдоль системы колонн или мостовых ферм, штриховая кривая на рис. 11 будет иметь осциллирующий характер. Аналогичные осцилляции возникнут и в том случае, когда имеются окна, периодически расположенные вдоль стены.
Корреляционная функция принимаемого излучения имеет вид:
(45)
$\left\langle {{{p}_{r}}\left( t \right){{p}_{r}}\left( {t + {\tau }} \right)} \right\rangle = {{R}_{p}}\left( {\tau } \right) = \overline {f\left( t \right)f\left( {t + {\tau }} \right)} {{R}_{i}}\left( {\tau } \right).$(46)
$\overline {f\left( t \right)f\left( {t + {\tau }} \right)} = \left\{ {\begin{array}{*{20}{c}} {1,\,\,\,\,{\tau } < \left( {{{t}_{2}} - {{t}_{1}}} \right);} \\ {0,\,\,\,\,{\tau } > \left( {{{t}_{2}} - {{t}_{1}}} \right).} \end{array}} \right.$Корректный расчет переходного излучения требует отдельного рассмотрения.
Следует заметить, что после обзора [15] появился ряд работ в Акустическом журнале, посвященных переходному излучению и задачам с подвижными границами (см., например, [16–20]). Среди них отметим классическую работу В.Л. Гинзбурга [19], напечатанную с разрешения автора в Юбилейном выпуске, посвященном 50‑летию Акустического журнала.
Работа поддержана грантом РФФИ 19-29-06048.
Список литературы
Весницкий А.И. Волны в системах с движущимися границами и нагрузками. М.: Физматлит, 2001. 320 с.
Поздеев В.А. Нестационарные волновые поля в областях с подвижными границами. Киев: Наукова Думка, 1991. 244 с.
Болотовский Б.М., Столяров С.Н. Отражение света от движущегося зеркала и родственные задачи // УФН. 1989. Т. 159. № 1. С. 155–180.
Блохинцев Д.И. Акустика неоднородной движущейся среды (2-е изд.). М.: Наука, 1981. 208 с.
Осташев В.Е. Распространение звука в движущихся средах. М., Наука, 1992. 206 с.
Корольков А.И., Князева К.С., Шуруп А.С. Теоретические и экспериментальные исследования корреляционных характеристик сигналов, отраженных вращающимся винтом // Акуст. журн. 2020. Т. 66. № 6. С. 681–689.
Руденко О.В. Нелинейное искажение волн, возбуждаемых в линейной среде конечными хаотическими колебаниями поршня // Докл. Акад. наук. 1998. Т. 360. № 6. С. 759–761.
Руденко О.В. Нелинейные взаимодействия регулярных и шумовых спектров при формировании интенсивного излучения поршнем в линейной среде // Акуст. журн. 1998. Т. 44. № 6. С. 823–828.
Абрамовиц М., Стиган И. Справочник по специальным функциям с формулами, графиками и математическими таблицами. М.: Наука, 1979. 832 с.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971. 1108 с.
Островский Л.А. Некоторые “парадоксы движущихся границ” в электродинамике // УФН. 1975. Т. 116. № 2. С. 315–326.
Гинзбург В.Л., Франк И.М. Излучение равномерно движущегося электрона, возникающее при его переходе из одной среды в другую // ЖЭТФ. 1946. Т. 16. № 1. С. 15–28.
Руденко О.В. Виталий Лазаревич Гинзбург – лауреат нобелевской премии // Акуст. журн. 2004. Т. 50. № 3. С. 293–297.
Денисов С.П. Переходное излучение: научное значение и практическое применение в физике высоких энергий // УФН. 2007. Т. 177. № 4. С. 394–396.
Павлов В.И., Сухоруков А.И. Переходное излучение акустических волн // УФН. 1985. Т. 147. № 1. С. 84–115.
Павлов В.И., Харин О.А., Холодова С.В. Переходное излучение акустических волн источником, движущимся вблизи локально реагирующей поверхности // Акуст. журн. 1991. Т. 37. № 5. С. 978–983.
Павлова Е.В., Харин О.А. Акустическое переходное излучение от источников, пересекающих хаотический экран // Акуст. журн. 1992. Т. 38. № 5. С. 911–915.
Поздеев В.А. Влияние подвижности возмущающей границы и нелинейности среды на волновое поле, вызванное нестационарным движением плоского поршня // Акуст. журн. 1995. Т. 41. № 1. С. 164–165.
Гинзбург В.Л. Излучение равномерно движущихся источников (эффект Вавилова–Черенкова, переходное излучение и некоторые другие явления) // Акуст. журн. 2005. Т. 51. № 1. С. 24–36.
Ерофеев В.И., Колесов Д.А., Лисенкова Е.Е. Особенности генерации волн источником, движущимся по одномерной гибкой направляющей, лежащей на упруго-инерционном основании // Акуст. журн. 2016. Т. 62. № 6. С. 539–647.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал