Акустический журнал, 2020, T. 66, № 6, стр. 613-621
Об адиабатическом распространении звука в мелком море с изогнутым подводным каньоном
М. С. Казак a, *, П. С. Петров a, **
a Федеральное государственное бюджетное учреждение науки Тихоокеанский океанологический институт
им. В.И. Ильичева ДВО РАН
690041 Владивосток, ул. Балтийская 43, Россия
* E-mail: kazak.ms@poi.dvo.ru
** E-mail: petrov@poi.dvo.ru
Поступила в редакцию 15.05.2020
После доработки 28.06.2020
Принята к публикации 07.07.2020
Аннотация
Рассматривается модельная задача о распространении звука в мелком море с изогнутым подводным каньоном. Каньон представляет собой кольцевидную неоднородность дна, наличие которой ведет к фокусировке звуковых волн в области над каньоном. Эта фокусировка является проявлением эффекта горизонтальной рефракции звука. В работе описана методика расчета акустического поля для волновода с неоднородностью такого типа, а также исследована геометрия горизонтальных лучей, захваченных каньоном. Методика основана на разделении переменных в уравнениях для модовых амплитуд и представлении решения в виде двойного ряда. Она имеет весьма общий характер и может быть использована для расчетов поля в любой задаче, где волновод имеет вращательную симметрию. Кроме того, установлено, какие члены этого ряда соответствуют горизонтальным лучам, сфокусированным над каньоном.
ВВЕДЕНИЕ
В настоящее время исследование трехмерных эффектов распространения звука в океане, а также разработка математических моделей, позволяющих выполнять расчет акустического поля с учетом этих эффектов, составляют одно из важнейших направлений в подводной акустике [1]. Такие эффекты, как правило, представляют собой различные проявления горизонтальной рефракции звука [2–4], т.е. явления искривления горизонтальных лучей (соответствующих вертикальным модам). Следствиями такого искривления могут быть, например, деформация волновых фронтов или локализация акустической энергии в некоторой части акватории.
Соответствующие эффекты рассматривались во многих теоретических и экспериментальных работах. Отметим, например, статью [5], в которой рассмотрена фокусировка звука над прямым подводным каньоном и формируемая им модовая структура в горизонтальной плоскости. В работе [6] исследована ситуация, когда акустическая энергия канализируется между двумя искривленными фронтами внутренних волн. Наконец, в недавней работе [7] показано, что в области мелкого моря с чашеобразным рельефом дна могут формироваться акустические волны особого типа, локазизованные в окрестности искривленной изобаты.
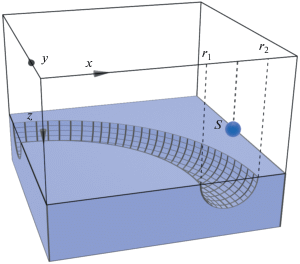
В настоящем исследовании рассматривается задача, которая в некотором смысле схожа с описанными в упомянутых выше работах. Будет рассматриваться распространение звука в волноводе мелкого моря с изогнутым подводным каньоном (см. схематическое изображение на рис. 1). В рамках данного исследования будем предполагать, что каньон имеет кольцевидную форму, т.е. является замкнутым и симметричным относительно вращений в горизонтальной плоскости относительно центра его кривизны. Хотя этот случай может показаться очень экзотическим и частным, из описания методики расчета поля будет ясно, что она применима для любого волновода с вращетельной симметрией, например, при наличии в дне чашеобразного углубления или при расчете распространения звука в волноводе глубокого океана в присутствии синоптического вихря. Заметим, что если каньон не образует полного кольца (например, если его проекция на горизонтальную плоскость представляет собой некоторый сектор кольца), то сфокусированная им компонента звукового поля может быть рассчитана по методу, описанному в работе [7]. В настоящей работе мы рассчитаем полное звуковое поле, состоящее как из расходящихся в горизонтальных направлениях волн, так и из волн, захваченных каньоном.
ПОСТАНОВКА ЗАДАЧИ И МОДОВОЕ ПРЕДСТАВЛЕНИЕ РЕШЕНИЯ
В этом разделе рассматривается общая методика расчета звукового поля в волноводе мелкого моря с вращательной симметрией в адиабатическом приближении. Она основана на модовом представлении поля и на решении несвязанных уравнений для модовых амплитуд (отделение уравнений друг от друга оказывается возможным благодаря отбрасыванию членов, описывающих взаимодействие мод). Тем не менее, расчеты такого рода, насколько нам известно, ранее не применялись в задачах акустики океана.
Рассмотрим трехмерное уравнение Гельмгольца
(1)
$\begin{gathered} \frac{1}{r}{{\left( {r{{P}_{r}}} \right)}_{r}} + \frac{1}{{{{r}^{2}}}}{{P}_{{{\theta \theta }}}} + {{P}_{{zz}}} + \frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}P = \\ = - \frac{1}{r}\delta \left( {r - {{r}_{s}}} \right)\delta \left( {\theta - {{\theta }_{s}}} \right)\delta \left( {z - {{z}_{s}}} \right) \\ \end{gathered} $Батиметрия в волноводе мелкого моря, показанном на рис. 1, описывается соотношением
где H0 – глубина моря вдали от каньона (“невозмущенная” глубина), $\delta H$ – глубина каньона, V(r) – функция, описывающая форму поперечного сечения каньона (радиальный профиль возмущения глубины), такая что max(V(r)) = 1. Мы будем считать, что носителем функции V(r) является отрезок [r1, r2], т.е. что горизонтальной проекцией каньона является кольцо с границами r = r1 и r = r2.На поверхности океана, как обычно, мы ставим условие Дирихле (условие мягкой границы)
На границе раздела вода–дно z = H(r, θ) поставим условия непрерывности акустического давления и нормальной компоненты колебательной скорости, которые имеют вид
(5)
${{\left( {\frac{1}{\rho }\frac{{\partial P}}{{\partial {\mathbf{n}}}}} \right)}_{ + }} = {{\left( {\frac{1}{\rho }\frac{{\partial P}}{{\partial {\mathbf{n}}}}} \right)}_{ - }},$Для того чтобы исключить появление непрерывного спектра, ограничим расчетную область снизу плоскостью z = Hmax. На этой границе потребуем выполнения условия Дирихле (условия мягкой границы)
В целях обеспечения единственности решения краевой задачи для уравнения Гельмгольца (1) потребуем также выполнения условия излучения [1] при
Решение краевой задачи для уравнения Гельмгольца (1) с граничными условиями (3), (6) и условиями на границе раздела (4), (5) будем искать в виде модового разложения
(7)
$P\left( {r,\theta ,z} \right) = \sum\limits_{j = 1}^N {{{A}_{j}}\left( {r,\theta } \right)} {{\phi }_{j}}\left( {z,r,\theta } \right),$(8)
$\left\{ {\begin{array}{*{20}{l}} {{{\phi }_{{zz}}} + \frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}\phi - {{k}^{2}}\phi = 0,} \\ {\phi \left( 0 \right) = 0,} \\ {\phi \left( {{{H}_{{{\text{max}}}}}} \right) = 0,} \\ {{{\phi }^{ + }} = {{\phi }^{ - }},} \\ {\frac{1}{{{{\rho }^{ + }}}}\phi _{z}^{ + } = \frac{1}{{{{\rho }^{ - }}}}\phi _{z}^{ - },} \end{array}} \right.$После подстановки (7) в уравнение (1) получаем
(9)
$\begin{array}{*{20}{c}} \begin{gathered} \frac{1}{r}{{\left( {r{{{\left( {\sum\limits_{j = 1}^N {{{A}_{j}}\left( {r,\theta } \right){{\phi }_{j}}\left( {r,\theta ,z} \right)} } \right)}}_{r}}} \right)}_{r}} + \\ + \,\,\frac{1}{{{{r}^{2}}}}{{\left( {\sum\limits_{j = 1}^N {{{A}_{j}}\left( {r,\theta } \right){{\phi }_{j}}\left( {r,\theta ,z} \right)} } \right)}_{{{\theta \theta }}}} + \\ \end{gathered} \\ \begin{gathered} + \,\,{{\left( {\sum\limits_{j = 1}^N {{{A}_{j}}\left( {r,\theta } \right){{\phi }_{j}}\left( {r,\theta ,z} \right)} } \right)}_{{zz}}} + \\ + \,\,\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}\sum\limits_{j = 1}^N {{{A}_{j}}\left( {r,\theta } \right){{\phi }_{j}}\left( {r,\theta ,z} \right)} = \\ \end{gathered} \\ { = - \frac{1}{r}\delta \left( {r - {{r}_{s}}} \right)\delta \left( {\theta - {{\theta }_{s}}} \right)\delta \left( {z - {{z}_{s}}} \right)~.} \end{array}$В условиях данной задачи, очевидно, функции ${{\phi }_{m}}\left( {z,r} \right)$ зависят только от горизонтальной переменной r (как от параметра).
После применения оператора $\int {( \cdot )} \frac{1}{\rho }{{\phi }_{j}}(r,\theta ,z)dz$ (где ρ(z) – зависимость плотности от глубины) к последнему уравнению и упрощения полученных выражений с помощью условия нормировки собственных функций
(10)
$\begin{gathered} \frac{{{{\partial }^{2}}{{A}_{j}}\left( {r,\theta } \right)}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{A}_{j}}\left( {r,\theta } \right)}}{{\partial r}} + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}{{A}_{j}}\left( {r,\theta } \right)}}{{\partial {{\theta }^{2}}}} + \\ + \,\,{{A}_{j}}\left( {r,\theta } \right)k_{j}^{2} = - \frac{1}{r}\frac{{{{\phi }_{j}}\left( {r,\theta ,{{z}_{s}}} \right)}}{\rho }\delta \left( {r - {{r}_{s}}} \right)\delta \left( {\theta - {{\theta }_{s}}} \right), \\ \end{gathered} $СТРУКТУРА ПОЛЯ В ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ: МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
Решение уравнения горизонтальной рефракции в случае волновода, обладающего вращательной симметрией, естественно искать с помощью метода разделения переменных. Рассмотрим однородный аналог уравнения (10)
(11)
$\begin{gathered} \frac{{{{\partial }^{2}}{{A}_{j}}\left( {r,\theta } \right)}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{A}_{j}}\left( {r,\theta } \right)}}{{\partial r}} + \\ + \,\,\frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}{{A}_{j}}\left( {r,\theta } \right)}}{{\partial {{\theta }^{2}}}} + {{A}_{j}}\left( {r,\theta } \right)k_{j}^{2} = 0 \\ \end{gathered} $Подставим это выражение в уравнение (11) и выполним разделение переменных, разделив полученное равенство на Q(r)ψ(θ) и умножив на r2:
(12)
$\frac{1}{Q}\left( {{{r}^{2}}\frac{{{{\partial }^{2}}\psi }}{{\partial {{r}^{2}}}} + rQ{{k}^{2}}} \right) + \frac{1}{\psi }\frac{{{{\partial }^{2}}\psi }}{{\partial {{\theta }^{2}}}} = 0.$Оставляя в (12) слагаемые, зависящие от r, в левой стороне уравнения, и перенося слагаемые, зависящие от θ, в правую сторону, получаем
(13)
$\frac{1}{Q}\left( {{{r}^{2}}\frac{{{{\partial }^{2}}\psi }}{{\partial {{r}^{2}}}} + rQ{{k}^{2}}} \right) = - \frac{1}{\psi }\frac{{{{\partial }^{2}}\psi }}{{\partial {{\theta }^{2}}}}.$Поскольку величина в левой части уравнения зависит только от r, а в правой – только от θ, обе они равны некоторой постоянной a2 (постоянная разделения). Тогда получим следующее уравнение для азимутальной компоненты частного решения $\psi \left( \theta \right)$
Добавляя к данному уравнению граничные условия и условие периодичности при θ = ±π, получаем “азимутальную” задачу Штурма–Лиувилля (ШЛ), где a2 есть спектральный параметр. Заметим, что на этом этапе обнаруживается принципиальное отличие описываемой здесь процедуры решения от метода построения поля шепчущей галереи в работе [7], где решалась задача ШЛ по радиальной координате.
Нетрудно заметить, что собственные значения задачи ШЛ для уравнения (14) с условиями периодичности суть $a_{m}^{2} = {{m}^{2}},$ m = 0, 1, 2,… Для каждого собственного значения m2 существуют две линейно независимых собственных функции, а именно: $\psi _{m}^{0}(\theta )$ = $\frac{1}{{\sqrt \pi }}\cos (m\theta )$ и $\psi _{m}^{1}(\theta )$ = $\frac{1}{{\sqrt \pi }}\sin (m\theta )$ (значение верхнего индекса 0 относится к косинусам, а 1 – к синусам). Для удобства будем полагать, что θs = 0 (очевидно, это не ограничивает общность). В этом предположении решение Am будет представлять собой суперпозицию $\left\{ {\psi _{m}^{0}} \right\},$ так как $\psi _{m}^{1}(0)$ = 0 при всех m.
Решение уравнения (10), таким образом, представимо в виде разложения
(15)
${{A}_{j}}\left( {r,\theta } \right) = \mathop \sum \limits_{m = 0}^{{{N}_{\theta }}} {{Q}_{{j,m}}}\left( r \right){{\psi }_{m}}\left( \theta \right) .$Подставляя суперпозицию гармоник (15) в уравнение (10), получаем
Пользуясь тем, что $\frac{{{{\partial }^{2}}{{\psi }_{m}}}}{{\partial {{\theta }^{2}}}}$ = –m2ψm, упростим последнее равенство, после чего применим к обеим его частям оператор $\int {( \cdot )} {{\psi }_{m}}(\theta )d\theta .$ Воспользовавшись ортогональностью системы собственных функций $\psi _{m}^{0}(\theta ),$ получим уравнения для радиальных компонент решения Qj,m(r)
(16)
$\begin{gathered} \frac{{{{\partial }^{2}}{{Q}_{{j,m}}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{Q}_{{j,m}}}}}{{\partial r}} + {{Q}_{{j,m}}}k_{j}^{2} - \frac{{{{m}^{2}}}}{{{{r}^{2}}}}{{Q}_{{j,m}}} = \\ = - \frac{1}{r}\frac{{{{\phi }_{m}}\left( {r,{{z}_{s}}} \right)}}{\rho }\delta \left( {r - {{r}_{s}}} \right){{\psi }_{m}}\left( 0 \right). \\ \end{gathered} $Вне отрезка [r1, r2] уравнение (16) имеет постоянные коэффициенты и фактически сводится к уравнению Бесселя. Из условия ограниченности решения при r = 0 мы делаем вывод, что при r ≤ r1 оно должно с точностью до константы представлять собой функцию Бесселя
(17)
${{Q}_{{jm}}}\left( r \right) = {{\alpha }_{{jm}}}{{J}_{m}}\left( {{{k}_{j}}r} \right)~~~{\text{при}}~~~r \leqslant {{r}_{1}}.$В то же время из условия излучения на бесконечности следует, что при r ≥ r2 решение должно обращаться в функцию Ганкеля первого рода, т.е.
(18)
${{Q}_{{jm}}}\left( r \right) = {{\beta }_{{jm}}}H_{m}^{{\left( 1 \right)}}\left( {{{k}_{j}}r} \right)~~~{\text{при}}~~~r \geqslant {{r}_{2}}.$Теперь осталось лишь найти значения функции Qj,m(r) на отрезке [r1, r2]. С этой целью составим нормальную систему, эквивалентную уравнению (16)
(19)
$\left\{ {\begin{array}{*{20}{l}} {\frac{{d{{Q}_{{jm}}}}}{{dr}} = {{P}_{{jm}}},} \\ {\frac{{d{{P}_{{jm}}}}}{{dr}} = - \frac{1}{r}{{P}_{{jm}}} + \left( {\frac{{{{m}^{2}}}}{{{{r}^{2}}}} - k_{j}^{2}} \right){{Q}_{{jm}}}.} \end{array}} \right.~$Решение этой системы может быть найдено методом двустороннего численного интегрирования. Сначала мы решаем ее на отрезке [r1, rs], начиная с точки r = r1 и используя начальное условие
(20)
$\left\{ {\begin{array}{*{20}{l}} {{{Q}^{0}}\left( {{{r}_{1}}} \right) = {{J}_{m}}\left( {{{k}_{j}}{{r}_{1}}} \right),} \\ {{{P}^{0}}\left( {{{r}_{1}}} \right) = d{{J}_{m}}\left( {{{k}_{j}}r} \right)/dr{{|}_{{r = {{r}_{1}}}}},} \end{array}} \right.~$(21)
$\left\{ {\begin{array}{*{20}{l}} {{{Q}^{0}}\left( {{{r}_{2}}} \right) = H_{m}^{{\left( 1 \right)}}\left( {{{k}_{j}}{{r}_{2}}} \right),} \\ {{{P}^{0}}\left( {{{r}_{2}}} \right) = dH_{m}^{{\left( 1 \right)}}\left( {{{k}_{j}}r} \right)/dr{\kern 1pt} {{|}_{{r = {{r}_{2}}}}},} \end{array}} \right.~$Наличие в правой части (16) дельта-функции (источника, сосредоточенного при r = rs) эквивалентно тому, что решения системы (19) удовлетворяют следующим условиям
(22)
$\left\{ {\begin{array}{*{20}{l}} {{{\beta }_{{jm}}}{{Q}^{{{\text{right}}}}} - {{\alpha }_{{jm}}}{{Q}^{{{\text{left}}}}} = 0,} \\ {{{\beta }_{{jm}}}{{P}^{{{\text{right}}}}} - {{\alpha }_{{jm}}}{{P}^{{{\text{left}}}}} = - \frac{{{{\phi }_{m}}\left( {{{z}_{s}}} \right)}}{{{{r}_{s}}}}} \end{array}} \right.~,$Равенства (22) образуют систему линейных алгебраических уравнений, из которой легко определить коэффициенты αjm и ${{\beta }_{{jm}}}$ и, таким образом, найти вид решения (16) на отрезке [r1, rs].
ПРИМЕР РАСЧЕТА ЗВУКОВОГО ПОЛЯ
Рассмотрим в качестве примера двухслойный волновод мелкого моря, глубина которого без учета каньона составляет H0 = 90 м, скорости звука принимают значения cw = 1500 м/с и cb = 2000 м/с в водном слое и дне соответственно, а плотности в этих в этих средах равны ρw = 1 г/см3, ρb = 2 г/см3. Пусть точечный источник с частотой f = 50 Гц располагается на глубине z = zs = 10 м и на удалении rs = 5000 м от оси симметрии каньона. Глубину каньона в нашем примере мы примем равной δH = 10 м, а его радиальный профиль на отрезке [r1, r2] зададим формулой
Таблица 1.
Таблица зависимости волновых чисел от глубины
| h, м | ${{k}_{1}}$ | ${{k}_{2}}$ | ${{k}_{3}}$ | ${{k}_{4}}$ |
|---|---|---|---|---|
| 90 | 0.2072 | 0.2003 | 0.1877 | 0.1682 |
| 92 | 0.2073 | 0.2007 | 0.1886 | 0.1700 |
| 94 | 0.2074 | 0.2010 | 0.1895 | 0.1717 |
| 96 | 0.2075 | 0.2013 | 0.1903 | 0.1733 |
| 98 | 0.2076 | 0.2016 | 0.1910 | 0.1747 |
| 100 | 0.2076 | 0.2019 | 0.1917 | 0.1761 |
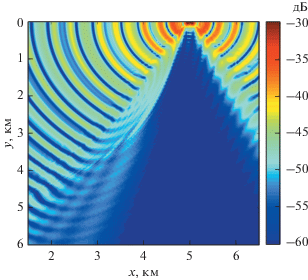
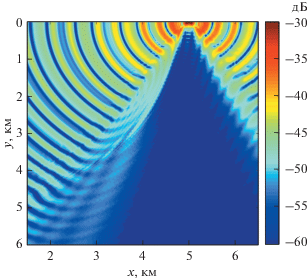
На рис. 2 и 3 показаны графики уровней акустического поля при ${{N}_{\theta }} = 800$ и ${{N}_{\theta }} = 1200$ (в дБ отн. уровня в 1 м от источника). Видно, что первые 800 членов ряда (15) (рис. 2) описывают компоненты поля, для которых волновые векторы образуют достаточно большие углы с касательной к окружности вида r = const, в то время как для захваченных каньоном волн волновые числа не превышают некоторых критических значений (они будут вычислены в следующих разделах). Интерференционная картина поля, представленная на рис. 3, стабилизируется, начиная с значения Nθ = 900. Таким образом, фактически при расчете поля во всех случаях достаточно суммирования лишь конечного числа членов ряда (15), однако это число зависит от rs. На рис. 3 хорошо видно, что часть акустической энергии источника фокусируется над каньоном, причем можно заметить, что поле в этой области имеет выраженную модовую структуру в горизонтальной плоскости.
Рис. 2.
Уровни акустического давления (в дБ отн. 1 м от источника), 4 вертикальные моды, Nθ = 800. Видно, что при суммировании такого количества членов ряда (15) в решение входят только волны Qm,n(r)ψn(θ), для которых отношение тангенциальной и радиальной компонент волнового вектора (см. ниже) достаточно мало.
Интeресно также отметить, что помимо фокусировки над каньоном наблюдается еще один эффект, связанный с горизонтальной рефракцией. Он заключается в формировании узкого пучка, распространяющегося в направлении, близком к касательному к окружности r = rs (более точно, пучок направлен из точки x = 5 км, y = 0 в точку x = 4 км, y = 6 км). Уровень акустического поля в этом пучке заметно превышает уровни, формируемые источником в других направлениях на том же расстоянии от точки излучения. Забегая вперед, отметим, что такому пучку соответствуют горизонтальные лучи, которые выходят из источника под углами относительно касательной к r = rs, близкими к нулю, но все же превышающими критический угол, при котором осуществляется их захват каньоном.
ГОРИЗОНТАЛЬНЫЕ ЛУЧИ И ОЦЕНКА ДОЛИ АКУСТИЧЕСКОЙ ЭНЕРГИИ, ФОКУСИРУЕМОЙ КАНЬОНОМ
Исследуем свойства решения краевой задачи для уравнения (10) с использованием теории горизонтальных лучей. Здесь и далее будем предполагать номер моды j фиксированным и опускать соответствующий нижний индекс во всех выражениях.
Модовые амплитуды Am в лучевом приближении представляются в виде
Для нахождения траектории лучей введем в рассмотрение касательные к ним векторы e = (er, eθ) = = ∇⊥S, где er и ${{e}_{{\theta }}}$ суть радиальная и тангенциальная компоненты данного вектора.
Система уравнений Гамильтона для лучевых траекторий имеет вид [8]
(24)
$\begin{gathered} \frac{{dr}}{{d\tau }} = {{e}_{r}},\,\,\,\frac{{d{{e}_{r}}}}{{d\tau }} = n\frac{{dn}}{{dr}} + \frac{1}{r}{{e}_{\theta }}^{2}, \\ \frac{{d\theta }}{{d\tau }} = \frac{1}{r}{{e}_{\theta }},\,\,\,\frac{{d{{e}_{\theta }}}}{{d\tau }} = - \frac{1}{r}{{e}_{r}}{{e}_{\theta }}, \\ \end{gathered} $(25)
$rn\left( r \right){\text{sin}}\left( {\chi \left( r \right)} \right) = {\text{const}} = \sigma ,$(26)
$\theta = \theta \left( r \right) = \int {\frac{\sigma }{{r\sqrt {{{n}^{2}}{{r}^{2}} - {{\sigma }^{2}}} }}} dr.$В первую очередь нас будут интересовать лучи, захваченные волноводом в горизонтальной плоскости, который формируется в связи с наличием подводного каньона (см. рис. 4). Для захваченных лучей характерно наличие точек заворота r = $r_{1}^{t}$ и r = $r_{2}^{t},$ лежащих внутри кольца r1 ≤ r ≤ r2. Так как в точках заворота sin(χ) = 1, то для луча, выходящего из источника под углом χ = χs, при r = rs из закона Снеллиуса получается следующее равенство
(27)
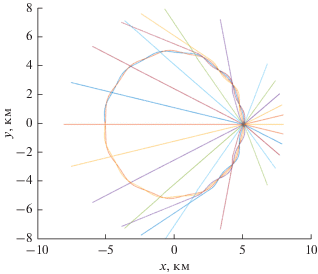
${{r}_{s}}{{k}_{j}}\left( {{{r}_{s}}} \right){\text{sin}}\left( {{{\chi }_{s}}} \right) = r_{l}^{t}{{k}_{j}}\left( {r_{l}^{t}} \right),$Рис. 4.
Горизонтальные лучи для четвертой вертикальной моды (j = 4). На рисунке хорошо видна группа захваченных каньоном лучей, описывающих полный круг, а также обычные лучи, для которых наблюдается расходимость. Кроме того, имеется группа лучей, образующих пучок с малой расходимостью, направленный вдоль касательной к окружности.
Рассмотрев график функции rkj(r), представленный (для j = 4) на рис. 5в, можно получить из последнего соотношения следующее неравенство для захваченных каньоном лучей
(28)
$\cos {{\alpha }_{s}} = \frac{{r_{l}^{t}{{k}_{j}}\left( {r_{l}^{t}} \right)}}{{{{r}_{s}}{{k}_{j}}\left( {{{r}_{s}}} \right)}} > \frac{{{{r}_{l}}{{k}_{j}}\left( {{{r}_{l}}} \right)}}{{{{r}_{s}}{{k}_{j}}\left( {{{r}_{s}}} \right)}}\,\,\,{\text{для}}\,\,\,l = 1,2.$Рис. 5.
(а) – График объема захватываемой каньоном энергии в зависимости от расположения источника; (б) – график глубины каньона; (в) – график функции $r{{k}_{j}}(r)$ при j = 4.
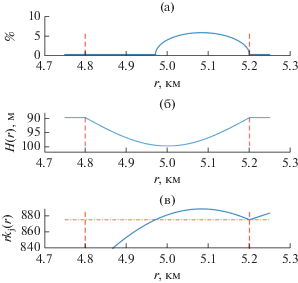
Каньоном захватываются только лучи с углами выхода из источника αs, для которых одновременно выполняются условия αs < αs, 1 и αs < αs, 2, где по определению
Отметим, что из рис. 5 видно, что первое неравенство является заведомо менее ограничительным, чем второе. Таким образом, долю D акустической энергии источника, переносимой данной модой и захваченной каньоном, можно оценить по формуле
Действительно, D совпадает с отношением углового сектора, заполняемого захваченными лучами (очевидно, что он равен 4αs, 2), к общей угловой мере 2π семейства лучей, выходящих из источника. Оценка этой величины в зависимости от радиальной координаты rs точки излучения показана на рис. 5а (все значения параметров – такие же, как в предыдущем разделе). Видно, что в этом случае в толще воды непосредственно над каньоном фокусируется около 5% энергии, переносимой четвертой водной модой.
СВЯЗЬ ГОРИЗОНТАЛЬНЫХ ЛУЧЕЙ С ЧЛЕНАМИ РЯДА В РАЗЛОЖЕНИИ МОДОВЫХ АМПЛИТУД
Пусть rmax – точка, в которой функция rk(r) имеет максимум (см. рис. 5). Тогда из закона Снеллиуса (25) следует, что самый большой угол α между некоторым захваченным лучом и касательной к окружности в данной точке будет именно при r = rmax. Для этого угла α(rm) будет выполняться пара неравенств
(30)
${{r}_{{{\text{max}}}}}k\left( {{{r}_{{{\text{max}}}}}} \right) > \cos \alpha \left( {{{r}_{{{\text{max}}}}}} \right){{r}_{{{\text{max}}}}}k\left( {{{r}_{{{\text{max}}}}}} \right) > {{k}_{{{\text{min}}}}}{{r}_{2}}.$Далее, волны вида cos(nθ)Qn(r) по азимутальной переменной являются стоячими, причем
Таким образом, n = rk(r)cos α(r) = rmaxk(rmax) × × cos α(rmax). Иными словами, лучевой инвариант Снеллиуса σ в волновой интерпретации и есть число n, определяющее зависимость компоненты решения от угловой переменной.
Из неравенства (30), которому удовлетворяют захваченные каньоном горизонтальные лучи, следует, что номера n соответствующих им компонент решения лежат в интервале
(31)
${{k}_{{{\text{min}}}}}{{r}_{2}} < n < {{r}_{{{\text{max}}}}}k\left( {{{r}_{{{\text{max}}}}}} \right).$В рассматриваемом нами примере максимальное значение функции rk4(r) на интервале [r1, r2] достигается в точке rmax = 5082 м и составляет rmaxk4(rmax) = 887.9959 (см. рис. 5в). Нижняя граница номеров n, соответствующих захваченным лучам, есть kminr2 = 874.6199. Таким образом, на основании этих данных неравенство (31) для рассматриваемой задачи выглядит следующим образом
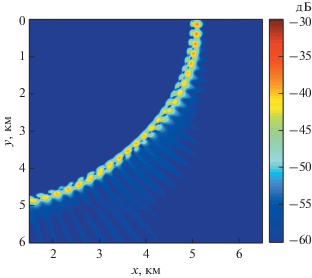
На рис. 6 показаны графики функций Q4,m(r). Видно, что энергия соответствующих компонент решения Q4,m(r)ψm(θ) локализована в горизонтальной плоскости в относительно узком кольце, являющемся проекцией “внешней” половины каньона. Контурный график акустического поля, формируемого этими компонентами, отдельно показан на рис. 7.
ЗАКЛЮЧЕНИЕ И ВЫВОДЫ
В настоящей работе изложена методика расчета звуковых полей в волноводах мелкого моря с симметрией относительно вращений в горизонтальной плоскости в случае, когда источник не находится в центре симметрии. Расчеты проведены в адиабатическом приближении, т.е. пренебрегается взаимодействием мод. В дальнейшем изложенная здесь методика будет расширена на случаи, когда взаимодействием мод пренебречь нельзя, в частности, на волноводы с такими вариациями глубины, которые приводят к отсечке одной или нескольких водных мод. С теоретической точки зрения такое обобщение почти очевидно, и вместо нормальной системы (19) просто получим связанную систему из 2N связанных обыкновенных дифференциальных уравнений, а условие согласования (22) сведется к решению системы линейных уравнений с 2N неизвестными. Такая процедура построения Qm(r), однако, приводит к некоторым вычислительным сложностям (в частности, матрица в аналоге системы (22) оказывается плохо обусловленной) и нуждается в регуляризации, которая выходит за рамки настоящей работы.
Изложенная здесь методика является весьма общей и может быть, например, использована для расчета рассеяния акустических волн на самых разных трехмерных неоднородностях скорости звука (например, синоптических вихрях) и рельефа дна (подводных горах, банках и т.п.).
Заметим также, что изложенный здесь подход в некоторых аспектах схож с методами расчета звукового поля, рассеянного подводной горой, предложенными в работах [9, 10]. Однако, в отличие от их авторов, мы уделяем особое внимание установлению связи между отдельными элементами разложения модовых амплитуд по гармоникам вида Q(r)ψ(θ) с физическими свойствами описываемых ими волн. Мы также устанавливаем связь этих компонент звукового поля некоторой моды с соответствующими ей горизонтальными лучами, что, в частности, позволяет нам получить простую лучевую оценку доли акустической энергии, сфокусированной в водном слое непосредственно над подводным каньоном. Несмотря на очевидную идеализацию в рассмотренной нами постановке задачи, выражающуюся в замкнутости каньона, лучевая оценка (29) остается справедливой и в случае каньона с открытыми концами (например, если его проекция на плоскость (x, y) представляет собой половину кольца).
Подчеркнем еще раз связь нашей работы с недавней статьей [7]. Глядя на рис. 5в, внимательный читатель легко заметит, что внутренняя граница каньона r = r1 фактически не принимает участия в фокусировке звукового поля, и его локализация происходит в кольце между r = r2 и второй точкой пересечения штрихпунктирной горизонтальной линии с графиком функции rk(r). По-видимому, в большинстве случаев, которые можно представить, эта точка будет находиться правее границы r = r1, и, таким образом, захваченные каньоном лучи в таких случаях будут фактически лучами шепчущей галереи [7].
Работа выполнена в рамках темы госзадания ТОИ ДВО РАН “Математическое моделирование и анализ динамических процессов в океане” (№ 0271-2019-0001) и поддержана грантами РФФИ 18-05-00057_а и 18-35-20081_мол_а_вед. Авторы также признательны д-ру А.В. Цветковой (ИПМех РАН) и рецензентам работы за ряд предложенных поправок, которые позволили существенно ее улучшить.
Список литературы
Jensen F.B., Kuperman W.A., Porter M.B., Schmidt H. Computational ocean acoustics. SpringerScience&BusinessMedia, 2011.
Кацнельсон Б.Г., Бади М., Линч Дж. Горизонтальная рефракция звука в мелком море и ее экспериментальные наблюдения // Акуст. журн. 2007. Т. 53. № 3. С. 362–376.
Кацнельсон Б.Г., Пересёлков С.А. Горизонтальная рефракция низкочастотного звукового поля, вызванная солитонами внутренних волн в мелководном волноводе // Акуст. журн. 2000. Т. 46. № 6. С. 779.
Katsnelson B., Petnikov V. and Lynch J. Fundamentals of shallow water acoustics. Springer Science & Business Media, 2012.
Petrov P.S., Petrova T.N. Asymptotic solution for the problem of sound propagation in a sea with an underwater canyon // J. Acoust. Soc. Am. 2014. V. 136. № 4. P. EL281–EL287.
Lynch J.F., Lin Y.-T., Duda T.F., Newhall A.E. Acoustic ducting, reflection, refraction, and dispersion by curved nonlinear internal waves in shallow water // IEEE J. Oceanic Engineering. 2010. V. 35. № 1. P. 12–27.
Katsnelson B. and Petrov P. Whispering gallery waves localized near circular isobaths in shallow water // J. Acoust. Soc. Am. 2019. V. 146. № 3. P. 1343–1352.
Kravtsov Yu. A. and Orlov Yu. I. Geometrical optics of inhomogeneous media. Spring-Verlag, Berlin, 1990.
Taroudakis M.I. A coupled–mode formulation for the solution of the Helmholtz equation in water in the presence of a conical sea-mount // J. Comp. Acoust. 1996. V. 4. № 01. P. 101–121.
Luo W., Schmidt H. Three-dimensional propagation and scattering around a conical seamount // J. Acoust. Soc. Am. 2009. V. 125. № 1. P. 52–65.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал