Акустический журнал, 2021, T. 67, № 1, стр. 65-71
Эффекты многократного рассеяния акустических мод на анизотропном ветровом волнении в мелком море
М. А. Раевский a, В. Г. Бурдуковская a, *
a Институт прикладной физики РАН
603950 Нижний Новгород, ул. Ульянова 46, БОКС-120, Россия
* E-mail: bvg@appl.sci-nnov.ru
Поступила в редакцию 14.10.2020
После доработки 12.11.2020
Принята к публикации 23.11.2020
Аннотация
Исследовано влияние анизотропии пространственного спектра ветрового волнения на многократное рассеяние акустических мод в рефракционном волноводе. Проанализированы затухание когерентной компоненты модовых амплитуд, изменение их интенсивности и коэффициента пространственной корреляции. Приведены результаты численного моделирования для гидрологических условий Баренцева моря в зимний период. Проведено сравнение результатов для анизотропного спектра ветрового волнения и упрощенной модели с изотропным спектром.
При разработке теоретической модели акустического поля в мелком море необходимо, наряду с эффектами регулярной рефракции и поглощения в донных осадках, учитывать и влияние случайных флуктуаций среды. Поскольку мелководные звуковые каналы частично или полностью открыты к поверхности, одним из основных флуктуационных факторов распространения является многократное рассеяние звука на ветровом волнении. На малых дистанциях влияние ветрового волнения можно учесть в приближении однократного рассеяния [1], но для прогнозирования статистических характеристик акустического поля на протяженных трассах необходимо разрабатывать теорию многократного рассеяния звука в рефракционных волноводах с нерегулярной границей. Несмотря на то, что ветровое волнение обладает высокой степенью анизотропии, ранее эффекты многократного рассеяния акустического поля в волноводе со взволнованной поверхностью изучались в рамках упрощенной модели изотропного ветрового волнения [2–5] (за исключением [6], где анализировался угловой спектр океанических шумов и учитывалась анизотропия волнения). Такое рассмотрение имеет определенный смысл, если прогнозируются энергетические и корреляционные характеристики сигнала, усредненные по направлению ветра. Но при конкретной метеорологической ситуации возникает вопрос о соотношении такого упрощенного подхода и более достоверной модели, учитывающей направление ветра, анизотропию спектра ветрового волнения и, соответственно, анизотропию эффектов многократного рассеяния акустического поля в волноводе.
Рассмотрим акустическое поле, которое создается тональным точечным источником в звуковом канале со взволнованной свободной поверхностью. Волновод предполагается горизонтально однородным с произвольным профилем скорости звука c(z) и плоскослоистой структурой дна. Для акустики мелкого моря наиболее интересен низкочастотный диапазон ($f \leqslant 500$ Гц), когда возможно распространение звука на десятки и даже сотни километров. Поле источника в дальней зоне представим в виде разложения по ортонормированным собственным функциям ${{\varphi }_{p}}\left( z \right)$ невозмущенного волновода:
(1)
$p\left( {r,z,t} \right) = \sum\limits_p {\frac{{{{a}_{p}}{{\varphi }_{p}}\left( z \right)}}{{\sqrt {{{k}_{p}}r} }}} \exp \left[ {i\left( {{{k}_{p}}r - {{\omega }_{0}}t - {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}} \right)} \right],$(2)
$\begin{gathered} \left\langle {p\left( {{{r}_{1}},{{z}_{1}},t} \right)p{\text{*}}\left( {{{r}_{2}},{{z}_{2}},t} \right)} \right\rangle = \sum\limits_{p,q} {\left\langle {{{a}_{p}}\left( {{{r}_{1}},t} \right)a_{q}^{*}\left( {{{r}_{2}},t} \right)} \right\rangle \times } \\ \times \,\,\frac{{{{\varphi }_{p}}\left( {{{z}_{1}}} \right){{\varphi }_{q}}\left( {{{z}_{2}}} \right)}}{{\sqrt {{{k}_{p}}{{k}_{q}}{{r}_{1}}{{r}_{2}}} }}\exp \left[ {i\left( {{{k}_{p}}{{r}_{1}} - {{k}_{q}}{{r}_{2}}} \right)} \right] \\ \end{gathered} $(3)
${{N}_{p}}\left( {\rho ,x} \right) = \left\langle {{{a}_{p}}\left( { - \frac{\rho }{2},x} \right)a_{p}^{*}\left( {\frac{\rho }{2},x} \right)} \right\rangle $(4)
$\begin{gathered} \frac{{\partial {{N}_{p}}\left( {\rho ,x} \right)}}{{\partial x}} = \sum\limits_{{{p}_{2}}} {{{W}_{{p{{p}_{2}}}}}\left( {\rho ,x} \right){{N}_{{{{p}_{2}}}}}\left( {\rho ,x} \right)} - \\ - \,\,2\left( {{{\gamma }_{p}} + \left| {\operatorname{Im} {{k}_{p}}} \right|} \right){{N}_{p}}\left( {\rho ,x} \right). \\ \end{gathered} $Здесь ${{\gamma }_{p}}$ – декремент затухания когерентной компоненты модовой амплитуды $\left\langle {{{a}_{p}}} \right\rangle $, в котором учтено рассеяние энергии данной моды как в другие моды дискретного спектра, так и в моды сплошного спектра, $\operatorname{Im} {{k}_{p}}$ – мнимая часть волнового числа, обусловленная потерями в донном грунте, ${{W}_{{p{{p}_{2}}}}}$ – вероятность перехода между модами, описывающая эффекты взаимного рассеяния мод, локализованных в волноводе. Функции ${{\gamma }_{p}}$ и ${{W}_{{p{{p}_{2}}}}}$ выражаются через частотно-угловой спектр ветрового волнения $B\left( {\Omega ,\theta } \right)$ следующим образом:
(5)
${{\gamma }_{p}} = \frac{{{{g}^{2}}}}{{4{{k}_{p}}}}{{\left( {\frac{{d{{\varphi }_{p}}}}{{dz}}} \right)}^{2}}\int\limits_0^{{{k}_{0}}} {\eta \sqrt {k_{0}^{2} - {{\eta }^{2}}} d\eta } \int\limits_{ - \pi }^\pi {B\left( {\Omega ,\theta } \right){{\Omega }^{{ - 3}}}d\varphi } ,$(6)
$\begin{gathered} \Omega = \sqrt g {{\left[ {{{{\left( {{{k}_{p}} - \eta \cos \varphi } \right)}}^{2}} + {{\eta }^{2}}{{{\sin }}^{2}}\varphi } \right]}^{{\frac{1}{4}}}}, \\ \theta = {\text{arctg}}\left( {\frac{{\eta \sin \varphi }}{{{{k}_{p}} - \eta \cos \varphi }}} \right), \\ \end{gathered} $(7)
$\begin{gathered} {{W}_{{p{{p}_{2}}}}}\left( {\rho ,x} \right) = \frac{{\pi {{g}^{2}}}}{{4{{k}_{p}}{{k}_{{{{p}_{2}}}}}}}{{\left( {\frac{{d{{\varphi }_{p}}}}{{dz}}} \right)}^{2}}{{\left( {\frac{{d{{\varphi }_{{{{p}_{2}}}}}}}{{dz}}} \right)}^{2}} \times \\ \times \,\,\int\limits_{ - \infty }^{ + \infty } {\frac{{B\left( {\tilde {\omega },\Phi } \right)}}{{{{{\tilde {\omega }}}^{3}}}}\cos \left( {{{k}_{y}}\frac{x}{R}\rho } \right)d{{k}_{y}}} , \\ \end{gathered} $(8)
$\tilde {\omega } = \sqrt g {{\left( {k_{y}^{2} + {{{\left( {{{k}_{p}} - {{k}_{{{{p}_{2}}}}}} \right)}}^{2}}} \right)}^{{\frac{1}{4}}}},\,\,\,\,\Phi = {\text{arctg}}\left( {\frac{{{{k}_{y}}}}{{{{k}_{p}} - {{k}_{{{{p}_{2}}}}}}}} \right),$Эмпирические спектры ветрового волнения обычно приводят в виде произведения частотного спектра $S\left( \Omega \right)$ и нормированного на единицу углового спектра $Q\left( {\Omega ,\theta } \right)$. В дальнейшем для частотного спектра $S\left( \Omega \right)$ будем использовать общепринятую модель JONSWAP [9]:
(9)
$\begin{gathered} S\left( \Omega \right) = \beta {{g}^{2}}{{\Omega }^{{ - 5}}}\exp \left[ { - 1.25{{{\left( {\frac{{{{\Omega }_{m}}}}{\Omega }} \right)}}^{4}}} \right] \times \\ \times \,\,{{\gamma }^{{\exp \left[ { - {{{{{\left( {\Omega - {{\Omega }_{m}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {\Omega - {{\Omega }_{m}}} \right)}}^{2}}} {2{{\sigma }^{2}}\Omega _{m}^{2}}}} \right. \kern-0em} {2{{\sigma }^{2}}\Omega _{m}^{2}}}} \right]}}}, \\ \sigma = \left\{ {\begin{array}{*{20}{c}} {0.07\,\,\,\,{\text{при}}\,\,\,\,\Omega \leqslant {{\Omega }_{m}},} \\ {0.09\,\,\,\,{\text{при}}\,\,\,\,\Omega > {{\Omega }_{m}},} \end{array}} \right. \\ \end{gathered} $ $1 \leqslant \gamma \leqslant 3.3$. Для углового распределения $Q\left( {\Omega ,\theta } \right)$ используют [9] аппроксимацию:
$1 \leqslant \gamma \leqslant 3.3$. Для углового распределения $Q\left( {\Omega ,\theta } \right)$ используют [9] аппроксимацию:
(10)
$Q\left( {\Omega ,\theta } \right) = G\left( s \right){{\left[ {\cos \left( {\frac{{\theta - \alpha }}{2}} \right)} \right]}^{{2s}}},$(11)
$G\left( s \right) = \frac{{\Gamma \left( {2s + 1} \right)}}{{{{2}^{{2s + 1}}}{{\Gamma }^{2}}\left( {s + \frac{1}{2}} \right)}},$(12)
$s = \left\{ \begin{gathered} 11.5{{\left( {\frac{g}{V}} \right)}^{{2.5}}}\Omega _{m}^{{ - 7.5}}{{\Omega }^{5}}\,\,\,\,{\text{при}}\,\,\,\,\Omega \leqslant {{\Omega }_{m}}, \hfill \\ 11.5{{\left( {\frac{g}{V}} \right)}^{{2.5}}}{{\Omega }^{{ - 2.5}}}\,\,\,\,{\text{при}}\,\,\,\,\Omega > {{\Omega }_{m}}. \hfill \\ \end{gathered} \right.$В дальнейшем нас будут интересовать три статистические характеристики акустических мод: декремент затухания когерентной компоненты ${{\gamma }_{p}}$, интенсивность ${{n}_{p}}\left( x \right) \equiv {{N}_{p}}\left( {\rho = 0,x} \right)$ и коэффициент корреляции ${{k}_{p}}\left( {\rho ,x} \right) \equiv $ ${{{{N}_{p}}\left( {\rho ,x} \right)} \mathord{\left/ {\vphantom {{{{N}_{p}}\left( {\rho ,x} \right)} {{{N}_{p}}\left( {\rho = 0,x} \right)}}} \right. \kern-0em} {{{N}_{p}}\left( {\rho = 0,x} \right)}}$. Помимо анализа зависимости этих характеристик от угла α (то есть направления ветра по отношению к акустической трассе), проведем также сравнение численных расчетов для развитого ветрового волнения с анизотропным угловым спектром (10)–(12) и изотропного волнения, соответствующего $s \equiv 0$. При этом ввиду очевидной симметрии величин ${{\gamma }_{p}}\left( \alpha \right)$, ${{n}_{p}}\left( {x,\alpha } \right)$ и ${{k}_{p}}\left( {\rho ,x,\alpha } \right)$ относительно замены α на (‑α), анализ достаточно провести в диапазоне углов 0 ≤ α ≤ π.
Численное моделирование выполнено нами для гидрологических условий Баренцева моря в зимний период, т.е. волновода с положительным градиентом скорости звука c(z). Расчеты проведены для волновода с линейным профилем c(z) и параметрами: c(0) = 1490 м/с, c(H) = 1500 м/с, глубина дна H = 200 м. В качестве модели дна выбрано жидкое полупространство с параметрами ${{c}_{l}} = 1600$ м/с, ρ0 = 2 г/см3 и коэффициентом затухания δ = 0.1 дБ/км Гц. Частота излучения f = = 240 Гц, глубина источника zи = 10 м. Анализ проводился для скорости ветра V = 10 м/с и V = 15 м/с, соответствующих умеренному и сильному ветровому волнению. Чтобы продемонстрировать характерные зависимости характеристик от номера акустических мод p, результаты приводятся для мод с номерами p = 1, 10 и 20 (всего в волноводе локализовано 23 моды).
На рис. 1 приведены результаты расчетов декремента затухания когерентной компоненты ${{\gamma }_{p}}\left( \alpha \right)$ для умеренного и сильного ветрового волнения. Чтобы наглядно продемонстрировать влияние анизотропии волнения, результаты нормированы на соответствующие значения для изотропного волнения ($s \equiv 0$). Видно, что угловые зависимости симметричны относительно α = π/2, причем для низших и средних номеров мод декременты максимальны при α = 0, π и минимальны при α = π/2. Для высших мод максимум, наоборот, наблюдается при α = π/2. Следует также отметить, что угловые изменения ${{\gamma }_{p}}\left( \alpha \right)$ максимальны для низших (слабозатухающих) мод. В целом можно сделать вывод об относительно малых отличиях значений ${{\gamma }_{p}}\left( \alpha \right)$ для анизотропной и изотропной моделей (не превышающих в нашем случае 30%). Таким образом, для практических расчетов когерентной компоненты акустического поля можно использовать упрощенную модель изотропного волнения. Чтобы иметь представление об абсолютных значениях коэффициентов затухания когерентной компоненты ${{\gamma }_{p}}\left( \alpha \right)$ и провести их сравнение с коэффициентами затухания мод в донном грунте, на рис. 2 приведены также величины $\operatorname{Im} \left( {{{k}_{p}}} \right)$ и ${{\gamma }_{p}}\left( {s = 0} \right)$, соответствующие изотропной модели рассеяния. Следует при этом отметить, что (за исключением первых шести мод, не проникающих в дно) при скорости ветра V = 10 м/с затухание мод, обусловленное рассеянием на ветровом волнении, сравнимо с потерями в дне, а при скорости ветра V = = 15 м/с на порядок превышает их.
Рис. 1.
Нормированный декремент затухания когерентной компоненты модовых амплитуд при скорости ветра (а) – V = 10 м/с и (б) – V = 15 м/с.
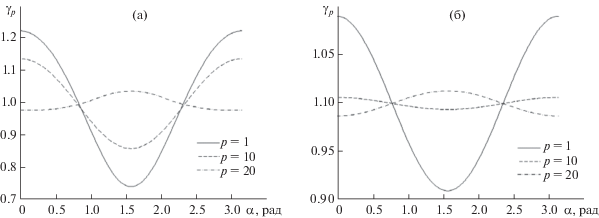
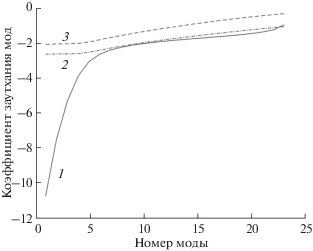
Рис. 2.
Абсолютные значения коэффициентов затухания нормальных мод (в расчете на километр) для изотропной модели рассеяния и коэффициентов затухания мод в донном грунте: кривая 1 – $\lg \left( {\left| {\operatorname{Im} \left( {{{k}_{p}}} \right)} \right|} \right)$, кривая 2 – $\lg \left( {{{\gamma }_{p}}\left( {s = 0} \right)} \right)$ при скорости ветра V = = 10 м/с, кривая 3 – $\lg \left( {{{\gamma }_{p}}\left( {s = 0} \right)} \right)$ при скорости ветра V = 15 м/с.
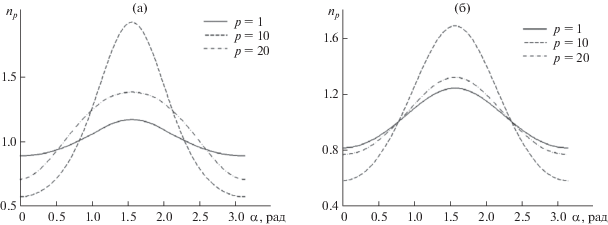
Рассмотрим теперь интенсивности мод ${{n}_{p}}\left( {r,\alpha } \right)$ и коэффициенты поперечной корреляции ${{k}_{p}}\left( {\rho ,r,\alpha } \right)$ для конкретной длины акустической трассы R. При увеличении дистанции эффекты многократного рассеяния, очевидно, проявляются сильнее. Но ввиду сильного затухания сигнала на больших расстояниях приведем основные результаты расчетов для R = 102 км. На рис. 3 приведены угловые зависимости интенсивности мод ${{n}_{p}}\left( \alpha \right)$ при умеренном и сильном ветровом волнении. Они также нормированы на соответствующие значения интенсивности, вычисленные для изотропного волнения ($s \equiv 0$). Видно, что расчетные кривые также симметричны относительно α = π/2. Во всех случаях угловые распределения интенсивности имеют максимум при α = π/2 и, соответственно, минимум при α = 0, π. Угловые изменения для ${{n}_{p}}\left( \alpha \right)$ более выражены, чем для ${{\gamma }_{p}}\left( \alpha \right)$, и могут достигать 5 дБ. Максимальное отличие результатов, рассчитанных для анизотропного и изотропного спектров волнения, составляет 3 дБ, что уже может быть значимым для прикладных задач гидроакустики.
Рис. 3.
Угловая зависимость нормированной интенсивности модовых амплитуд при скорости ветра (а) – V = 10 м/с и (б) – V = 15 м/с.
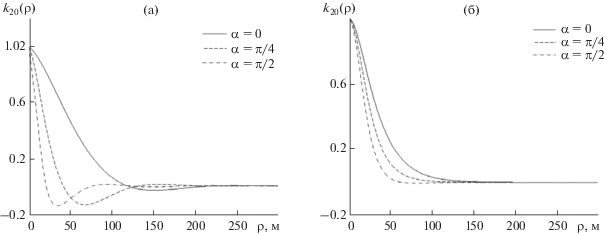
Проанализируем теперь результаты численных расчетов при R = 102 км коэффициента поперечной корреляции акустических мод ${{k}_{p}}\left( {\rho ,\alpha } \right)$. Чтобы не рассматривать многомерные распределения от ρ и α, угловая зависимость ${{k}_{p}}\left( {\rho ,\alpha } \right)$ приводится при трех фиксированных значениях угла: α = 0, π/4, π/2. Сразу отметим, что угловые зависимости коэффициента корреляции также симметричны относительно α = π/2, поэтому ${{k}_{p}}\left( {\rho ,\alpha = \pi } \right)$ = ${{k}_{p}}\left( {\rho ,\alpha = 0} \right)$, ${{k}_{p}}\left( {\rho ,\alpha = {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 4}} \right. \kern-0em} 4}} \right)$ = = ${{k}_{p}}\left( {\rho ,\alpha = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}} \right)$. На рис. 4 для дальнейшего сравнения приведены результаты расчетов коэффициентов корреляции для модели изотропного спектра для p = 1, 10, 20 при двух значениях скорости ветра. Для первой моды характерно высокое значение коэффициента корреляции для всех значений ρ. Для p = 10 и p = 20 четко выражен корреляционный максимум с шириной (радиусом корреляции) ρcor ≈ 50…70 м. Уровень остаточных корреляций (при больших значениях ρ) определяется когерентной компонентой поля и уменьшается как с ростом номера моды, так и с увеличением скорости ветра (для фиксированной дистанции). На рис. 5–7 приведены расчетные кривые для анизотропного волнения. Видно, что качественный вид коэффициента корреляции не изменился, но его количественные характеристики зависят от угла α. Во всех случаях спадание коэффициента корреляции (с увеличением ρ) минимально для α = 0, максимально для α = π/2. При α = π/4 расчетные данные для анизотропного волнения близки к результатам расчетов для изотропной модели. Так, например, для первой и десятой моды их отличие не превышает нескольких процентов. Аналогичное численное моделирование, проведенное для других значений угла α и номеров мод, показывает, что всегда в диапазоне углов $0 \leqslant \alpha \leqslant \frac{\pi }{4}$ (и соответственно $\frac{{3\pi }}{4} \leqslant \alpha \leqslant \pi $) расчеты, выполненные на основании модели изотропного волнения, приводят к завышенным значениям ${{k}_{p}}\left( {\rho ,\alpha } \right)$, а в диапазоне углов $\frac{\pi }{4} \leqslant \alpha \leqslant \frac{\pi }{2}$ (либо $\frac{\pi }{2} \leqslant \alpha \leqslant \frac{{3\pi }}{4}$) — наоборот, к заниженным значениям коэффициента поперечной корреляции для всех акустических мод. Численное расхождение может превышать 3 дБ, а сами угловые изменения коэффициента ${{k}_{p}}\left( {\rho ,\alpha } \right)$ могут иметь еще большие значения (особенно в области центрального максимума).
Рис. 4.
Коэффициент пространственной корреляции акустических мод для упрощенной модели изотропного спектра волнения при скорости ветра (а) – V = 10 м/с и (б) – V = 15 м/с.
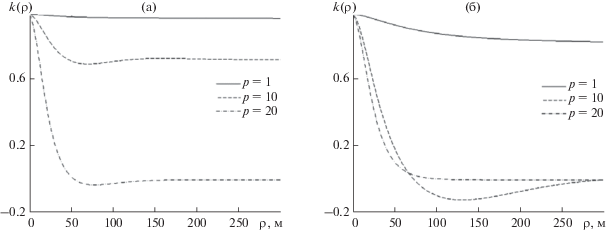
Рис. 5.
Угловая зависимость коэффициента пространственной корреляции первой моды при скорости ветра (а) – V = = 10 м/с и (б) – V = 15 м/с.
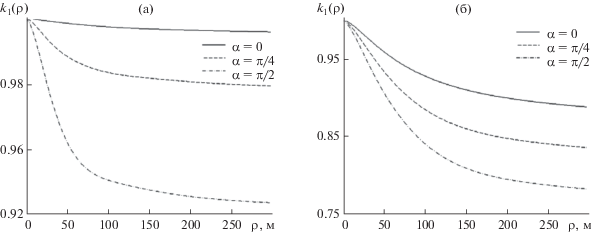
Рис. 6.
Угловая зависимость коэффициента пространственной корреляции десятой моды при скорости ветра (а) – V = = 10 м/с и (б) – V = 15 м/с.
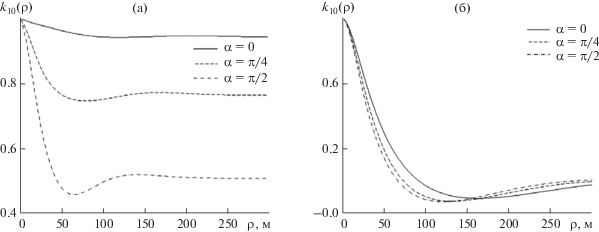
Рис. 7.
Угловая зависимость коэффициента пространственной корреляции двадцатой моды при скорости ветра (а) – V = 10 м/с и (б) – V = 15 м/с.
Таким образом, можно сделать вывод о существенном влиянии типичной для развитого ветрового волнения анизотропии на статистические характеристики нормальных мод акустического поля удаленного источника в открытых к поверхности подводных каналах. Приведенные результаты показывают, что лишь при расчете когерентной компоненты акустических мод анизотропия ветрового волнения не столь важна для прикладных задач. При расчете интенсивности мод и коэффициента пространственной корреляции учет анизотропии ветрового волнения и, соответственно, анизотропного характера эффектов многократного рассеяния звука может значимо уточнить результаты изотропной модели.
Авторы благодарят А.И. Малеханова (ИПФ РАН) за внимание к работе и полезные замечания.
Данная работа выполнена при поддержке гранта РНФ № 20-19-00383.
Список литературы
Бреховских Л.М., Лысанов Ю.П. Теоретические основы акустики океана. М.: Наука, 2007. 370 с.
Городецкая Е.Ю., Малеханов А.И., Сазонтов А.Г., Фарфель В.А. Влияние эффектов дальнего распространения звука в случайно-неоднородном океане на потери усиления горизонтальной антенной решетки // Акуст. журн. 1996. Т. 42. № 5. С. 615–622.
Gorodetskaya E.Yu., Malekhanov A.I., Sazontov A.G., Vdovicheva N.K. Coherence effects on array beamforming in shallow water // Proc. Fifth European Conf. on Underwater Acoustics: ECUA, 2000 (Lyon, France, 2000). P. 1031–1036.
Раевский М.А., Хилько А.И. О пространственно-временной когерентности низкочастотных акустических волн в мелком море с флуктуирующими параметрами // Акуст. журн. 2015. Т. 61. № 3. С. 369–376.
Завольский Н.А., Малеханов А.И., Раевский М.А. Сравнительный анализ методов пространственной обработки сигналов, принимаемых горизонтальной антенной решеткой в канале мелкого моря со взволнованной поверхностью // Акуст. журн. 2019. Т. 65. № 5. С. 608–618.
Завольский Н.А., Раевский М.А. Горизонтальная анизотропия динамических шумов в глубоком и мелком море // Акуст. журн. 2019. Т. 65. № 2. С. 197–202.
Артельный В.В., Раевский М.А. О статистических характеристиках нормальных волн в волноводе с объемными неоднородностями // Изв. ВУЗов. Радиофизика. 1984. Т. 27. № 9. С. 1142–1150.
Горская Н.С., Раевский М.А. О многократном рассеянии низкочастотных акустических волн на поверхностном волнении // Акуст. журн. 1986. Т. 32. № 2. С. 165–171.
Давидан И.Н., Лопатухин Л.И., Рожков В.А. Ветровое волнение в Мировом океане. Л.: Гидрометеоиздат, 1985. 256 с
Mitsuyasu H., Tasai F., Suhara T., Mizuno S., Ohkusu M., Honda T., Rikiishi K. Observations of the power spectrum of ocean waves using a clover-leaf buoy // J. Phys. Oceanogr. 1980. V. 10. P. 286–296.
Дополнительные материалы отсутствуют.
Инструменты
Акустический журнал


