1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 67, № 2, 2021

Акустический журнал, 2021, T. 67, № 2, стр. 119-125

Исследование волновых процессов в упругих топографических волноводах

А. О. Ватульян a, b, *, Л. И. Паринова a, **

a Южный федеральный университет
344006 Ростов-на-Дону, ул. Большая Садовая 105/42, Россия

b Южный математический институт-филиал ВНЦ РАН
362027 Владикавказ, ул. Маркуса 22, Россия

* E-mail: vatulyan@math.rsu.ru
** E-mail: parinovali@mail.ru

Поступила в редакцию 08.07.2020
После доработки 06.11.2020
Принята к публикации 22.12.2020

Полный текст (PDF)

Аннотация

Изучены особенности распространения акустических волн в ортотропных упругих топографических волноводах – протяженных цилиндрических структурах с симметричными поперечными сечениями различных форм (прямоугольным, трапециевидным). Предложен способ приближенного исследования задач в рамках моделей пластин переменной жесткости, опирающийся на вариационный принцип Гамильтона–Остроградского. В рамках гипотезы о структуре полей, аналогичной модели Тимошенко в теории пластин, построен функционал, зависящий от 3 функций одной переменной. Стационарное значение функционала находилось с помощью метода Ритца. Исследована его сходимость в зависимости от числа координатных функций. Сформирована алгебраическая система, равенство нулю определителя которой дает возможность построить дисперсионное уравнение задачи. Построены дисперсионные зависимости для сечений различной геометрии. Проведено сравнение дисперсионных кривых, построенных в рамках модели типа Тимошенко и в рамках изученной ранее модели Кирхгофа. Определены частоты запирания для упругих волноводов с треугольным, прямоугольным и трапециевидным поперечным сечением, проведен сравнительный анализ.

Ключевые слова: топографический волновод, упругая волна, пластина переменной жесткости, дисперсионное соотношение, модель типа Тимошенко

ВВЕДЕНИЕ

Изучение кинематики волновых процессов, возникающих в топографических волноводах, актуально для совершенствования методов неразрушающего контроля, широко применяющихся для выявления дефектов. Исследование упругих волн с различными типами локализации имеет практический интерес для разработки эффективных фильтров и линий задержки, мониторинга состояния режущего инструмента и выявления дефектов в сварочных и спаечных структурах.

К настоящему времени в научной литературе достаточно подробно описаны особенности формирования волновых процессов в изотропных и анизотропных волноводах, проанализированы дисперсионные зависимости и особенности их строения для слоистых и цилиндрических структур, в том числе и для неоднородных по поперечной координате. Гораздо меньше изучены волновые процессы в топографических волноводах, для которых построение дисперсионных зависимостей является непростой задачей; при построении ветвей дисперсионного множества обычно используются КЭ–пакеты. Отметим, что практически отсутствуют работы, посвященные изучению волновых процессов в клиновидных структурах из ортотропных материалов.

Изучение волновых процессов, возникающих в упругих клиновидных волноводах в изотропном случае, тесно связано с исследованиями особенностей распространения акустических волн вдоль ребра пространственного клина, которые проводились еще в 70-годах прошлого века. В работах [1, 2] при помощи метода конечных элементов исследованы колебания изотропного бесконечного клиновидного волновода с произвольным углом раскрыва. Установлено, что в рассматриваемом случае отсутствует дисперсия и волновое поле локализуется вдоль ребра пространственного клина.

В [3] в рамках теории возмущений исследованы некоторые факторы, влияющие на возникновение дисперсии в бесконечном клине: усечение вершины клина и замена острия другим материалом, покрытие одной или обеих поверхностей клина, модификация упругих постоянных материала в области около вершины клина.

Локализация упругих волновых полей, бегущих вдоль вершин анизотропных клиньев с различными видами симметрии, и взаимодействие локализованных волн с другими видами волн, изучены в работе [4], где проведено экспериментальное измерение фазовых скоростей и распределения волновых полей, а также выполнено теоретическое исследование клиновых мод, опирающееся на функции Лагерра.

В [5] с использованием вариационного подхода получены условия существования симметричных и антисимметричных мод для бесконечного клинообразного волновода. Существование клиновых волн в некотором диапазоне изменения угла раскрыва было строго доказано в работах [6, 7], а в [8] представлено доказательство существования волн в топографических волноводах с более сложной формой поперечного сечения. В [9] строгое доказательство существования локализованных акустических клиновых волн, предложенное Камоцким, Заворохиным и Назаровым, распространяется на случай клина с прямым углом.

Отметим также, что особое внимание при исследовании волновых процессов в топографических волноводах уделяется изучению пластинчатых и балочных моделей. Первопроходцем в изучении волн у кромки пластин считается Коненков. В работе [10], опубликованной в 1960 году, приведено пионерское исследование распространения изгибной краевой волны вдоль свободного края полубесконечной пластины.

Исследование акустического отклика жестко защемленной по контуру пластины в рамках моделей Тимошенко и Кирхгофа–Лява представлено в работе [11], где для сравнения значений функции прогиба для различных вариантов параметров применялся метод Галеркина.

В [12] с использованием бесконтактного метода оптического зондирования изучены линейные одномерные сверхзвуковые и основные моды клиновой волны, направляемой краем кристалла кремния, определены скорость клиновых волн и глубина их проникновения, проведено сравнение теоретических и экспериментальных данных.

В работе [13] показано, что, анализируя особенности колебаний неоднородных цилиндрических волноводов и зная информацию о поле смещений на поверхности, можно определить неоднородные упругие свойства этой структуры.

Периодический гофрированный волновод из пористого материала исследуется в работе [14], где показано, что дополнительная извилистость усиливает звукопоглощение для низких частот.

Закономерности, возникающие при нахождении дисперсионных соотношений для неоднородного пьезоэлектрического волновода с затуханием, обсуждены в [15], где для исследования применяется асимптотический метод.

В предыдущих работах авторов настоящей работы [16–19] в рамках теории пластин переменной жесткости Кирхгофа были проанализированы волновые процессы в топографических волноводах из изотропных и ортотропных материалов. Для изотропного случая проведено сравнение скоростей клиновых волн, полученных в рамках вариационного подхода, с аналогичными результатами, но найденными по геометроакустической теории, представленной в [20]. Для антисимметричных мод в клиновидных структурах с ортотропных типом анизотропии построены дисперсионные соотношения.

Исследования волновых процессов в топографических волноводах можно проводить на основе моделей пластин переменной жесткости Кирхгофа или типа Тимошенко, для которых можно сформулировать краевые задачи для операторов с переменными коэффициентами. В работе [21] с использованием обобщенных гипотез теории пластин переменной жесткости типа Тимошенко авторы настоящей работы изучили особенности волновых процессов в клиновидных волноводах конечной высоты с закрепленным основанием.

Цель настоящей работы – в рамках теории пластин переменной жесткости типа Тимошенко разработать подход для изучения дисперсионных зависимостей для топографических волноводов, представляющих собой упругие структуры с трапециевидным поперечным сечением конечных размеров, а также совершить предельный переход к треугольному и прямоугольному случаю. В настоящем исследовании на основе вариационной трактовки исходной задачи при анализе дисперсионного множества использован метод Ритца.

ПОСТАНОВКА ЗАДАЧИ

Под топографическим волноводом будем понимать бесконечную упругую структуру, ограниченную цилиндрической поверхностью, в поперечном сечении которой находится многоугольник (в настоящем исследовании в общем случае это трапеция); одна из граней волновода закреплена. Особенности распространения упругих волн в волноводах с конечным поперечным сечением изучены недостаточно. Для бесконечного клина известно о локализации энергии в поперечном сечении около ребра и отсутствии дисперсии; интерес представляет исследование волновых процессов и дисперсионных соотношений для волноводов с прямоугольным и трапециевидным поперечным сечением.

Задача для ограниченного по высоте клиновидного волновода, поперечное сечение которого – конечный треугольник, подробно изучена в работе [21]. В настоящем исследовании рассмотрим упругие волны, распространяющиеся вдоль оси упругого топографического волновода из ортотропного материала с сечением S, которое в общем случае представляет собой равнобедренную трапецию с высотой h, углом при основании π/2 – α и меньшим основанием длины 2l (рис. 1). Введем связанную с осями упругой симметрии декартову систему координат Ox1x2x3. Будем считать, что ось Ox3 направлена перпендикулярно плоскости поперечного сечения волновода и проходит через середину меньшего основания трапеции. Нижняя граница волноводной структуры защемлена. Нагрузки на верхней и боковых гранях отсутствуют.

Рис. 1.

Поперечное сечение волновода.

Как и в работе [21], решение задачи для цилиндрического волновода с сечением в виде трапеции будем искать в виде волн, распространяющихся вдоль оси Ox3 изучаемой упругой структуры:

$\begin{gathered} {{u}_{1}}({{x}_{1}},{{x}_{2}},{{x}_{3}},t){\text{ }} = {{U}_{1}}({{x}_{1}},{{x}_{2}})\cos (\gamma {{x}_{3}} - \omega t), \\ {{u}_{2}}({{x}_{1}},{{x}_{2}},{{x}_{3}},t){\text{ }} = {{U}_{2}}({{x}_{1}},{{x}_{2}})\cos (\gamma {{x}_{3}} - \omega t), \\ {{u}_{3}}({{x}_{1}},{{x}_{2}},{{x}_{3}},t){\text{ }} = {{U}_{3}}({{x}_{1}},{{x}_{2}})\sin (\gamma {{x}_{3}} - \omega t), \\ \end{gathered} $
где γ – волновое число, Um(x1,x2), m = 1, 2, 3 – проекции вектора смещений в плоскости Ox1x2, ω – частота вибраций волновода.

Для перехода к безразмерной задаче введем следующие параметры: γi = Cii/C55, где i = 1–4, 6, γ5 = C12/C55, γ7 = C23/C55, γ8 = C13/C55, β = ρω2h2/C55, µ = γ2h2, где ρ – плотность материала, Cij – упругие постоянные ортотропного материала. Задачу о распространении волны для усеченного клиновидного волновода сводим к определению стационарного значения квадратичного функционала M:

(1)
$M[{{U}_{i}}] = \int\limits_S {{{M}_{0}}dS} ,$
который после отделения временного сомножителя формируется на основе принципа Гамильтона–Остроградского [18].

Подынтегральная функция в (1) есть квадратичная функция амплитуд и их производных и имеет следующий вид:

$\begin{gathered} M{\kern 1pt} {}_{0}\,\, = ({{\gamma }_{1}}{{U}_{{1,1}}} + {{\gamma }_{5}}{{U}_{{2,2}}} + {{\gamma }_{8}}{{U}_{{3,3}}}){{U}_{{1,1}}} + \\ + \,\,({{\gamma }_{5}}{{U}_{{1,1}}} + {{\gamma }_{2}}{{U}_{{2,2}}} + {{\gamma }_{7}}{{U}_{{3,3}}}){{U}_{{2,2}}} + \\ + \,\,({{\gamma }_{8}}{{U}_{{1,1}}} + {{\gamma }_{7}}{{U}_{{2,2}}} + {{\gamma }_{3}}{{U}_{{3,3}}}){{U}_{{3,3}}} + {{\gamma }_{6}}{{({{U}_{{1,2}}} + {{U}_{{2,1}}})}^{2}} + \\ + \,\,{{({{U}_{{1,3}}} + {{U}_{{3,1}}})}^{2}} + {{\gamma }_{4}}{{({{U}_{{2,3}}} + {{U}_{{3,2}}})}^{2}} - \\ - \,\,\beta \,(U_{1}^{2} + U_{2}^{2} + U_{3}^{2}). \\ \end{gathered} $

Здесь нижний индекс после запятой обозначает производную по соответствующей координате.

Из условия стационарности функционала δM[Ui] = 0 можно получить однородную краевую задачу с двумя спектральными параметрами µ и β; те соотношения между спектральными параметрами µ и β, при которых эта задача имеет нетривиальное решение, порождает дисперсионное множество задачи. Построим первые ветви этого множества, используя вариационную трактовку и упростив функционал.

МОДЕЛЬ ПЛАСТИНЫ ТИПА ТИМОШЕНКО

Для нахождения приближенного решения задачи в случае малого угла раскрыва используем гипотезы, подобные гипотезам теории пластин.

Отметим, что колебания волновода по типу движений подразделяются на два типа: симметричные и антисимметричные. Учитывая, что свободные симметричные колебания топографического волновода с симметричным поперечным сечением обычно отсутствуют [5], подробно исследуем антисимметричный случай.

Считая, что углы при основании трапециевидного поперечного сечения мало отличаются от π/2, предположим, что компоненты амплитуд смещений соответствуют гипотезам, аналогичным гипотезам теории пластин для модели Тимошенко [11]:

${{U}_{1}} = {{x}_{2}}{{W}_{1}}\left( {{{x}_{1}}} \right),\,\,\,{{U}_{2}} = h{{W}_{2}}\left( {{{x}_{1}}} \right),\,\,\,{{U}_{3}} = \gamma {{x}_{2}}h{{W}_{3}}\left( {{{x}_{1}}} \right).$

Совершая переход к безразмерным величинам, сделаем замену переменных: z = x1/h и учтем обобщенные гипотезы. В выражении для функционала (1) осуществим интегрирование по x2. Таким образом, найдем упрощенное значение функционала (1) и задачу об анализе волновых полей для топографических волноводов сведем к задаче об исследовании стационарного значения функционала M:

(2)
$M[{{W}_{j}}] = \int\limits_0^1 {M_{0}^{*}} dz,$
где

$\begin{gathered} M_{0}^{*} = 2h\left( {\frac{1}{3}{{{\left( {zt + s} \right)}}^{3}}\left( {\left( {{{\gamma }_{1}}W_{1}^{{'2}} + 2\mu {{\gamma }_{8}}W_{1}^{'}{{W}_{3}} + {{\mu }^{2}}{{\gamma }_{3}}{{W}_{3}}^{2} + \mu {{{( - {{W}_{1}} + W_{3}^{'})}}^{2}}} \right) - \beta (W_{1}^{2} + \mu W_{3}^{2})} \right) + } \right. \\ \left. {\,\, + \left( {zt + s} \right)\left( {{{\gamma }_{6}}{{{({{W}_{1}} + W_{2}^{1})}}^{2}} + {{\gamma }_{4}}\mu {{{\left( { - {{W}_{2}} + {{W}_{3}}} \right)}}^{2}} - \beta {{W}_{2}}^{2}} \right)} \right) \\ \end{gathered} $

и введены обозначения t = tg α, s = l/h. Отметим, что исходя из представления (2), можно с единых позиций исследовать дисперсионные множества для различных поперечных сечений, варьируя параметры. Так, например, задавая s = 0, можно получить функционал для волновода с треугольным поперечным сечением, исследование которого осуществлено в работе [21].

Определим стационарное значение функционала $M[{{W}_{j}}]$, основываясь на методе Ритца. Учитывая известные требования к координатным функциям, выберем решение из класса функций W(z), ограниченных при z = 0 и удовлетворяющих граничным условиям жесткого защемления при z = 1. Решение о нахождении стационарного значения функционала (2) будем искать в следующем виде:

${{W}_{1}} = {{(1 - z)}^{2}}\sum\limits_{n = 1}^N {{{a}_{n}}{{\varphi }_{n}}\left( z \right)} ,$
${{W}_{2}} = {{(1 - z)}^{2}}\sum\limits_{n = 1}^N {{{b}_{n}}{{\varphi }_{n}}\left( z \right)} ,$
${{W}_{3}} = {{(1 - z)}^{2}}\sum\limits_{n = 1}^N {{{c}_{n}}{{\varphi }_{n}}\left( z \right)} .$

В качестве координатных функций выберем систему функций φn(z) = zn – 1, n = 1, 2, 3, … Тогда функционал (2) можно представить в виде квадратичной формы 3N переменных относительно коэффициентов разложений.

Условие стационарности функционала (2) позволяет сформулировать однородную систему линейных однородных уравнений; приравнивая к нулю ее определитель, получим приближенный вид дисперсионного уравнения. Определяя его нули в окрестности начала координат, найдем ветви дисперсионного множества.

В качестве примера рассмотрим частный случай при N = 2. Проинтегрировав (2) по z, получаем функционал, представляющий собой квадратичную форму 6 переменных.

$\begin{gathered} M\left( {{{a}_{1}},{{b}_{1}},{{c}_{1}},{{a}_{2}},{{b}_{2}},{{c}_{2}}} \right) = {{k}_{{11}}}a_{1}^{2} + {{k}_{{12}}}{{a}_{1}}{{b}_{1}} + {{k}_{{13}}}{{a}_{1}}{{c}_{1}} + \\ + \,\,{{k}_{{14}}}{{a}_{1}}{{a}_{2}} + {{k}_{{15}}}{{a}_{1}}{{b}_{2}} + {{k}_{{16}}}{{a}_{1}}{{c}_{2}} + {{k}_{{22}}}b_{1}^{2} + {{k}_{{23}}}{{b}_{1}}{{c}_{1}} + \\ + \,\,{{k}_{{24}}}{{b}_{1}}{{a}_{2}} + {{k}_{{25}}}{{b}_{1}}{{b}_{2}} + {{k}_{{26}}}{{b}_{1}}{{c}_{2}} + {{k}_{{33}}}c_{1}^{2} + {{k}_{{34}}}{{c}_{1}}{{a}_{2}} + \\ + \,\,{{k}_{{35}}}{{c}_{1}}{{b}_{2}} + {{k}_{{36}}}{{c}_{1}}{{c}_{2}} + {{k}_{{44}}}a_{2}^{2} + {{k}_{{45}}}{{a}_{2}}{{b}_{2}} + \\ + \,\,{{k}_{{46}}}{{a}_{2}}{{c}_{2}} + {{k}_{{55}}}b_{2}^{2} + {{k}_{{56}}}{{b}_{2}}{{c}_{2}} + {{k}_{{66}}}a_{6}^{2}, \\ \end{gathered} $
где все kij = kij(β,µ), i, j = 1–6 полиномиальным образом зависят от спектральных параметров. В силу громоздкости они не приводятся; приведем, например:

$\begin{gathered} {{k}_{{11}}} = \left( { - \frac{1}{{15}}{{s}^{3}} - \frac{1}{{30}}{{s}^{2}}t - \frac{1}{{840}}{{t}^{3}} - \frac{1}{{105}}s{{t}^{2}}} \right)\beta + \\ + \,\,\frac{1}{{30}}{{\gamma }_{6}}t + \frac{1}{5}{{\gamma }_{6}}s + \left( {\frac{2}{{15}}{{\gamma }_{1}} + \frac{1}{{105}}\mu } \right)s{{t}^{2}} + \\ + \,\,\left( {\frac{1}{3}{{\gamma }_{1}} + \frac{1}{{30}}\mu } \right){{s}^{2}}t + \left( {\frac{1}{{45}}{{\gamma }_{1}} + \frac{1}{{840}}\mu } \right){{t}^{3}} + \left( {\frac{4}{9}{{\gamma }_{1}} + \frac{1}{{15}}\mu } \right){{s}^{3}}. \\ \end{gathered} $

Стоит отметить, что, совершая предельный переход при s → 0, при нахождении стационарного значения функционала (2) можно получить уравнение для определения дисперсионного множества такое же, как и при исследовании волновых процессов для клиновидного волновода, представленного в [21].

Можно также заметить, что при наличии связей W1 = –W', W2 = W3 = W модель пластины переменной жесткости типа Тимошенко сводится к частному случаю – к модели типа Кирхгофа. Функционал (2) преобразуется в функционал, который зависит от одной переменной W и имеет вид:

Полученное дисперсионное множество для пластины Кирхгофа исследовано в работе [18].

ВЫЧИСЛИТЕЛЬНЫЕ ЭКСПЕРИМЕНТЫ

В ходе исследований рассматриваются топографические волноводы со следующими геометрическими параметрами α = 5° и s = 0.01. На основе приближенного подхода с использованием метода Ритца получены дисперсионные зависимости для различного числа координатных функций. Серия вычислительных экспериментов проводится для ортотропного материала – аустенитной стали, которая характеризуется следующими безразмерными параметрами [22]: γ1 = 2.036, γ2 = 2.036, γ3 = 1.674, γ4 = 1.000, γ5 = 0.761, γ6 = 0.598, γ7 = 1.124, γ8 = 1.124.

В табл. 1 для различного числа координатных функций показаны найденные значения µ(β). Отметим, что значения безразмерного параметра µ монотонно увеличиваются с увеличением числа координатных функций, что подтверждает характер сходимости при реализации метода Ритца [23]. Стабилизация значений параметра µ для первой моды и для второй моды достигнута при N = 10. При этом относительная разница между значениями µ, которые соответствуют N = 9 и N = 10, не превосходит 1%.

Таблица 1.  

Значения µ для первой и второй моды

№ моды β Число координатных функций
N = 6 N = 7 N = 8 N = 9 N = 10
1 мода 1 34.442 34.451 34.475 34.483 34.499
2 60.671 60.681 60.708 60.723 60.745
3 82.798 82.821 82.859 82.889 82.922
4 102.614 102.653 102.703 102.750 102.798
5 120.841 120.943 120.959 121.024 121.088
2 мода 2 8.894 9.073 9.167 9.240 9.293
3 19.857 20.068 20.137 20.207 20.251
4 29.737 29.563 29.611 29.677 29.714
5 37.825 38.088 38.120 38.184 38.216

Графики дисперсионных зависимостей µ от параметра β для первых двух мод приведены на рис. 2 для различного числа координатных функций. Черной сплошной линией показаны зависимости для N = 3, серой сплошной – для N = 5 и черной штрихпунктирной – для N = 10.

Рис. 2.

Графики дисперсионных зависимостей µ(β).

Сравнение дисперсионных соотношений для модели Кирхгофа и модели типа Тимошенко для волноводов из аустенитной стали с различными поперечными сечениями представлено на рис. 3. Метками 1–5 отмечены соответствующие моды. Дисперсионные ветви для модели типа Тимошенко показаны черной сплошной линией, а для модели Кирхгофа – точками. Результаты вычислительных экспериментов показали, что дисперсионные множества, найденные в рамках различных гипотез, отличаются незначительно в низкочастотной области.

Рис. 3.

Графики зависимости µ(β) для модели Кирхгофа и модели типа Тимошенко для случая N = 10 для топографического волновода с сечением в виде (а) – трапеции, (б) – прямоугольника и (в) – треугольника.

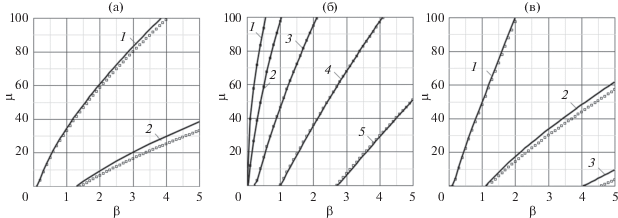
Из общей теории волноводов известно, что для слоистого волновода имеется частота запирания, т.е. такое критическое значение β, при котором в волноводе отсутствует распространение мод µ = 0 и имеется стоячая волна. Для изучаемого топографического волновода также были проанализированы аналогичные ситуации. Для волноводов с поперечным сечением в виде равнобедренного треугольника, прямоугольника и равнобочной трапеции были найдены критические значения, которые представлены в табл. 2.

Таблица 2.  

Значения частот запирания β для изучаемых сечений

Трапециевидное сечение 0.133 1.286 5.536 15.497 33.706
Треугольное сечение 0.143 1.112 4.061 10.370 21.446
Прямоугольное сечение 0.001 0.034 0.266 1.015 2.749

В табл. 3 представлена зависимость для частот запирания β(s) при фиксированном значении α = 5°. Из анализа полученных значений следует, что с увеличением значения параметра s, представляющего собой отношение половины длины меньшего основания трапеции к ее высоте, монотонно возрастают и значения спектрального параметра β, при котором в волноводе отсутствует распространение мод и имеется стоячая волна.

Таблица 3.  

Значения частот запирания β для волновода с трапециевидным поперечным сечением при фиксированном значении α = 5°

s Значения частот запирания β
0.01 0.133 1.286 5.536 15.497 33.706
0.02 0.141 1.623 7.388 20.663 44.124
0.03 0.155 1.981 9.145 25.168 52.583
0.04 0.171 2.339 10.776 29.087 59.605
0.05 0.189 2.690 12.273 32.494 65.471

Представленная в табл. 4 зависимость значений частот запирания β от параметра α при фиксированном значении s = 0.01 демонстрирует, что с увеличением угла раскрыва значения спектрального параметра β, при котором в волноводе отсутствует распространение мод и имеется стоячая волна, возрастают.

Таблица 4.

  Значения частот запирания β для волновода с трапециевидным поперечным сечением при фиксированном значении s = 0.01

α Значения частот запирания β
π/180 0.008 0.152 0.925 3.212 8.193
π/90 0.025 0.342 1.841 5.989 14.572
π/60 0.051 0.600 2.953 9.081 21.216
π/45 0.087 0.917 4.202 12.294 27.656
π/36 0.133 1.286 5.536 15.497 33.706

ЗАКЛЮЧЕНИЕ

На основе вариационного принципа Гамильтона–Остроградского, приближенного подхода Ритца и модели пластины переменной жесткости типа Тимошенко разработан полуаналитический метод для нахождения дисперсионных зависимостей и проведены вычислительные эксперименты. Для топографических волноводов из ортотропного материала с треугольным, прямоугольным и трапециевидным поперечным сечением получены дисперсионные зависимости и найдены точки, соответствующие частотам запирания. Проведен анализ частот запирания в зависимости от угла раскрыва и от параметра, представляющего собой отношение половины длины меньшего основания трапеции к ее высоте. Проведено сравнение полученных результатов в рамках модели пластины типа Тимошенко с результатами для изученной ранее модели Кирхгофа. Показано, что при малых частотах касательные напряжения практически не влияют на дисперсионное множество для первой и второй моды. Для третьей моды появляется более существенное различие и учет касательных напряжений весьма существенен для расчета волновых полей.

Исследование выполнено при частичной финансовой поддержке РФФИ в рамках научного проекта № 19-31-90079-А.

Список литературы

  1. Ash E.A., Rue R.M.D.L., Humphryes R.F. Microsound surface waveguide // IEEE Trans. Microw. Theory. Tech. 1969. V. 17. № 11. P. 882–892.

  2. Lagasse P.E., Mason I.M., Ash E.A. Acoustic surface waveguides – analysis and assessment // IEEE Trans. Microw. Theory Tech. 1973. V. MTT-21. P. 225–226.

  3. Sokolova E.S., Timler R., Mayer A.P., Kovalev A.S. On the dispersion of wedge acoustic waves // Wave Motion. 2013. T. 50. № 2. P. 233–245.

  4. Pupyrev P.D., Lomonosov A.M., Mayer A.P., Hess P. Symmetry effects on elastic wedge waves at anisotropic edges // J. Appl. Phys. 2014. V. 115. № 24. P. 243504.

  5. Tiersten H.F., Rubin D. On the fundamental antisymmetric mode of the wedge guide // Proc. IEEE Ultrasonic Symposium. 1974. P. 117–120.

  6. Заворохин Г.Л., Назаров А.И. Об упругих волнах в клине // Записки научных семинаров ЛОМИ. 2010. Т. 380. С. 45–52.

  7. Камоцкий И.В. О поверхностной волне, бегущей вдоль ребра упругого клина // Алгебра и анализ. 2008. Т. 20. № 1. С. 86–92.

  8. Бабич В.М. Об одном классе топографических волноводов // Алгебра и анализ. 2010. Т. 22. № 1. С. 98–107.

  9. Pupyrev P.D., Lomonosov A.M., Nikodijevic A., Mayer A.P. On the existence of guided acoustic waves at rectangular anisotropic edges // Ultrasonics. 2016. V. 71. P. 278–287.

  10. Коненков Ю.К. Об изгибной волне “рэлеевского” типа // Акуст. журн. 1960. Т. 6. № 1. С. 124–126.

  11. Богачев И.В., Ватульян А.О., Дударев В.В., Недин Р.Д. Идентификация свойств неоднородной пластины в рамках модели Тимошенко // Известия Саратовского университета. Новая серия. Серия: Математика. Механика. Информатика. 2017. Т. 17. № 4. С. 419–430.

  12. Lomonosov A.M., Hess P., Mayer A.P. Silicon edges as one-dimensional waveguides for dispersion-free and supersonic leaky wedge waves // Appl. Phys. Lett. 2012. V. 101. № 3. P. 031904.

  13. Ватульян А.О., Юров В.О. Об оценке законов радиальной неоднородности в цилиндрическом волноводе // Акуст. журн. 2020. Т. 66. № 2. С. 119–127.

  14. Changyong Jiang, Lixi Huang. Characterization of low-frequency acoustic wave propagation through a periodic corrugated waveguide // J. Sound Vib. 2018. V. 418. P. 79–99.

  15. Ватульян А.О., Юров В.О. Исследование дисперсионных свойств неоднородного пьезоэлектрического волновода при наличии затухания // Акуст. журн. 2017. Т. 63. № 4. С. 339–348.

  16. Ватульян А.О., Паринова Л.И. Исследование клиновых волн в ортотропной среде // Вестник ДГТУ. 2005. Т. 5. № 4(26). С. 491–499.

  17. Vatulyan A.O., Parinova L.I. On the elastic waves propagating along the edge of the wedge with small opening angle // Advanced Materials–Techniques, Physics, Mechanics and Applications. Springer Proceeding in Physics. Eds. Ivan A. Parinov, Shun-Hsyung Chang, Muaffaq A. Jani. Springer, Cham, 2017. V. 193. P. 309–319.

  18. Ватульян А.О., Паринова Л.И. Об исследовании дисперсионных свойств топографических волноводов // Изв. вузов. Сев-Кавк. регион. Естеств. науки. 2018. № 3. С. 10–17.

  19. Parinova L.I. On the wave propagating along the plate-like waveguide // Advanced Materials – Proc. of the Int. Conf. on “Physics and Mechanics of New Materials and Their Applications”, PHENMA 2018, Springer Proceeding in Physics, V. 224. Eds. Ivan A. Parinov, Shun-Hsyung Chang, Yun-Hae Kim. 2019. P. 487–494.

  20. Бирюков С.В., Гуляев Ю.В., Крылов В.В., Плесский В.П. Поверхностные акустические волны в неоднородных средах. М.: Наука, 1991. 414 с.

  21. Vatulyan A., Parinova L. On the use of models of the Tymoshenko type in the analysis of wave processes in wedge-shaped waveguides // Advanced Materials – Proc. of the Int. Conf. on “Physics and Mechanics of New Materials and Their Applications”, PHENMA 2019, Springer Proceedings in Materials. Eds. Ivan A. Parinov, Shun-Hsyung Chang, Banh Tien Long. Springer Nature, Cham, Switzerland, 2020. V. 6. P. 383–389.

  22. Блистанов В.С., Бондаренко В.С., Перемолова Н.В. Стрижевская Ф.Н., Чкалова В.В., Шаскольская М.П. Акустические кристаллы: Справочник / Под ред. Шаскольской М.П. М.: Наука, 1982. 632 с.

  23. Михлин С.Г. Вариационные методы в математической физике. М.: Гостехиздат, 1957. 476 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал